Hierarchical Line Loss Allocation Methods for Low-Voltage Distribution Networks with Distributed Photovoltaics
Abstract
1. Introduction
2. Theoretical Foundation of Line Loss Allocation for Low-Voltage Distribution Networks with Distributed Photovoltaics
2.1. Mathematical Model of Line Loss in Low-Voltage Distribution Networks
- (1)
- All physical power losses in the distribution network occur in the branches with impedance, such as transmission lines, cables, and transformers, not at the bus nodes themselves. Nodes are merely electrical connection points that satisfy Kirchhoff’s Current Law (KCL).
- (2)
- In loss allocation studies, “node losses” refer to the marginal contribution or allocated share of each node to the total system losses. This concept is used to quantify each node’s responsibility and impact on loss formation. It is not a physical measurement. This distinction is key to understanding loss allocation mechanisms. In this paper, “node loss allocation” refers to the loss shares allocated to nodes using specific methods, not the physical losses at the nodes.
2.2. Impact Mechanism of PV Integration
2.3. Electrical Distance and Node Correlation
2.4. Problem Description of Line Loss Allocation
- (1)
- Cost recovery constraint:
- (2)
- Non-negativity constraint:
- (3)
- Physical rationality constraint: Line loss allocation results should reflect the actual contribution of each node to line losses.
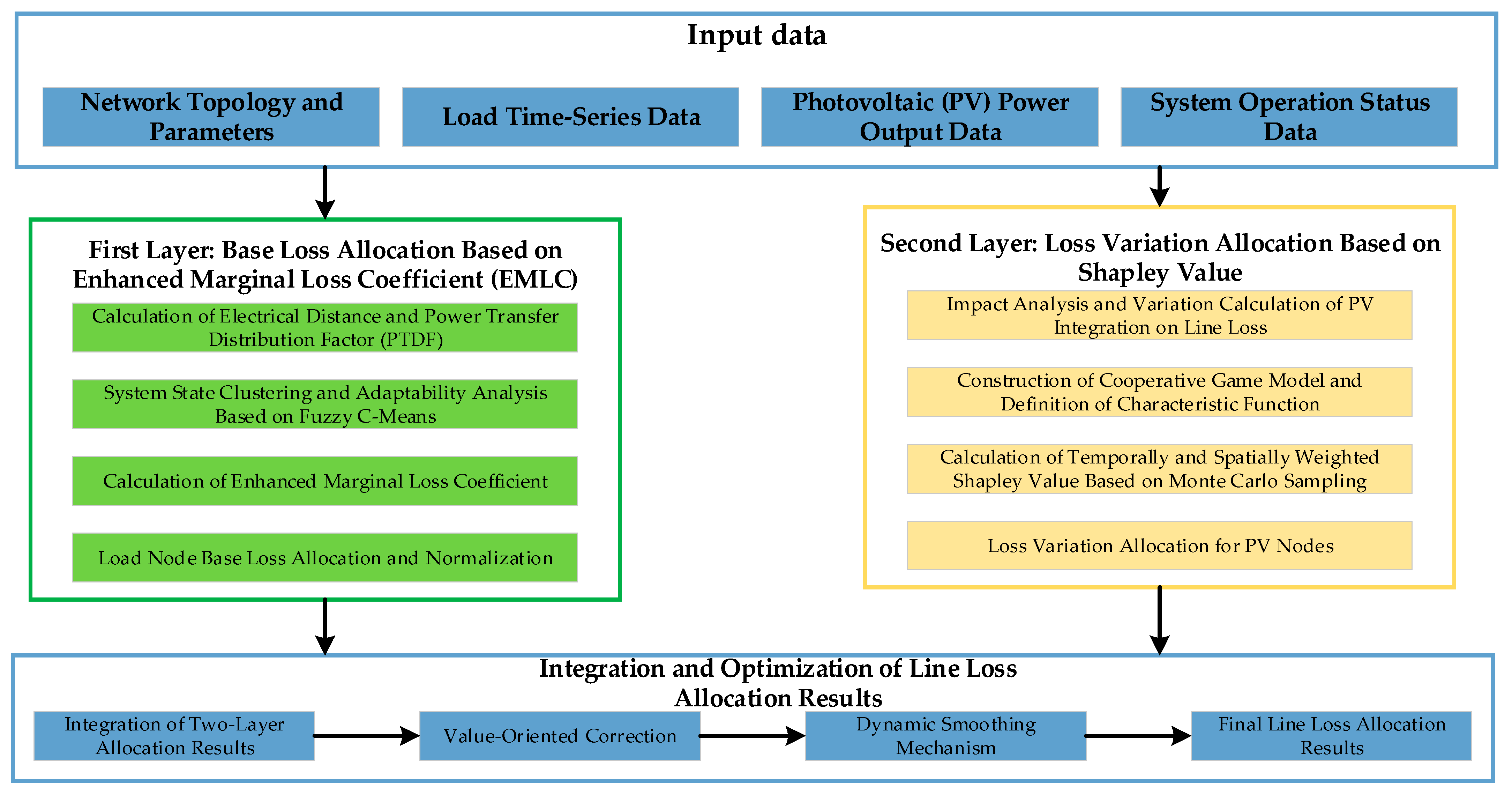
3. Hierarchical Line Loss Allocation Method
3.1. Basic Line Loss Allocation Based on EMLC
3.2. Game Theory Incremental Allocation
3.3. Comprehensive Model of Hierarchical Line Loss Allocation
- (1)
- Baseline Establishment
- (2)
- Baseline-Referenced Incremental Allocation
- (3)
- Final Allocation
3.4. Multi-Dimensional Value-Oriented Line Loss Allocation Correction Mechanism
3.4.1. Architecture of Multi-Dimensional Value Correction System
- (1)
- Maintaining unchanged total line loss allocation of the distribution network to ensure cost recovery.
- (2)
- Forming clear economic incentive signals to guide system optimization, but only fine-tuning the basic allocation rather than making fundamental changes.
3.4.2. Multi-Dimensional Value Assessment
- Local Consumption Service Value Assessment
- 2.
- Spatiotemporal Matching Optimization Value Assessment
- 3.
- Voltage Support Capability Value Assessment
3.4.3. Line Loss Allocation Mechanism with Multi-Dimensional Value Synergistic Correction
4. Simulation Verification and Analysis
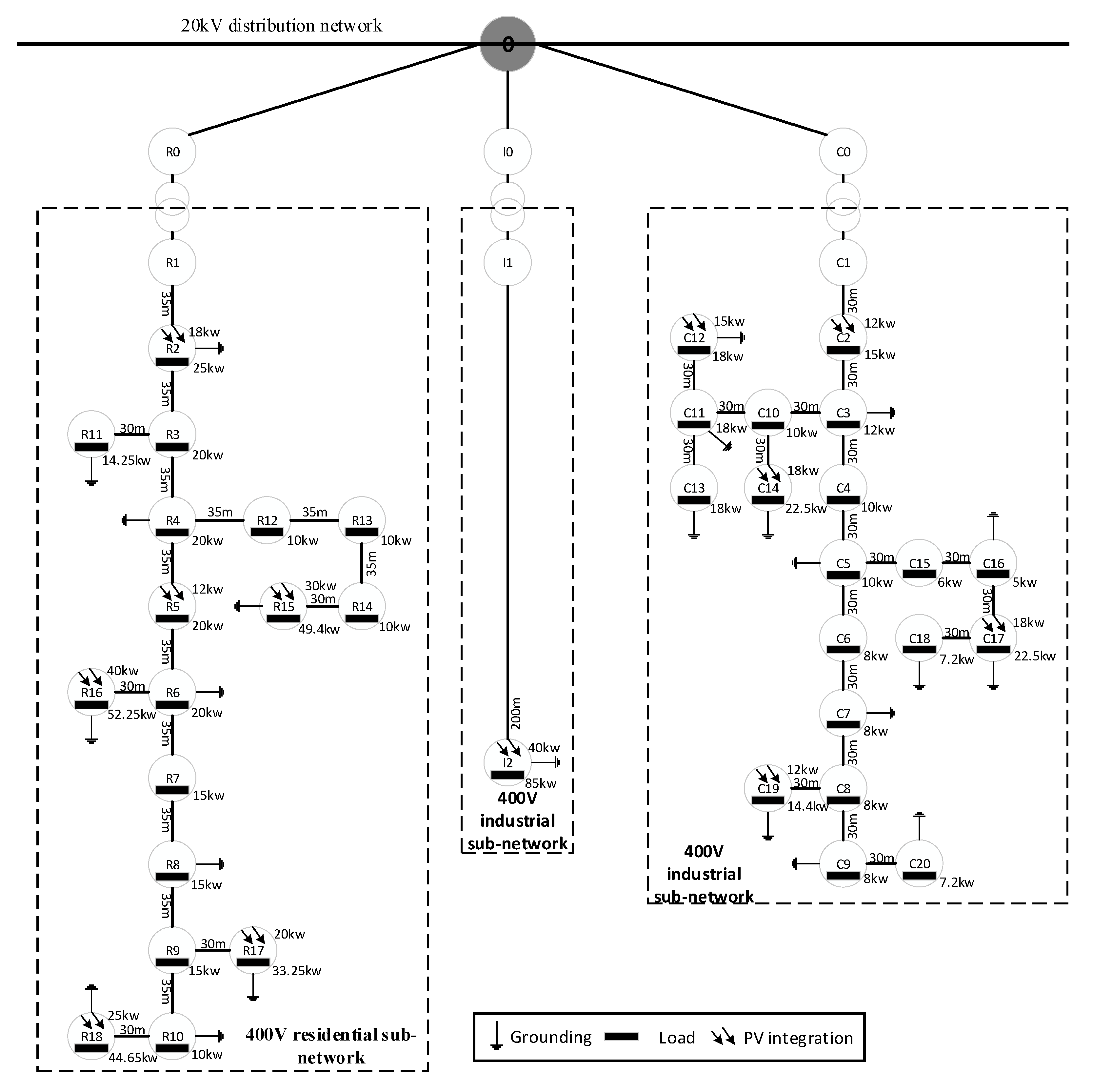
4.1. Test System Construction
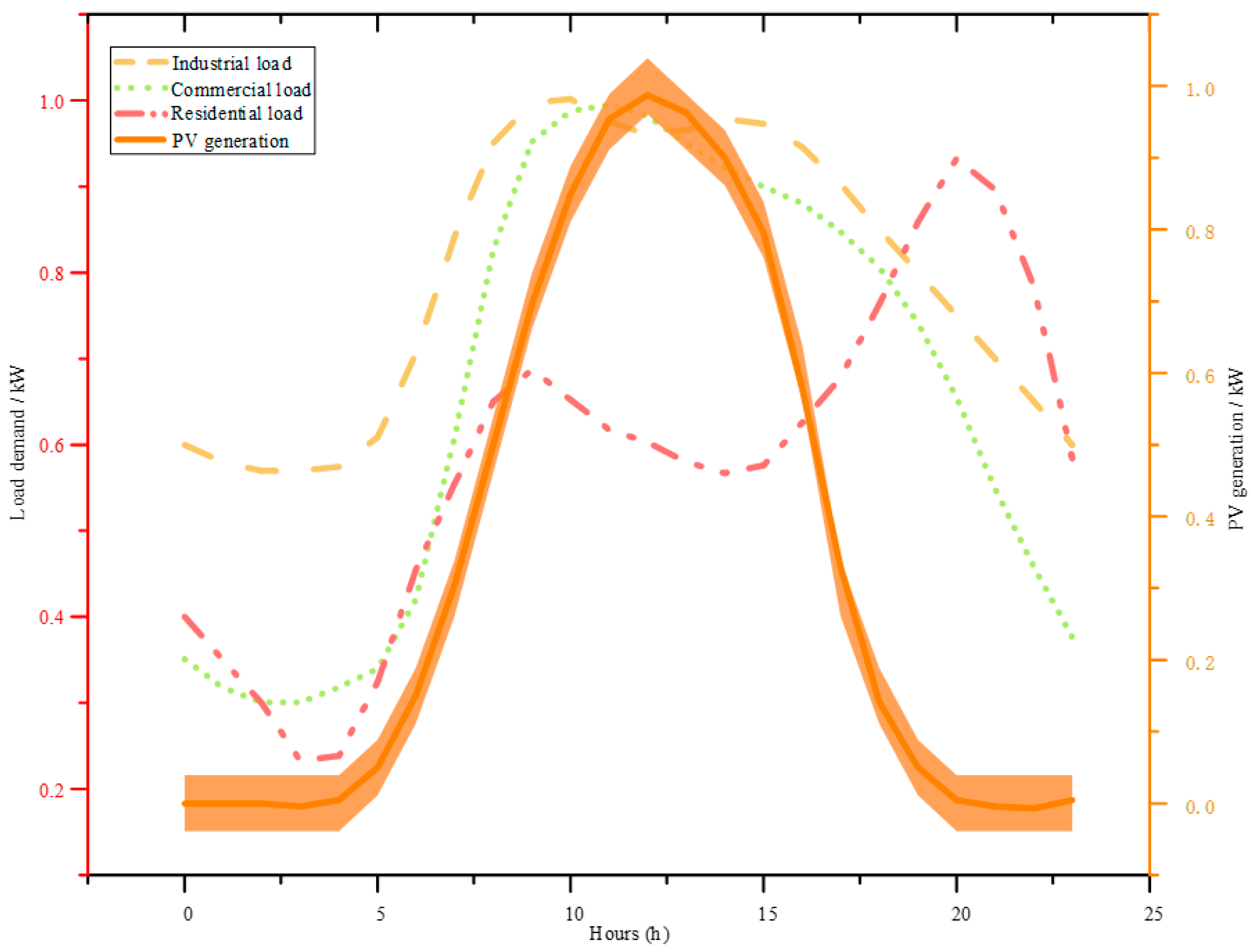
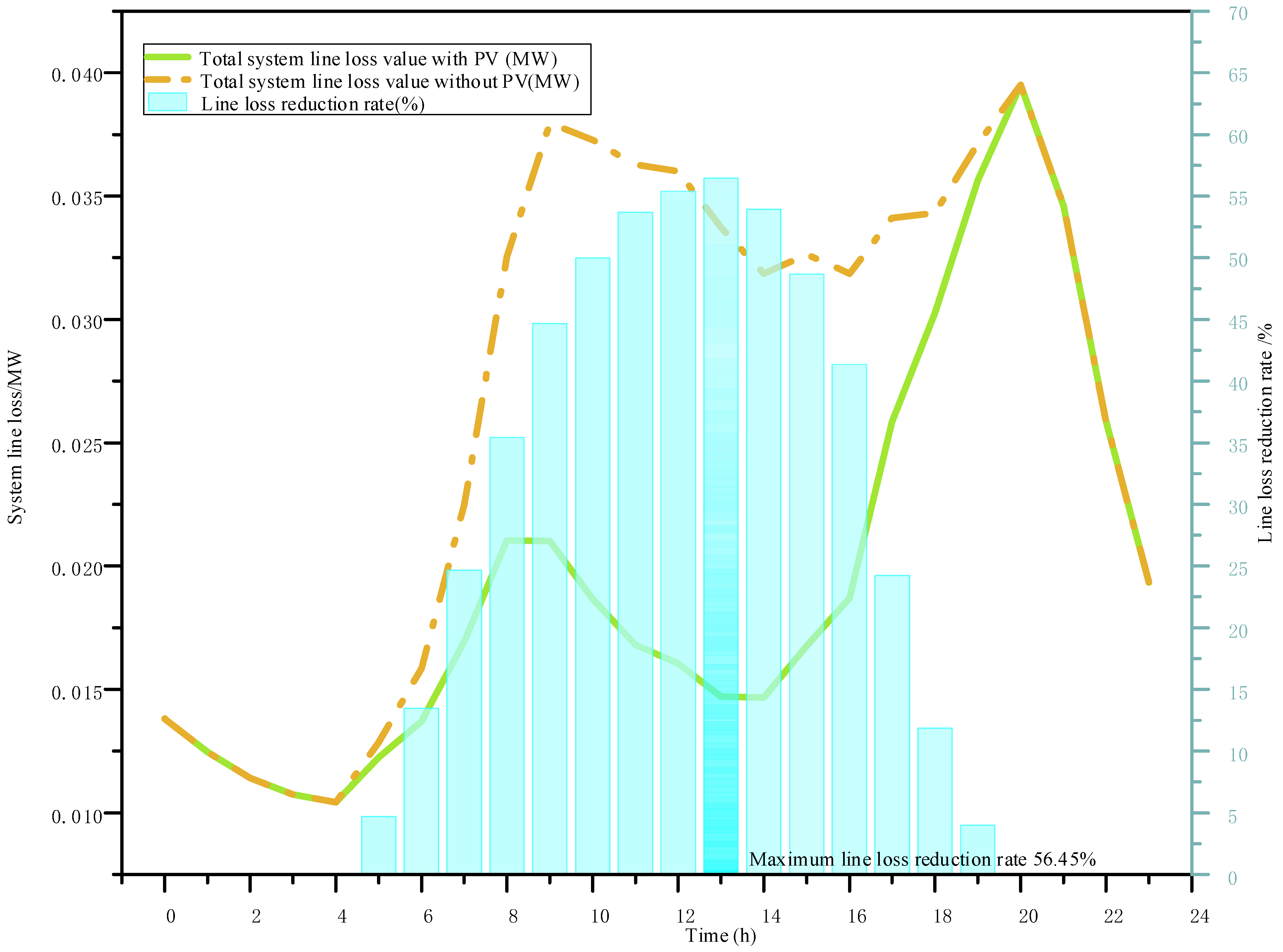
4.2. Impact Assessment of PV Integration on Line Losses
4.3. Node Shapley Value Analysis
4.4. Line Loss Allocation with Multi-Dimensional Value Synergistic Correction
4.5. Horizontal Comparative Analysis with Existing Methods
4.6. Robustness Comparative Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Node | First Layer Allocation/MW | Second Layer Allocation/MW | Final Allocation/MW | Node | First Layer Allocation/MW | Second Layer Allocation/MW | Final Allocation/MW |
| R2 | 0.00425 | 0.00217 | 0.00208 | C2 | 0.00563 | 0.00364 | 0.00199 |
| R3 | 0.00689 | 0 | 0.00689 | C3 | 0.00928 | 0 | 0.00928 |
| R4 | 0.00998 | 0 | 0.00998 | C4 | 0.01018 | 0 | 0.01018 |
| R5 | 0.01194 | 0.00482 | 0.00711 | C5 | 0.01258 | 0 | 0.01258 |
| R6 | 0.01388 | 0 | 0.01388 | C6 | 0.01107 | 0 | 0.01107 |
| R7 | 0.01145 | 0 | 0.01145 | C7 | 0.01197 | 0 | 0.01197 |
| R8 | 0.01237 | 0 | 0.01237 | C8 | 0.01273 | 0 | 0.01273 |
| R9 | 0.01314 | 0 | 0.01314 | C9 | 0.01307 | 0 | 0.01307 |
| R10 | 0.00893 | 0 | 0.00893 | C10 | 0.01134 | 0 | 0.01134 |
| R11 | 0.00562 | 0 | 0.00562 | C11 | 0.01109 | 0 | 0.01109 |
| R12 | 0.00704 | 0 | 0.00704 | C12 | 0.02613 | 0.01794 | 0.00819 |
| R13 | 0.00874 | 0 | 0.00874 | C13 | 0.02933 | 0 | 0.02933 |
| R14 | 0.01006 | 0 | 0.01006 | C14 | 0.02733 | 0.01877 | 0.00855 |
| R15 | 0.0532 | 0.02068 | 0.03252 | C15 | 0.00882 | 0 | 0.00882 |
| R16 | 0.03844 | 0.02013 | 0.01831 | C16 | 0.00792 | 0 | 0.00792 |
| R17 | 0.0306 | 0.01233 | 0.01827 | C17 | 0.03489 | 0.0224 | 0.01249 |
| R18 | 0.04301 | 0.01763 | 0.02537 | C18 | 0.01229 | 0 | 0.01229 |
| I2 | 0.06348 | 0.01616 | 0.04732 | C19 | 0.02376 | 0.01629 | 0.00747 |
| C20 | 0.01266 | 0 | 0.01266 |
References
- Han, M.Y.; Xiong, J.; Liu, W.D. Spatio-temporal distribution, competitive development and emission reduction of China‘s photovoltaic power generation. J. Nat. Resour. 2022, 37, 1338–1351. [Google Scholar] [CrossRef]
- Shchemeleva, Y.B.; Shchemelev, A.N.; Davidov, S.K. Analysis of the Electrical Energy Losses Structure. In Proceedings of the 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 6–9 October 2020; pp. 1–5. [Google Scholar]
- Koochaki, M.; Davoudi, M.; Aghtaie, M. A novel loss allocation method applicable for any desired network topology. Electr. Power Syst. Res. 2023, 224, 109733. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, Y.G.; Liu, D.H.; Liang, X.W.; Wu, K.; Li, L. Calculation and analysis of theoretical line loss in low voltage station area based on Adaboost integrated learning. Electr. Meas. Instrum. 2025; in press. [Google Scholar]
- Cheng, L.; Yu, F.; Huang, P.; Liu, G.; Zhang, M.; Sun, R. Game-theoretic evolution in renewable energy systems: Advancing sustainable energy management and decision optimization in decentralized power markets. Renew. Sustain. Energy Rev. 2025, 217, 115776. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, D.Z.; Li, P.D.; Ji, K.L.; Liu, X.F.; Tan, H. A three-phase power flow model for low-voltage distribution networks considering balanced bus phase asymmetry and photovoltaic access. Electr. Power China 2024, 57, 190–198. [Google Scholar]
- Hou, X.Z.; Wang, S.W.; Su, Y.; Cheng, Y.Y.; Chen, W.L.; Chen, F.Y.; Wu, Z.Y.; Huang, H.C.; He, Y.M.; Yan, W. Daily theoretical line loss rate probability analysis for low voltage distribution networks. J. Chongqing Univ. 2025, 48, 27–37. [Google Scholar]
- Yang, L.; Wang, X.J.; Wang, Z.J.; Zhao, W.H.; Li, P.; Li, M.X. Data-driven Voltage Coordination Control for Low-voltage Distribution Networks with High Household Photovoltaics Penetration. Electr. Drive 2025, 55, 51–60. [Google Scholar]
- Xiao, J.X.; Ye, Y.; Wang, F.; Shen, J.S.; Gao, F. Comprehensive evaluation index system of distribution network for distributed photovoltaic access. Front. Energy Res. 2022, 10, 1–15. [Google Scholar] [CrossRef]
- Tang, W.H.; Huang, K.C.; Qian, T.; Li, W.W.; Xie, X.H. Spatio-temporal prediction of photovoltaic power based on broad learning system and improved backtracking search optimization algorithm. Front. Energy Res. 2024, 12, 1–18. [Google Scholar] [CrossRef]
- Cheng, L.; Peng, P.; Huang, P.; Zhang, M.; Meng, X.; Lu, W. Leveraging evolutionary game theory for cleaner production: Strategic insights for sustainable energy markets, electric vehicles, and carbon trading. J. Clean. Prod. 2025, 512, 145682. [Google Scholar] [CrossRef]
- Wang, L.C.; Yan, R.F.; Saha, T.K. Voltage regulation challenges with unbalanced PV integration in low voltage distribution systems and the corresponding solution. Appl. Energy 2019, 256, 113927. [Google Scholar] [CrossRef]
- Zheng, S. Analysis of Voltage Stability of Receiving-End Power Grid Adapted to Photovoltaic and DC. Master’s Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, 2021. [Google Scholar]
- Ma, Z.; Chen, H.Y.; Deng, C.; Chen, Y.; Guan, L. Analysis on the Spatiotemporal Distribution Characteristics of the Frequency Response in Large-scale New Energy Access Sending-end Power Grid. Electr. Drive 2025, 55, 56–65. [Google Scholar]
- He, Z.H.; Cao, R.; Liu, H.P.; Zhou, C. Research on improving photovoltaic fault voltage support capability by virtual impedance and reactive current control. Power Capacit. React. Power Compens. 2022, 43, 42–49. [Google Scholar]
- Ren, Y.F.; Zhao, Y.X.; Chen, S.N.; Sun, Q.; Li, M.Y.; Zhang, W.; Liu, L. Compatibility evaluation of photovoltaic and hydroelectric power generation potential in the Beijiang River Basin based on climate resources. Appl. Meteor. Sci. 2025, 36, 164–177. [Google Scholar]
- Chen, H.; Zhang, T.; Pei, H.M.; Shi, W.; Zhang, X.Y. Analysis of distributed photovoltaic power influence on grid voltage and power losses. Electr. Meas. Instrum. 2015, 52, 63–69. [Google Scholar]
- Singh, N.; Mohapatra, A.; Singh, S.N. Loss allocation methods in distribution networks: Present status and challenges. Electr. Power Syst. Res. 2024, 236, 110966. [Google Scholar] [CrossRef]
- Hota, A.P.; Mishra, S.; Mishra, D.P. Active power loss allocation in radial distribution networks with different load models and DGs. Electr. Power Syst. Res. 2022, 205, 107764. [Google Scholar] [CrossRef]
- Atanasovski, M.; Mijoski, T.; Kostov, M.; Arapinoski, B. Real case study of loss allocation in distribution systems with RES. In Proceedings of the 2022 57th International Scientific Conference on Information, Communication and Energy Systems and Technologies (ICEST), Ohrid, North Macedonia, 16–18 June 2022; pp. 1–4. [Google Scholar]
- Wang, Y.H. Research on Allocation of Energy Losses of Distribution System Including Distributed Generation. Master‘s Thesis, North China Electric Power University, Beijing, China, 2013. [Google Scholar]
- Huang, X.; Ouyang, S.; Ma, S.H. Line loss allocation method considering the contribution rate of the distributed generation to distribution network. Electr. Meas. Instrum. 2019, 56, 16–24. [Google Scholar]
- Kumar, H.; Khatod, D.K. Loss allocation in three-phase distribution network using τ-Value. IEEE Trans. Power Syst. 2024, 39, 4924–4934. [Google Scholar] [CrossRef]
- Kumar, H.; Khatod, D.K. τ-Value Based approach for loss allocation in radial and weakly meshed distribution networks with distributed generation. IEEE Trans. Power Deliv. 2022, 37, 1845–1855. [Google Scholar] [CrossRef]
- Gui, J.P.; Zhou, B.T.; Rao, Y.; Wang, W.Z.; Liang, C.; Ding, S.; Xu, C.Y. Loss allocation method for distribution network with DG based on knowledge graph and network topology. J. Wuhan Univ. (Eng. Ed.), 2025; in press. [Google Scholar]
- Liu, W.Y.; Chen, X.X.; Wang, F.Y.; Liu, F.C.; Wang, G. Network loss allocation based on graph theory and power flow tracking. J. North China Electr. Power Univ. (Nat. Sci. Ed.) 2020, 47, 1–9. [Google Scholar]
- Jagtap, K.M. Average marginal loss allocation of distribution networks. In Proceedings of the 2021 13th IEEE PES Asia Pacific Power & Energy Engineering Conference (APPEEC), Thiruvananthapuram, India, 21–23 November 2021; pp. 1–5. [Google Scholar]
- Li, M.Z.; Huo, C.J.; Wang, W.R.; Yu, K.; Zhang, F.R.; Zhang, Y.F. Loss allocation of distribution network with distributed generations based on improved marginal loss coefficients method. Electr. Power Eng. Technol. 2022, 41, 180–184. [Google Scholar]
- Cheng, L.; Wei, X.; Li, M.; Tan, C.; Yin, M.; Shen, T.; Zou, T. Integrating evolutionary game-theoretical methods and deep reinforcement learning for adaptive strategy optimization in user-side electricity markets: A comprehensive review. Mathematics 2024, 12, 3241. [Google Scholar] [CrossRef]
- Zhao, J.; Du, S.; Dong, Y.; Su, J.; Xia, Y. A bidirectional loss allocation method for active distributed network based on virtual contribution theory. Int. J. Electr. Power Energy Syst. 2023, 153, 109112. [Google Scholar] [CrossRef]
- Zare, A.; Mehdinejad, M.; Abedi, M. Designing a decentralized peer-to-peer energy market for an active distribution network considering loss and transaction fee allocation, and fairness. Appl. Energy 2024, 358, 122527. [Google Scholar] [CrossRef]
- Chaitra, A.S.; Sudarshana Reddy, H.R. Improving Reliability in Distribution Systems through Optimal Allocation of Distributed Generators, Network Reconfiguration and Capacitor Placement. SN Comput. Sci. 2024, 5, 456. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Kirk-Davidoff, D.B.; Bloomfield, H.; Bracken, C.; Sharp, J. Wind and solar energy droughts: Potential impacts on energy system dynamics and research needs. J. Renew. Sustain. Energy 2025, 17, 022301. [Google Scholar] [CrossRef]
- Hjalmarsson, J.; Thomas, K.; Boström, C. Service stacking using energy storage systems for grid applications – A review. J. Energy Storage 2023, 60, 106639. [Google Scholar] [CrossRef]
- Mitchell, R.; Cooper, J.; Frank, E.; Holmes, G. Sampling permutations for Shapley value estimation. J. Mach. Learn. Res. 2022, 23, 1–46. [Google Scholar]
- Atanasovski, M.; Taleski, R. Power Summation Method for Loss Allocation in Radial Distribution Networks With DG. IEEE Trans. Power Syst. 2011, 26, 2491–2499. [Google Scholar] [CrossRef]
- Grainger, J.J.; Stevenson, W.D., Jr.; Chang, G.W. Power System Analysis, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2016; ISBN 978-1-259-00835-1. [Google Scholar]
- Shang, C.; Gao, J.; Liu, H.; Liu, F. Short-Term Load Forecasting Based on PSO-KFCM Daily Load Curve Clustering and CNN-LSTM Model. IEEE Access 2021, 9, 50344–50357. [Google Scholar] [CrossRef]
- Leng, D.; Qiu, Z. Identification of Anomaly Detection in Power System State Estimation Based on Fuzzy C-Means Algorithm. Int. Trans. Electr. Energy Syst. 2023, 7553080. [Google Scholar] [CrossRef]
- Serrano, R. Cooperative games: Core and Shapley value. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 1729–1746. [Google Scholar]
- Shapley, L.S. A value for n-person games. In Contributions to the Theory of Games; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; Volume II, pp. 307–317. [Google Scholar]
- Singh, V.P.; Ahmad, A.; Jagtap, K.M. Weighted Shapley value: A cooperative game theory for loss allocation in distribution systems. Front. Energy Res. 2023, 11, 1129846. [Google Scholar] [CrossRef]
- Touati, S.; Radjef, M.S.; Sais, L. A Bayesian Monte Carlo method for computing the Shapley value: Application to weighted voting and bin packing games. Comput. Oper. Res. 2021, 125, 105094. [Google Scholar] [CrossRef]
- Hu, R.Z.; Lv, S.X.; Zhang, C.; Geng, P.L.; We, H.; Zheng, L.J. Real time comprehensive evaluation method of power quality based on state entropy and dual track TOPSIS. Power Syst. Prot. Control 2023, 51, 102–114. [Google Scholar]
- Patro, S.G.K.; Sahu, K.K. Normalization: A Preprocessing Stage. IARJSET 2015, 20–22. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Luo, Y. Integration of correlations with standard deviations for determining attribute weights in multiple attribute decision making. Math. Comput. Model. 2010, 51, 1–12. [Google Scholar] [CrossRef]
- Mukhoti, J.; Kirsch, A.; van Amersfoort, J.; Torr, P.H.S.; Gal, Y. Deep Deterministic Uncertainty: A New Simple Baseline. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 7 June 2023; pp. 24384–24394. [Google Scholar]
- Barsali, S. Benchmark Systems for Network Integration of Renewable and Distributed Energy Resources; Technical Brochure 575; CIGRE: Paris, France, 2014. [Google Scholar]
- Dickert, J.; Domagk, M.; Schegner, P. Benchmark low voltage distribution networks based on cluster analysis of actual grid properties. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- Thurner, L.; Scheidler, A.; Schäfer, F.; Menke, J.-H.; Dollichon, J.; Meier, F.; Meinecke, S.; Braun, M. pandapower—An Open-Source Python Tool for Convenient Modeling, Analysis, and Optimization of Electric Power Systems. IEEE Trans. Power Syst. 2018, 33, 6510–6521. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, X.P.; Sterling, M. Solar Power Generation Intermittency and Aggregation. Sci. Rep. 2022, 12, 1363. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Wang, Y.; Guo, J.; Xia, Q.; Tu, Y.; Nie, P. Compensation Benefits Allocation and Stability Evaluation of Cascade Hydropower Stations Based on Variation Coefficient-Shapley Value Method. J. Hydrol. 2021, 599, 126277. [Google Scholar] [CrossRef]
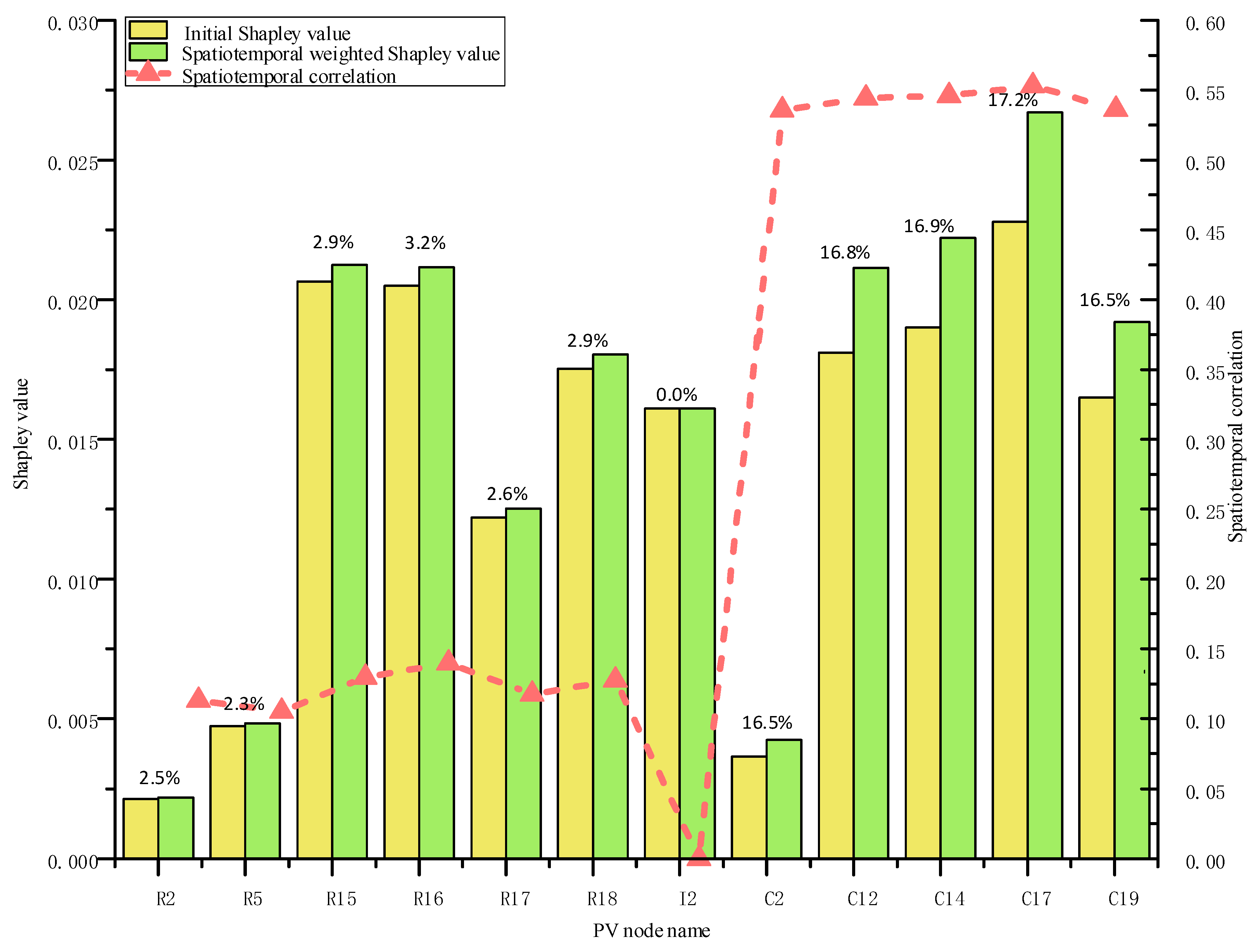
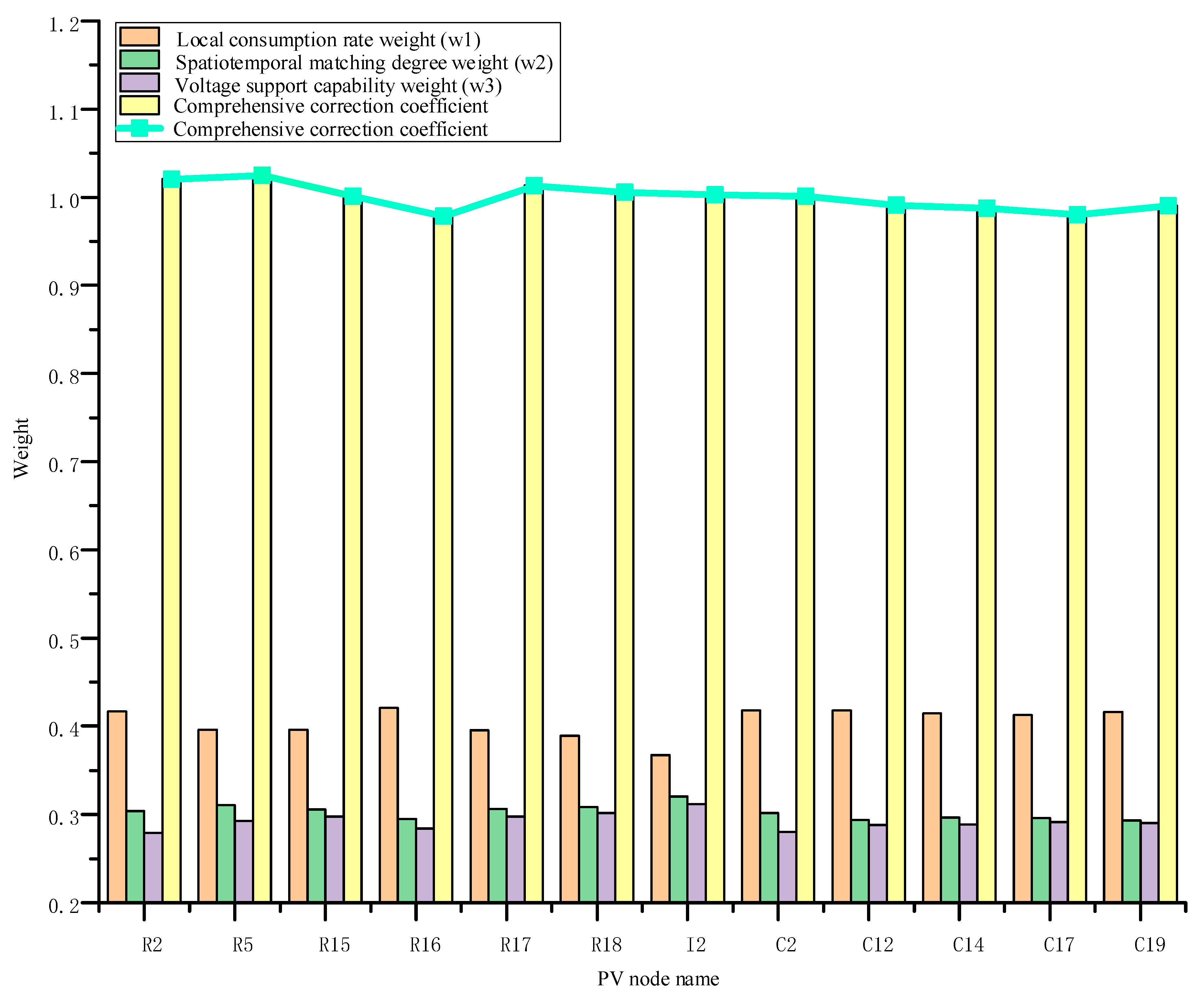

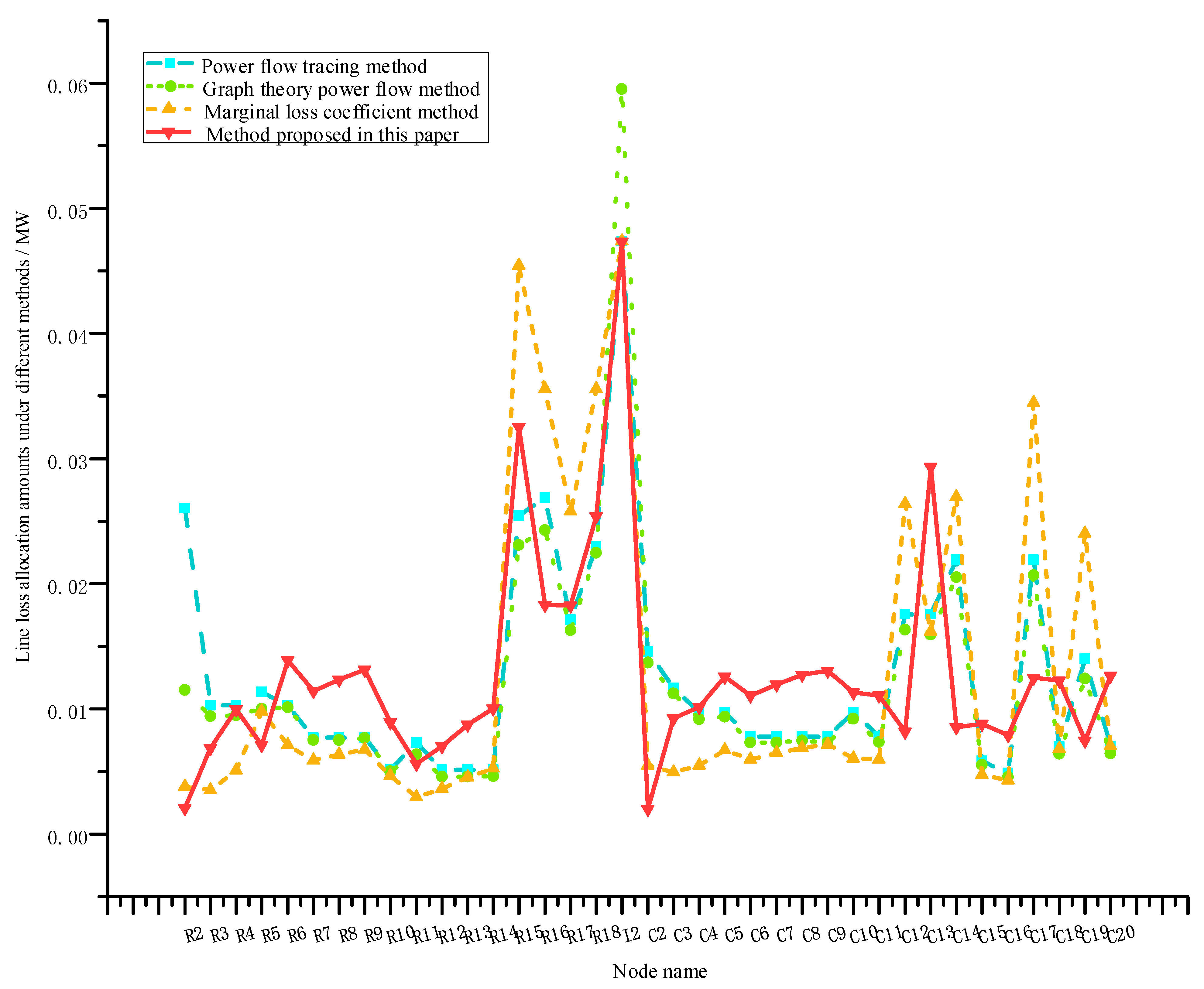

| Node | Power Flow Tracing/MW | Graph Theory–Power Flow/MW | Marginal Loss Coefficient/MW | Proposed Method/MW |
|---|---|---|---|---|
| R5 | 0.011356 | 0.010013 | 0.009803 | 0.007115 |
| R16 | 0.026896 | 0.024266 | 0.035561 | 0.01831 |
| R17 | 0.017116 | 0.016256 | 0.025778 | 0.018269 |
| R18 | 0.022984 | 0.022469 | 0.035555 | 0.025373 |
| C2 | 0.014602 | 0.013696 | 0.005513 | 0.001992 |
| C12 | 0.017522 | 0.016314 | 0.026382 | 0.008185 |
| C17 | 0.021903 | 0.020658 | 0.034462 | 0.012491 |
| C19 | 0.014018 | 0.012499 | 0.023999 | 0.007468 |
| Indicator | Power Flow Tracing | Graph Theory–Power Flow | Marginal Loss Coefficient | Proposed Method |
|---|---|---|---|---|
| Average CV | 0.139036 | 0.125587 | 0.141561 | 0.166424 |
| Median CV | 0.1478 | 0.1172 | 0.1712 | 0.0402 |
| QCD | 0.084054 | 0.076455 | 0.086533 | 0.10611 |
| Max Deviation % | 33.52865 | 30.48456 | 34.39774 | 40.54669 |
| Variation Range | 0.004316 | 0.003921 | 0.003359 | 0.004444 |
| Indicator | Power Flow Tracing | Graph Theory–Power Flow | Marginal Loss Coefficient | Proposed Method |
|---|---|---|---|---|
| Average CV | 0.13669 | 0.114086 | 0.181583 | 0.032544 |
| Median CV | 0.1478 | 0.1104 | 0.1812 | 0.0332 |
| QCD | 0.082651 | 0.069437 | 0.111201 | 0.019426 |
| Max Deviation % | 33.00416 | 27.63405 | 44.15734 | 7.745019 |
| Variation Range | 0.00273 | 0.002198 | 0.002764 | 0.00083 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Q.; Zhang, H.; Cai, H.; Li, H.; Wang, X.; Peng, X.; Zhao, Z. Hierarchical Line Loss Allocation Methods for Low-Voltage Distribution Networks with Distributed Photovoltaics. Mathematics 2025, 13, 3366. https://doi.org/10.3390/math13213366
Peng Q, Zhang H, Cai H, Li H, Wang X, Peng X, Zhao Z. Hierarchical Line Loss Allocation Methods for Low-Voltage Distribution Networks with Distributed Photovoltaics. Mathematics. 2025; 13(21):3366. https://doi.org/10.3390/math13213366
Chicago/Turabian StylePeng, Qingjiong, Haobo Zhang, Haotian Cai, Hongwe Li, Xiaolong Wang, Xiangang Peng, and Zhuoli Zhao. 2025. "Hierarchical Line Loss Allocation Methods for Low-Voltage Distribution Networks with Distributed Photovoltaics" Mathematics 13, no. 21: 3366. https://doi.org/10.3390/math13213366
APA StylePeng, Q., Zhang, H., Cai, H., Li, H., Wang, X., Peng, X., & Zhao, Z. (2025). Hierarchical Line Loss Allocation Methods for Low-Voltage Distribution Networks with Distributed Photovoltaics. Mathematics, 13(21), 3366. https://doi.org/10.3390/math13213366








