Study on Gas Pre-Extraction Law of Along-Layer Boreholes Based on Thermo-Hydro-Mechanical-Damage Coupled Model
Abstract
1. Introduction
2. A Coupled THMD Model Considering Coal Matrix Damage
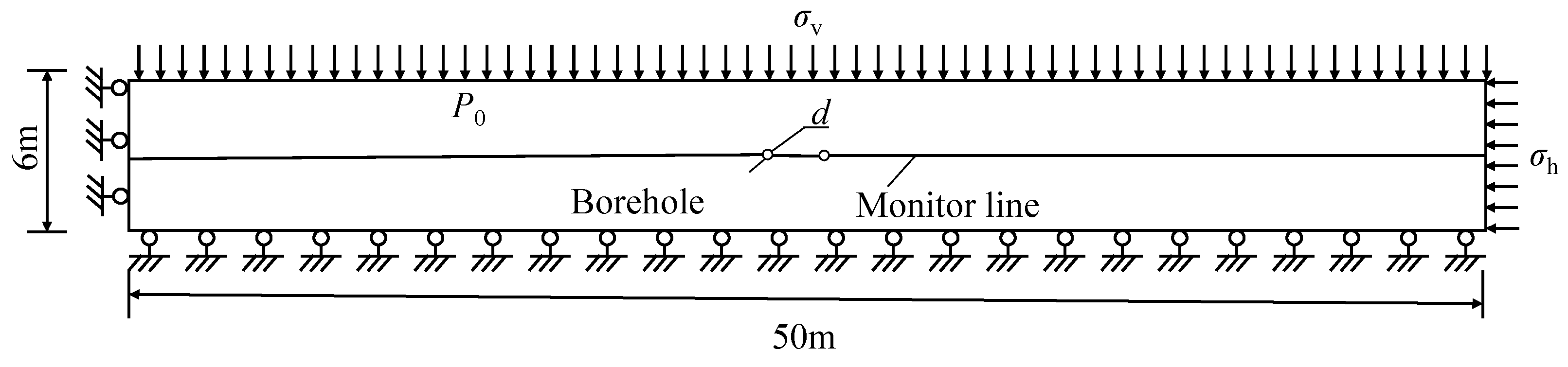
2.1. Physical System and Conceptual Model
2.2. The Thermo-Hydro-Mechanical Damage Coupled Model
2.2.1. Basic Assumptions
2.2.2. Coal Body Energy Conservation Equation
2.2.3. Gas Seepage Equation
2.2.4. Control Equation of Coal Body Deformation Field
2.3. Damage Evolution Equations
2.3.1. Impact of Damage on Coal Body
2.3.2. Thermo-Hydro-Mechanical Damage Coupling Relationship
3. Numerical Methodology
3.1. Finite Element Implementation
3.2. Numerical Model Construction
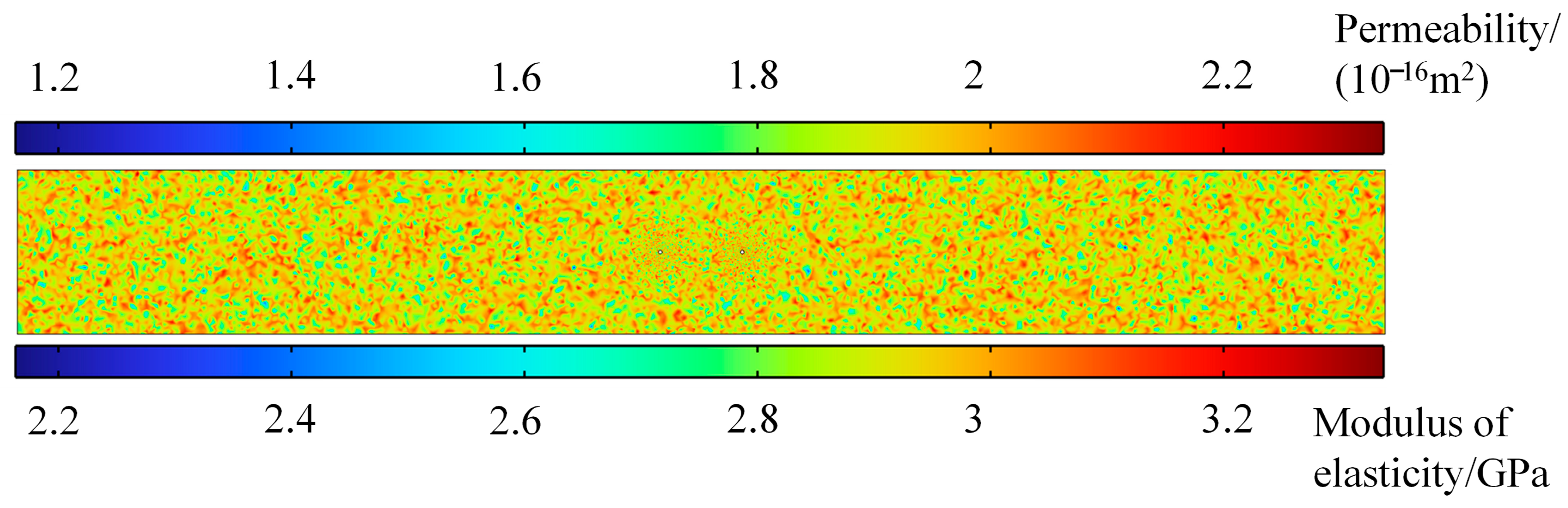
3.2.1. Construction of Heterogeneous Coal Bodies
3.2.2. Model Calculation Parameters
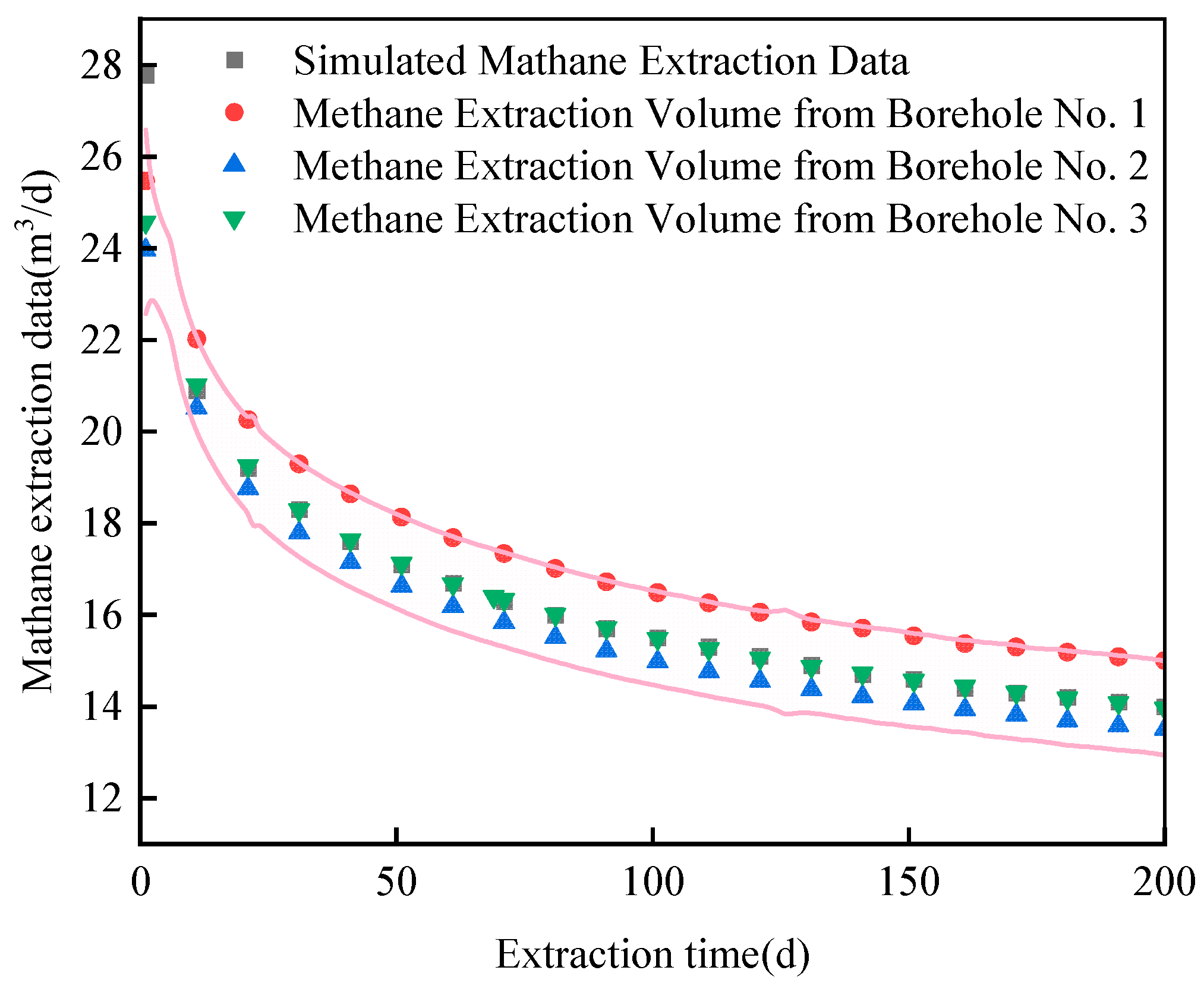
3.3. Model Validation
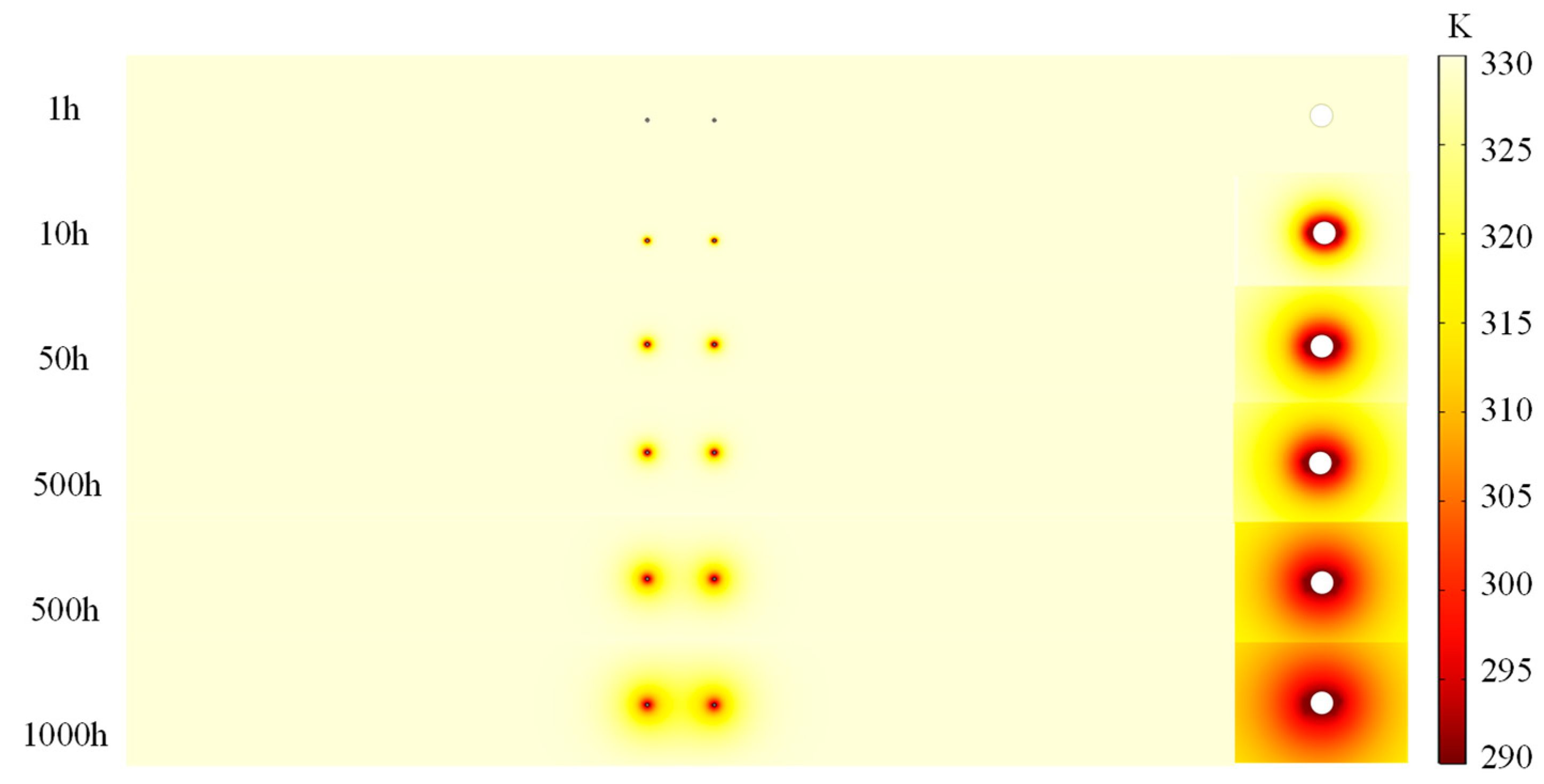
3.4. Simulation Results
3.4.1. Temperature Distribution
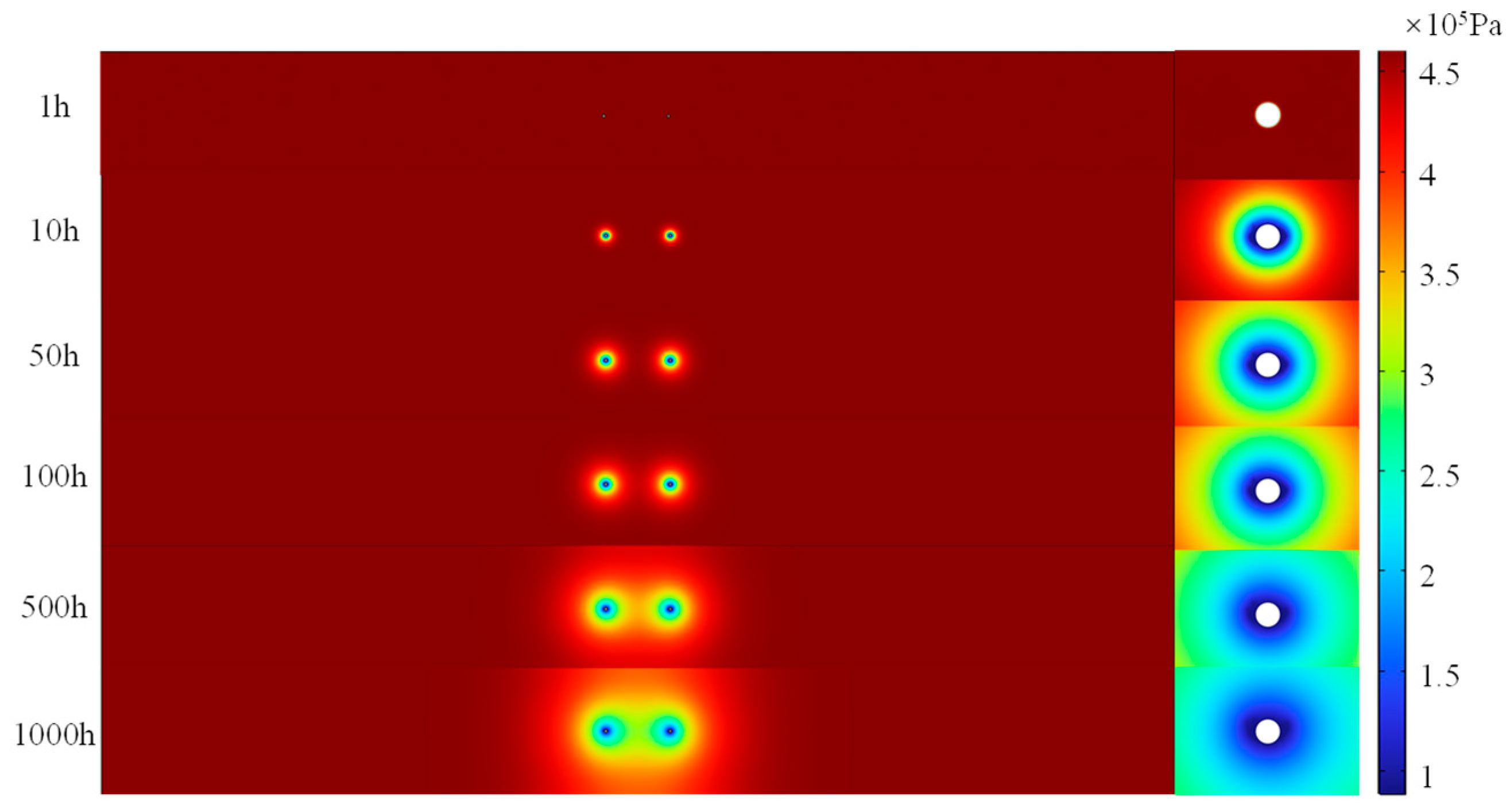
3.4.2. Gas Pressure Distribution
3.4.3. Borehole Damage Zone Area
4. Multi-Factor Sensitivity Analysis of Borehole Pre-Extraction Effectiveness
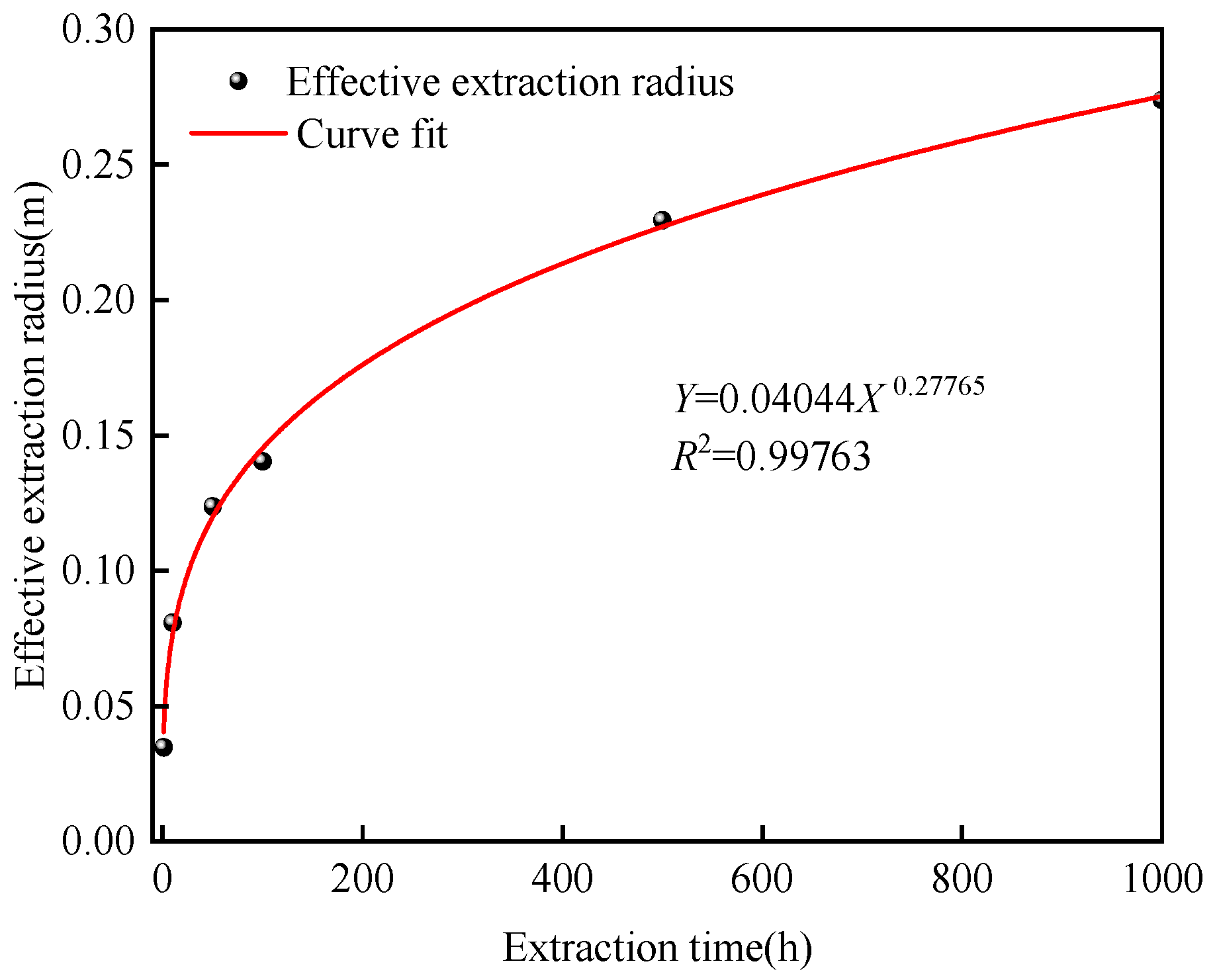
4.1. Effective Extraction Radius
4.2. Sensitivity Analysis of Effective Extraction Radius and Damage Zone Area
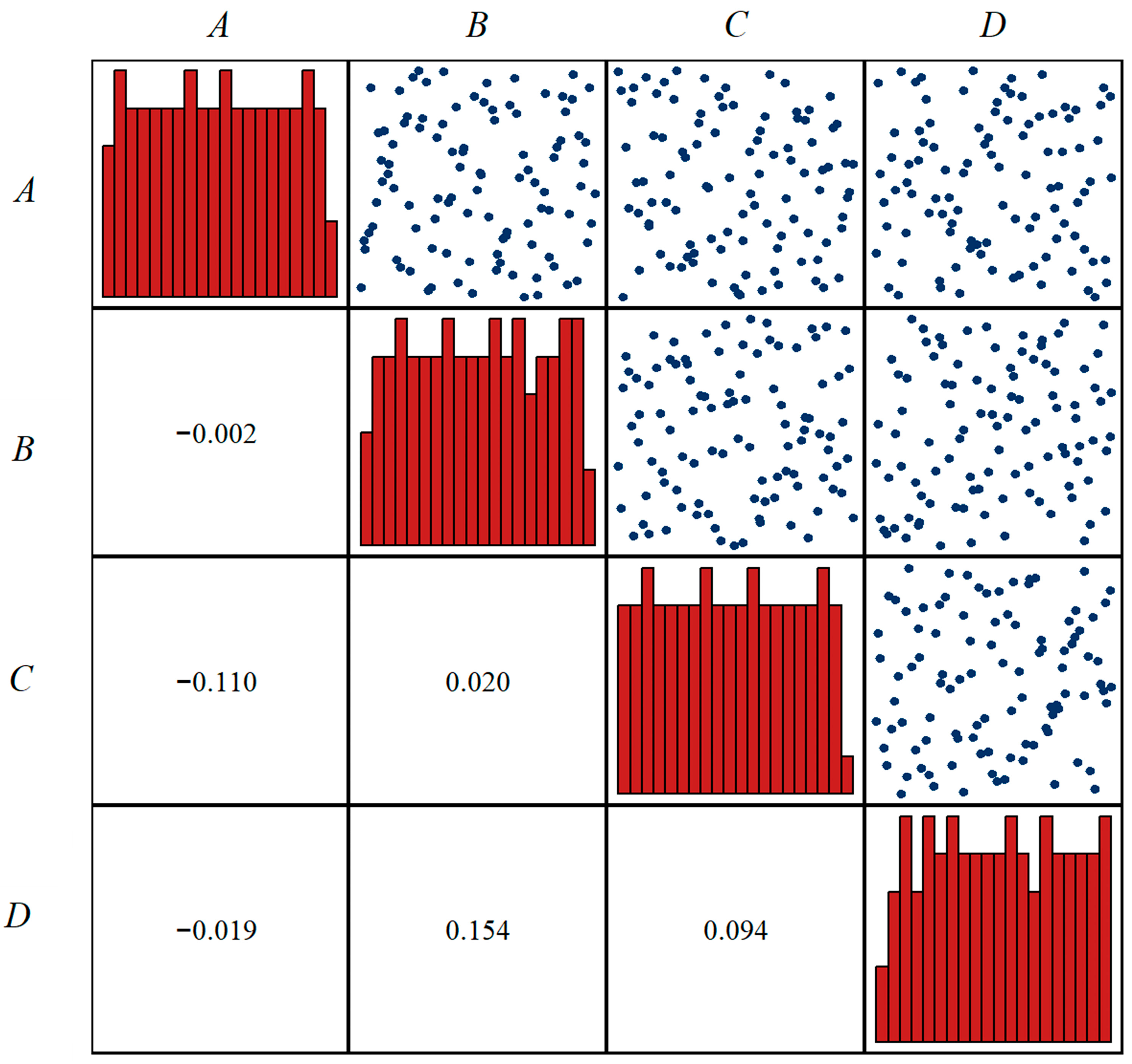
4.2.1. Response Surface Analysis Method
− 3.5091 × 10−7 × AC + 1.14099 × 10−6 × AD + 2.23757 × 10−5 × BC + 7.3526 × 10−6× BD + 2.71634 × 10−6 × CD + 6.48457 × 10−7 × A2
− 2.78064 × 10−5 × B2 − 4.06081 × 10−8 × C2 + 3.43143 × 10−6 × D2
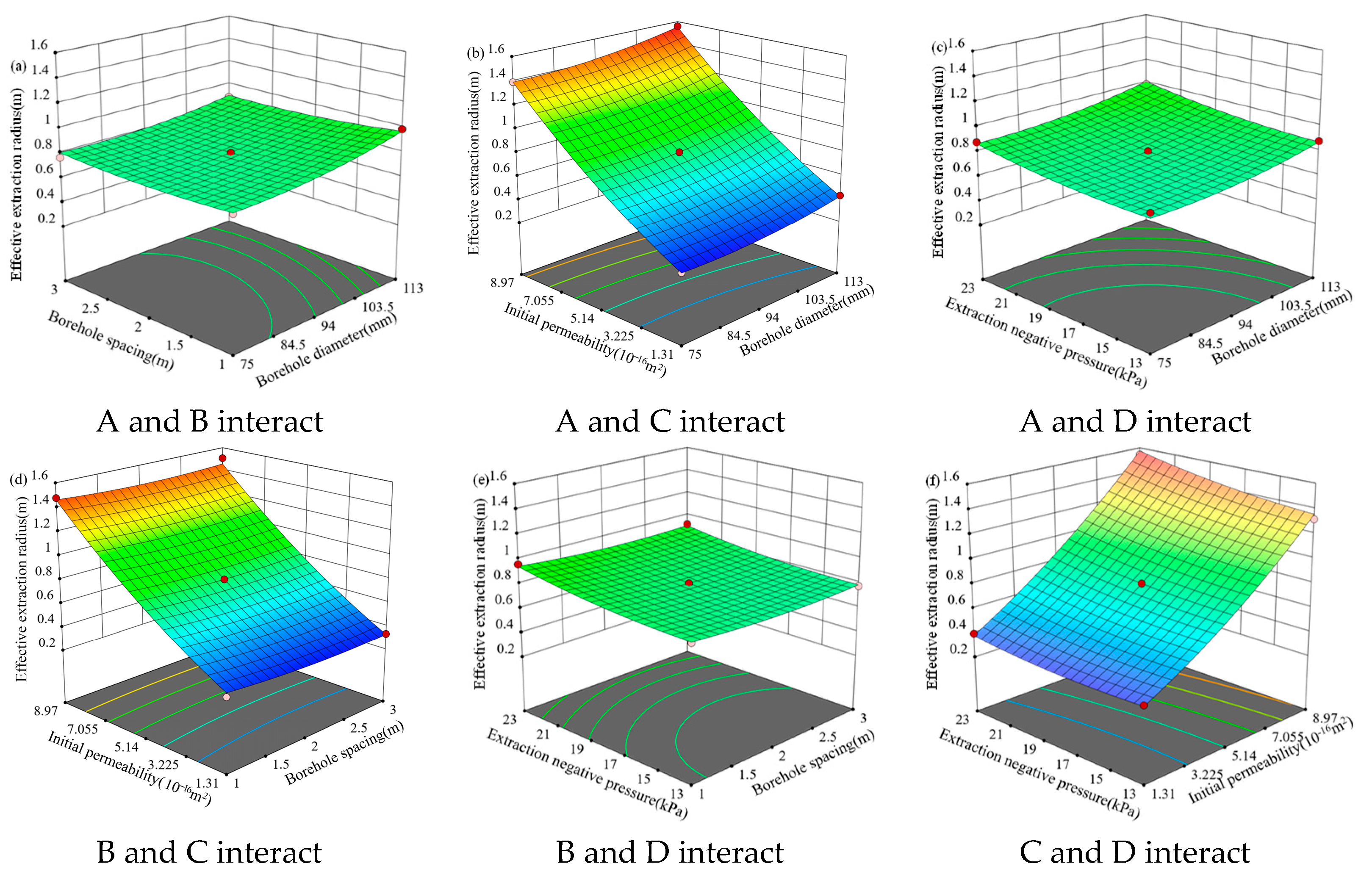
4.2.2. Sensitivity Analysis
4.3. Limitations and Future Outlook
5. Conclusions
- (1)
- A fully coupled thermo-hydro-mechanical damage (THMD) model that accounts for the heterogeneous distribution of coal’s physical properties was established and successfully validated against field data, demonstrating good consistency.
- (2)
- The simulations revealed complex, non-uniform evolution patterns for the physical fields around the boreholes. The inherent material heterogeneity led to localized stress concentrations and preferential flow paths, confirming a more realistic response than a uniform material model would predict. The subsequent multi-factor sensitivity analysis provided a definitive, quantitative ranking of these influences. It was demonstrated that the effective extraction radius (Y1) is predominantly governed by the initial permeability (F-value of 4219.59), while the extent of the damage zone area (Y2) is overwhelmingly dictated by the borehole diameter (F-value of 2531.51), with both factors being highly significant (p < 0.0001).
- (3)
- These findings provide crucial, data-driven directives for engineering practice. To enhance the drainage radius in low-permeability seams, engineering interventions should prioritize measures that improve permeability (e.g., hydraulic fracturing), as this is the most influential factor. Conversely, to manage borehole stability and mitigate safety risks associated with excessive fracturing, the precise control of borehole diameter is the most critical lever. Ultimately, this research showcases the significant potential of integrating high-fidelity numerical modeling with statistical analysis to guide and optimize gas extraction strategies in complex deep-mining environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, D.; Liu, Q.; Qiu, L.; Zhang, J.; Majid, K.; Peng, Y.; Zhao, Y.; Wang, M.; Guo, M.; Hong, T. Experimental Study on Resistivity Evolution Law and Precursory Signals in the Damage Process of Gas-Bearing Coal. Fuel 2024, 362, 130798. [Google Scholar] [CrossRef]
- Qiu, L.; Dang, J.; Zhang, J.; Wang, M.; Liu, Q.; Si, L.; Jiang, Z.; Khan, M. Investigating Nonlinear Resistivity Characteristics and Mechanisms of Coal during Various Loading Stages. J. Appl. Geophys. 2025, 238, 105705. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, E. Risk Identification for Coal and Gas Outburst in Underground Coal Mines: A Critical Review and Future Directions. Gas Sci. Eng. 2023, 118, 205106. [Google Scholar] [CrossRef]
- Hu, B.; Gou, R.; Song, Z.; Li, S.; Liu, S.; Liu, S.; Han, T.; Yang, W.; Shuang, H. Evolution of Overlying Strata Fractures in Variable Mining Heights of Deeply Buried Thick Coal Seams. Results Eng. 2025, 28, 107415. [Google Scholar] [CrossRef]
- Hu, B.; Ren, Z.; Li, S.; He, X.; Long, H.; Cheng, L.; Luo, R. The Distribution Characteristics of Adsorbed CH4 in Various-Sized Pore Structures of Coal Seams. Mathematics 2025, 13, 2931. [Google Scholar] [CrossRef]
- Liu, L.; Jin, J.; Liu, J.; Cheng, W.; Zhao, M.; Luo, S.; Luo, Y.; Wang, T. Mechanical Properties of Sandstone under In-Situ High-Temperature and Confinement Conditions. Int. J. Miner. Metall. Mater. 2025, 32, 778–787. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Z.; Shen, W.; Feng, T.; Zhang, G. Mechanical Property and Thermal Degradation Mechanism of Granite in Thermal-Mechanical Coupled Triaxial Compression. Int. J. Rock Mech. Min. Sci. 2022, 160, 105270. [Google Scholar] [CrossRef]
- Dong, Z.; Tian, S.; Xue, H.; Lu, S.; Liu, B.; Erastova, V.; Wu, M.; Wu, R. Analysis of Pore Types in Lower Cretaceous Qingshankou Shale Influenced by Electric Heating. Energy Fuels 2024, 38, 20577–20590. [Google Scholar] [CrossRef]
- Gao, F.; Xue, Y.; Gao, Y.; Zhang, Z.; Teng, T.; Liang, X. Fully Coupled Thermo-Hydro-Mechanical Model for Extraction of Coal Seam Gas with Slotted Boreholes. J. Nat. Gas Sci. Eng. 2016, 31, 226–235. [Google Scholar] [CrossRef]
- Li, H.; Huang, B.; Zheng, W.; Zhao, X.; Tannant, D. Effect of Proppant Distribution in Hydraulic Fractures on Coalbed Methane Extraction. Results Eng. 2023, 20, 101550. [Google Scholar] [CrossRef]
- Zou, X.; Ma, T.; Liu, G.; Ye, D.; Wang, X.; Guo, K. A New Hydro-Mechanics Coupling Model for Gas Extraction of Coal Seam Considering Slippage Effect and Tortuosity. Phys. Fluids 2025, 37, 067106. [Google Scholar] [CrossRef]
- Rong, T.; Yang, Y.; Zhou, Y.; Zhang, S.; Niu, R.; Nan, P.; Wang, C. Development of an Anisotropic Coal Permeability Model Incorporating Damage and Its Application in Gas Drainage. Phys. Fluids 2025, 37, 053110. [Google Scholar] [CrossRef]
- Peng, J.; Shi, S.; Shi, X. Research on Prediction of Coal and Gas Outburst Risk Based on TIWTD-CNSA. Results Eng. 2023, 18, 101195. [Google Scholar] [CrossRef]
- Sun, C.; Liu, W.; Yang, R.; Ma, T. Sensitivity Analysis on the Microwave Irradiation Enhancing Coal Seam Gas Recovery: A Coupled Electromagnetic-Thermo-Hydro-Mechanical Model. J. Nat. Gas Sci. Eng. 2022, 100, 104457. [Google Scholar] [CrossRef]
- Du, F.; Zhang, Y.; Wang, K.; Sun, J.; Xu, Y. Nitrogen Injection for Enhanced Coal Seam Gas Extraction (N2-ECGE): A Simulation Study. Earth Energy Sci. 2025, 1, 193–202. [Google Scholar] [CrossRef]
- Wang, J.G.; Liu, J.; Kabir, A. Combined Effects of Directional Compaction, Non-Darcy Flow and Anisotropic Swelling on Coal Seam Gas Extraction. Int. J. Coal Geol. 2013, 109–110, 1–14. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Y.; Zhao, Z.; Wei, M.; Wang, Z.; Zhang, J. Time Dependency of Permeability and Deformation of Coal during Gas Storage in Deep Coal Reservoirs. Int. J. Hydrog. Energy 2025, 98, 341–352. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Chang, J.; Yan, F.; Li, A.; Wang, S.; Guo, J.; Lei, Q.; Yang, S. Pressure-Relief Gas Flow Behavior in the Hydraulic Flushing Coal Mass Considering Creep Effect: Theoretical Modeling and Numerical Simulation. Gas Sci. Eng. 2025, 142, 205691. [Google Scholar] [CrossRef]
- Hu, B.; Ren, Z.; Li, S.; He, X.; Lin, H.; Bai, Y.; Yan, D.; Luo, R. A New Quantitative Characterization Method of Absolute Methane Adsorption Isotherm in Coal. Chem. Eng. J. 2025, 522, 167551. [Google Scholar] [CrossRef]
- Feng, X.; Deng, S.; Liu, Q.; Kong, X.; Zhang, X. Moisture Content Modulates Pressure-Dependent Gas Diffusion in Coal Particles: Mechanistic Insights. Int. J. Heat Mass Transf. 2025, 252, 127455. [Google Scholar] [CrossRef]
- Zhang, M.; Fan, J.; Du, J.; Jiang, D.; Chen, J.; Yuan, Q.; Hao, L.; Wang, Y. Experimental Study on Effects of Load Damage Precursor Information and Response Characteristic of Gas-Containing Coal for Mining Safety Based on Acoustic Emission. Process Saf. Environ. Prot. 2024, 184, 993–1010. [Google Scholar] [CrossRef]
- Song, W.; Yu, S.; Rong, H. Study on the Mechanism of Structural Coal Permeability Law on Coal and Gas Outburst under Multi-Field Coupling. Phys. Fluids 2025, 37, 076641. [Google Scholar] [CrossRef]
- Zhao, J.; Jin, J.; Li, Y. Macro-Micro Failures of Shear Creep and Creep Damage Model of Deep Hard Rocks Induced by Initial Disturbances. Eng. Fract. Mech. 2025, 324, 111269. [Google Scholar] [CrossRef]
- Lin, C.; Wang, Z.; Shi, J.; Ma, B.; Liang, R.; Luo, X. Elasto-Plastic Solution for Tunnelling-Induced Nonlinear Responses of Overlying Jointed Pipelines in Sand. Tunn. Undergr. Space Technol. 2024, 152, 105953. [Google Scholar] [CrossRef]
- Du, M.; Zhou, C.; Cai, C.; Xue, Y.; Hou, P.; Gao, F.; Han, W.; Ren, R.; Ren, H.; Su, S. Damage Evolution Law and Permeability Enhancement Effect of Coal Subjected to Liquid Nitrogen Fracturing in Coalbed Methane Mining. Phys. Fluids 2025, 37, 046614. [Google Scholar] [CrossRef]
- Peng, L.; Zhang, G.; Wang, H.; Sun, S.; Zhang, Y.; Liu, Z.; Wang, Z. Research on Strata Movement Control in Deep Areas of Super-Thick and Weak-Cemented Overlying Strata during Local Backfill Mining—A Case Study Based on Yingpanhao Coal Mine. Results Eng. 2025, 27, 105579. [Google Scholar] [CrossRef]
- Chen, X.; Han, P.; Hu, J.; Yang, T.; Zhou, A.; Sun, J. Air Leakage Mechanism and Hole Sealing Technology in Directional Long-Drilled Perimeter Rock-Borehole Composite Fissures: For Gas Enrichment in Varying Coal-Seam Thickness Change Areas. Process Saf. Environ. Prot. 2024, 192, 1367–1381. [Google Scholar] [CrossRef]
- Xu, C.; Yuan, Y.; Wang, K.; Hu, Y.; Nie, Z.; Shi, Y. Coalbed Methane Extraction: Characteristics of Damage-Seepage Evolution and Dynamic Response of Methane Transport in Non-Homogeneous Coal Seams under Cavitation. Gas Sci. Eng. 2025, 142, 205689. [Google Scholar] [CrossRef]
- Jia, L.; Wang, L.; Cheng, Y.; Xu, J.; Nie, B.; Peng, S. Dynamic Evolution of Fluid Energy in Gas Extraction: Insights from Physical Simulation and Mathematical Modeling. Phys. Fluids 2025, 37, 073355. [Google Scholar] [CrossRef]
- Zhang, E.; Zhou, B.; Yang, L.; Li, C.; Li, P. Experimental Study on the Microseismic Response Characteristics of Coal and Gas Outbursts. Process Saf. Environ. Prot. 2023, 172, 1058–1071. [Google Scholar] [CrossRef]
- Lin, H.; Li, B.; Li, S.; Song, Z.; Wang, P.; Luo, R.; Wei, Z.; Qin, L. A Coupled Thermo-Hydro-Mechanical-Damage Model and Numerical Simulation for Layered Coal Subjected to Liquid Nitrogen Fracturing. Chin. J. Rock Mech. Eng. 2024, 43, 1110–1123. [Google Scholar] [CrossRef]
- Liu, L.; Li, Y.; Cao, W.; Wang, T.; Zhang, L.; Feng, X. Coupled Thermo-Hydro-Mechanical-Damage Modeling of Cold-Water Injection in Deep Geothermal Reservoirs. J. Rock Mech. Geotech. Eng. 2025; in press. [Google Scholar] [CrossRef]
- Xi, B.; Wu, Y.; Zhao, Y. Experimental Study on the Correlation between Macroscopic Mechanical Parameters and Thermal Shock Velocity of Granite under Thermal Shock. Chin. J. Rock Mech. Eng. 2019, 38, 2194–2207. [Google Scholar] [CrossRef]
- Liu, L.; Ji, H.; Elsworth, D.; Zhi, S.; Lv, X.; Wang, T. Dual-Damage Constitutive Model to Define Thermal Damage in Rock. Int. J. Rock Mech. Min. Sci. 2020, 126, 104185. [Google Scholar] [CrossRef]
- Zhu, W.C.; Liu, J.; Sheng, J.C.; Elsworth, D. Analysis of Coupled Gas Flow and Deformation Process with Desorption and Klinkenberg Effects in Coal Seams. Int. J. Rock Mech. Min. Sci. 2007, 44, 971–980. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, Y.; Li, W.; Jin, K.; He, T.; Zhao, W. Gas-Solid Coupling Model for Coal and Gas in Deep Low-Permeability First-Mining Seams. Chin. J. Rock Mech. Eng. 2015, 34, 2749–2758. [Google Scholar] [CrossRef]
- Lin, H.; Li, B.; Li, S.; Qin, L.; Wei, Z.; Wang, P.; Luo, R. Numerical Investigation of Temperature Distribution and Thermal Damage of Heterogeneous Coal under Liquid Nitrogen Freezing. Energy 2023, 267, 126592. [Google Scholar] [CrossRef]
- Guo, T.; Tang, S.; Liu, S.; Liu, X.; Zhang, W.; Qu, G. Numerical Simulation of Hydraulic Fracturing of Hot Dry Rock under Thermal Stress. Eng. Fract. Mech. 2020, 240, 107350. [Google Scholar] [CrossRef]
- Zhu, W.C.; Tang, C.A. Numerical Simulation on Shear Fracture Process of Concrete Using Mesoscopic Mechanical Model. Constr. Build. Mater. 2002, 16, 453–463. [Google Scholar] [CrossRef]
- Zhu, W.C.; Tang, C.A. Micromechanical Model for Simulating the Fracture Process of Rock. Rock Mech. Rock Eng. 2004, 37, 25–56. [Google Scholar] [CrossRef]
- Williams, E. Hooke’s Law and the Concept of the Elastic Limit. Ann. Sci. 1956, 12, 74–83. [Google Scholar] [CrossRef]
- Hassanzadegan, A.; Blöcher, G.; Milsch, H.; Urpi, L.; Zimmermann, G. The Effects of Temperature and Pressure on the Porosity Evolution of Flechtinger Sandstone. Rock Mech. Rock Eng. 2014, 47, 421–434. [Google Scholar] [CrossRef]
- Lin, H.; Li, B.; Li, S.; Qin, L.; Wei, Z.; Wang, P.; Luo, R. Enhancing Coalbed Methane Recovery Using Liquid Nitrogen as a Fracturing Fluid: A Coupled Thermal-Hydro-Mechanical Modeling and Evaluation in Water-Bearing Coal Seam. Energy 2024, 291, 130445. [Google Scholar] [CrossRef]
- Baqer, Y.; Chen, X. A Review on Reactive Transport Model and Porosity Evolution in the Porous Media. Environ. Sci. Pollut. Res. 2022, 29, 47873–47901. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, C.H. Numerical Simulation on Mining-Induced Water Inrushes Related to Geologic Structures Using a Damage-Based Hydromechanical Model. Environ. Earth Sci. 2011, 62, 43–54. [Google Scholar] [CrossRef]
- Qiu, Y.; Liang, W.; Li, J.; He, W. Study on Fracture Morphology of Heterogeneous Elasto-Plastic Coal under Hydraulic Fracturing. J. China Coal Soc. 2022, 47, 3668–3679. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, J.; Su, X. A New Test and Calculation Method for the Permeability Coefficient of Coal Seams. J. China Coal Soc. 2024, 49, 833–844. [Google Scholar] [CrossRef]
- Nazarpour, M.; Taghizadeh-Alisaraei, A.; Asghari, A.; Abbaszadeh-Mayvan, A.; Tatari, A. Optimization of Biohydrogen Production from Microalgae by Response Surface Methodology (RSM). Energy 2022, 253, 124059. [Google Scholar] [CrossRef]
- Qatan, H.S.O.; Ghani, W.A.W.A.K.; Said, M.S.M. Prediction and Optimization of Syngas Production from Napier Grass Air Gasification via Kinetic Modelling and Response Surface Methodology. Energy 2023, 270, 126883. [Google Scholar] [CrossRef]
- Allahyarzadeh-Bidgoli, A.; Dezan, D.J.; Salviano, L.O.; de Oliveira Junior, S.; Yanagihara, J.I. FPSO Fuel Consumption and Hydrocarbon Liquids Recovery Optimization over the Lifetime of a Deep-Water Oil Field. Energy 2019, 181, 927–942. [Google Scholar] [CrossRef]
- Deutsch, J.L.; Deutsch, C.V. Latin Hypercube Sampling with Multidimensional Uniformity. J. Stat. Plan. Inference 2012, 142, 763–772. [Google Scholar] [CrossRef]
- Posadas, H.; Real, S.; Villar, E. M3-SCoPE: Performance Modeling of Multi-Processor Embedded Systems for Fast Design Space Exploration. In Multi-Objective Design Space Exploration of Multiprocessor SoC Architectures; Silvano, C., Fornaciari, W., Villar, E., Eds.; Springer: New York, NY, USA, 2011; pp. 19–50. ISBN 978-1-4419-8836-2. [Google Scholar]
- Guo, T.; Tang, S.; Sun, J.; Gong, F.; Liu, X.; Qu, Z.; Zhang, W. A Coupled Thermal-Hydraulic-Mechanical Modeling and Evaluation of Geothermal Extraction in the Enhanced Geothermal System Based on Analytic Hierarchy Process and Fuzzy Comprehensive Evaluation. Appl. Energy 2020, 258, 113981. [Google Scholar] [CrossRef]




| Material Properties | Value | Material Properties | Value |
|---|---|---|---|
| Coal density ρc (kg/m−3) | 1519 | Gas molar mass M (g·mol−1) | 16 |
| Langmuir adsorption constant a (m3·kg−1) | 0.0257 | Langmuir pressure constant b (MPa−1) | 0.5159 |
| Shear modulus G (MPa) | 2570 | Poisson’s ratio ν | 0.27 |
| Gas dynamic viscosity μ (Pa·s) | 1.84 × 10−5 | Initial permeability of coal k0 (m2) | 9.869 × 10−16 |
| Gas diffusion coefficient D (m2·s−1) | 1.2 × 10−11 | Biot coefficient β | 0.3759 |
| Initial porosity φ0 (%) | 8.7989 | Uniaxial compressive strength (MPa) | 13.5 |
| Bulk modulus K (MPa) | 4730 | Shear strain rate τ (s−1) | 1.3992 × 10−3 |
| Gas constant R (J·(mol·K)−1) | 8.3145 | Gas density ρga (kg·m−3) | 0.717 |
| Gas pressure P0 (MPa) | 0.46 |
| Variable | Parameter | −1 | 0 | 1 |
|---|---|---|---|---|
| Borehole diameter (mm) | A | 75 | 94 | 113 |
| Borehole spacing (m) | B | 1 | 2 | 3 |
| Initial permeability (10−16 m2) | C | 1.31 | 5.14 | 8.97 |
| Extraction negative pressure (kPa) | D | 13 | 18 | 23 |
| Run | A-Borehole Diameter (mm) | B-Borehole Spacing (m) | C-Initial Permeability (m2) | D-Extraction Negative Pressure (kPa) | Y1-Effective Extraction Radius (m) | Y2-Area of the Damaged Region (m2) |
|---|---|---|---|---|---|---|
| 1 | 75 | 1 | 5.14 | 18 | 0.7929 | 0.0051 |
| 2 | 113 | 1 | 5.14 | 18 | 0.9894 | 0.0097 |
| 3 | 75 | 3 | 5.14 | 18 | 0.7682 | 0.0051 |
| 4 | 113 | 3 | 5.14 | 18 | 0.8884 | 0.0096 |
| 5 | 94 | 2 | 1.31 | 13 | 0.3449 | 0.0076 |
| 6 | 94 | 2 | 8.97 | 13 | 1.3171 | 0.0068 |
| 7 | 94 | 2 | 1.31 | 23 | 0.3939 | 0.0076 |
| 8 | 94 | 2 | 8.97 | 23 | 1.5404 | 0.0070 |
| 9 | 75 | 2 | 5.14 | 13 | 0.7929 | 0.0053 |
| 10 | 113 | 2 | 5.14 | 13 | 0.8811 | 0.0096 |
| 11 | 75 | 2 | 5.14 | 23 | 0.8800 | 0.0052 |
| 12 | 113 | 2 | 5.14 | 23 | 0.9894 | 0.0099 |
| 13 | 94 | 1 | 1.31 | 18 | 0.3449 | 0.0076 |
| 14 | 94 | 3 | 1.31 | 18 | 0.3312 | 0.0072 |
| 15 | 94 | 1 | 8.97 | 18 | 1.4780 | 0.0069 |
| 16 | 94 | 3 | 8.97 | 18 | 1.5058 | 0.0069 |
| 17 | 75 | 2 | 1.31 | 18 | 0.3137 | 0.0052 |
| 18 | 113 | 2 | 1.31 | 18 | 0.4263 | 0.0096 |
| 19 | 75 | 2 | 8.97 | 18 | 1.3929 | 0.0049 |
| 20 | 113 | 2 | 8.97 | 18 | 1.5576 | 0.0092 |
| 21 | 94 | 1 | 5.14 | 13 | 0.8043 | 0.0071 |
| 22 | 94 | 3 | 5.14 | 13 | 0.7759 | 0.0070 |
| 23 | 94 | 1 | 5.14 | 23 | 0.9626 | 0.0070 |
| 24 | 94 | 3 | 5.14 | 23 | 0.9197 | 0.0071 |
| 25 | 94 | 2 | 5.14 | 18 | 0.8043 | 0.0071 |
| 26 | 94 | 2 | 5.14 | 18 | 0.8043 | 0.0071 |
| 27 | 94 | 2 | 5.14 | 18 | 0.8043 | 0.0071 |
| 28 | 94 | 2 | 5.14 | 18 | 0.8043 | 0.0071 |
| 29 | 94 | 2 | 5.14 | 18 | 0.8043 | 0.0071 |
| Effective Extraction Radius | Sum of Squares | df | Mean Square | F-Value | p-Value | Area of Damage Region | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|
| model | 3.83 | 14 | 0.2734 | 314.32 | <0.0001 | model | 0.0001 | 14 | 4.43 × 10−6 | 185.07 | <0.0001 |
| A-Borehole diameter | 0.0522 | 1 | 0.0522 | 60.02 | <0.0001 | A-Borehole diameter | 0.0001 | 1 | 0.0001 | 2531.51 | <0.0001 |
| B-Borehole spacing | 0.0028 | 1 | 0.0028 | 3.2 | 0.0953 | B-Borehole spacing | 2.96 × 10−8 | 1 | 2.96 × 10−8 | 1.23 | 0.2853 |
| C-Initial permeability | 3.67 | 1 | 3.67 | 4219.59 | <0.0001 | C-Initial permeability | 8.44 × 10−7 | 1 | 8.44 × 10−7 | 35.22 | <0.0001 |
| D-Extraction negative pressure | 0.0494 | 1 | 0.0494 | 56.77 | <0.0001 | D-Extraction negative pressure | 2.84 × 10−8 | 1 | 2.84 × 10−8 | 1.19 | 0.2945 |
| AB | 0.0015 | 1 | 0.0015 | 1.67 | 0.217 | AB | 5.21 × 10−9 | 1 | 5.21 × 10−9 | 0.2173 | 0.6483 |
| AC | 0.0007 | 1 | 0.0007 | 0.7779 | 0.3927 | AC | 2.61 × 10−9 | 1 | 2.61 × 10−9 | 0.1089 | 0.7463 |
| AD | 0.0001 | 1 | 0.0001 | 0.129 | 0.7248 | AD | 4.70 × 10−8 | 1 | 4.70 × 10−8 | 1.96 | 0.1831 |
| BC | 0.0004 | 1 | 0.0004 | 0.4955 | 0.493 | BC | 2.94 × 10−8 | 1 | 2.94 × 10−8 | 1.23 | 0.2868 |
| BD | 0.0001 | 1 | 0.0001 | 0.0608 | 0.8088 | BD | 5.41 × 10−9 | 1 | 5.41 × 10−9 | 0.2256 | 0.6421 |
| CD | 0.0076 | 1 | 0.0076 | 8.72 | 0.0105 | CD | 1.08 × 10−8 | 1 | 1.08 × 10−8 | 0.4517 | 0.5125 |
| A2 | 0.0107 | 1 | 0.0107 | 12.32 | 0.0035 | A2 | 3.56 × 10−7 | 1 | 3.56 × 10−7 | 14.83 | 0.0018 |
| B2 | 0.0046 | 1 | 0.0046 | 5.32 | 0.0369 | B2 | 5.02 × 10−9 | 1 | 5.02 × 10−9 | 0.2093 | 0.6543 |
| C2 | 0.0363 | 1 | 0.0363 | 41.78 | <0.0001 | C2 | 2.30 × 10−12 | 1 | 2.30 × 10−12 | 0.0001 | 0.9923 |
| D2 | 0.0066 | 1 | 0.0066 | 7.55 | 0.0157 | D2 | 4.77 × 10−8 | 1 | 4.77 × 10−8 | 1.99 | 0.18 |
| Residual | 0.0122 | 14 | 0.0009 | Residual | 3.36 × 10−7 | 14 | 2.40 × 10−8 | ||||
| Lack of Fit | 0.0122 | 10 | 0.0012 | 3.38 × 107 | <0.0001 | Lack of Fit | 3.35 × 10−7 | 10 | 3.35 × 10−8 | 1018.71 | <0.0001 |
| Pure Error | 1.44 × 10−10 | 4 | 3.61 × 10−11 | Pure Error | 1.32 × 10−10 | 4 | 3.29 × 10−11 | ||||
| Cor Total | 3.84 | 28 | Cor Total | 0.0001 | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Lei, X.; Zhang, L.; Long, H.; Ji, P.; Wang, L.; Ding, Y.; Wang, C. Study on Gas Pre-Extraction Law of Along-Layer Boreholes Based on Thermo-Hydro-Mechanical-Damage Coupled Model. Mathematics 2025, 13, 3375. https://doi.org/10.3390/math13213375
Hu B, Lei X, Zhang L, Long H, Ji P, Wang L, Ding Y, Wang C. Study on Gas Pre-Extraction Law of Along-Layer Boreholes Based on Thermo-Hydro-Mechanical-Damage Coupled Model. Mathematics. 2025; 13(21):3375. https://doi.org/10.3390/math13213375
Chicago/Turabian StyleHu, Biao, Xuyang Lei, Lu Zhang, Hang Long, Pengfei Ji, Lianmeng Wang, Yonghao Ding, and Cuixia Wang. 2025. "Study on Gas Pre-Extraction Law of Along-Layer Boreholes Based on Thermo-Hydro-Mechanical-Damage Coupled Model" Mathematics 13, no. 21: 3375. https://doi.org/10.3390/math13213375
APA StyleHu, B., Lei, X., Zhang, L., Long, H., Ji, P., Wang, L., Ding, Y., & Wang, C. (2025). Study on Gas Pre-Extraction Law of Along-Layer Boreholes Based on Thermo-Hydro-Mechanical-Damage Coupled Model. Mathematics, 13(21), 3375. https://doi.org/10.3390/math13213375






