Piecewise Analytical Approximation Methods for Initial-Value Problems of Nonlinear Ordinary Differential Equations

Abstract

Piecewise analytical solutions to scalar, nonlinear, first-order, ordinary differential equations based on the second-order Taylor series expansion of their right-hand sides that result in Riccati’s equations are presented. Closed-form solutions are obtained if the dependence of the right-hand side on the independent variable is not considered; otherwise, the solution is given by convergent series. Discrete solutions also based on the second-order Taylor series expansion of the right-hand side and the discretization of the independent variable that result in algebraic quadratic equations are also reported. Both the piecewise analytical and discrete methods are applied to two singularly perturbed initial-value problems and the results are compared with the exact solution and those of linearization procedures, and implicit and explicit Taylor’s methods. It is shown that the accuracy of piecewise analytical techniques depends on the number of terms kept in the series expansion of the solution, whereas that of the discrete methods depends on the location where the coefficients are evaluated. For Riccati equations with constant coefficients, the piecewise analytical method presented here provides the exact solution; it also provides the exact solution for linear, first-order ordinary differential equations with constant coefficients.

1. Introduction

Nonlinear, first-order ordinary differential equations arise in numerous science and engineering models, such as lumped models in heat and mass transfer [1,2,3,4], blood perfusion [5], electrical circuits, chemical kinetics modeling [6], combustion, pyrolysis [7], bubble dynamics [8,9], etc. Despite a large body of research, e.g., [10,11,12,13], most of these equations do not have closed-form analytical solutions. As a consequence, they are frequently solved by means of finite-difference methods that provide discrete solutions at fixed times. However, piecewise analytical approximations to the solution of these equations may be obtained by linearization [14,15,16] and approximating their right-hand sides by the constant and linear terms of their Taylor series expansions. This linearization results in piecewise exponential solutions, requires the existence of the first-order partial derivatives of the right-hand side of the ordinary differential equation with respect to both the independent and dependent variables, and has been used in the development of exponential integrators, e.g., [17], that integrate exactly the linear terms and use quadrature rules for the nonlinear ones [17,18,19]. For systems of nonlinear, first-order ordinary differential equations, linearization results in matrix exponentials.

In this paper, piecewise approximate analytical solutions to scalar, first-order, nonlinear ordinary differential equations based on second-order Taylor’s approximations of the right-hand side are presented. These approximations require the existence of the second-order derivatives of the right-hand side with respect to the dependent and independent variables, and result in Riccati equations whose solutions are obtained analytically in terms of series if the coefficients of the Riccati equation are not constant and in closed form if they are assumed to be piecewise constant; these piecewise analytical solutions coincide with the exact ones if the coefficients of the generalized Riccati equation are constant. If the second-order derivatives of the right-hand side are not considered, the methods presented in this paper reduce to the linearization techniques described in the previous paragraph, and these linearization techniques provide the exact solution for first-order, linear ordinary differential equations with constant coefficients.

Riccati equations have played an important role in mathematical finance [20] where symbolic computations have been used to classify solutions to an important class of mathematical finance models [21]; control theory, separation of variables, and continued fractions [22,23]; integrability [24]; nonlinear wave propagation [25,26,27]; Painlevé equations, nonlinear special functions, and orthogonal polynomials [28,29], etc. In addition, Riccati hierarchies may be treated by means of Painlevé and symmetry analysis, e.g., [30,31,32].

Finite-difference methods based on the second-order Taylor’s approximations of the right-hand side are also presented in this paper. These methods result in quadratic equations and provide finite-difference equations whose solutions are compared with those of the continuous techniques presented herein.

The manuscript has been arranged as follows. In Section 2 and Section 3, piecewise analytical approximate solutions based on the second-order Taylor series expansion of the right-hand side of the first-order, nonlinear ordinary differential equations are reported for the cases where the dependence of the coefficients on the independent variable is and is not considered, respectively. The explicit finite-difference expressions or nonlinear, one-dimensional mappings corresponding to the piecewise analytical presented in Section 2 and Section 3 are summarized in Section 4. Explicit finite-difference methods based on the quadratic approximations of the right-hand side presented in Section 2 and Section 3 are reported in Section 5 and Section 6, respectively. It is important to keep in mind that the finite-difference equations presented in Section 2, Section 3 and Section 4 are based on continuous solutions, whereas those of Section 5 and Section 6 are based on the discretization of both the dependent and independent variables. Some results for two singularly perturbed problems are presented in Section 7 where the accuracy of continuous and discrete approximations is assessed by comparing them with the exact solution. A final section on conclusions summarizes the most important findings of the paper. For the sake of convenience, continuous and discrete approximations based on linear approximations of the right-hand side of the ordinary differential equations are collected in Appendix A and Appendix B, while Appendix C presents three well-known explicit Taylor’s methods.

2. Piecewise Continuous Solutions Based on Quadratic Approximations

Consider the following nonlinear, initial-value problem:

$${\displaystyle \frac{dy}{dx}}=f(x,y),x>0,y\left(0\right)=y_0,y\in \Re ,$$

(1)

where x and y denote the independent (time) and dependent variables, respectively, $f(x,y)$ is a nonlinear function of both x and y, and $y_0$ denotes a constant (initial) value.

Let the time interval $[0,L]$ ($L>0$) be divided into N non-overlapping subintervals $I_n=[x^n,x^{n+1}]$ with $x^0=0$, $x^{n+1}>x^n$ and $x^N=L$, and, in each subinterval $I_n$, approximate the right-hand side of Equation (1) by its second-order Taylor series expansion about $(x^n,y^n)$, i.e., Equation (1) is approximated by

$${\displaystyle \frac{dY}{dX}}=P^n\left(X\right)+Q^n\left(X\right)Y+H^n{Y}^2,x\in (x^n,x^{n+1}],$$

(2)

where $X\equiv x-x^n\in (0,x^{n+1}-x^n]$, $Y\equiv y-y^n$,

$$\begin{array}{cc}\hfill & P^n\left(X\right)=f^n+A^{n}X+B^n{X}^2,Q^n\left(X\right)=J^n+C^{n}X,H^n={\displaystyle \frac{1}{2}}{f}_{yy}(x^n,y^n),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & f^n=f(x^n,y^n),A^n=f_x(x^n,y^n),B^n={\displaystyle \frac{1}{2}}{f}_{xx}(x^n,y^n),\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & J^n=f_y(x^n,y^n),C^n=f_{xy}(x^n,y^n),\hfill \end{array}$$

(5)

$y^n=y\left(x^n\right)$, $f_r={\displaystyle \frac{\partial f}{\partial r}}$, $f_{pq}={\displaystyle \frac{{\partial }^{2}f}{\partial p\partial q}}$, and $Y(X=0)=Y^n=0$.

Equation (2) is the (generalized) Riccati equation [33,34,35], which may transformed into a second-order, linear, ordinary differential equation [33,36,37]. However, very few analytical solutions to the generalized Riccati equation are available in the literature [10,11,12,13].

2.1. Piecewise Continuous Solutions of the Generalized Riccati Equation (2) for $H^n=0$

If $H^n=0$ in the generalized Riccati Equation (2), then a linear ordinary differential equation is obtained whose solution may be written as

$$Y\left(X\right)={\int }_0^X{P}^n\left(s\right)exp(U\left(X\right)-U\left(s\right))ds,$$

(6)

where $U\left(X\right)=J^{n}X+{\displaystyle \frac{1}{2}}{C}^n{X}^2$.

For $H^n=0$, $C^n=0$ and $J^n\ne 0$, Equation (6) becomes

$$Y\left(X\right)=V^{n}exp\left(J^{n}X\right)-{\displaystyle \frac{1}{J^n}}\left(f^n+A^n\left(X+{\displaystyle \frac{1}{J^n}}\right)+B^n\left(X^2+{\displaystyle \frac{2}{J^n}}\left(X+{\displaystyle \frac{1}{J^n}}\right)\right)\right),$$

(7)

where

$$V^n={\displaystyle \frac{1}{J^n}}\left(f^n+{\displaystyle \frac{A^n}{J^n}}+B^n{\displaystyle \frac{2}{{\left(J^n\right)}^2}}\right).$$

(8)

For $H^n=0$, $C^n=0$ and $J^n=0$, the solution to Equation (6) is

$$Y\left(X\right)=\left(f^n+{\displaystyle \frac{1}{2}}{A}^{n}X+{\displaystyle \frac{1}{3}}{B}^n{X}^2\right)X.$$

(9)

On the other hand, if $H_n=0$ and $C_n>0$, Equation (6) may be written as

$$Y\left(X\right)=exp\left({\alpha }^n{z}^2\right)\left({\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{\pi }{{\alpha }^n}}}\left(p^n+{\displaystyle \frac{r^n}{2{\alpha }^n}}\right)(M\left(z^{+}\right)-M\left(z^{-}\right))-(N\left(z^{+}\right)-N\left(z^{-}\right))\right),$$

(10)

where

$$\begin{array}{cc}\hfill p^n& =f^n+A^n{\displaystyle \frac{J^n}{C^n}}+B^n{\left({\displaystyle \frac{J^n}{C^n}}\right)}^2,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill q^n& =A^n+2B^n{\displaystyle \frac{J^n}{C^n}},r^n=B^n,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill M\left(z\right)& =erf\left(z\sqrt{{\alpha }^n}\right),N\left(z\right)={\displaystyle \frac{1}{2{\alpha }^n}}(r^{n}z+q^n)exp(-{\alpha }^n{z}^2),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill z& =z^{+}=X+{\displaystyle \frac{J^n}{C^n}},z^{-}={\displaystyle \frac{J^n}{C^n}},{\alpha }^n={\displaystyle \frac{1}{2}}{C}^n,\hfill \end{array}$$

(14)

and $erf\left(z\right)={\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_0^{\infty }{e}^{-z^2}dz$ is the error function integral.

For $H_n=0$ and $C_n<0$, Equation (6) may be written as

$$Y\left(X\right)=exp\left({\alpha }^n{z}^2\right)\left({\displaystyle \frac{1}{2}}\sqrt{{\displaystyle \frac{\pi }{-{\alpha }^n}}}\left(p^n-{\displaystyle \frac{r^n}{-2{\alpha }^n}}\right)(M\left(z^{+}\right)-M\left(z^{-}\right))+N\left(z^{+}\right)-N\left(z^{-}\right)\right),$$

(15)

where

$$M\left(z\right)=erfi\left(z\sqrt{-{\alpha }^n}\right),N\left(z\right)={\displaystyle \frac{1}{2{\alpha }^n}}(r^{n}z+q^n)exp(-{\alpha }^n{z}^2),$$

(16)

$erfi\left(z\right)=-\mathrm{i}erf\left(\mathrm{i}z\right)={\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_0^{\infty }{e}^{z^2}dz$ is related to Dawson’s integral or function $F\left(x\right)={\displaystyle \frac{\sqrt{\pi }}{2}}{e}^{-x^2}erfi\left(x\right)$ [10,38,39,40,41] and ${\mathrm{i}}^2=-1$.

2.2. Piecewise Continuous Solutions of the Generalized Riccati Equation (2) for $H^n\ne 0$

For $H^n\ne 0$, Equation (2) is a (generalized) Riccati equation with polynomial coefficients of the independent variable which may not have a closed-form compact analytical solution. However, its solution may be obtained as a series, as follows. First, by introducing

$$Y\left(X\right)=\mu {\displaystyle \frac{w^{\prime }\left(X\right)}{w\left(X\right)}},$$

(17)

where the prime denotes differentiation with respect to X and $\mu =-{\displaystyle \frac{1}{H^n}}$, Equation (2) becomes the following linear second-order ordinary differential equation:

$$w^{″}-Q^n\left(X\right)w^{\prime }+H^n{P}^n\left(X\right)w=0.$$

(18)

For the sake of convenience and in order to avoid the cumbersome use of superscripts, hereon, we shall use the following nomenclature:

$$\begin{array}{cc}\hfill Q^n\left(X\right)& =J^n+C^{n}X\equiv \delta +ϵX,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill P^n\left(X\right)& =(f^n+B^{n}X+C^n{X}^2)H^n\equiv \alpha +\beta X+\gamma X^2,\hfill \end{array}$$

(20)

which, when substituted into Equation (2) together with

$$w\left(X\right)=\sum _{k=0}^{\infty }{a}_k{X}^k,$$

(21)

results in the following sequence of equations for the coefficients $a_k$

$$\begin{array}{cc}\hfill & 2a_2-\delta a_1+\alpha a_0=0,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & 6a_3-2\delta a_2+(\alpha -ϵ)a_1+\beta a_0=0,\hfill \end{array}$$

(23)

and, for $k\ge 2$,

$$(k+2)(k+1)a_{k+2}-(k+1)\delta a_{k+1}+(\alpha -kϵ)a_k+\beta a_{k-1}+\gamma a_{k-2}=0.$$

(24)

With Equations (22)–(24), it is an easy exercise to show that, for $k\ge 2$,

$$a_k=a_{k0}{a}_0+a_{k1}{a}_1,$$

(25)

where, for example,

$$\begin{array}{cc}\hfill & a_{20}=-{\displaystyle \frac{\alpha }{2}},a_{21}=-{\displaystyle \frac{\delta }{2}},\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & a_{30}=-{\displaystyle \frac{1}{6}}(\alpha \delta +\beta ),a_{31}=-{\displaystyle \frac{1}{6}}({\delta }^2-\alpha +ϵ),\hfill \end{array}$$

(27)

and all $a_k$s for $k>2$ may be written as linear combinations of $a_0$ and $a_1$. This means that $w\left(X\right)$ (cf. Equation (21)) may be written as

$$w\left(X\right)=a_0{S}_0\left(X\right)+a_1{S}_1\left(X\right),$$

(28)

where

$$\begin{array}{c}\hfill S_0\left(X\right)=1+a_{20}{X}^2+a_{30}{X}^3+\mathcal{O}\left(X^4\right),\end{array}$$

(29)

$$\begin{array}{c}\hfill S_1\left(X\right)=X(1+a_{21}X+a_{31}{X}^2+\mathcal{O}\left(X^4\right)),\end{array}$$

(30)

and the coefficients $a_{k0}$ and $a_{k1}$ for $k\ge 2$ may be easily obtained from Equations (22)–(27).

The use of Equations (28)–(30) in Equation (20) yields

$$Y\left(X\right)=\mu {\displaystyle \frac{w^{\prime }\left(X\right)}{w\left(X\right)}}=-{\displaystyle \frac{1}{H^n}}{\displaystyle \frac{S_0^{\prime }\left(X\right)+F{S}_1^{\prime }\left(X\right)}{S_0\left(X\right)+F{S}_1\left(X\right)}},$$

(31)

where $F={\displaystyle \frac{a_1}{a_0}}$ is an unknown constant.

Use of the (initial) condition $Y\left(0\right)=0$ in Equation (31) results in the following expression:

$$Y\left(X\right)=\mu {\displaystyle \frac{W^{\prime }\left(X\right)}{W\left(X\right)}}=-{\displaystyle \frac{1}{H^n}}{\displaystyle \frac{S_0^{\prime }\left(X\right)}{S_0\left(X\right)}},$$

(32)

which contains the ratio of two series; both of them are convergent because the point $X=0$ is a regular point for the ordinary differential Equation (18).

3. Piecewise Continuous Solutions Based on Quadratic Approximations with Frozen Coefficients

As shown in the previous subsection, the solution to Equation (2) for $H^n\ne 0$, i.e., Equation (32), is given by the ratio of two series. This is a consequence of the fact that the coefficients $A^n$, $B^n$ and $C^n$ in Equations (4) and (5) which arise through $f_x$ and $f_{xx}$, and $f_{xy}$, respectively, account for the dependence of $f(x,y)$ on x. However, if we assume that, in each interval $I_n$, $f(x,y)$ is approximated by $f(x^{*},y)$, where $x^{*}\in [x^n,x^{n+1}]$, then by using a second-order Taylor series expansion for $f(x^{*},y)$ around $y^n$, Equation (1) may be approximated by

$${\displaystyle \frac{dY}{dX}}=P^n+Q^{n}Y+H^n{Y}^2,x\in (x^n,x^{n+1}],X\in (0,x^{n+1}-x^n],$$

(33)

where (abusing notation) $P^n=f(x^{*},y^n)$, $Q^n=f_y(x^{*},y^n)$ and $H^n={\displaystyle \frac{1}{2}}{f}_{yy}(x^{*},y^n)$ are now constant in each subinterval $I_n$. Hereon, we shall refer to the approximation methods that do not account for $f_x$, $f_{xy}$ and $f_{xx}$ as piecewise continuous frozen-coefficient techniques based on quadratic approximations for the dependent variable.

3.1. Piecewise Continuous Solutions for $H^n=0$

If $H^n=0$ and $Q^n=f_y(x^{*},y^n)\ne 0$, the solution to Equation (33) subject to $Y\left(0\right)=0$ is

$$Y\left(X\right)={\displaystyle \frac{P^n}{Q^n}}\left(exp\left(Q^{n}X\right)-1\right),$$

(34)

which is used in the development of exponential integrators, e.g., [14,17,42]. On the other hand, for $H^n=0$ and $Q^n=0$, the solution to Equation (33) subject to $Y\left(0\right)=0$ is

$$Y\left(X\right)=P^{n}X,$$

(35)

which yields Euler’s forward or explicit method for $x^{*}=x^n$ and $X^{n+1}=h$, where h is the step size.

3.2. Piecewise Continuous Solutions for $H^n\ne 0$

If $H^n\ne 0$, Equation (33) is a constant-coefficient Riccati equation whose solution may be obtained by using Equation (17), which results in the following constant-coefficient, linear, second-order ordinary differential equation

$$W^{″}-Q^n{W}^{\prime }+P^n{H}^{n}W=0,$$

(36)

whose solution depends on the sign of the radicand ${\left(Q^n\right)}^2-4P^n{Q}^n$, as discussed next.

If the radicand is positive, then Equations (36) and (17) subject to $Y\left(0\right)=0$ yield

$$Y\left(X\right)=y\left(x\right)-y\left(x^n\right)=-P^n{\displaystyle \frac{1-exp\left(({\lambda }^{-}-{\lambda }^{+})X\right)}{{\lambda }^{-}-{\lambda }^{+}exp\left(({\lambda }^{-}-{\lambda }^{+})X\right))}},$$

(37)

where ${\lambda }^{\pm }={\displaystyle \frac{1}{2}}(-Q^n\pm \sqrt{{\left(Q^n\right)}^2-4P^n{Q}^n})$, while if the radicand is nil,

$$Y\left(X\right)=y\left(x\right)-y\left(x^n\right)={\displaystyle \frac{{\lambda }^2}{H^n}}{\displaystyle \frac{X}{1-\lambda X}}=P^n{\displaystyle \frac{X}{1-\lambda X}},$$

(38)

where $\lambda =-{\displaystyle \frac{Q^n}{2}}$.

If the radicand is negative, then the solution to Equations (36) and (17) subject to $Y\left(0\right)=0$ is

$$Y\left(X\right)=y\left(x\right)-y\left(x^n\right)=P^n{\displaystyle \frac{sin\left(\omega X\right)}{\omega cos\left(\omega X\right)-\lambda sin\left(\omega X\right)}},$$

(39)

where $\lambda =-{\displaystyle \frac{Q^n}{2}}$ and $\omega =\sqrt{4P^n{H}^n-{\left(Q^n\right)}^2}$.

4. Discrete Mappings/Finite-Difference Techniques for Piecewise Continuous Methods Based on Quadratic Approximations

The solutions corresponding to Equations (7), (9), (32), (34), (35) and (37)–(39) result in the following one-dimensional mappings or explicit finite-difference equations:

$$\begin{array}{cc}\hfill & y^{n+1}=y^n+{\displaystyle \frac{1}{J^n}}\left(f^n+{\displaystyle \frac{A^n}{J^n}}+B^n{\displaystyle \frac{2}{{\left(J^n\right)}^2}}\right)(exp\left(J^{n}h\right)-1)-{\displaystyle \frac{h}{J^n}}\left(A^n+2B^n{\displaystyle \frac{h}{J^n}}\right)h,\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill & y^{n+1}=y^n+\left(f^n+{\displaystyle \frac{1}{2}}{A}^{n}h+{\displaystyle \frac{1}{3}}{B}^n{h}^2\right)h,\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill & y^{n+1}=y^n-{\displaystyle \frac{1}{H^n}}{\displaystyle \frac{S_0^{\prime }\left(h\right)}{S_0\left(h\right)}},\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & y^{n+1}=y^n+{\displaystyle \frac{P^n}{Q^n}}\left(exp\left(Q^{n}h\right)-1\right),\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & y^{n+1}=y^n+P^{n}h,\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill & y^{n+1}=y^n-P^n{\displaystyle \frac{1-exp\left(({\lambda }^{-}-{\lambda }^{+})h\right)}{{\lambda }^{-}-{\lambda }^{+}exp\left(({\lambda }^{-}-{\lambda }^{+})h\right))}},\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill & y^{n+1}=y^n+{\displaystyle \frac{{\lambda }^2}{P^n{H}^n}}{\displaystyle \frac{h}{1-\lambda h}}=y^n+P^n{\displaystyle \frac{2h}{2-Q^{n}h}},\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & y^{n+1}=y^n+P^n{\displaystyle \frac{sin\left(\omega h\right)}{\omega cos\left(\omega h\right)-\lambda sin\left(\omega h\right)}},\hfill \end{array}$$

(47)

respectively, where $h=x^{n+1}-x^n$ is the step size.

Equations (10) and (15) also result in one-dimensional mappings that are not reported here. Note, however, that these mappings involve the error function and the erfi function.

For autonomous differential equations, i.e., $f(x,y)=f\left(y\right)$, $A^n=B^n=C^n=0$, $P^n=f^n=\alpha$, and $Q^n=0$, all the above mappings preserve the fixed points of the original differential equation, i.e., Equation (1).

For the sake of convenience, we shall refer to the finite-difference Equation (42) as CRsm where C, R and s denote continuous, Riccati/quadratic, and series, respectively, and m stands for a natural number that corresponds to the number of terms of the series $S_0\left(X\right)$ used in these methods (cf. Equations (29) and (32)); CR corresponds to Equation (2) when $f(x,y)$ does not depend on x. We shall also refer to Equations (45)–(47) as CRF, where F stands for frozen, i.e., the dependence of $f(x,y)$ on x has not been considered (cf. Equation (33)). Furthermore, we shall refer to Equation (42) with $A^n=B^n=C^n=0$ (cf. Equations (4) and (5)) as CRFsm. For both CRF and CRFsm, $A^n=B^n=C^n=0$; however, the former employs the exact solutions given by Equations (45)–(47) (cf. Equations (37)–(39)), whereas the latter employs Equations (32) and (42) which depend on the series $S_0\left(X\right)$. This means that the solutions provided by CRF and CRFsm will in general differ because the latter make use of a finite number of terms in $S_0\left(X\right)$ (cf. Equation (29)). Moreover, CRF and CR are identical if $f(x,y)$ does not depend on x.

5. Discrete Methods Based on Quadratic Approximations

The use of a $\theta$-method in Equation (1) in the interval $I_n$ yields

$$\Delta y=h(\theta f(x^{n+1},y^{n+1})+(1-\theta )f(x^n,y^n)),$$

(48)

where $\Delta y=y^{n+1}-y^n$, $0\le \theta \le 1$. $\theta =0$, ${\displaystyle \frac{1}{2}}$ and 1 correspond to the well-known Euler’s forward or explicit, trapezoidal and Euler’s backward or implicit methods, respectively; the latter two techniques result in nonlinear algebraic equations if $f(x,y)$ is a nonlinear function of y and their corresponding finite-difference expressions must be solved iteratively by means of, for example, the Newton–Raphson technique. Hereon, we shall refer to the implicit, finite-difference expressions corresponding to Equation (48) for $\theta ={\displaystyle \frac{1}{2}}$ and 1 as Dt and either D or Dn which are $\mathcal{O}\left(h^2\right)$ and $\mathcal{O}\left(h\right)$ accurate, respectively, where D, t and n stand for discrete, trapezoidal, and implicit, respectively.

5.1. Discrete Methods Based on Quadratic Approximations for $P\ne 0$

In this section, some methods based on the approximation of $f(x^{n+1},y^{n+1})$ by its second-order Taylor expansion, i.e.,

$$f(x^{n+1},y^{n+1})\approx f^n+f_x^{n}h+f_y^n\Delta y+{\displaystyle \frac{1}{2}}(f_{xx}^n{h}^2+2f_{xy}^{n}h\Delta y+f_{yy}^n\Delta y^2),$$

(49)

are presented, where $F^n=F(x^n,y^n)$.

Substitution of Equation (49) into Equation (48) yields the following quadratic expression:

$$P\Delta y^2+Q\Delta y+R=0,$$

(50)

where

$$P={\displaystyle \frac{1}{2}}{f}_{yy}^n,Q=\theta (f_y^n+f_{xy}^{n}h)-{\displaystyle \frac{1}{h}},R=f^n+\theta h\left(f_x^n+{\displaystyle \frac{1}{2}}h{f}_{xx}^n\right).$$

(51)

If $P\ne 0$, the two roots of Equation (50) may be easily determined; they are real provided that $Q^2-4PR\ge 0$, and the valid root may be easily determined by Taylor series expansion of the radicand. Hereon, we shall refer to the finite-difference methods corresponding to Equations (50) and (51) as DRn and DRt for $\theta =1$ and ${\displaystyle \frac{1}{2}}$, respectively, where R stands for Riccati (quadratic). Note that Equation (50) provides $\Delta y$ in an explicit manner.

5.2. Discrete Methods Based on Quadratic Approximations for $P=0$ and $Q\ne 0$

If $P=0$ and $Q\ne 0$, Equation (50) is linear and provides the following solution:

$$y^{n+1}=y^n-{\displaystyle \frac{R}{Q}},$$

(52)

which accounts for the dependence of the solution on $f_x$, $f_{xy}$ and $f_{xx}$ through Equations (50) and (51) for $0<\theta \le 1$.

The explicit finite-difference methods corresponding to Equation (52) will be referred to as DLn and DLt for $\theta =1$ and ${\displaystyle \frac{1}{2}}$, respectively, where L stands for linear; these methods account for the dependence of $f(x,y)$ on x, as indicated in Equation (51).

If such a dependence is not considered, i.e., if $f(x^{n+1},y^{n+1})$ is approximated by

$$f(x^{n+1},y^{n+1})\approx f^n+f_y^n\Delta y,$$

(53)

where $F^n=F(x^n,y^n)$, then Equation (50) or (52) yields

$$y^{n+1}=y^n-{\displaystyle \frac{f^n}{\theta h{f}_y^n-1}},$$

(54)

which results in the first-order accurate Euler’s forward or explicit method for $\theta =0$. The explicit finite-difference Equation (54) will be referred to as DLFn and DLFt for $\theta =1$ and ${\displaystyle \frac{1}{2}}$, respectively.

6. Discrete Methods Based on Frozen-Coefficient Approximations

Equation (51) shows that Q and R depend on $f_{xy}^n$, and $f_x^n$ and $f_{xx}^n$, respectively. If these three terms are not considered in Equation (49), Equation (51) remains valid and the resulting finite-difference methods will be referred to as DRFn and DRFt for $\theta =1$ and ${\displaystyle \frac{1}{2}}$, respectively, where F stands for frozen, i.e., $f(x^{n+1},y^{n+1})$ is approximated by the second-order Taylor expansion (compared with Equation (49))

$$f(x^{n+1},y^{n+1})\approx f^{(n+1,n)}+f_y^{(n+1,n)}\Delta y+{\displaystyle \frac{1}{2}}{f}_{yy}^{(n+1,n)}\Delta y^2,$$

(55)

where $F^{(n+1,n)}=F(x^{n+1},y^n)$.

In the interval $I_n$, Equation (1) may also be approximated by

$${\displaystyle \frac{dy}{dx}}\approx f(x^{*},y^{*}),$$

(56)

where $x^{*}\in I_n$.

If $x^{*}=x^n$, first-order discretization of Equation (56) results in the well-known Euler’s explicit or forward method, i.e.,

$$y^{n+1}=y^n+h{f}^n,f^n=f(x^n,y^n),$$

(57)

whereas for $x^n<x^{*}\le x^{n+1}$, the discretization of Equation (56) yields

$$y^{n+1}=y^n+h(f(x^{*},y^n)+f_y(x^{*},y^n)(y^{*}-y^n)),$$

(58)

which, for $x^{*}=x^{n+1}$, yields

$$y^{n+1}=y^n+h(f(x^{n+1},y^n)+f_y(x^{n+1},y^n)(y^{n+1}-y^n)),$$

(59)

and, for $x^{*}=x^{n+{\displaystyle \frac{1}{2}}}$,

$$y^{n+1}=y^n+h(f(x^{n+{\displaystyle \frac{1}{2}}},y^n)+{\displaystyle \frac{1}{2}}{f}_y(x^{n+{\displaystyle \frac{1}{2}}},y^n)),$$

(60)

where $y^{n+{\displaystyle \frac{1}{2}}}$ has been approximated by ${\displaystyle \frac{1}{2}}(y^n+y^{n+1})$.

Equations (59) and (60) provide the following explicit finite-difference expressions:

$$y^{n+1}=y^n+h{\displaystyle \frac{f(x^{n+1},y^n)}{1-h{f}_y(x^{n+1},y^n)}},$$

(61)

and

$$y^{n+1}=y^n+2h{\displaystyle \frac{f(x^{n+\frac{1}{2}},y^n)}{2-h{f}_y(x^{n+\frac{1}{2}},y^n)}},$$

(62)

which we will refer to as DLFnp1 and DLFmp, respectively, where np1 and mp stand for $n+1$ and the midpoint, i.e., $n+{\displaystyle \frac{1}{2}}$, respectively.

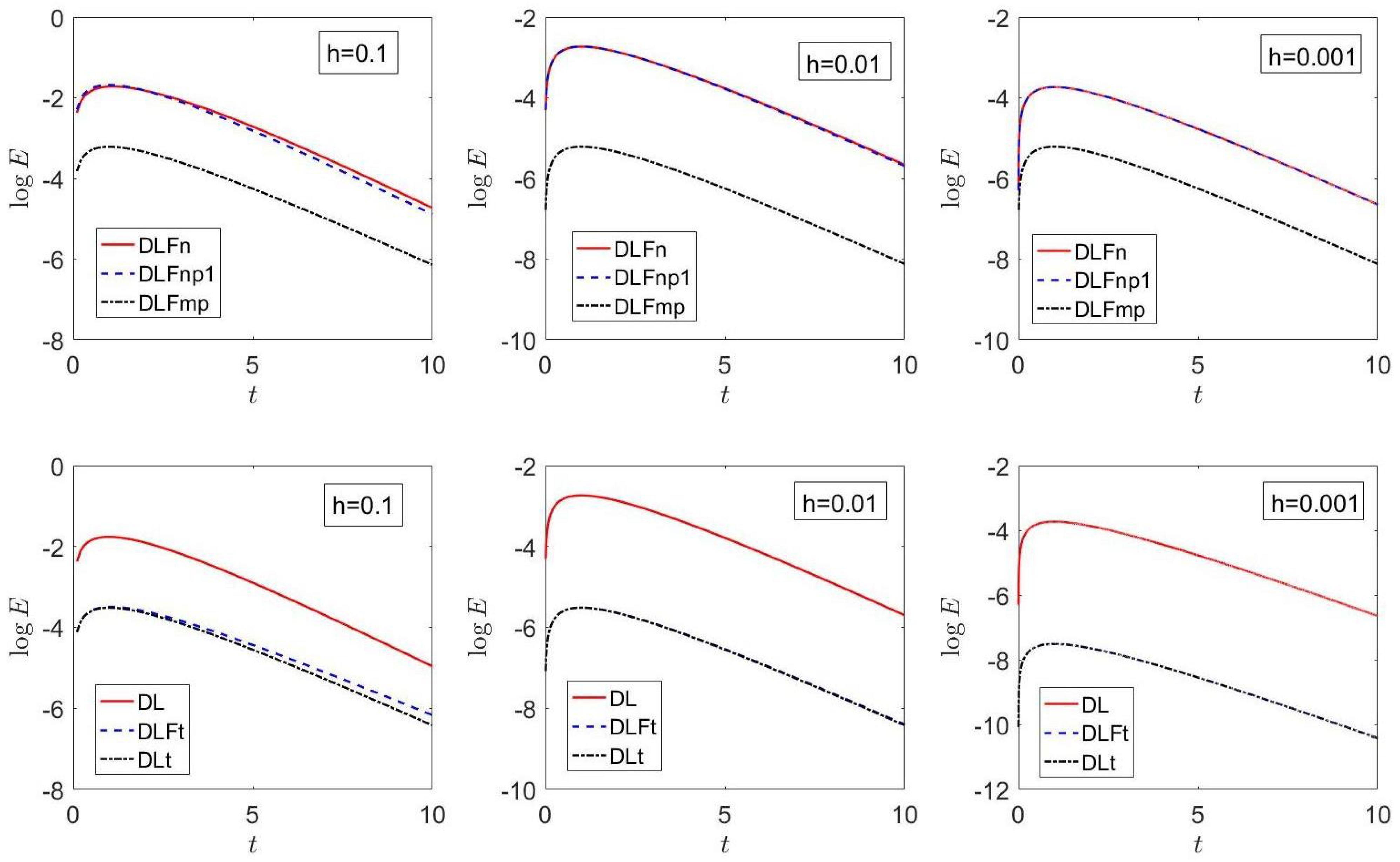
7. Results

As indicated in Section 2, Section 3, Section 4, Section 5 and Section 6, a large variety of continuous and discrete methods for the solution of scalar, first-order, nonlinear ordinary differential equations have been developed in this manuscript. In order to ease the reading of this section where the accuracy of some of the methods presented in this paper is reported for two singularly perturbed initial-value problems that have exact solutions, it seems convenient to recall that the techniques reported here have been identified by some letters and numbers whose meaning is as follows: C and D refer to the continuous and discrete formulations presented in Section 2, Section 3 and Section 4 and Section 5 and Section 6, respectively; F indicates that the dependence on the independent variable is not accounted for, but may change in each interval of integration; and L and R indicate first- and second-order Taylor series expansions, respectively, of the right-hand side of Equation (1) (cf. Section 2, Section 3 and Section 4) or linear and quadratic approximations of the dependent variable (cf. Section 5 and Section 6), respectively. Other symbols such as n indicate that the Taylor series expansion or approximation is evaluated at the n-th time level. Furthermore, the figures and tables for each example are presented in the corresponding subsection. In addition, in the tables, the section or appendix where the methods have been presented is also reported.

Unless stated otherwise, all the results presented in this section were obtained using a constant step size. It must be noted, however, that, since both the piecewise analytical and discrete methods presented in this paper make use of the first- and/or second-order derivatives of $f(x,y)$ with respect to x and y, the step size could be controlled according to the magnitude of these derivatives, thus resulting in step-adaptive procedures. However, adaptive procedures are not reported in this paper.

7.1. Example 1

Here, we consider the following (autonomous) singularly perturbed, Bernoulli equation:

$$ϵ{\displaystyle \frac{dy}{dt}}=-{\displaystyle \frac{1}{80}}(y^2-20y),t>0,$$

(63)

subject to $y\left(0\right)=1$, whose exact solution is

$$y\left(t\right)={\displaystyle \frac{20}{1+19exp\left(-\frac{t}{4ϵ}\right)}},$$

(64)

and $0<ϵ<<1$.

Equation (63) exhibits an initial layer of thickness $\mathcal{O}\left(ϵ\right)$ and has two fixed points $y=0$ and $y=20$ which are unstable and stable, respectively. Upon introducing $\tau \equiv {\displaystyle \frac{t}{ϵ}}$, Equation (63) becomes

$${\displaystyle \frac{dy}{d\tau }}=-{\displaystyle \frac{1}{80}}(y^2-20y),$$

(65)

also subject to $y\left(0\right)=0$. Furthermore, upon using $z\equiv {\displaystyle \frac{1}{y}}$, Equation (63) becomes the following linear, constant-coefficient, first-order ordinary differential equation:

$$ϵ{\displaystyle \frac{dz}{dt}}={\displaystyle \frac{1}{80}}(1-20z),$$

(66)

subject to $z\left(0\right)=1$.

The errors of some of the continuous and discrete approximate methods presented in Section 2, Section 3 and Section 4 and Section 5 and Section 6, respectively, and in Appendix A, Appendix B and Appendix C for Equation (63) are reported in Figure 1 and Figure 2 and

Table 1. Largest values of $e\left(t\right)\equiv logE=log|y\left(t\right)-y_{ex}\left(t\right)|$ for some piecewise analytical continuous and discrete methods and different values of ${\displaystyle \frac{ϵ}{h}}$ for Example 1. (The Sect/App column indicates the section or appendix where the methods listed in the first column appear; the subscript $ex$ stands for exact solution).

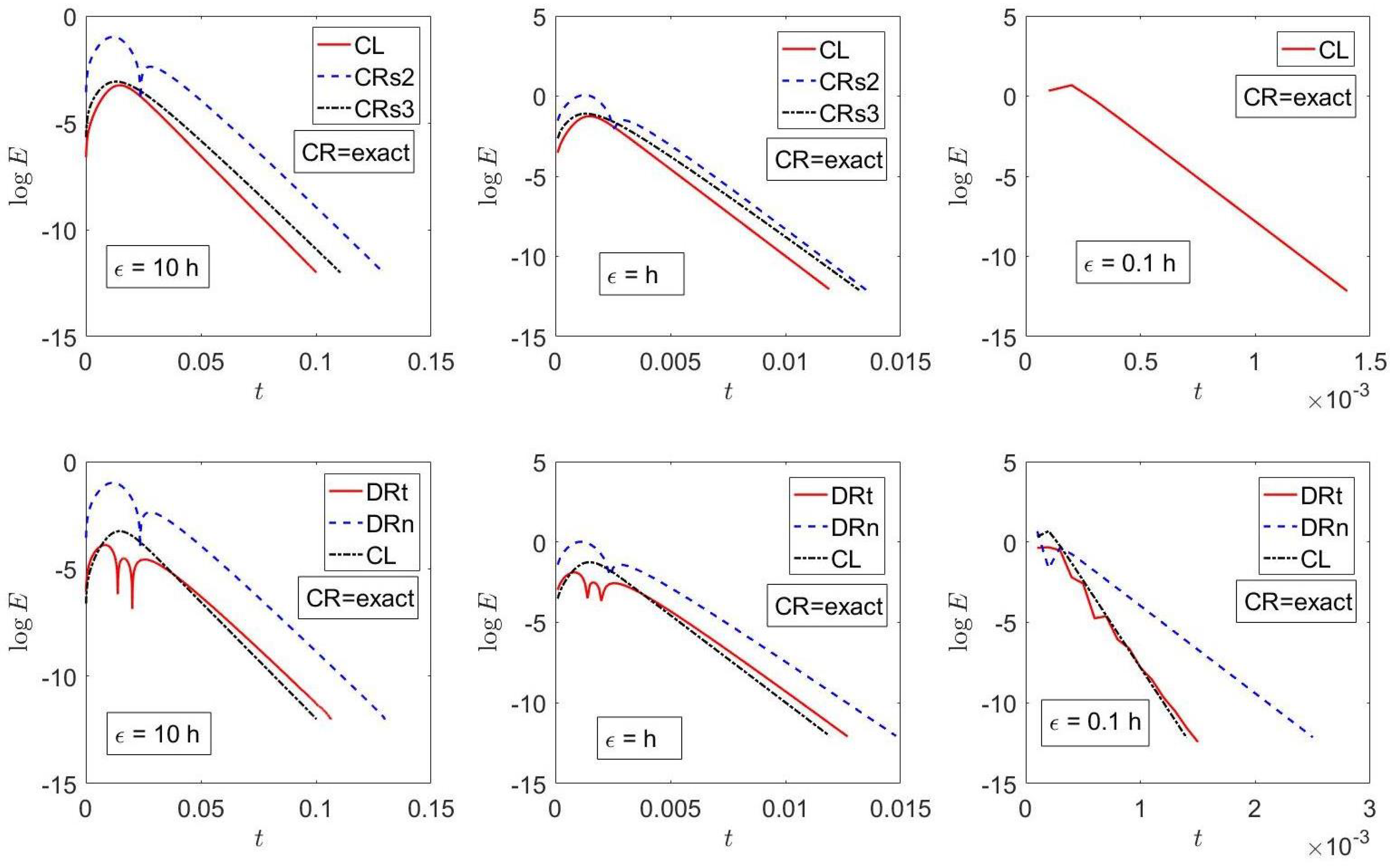
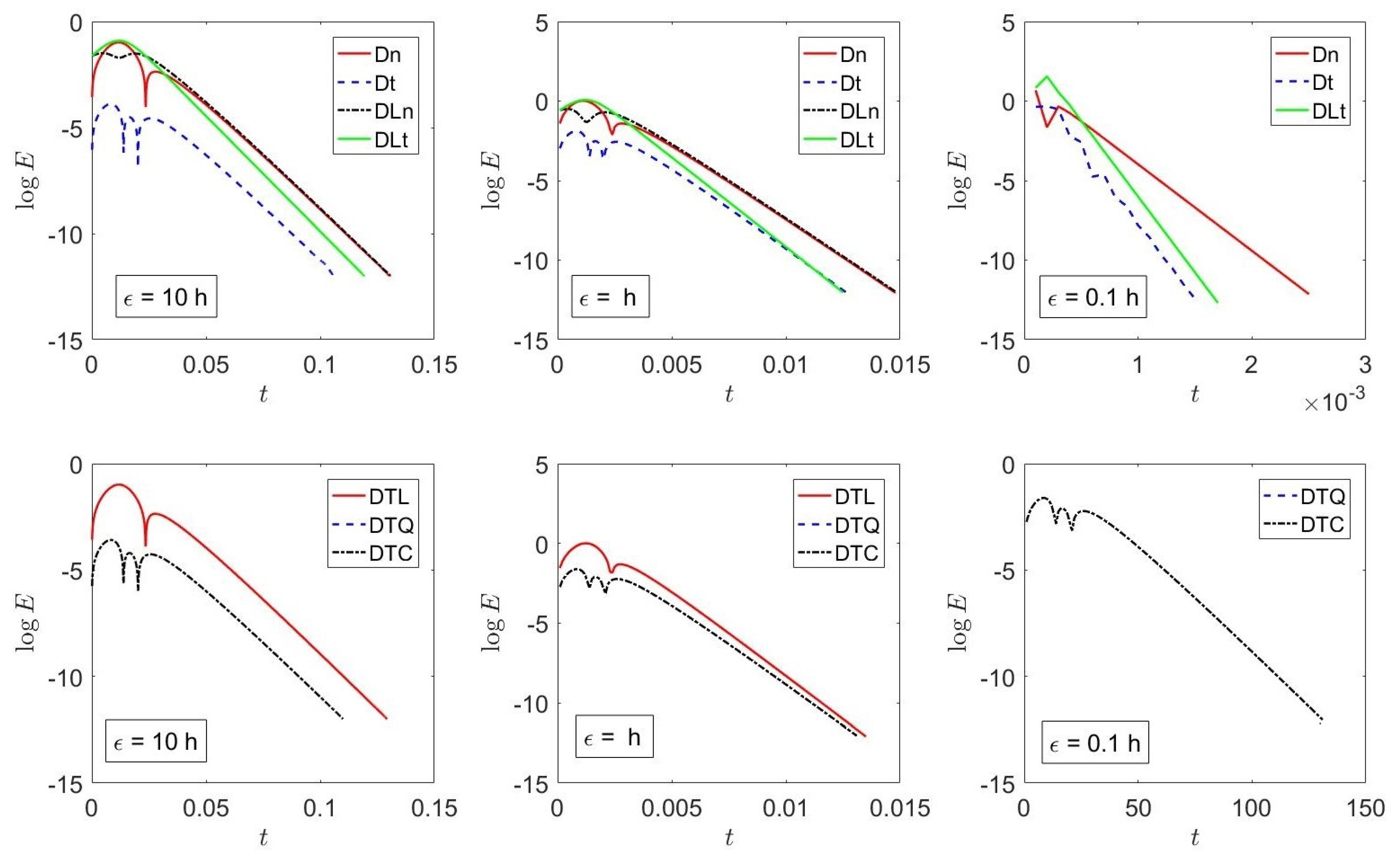
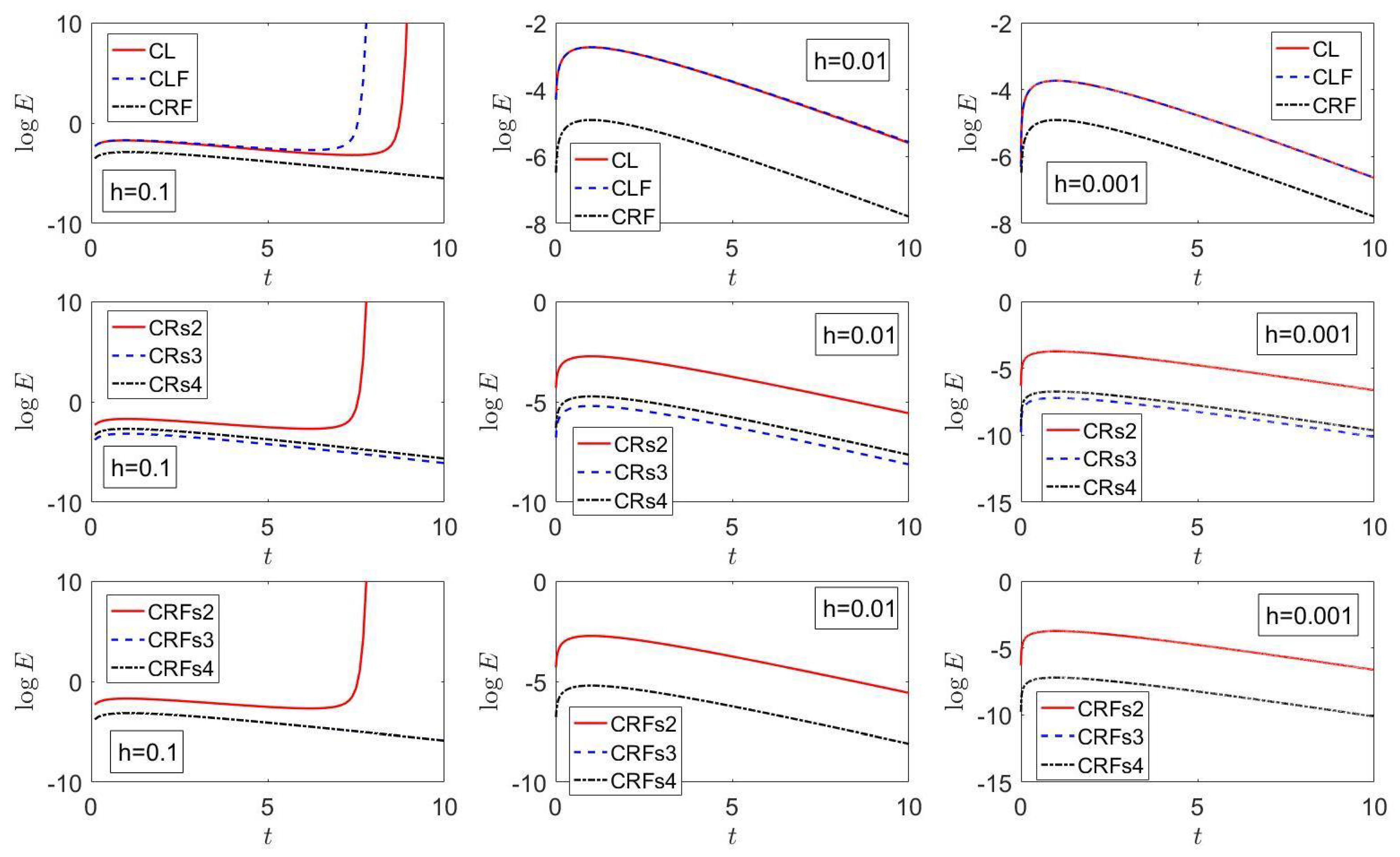
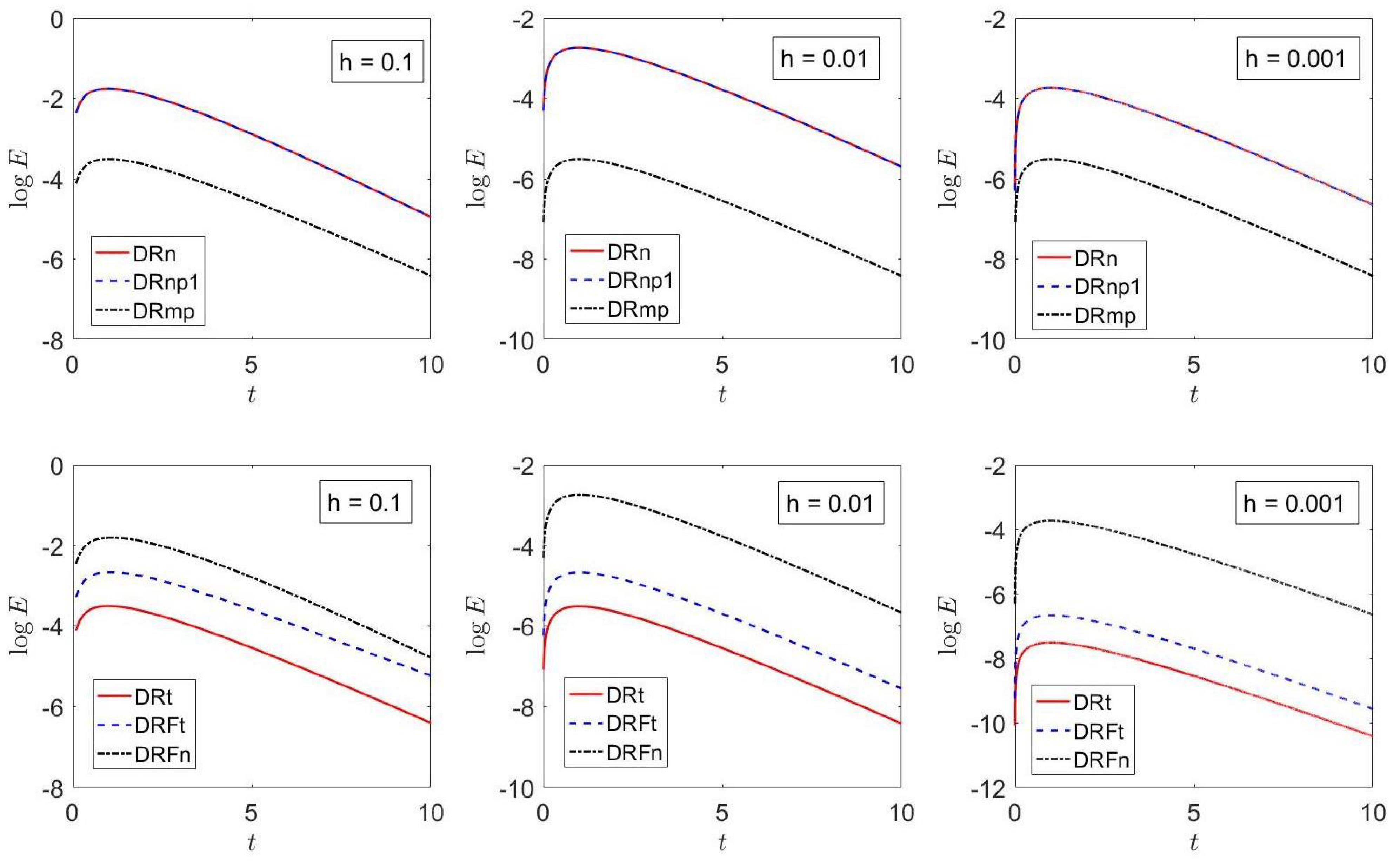
Method	Sect/App	${\mathit{e}}_{max}$ ($\mathit{ϵ}=10\mathit{h}$)	${\mathit{e}}_{max}$ ($\mathit{ϵ}=\mathit{h}$)	${\mathit{e}}_{max}$ ($\mathit{ϵ}=0.1\mathit{h}$)
CR	Section 4	$-\infty$	$-\infty$	$-\infty$
CRF	Section 4	$-\infty$	$-\infty$	$-\infty$
CRs2	Section 4	−0.978	+0.064	Diverges
CRs3	Section 4	−3.073	−1.098	Diverges
CL	Appendix A	−3.245	−1.256	+0.681
DRtn	Section 5.1	−3.884	−1.886	−0.365
DRn	Section 5.1	−0.984	+0.018	−0.984
Dtn	Section 5	−3.586	−1.886	−0.327
Dn	Section 5	−0.984	+0.018	+0.683
DLn	Appendix B	−1.492	−0.499	Diverges
DLtn	Appendix B	−0.906	−0.070	+1.553
DTL	Appendix C	−0.984	+0.011	Diverges
DTQ	Appendix C	−3.589	−1.611	Diverges
DTC	Appendix C	−3.589	−1.611	Diverges

.

Figure 1 shows the decimal logarithm of $E_M\left(t\right)=|y_M\left(t\right)-y_{ex}\left(t\right)|$ which is the error of the method M applied to Equation (63), for $h={10}^{-4}$, where the subscript $ex$ stands for exact solution, i.e., Equation (64). Since the right-hand side of Equation (63) is quadratic and does not depend explicitly on t, CR and CRF provide the exact solution, i.e., $E_{\mathsf{CR}}\left(t\right)=E_{\mathsf{CRF}}\left(t\right)=0$; this is not the case for CRs2 and CRs3, which use two and three terms of the series $S_0\left(t\right)$, as discussed previously (cf. Equation (29)).

Figure 1 indicates that throughout the whole domain, CR is more accurate than CRs3, and the latter is more accurate than CRs2 except in a very small region for $ϵ=10h$ and h, i.e., when the initial layer near $t=0$ contains roughly ten and one (grid) points, respectively. However, if the initial layer does not contain any grid points, neither CRs2 nor CRs3 provides bounded solutions as indicated in Figure 1 for $ϵ=0.1h$, i.e., $ϵ={10}^{-5}$; this is in marked contrast to the (linear) CL and CLF methods, which provide a solution for $ϵ=0.1h$ that is very accurate away from the initial layer, but extremely inaccurate in that layer as illustrated in Figure 1 and Table 1, which show that the logarithm of the error is positive near $t=0$ for CL.

Figure 1 also shows that DRt and DRn do not diverge even when the initial layer is not resolved, i.e., for $ϵ=0.1h$, and that DRt is more accurate than DRn except in a small region located in the initial layer; this is somewhat expected owing to the higher accuracy of the trapezoidal discretization used in DRt. Figure 1 also shows that, in the initial layer, DRt is more accurate than CL which in turn is more accurate than DRn; however, away from the initial layer, CL is more accurate than DRt which in turn is more accurate than DRn. Figure 1 also indicates that, away from the initial layer, Dt is more accurate than DLt, which in turn is more accurate than Dn, which in turn is more accurate than DLn; this is consistent with the fact that linearization and first-order accurate implicit techniques are less accurate than nonlinearized and second-order accurate implicit methods, respectively. In addition, CL, DRt, and DRn are very inaccurate near $t=0$ for $ϵ=0.1h$, owing to the lack of resolution of the initial layer.

In Figure 2, the errors of the implicit and trapezoidal methods, i.e., Dn and Dt, respectively; linearized implicit and trapezoidal techniques, i.e., DLn and DLt, respectively; and the first-, second- and third-order accurate methods presented in Appendix A, Appendix B and Appendix C, respectively, are reported for $ϵ=10h$, h and $0.1h$.

For $ϵ=0.1h$, i.e., when there are no grid points in the initial layer, Figure 2 shows that DLn and DTL do not provide bounded solutions. On the other hand, Dn and DLt do not diverge but are very inaccurate near $t=0$. Figure 2 also shows that the accuracy of Dn, Dt, DLn, DLt, DTL, DTQ and DTC increases as $ϵ/h$ increases, i.e., as the number of grid points in the initial layer increases.

For $ϵ=10h$ and h, the accuracy of DTQ illustrated in Figure 2 is almost identical to that of DTC and higher than that of DTL, in accordance with the truncation errors of these techniques. Figure 2 clearly indicates that Dt is more accurate than DLt which, in turn, is more accurate than DLn and Dn; DLn and DLt are less accurate than Dn near $t=0$; and the accuracy of Dn is slightly higher than that of DLn away from the initial layer.

CL and CR provide the exact solution when applied to the linear Equation (66). This indicates that the accuracy of these methods depends on how the original differential equation is treated (cf. Equations (63) and (66)).

If E is assumed to be equal to $A{ϵ}^p$ where $A>0$, the results shown in Table 1 for $ϵ=h$ and $ϵ=10h$ indicate that $p\approx 2$ for CRs3 and CL, DRtn and Dtn, and DTQ and DTC; $p=-\infty$ for CR and CRF; and $p=1$ for the rest of the methods presented in that table. Furthermore, Table 1 indicates that CR and CRF provide the exact solution for Example 1 and, therefore, are the most accurate methods presented in this paper for this example.

7.2. Example 2

In this subsection, we consider the following singularly perturbed initial-value problem:

$$ϵ{\displaystyle \frac{dy}{dx}}=-exp\left({\displaystyle \frac{x}{ϵ}}\right)y^2+y-exp\left(-{\displaystyle \frac{x}{ϵ}}\right),x>0,$$

(67)

subject to $y\left(0\right)=1$, with $0<ϵ<<1$.

Equation (67) contains a transcendentally small term, i.e., $exp\left(-{\displaystyle \frac{x}{ϵ}}\right)$, and a transcendentally large coefficient, i.e., $exp\left({\displaystyle \frac{x}{ϵ}}\right)$. However, upon making use of $t\equiv {\displaystyle \frac{x}{ϵ}}$, Equation (67) becomes

$${\displaystyle \frac{dy}{dt}}=-y^2{e}^t+y-e^{-t},$$

(68)

subject to $y\left(0\right)=1$, whose analytical solution is $y\left(t\right)=e^{-t}$ or $y\left(x\right)=exp\left(-{\displaystyle \frac{x}{ϵ}}\right)$.

Figure 3, Figure 4 and Figure 5 and

Table 2. Largest values of $e\left(t\right)\equiv logE=log|y\left(t\right)-y_{ex}\left(t\right)|$ for some piecewise analytical continuous and discrete methods and different values of h for Example 2. (The Sect/App column indicates the section or appendix where the methods listed in the first column appear; the subscript $ex$ stands for the exact solution).

Method	Sect/App	${\mathit{e}}_{max}$ ($\mathit{h}=0.001$)	${\mathit{e}}_{max}$ ($\mathit{h}=0.01$)	${\mathit{e}}_{max}$ ($\mathit{h}=0.1$)
CRF	Section 4	−6.911	−4.909	−2.890
CRs2	Section 4	−3.735	−2.733	Diverges
CRs3	Section 4	−7.212	−5.209	−3.180
CRs4	Section 4	−6.735	−4.731	−2.696
CRFs2	Section 4	−3.735	−2.733	Diverges
CRFs3	Section 4	−7.212	−5.207	−3.158
CRFs4	Section 4	−7.212	−5.207	−3.159
CL	Appendix A	−3.735	−2.735	−1.731
CLF	Appendix A	−3.735	−2.733	Diverges
DRt	Section 5.1	−7.513	−5.513	−3.507
DRFt	Section 6	−6.668	−4.668	−2.663
DRn	Section 5.1	−3.736	−2.739	−1.761
DRFn	Section 6	−3.736	−2.742	−1.808
DRmp	Section 5.1	−7.514	−5.513	−3.513
DRnp1	Section 5.1	−3.736	−2.738	−1.760
DLt	Section 6	−7.513	−5.513	−3.514
DLFt	Section 6	−7.513	−5.513	−3.493
DLnp1	Section 6	−3.735	−2.729	−1.682
DLn	Section 6	−3.736	−2.738	−1.762
DLFn	Section 6	−3.735	−2.734	−1.720
DLmp	Section 6	−7.212	−5.212	−3.214

provide the errors of some of the continuous and discrete approximate methods presented in Section 2, Section 3, Section 4, Section 5 and Section 6 for Equation (68).

The top row of Figure 3 shows that, away from the initial layer, CRF is more accurate than CL, which in turn is more accurate than CLF, in accordance with the fact that CRF uses a quadratic approximation, whereas CL employs a linear one, and CLF does not account for the dependence of $f(x,y)$ on the independent variable x in each interval. The top row of Figure 3 also shows that CL and CLF diverge for $h=0.1$ but provide almost the same errors for $h=1$ and 10, and that the accuracy of CRF, CL and CLF increases as the step size is decreased, in accordance with the improvement of the accuracy of the Taylor series expansion as the step size is decreased.

The middle row of Figure 3 shows that, for $h=0.1$, CRs2 diverges and CRs3 is slightly more accurate than CRs4. For $h=0.01$ and 0.001, the middle row of Figure 3 indicates that CRs2 is less accurate than CRs4, and the latter, in turn, is less accurate than CRs3. This may seem a bit counter-intuitive at first sight since CRs4 contains one term more than CRs3 in the truncation of the series $S_0\left(X\right)$ (cf. Equations (29) and (32)); however, both methods truncate the series $S_0\left(X\right)$ and their solutions are given by the ratio of a truncated series to the derivative of such a truncated series. Furthermore, the higher accuracy of CRs3 shown in the middle row of Figure 3 has not been observed in numerical experiments on other ordinary differential equations not reported here.

Figure 3 also indicates that, for $h=0.001$, CRs3 and CRs4 are more accurate than CRF, and the (absolute value of the) slope of $logE$ beyond the maximum value of E for CRs2, CRs3 and CRs4 decreases much more slowly with time than that of CL, CLF and CRF.

The bottom row of Figure 3 shows the errors for CRFs2, CRFs3 and CRFs4, which exhibit similar trends to those for CRs2, CRs3 and CRs4 illustrated in the middle row of that figure. For $h=0.1$, CRFs2 diverges, but the errors of CRFs3 are almost identical to those of CRFs4.

Figure 4 indicates that DRmp is more accurate than DRn and DRnp1; this is in accordance with the fact that, in DRmp, the coefficients are evaluated at the midpoint $x^{n+{\displaystyle \frac{1}{2}}}$, whereas they are evaluated at $x^n$ and $x^{n+1}$ in DRn and DRnp1, respectively. Figure 4 also shows that DRnp1 is more accurate than DRn.

The bottom row of Figure 4 shows that DRt is more accurate than DRFt; the latter, in turn, is more accurate than DRFn. This is to be expected because the coefficients of Equation (68) depend on t and are assumed to be (frozen) constant in DRFt and DRFn. In addition, DFRt is based on a trapezoidal rule evaluation.

The results presented in the top row of Figure 5 show that the accuracy of DLFn is very close to that of DLFnp1 but lower than that of DLFmp in accordance with results previously shown in this paper, thus indicating that the accuracy of constant-coefficient (frozen) approximations is higher when these coefficients are evaluated at the midpoint $t^{n+{\displaystyle \frac{1}{2}}}$ than when evaluated at $t^n$ or $t^{n+1}$.

The bottom row of Figure 5 shows that DLt is more accurate than DLFt and this, in turn, is more accurate than DLn or DL. The error of DLt is very close to that of DLFt for $h=0.01$ and 0.001, and smaller than that for DLFt for $h=0.1$, in accordance with the fact that the accuracy of the linearization of $f(x,y)$ increases as the step size is decreased.

A comparison of the results presented in the two rows of Figure 5 clearly shows that DLt is more accurate than DLFt; the latter is more accurate than DLFmp, which, in turn, is more accurate than DLFn and DLFnp1.

If E is assumed to be equal to $B{h}^p$ where $B>0$ is a constant and p is the order, the results shown in Table 2 clearly indicate that piecewise analytical methods CRF, CRs3, CRs4, CRFs3 and CRFs4 and the discrete techniques DRt, DRFt and DRmp, which are based on the second-order Taylor series expansion of $f(x,y)$ and quadratic approximations, respectively, are second-order accurate. Table 2 also indicates that the linear methods DLt, DLFt and DLmp are also second-order accurate; the remaining methods reported in Table 2 are first-order accurate.

Table 2 also shows that the accuracy of CRs3 is about the same as that of CRFs3 and CRFs4 and higher than that of CRF; the latter is more accurate than CRs4. On the other hand, Table 2 shows that DLt and DLFt exhibit almost the same accuracy, thus indicating that the dependence of the coefficients on the independent variable does not play much a role in discrete linearization methods for Equation (68). However, the location where these coefficients are evaluated plays an important role as a comparison between the errors of DLt and DLmp indicates.

Table 2 also shows that the error of DRmp is about the same as that of DRt and smaller than that of DRFt, thus indicating once again that the accuracy of the discrete methods presented in this paper depends on the location where the coefficients are evaluated.

8. Conclusions

Piecewise analytical, continuous and discrete (approximate) solutions to scalar, nonlinear, first-order, ordinary differential equations based on the use of the second-order Taylor series expansion of their right-hand sides have been reported. The continuous approximation results in Riccati equations whose analytical solutions are given in terms of convergent series if the dependence of the right-hand side on the independent variable is taken into account, and, in closed form, this involves exponential, linear polynomials, or trigonometric functions depending on the sign and value of a (local) radicand, otherwise. On the other hand, the discrete approximation results in quadratic equations.

It has been shown that, for a singularly perturbed, constant-coefficient Bernoulli equation, the piecewise analytical continuous method provides the exact solution, whereas it provides a second-order accurate one for a Riccati equation whose coefficients depend exponentially on the independent variable. It has also been shown that linearization methods that only account for the constant and linear terms in the Taylor’s series expansion of the right-hand side provide very accurate solutions if the initial layer is adequately resolved; otherwise, they may result in errors which may be larger than the exact solution, not only in that layer but also away from it. A similar behavior has been observed for the discrete, analytical methods reported in this paper.

For a Riccati equation whose coefficients depend exponentially on the dependent variable, it has been shown that the piecewise analytical continuous method presented in this paper which does not account for the dependence of the right-hand side on the independent variable provides slightly less accurate solutions than piecewise analytical continuous methods that account for such a dependence, provided that at least three terms in the series expansion are used. It has also been shown that the accuracy of the discrete, analytical, approximate methods presented here depends strongly on the locations where the right-hand side and its first- and second-order derivatives are evaluated. The highest accuracy has been found when such an evaluation is performed at the midpoint or when a trapezoidal method is used.