Maxima of the Aα-Index of Non-Bipartite C3-Free Graphs for 1/2 < α < 1
Abstract
:1. Introduction
2. Some Lemmas
- (i)
- is the largest root of ;
- (ii)
- for ;
- (iii)
- for ;
- (iv)
- for and .
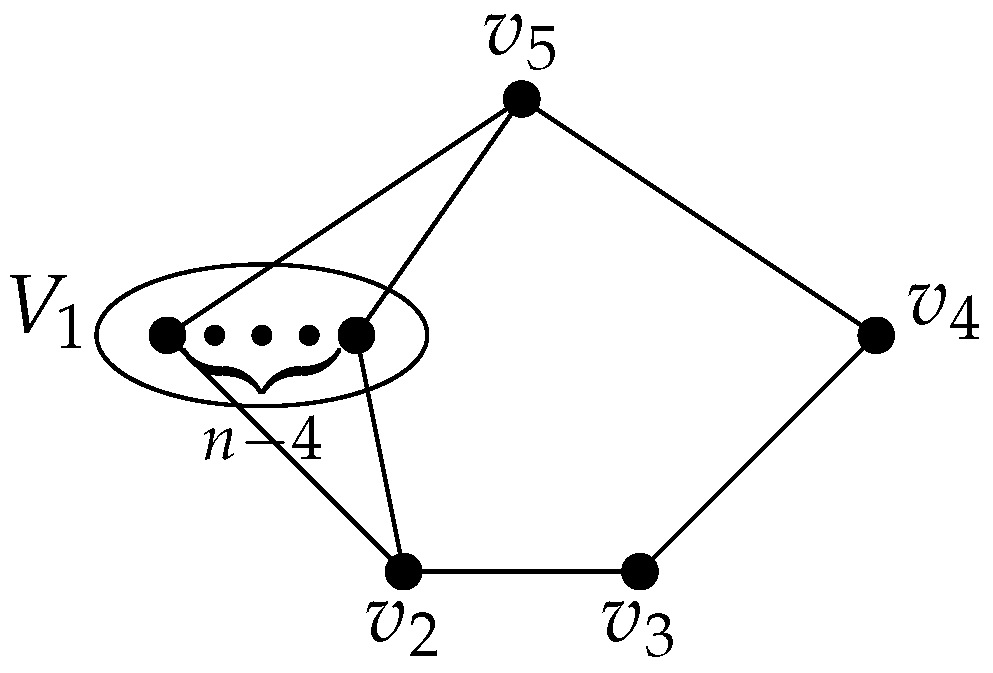
3. The -Index of
- (i)
- , and ;
- (ii)
- , and , ;
- (iii)
- , ;
- (iv)
- , and .
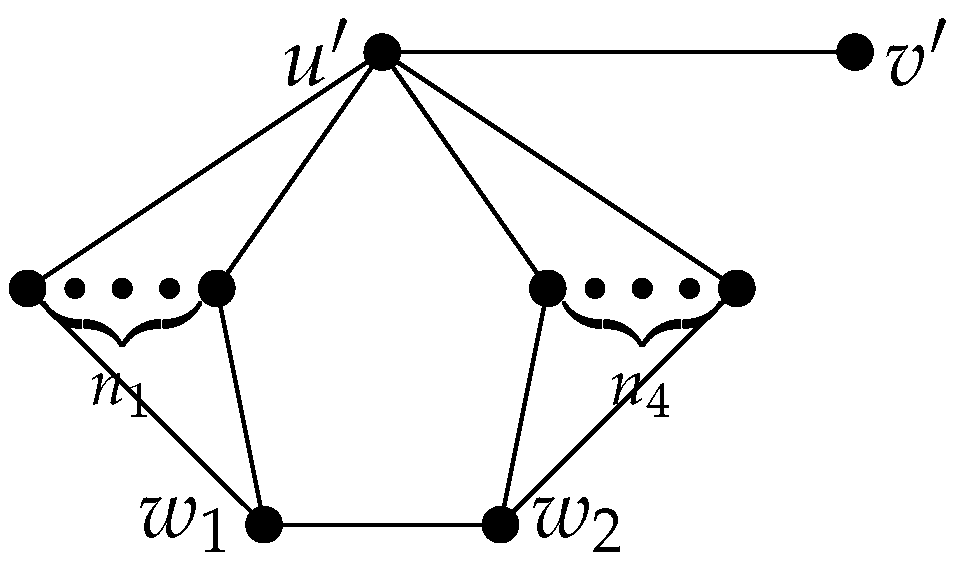
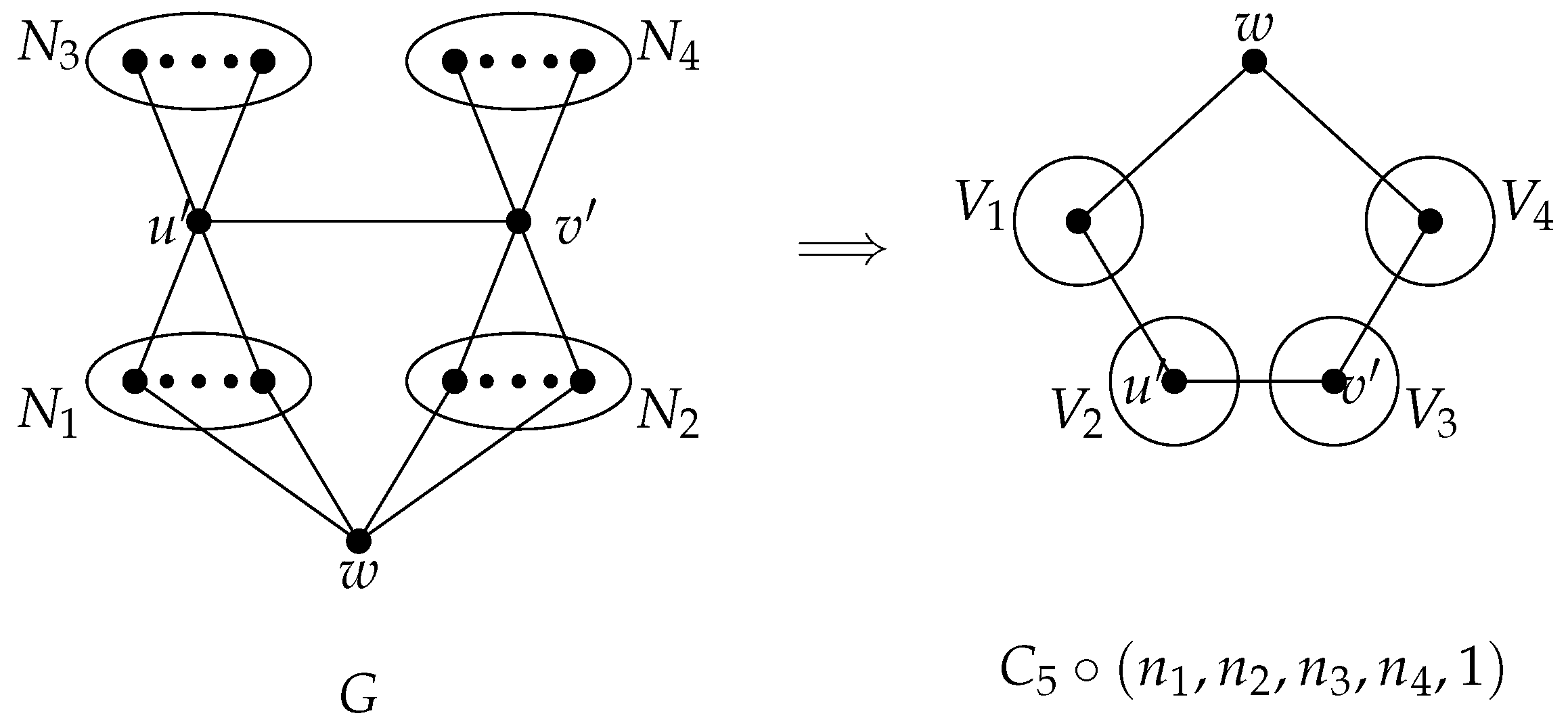
4. Proof of Theorem 2
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nikiforov, V. Merging the A- and Q- spectral theories. Appl. Anal. Discret. Math. 2017, 11, 81–107. [Google Scholar] [CrossRef]
- Füredi, Z.; Simonovits, M. The history of degenerate (bipartite) extremal graph problems. Bolyai Soc. Stud. Erdős Centen. 2013, 25, 167–262. [Google Scholar]
- Nikiforov, V. The spectral radius of graphs without paths and cycles of specified length. Linear Algebra Appl. 2010, 432, 2243–2256. [Google Scholar] [CrossRef]
- de Freitas, M.A.A.; Nikiforov, V.; Patuzzi, L. Maxima of the Q-index: Forbidden 4-cycle and 5-cycle. Electron. J. Linear Algebra 2013, 26, 905–916. [Google Scholar] [CrossRef]
- Zhai, M.Q.; Wang, B. Proof of a conjecture on the spectral radius of C4-free graphs. Linear Algebra Appl. 2012, 437, 1641–1647. [Google Scholar] [CrossRef]
- Zhai, M.Q.; Lin, H.Q. Spectral extrema of graphs: Forbidden hexagon. Discret. Math. 2020, 343, 112028. [Google Scholar] [CrossRef]
- Nikiforov, V.; Yuan, X.Y. Maxima of the Q-index: Forbidden even cycles. Linear Algebra Appl. 2015, 471, 636–653. [Google Scholar] [CrossRef]
- Yuan, X.Y. Maxima of the Q-index: Forbidden odd cycles. Linear Algebra Appl. 2014, 458, 207–216. [Google Scholar] [CrossRef]
- He, B.; Jin, Y.L.; Zhang, X.D. Sharp bounds for the signless Laplacian spectral radius in terms of clique number. Linear Algebra Appl. 2013, 438, 3851–3861. [Google Scholar] [CrossRef]
- Nikiforov, V. Some new results in extremal graph theory. In Surveys in Combinatorics; Cambridge University Press: Cambridge, MA, USA, 2011; pp. 141–182. [Google Scholar]
- Cioabǎ, S.; Desai, D.N.; Tait, M. The spectral even cycle problem. arXiv 2022, arXiv:2205.00990. [Google Scholar] [CrossRef]
- de Freitas, M.A.A.; Nikiforov, V.; Patuzzi, L. Maxima of the Q-index: Graphs with no Ks,t. Linear Algebra Appl. 2016, 496, 381–391. [Google Scholar] [CrossRef]
- Liu, R.F.; Miao, L.; Xue, J. Maxima of the Q-index of non-bipartite C3-free graphs. Linear Algebra Appl. 2023, 673, 1–13. [Google Scholar] [CrossRef]
- Lin, H.Q.; Zhai, M.Q.; Zhao, Y.H. Spectral radius, edge-disjoint cycles and cycles of the same length. Electron. J. Comb. 2022, 29, P2.1. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Kang, L.Y.; Xue, X.S. On a conjecture of spectral extremal problems. J. Comb. Theory B 2023, 159, 20–41. [Google Scholar] [CrossRef]
- Zhai, M.Q.; Lin, H.Q.; Shu, J.L. Spectral extrema of graphs with fixed size: Cycles and complete bipartite graphs. Eur. J. Comb. 2021, 95, 103322. [Google Scholar] [CrossRef]
- Brouwer, A.E.; Haemers, W.H. Spectra of Graphs; Springer: Berlin, Germany, 2011. [Google Scholar]
- Godsil, C.; Royle, G. Algebraic Graph Theory. In Graduate Texts in Mathematics; Springer Verlag: New York, NY, USA, 2001; Volume 207. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Lei, Y. Maxima of the Aα-Index of Non-Bipartite C3-Free Graphs for 1/2 < α < 1. Mathematics 2025, 13, 454. https://doi.org/10.3390/math13030454
Zhang H, Lei Y. Maxima of the Aα-Index of Non-Bipartite C3-Free Graphs for 1/2 < α < 1. Mathematics. 2025; 13(3):454. https://doi.org/10.3390/math13030454
Chicago/Turabian StyleZhang, Haixia, and Yu Lei. 2025. "Maxima of the Aα-Index of Non-Bipartite C3-Free Graphs for 1/2 < α < 1" Mathematics 13, no. 3: 454. https://doi.org/10.3390/math13030454
APA StyleZhang, H., & Lei, Y. (2025). Maxima of the Aα-Index of Non-Bipartite C3-Free Graphs for 1/2 < α < 1. Mathematics, 13(3), 454. https://doi.org/10.3390/math13030454





