Numerical Transformation Methods for a Moving-Wall Boundary Layer Flow of a Rarefied Gas Free Stream over a Moving Flat Plate

Abstract

In this paper, we present an original numerical method for the solution of a Blasius problem with extended boundary conditions. To this end, we extend to the proposed problem the non-iterative transformation method, proposed by Töpfer more than a century ago and defined for the numerical solution of the Blasius problem. The proposed method, which makes use of the invariance of two physical parameters with respect to an extended scaling group of point transformations, allows us to solve the Blasius problem numerically with extended boundary conditions by solving a related initial value problem and then rescaling the obtained numerical solution. Therefore, our method is an initial value method. However, in this way, we cannot fix the values of the physical parameters in advance, and if we just need to compute the numerical solution for given values of the two parameters, we have to define an iterative extension of the transformation method. Thus, in this paper, for the problem under study, we define a non-ITM and an ITM based on Lie groups scaling invariance theory.

1. Introduction

It was Prandtl [1] who in 1904 fixed the terms for the validity of boundary layer theory. Within this theory, the problem of determining the steady two-dimensional motion of fluid flow past a flat plate placed edge-ways to the mainstream was formulated in general terms and investigated in detail by Blasius [2]. The engineering interest was to calculate the shear at the plate (skin friction), which leads to the determination of the viscous drag on the plate (see, for instance Schlichting and Gersten [3]). The Blasius problem is a non-linear boundary value problem (BVP) defined on the semi-infinite interval $[0,\infty )$. It is possible to prove (see Weyl [4]) that the unique solution of the Blasius problem has a positive second-order derivative, which is a monotone decreasing function on $[0,\infty )$ and approaches zero as $\eta$ goes to infinity. The governing differential equation and the two boundary conditions at the origin in the Blasius problem are invariant with respect to a scaling group of point transformations and this has several consequences. From a numerical viewpoint, a non-iterative transformation method (ITM) reducing the solution of the Blasius problem to the solution of a related initial value problem (IVP) was defined by Töpfer [5]. From a theoretical point of view, by applying the scaling invariance properties, a simple existence and uniqueness Theorem was given by J. Serrin (see Meyer [6]: pp. 104–105). Furthermore, let us note here that the mentioned invariance property is essential to the error analysis of the truncated boundary solution offered by Rubel [7]. Recently, the Blasius problem was used, by Boyd [8], as an example, where some good analysis allowed researchers of the past to solve problems, governed by partial differential equations, which might be otherwise have been impossible to face before the invention of the computer.

The present paper is concerned with the numerical solution of a Blasius problem with extended boundary conditions, as described by White [9], Klemp and Acrivos [10], Fang and Lee [11], and Lu and Law [12]. This problem allows us to define both a non-ITM, where we are forced to accept the transformed values of the two physical parameters, and an ITM, where we can fix the values of interest of these parameters and compute the numerical solution by using the invariance properties of an extended scaling group of point transformations. Therefore, we are able to illustrate the differences between the two proposed numerical methods.

Non-ITMs have been applied to several problems of practical interest within the applied sciences. First of all, a non-ITM was applied to the Blasius equation with a slip boundary condition, arising within the study of gas and liquid flows at the micro-scale regime [13,14]. A non-ITM has also been applied to the Blasius equation with moving wall, as considered by Ishak et al. [15], surface gasification, as studied by Emmons [16] and recently by Lu and Law [12], and slip boundary conditions, as investigated by Gad-el-Hak [13] and Martin and Boyd [14]. In particular, within these applications, we found a way to solve the Sakiadis problem non-iteratively [17,18]. The application of a non-ITM to an extended Blasius problem has been the subject of a recent paper [19]. Furthermore, another application has been considered for boundary layer problems with power-law viscosity for non-Newtonian fluids (see Fazio [20]). As far as the non-ITM is concerned, a recent review dealing with all the cited problems can be be found in ([21]).

Moreover, Töpfer’s method has been extended to classes of problems in boundary layer theory involving one or more physical parameters. This kind of extension was first considered by Na [22]; see also the book by Na [23] (Chapters 8–9) for an extensive survey on this subject.

Finally, an iterative extension of the transformation method has been introduced by Fazio for the numerical solution of free BVPs [24]. This iterative extension has been applied to several problems of interest: free boundary problems [24]; a moving boundary hyperbolic problem [25]; and two variants of the Blasius problem [26], namely a boundary layer problem over moving surfaces, first studied by Klemp and Acrivos [27], and a boundary layer problem with slip boundary conditions, which has found applications in the study of gas and liquid flows at the micro-scale regime [13,14]. In addition (see [28]), a further variant of the Blasius problem in boundary layer theory has recently been introduced: the so-called Sakiadis problem [17,18]. A recent review dealing with the derivation and application of the ITM can be be found, by the interested reader, in [29].

2. The Blasius Problem with Extended Boundary Conditions

The Blasius problem with extended boundary conditions is given in White [9], Klemp and Acrivos [10], Fang and Lee [11], and Lu and Law [12]

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d^{3}f}{d{\eta }^3}}+f{\displaystyle \frac{d^{2}f}{d{\eta }^2}}=0\hfill \\ \hfill & \\ \hfill & f\left(0\right)=0,{\displaystyle \frac{df}{d\eta }}\left(0\right)=P_1+P_2{\displaystyle \frac{d^{2}f}{d{\eta }^2}}\left(0\right),{\displaystyle \frac{df}{d\eta }}\left(\eta \right)\to 1\mathrm{as}\eta \to \infty ,\hfill \end{array}$$

(1)

where $P_1={\displaystyle \frac{U_w}{U_{\infty }}}$, which for $U_w>0$ is positive with the same direction as the free stream velocity and for $U_w<0$ is negative opposite to the free stream velocity, and $P_2={\displaystyle \frac{U_{slip}}{U_{\infty }}}=\left({\displaystyle \frac{2}{P_3}}-1\right)K_{n,x}R{e}_x^{1/2}$ is a dimensionless parameter with $K_{n,x}={\displaystyle \frac{1}{x}}$, and $R{e}_x={\displaystyle \frac{U_{\infty }x}{2\nu }}$. In the current derivations, it is assumed that the positive x points in the direction of the free stream. The slip velocity at an isothermal wall can be obtained based on Maxell’s first-order approximation as

$$U_{slip}=\left({\displaystyle \frac{2}{\sigma }}-1\right)\ell {\displaystyle \frac{du}{dy}}{|}_w,$$

(2)

where $\sigma$ is the tangential momentum accommodation coefficient, ℓ is the mean free path, and the notation ${\displaystyle \frac{du}{dy}}{|}_w$ means the derivative of u with respect to y at constant w. The dimensionless parameter $\gamma$ can also be arranged as

$$\gamma =\left({\displaystyle \frac{2}{\sigma }}-1\right){\eta }_{99\%}{\displaystyle \frac{\mathsf{\ell }}{\delta }}=\left({\displaystyle \frac{2}{\sigma }}-1\right){\eta }_{99\%}{K}_{n,\delta },$$

(3)

where $\delta$ is the boundary layer thickness defined as $\delta ={\eta }_{99\%}\sqrt{{\displaystyle \frac{2\nu x}{U_{\infty }}}}$ in which ${\eta }_{99\%}$ is the value satisfying $f^{\prime }\left({\eta }_{99\%}\right)=0.99$. It is seen from Equation (3) that this non-dimensional parameter shows the relationship between the molecular mean free path to the boundary layer thickness. As pointed out by the previously cited researchers, because $P_2$ is dependent on x, the boundary layer flow is not self-similar any more. However, since the approach preserves the mass and momentum conservation, it is still valid to study the behaviour of velocity and stress within the fluid.

We notice here, that the problem (1) when $P_1=P_2=0$ reduces to the celebrated Blasius problem.

2.1. The Non-ITM

In this section, we assume that we need to find the behaviour of the missing initial condition with respect to the variation of the values of the involved parameters; that is, $P_1$ and $P_2$ should have several different values, but these values are not fixed in advance. The applicability of a non-ITM to the Blasius problem is a consequence of both the invariance of the governing differential equation and the two boundary conditions at $\eta =0$, and the non-invariance of the asymptotic boundary condition, as $\eta$ goes to infinity, under the scaling group of point transformations. In order to apply a non-ITM to the BVP (1) we investigate its invariance with respect to the extended scaling group

$$f^{*}=\lambda f,{\eta }^{*}={\lambda }^{-1}\eta ,P_1^{*}={\lambda }^{{\delta }_1}{P}_1,P_2^{*}={\lambda }^{{\delta }_2}{P}_2.$$

(4)

We find that the Blasius problem with extended boundary conditions (1) is invariant under (4) if

$${\delta }_1=2,{\delta }_2=-1.$$

(5)

Now, we can integrate the Blasius equation in (1) written in the starred variables on $[0,{\eta }_{\infty }^{*}]$, where ${\eta }_{\infty }^{*}$ is a suitable truncated boundary, with initial conditions

$$f^{*}\left(0\right)=0,{\displaystyle \frac{d{f}^{*}}{d{\eta }^{*}}}\left(0\right)=P_1^{*}+P_2^{*},{\displaystyle \frac{d^2{f}^{*}}{d{\eta }^{*2}}\left(0\right)}=1,$$

(6)

in order to compute an approximation ${\displaystyle \frac{d{f}^{*}}{d{\eta }^{*}}}\left({\eta }_{\infty }^{*}\right)$ for ${\displaystyle \frac{d{f}^{*}}{d{\eta }^{*}}}(\infty )$ and the corresponding value of $\lambda$ according to the equation

$$\lambda ={\left[{\displaystyle \frac{d{f}^{*}}{d{\eta }^{*}}}\left({\eta }_{\infty }^{*}\right)\right]}^{1/2}.$$

(7)

Once the value of $\lambda$ has been computed by Equation (7), we can find the missed initial condition by the equation

$${\displaystyle \frac{d^{2}f}{d{\eta }^2}}\left(0\right)={\lambda }^{-3}{\displaystyle \frac{d^2{f}^{*}}{d{\eta }^{*2}}}\left(0\right),$$

(8)

and the values of $P_1$ and $P_2$ by the relations

$$P_1={\lambda }_1^{-2}{P}_1^{*},P_2={\lambda }_2{P}_2^{*}.$$

(9)

Moreover, the numerical solution of the original BVP (1) can be computed by rescaling the numerical solution of the IVP. In this way, we obtain the solution of a given BVP by solving a related IVP. Then, in this author’s opinion, the computational complexity to solve the problem at hand will be greatly reduced.

Let us notice here that the used initial condition ${\displaystyle \frac{d^2{f}^{*}}{d{\eta }^{*2}}\left(0\right)}$ equal to one might be replaced by any value different from zero on the condition that this choice is taken into consideration in the subsequent analysis. The value one was chosen by this author in order to simplify the initial conditions used (see (8)).

2.2. The ITM

In this section, we assume that we need to compute the numerical solution for the given values of the involved parameters; that is, $P_1$ and $P_2$ are now fixed. We need now to consider the invariance of the initial conditions with respect to the extended scaling group of point transformations

$$f^{*}=\lambda f,{\eta }^{*}={\lambda }^{-1}\eta ,h^{*}={\lambda }^{\sigma }h.$$

(10)

This new scaling group involves the scaling of the fictitious parameter h that will be used to force the initial conditions to be invariant. Now, we can integrate the Blasius equation in (1) written in the star variables on $[0,{\eta }_{\infty }^{*}]$, where ${\eta }_{\infty }^{*}$ is a suitable truncated boundary, with initial conditions

$$f^{*}\left(0\right)=0,{\displaystyle \frac{d{f}^{*}}{d{\eta }^{*}}}\left(0\right)=h^{*2/\sigma }{P}_1+h^{*-1/\sigma }{P}_2,{\displaystyle \frac{d^2{f}^{*}}{d{\eta }^{*2}}\left(0\right)}=1,$$

(11)

in order to compute an approximation ${\displaystyle \frac{d{f}^{*}}{d{\eta }^{*}}}\left({\eta }_{\infty }^{*}\right)$ for ${\displaystyle \frac{d{f}^{*}}{d{\eta }^{*}}}(\infty )$ and the corresponding value of $\lambda$ again by Equation (7). Once the value of $\lambda$ has been computed by Equation (7), we can find the missed initial condition again from Equation (8). In the ITM, we proceed as follows: We set the values of $P_1$, $P_2$, $h^{*}$, $\sigma$ and ${\eta }_{\infty }^{*}$ and integrate the IVP on $[0,{\eta }_{\infty }^{*}]$. Naturally, choosing $h^{*}$ arbitrarily, we do not obtain the value $h=1$; however, we can apply a root-finder method like bisection, secant, regula-falsi, Newton, or quasi-Newton root-finder because the required value of h can be considered to be the root of the implicitly defined, transformation function

$$\Gamma \left(h^{*}\right)={\lambda }^{-\sigma }h-1.$$

(12)

Of course, any positive value of $\sigma$ can be chosen, and in the following, for the sake of simplicity, we set $\sigma =10$. Moreover, as a termination criterion for our root-finder, we used $|\Gamma (h^{*}\left)\right|<Tol$ with $Tol={10}^{-5}$.

3. Numerical Results

In this section, we report the numerical results computed with our non-ITM and ITM. To compute the numerical solution, we used the eighth-order Runge–Kutta method (see Butcher [30] (p. 180) for details), with constant step size.

First of all, we start with the results obtained by the non-ITM. In

Table 1. Numerical data and results.

${\mathit{P}}_1^{*}$	${\mathit{P}}_2^{*}$	${\mathit{P}}_1$	${\mathit{P}}_2$	$\frac{{\mathit{d}}^2\mathit{f}}{\mathit{d}{\mathit{\eta }}^2}\left(0\right)$
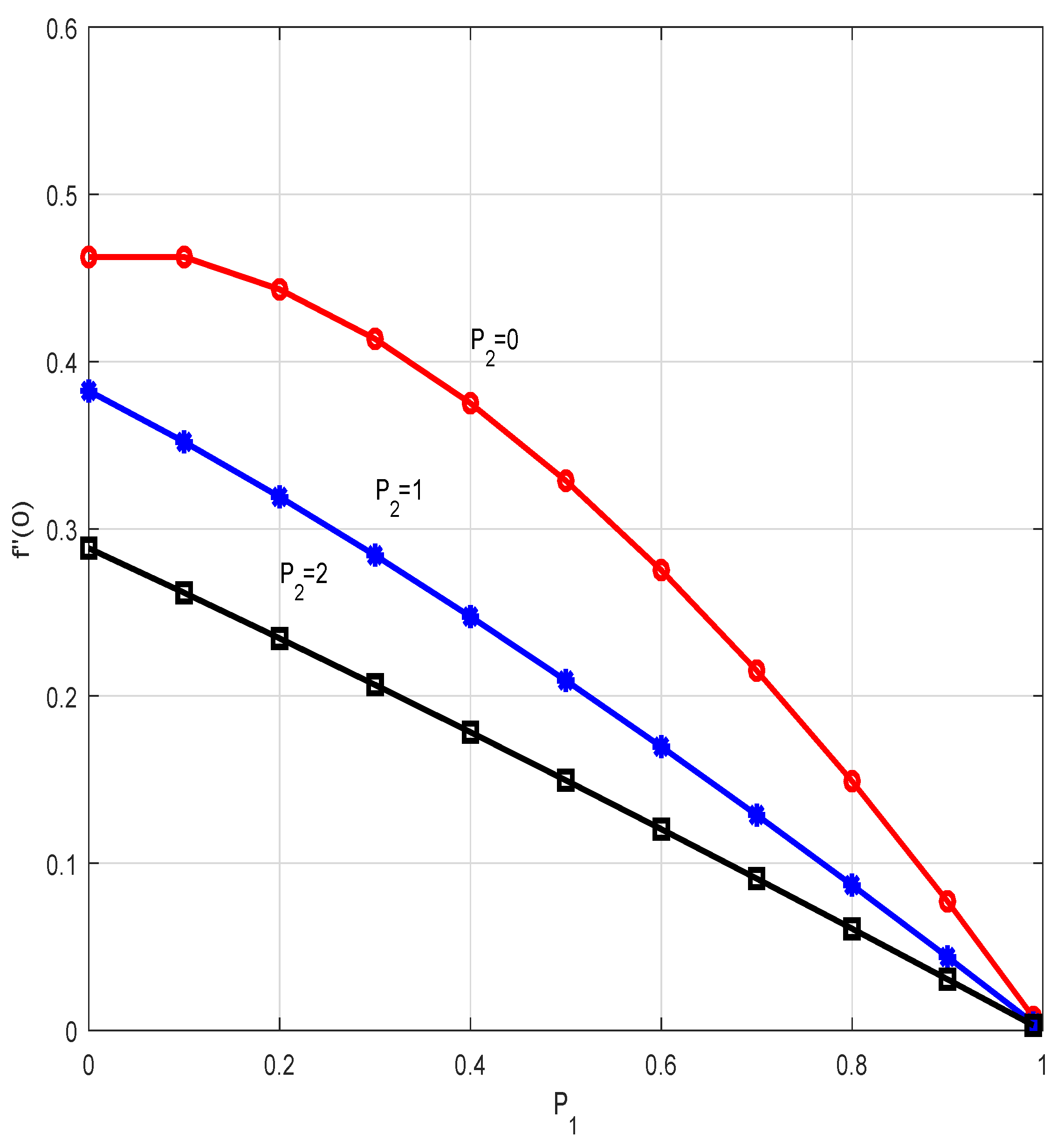
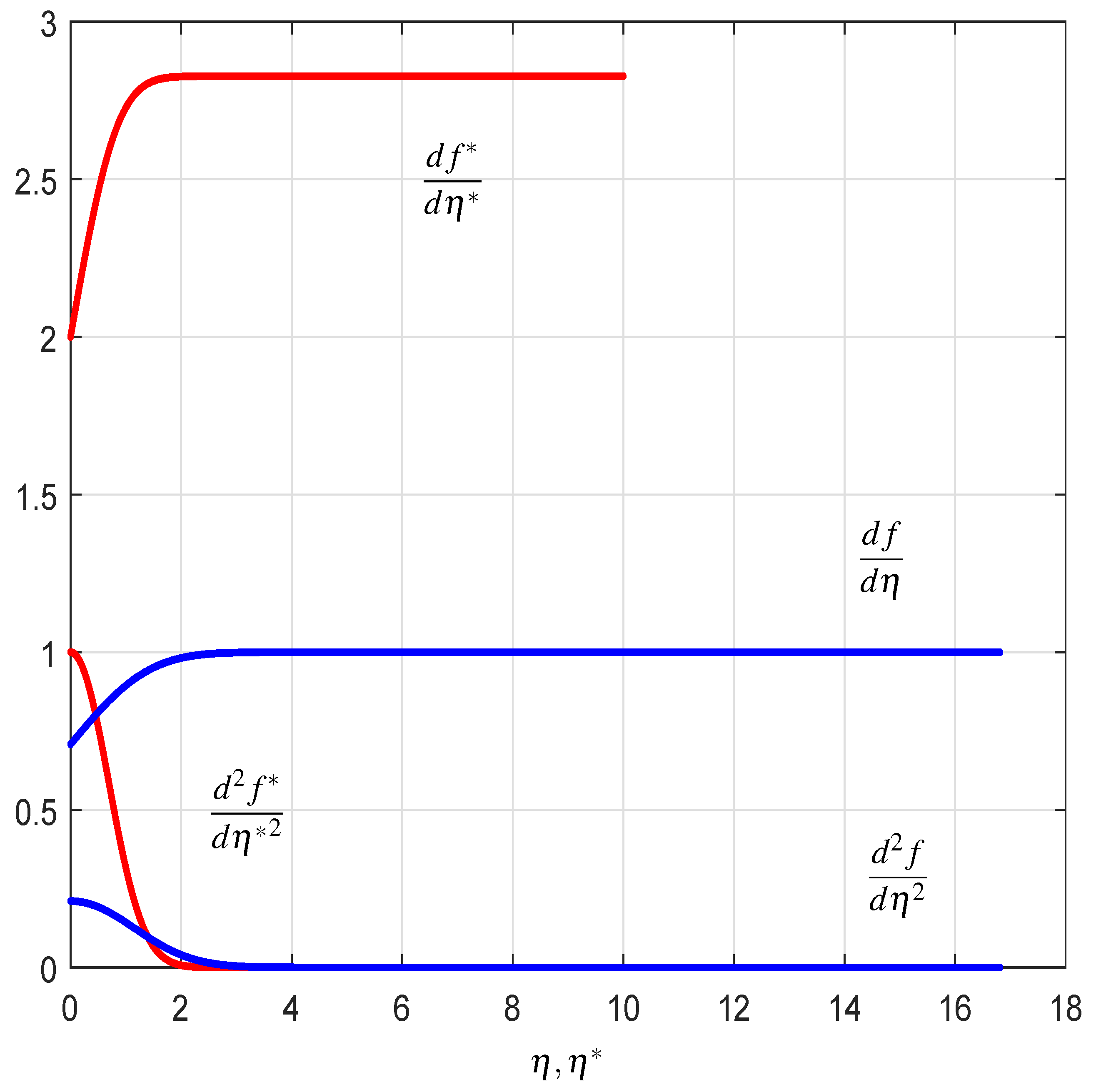
0.25	0.25	0.140225769	0.333807506	0.42007973468
0.5	0.5	0.241979004	0.336675506	0.33667550559
0.75	0.75	0.309184205	1.168108665	0.26468787856
1	1	0.353764405	1.681291175	0.21041233684
1.5	1.5	0.405947260	2.883381325	0.14078861396
2	2	0.433836425	4.294197226	0.10102852811
2.5	2.5	0.450478633	5.889425257	0.07648940496
5	5	0.481068451	16.119500068	0.02984388156

, we report the chosen parameter values, the computed values of the involved parameters, and the missing initial condition ${\displaystyle \frac{d^{2}f}{d{\eta }^2}}\left(0\right)$. As can easily be seen from the results listed in Table 1, we are not in a position to plot the data by fixing one of the two parameters, usually $P_1$, and plotting the missing initial condition versus the other parameter. Of course, this is a drawback of our non-ITM. However, when we are required to produce just these kinds of plots, we can apply the described ITM.

We report now the numerical results obtained by the ITM. As a root-finder, we applied the simple bisection method with the termination criterion $|\Gamma (h^{*}\left)\right|<Tol$ with $Tol={10}^{-5}$. In

Table 2. Bisection method iterations for $P_1=0.5$ and $P_2=0$.

${\mathit{h}}^{*}$	$\mathit{\lambda }$	$\mathbf{\Gamma }\left({\mathit{h}}^{*}\right)$
0.75		−0.424804078
1.75		0.118076477
1.25	1.389163618	−0.100177989
1.5	1.466575876	0.022790586
1.375	1.425023536	−0.035103656
1.4375	1.445108710	−0.005265147
1.46875	1.455672550	0.008983786
1.453125	1.450347802	0.001914850
1.4453125	1.447717501	−0.001661237
1.44921875	1.449029969	0.000130281
1.447265625	1.448373064	−0.0007646088
1.4482421875	1.448701349	−0.0003169467
1.44873046875	1.448865617	−0.0000932785
1.448974609375	1.448947782	0.0000185148
1.4488525390625	1.448906697	−0.0000373785
1.44891357421875	1.448927239	−0.0000094310

, we report a sample iteration of the bisection method.

Figure 1 shows the behaviour of the missing initial condition versus $P_1$ with three values of the other parameter, namely $P_2=0,1,2$.

As an example, Figure 2 shows the solution of the Blasius problem with extended boundary conditions in the particular case when we set $P_1^{*}=P_2^{*}=$ 1. For the results shown in this figure, we used $\Delta \eta =0.001$ and ${\eta }_{\infty }^{*}=10$. Let us notice here that, by rescaling, we obtain ${\eta }_{\infty }^{*}<{\eta }_{\infty }$, and this is convenient for the user because it means that we need to make less computational effort to achieve the wanted numerical solution.

As mentioned before, the case $P_1=P_2=0$ is the Blasius problem. In this particular case, our non-ITM reduces to the original method defined by Töpfer [5], and the computed skin friction coefficient value, namely $0.469599988361$, obtained with $\Delta \eta =0.0001$ and ${\eta }_{\infty }^{*}=10$, is in very good agreement with the values available in the literature (see for instance the value $0.469599988361$ computed by Fazio [31] by a free boundary formulation of the Blasius problem).

4. Concluding Remarks

The main contribution of this paper is the extension of the non-ITM, proposed by Töpfer [5] and defined for the numerical solution of the celebrated Blasius problem [2], to a Blasius problem with extended boundary conditions. This method, which makes use of the invariance of two physical parameters, allows us to numerically solve the Blasius problem with extended boundary conditions by solving a related IVP and then rescaling the obtained numerical solution. However, in this way, we cannot fix the physical parameters in advance, and if we just need to compute the numerical solution for the given values of the two parameters, we have to apply an iterative extension of our TM. Let us notice, here, that an alternative way to face the above essay is to consider tabulated values of the quantities of interest and then apply some kind of interpolation in order to find the wanted quantities for the chosen values of the involved parameters.

In the Appendix A we list, for the reader convenience, the MATLAB (latest v. R2024b) script files used to implement the numerical methods defined in the previous sections.