A Unified Control System with Autonomous Collision-Free and Trajectory-Tracking Abilities for Unmanned Surface Vessels Under Effects of Modeling Certainties and Ocean Environmental Disturbances
Abstract
1. Introduction
2. Unified Control System for Unmanned Surface Vessels
3. Design of the Collision-Free Trajectory Generator
3.1. Rapid Collision-Free Trajectory Generator
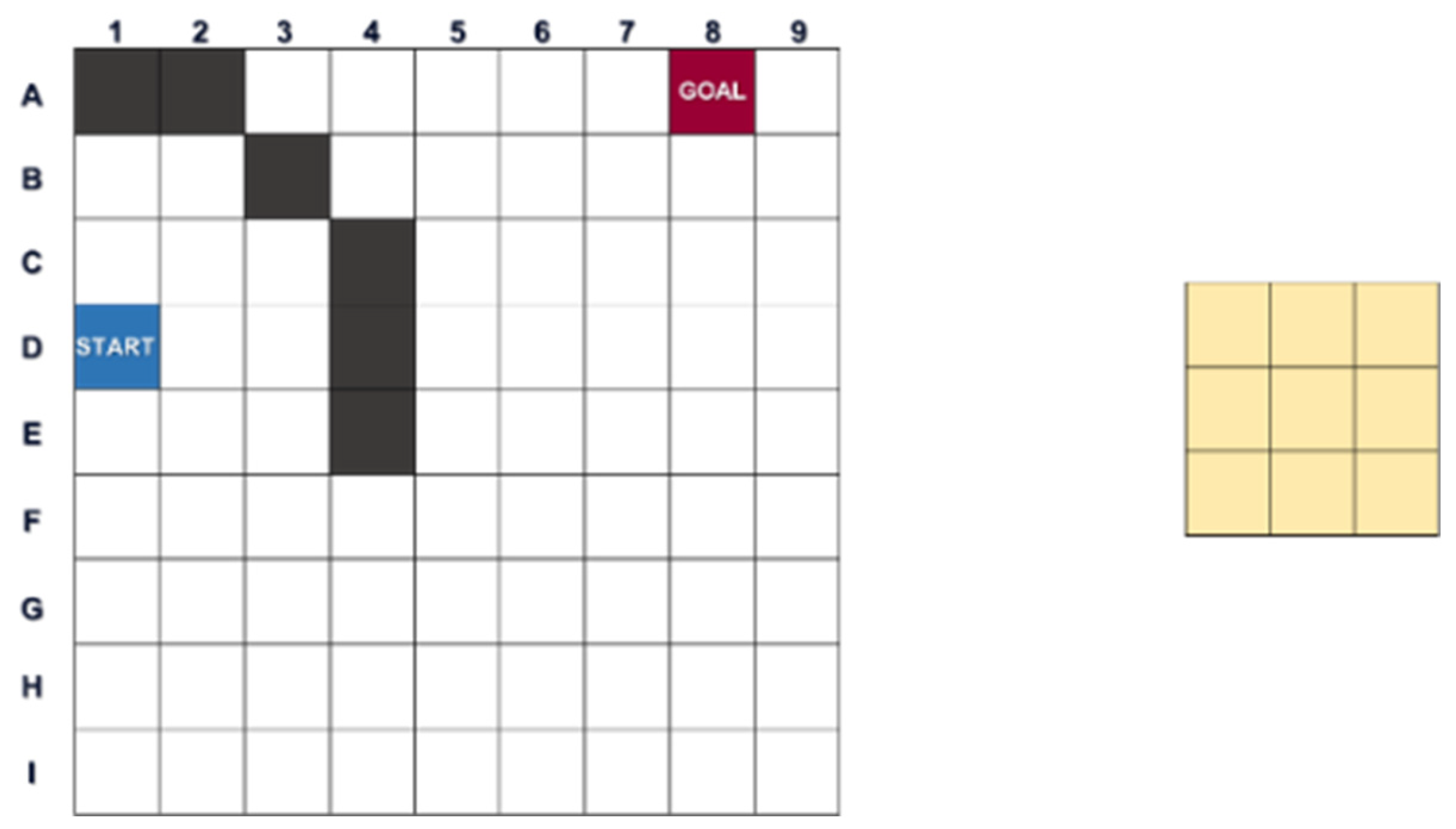
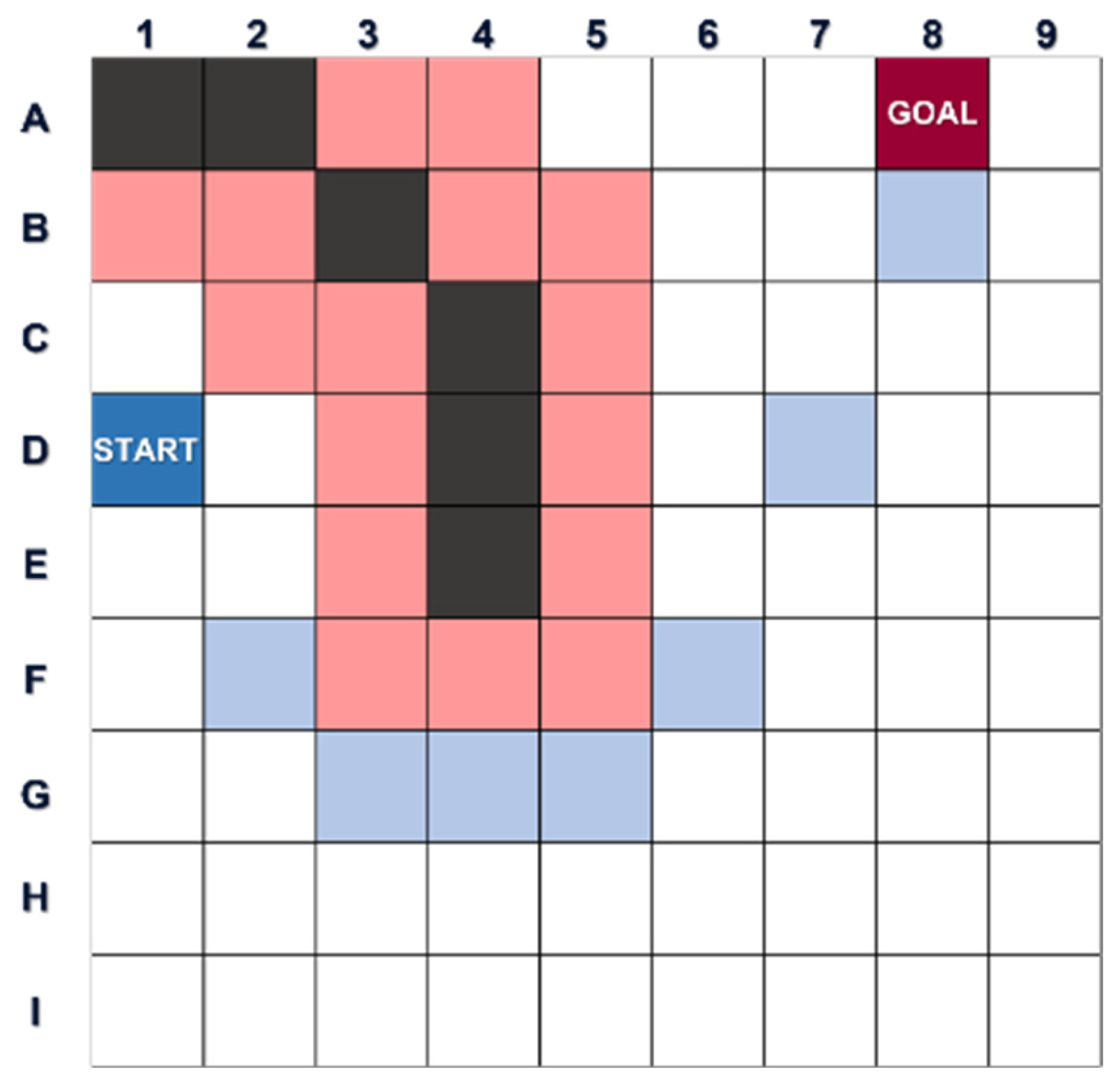
3.1.1. Edge Detection and Geofencing Construction
3.1.2. Collision-Free Waypoint-Searching Method with a Multi-Sided Finite Angle A* (FAA*) Algorithm
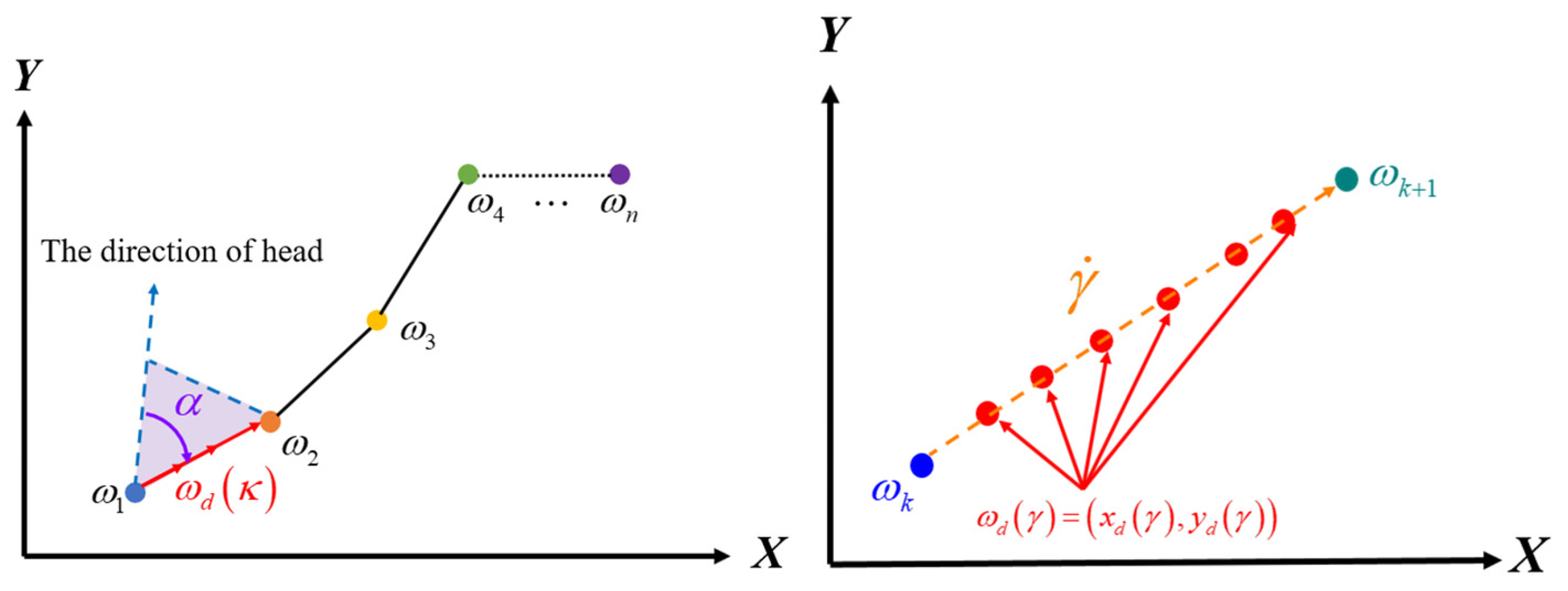
3.1.3. Continuous Trajectory Generator
3.1.4. Continuous and Smooth Trajectory Generator
4. Nonlinear Robust Control Law Design for USVs with Modeling Uncertainties and Ocean Disturbances
Robust Eliminator Design
- adjusting and can decrease the tracking errors in a steady state period;
- adjusting can speed up the transient response and quickly converge tracking errors.
5. Control Allocation Methodology for Installed Actuators
5.1. Configuration and Input–Output Model of Actuators
5.2. Optimization for Actuators’ Output Commands
6. Performance Validation of the Proposed Unified Control System
6.1. System Parameters of the Controlled USV
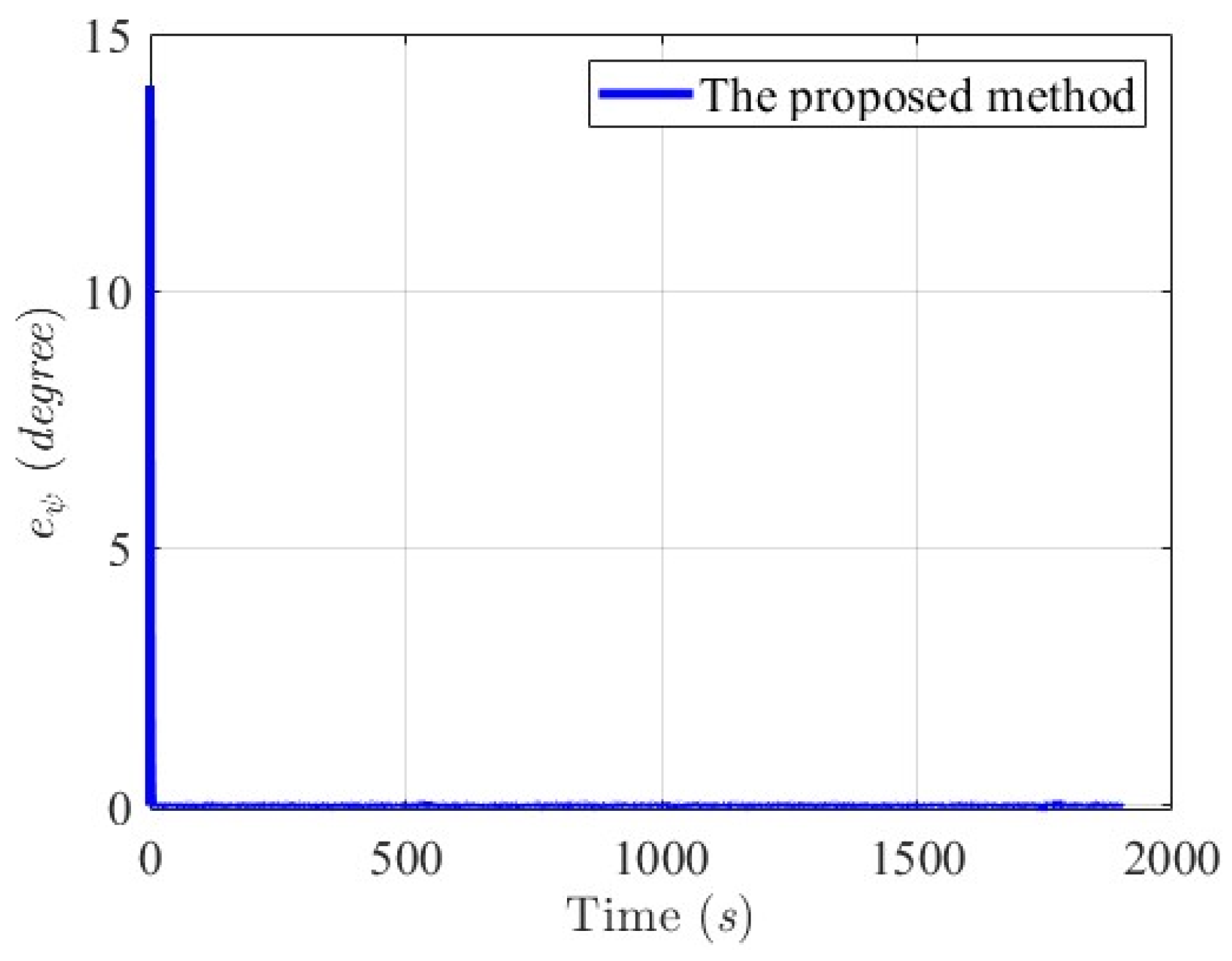
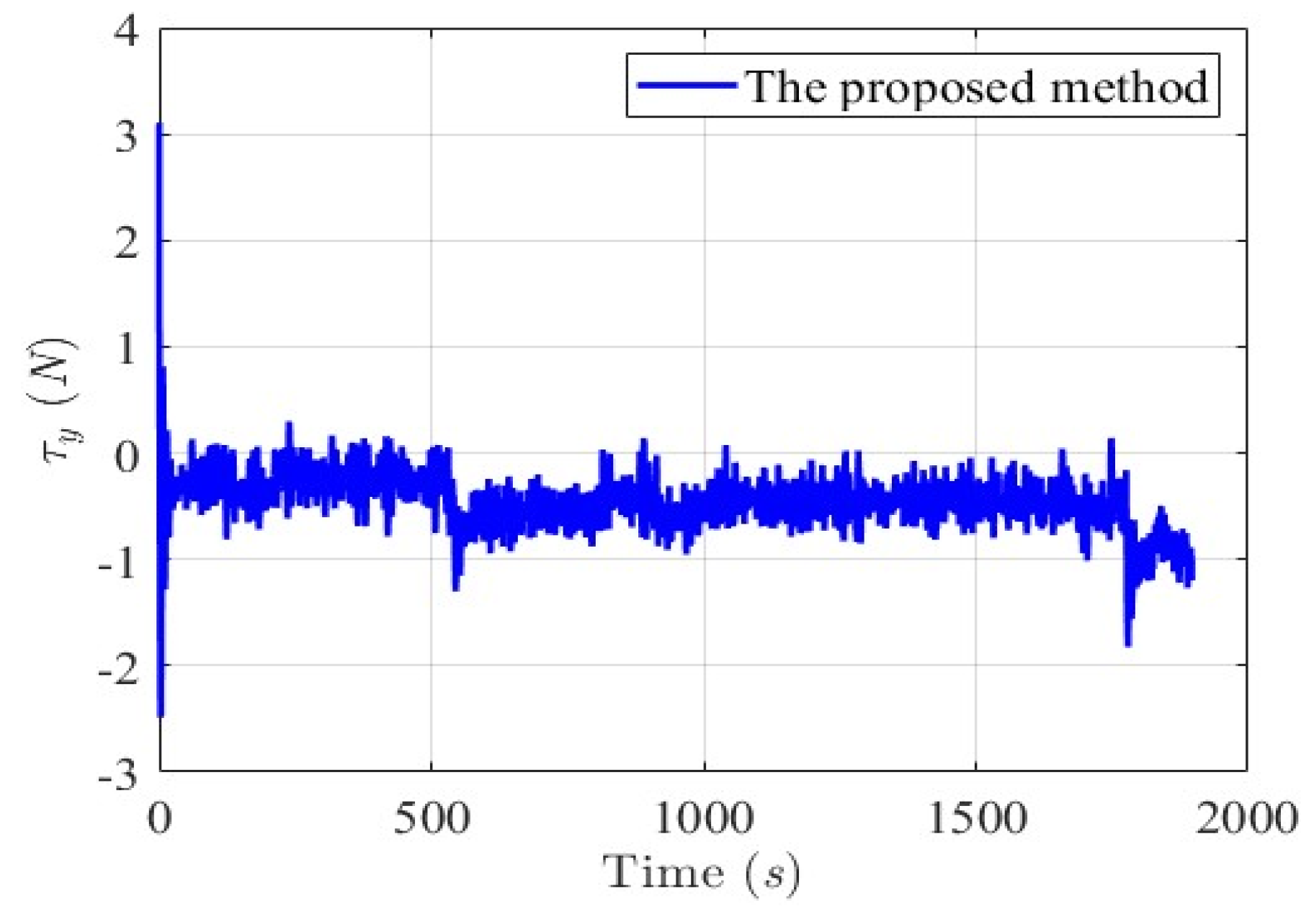
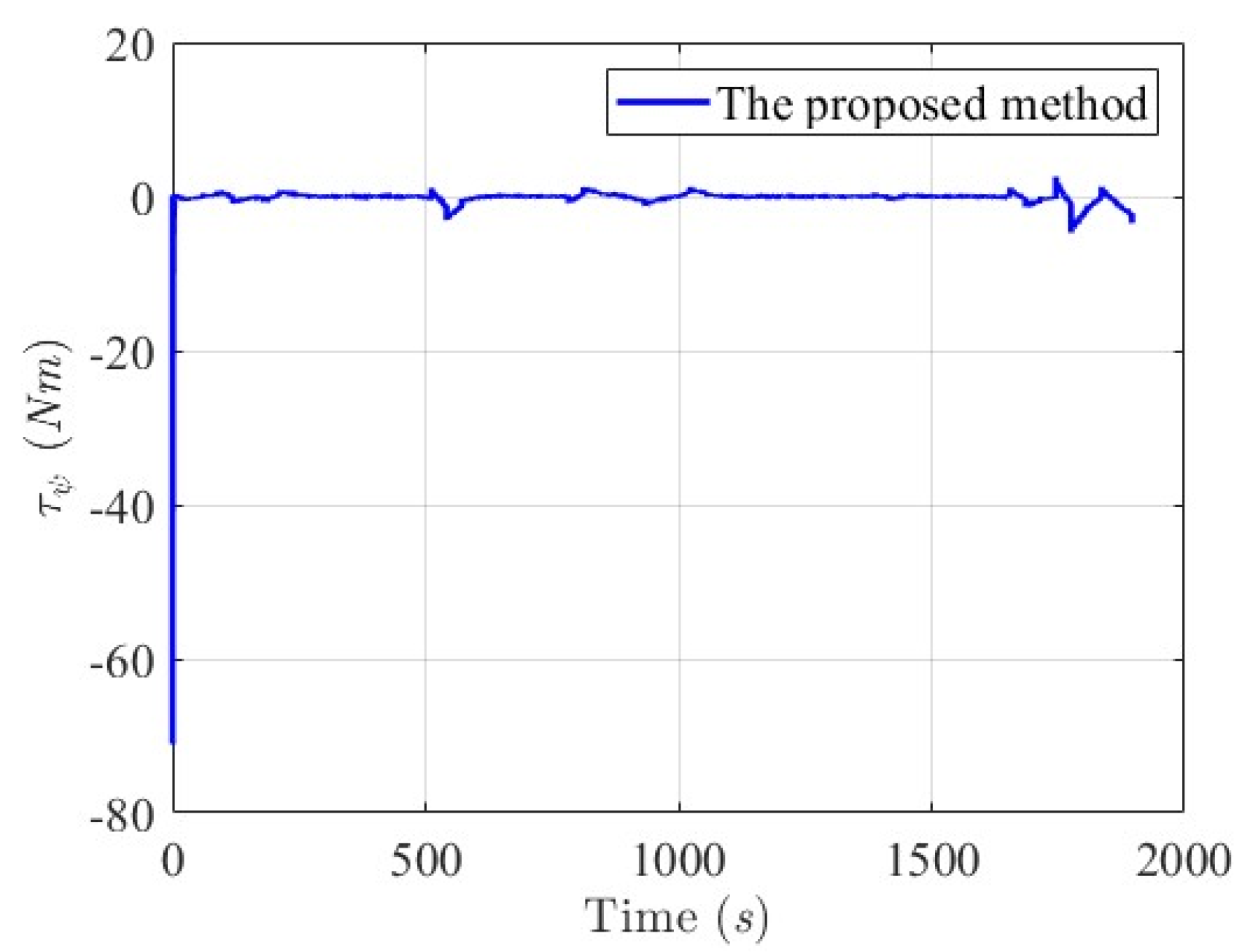
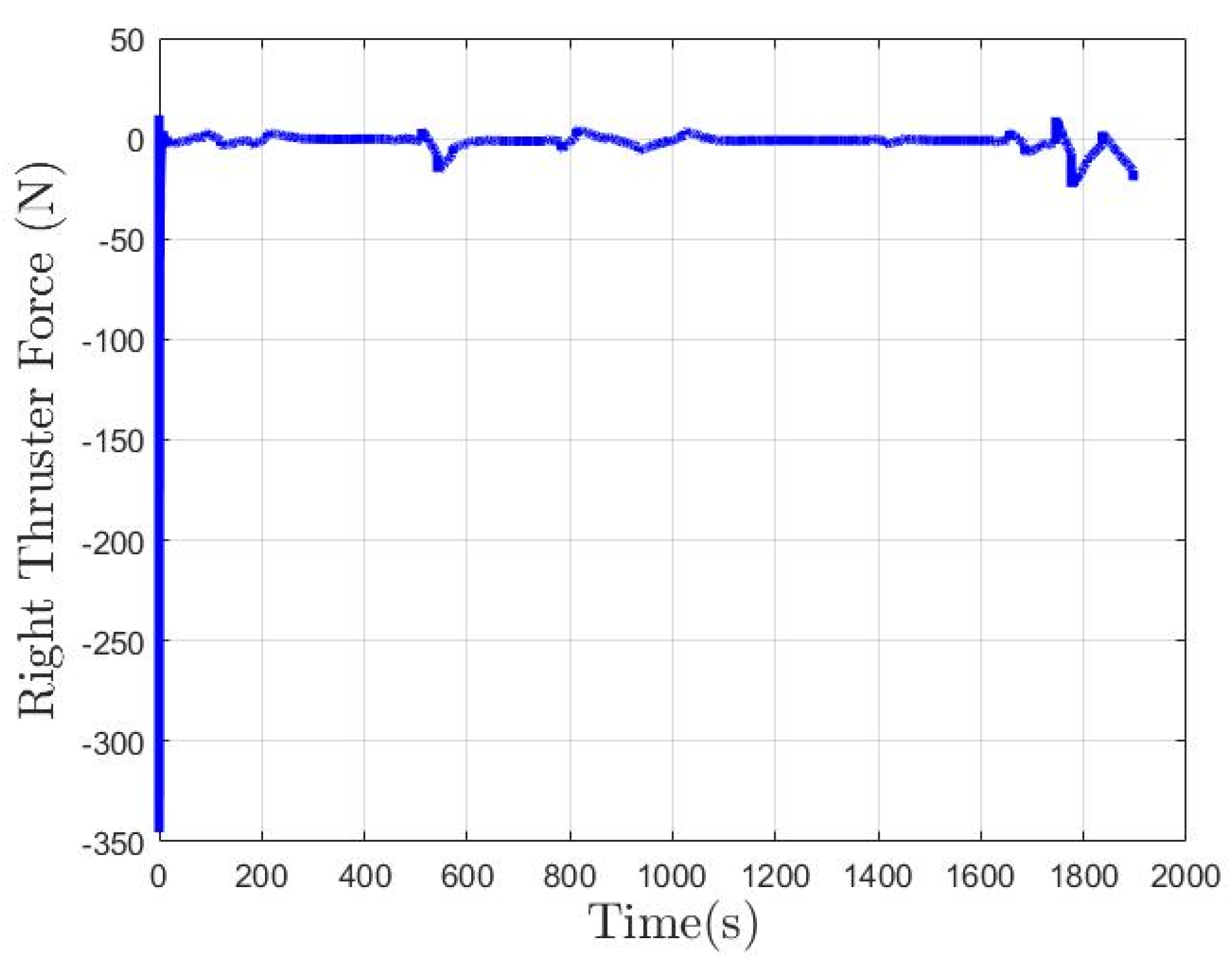
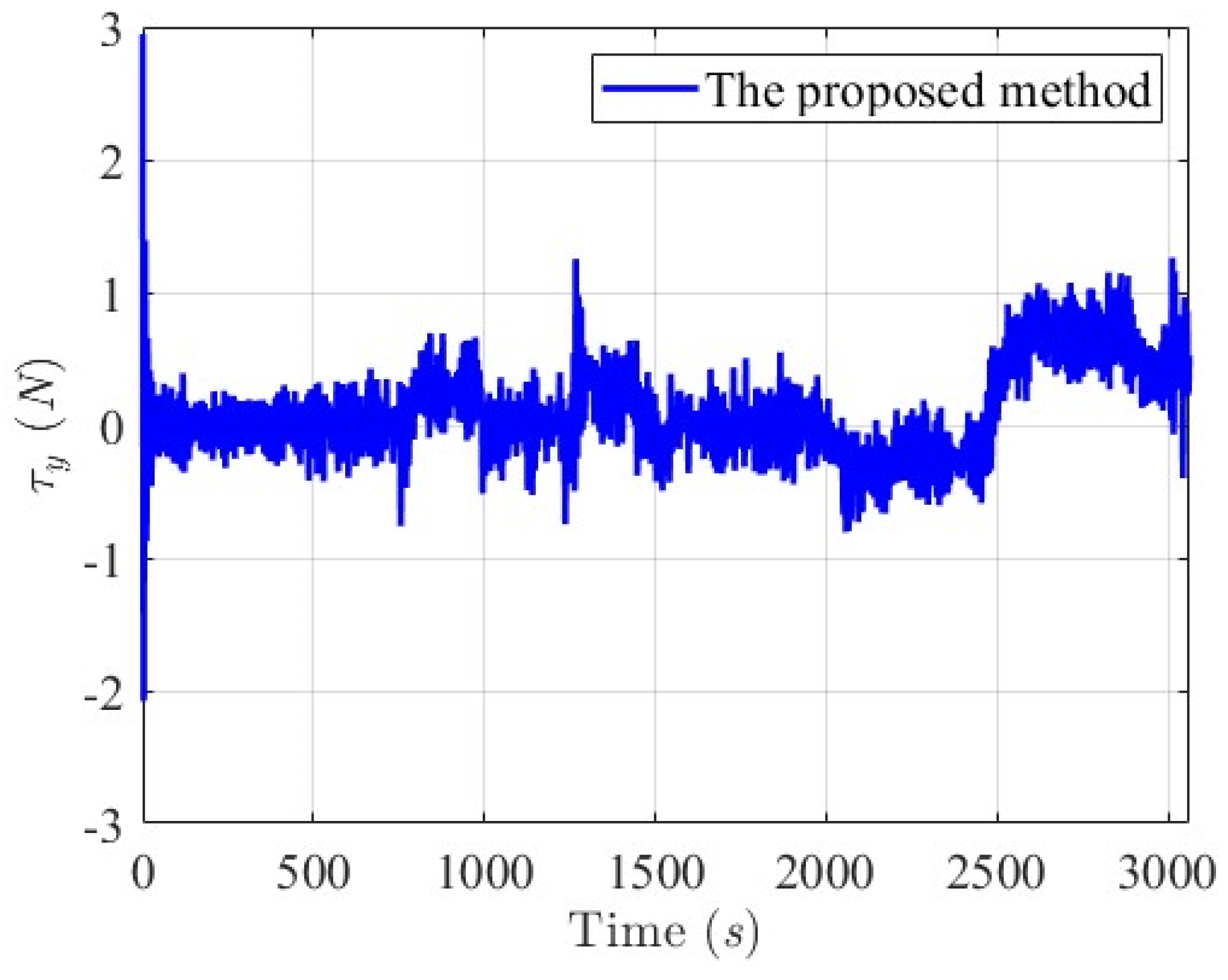
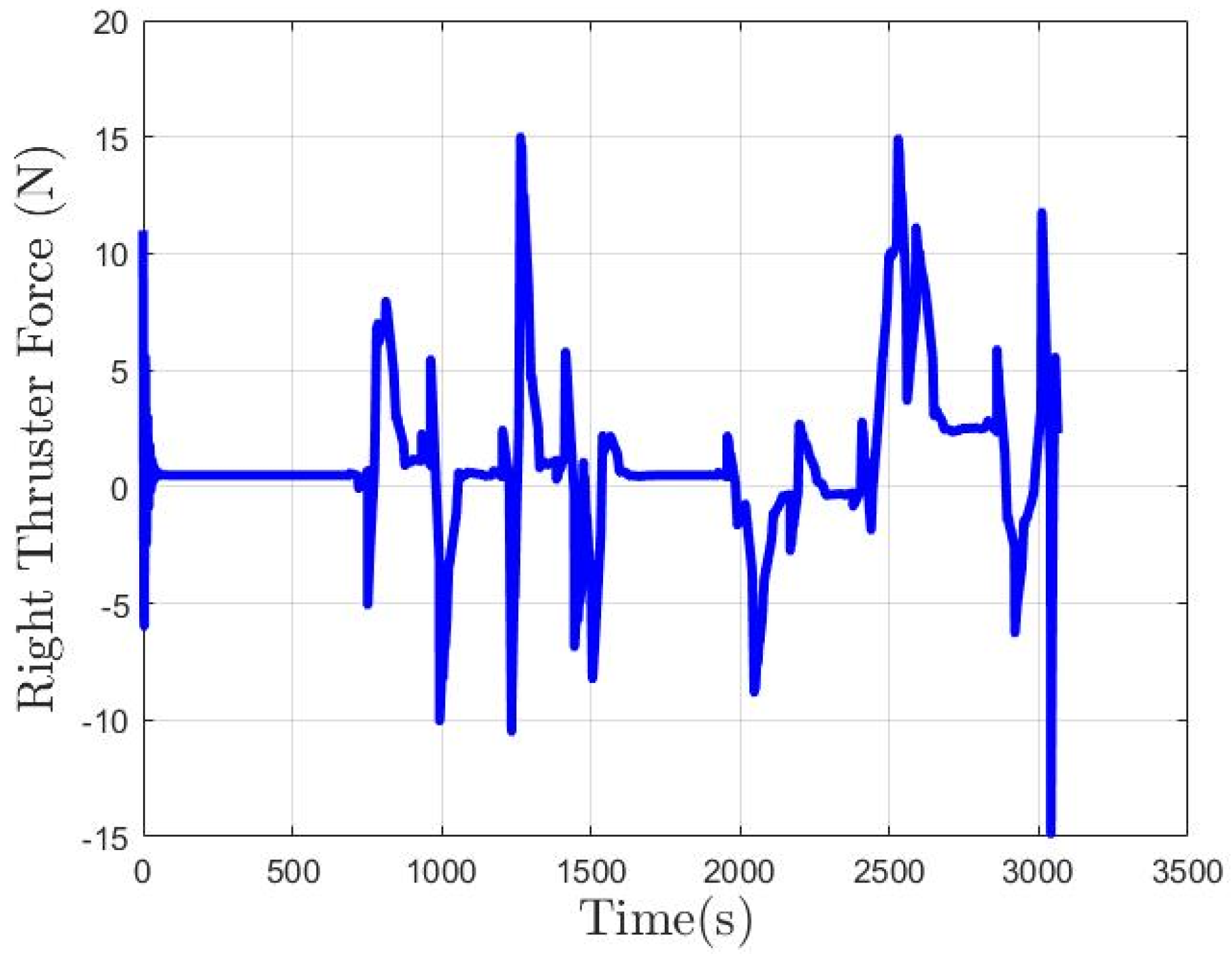
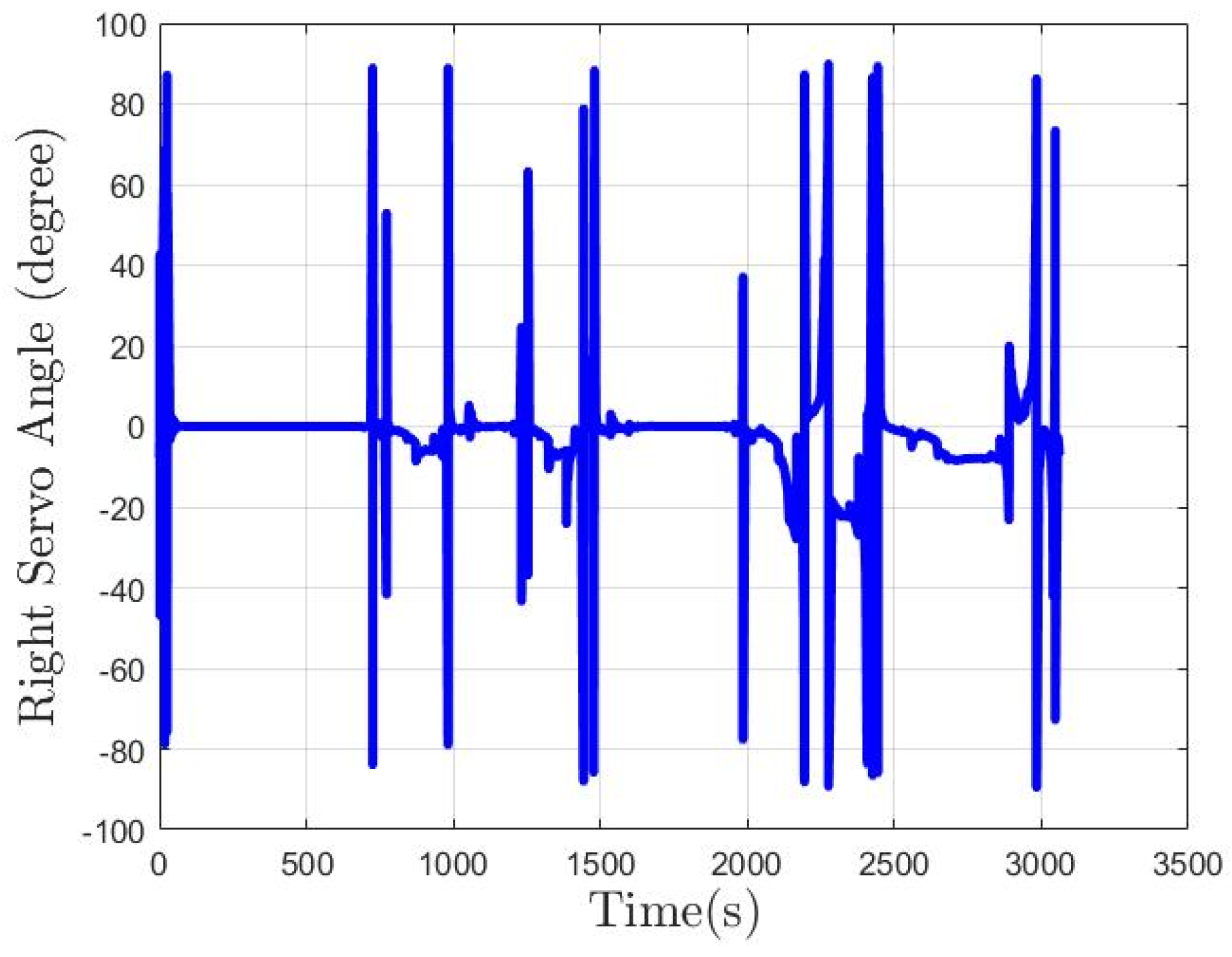
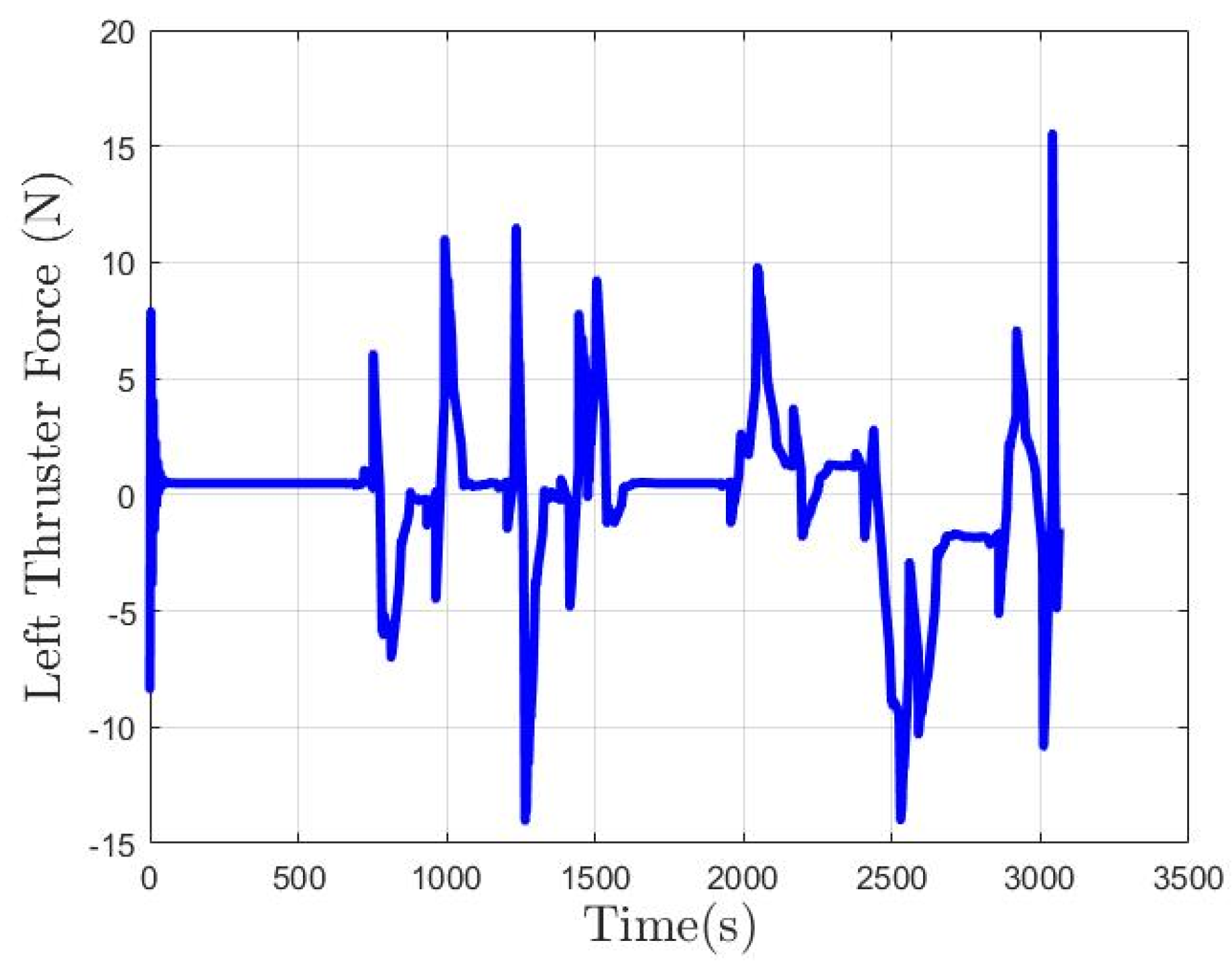
6.2. Simulation Results for Collision-Free and Trajectory-Tracking Verification
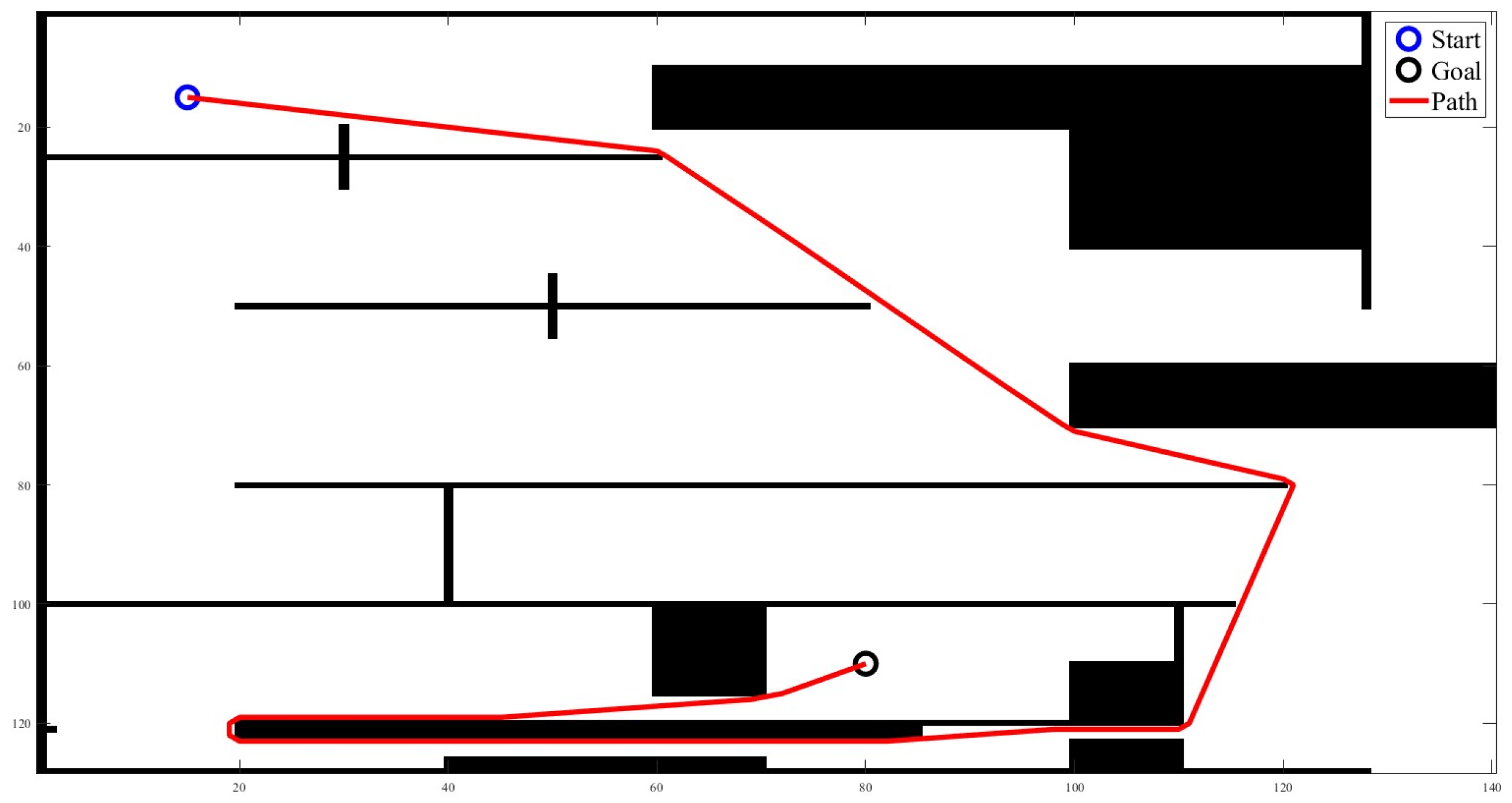
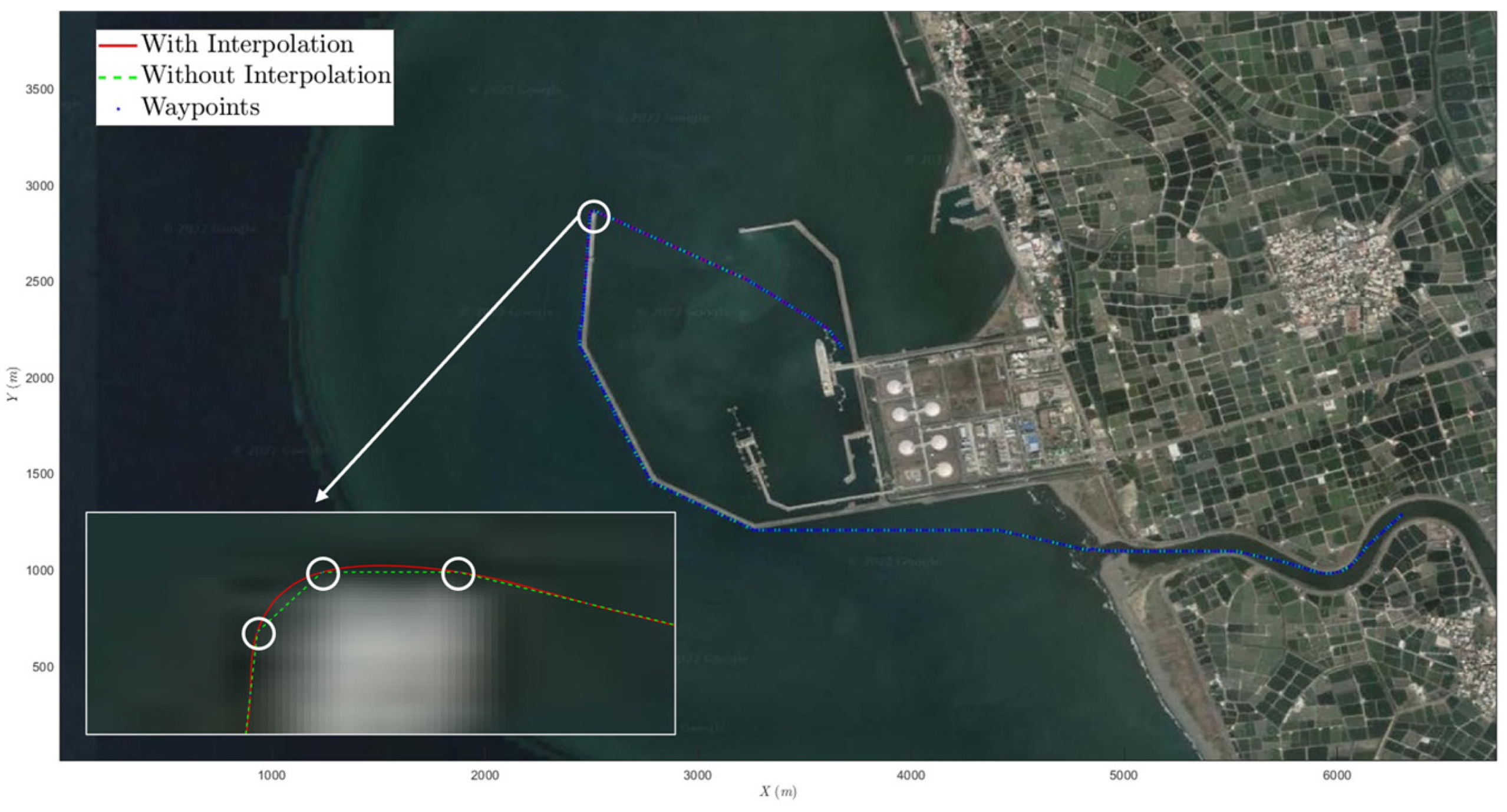
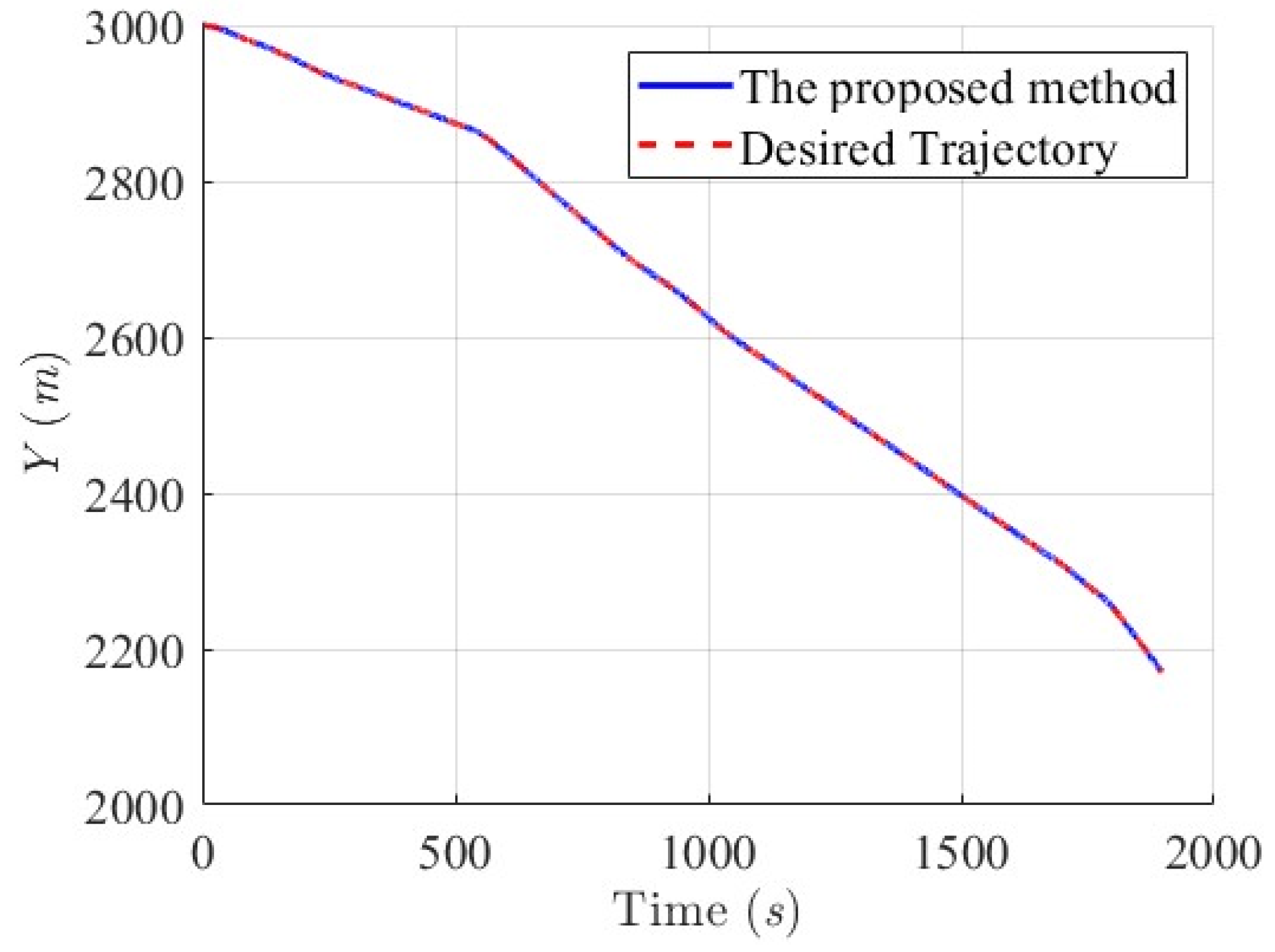
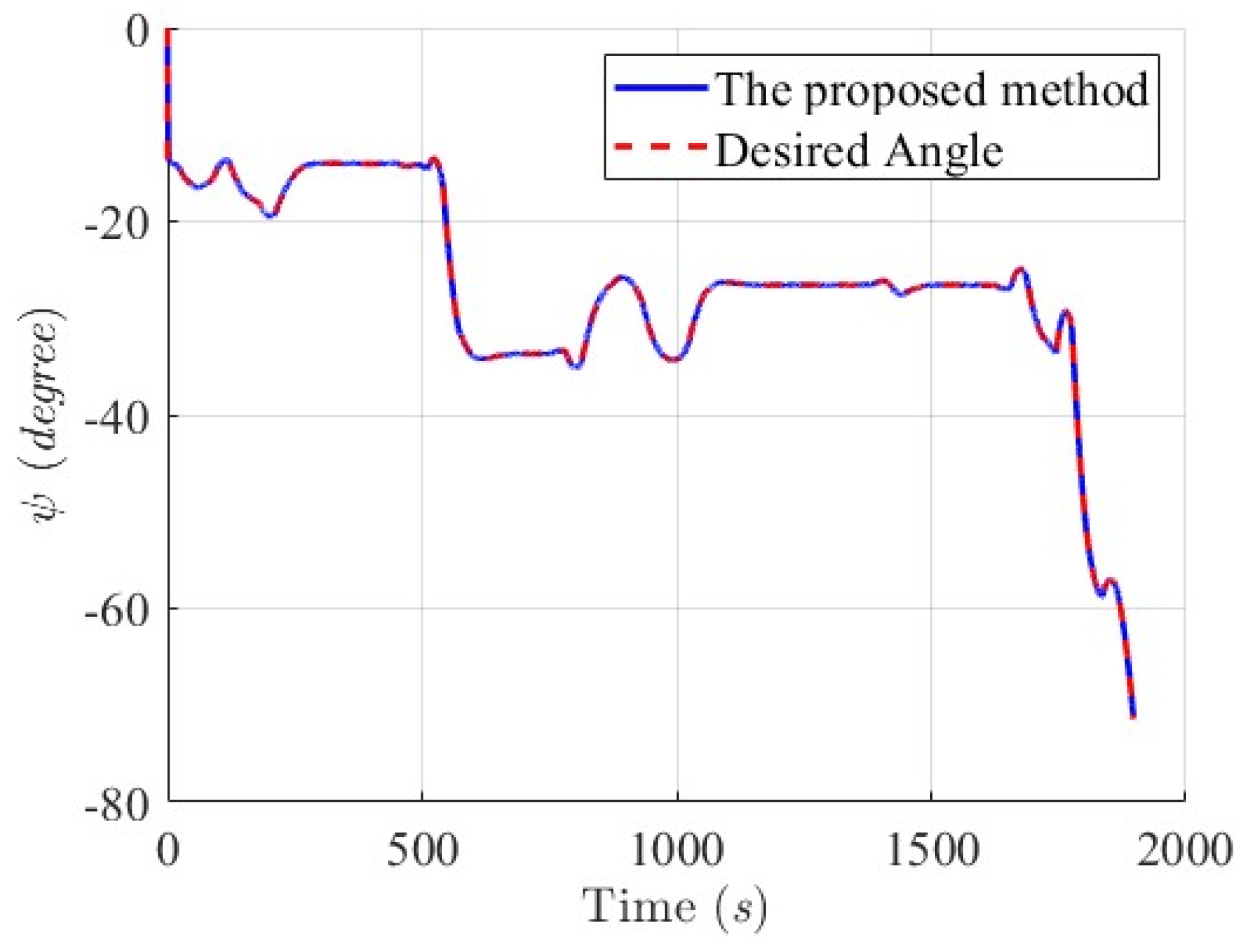
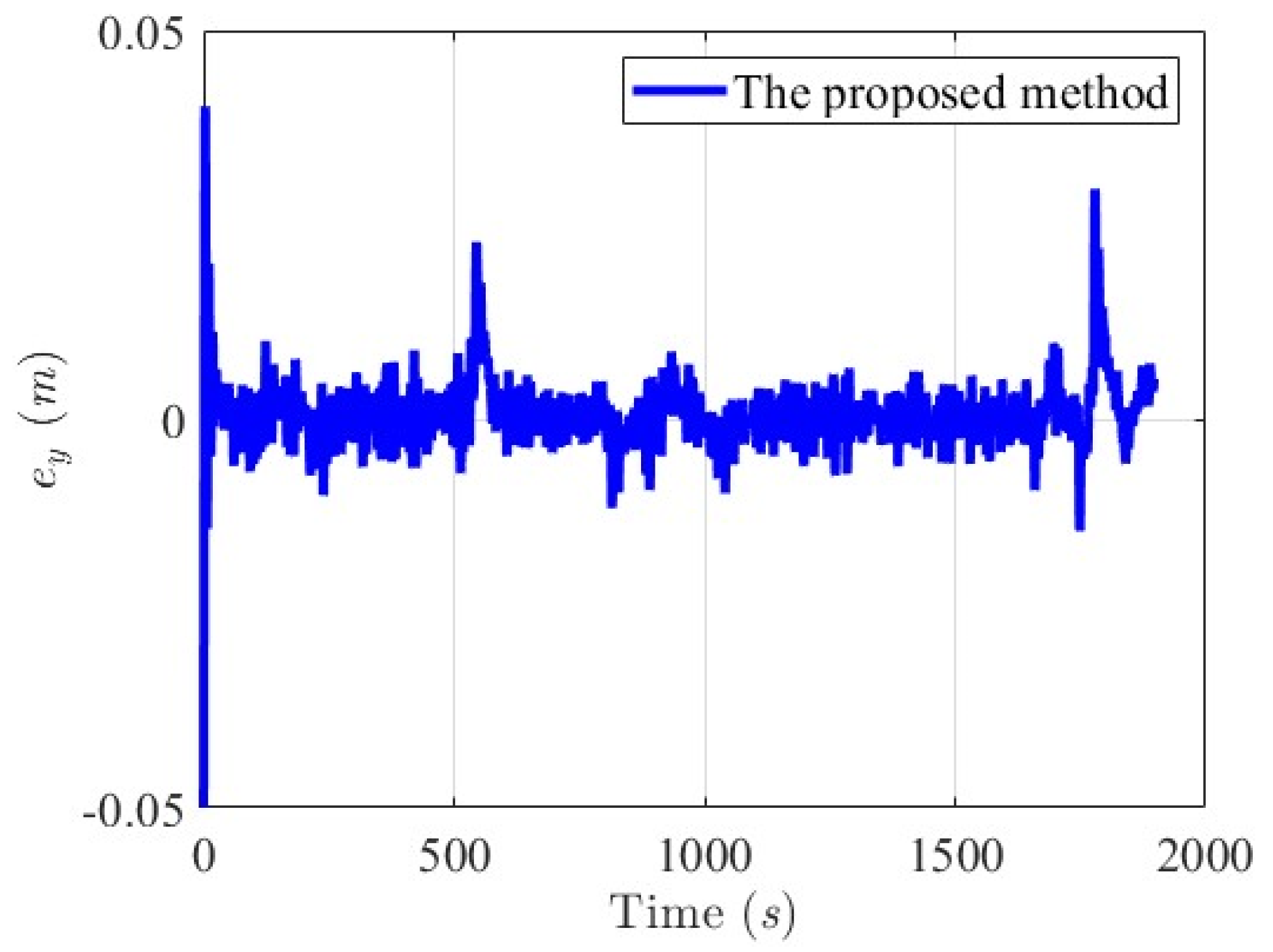
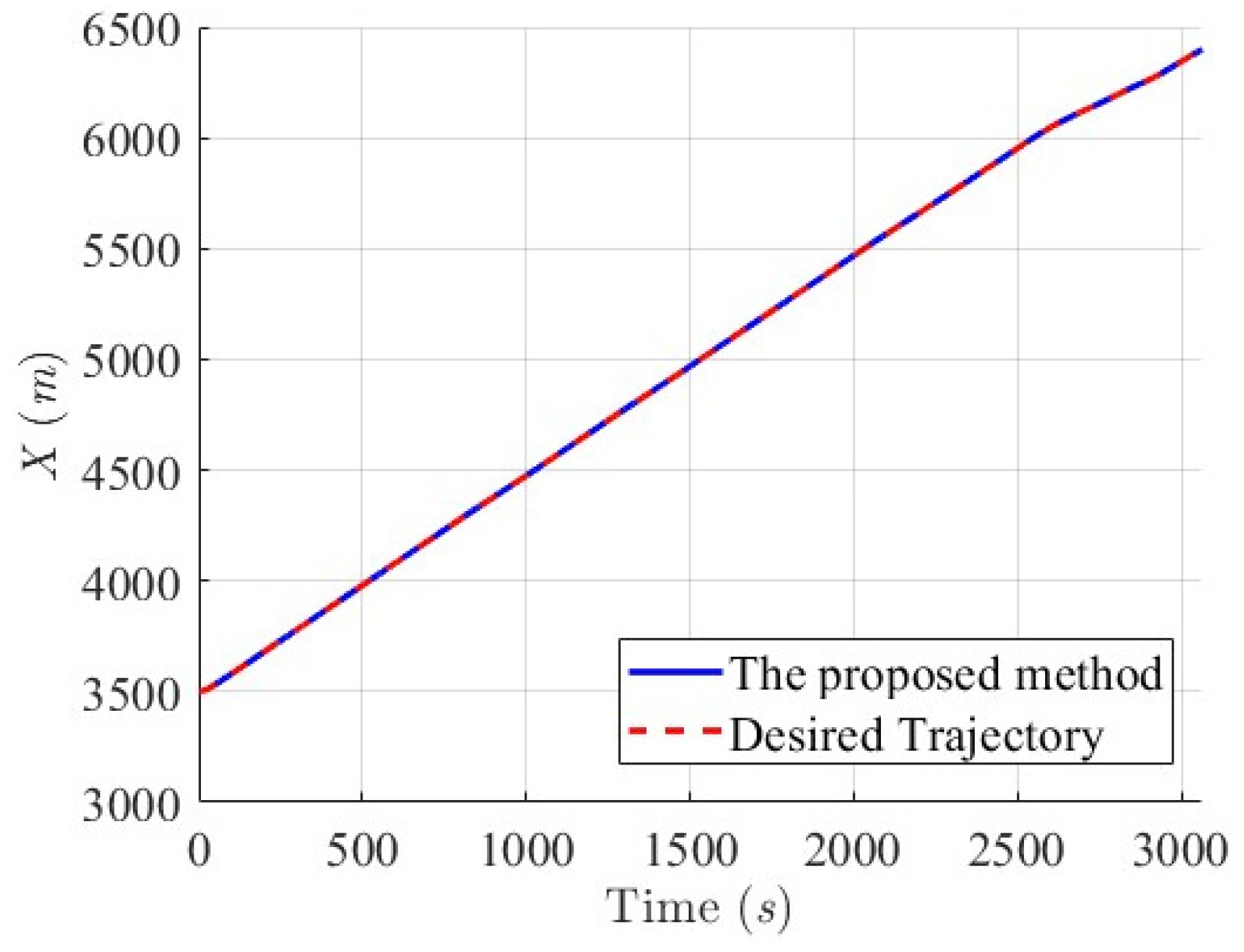
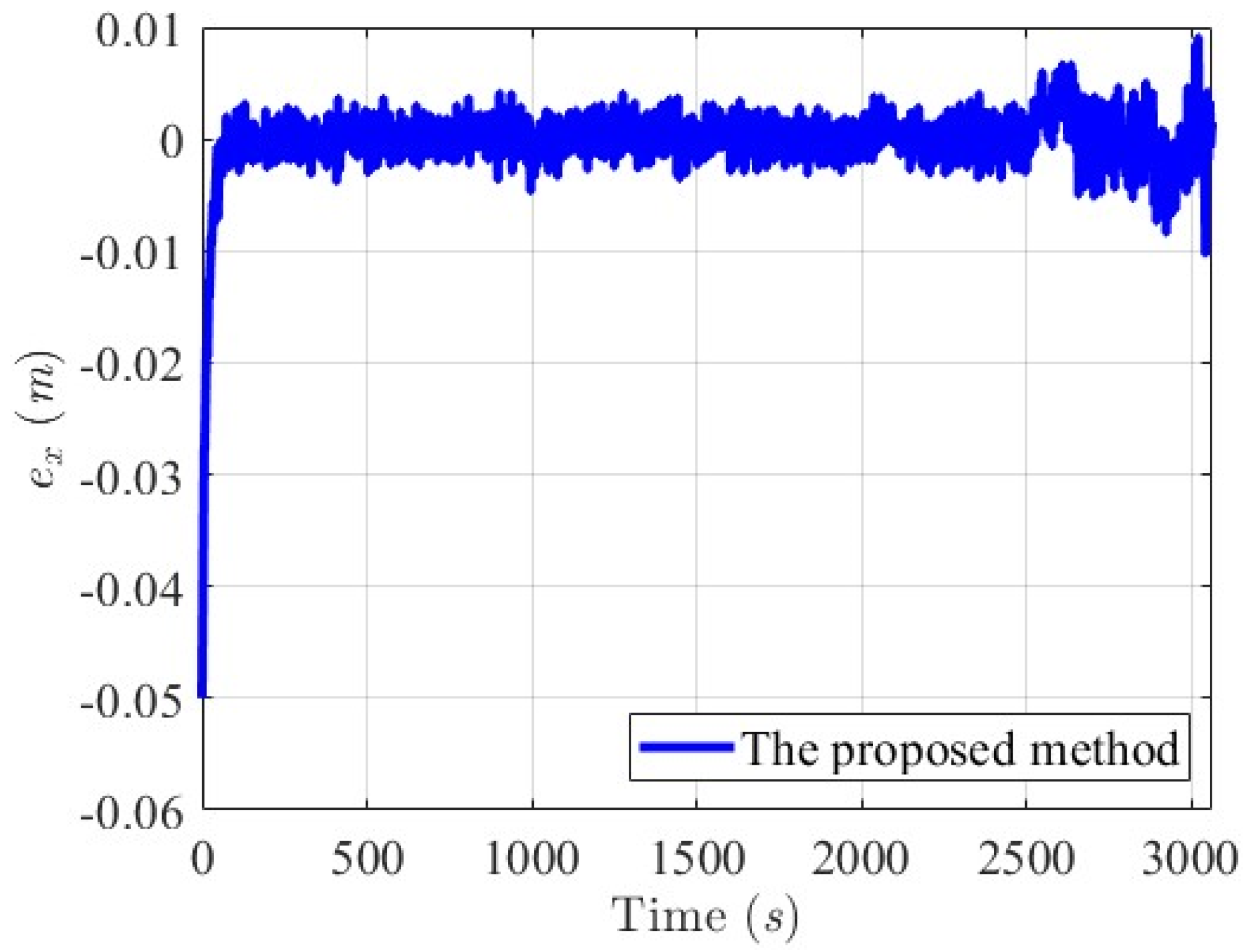
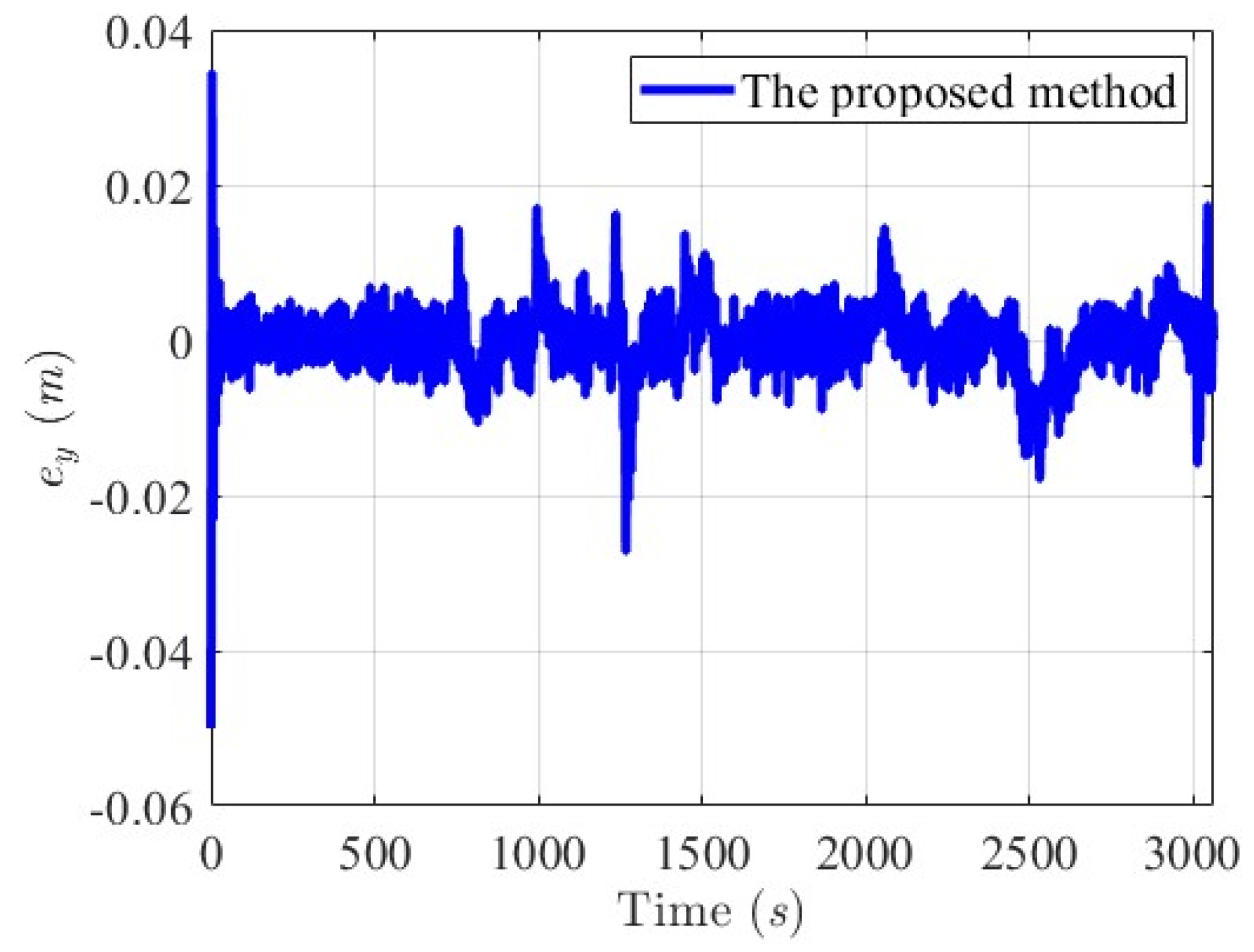
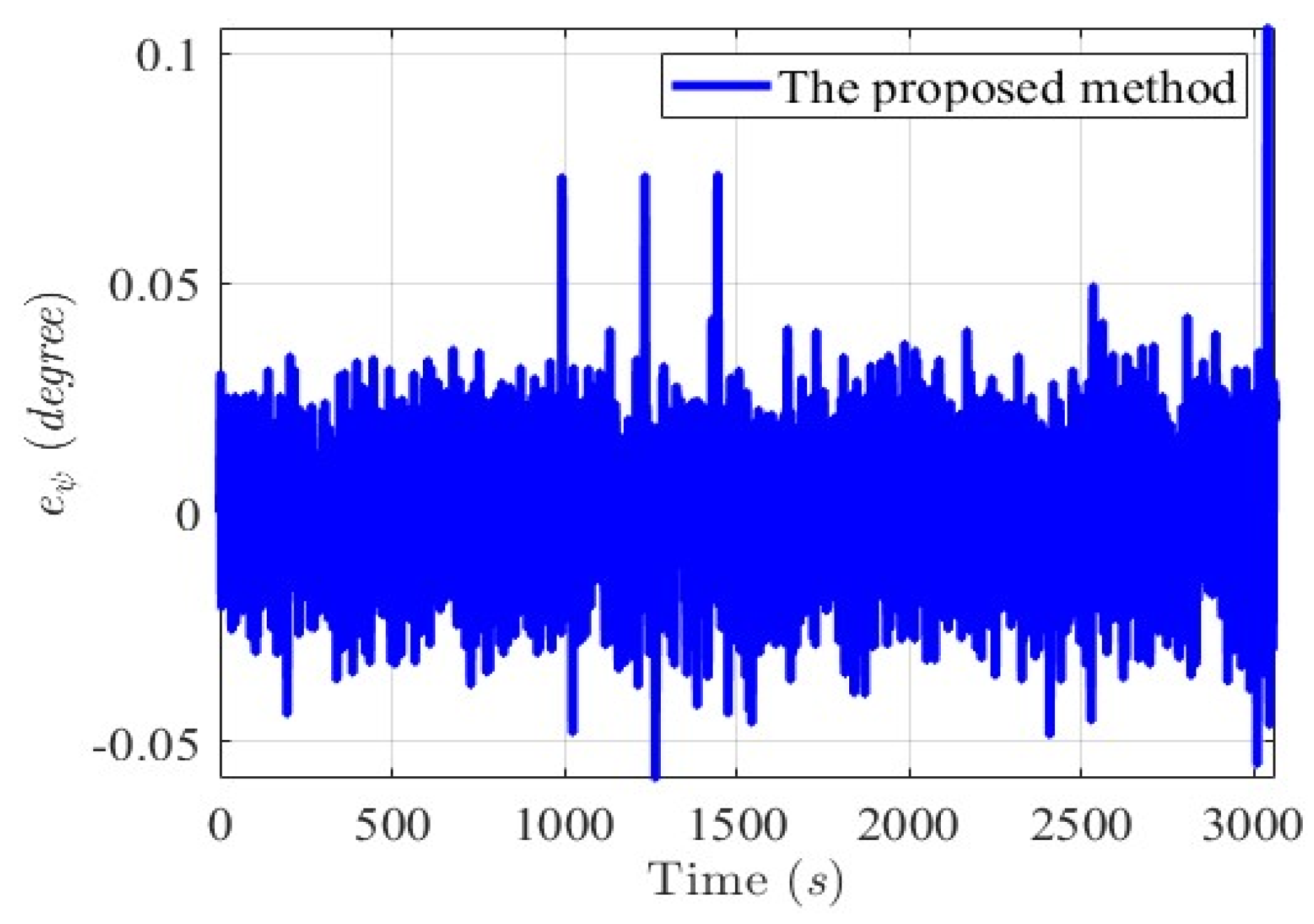
6.2.1. Scenario 1—USV Sails from Open Sea to Yongxin Harbor
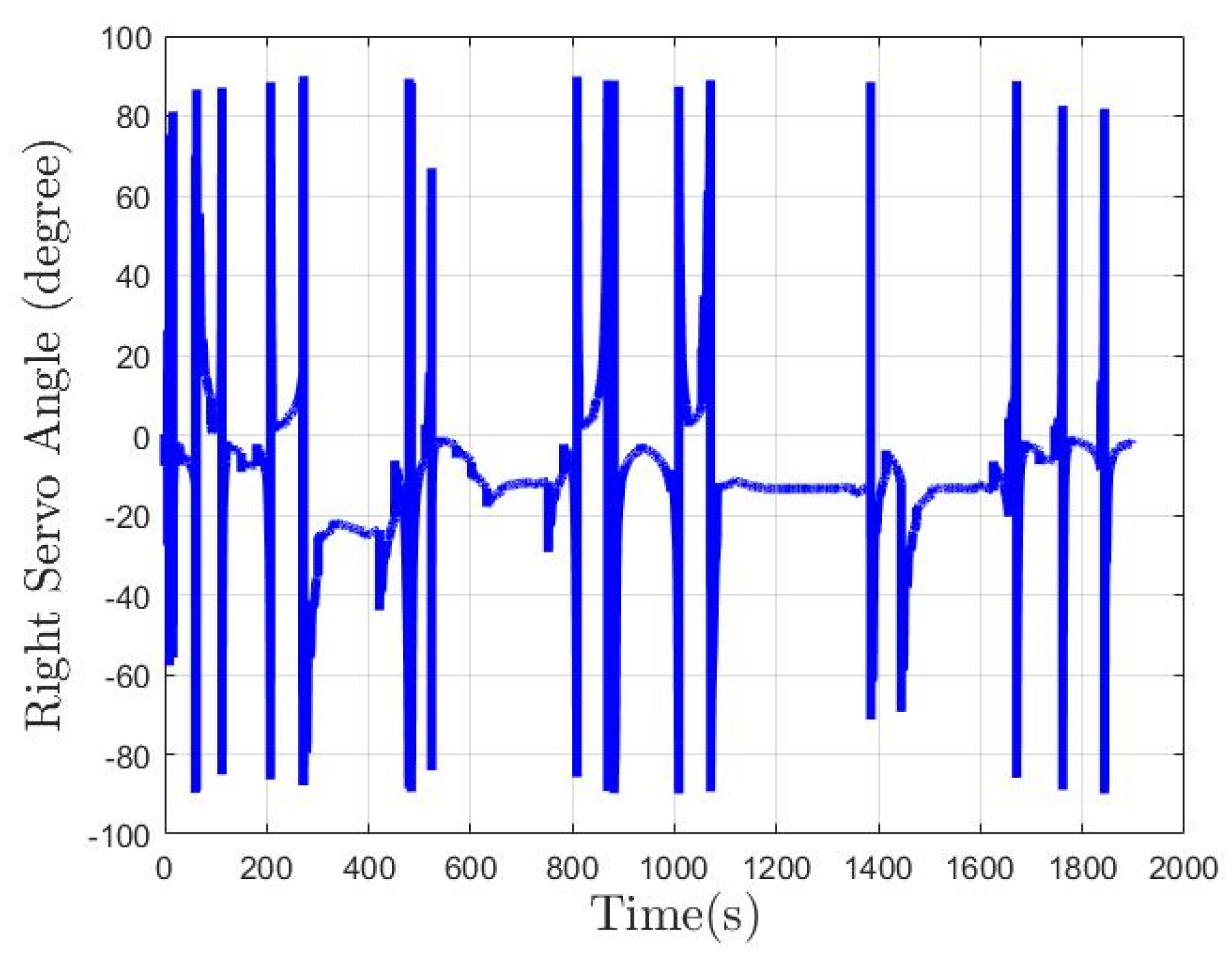
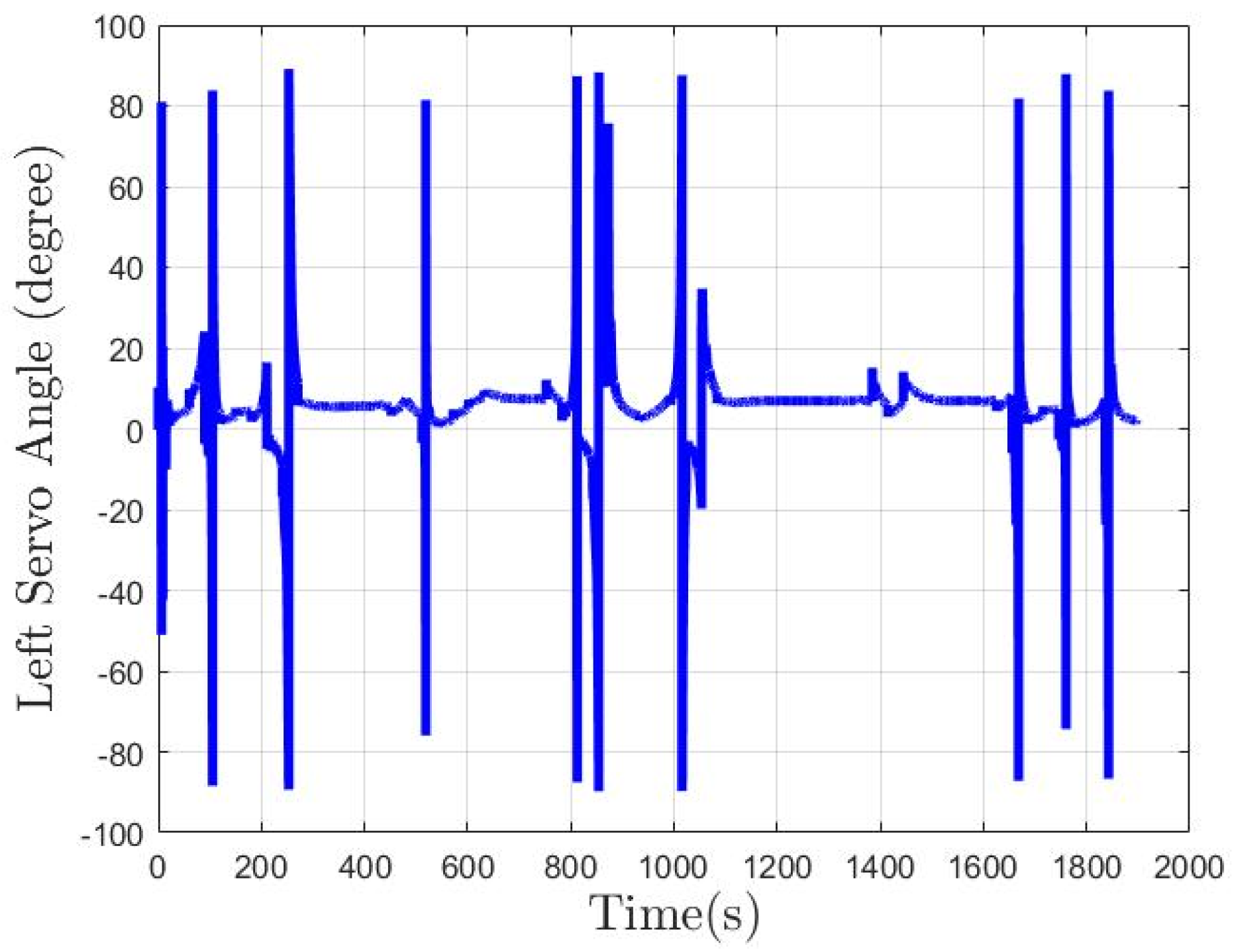
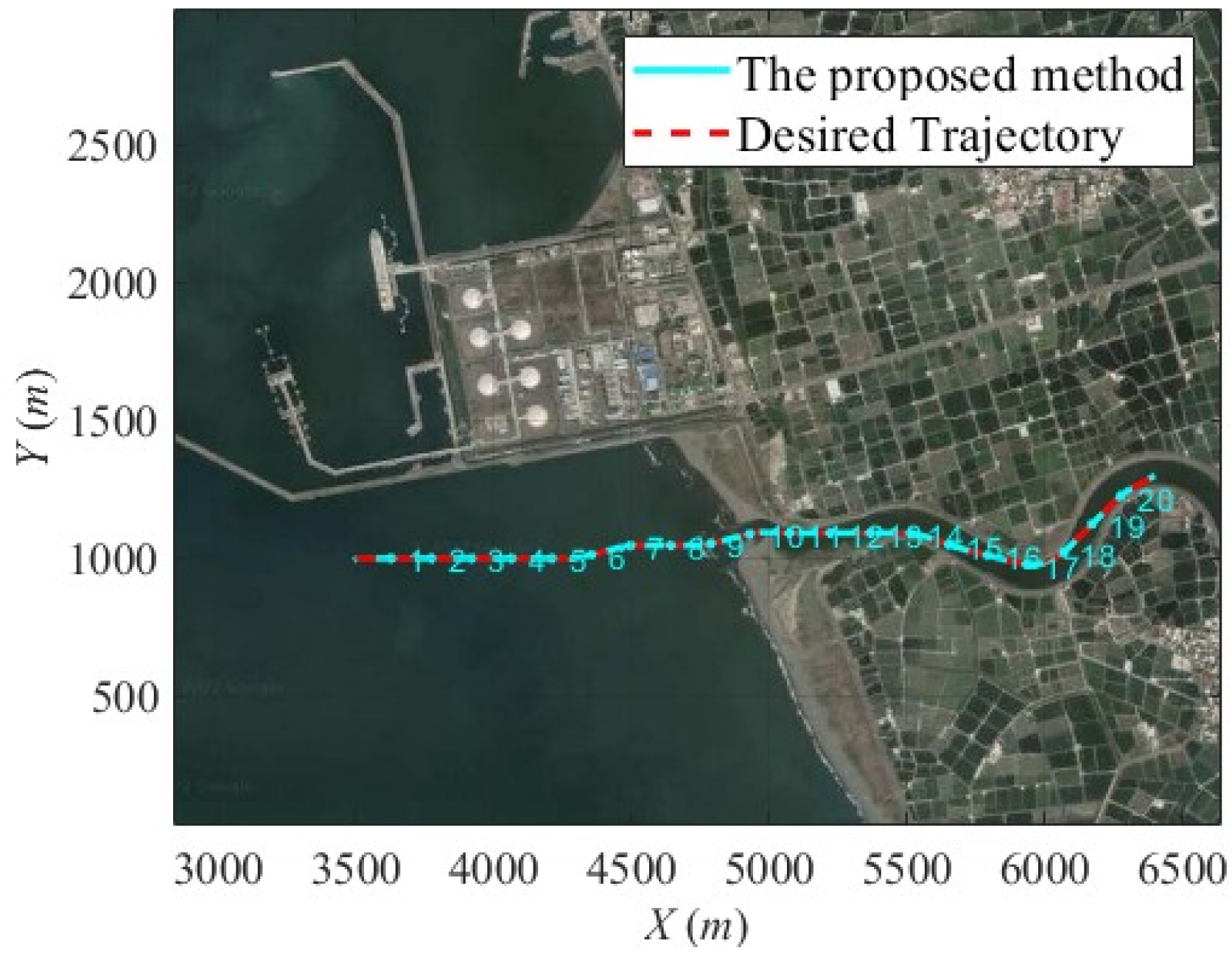
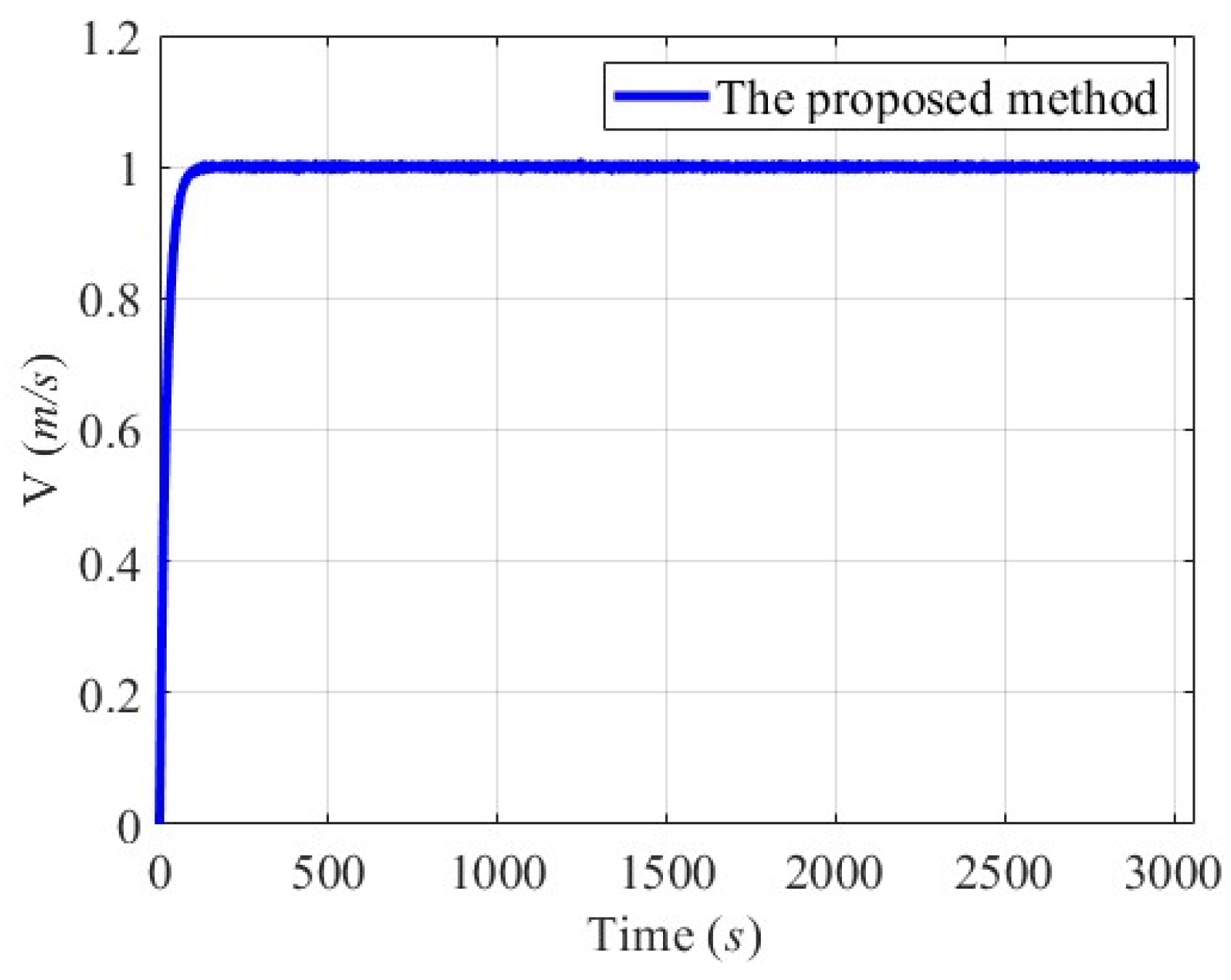
6.2.2. Scenario 2—Agongdian River
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorem 1
References
- Ships and Shipping of Tomorrow. Available online: https://books.google.com.tw/books/about/Ships_and_Shipping_of_Tomorrow.html?id=WC1UAAAAMAAJ&redir_esc=y (accessed on 1 January 1983).
- Autonomous Ships Market Expected to Reach US$ 235.73 Bn by 2028. Acute Market Reports. Available online: https://www.acutemarketreports.com/press/global-autonomous-ships-market (accessed on 15 March 2022).
- Avikus, H.D.H. Successfully Conducts the World’s First Transoceanic Voyage of a Large Merchant Ship Relying on Autonomous Navigation Technologies; HD Hyundai: Seoul, Republic of Korea, 2022. [Google Scholar]
- Ma, H.; Smart, E.; Ahmed, A.; Brown, D. Radar image-based positioning for USV under GPS denial environment. IEEE Trans. Intell. Transp. Syst. 2018, 19, 72–80. [Google Scholar] [CrossRef]
- Campbell, S.; Naeem, W.; Irwin, G.W. A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres. Annu. Rev. Control 2012, 36, 267–283. [Google Scholar] [CrossRef]
- Song, R.; Liu, Y.; Bucknall, R. Smoothed A* algorithm for practical unmanned surface vehicle path planning. Appl. Ocean Res. 2019, 83, 9–20. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S.-H.; Jeon, M.; Kim, J.; Song, S.; Paik, K.-J. A study on path optimization method of an unmanned surface vehicle under environmental loads using genetic algorithm. Ocean Eng. 2017, 142, 616–624. [Google Scholar] [CrossRef]
- Liu, Y.; Bucknall, R.; Zhang, X. The fast marching method based intelligent navigation of an unmanned surface vehicle. Ocean Eng. 2017, 142, 363–376. [Google Scholar] [CrossRef]
- Wang, N.; Ahn, C.K. Hyperbolic-tangent LOS guidance-based finite time path following of underactuated marine vehicles. IEEE Trans. Ind. Electron. 2020, 67, 8566–8575. [Google Scholar] [CrossRef]
- Zheng, Z.; Sun, L.; Xie, L. Error-constrained LOS path following of a surface vessel with actuator saturation and faults. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1794–1805. [Google Scholar] [CrossRef]
- Li, J.-H.; Lee, P.-M.; Jun, B.-H.; Lim, Y.-K. Point-to-point navigation of underactuated ships. Automatica 2008, 44, 3201–3205. [Google Scholar] [CrossRef]
- Chen, Y.-Y.; Lee, C.-Y.; Tseng, S.-H.; Hu, W.-M. Nonlinear Optimal Control Law of Autonomous Unmanned Surface Vessels. Appl. Sci. 2020, 10, 1686. [Google Scholar] [CrossRef]
- Yi, B.; Qiao, L.; Zhang, W. Two-time scale path following of underactuated marine surface vessels: Design and stability analysis using singular perturbation methods. Ocean Eng. 2016, 124, 287–297. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Tiew, M.Z.E.; Chan, Y.-H.; Lin, G.-W.; Chen, Y.-Y. Trajectory Tracking Design for Unmanned Surface Vessels: Robust Control Approach. J. Mar. Sci. Eng. 2023, 8, 1612. [Google Scholar] [CrossRef]
- Qin, H.; Chen, H.; Sun, Y.; Chen, L. Distributed finite-time fault tolerant containment control for multiple ocean bottom flying node systems with error constraints. Ocean Eng. 2019, 189, 106341. [Google Scholar] [CrossRef]
- Abdelhamid, B.; Mohamed, C. Adaptive fuzzy fault-tolerant control using Nussbaum-type function with state-dependent actuator failures. Neu Comp. App 2021, 33, 191–208. [Google Scholar]
- Yue, H.; Xue, A.; Li, J. Adaptive fuzzy finite-time output feedback fault-tolerant control for MIMO stochastic nonlinear systems with non-affine nonlinear faults. J. Low Freq. Noise Vib. Act. Control 2024, 43, 1312–1338. [Google Scholar] [CrossRef]
- Sofiane, B.; Mohammed, C.; Salim, Z. The International Conference on Electrical Engineering and Control Applications. In Proceedings of the 4th International Conference on Electrical Engineering and Control Applications, Constantine, Algeria, 17–19 December 2019. [Google Scholar]
- Yang, J.M.; Chen, Y.-Y.; Tseng, P.S. Real-Time Path Planning for Unmanned Surface Vehicle by using Finite Angle A* Algorithm. J. Taiwan Soc. Nav. Archit. Mar. Eng. 2015, 34, 165–172. [Google Scholar]


















| Length L | 1.72 m |
| Width B | 0.4 m |
| Draft T | 0.3 m |
| Mass m | 41 kg |
| Iz | 6.522 kg∙m |
| xg | 0 m |
| −1.291 kg | |
| −40.326 kg | |
| −39.04525 N∙s2/m2 | |
| 200.79808 N∙m∙s | |
| −0.98 N∙s2/m2 | |
| −38.808 N∙s2/m2 | |
| −16.43778 N∙s | |
| −14.340 N∙s2/m2 | |
| −236.5 N∙m∙s |
| Thrust force of single waterjet | 400 N |
| Rotatable angle | ±120° |
| Starting Point | (3000 m, 2000 m) |
| Destination | (2100 m, 3600 m) |
| Sailing velocity of the controlled USV | 1 m/s |
| Initial Condition |
| Starting Point | (3500, 1000) |
| Destination | (6400, 1300) |
| Desired Velocity | 1 m/s |
| Initial Condition |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-Y.; Sun, C.-Y.; Hung, I.-C.; Chen, Y.-Y. A Unified Control System with Autonomous Collision-Free and Trajectory-Tracking Abilities for Unmanned Surface Vessels Under Effects of Modeling Certainties and Ocean Environmental Disturbances. Mathematics 2025, 13, 609. https://doi.org/10.3390/math13040609
Lee C-Y, Sun C-Y, Hung I-C, Chen Y-Y. A Unified Control System with Autonomous Collision-Free and Trajectory-Tracking Abilities for Unmanned Surface Vessels Under Effects of Modeling Certainties and Ocean Environmental Disturbances. Mathematics. 2025; 13(4):609. https://doi.org/10.3390/math13040609
Chicago/Turabian StyleLee, Chun-Yen, Cheng-Yen Sun, I-Ching Hung, and Yung-Yue Chen. 2025. "A Unified Control System with Autonomous Collision-Free and Trajectory-Tracking Abilities for Unmanned Surface Vessels Under Effects of Modeling Certainties and Ocean Environmental Disturbances" Mathematics 13, no. 4: 609. https://doi.org/10.3390/math13040609
APA StyleLee, C.-Y., Sun, C.-Y., Hung, I.-C., & Chen, Y.-Y. (2025). A Unified Control System with Autonomous Collision-Free and Trajectory-Tracking Abilities for Unmanned Surface Vessels Under Effects of Modeling Certainties and Ocean Environmental Disturbances. Mathematics, 13(4), 609. https://doi.org/10.3390/math13040609





