Golden Ratio Function: Similarity Fields in the Vector Space
Abstract
1. Introduction
- The concept of the golden ratio has generalization in the multi-dimensional vector space;
- The general golden ratio is a function of one or more angles, and this is one of four solutions to the golden equation presented here;
- Each vector in space corresponds to a set of similarities or a set of vectors in the golden ratio with ;
- GGR can be used to describe similar figures, such as a vector space of triangles;
- Each vector affects its environment, exerting its influence through the imposition of its likeness or similarities;
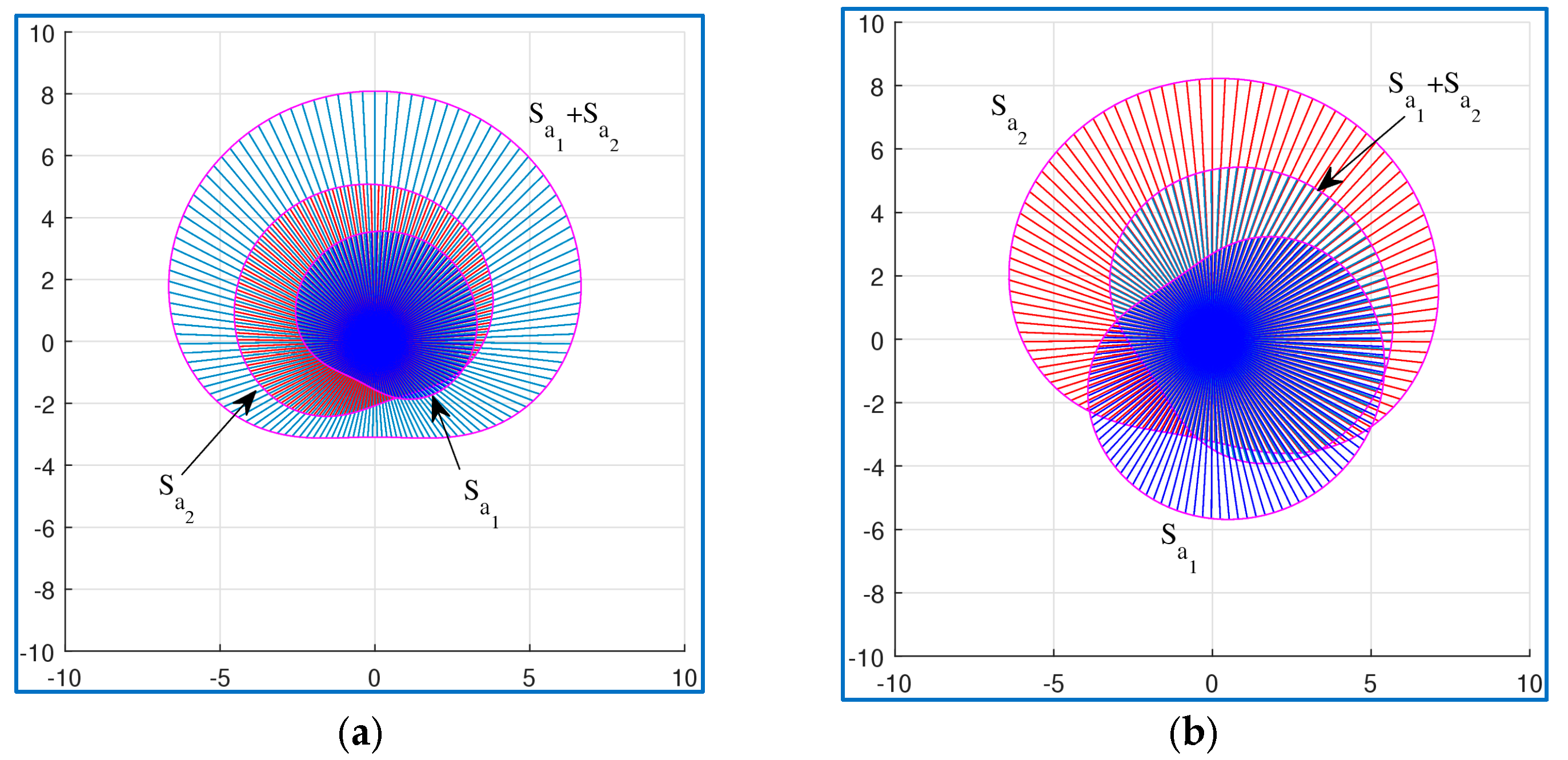
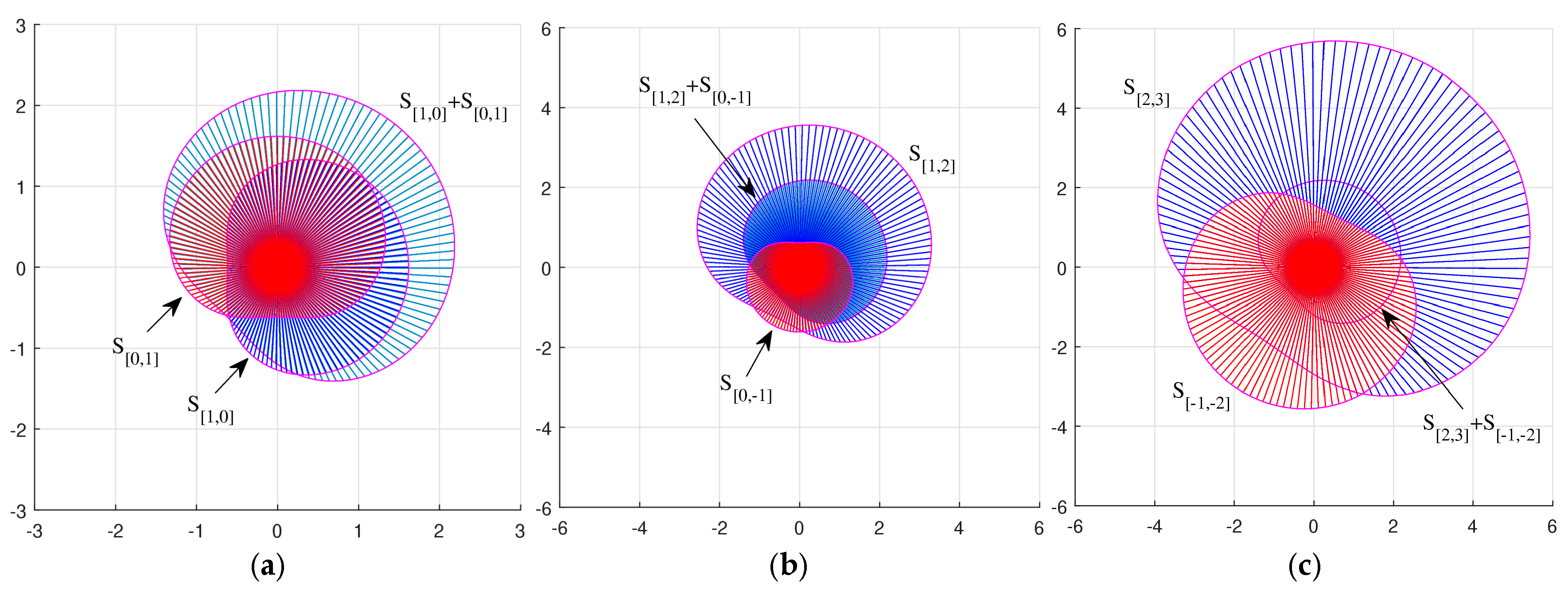
- The sets of similarities of vectors can be summed.
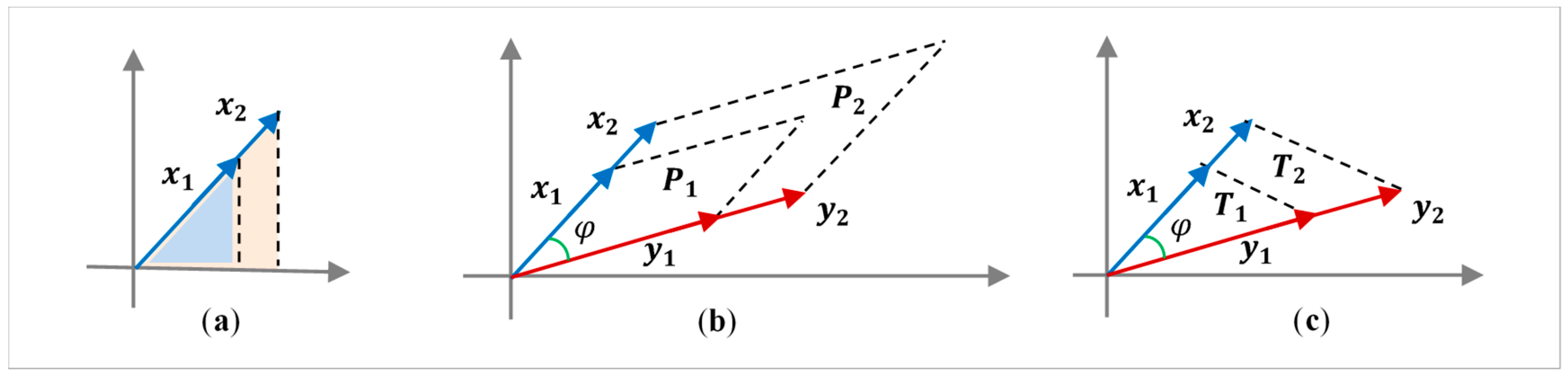
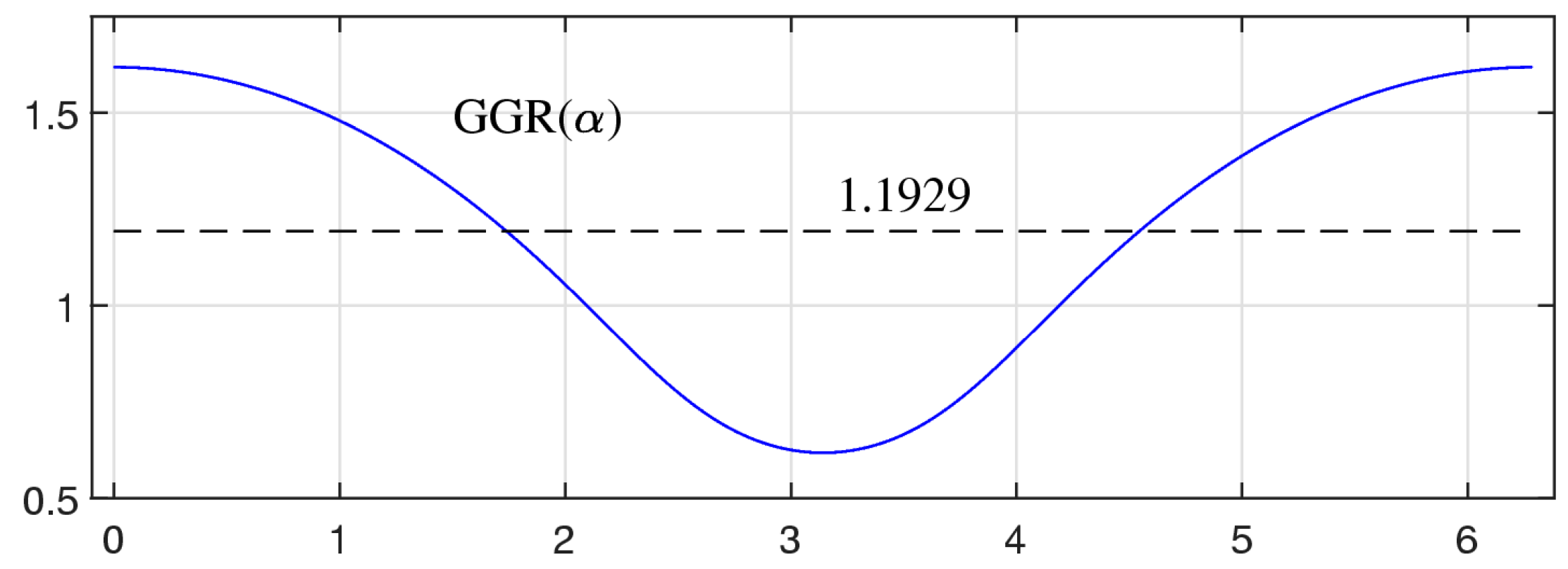
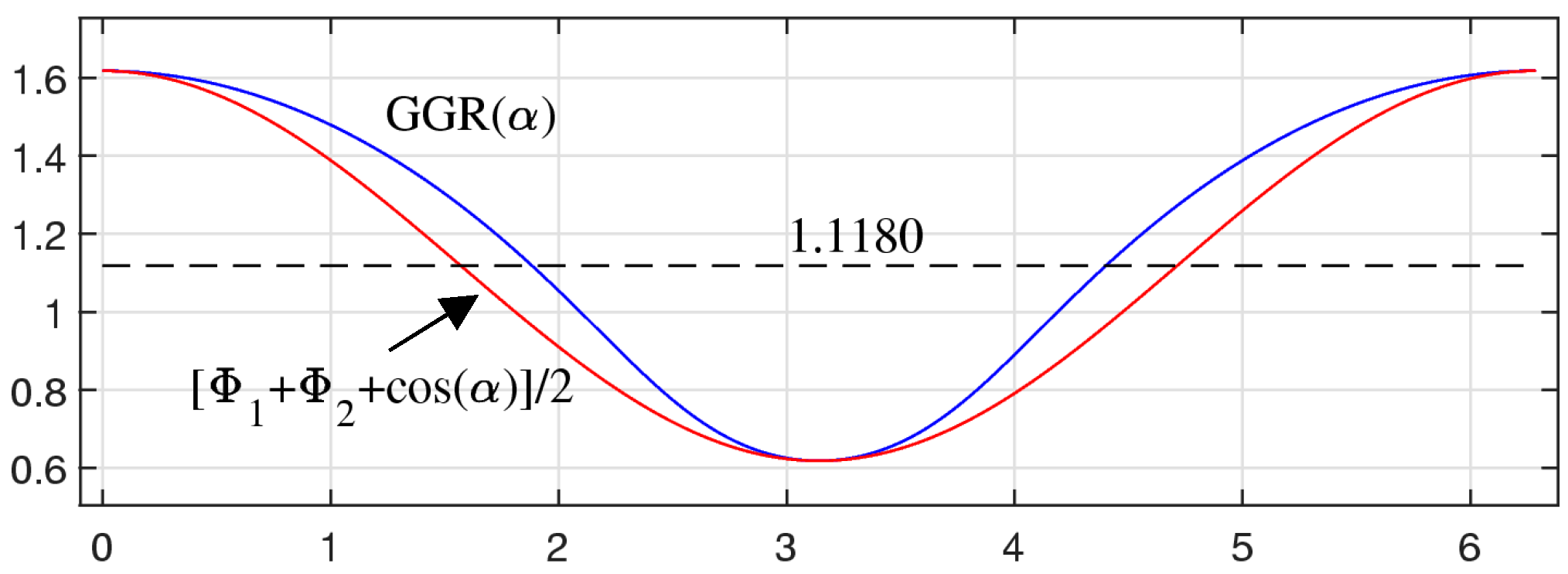
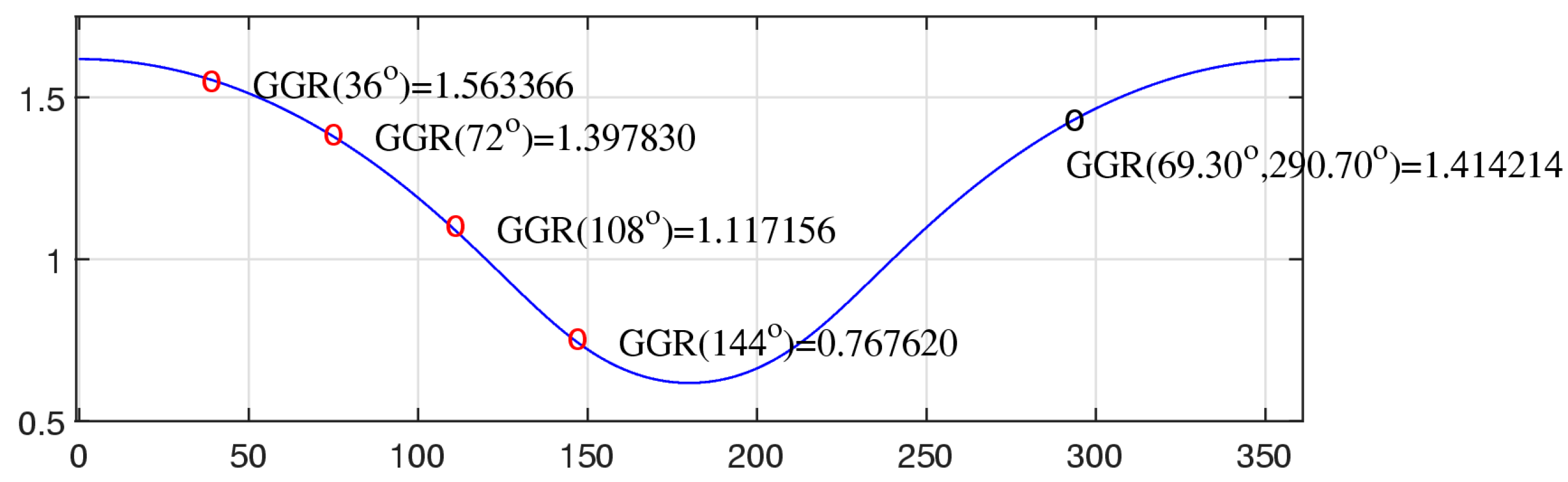
2. The Generalized Golden Ratio (GGR)
- , and means that
- , for any real number
- , for any elements and .
- , for any elements and
- If
- If
- For any real number, ,
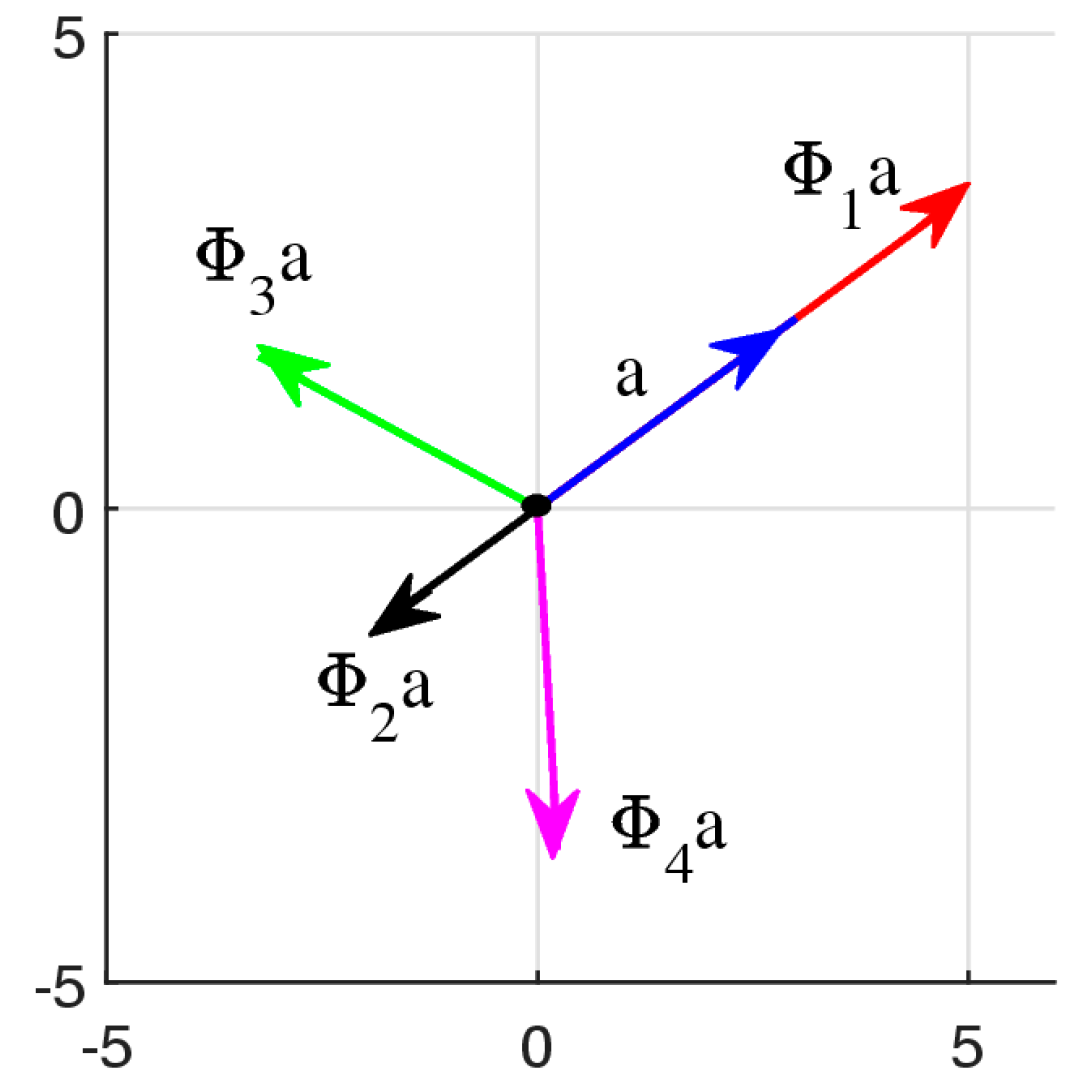
- Case : the equation to be solved isThe solutions areSuch numbers are real only when ; that is, the angle between the elements and is . Therefore,A golden ratio is a positive number. The first number is considered, but the second number is not considered, since it is negative. Thus, the golden ratio is
- 2.
- Case : The following equation is considered:with the solutionsSuch numbers are real only when ; that is, the angle between the elements and is . Therefore,
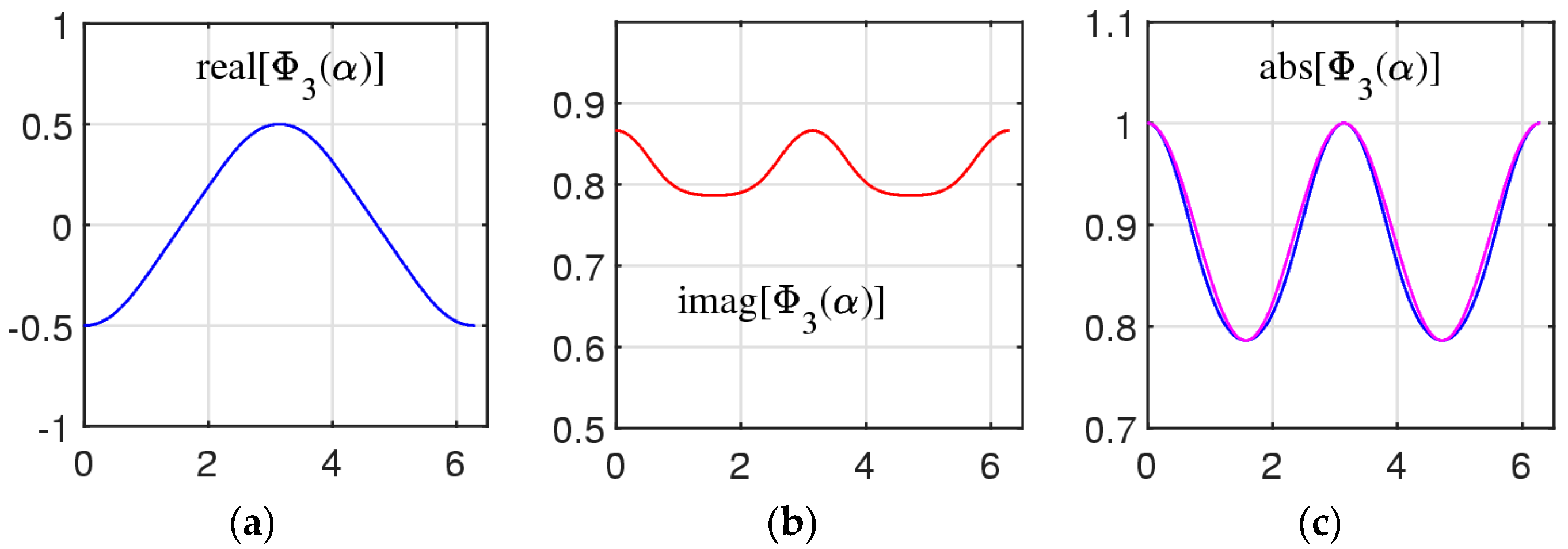
3. Main Equation of Golden Ratio and Its Analytical Solution
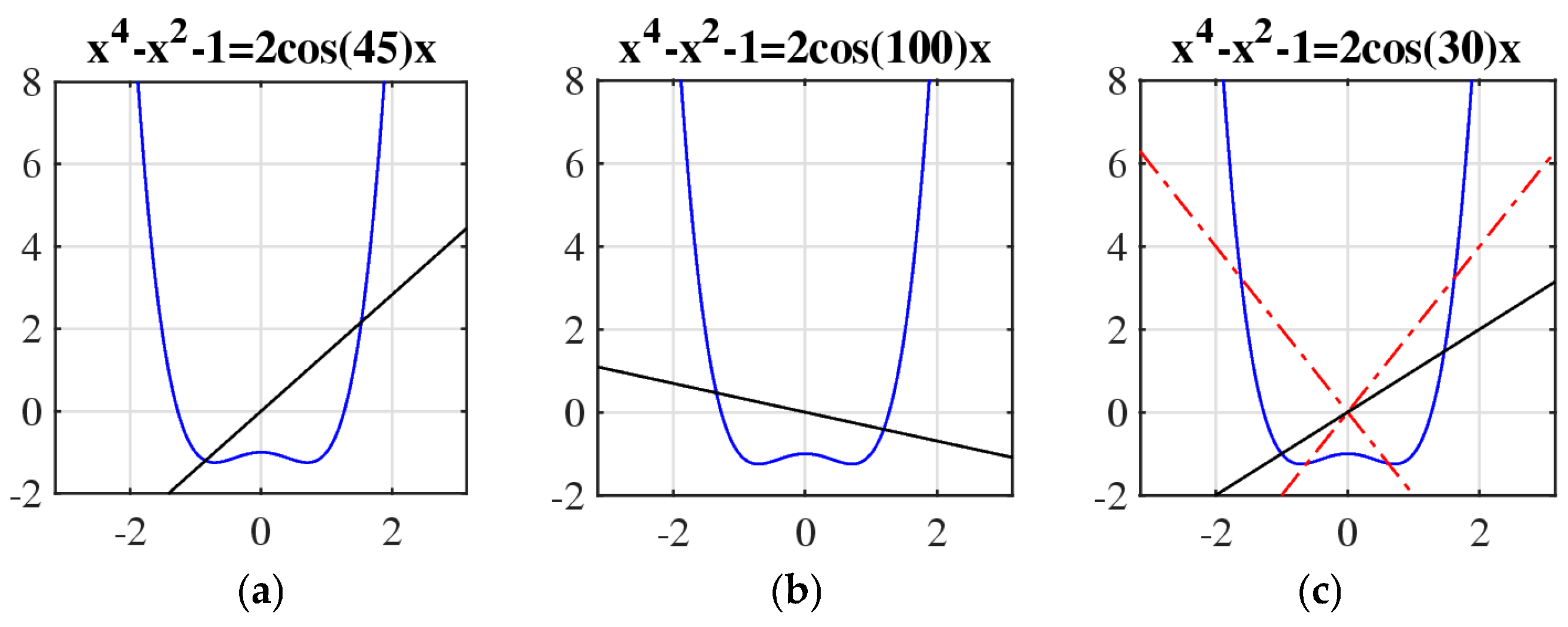
3.1. Similarity Equation and Its Roots
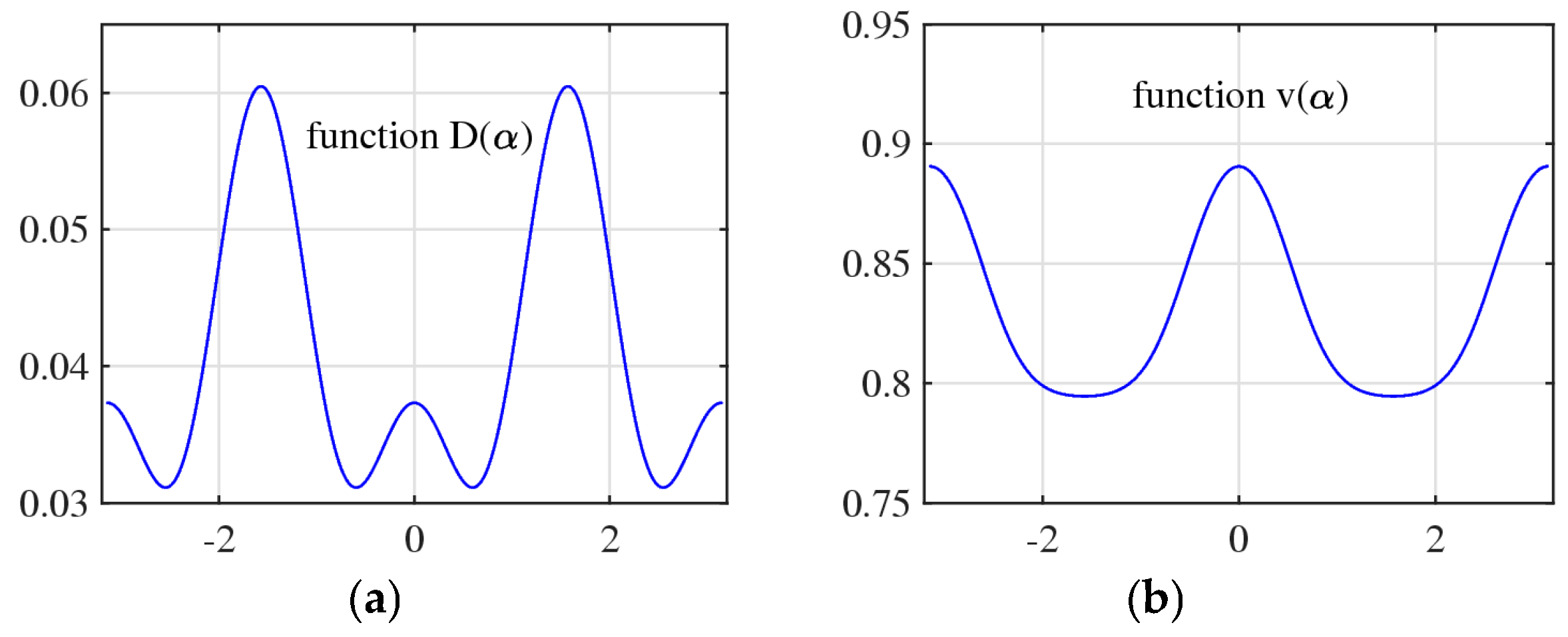
3.2. Analyze of Solutions
3.3. Properties of the Roots
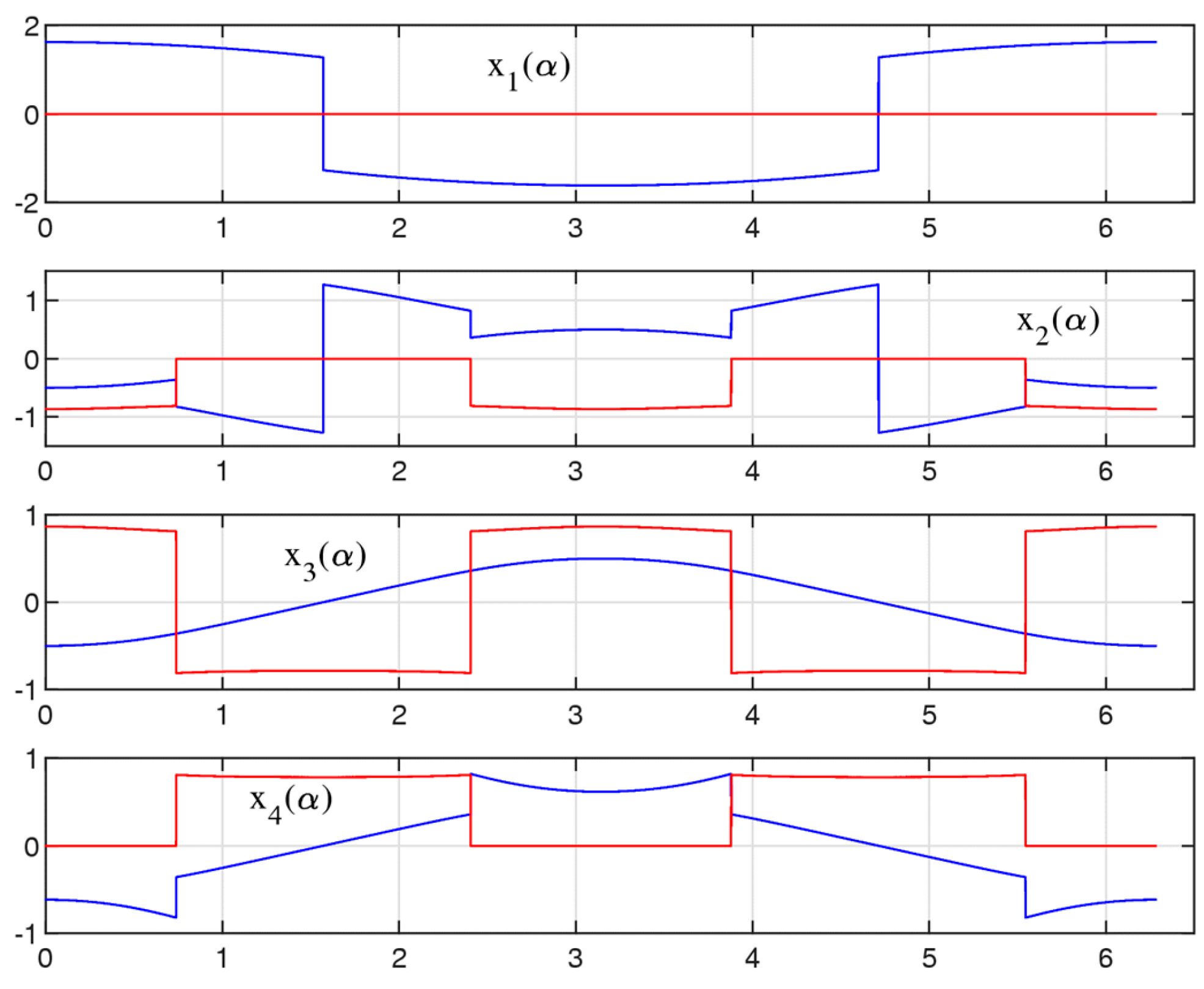
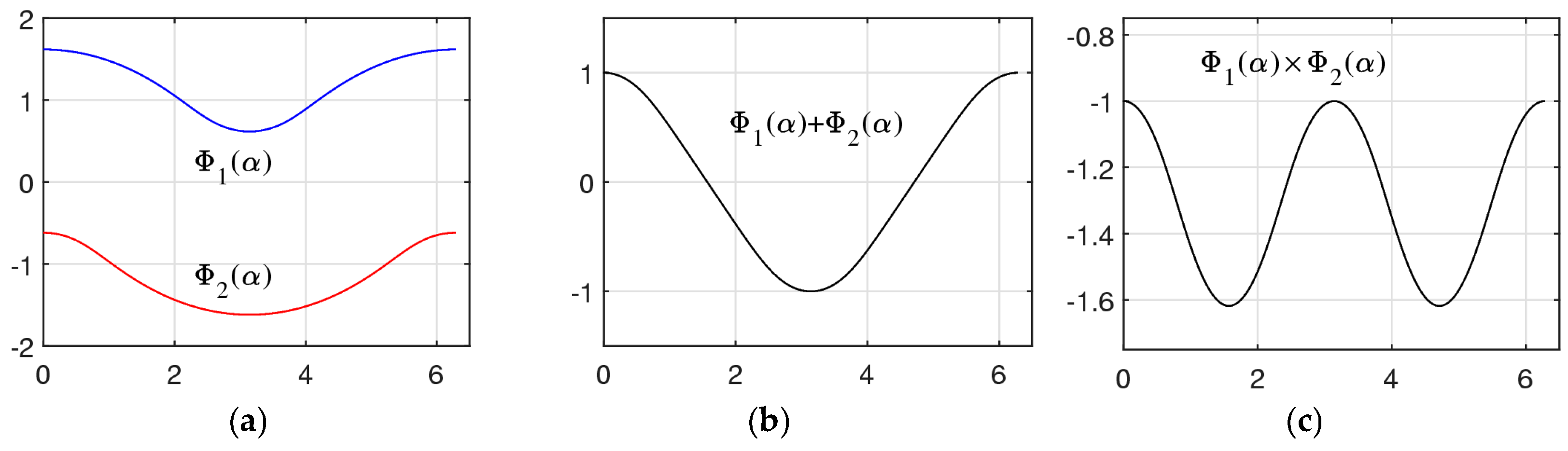
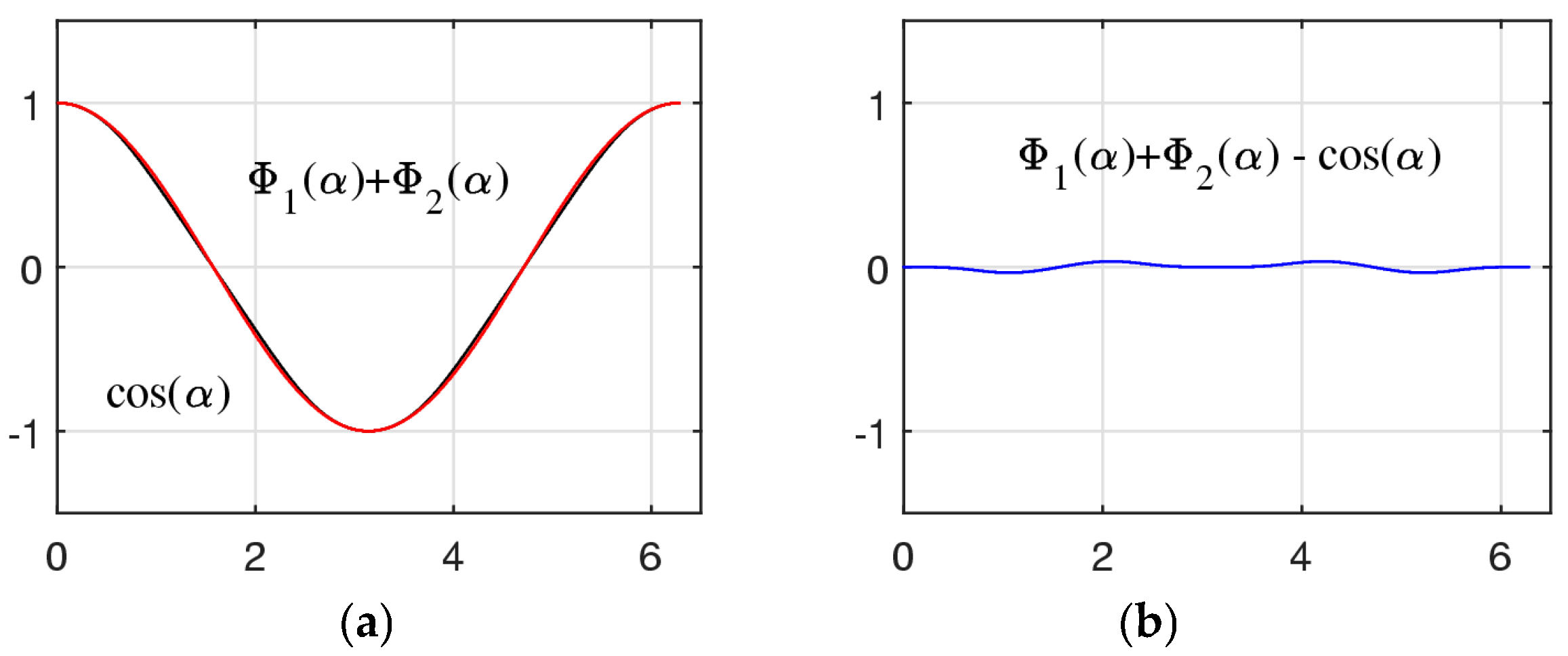
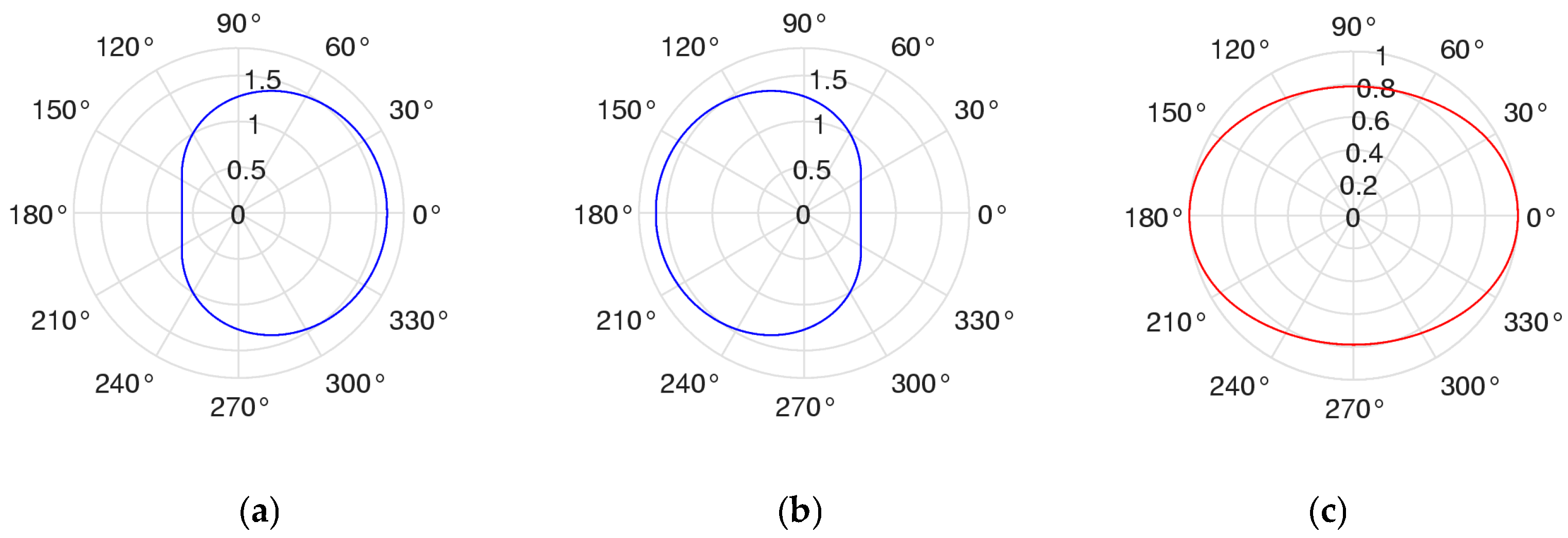
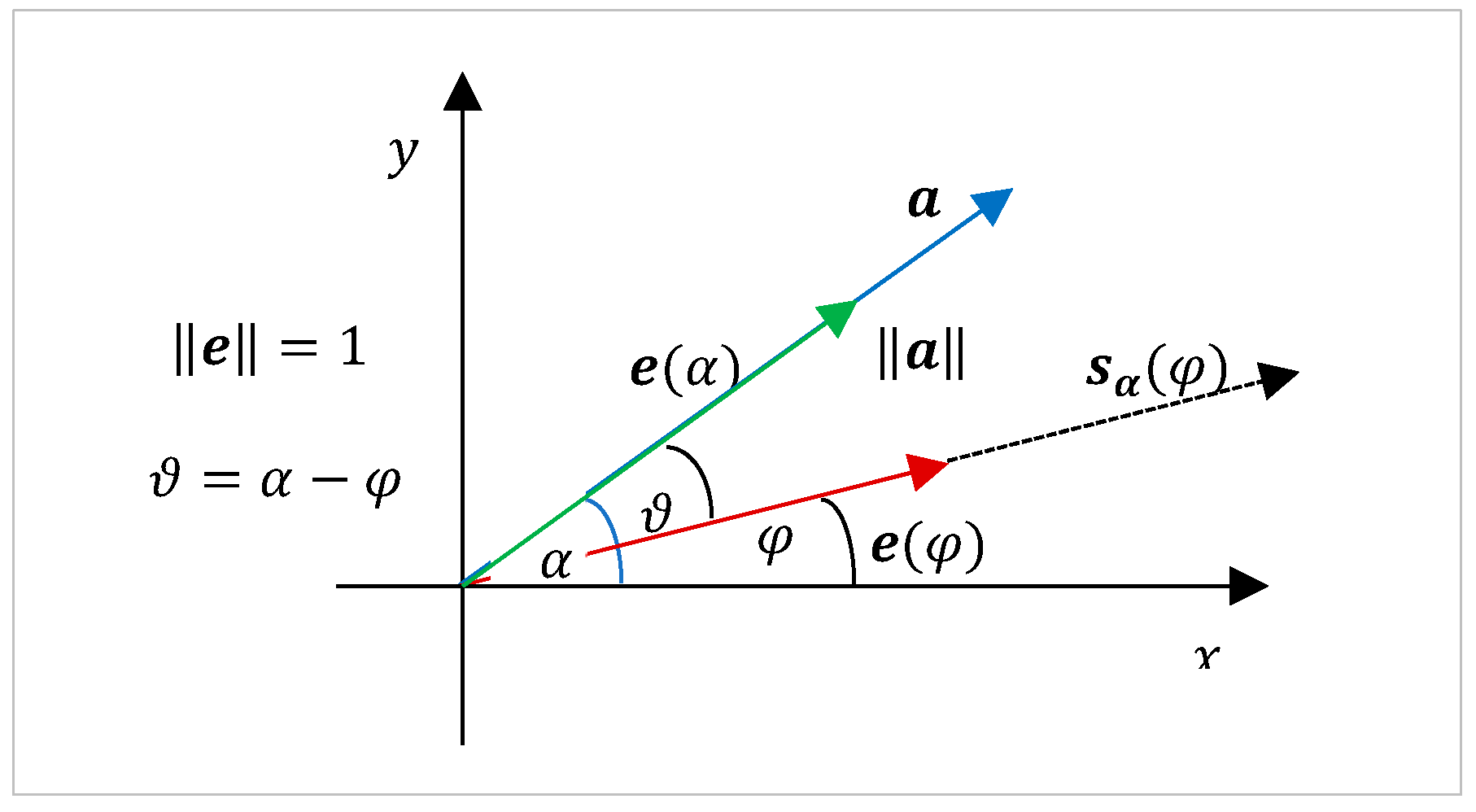
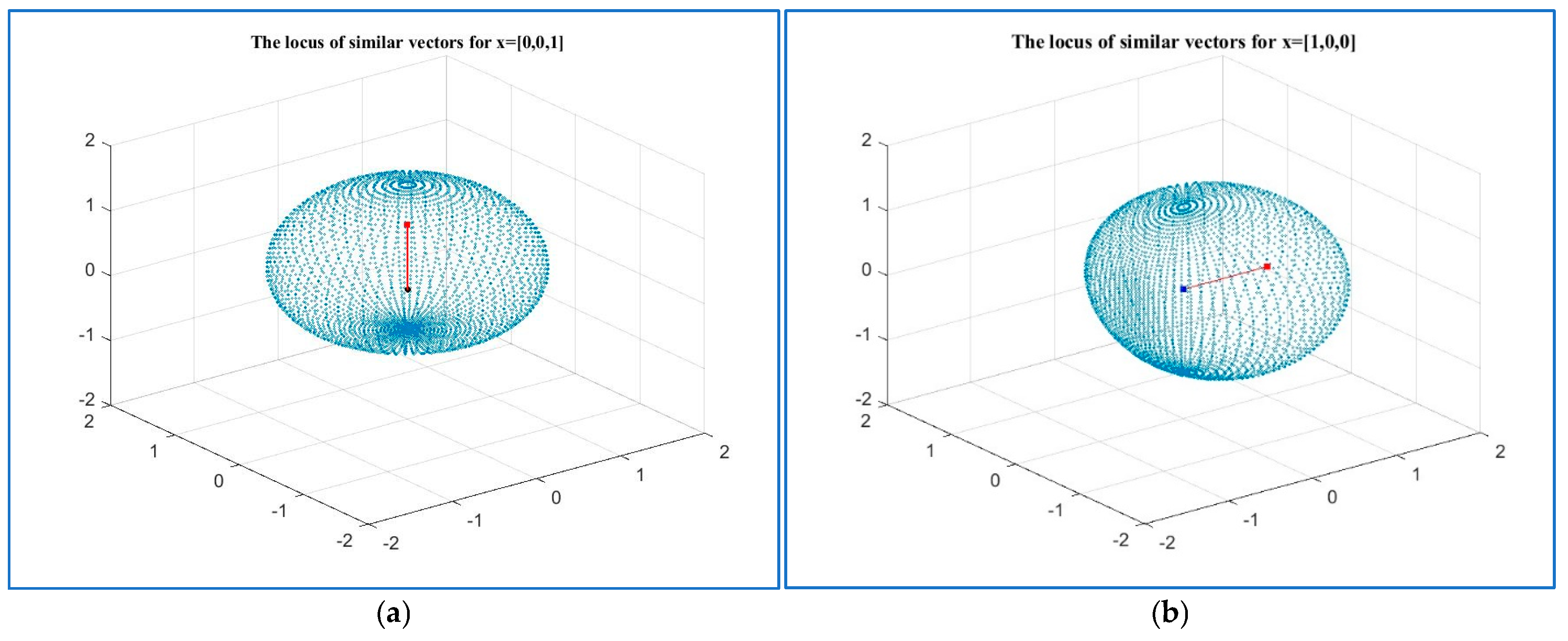
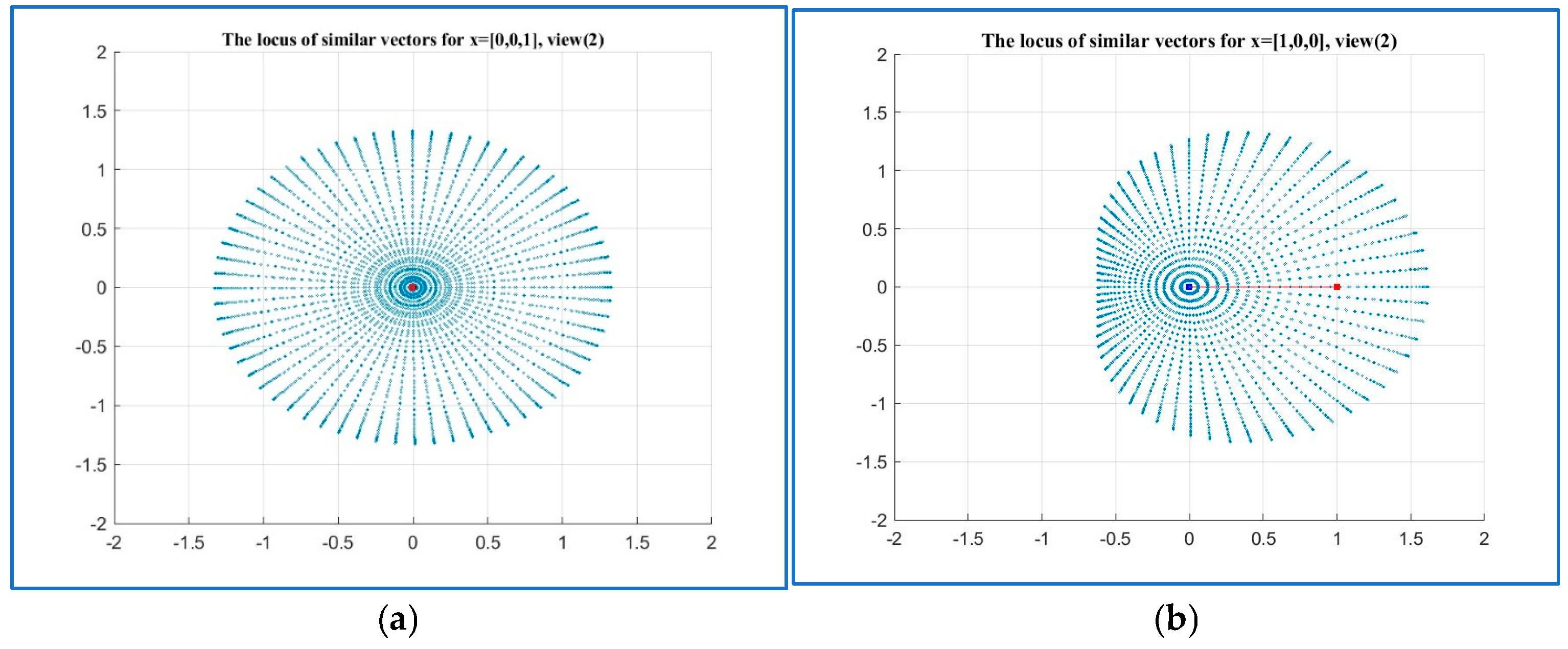
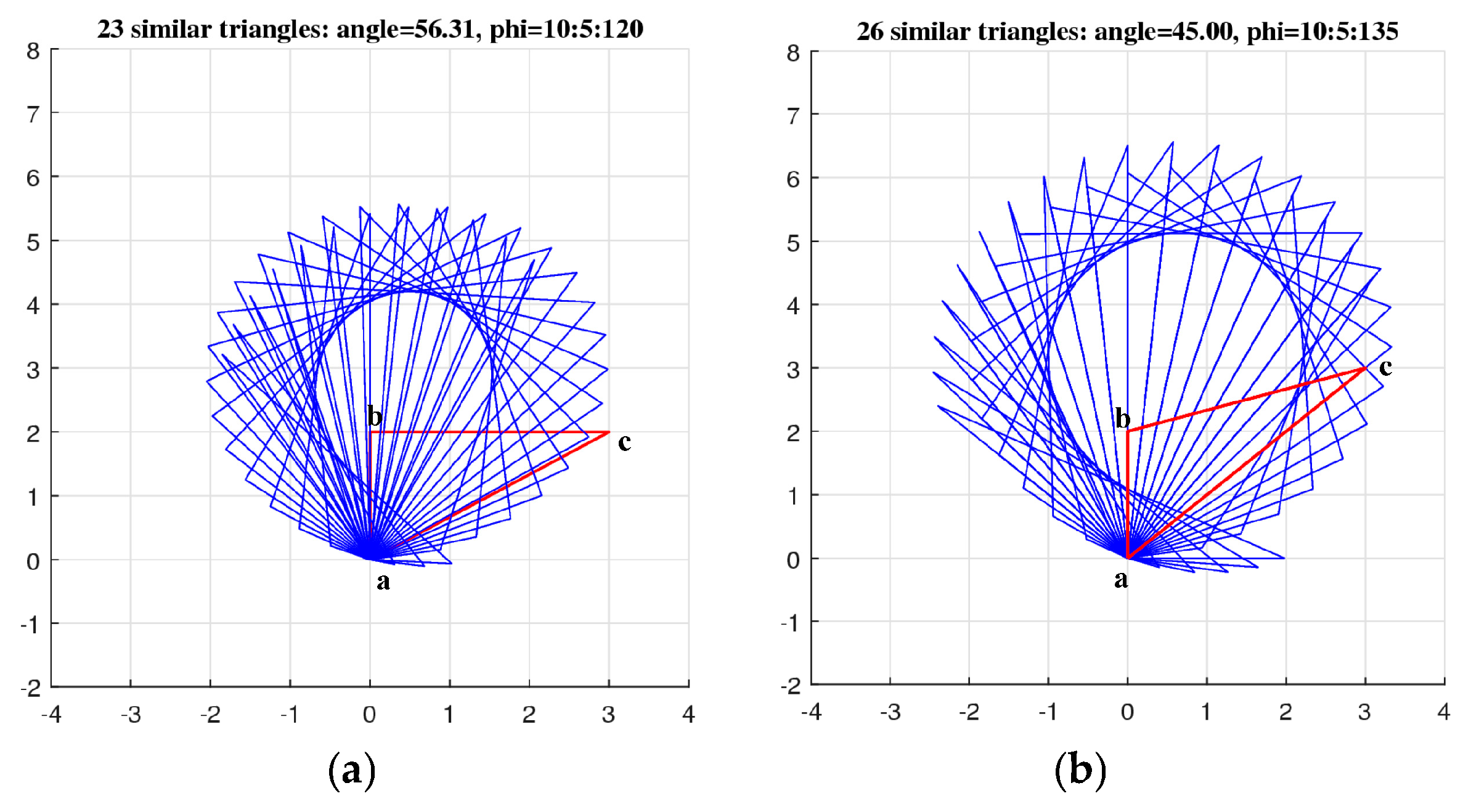
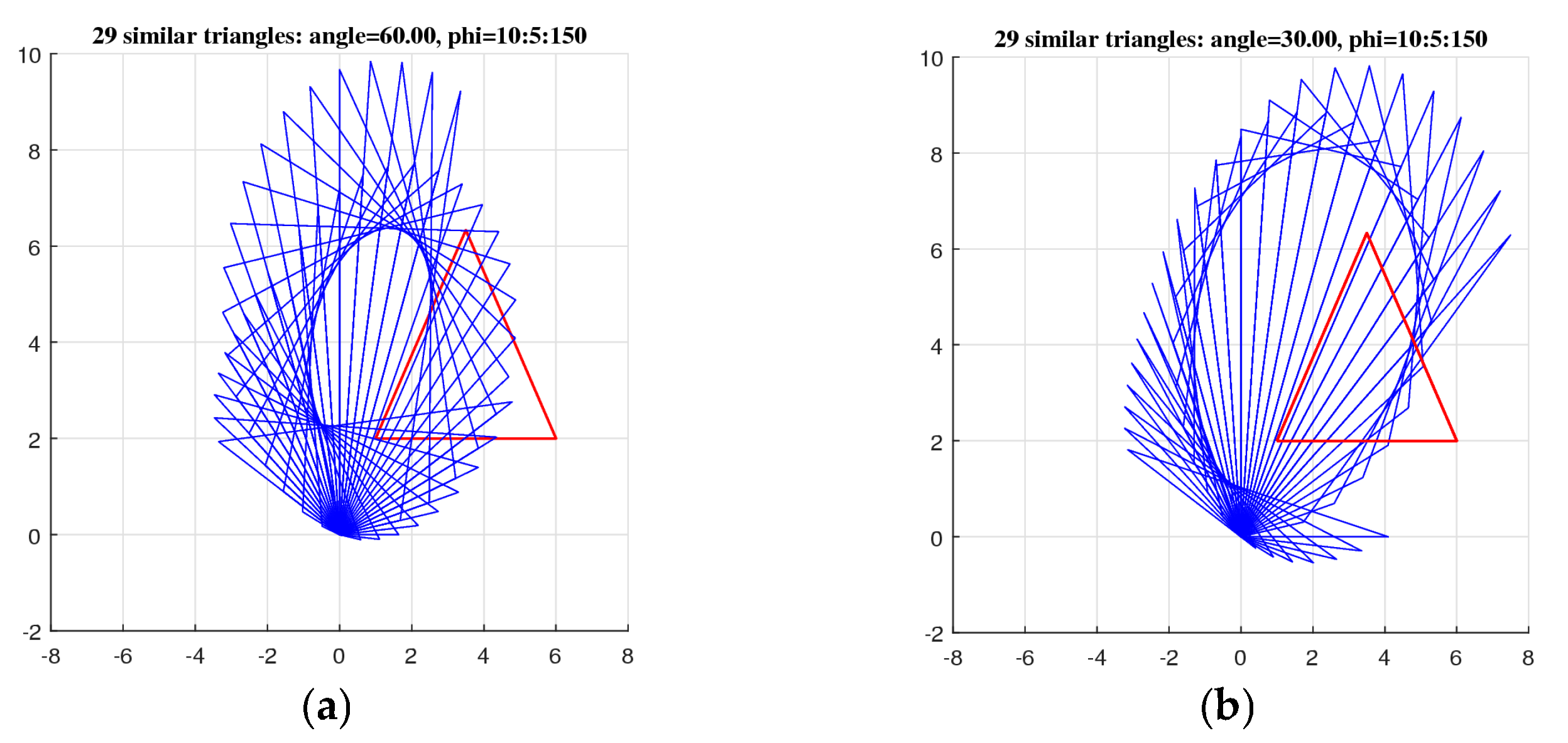
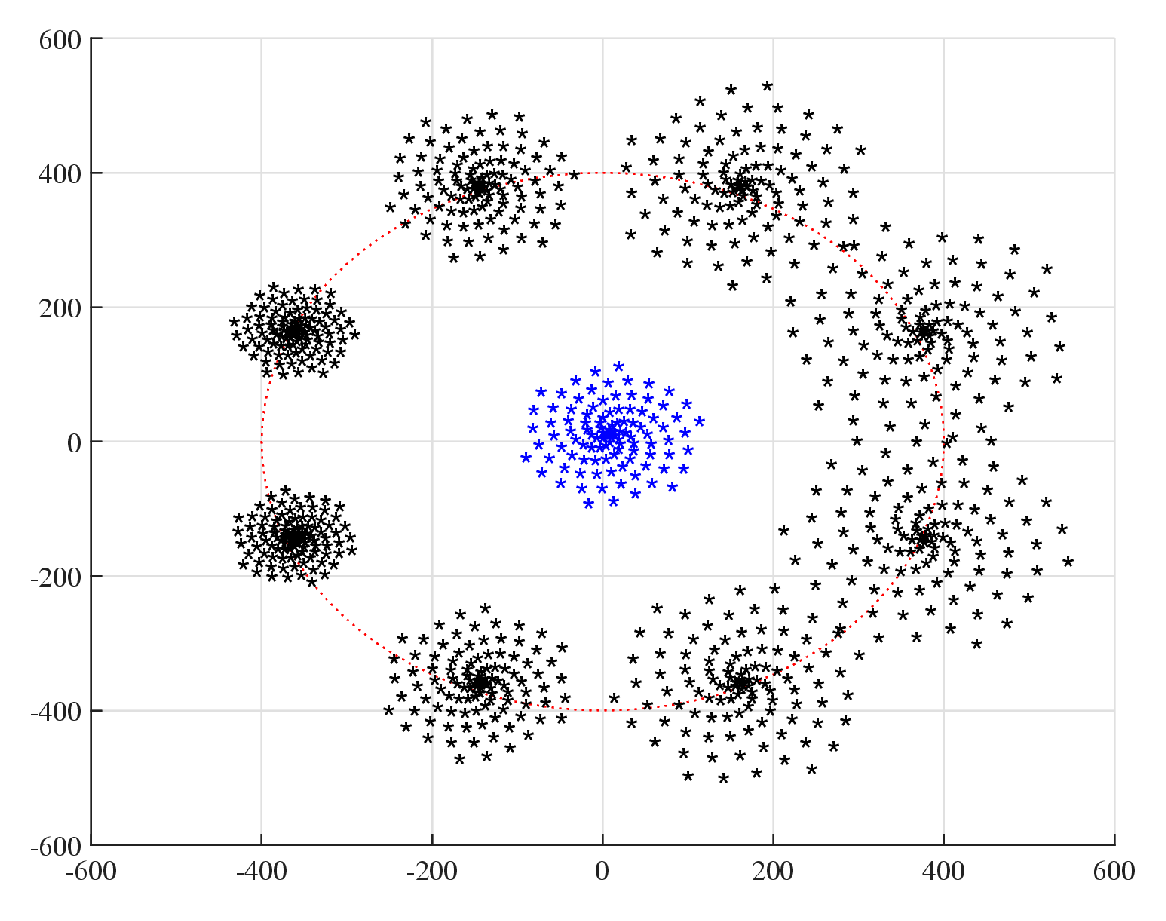
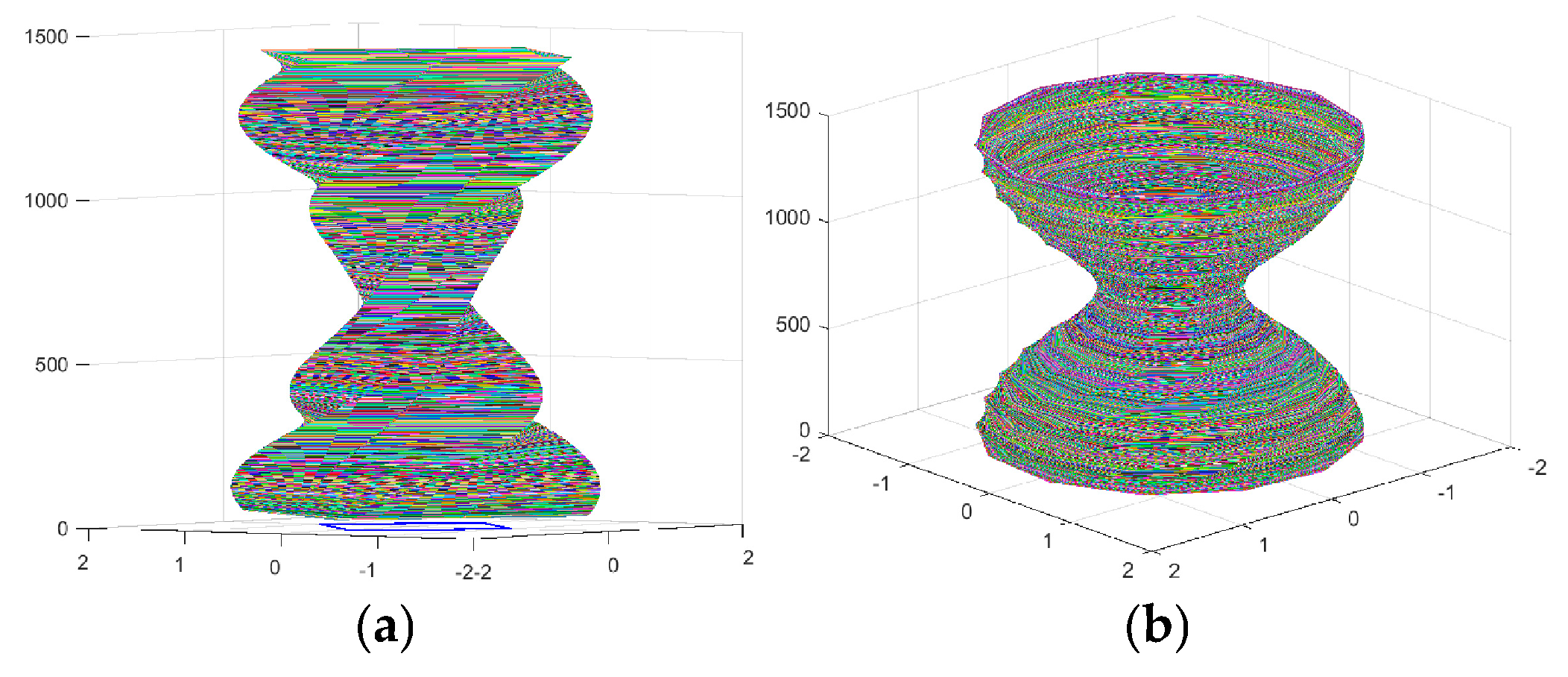
4. The Set of Similarity of a Vector
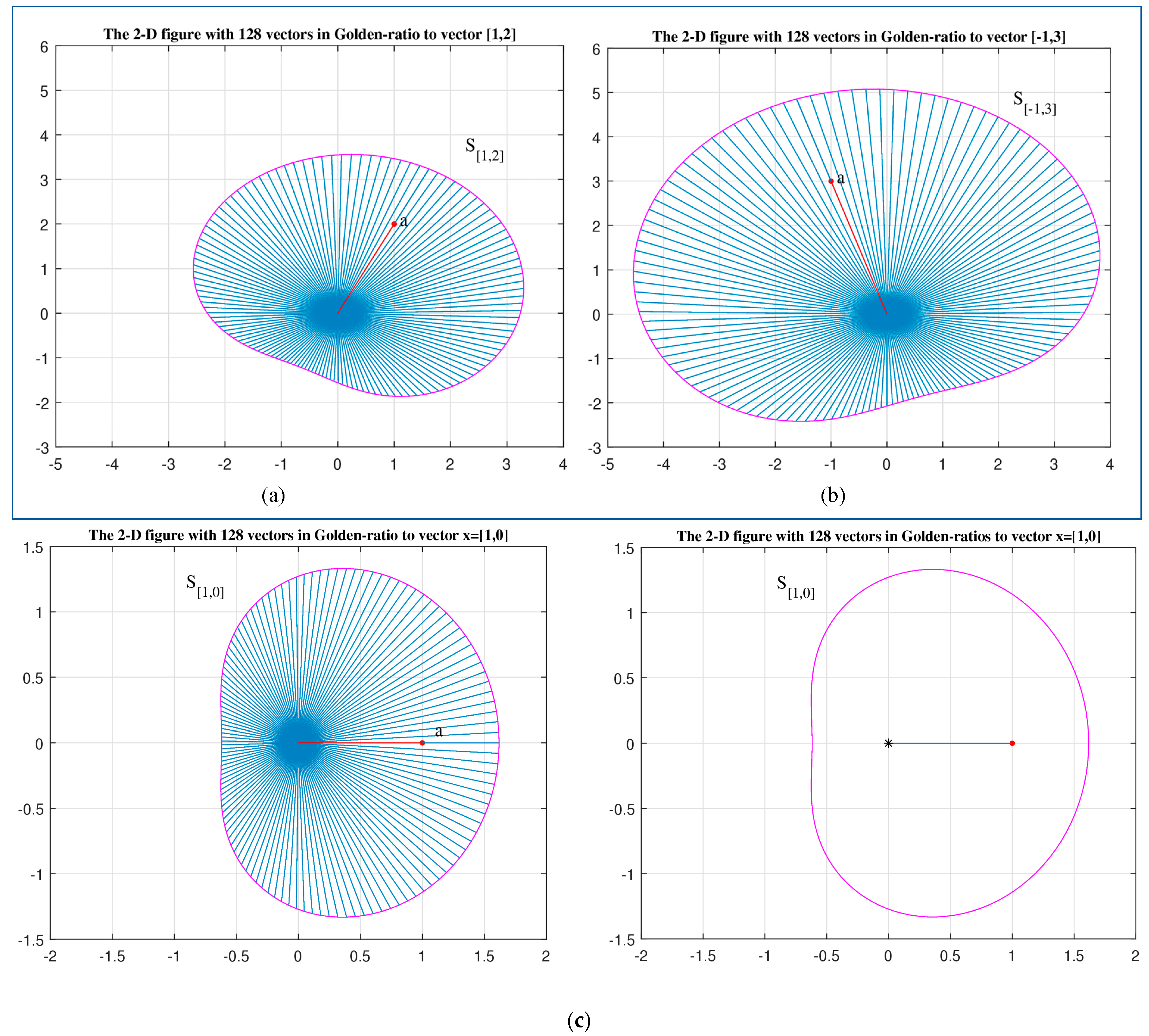
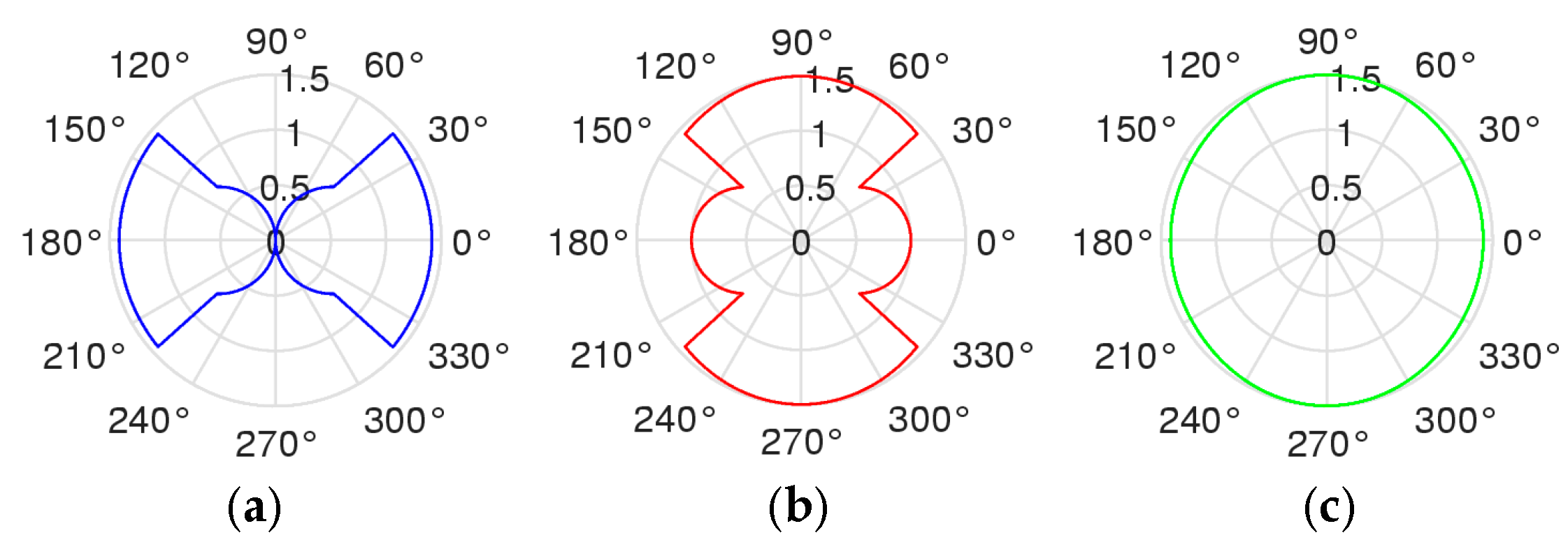
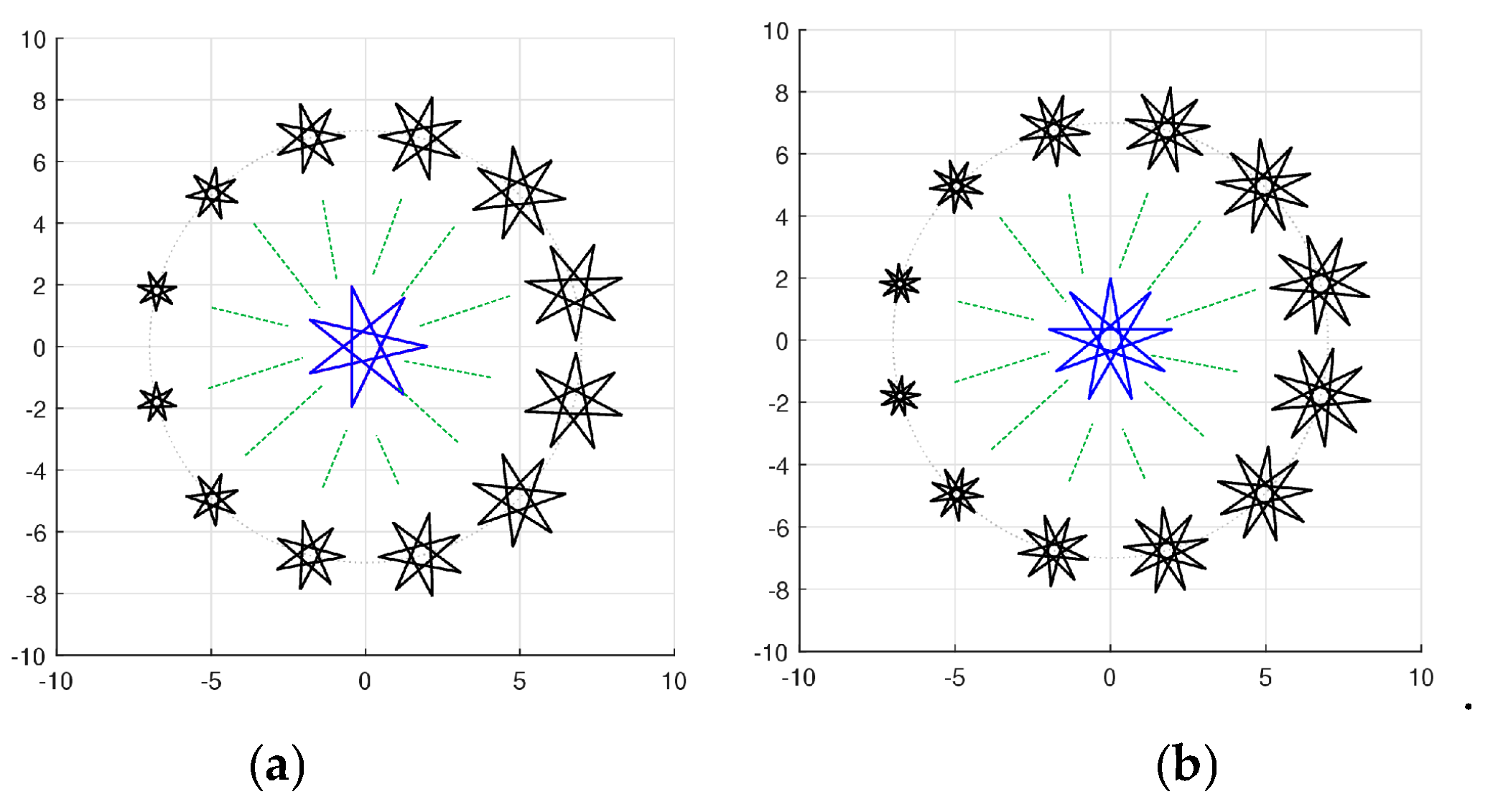
5. Field of Similarities
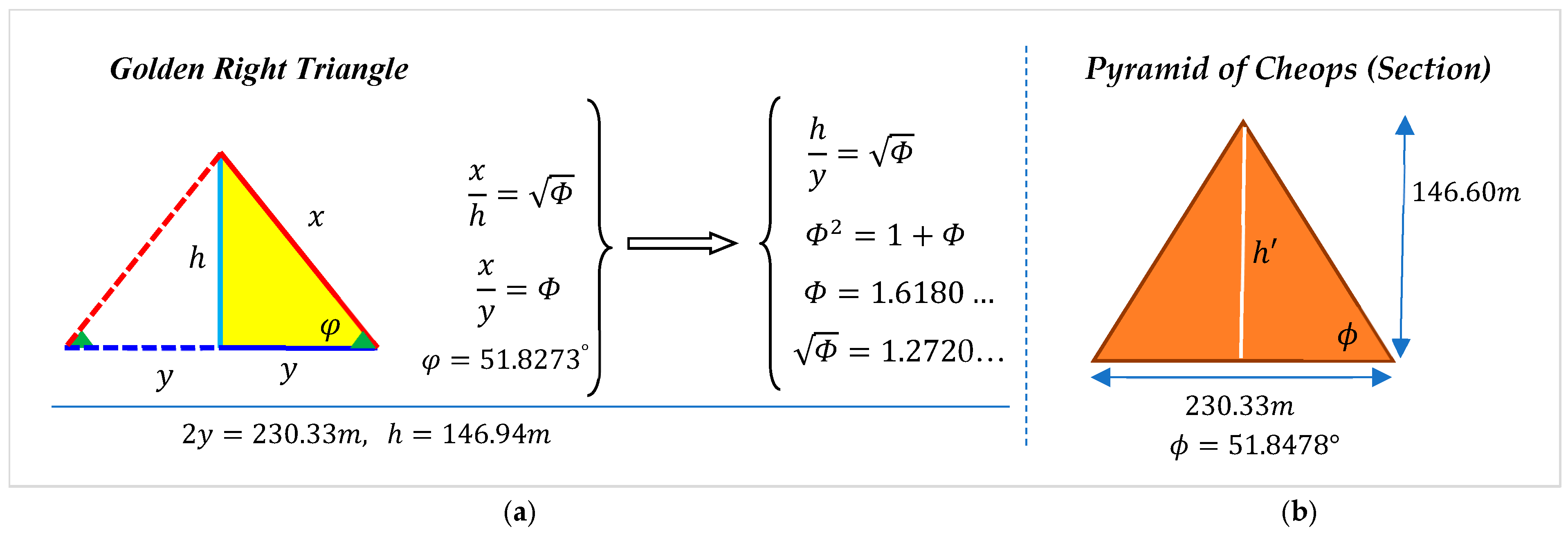
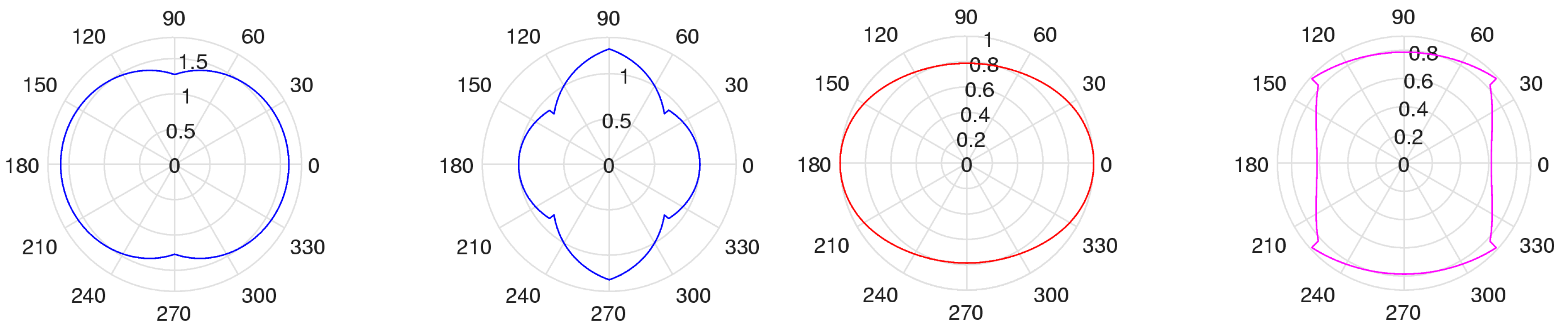
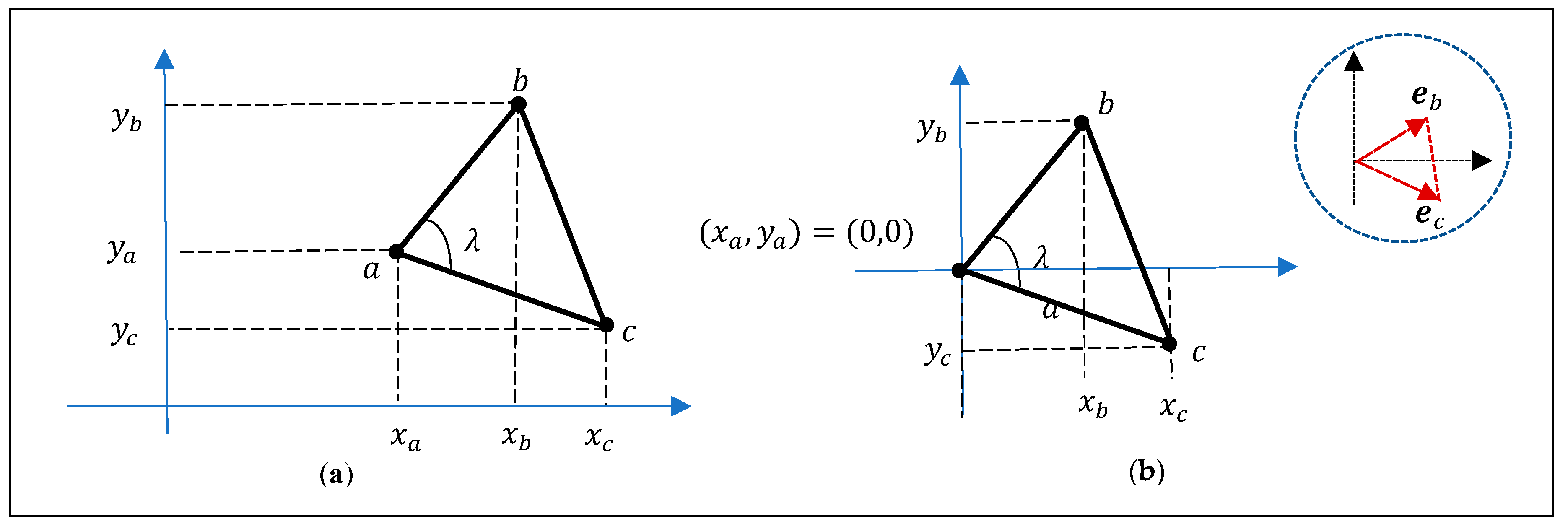
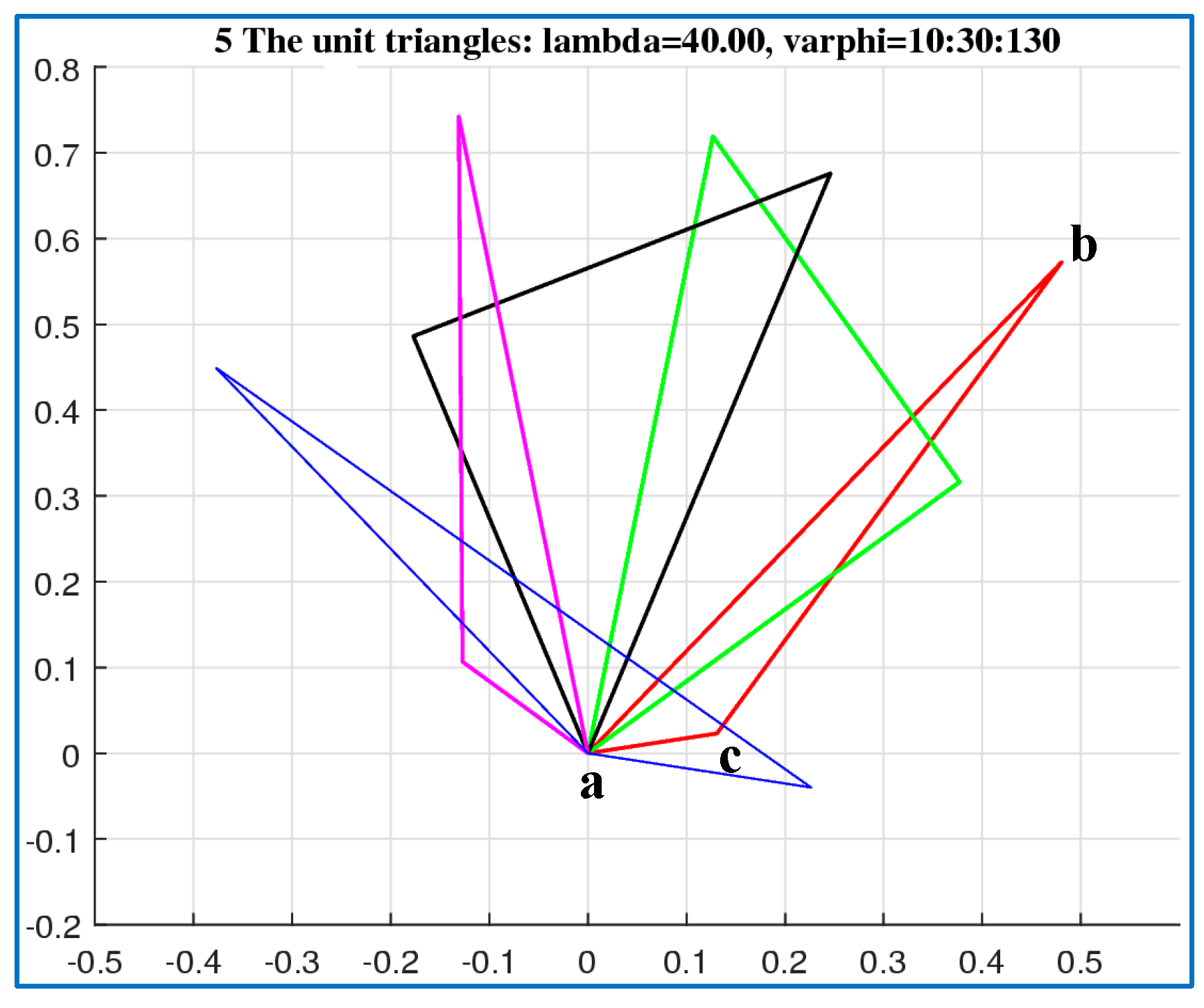
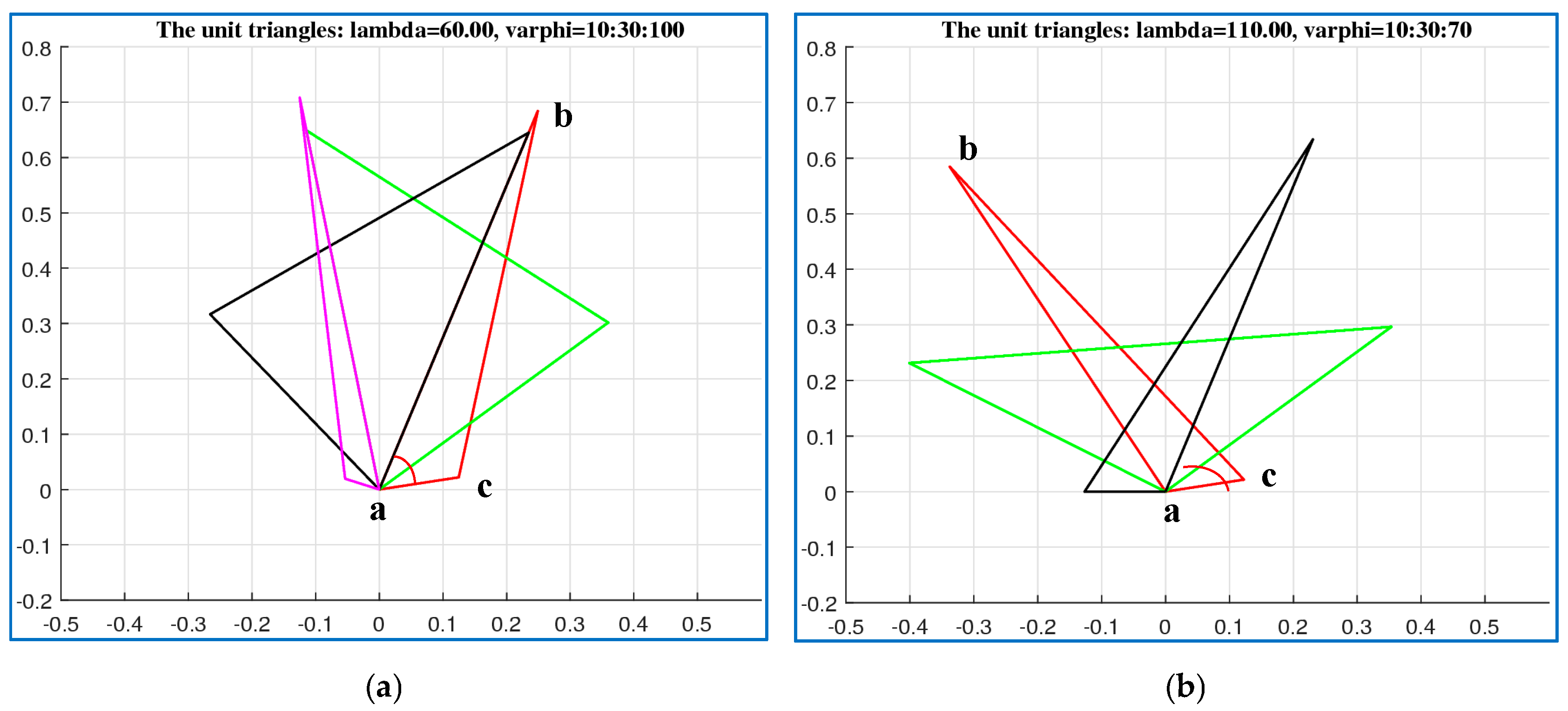
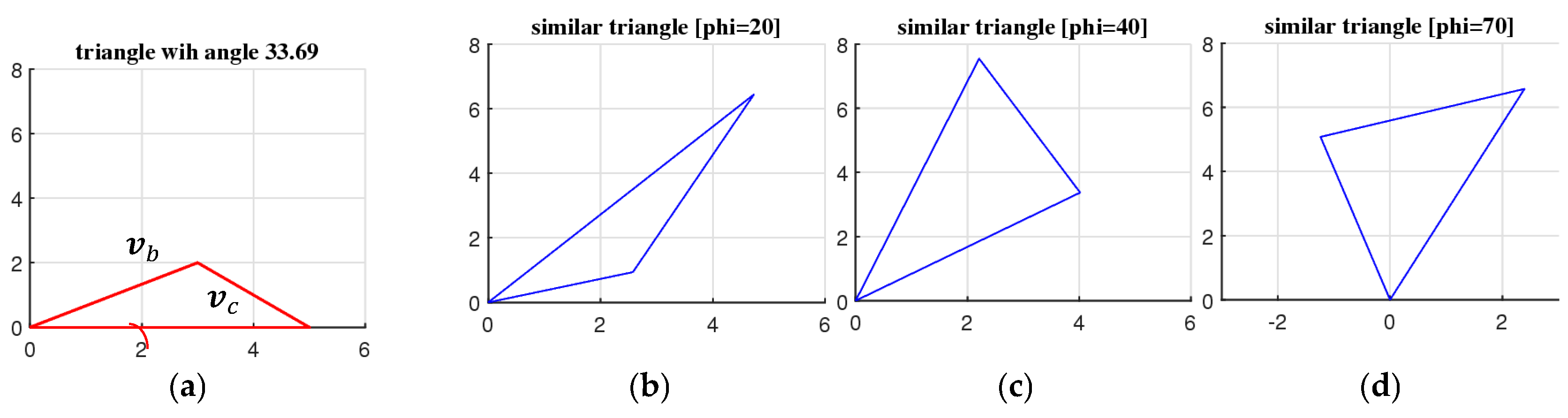
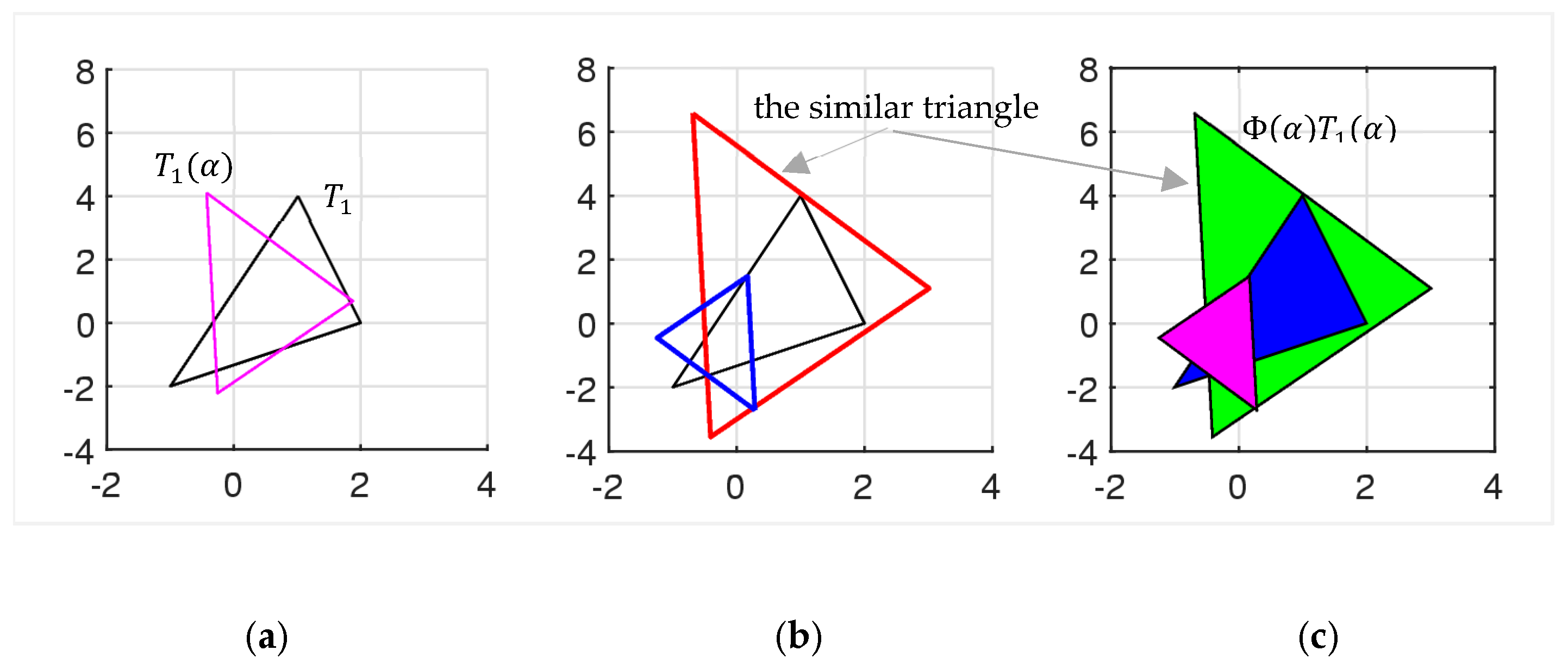
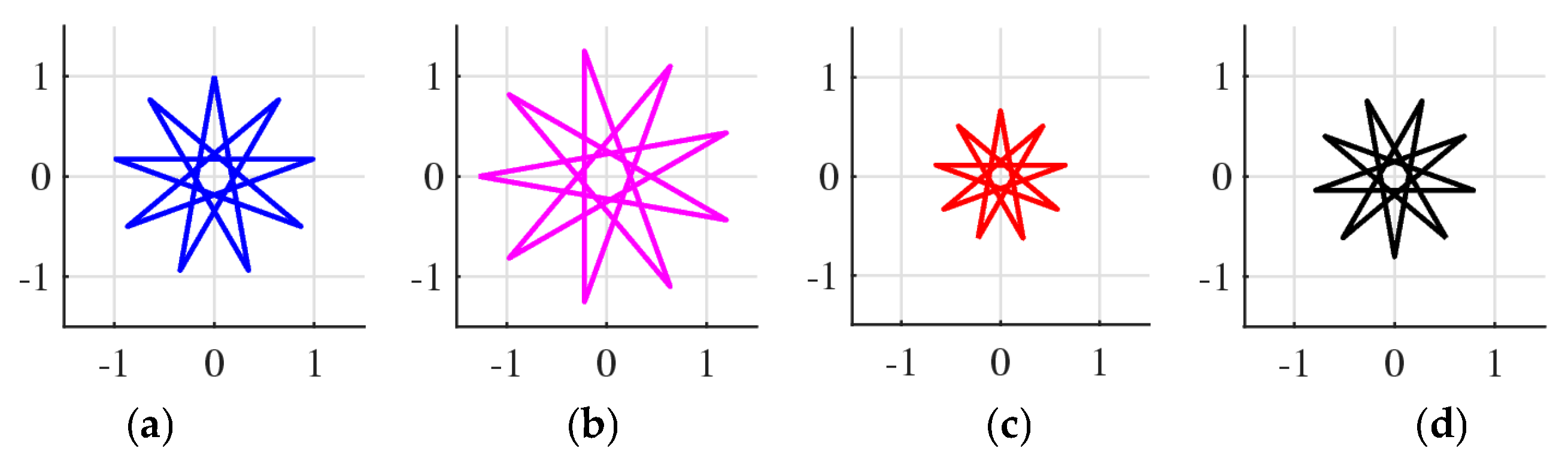
6. Similarity Triangles in Golden Ratio

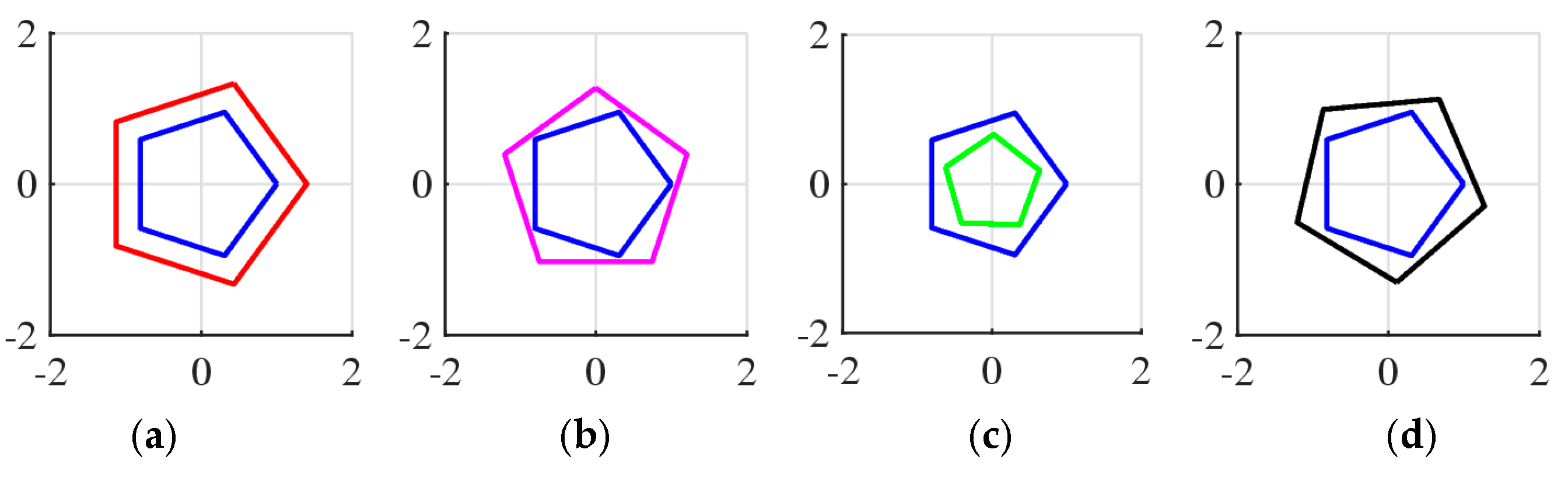
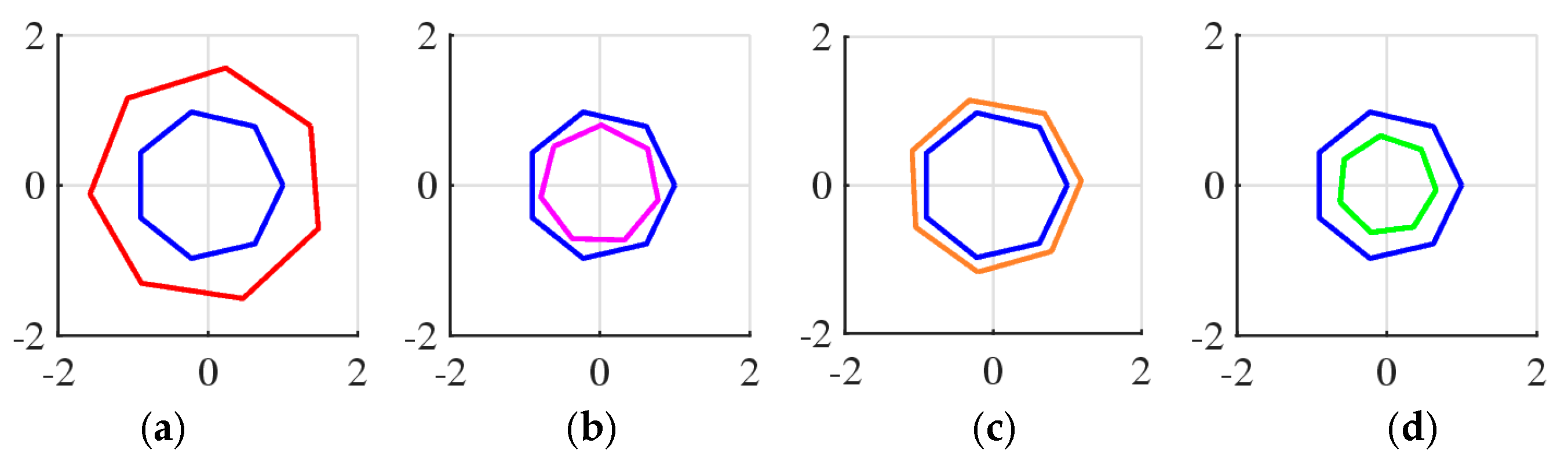
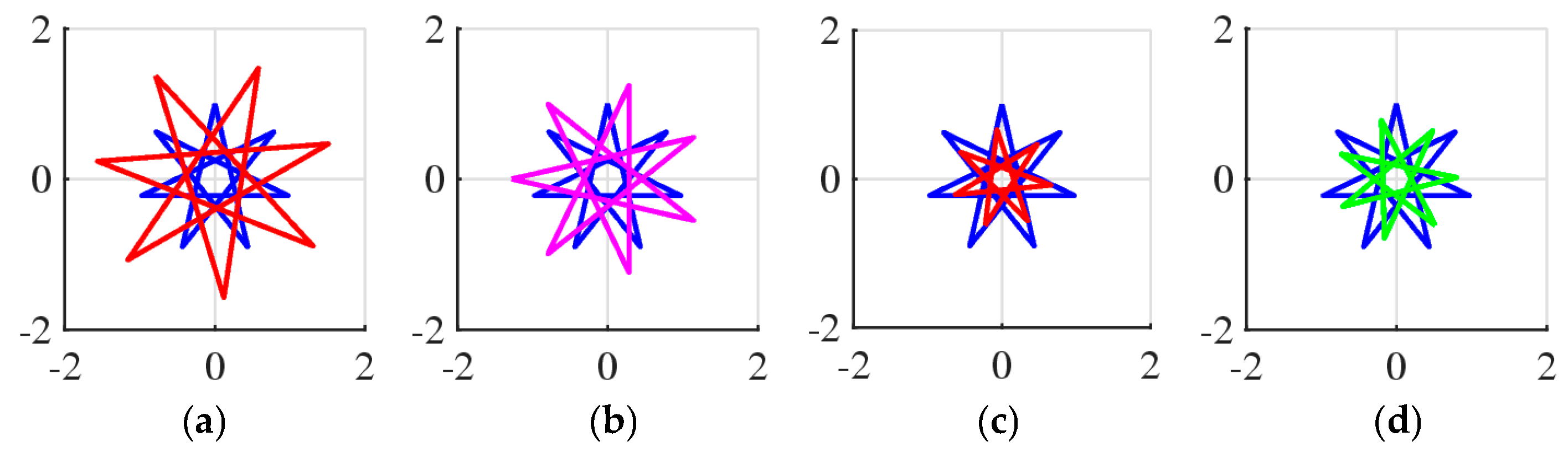
7. Similarity of Figures (Not Vectors)
Other Figures
8. Afterword and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- golden_ratio1.m (for , given an angle ),
- (2)
- golden_ratio2.m (for , given an angle ),
- (3)
- golden_ratio3.m (for , given an angle ),
- (4)
- golden_ratio4.m (for , given an angle ).

References
- Stakhov, A. The golden section and modern harmony mathematics. In Applications of Fibonacci Numbers; Springer: Dordrecht, The Netherlands, 1998; Volume 7, pp. 393–399. [Google Scholar]
- Bradley, S. A geometric connection between generalized Fibonacci sequences and nearly golden sections. Fibonacci Q. 1999, 38, 174–180. [Google Scholar] [CrossRef]
- Antonelli, P.; Leandro, C.; Rutz, S. Mario Livio-The Golden Ratio The Story of PHI, the World’s Most Astonishing Number-Broadway Books (2003); Crown: New York, NY, USA, 2016. [Google Scholar]
- Timerding, H.E. Der Goldene Schnitt, 1999; The Digital Collection; University of Michigan Historical Math Collection; University of Michigan: Ann Arbor, MI, USA, 2025. [Google Scholar]
- Vorobiev, N. The Fibonacci Numbers, 2nd ed.; Nauka: Moscow, Russia, 1964. [Google Scholar]
- Herz-Fischler, R. The Shape of the Great Pyramid; Wilfrid Laurier University Press: Waterloo, ON, Canada, 2000. [Google Scholar]
- Van Zanten, A. The golden ratio in the arts of painting, building and mathematic. Nieuw Arch. Wisk. 1999, 17, 229–245. [Google Scholar]
- Olariu, A. Golden Section and the Art of Painting; National Institute for Physics and Nuclear Engineering: Bucharest, Romania, 1999; pp. 1–4. [Google Scholar]
- Grigoryan, A.M.; Agaian, S.S. Evidence of golden and aesthetic proportions in colors of paintings of the prominent artists. IEEE Multimedia 2020, 27, 8–16. [Google Scholar] [CrossRef]
- Kazlacheva, Z.; Ilieva, J. The golden and Fibonacci geometry in fashion and textile design. Proc. eRA 2016, 10, 15–64. [Google Scholar]
- Chan, J.Y.; Chang, G.H. The golden ratio optimizes cardiomelic form and function. J. Med. Hypotheses Ideas 2009, 3, 2. [Google Scholar]
- Henein, M.Y.; Zhao, Y.; Nicoll, R.; Sun, L.; Khir, A.W.; Franklin, K.; Lindqvist, P.; Golden Ratio Collaborators. The human heart: Application of the golden ratio and angle. Int. J. Cardiol. 2011, 150, 239–242. [Google Scholar] [CrossRef] [PubMed]
- Hassaballah, M.; Murakami, K.; Ido, S. Face detection evaluation: A new approach based on the golden ratio. Signal Image Video Process. 2013, 7, 307–316. [Google Scholar] [CrossRef]
- Grigoryan, A.M.; Agaian, S.S. Monotonic sequences for image enhancement and segmentation. Digit. Signal Process. 2015, 41, 70–89. [Google Scholar] [CrossRef]
- Nave, F.L.; Mazur, B. Reading Bombelli. Math. Intell. 2002, 24, 12–21. [Google Scholar] [CrossRef]
- Katz, V.J. A History of Mathematics; Addison Wesley: Boston, MA, USA, 2004; p. 220. Available online: https://archive.org/details/historyofmathema0000katz (accessed on 12 January 2025).
- Nickalls, R.W.D. Viète, Descartes, and the cubic equation. Math. Gaz. 2006, 90, 203–208. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Section 5.6 Quadratic and Cubic Equations, Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Cardano’s Ars Magna in 1545 (Boyer and Merzbach 1991, p. 283). Available online: https://archive.org/details/arsmagnaorruleso0000card (accessed on 15 February 2025).
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information, 2nd ed.; Cambridge UP: Cambridge, UK, 2001. [Google Scholar]



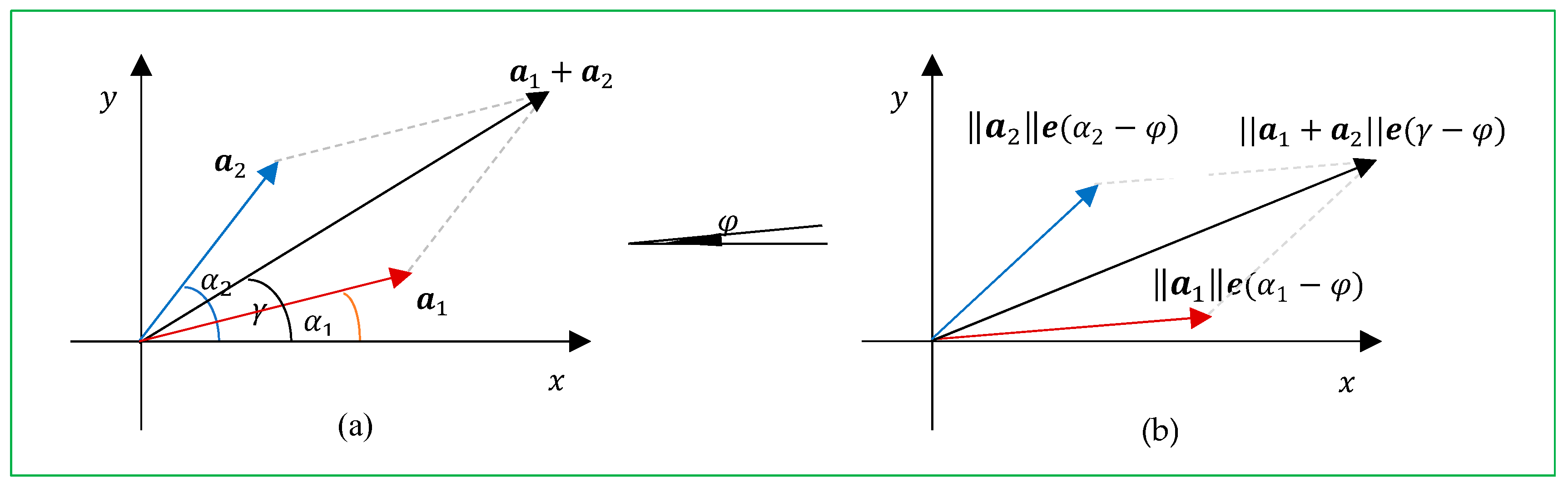






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigoryan, A.; Grigoryan, M. Golden Ratio Function: Similarity Fields in the Vector Space. Mathematics 2025, 13, 699. https://doi.org/10.3390/math13050699
Grigoryan A, Grigoryan M. Golden Ratio Function: Similarity Fields in the Vector Space. Mathematics. 2025; 13(5):699. https://doi.org/10.3390/math13050699
Chicago/Turabian StyleGrigoryan, Artyom, and Meruzhan Grigoryan. 2025. "Golden Ratio Function: Similarity Fields in the Vector Space" Mathematics 13, no. 5: 699. https://doi.org/10.3390/math13050699
APA StyleGrigoryan, A., & Grigoryan, M. (2025). Golden Ratio Function: Similarity Fields in the Vector Space. Mathematics, 13(5), 699. https://doi.org/10.3390/math13050699






