New Approximation Formula of Digamma Function with Bounded Remainder
Abstract
1. Introduction
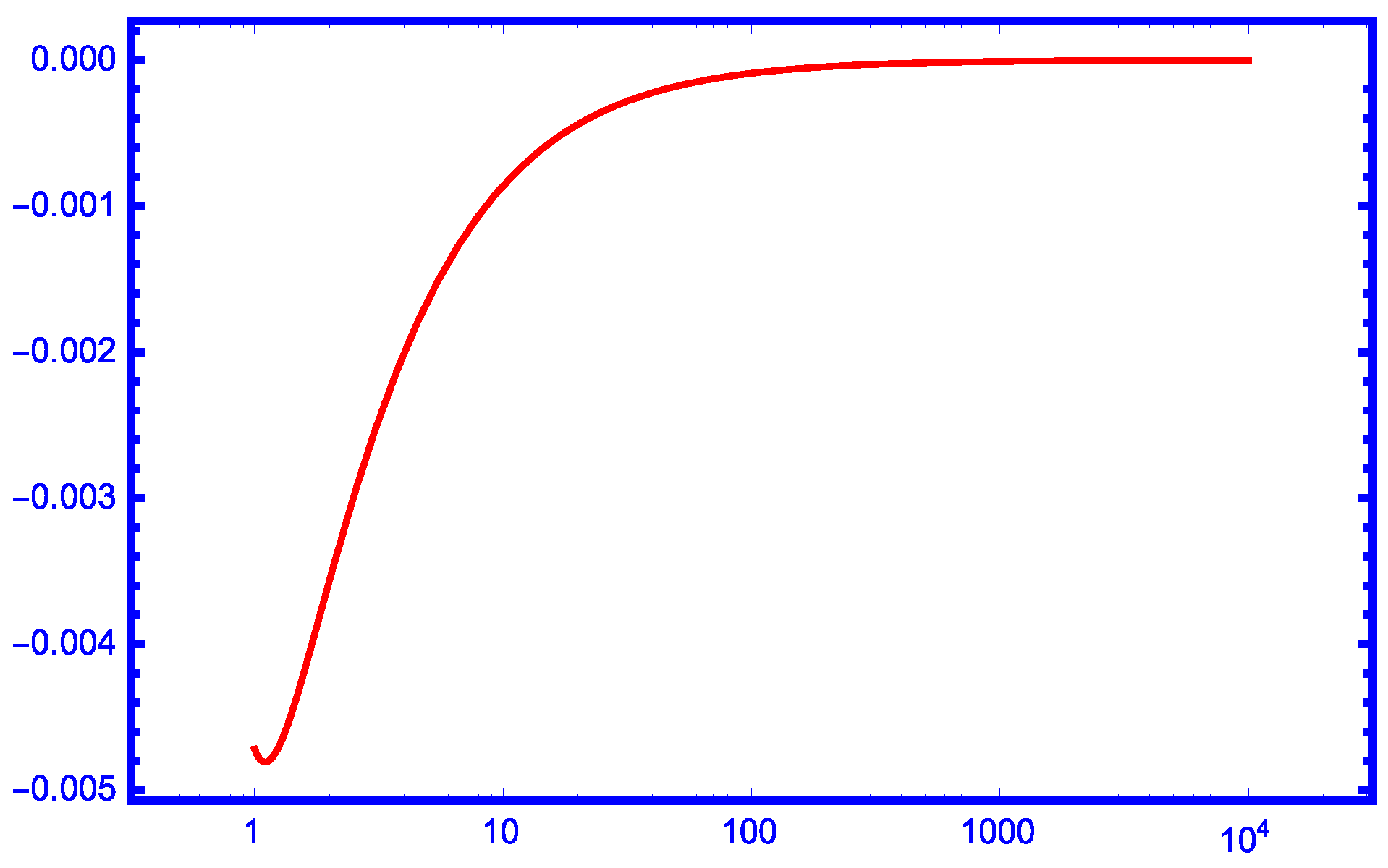
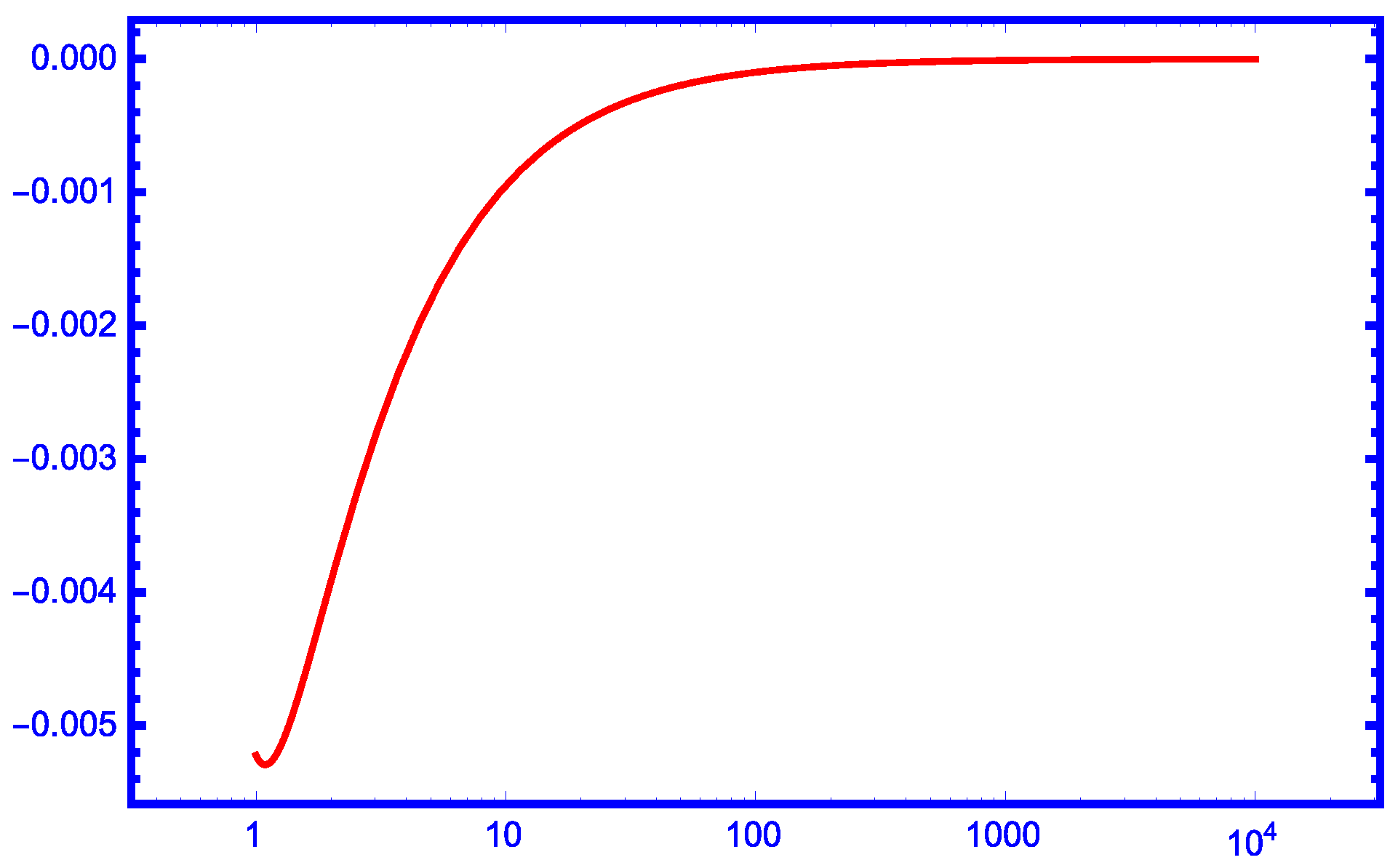
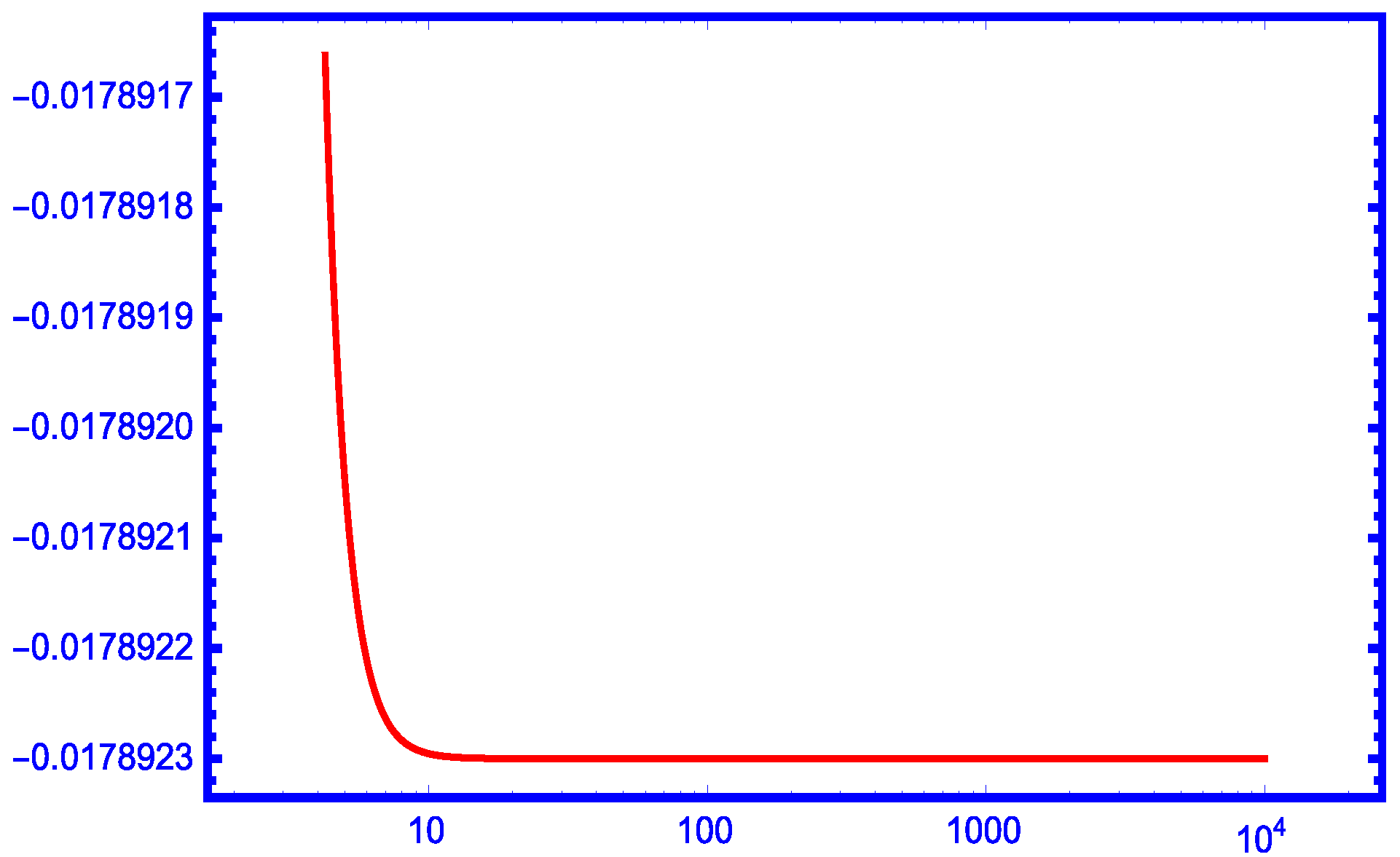
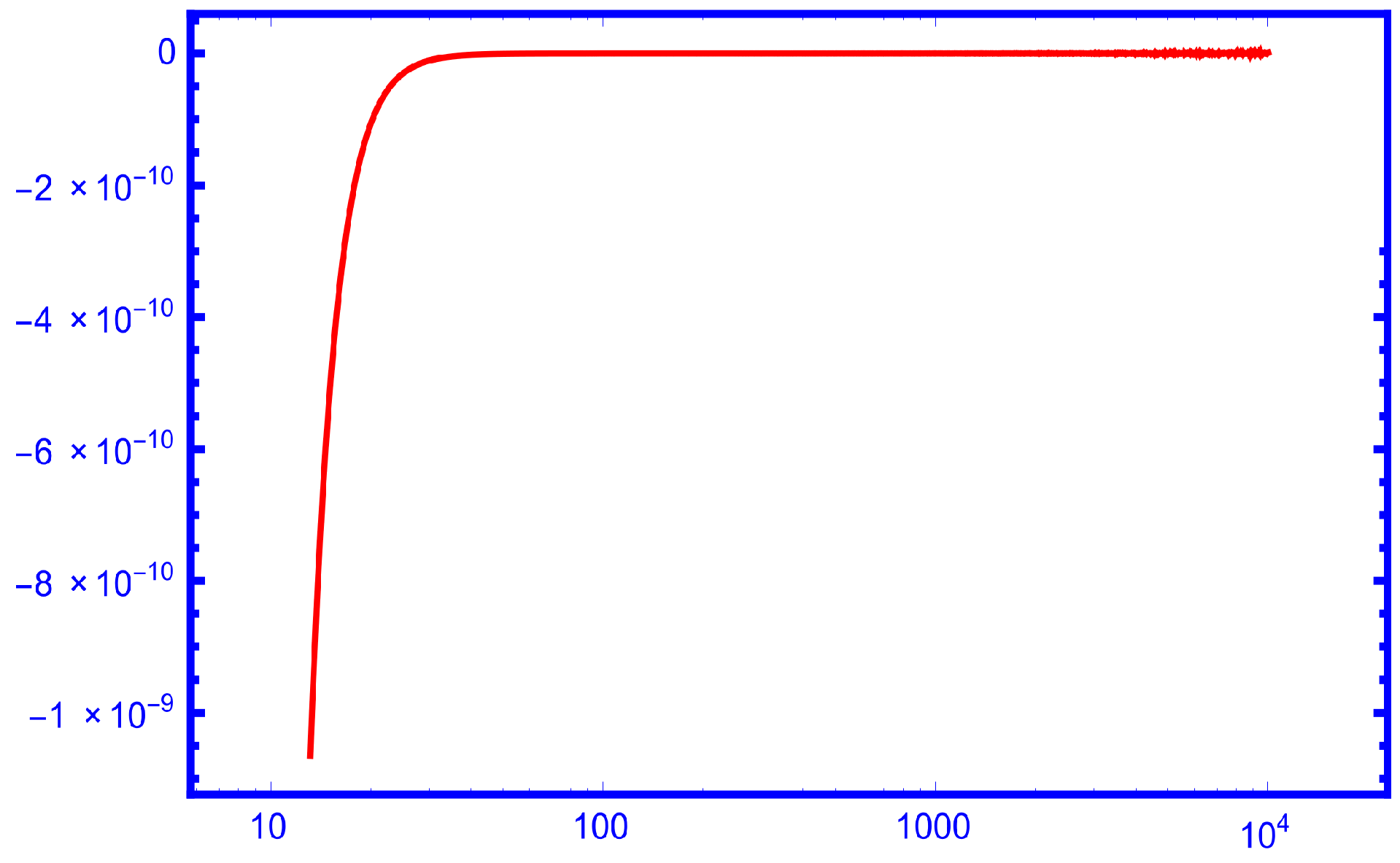
2. Main Results
3. Comparisons
4. Open Problem
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Andrews, G.E.; Askey, R.A.; Roy, R. Special Functions; Encyclopedia of Mathematics and Its Applications 71; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Apostol, T.M. Introduction to Analytic Number Theory; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Moll, V.H. Special Integrals of Gradshteyn and Ryzhik: The Proofs-Volume II; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M.; Jeffrey, A.; Zwillinger, D.; Moll, V. Table of Integrals, Series, and Products, 8th ed.; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards; Applied Mathematics Series 55; 9th Printing; Dover Publications: New York, NY, USA; Washington, DC, USA, 1972. [Google Scholar]
- Anderson, G.D.; Qiu, S.L. A monotonicity property of the gamma function. Proc. Am. Math. Soc. 1997, 125, 3355–3362. [Google Scholar] [CrossRef]
- Elezović, N.; Giordano, C.; Pečarić, J. The best bounds in Gautschi’s inequalitity. Math. Inequal. Appl. 2000, 3, 239–252. [Google Scholar]
- Guo, B.-N.; Qi, F. Sharp inequalities for the psi function and harmonic numbers. Analysis 2014, 34, 1–10. [Google Scholar] [CrossRef][Green Version]
- Allasia, G.; Giordano, C.; Pečarić, J. Inequalities for the gamma function relating to asymptotic expasions. Math. Inequal. Appl. 2002, 5, 543–555. [Google Scholar]
- Batir, N. Some new inequalities for Gamma and Polygamma functions. J. Inequal. Pure Appl. Math. 2005, 6, 103. [Google Scholar]
- Mortici, C. Sharp bounds for gamma and digamma function arising from Burnside’s formula. Rev. Anal. Numer. Th. Approx. 2010, 39, 69–72. [Google Scholar] [CrossRef]
- Mortici, C. Estimating the digamma and trigamma functions by com- pletely monotonicity arguments. Appl. Math. Comp. 2010, 217, 4081–4085. [Google Scholar] [CrossRef]
- Batir, N. Sharp bounds for the psi function and harmonic numbers. Math. Inequal. Appl. 2011, 14, 917–925. [Google Scholar] [CrossRef]
- Sun, B.-C.; Liu, Z.-M.; Li, Q.; Zheng, S.-Z. The monotonicity and convexity of a function involving psi function with applications. J. Inequalities Appl. 2016, 2016, 151. [Google Scholar] [CrossRef]
- Mahmoud, M.; Almuashi, H. An Approximation Formula for Nielsen’s Beta Function Involving the Trigamma Function. Mathematics 2022, 10, 4729. [Google Scholar] [CrossRef]
- Mahmoud, M.; Almuashi, H. Two Approximation Formulas for Bateman’s G-Function with Bounded Monotonic Errors. Mathematics 2022, 10, 4787. [Google Scholar] [CrossRef]
- Qi, F.; Lim, D.; Nantomah, K. Monotonicity and positivity of several functions involving ratios and products of polygamma functions. J. Inequal. Appl. 2025, 5, 2025. [Google Scholar] [CrossRef]
- Qi, F.; Agarwal, R.P. Several Functions Originating from Fisher-Rao Geometry of Dirichlet Distributions and Involving Polygamma Functions. Mathematics 2024, 12, 44. [Google Scholar] [CrossRef]
- Yin, H.-P.; Han, L.-X.; Qi, F. Decreasing and complete monotonicity of functions defined by derivatives of completely monotonic function involving trigamma function. Demonstr. Demonstr. Math. 2024, 57, 20240041. [Google Scholar] [CrossRef]
- Widder, D.V. The Laplace Transform; Princeton University Press: Princeton, NJ, USA, 1946. [Google Scholar]
- Qi, F.; Wang, S.-H. Complete monotonicity, completely monotonic degree, integral representations, and an inequality related to the exponential, trigamma, and modified Bessel functions. Glob. J. Math. Anal. 2014, 2, 91–97. [Google Scholar] [CrossRef]
- Gautschi, W. A harmonic mean inequality for the gamma function. SIAM J. Math. Anal. 1974, 5, 278–281. [Google Scholar] [CrossRef]
- Alzer, H.; Jameson, G. A harmonic mean inequality for the digamma function and related results. Rend. Semin. Mat. Univ. Padova 2017, 137, 203–209. [Google Scholar] [CrossRef] [PubMed]
- Alzer, H. A Mean Value Inequality for the Digamma Function, Rendiconti Sem. Mat. Univ. Pol. Torino 2017, 75, 19–25. [Google Scholar]
- Nantomah, K.; Abe-I-Kpeng, G.; Sandow, S. On some properties of the Trigamma function. arXiv 2023, arXiv:2304.12081v1. [Google Scholar]
- Alzer, H.; Salem, A. A harmonic mean inequality for the q-gamma function. Ramanujan J. 2022, 58, 1025–1041. [Google Scholar] [CrossRef]
- Bouali, M. A harmonic mean inequality for the q-gamma and q-digamma functions. Filomat 2021, 35, 4105–4119. [Google Scholar] [CrossRef]
- Yildirim, E. Monotonicity Properties on k-Digamma Function and its Related Inequalities. J. Math. Inequal. 2020, 14, 161–173. [Google Scholar] [CrossRef]
- Yin, L.; Huang, L.-G.; Lin, X.-L.; Wang, Y.-L. Monotonicity, concavity, and inequalities related to the generalized digamma function. Adv. Differ. Equ. 2018, 2018, 246. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, M.; Alofi, A.S.; Zurayyir, M.A. New Approximation Formula of Digamma Function with Bounded Remainder. Mathematics 2025, 13, 720. https://doi.org/10.3390/math13050720
Mahmoud M, Alofi AS, Zurayyir MA. New Approximation Formula of Digamma Function with Bounded Remainder. Mathematics. 2025; 13(5):720. https://doi.org/10.3390/math13050720
Chicago/Turabian StyleMahmoud, Mansour, Abdulaziz S. Alofi, and Mohammed A. Zurayyir. 2025. "New Approximation Formula of Digamma Function with Bounded Remainder" Mathematics 13, no. 5: 720. https://doi.org/10.3390/math13050720
APA StyleMahmoud, M., Alofi, A. S., & Zurayyir, M. A. (2025). New Approximation Formula of Digamma Function with Bounded Remainder. Mathematics, 13(5), 720. https://doi.org/10.3390/math13050720





