Domain Generalization Through Data Augmentation: A Survey of Methods, Applications, and Challenges
Abstract
1. Introduction
2. Background
2.1. Formalization of Domain Generalization
2.2. Related Research Areas
3. Taxonomy of Data Augmentation Techniques for Domain Generalization
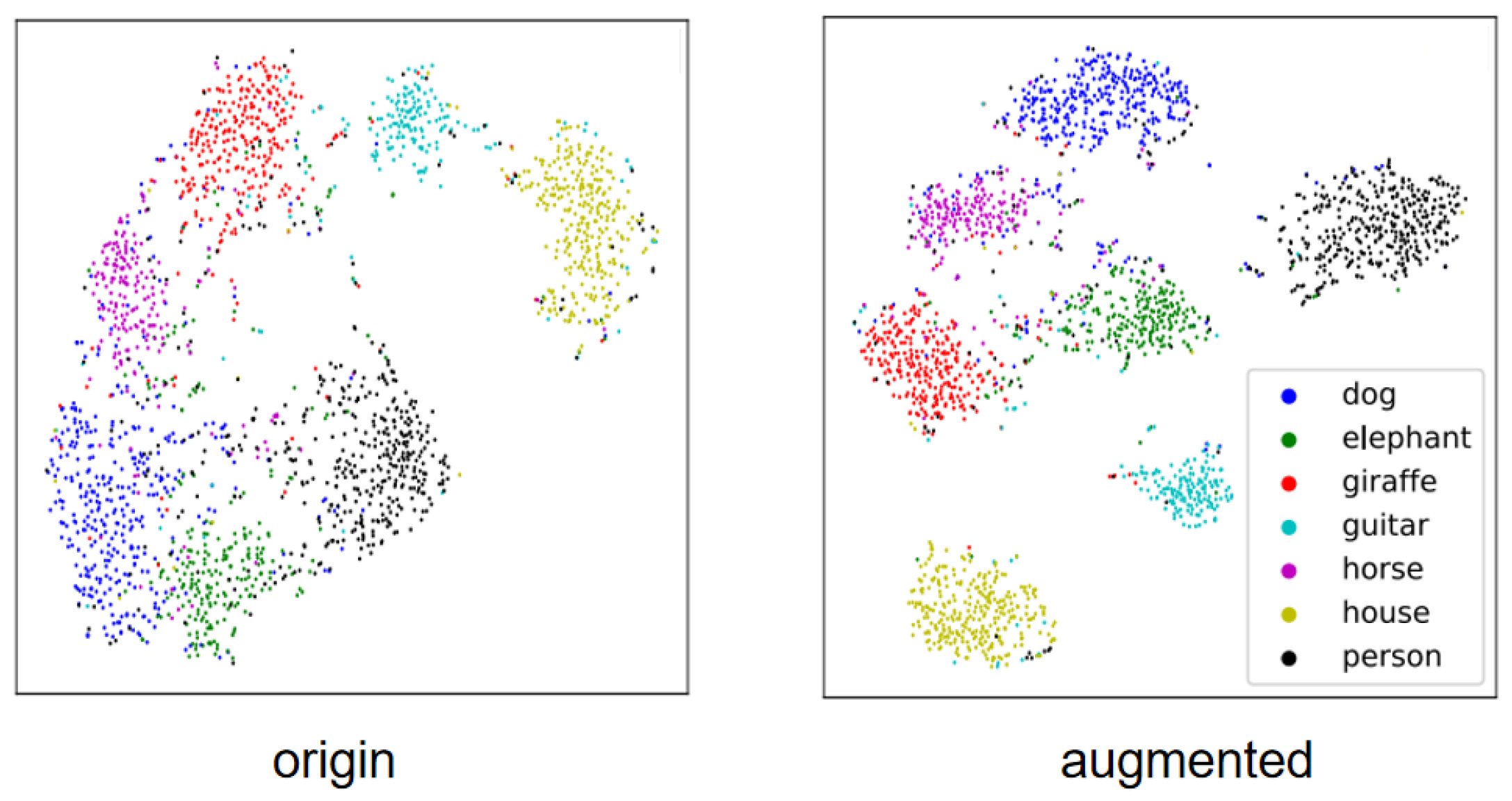
- Scope of Data Augmentation. This dimension identifies where data augmentation is applied, distinguishing between methods that operate in the image space and those in the feature space. Methods in the image space modify raw input data to indirectly influence the high-level features extracted by the model, while feature space methods directly alter high-level features to improve generalization.
- Nature of Data Augmentation. This dimension reflects the principles underlying the augmentation methods. It includes gradient-based methods that utilize backpropagation, generative methods that generate synthetic data by altering latent representations, and rule-based methods that apply predefined transformations to modify the data.
- Training Dependency. This dimension evaluates the reliance of data augmentation methods on the training process within the DG pipeline. It categorizes methods into those that can be integrated without requiring additional training, methods leveraging pretrained models directly for augmentation, and methods requiring the simultaneous training of augmentation-related parameters alongside the DG model.
3.1. Scope of Data Augmentation
3.2. Nature of Data Augmentation
3.3. Training Dependency
3.4. Comparative Summary of Taxonomy
| Scope | Methods | Nature | Td | Methods | Nature | Td |
|---|---|---|---|---|---|---|
| Input | VIPAug [69] | R | F | CrossGrad [72] | Gr | S |
| RCT [115] | R | F | ED-SAM [105] | Ge | P | |
| Pro-RandConv [71] | R | F | CDGA [106] | Ge | P | |
| APR [109] | R | F | DIDEX [107] | Ge | P | |
| FACT [68] | R | F | GeomTex [66] | Ge | P | |
| RandAugment [64] | R | F | EFDM [101] | Ge | P | |
| RandConv [70] | R | F | DAI [102] | Ge | S | |
| AugMix [63] | R | F | FDS [108] | Ge | S | |
| ALT [75] | Gr | S | [95] | Ge | S | |
| MODE [74] | Gr | S | GINet [98] | Ge | S | |
| TeacherAugment [73] | Gr | S | VDN [100] | Ge | S | |
| AdvStyle [116] | Gr | S | DIVA [117] | Ge | S | |
| [89] | Gr | S | L2A-OT [97] | Ge | S | |
| DFDG [90] | Gr | S | DDAIG [118] | Ge | S | |
| Feature | TFS-ViT [108] | R | F | DSU [81] | R | F |
| START [119] | R | F | SFA [76] | R | F | |
| CPerb [110] | R | F | MixStyle [79] | R | F | |
| CSU [82] | R | F | DFP [86] | Gr | S | |
| MRFP [120] | R | F | RASP [87] | Gr | S | |
| CDSA [78] | R | F | ASRConv [88] | Gr | S | |
| ALOFT [85] | R | F | DFF [33] | Gr | S | |
| Style Neophile [80] | R | F | [103] | Ge | S |
| Scope | Strengths | Weakness | Use Cases |
|---|---|---|---|
| Input | Simple to implement, no model modification needed, visually interpretable | Limited control over feature variations, potential distortions | Image-based tasks (e.g., object classification and medical imaging) |
| Feature | Directly manipulates learned representations, better generalization | Requires model modifications, harder to visualize, dependency on model’s representation learning capability | Feature-driven tasks (e.g., NLP, speech and ViT-based models) |
| Scope | Methods | PACS avg. | Office-Home avg. |
|---|---|---|---|
| BaseLine | ERM | 78.3 | 63.9 |
| Input | CrossGrad [72] | 80.7 | 64.4 |
| DDAIG [118] | 83.1 | 65.5 | |
| L2A-OT [97] | 82.8 | 65.6 | |
| FACT [68] | 84.5 | 66.5 | |
| CIRL [30] | 86.3 | 67.1 | |
| MODE [74] | 86.9 | 66.9 | |
| GINet [98] | 83.7 | 66.9 | |
| GeomTex [66] | 86.6 | 66.8 | |
| Pro-RandConv [71] | 84.3 | 64.6 | |
| CDGA [106] | 88.4 | 70.2 | |
| Feature | MixStyle [79] | 83.7 | 65.5 |
| RASP [87] | 84.7 | 67.3 | |
| Style Neophile [80] | 85.5 | 65.9 | |
| CDSA [78] | 89.3 | 73.0 | |
| DSU [81] | 84.1 | 66.1 | |
| CSU [82] | 85.2 | 66.8 | |
| [103] | 86.0 | 66.6 | |
| DFP [86] | 83.0 | 63.7 |
3.5. Discussion of the Taxonomy Design
4. Applications of Data Augmentation in Domain Generalization
5. Challenges and Open Problems
6. Emerging Trends and Future Directions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Quionero-Candela, J.; Sugiyama, M.; Schwaighofer, A.; Lawrence, N. Dataset Shift in Machine Learning; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar] [CrossRef]
- Khosla, A.; Zhou, T.; Malisiewicz, T.; Efros, A.A.; Torralba, A. Undoing the damage of dataset bias—Proceedings, Part I 12. In Proceedings of the Computer Vision–ECCV 2012: 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 158–171. [Google Scholar]
- Xie, Q.; Li, Y.; He, N.; Ning, M.; Ma, K.; Wang, G.; Lian, Y.; Zheng, Y. Unsupervised domain adaptation for medical image segmentation by disentanglement learning and self-training. IEEE Trans. Med. Imaging 2022, 43, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Schwonberg, M.; Niemeijer, J.; Termöhlen, J.A.; Schäfer, J.P.; Schmidt, N.M.; Gottschalk, H.; Fingscheidt, T. Survey on unsupervised domain adaptation for semantic segmentation for visual perception in automated driving. IEEE Access 2023, 11, 54296–54336. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 1–48. [Google Scholar] [CrossRef]
- Wang, J.; Perez, L. The effectiveness of data augmentation in image classification using deep learning. Convolutional Neural Netw. Vis. Recognit 2017, 11, 1–8. [Google Scholar]
- Zhou, K.; Liu, Z.; Qiao, Y.; Xiang, T.; Loy, C.C. Domain generalization: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 4396–4415. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Lan, C.; Liu, C.; Ouyang, Y.; Qin, T.; Lu, W.; Chen, Y.; Zeng, W.; Philip, S.Y. Generalizing to unseen domains: A survey on domain generalization. IEEE Trans. Knowl. Data Eng. 2022, 35, 8052–8072. [Google Scholar] [CrossRef]
- Kumar, T.; Brennan, R.; Mileo, A.; Bendechache, M. Image data augmentation approaches: A comprehensive survey and future directions. IEEE Access 2024. [Google Scholar] [CrossRef]
- Wang, M.; Deng, W. Deep visual domain adaptation: A survey. Neurocomputing 2018, 312, 135–153. [Google Scholar] [CrossRef]
- Liu, X.; Yoo, C.; Xing, F.; Oh, H.; El Fakhri, G.; Kang, J.W.; Woo, J. Deep unsupervised domain adaptation: A review of recent advances and perspectives. APSIPA Trans. Signal Inf. Process. 2022, 11, 1. [Google Scholar] [CrossRef]
- Li, B.; Wang, Y.; Zhang, S.; Li, D.; Keutzer, K.; Darrell, T.; Zhao, H. Learning invariant representations and risks for semi-supervised domain adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1104–1113. [Google Scholar]
- Ganin, Y.; Lempitsky, V. Unsupervised domain adaptation by backpropagation. In Proceedings of the International Conference on Machine Learning. PMLR, Lille, France, 7–9 July 2015; pp. 1180–1189. [Google Scholar]
- Long, M.; Cao, Y.; Wang, J.; Jordan, M. Learning transferable features with deep adaptation networks. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015; pp. 97–105. [Google Scholar]
- Li, H.; Pan, S.J.; Wang, S.; Kot, A.C. Domain generalization with adversarial feature learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5400–5409. [Google Scholar]
- Albuquerque, I.; Monteiro, J.; Darvishi, M.; Falk, T.H.; Mitliagkas, I. Generalizing to unseen domains via distribution matching. arXiv 2019, arXiv:1911.00804. [Google Scholar]
- Zhu, W.; Lu, L.; Xiao, J.; Han, M.; Luo, J.; Harrison, A.P. Localized adversarial domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 7108–7118. [Google Scholar]
- Nguyen, T.; Do, K.; Duong, B.; Nguyen, T. Domain Generalisation via Risk Distribution Matching. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 2790–2799. [Google Scholar]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Agarwal, N.; Sondhi, A.; Chopra, K.; Singh, G. Transfer learning: Survey and classification. In Smart Innovations in Communication and Computational Sciences: Proceedings of International Conference on Smart Innovations in Communication and Computational Sciences, online, 7–9 April 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 145–155. [Google Scholar]
- Zhang, Y.; Yang, Q. A survey on multi-task learning. IEEE Trans. Knowl. Data Eng. 2021, 34, 5586–5609. [Google Scholar] [CrossRef]
- Vandenhende, S.; Georgoulis, S.; Proesmans, M.; Dai, D.; Van Gool, L. Revisiting multi-task learning in the deep learning era. arXiv 2020, arXiv:2004.13379. [Google Scholar]
- Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; et al. Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. USA 2017, 114, 3521–3526. [Google Scholar] [CrossRef]
- Zhang, Z.; Ning, G.; Cen, Y.; Li, Y.; Zhao, Z.; Sun, H.; He, Z. Progressive neural networks for image classification. arXiv 2018, arXiv:1804.09803. [Google Scholar]
- Parisi, G.I.; Kemker, R.; Part, J.L.; Kanan, C.; Wermter, S. Continual lifelong learning with neural networks: A review. Neural Netw. 2019, 113, 54–71. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning PMLR, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Baik, S.; Choi, J.; Kim, H.; Cho, D.; Min, J.; Lee, K.M. Meta-learning with task-adaptive loss function for few-shot learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Online, 11–17 October 2021; pp. 9465–9474. [Google Scholar]
- Khoee, A.G.; Yu, Y.; Feldt, R. Domain generalization through meta-learning: A survey. Artif. Intell. Rev. 2024, 57, 285. [Google Scholar] [CrossRef]
- Zhang, X.; Cui, P.; Xu, R.; Zhou, L.; He, Y.; Shen, Z. Deep Stable Learning for Out-Of-Distribution Generalization. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 5368–5378. [Google Scholar] [CrossRef]
- Lv, F.; Liang, J.; Li, S.; Zang, B.; Liu, C.H.; Wang, Z.; Liu, D. Causality inspired representation learning for domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LO, USA, 21–24 June 2022; pp. 8046–8056. [Google Scholar]
- Nam, H.; Lee, H.; Park, J.; Yoon, W.; Yoo, D. Reducing Domain Gap by Reducing Style Bias. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 8686–8695. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Liu, W.; Weller, A.; Schölkopf, B.; Xing, E. Towards Principled Disentanglement for Domain Generalization. In Proceedings of the EEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Lin, S.; Zhang, Z.; Huang, Z.; Lu, Y.; Lan, C.; Chu, P.; You, Q.; Wang, J.; Liu, Z.; Parulkar, A.; et al. Deep frequency filtering for domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 11797–11807. [Google Scholar]
- Chen, Y.; Wang, Y.; Pan, Y.; Yao, T.; Tian, X.; Mei, T. A Style and Semantic Memory Mechanism for Domain Generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Jin, X.; Lan, C.; Zeng, W.; Chen, Z. Style Normalization and Restitution for Domain Generalization and Adaptation. IEEE Trans. Multimed. 2022, 24, 3636–3651. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Q.; Huang, Z.; Wang, H.; Zhao, J. Towards domain-specific features disentanglement for domain generalization. arXiv 2023, arXiv:2310.03007. [Google Scholar]
- Pei, S.; Sun, J.; Da Xu, R.Y.; Xiang, S.; Meng, G. Domain decorrelation with potential energy ranking. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 9–14 February 2023; Volume 37, pp. 2020–2028. [Google Scholar]
- Li, T.; Qiao, F.; Ma, M.; Peng, X. Are Data-driven Explanations Robust against Out-of-distribution Data? In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 3821–3831. [Google Scholar]
- Chen, L.; Zhang, Y.; Song, Y.; Van Den Hengel, A.; Liu, L. Domain generalization via rationale invariance. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 1751–1760. [Google Scholar]
- Huang, Z.; Wang, H.; Zhao, J.; Zheng, N. IDAG Invariant dag searching for domain generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 19169–19179. [Google Scholar]
- Zhang, X.; Su, H.; Liu, X. Graph convolutional network for adversarial domain generalization. IEEE Trans. Comput. Soc. Syst. 2024. [CrossRef]
- Huang, K.; Ren, Z.; Zhu, L.; Lin, T.; Zhu, Y.; Zeng, L.; Wan, J. Intra-domain self generalization network for intelligent fault diagnosis of bearings under unseen working conditions. Adv. Eng. Inform. 2025, 64, 102997. [Google Scholar] [CrossRef]
- Qu, S.; Pan, Y.; Chen, G.; Yao, T.; Jiang, C.; Mei, T. Modality-agnostic debiasing for single domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 24142–24151. [Google Scholar]
- Yu, G.; Hwang, H. A2XP: Towards Private Domain Generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 23544–23553. [Google Scholar]
- Li, B.; Shen, Y.; Yang, J.; Wang, Y.; Ren, J.; Che, T.; Zhang, J.; Liu, Z. Sparse mixture-of-experts are domain generalizable learners. arXiv 2022, arXiv:2206.04046. [Google Scholar]
- Zhang, L.; Liu, Z.; Zhang, W.; Zhang, D. Style uncertainty based self-paced meta learning for generalizable person re-identification. IEEE Trans. Image Process. 2023, 32, 2107–2119. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Qin, L.; Xu, M.; Chen, W.; Pu, S.; Zhang, W. Randomized Spectrum Transformations for Adapting Object Detector in Unseen Domains. IEEE Trans. Image Process. 2023, 32, 4868–4879. [Google Scholar] [CrossRef]
- Li, M.; Wang, Z.; Hu, X. Restoration towards decomposition: A simple approach for domain generalization. Inf. Sci. 2024, 679, 121053. [Google Scholar] [CrossRef]
- Lv, F.; Liang, J.; Li, S.; Zhang, J.; Liu, D. Improving generalization with domain convex game. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 24315–24324. [Google Scholar]
- Zhang, J.; Qi, L.; Shi, Y.; Gao, Y. Mvdg: A unified multi-view framework for domain generalization. In Proceedings of the European Conference on Computer Vision. Springer, Tel Aviv, Israel, 23–27 October 2022; pp. 161–177. [Google Scholar]
- Huang, C.; Cao, Z.; Wang, Y.; Wang, J.; Long, M. Metasets: Meta-learning on point sets for generalizable representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8863–8872. [Google Scholar]
- Cha, J.; Chun, S.; Lee, K.J.; Cho, H.C.; Park, S.H.; Lee, Y.; Park, S. SWAD: Domain Generalization by Seeking Flat Minima. Adv. Neural Inf. Process. Syst. 2021, 34, 22405–22418. [Google Scholar]
- Zhang, X.; Xu, R.; Yu, H.; Dong, Y.; Tian, P.; Cui, P. Flatness-aware minimization for domain generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 5166–5179. [Google Scholar]
- Wang, P.; Zhang, Z.; Lei, Z.; Zhang, L. Sharpness-aware gradient matching for domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 3769–3778. [Google Scholar]
- Zhang, R.; Fan, Z.; Yao, J.; Zhang, Y.; Wang, Y. Domain-Inspired Sharpness-Aware Minimization Under Domain Shifts. arXiv 2024, arXiv:2405.18861. [Google Scholar]
- Zhang, J.; Qi, L.; Shi, Y.; Gao, Y. Exploring Flat Minima for Domain Generalization with Large Learning Rates. IEEE Trans. Knowl. Data Eng. 2024, 36, 6145–6185. [Google Scholar] [CrossRef]
- Lee, K.; Kim, S.; Kwak, S. Cross-domain ensemble distillation for domain generalization. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–20. [Google Scholar]
- Cha, J.; Lee, K.; Park, S.; Chun, S. Domain generalization by mutual-information regularization with pre-trained models. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 440–457. [Google Scholar]
- Wang, Y.; Wu, X.; Liu, X.; Chu, F.; Liu, H.; Han, Z. Label smoothing regularization-based no hyperparameter domain generalization. Knowl. Based Syst. 2024, 309, 112877. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, W.; Zhao, Z.; Su, F.; Men, A.; Meng, H. PracticalDG: Perturbation Distillation on Vision-Language Models for Hybrid Domain Generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 23501–23511. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Matsuura, T.; Harada, T. Domain generalization using a mixture of multiple latent domains. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11749–11756. [Google Scholar]
- Hendrycks, D.; Mu, N.; Cubuk, E.D.; Zoph, B.; Gilmer, J.; Lakshminarayanan, B. Augmix: A simple data processing method to improve robustness and uncertainty. arXiv 2019, arXiv:1912.02781. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Shlens, J.; Le, Q.V. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 702–703. [Google Scholar]
- Chun, S.; Park, S. Styleaugment: Learning texture de-biased representations by style augmentation without pre-defined textures. arXiv 2021, arXiv:2108.10549. [Google Scholar]
- Liu, X.C.; Yang, Y.L.; Hall, P. Geometric and textural augmentation for domain gap reduction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–25 June 2022; pp. 14340–14350. [Google Scholar]
- Liu, X.C.; Yang, Y.L.; Hall, P. Learning to warp for style transfer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 3702–3711. [Google Scholar]
- Xu, Q.; Zhang, R.; Zhang, Y.; Wang, Y.; Tian, Q. A fourier-based framework for domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14383–14392. [Google Scholar]
- Lee, I.; Lee, W.; Myung, H. Domain Generalization with Vital Phase Augmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 23–28 February 2024; Volume 38, pp. 2892–2900. [Google Scholar]
- Xu, Z.; Liu, D.; Yang, J.; Raffel, C.; Niethammer, M. Robust and generalizable visual representation learning via random convolutions. arXiv 2020, arXiv:2007.13003. [Google Scholar]
- Choi, S.; Das, D.; Choi, S.; Yang, S.; Park, H.; Yun, S. Progressive random convolutions for single domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 10312–10322. [Google Scholar]
- Shankar, S.; Piratla, V.; Chakrabarti, S.; Chaudhuri, S.; Jyothi, P.; Sarawagi, S. Generalizing Across Domains via Cross-Gradient Training. In Proceedings of the International Conference on Learning Representations, International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Suzuki, T. Teachaugment: Data augmentation optimization using teacher knowledge. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–25 June 2022; pp. 10904–10914. [Google Scholar]
- Dai, R.; Zhang, Y.; Fang, Z.; Han, B.; Tian, X. Moderately Distributional Exploration for Domain Generalization. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 6786–6817. [Google Scholar]
- Gokhale, T.; Anirudh, R.; Thiagarajan, J.J.; Kailkhura, B.; Baral, C.; Yang, Y. Improving Diversity with Adversarially Learned Transformations for Domain Generalization. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 434–443. [Google Scholar]
- Li, P.; Li, D.; Li, W.; Gong, S.; Fu, Y.; Hospedales, T.M. A Simple Feature Augmentation for Domain Generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 8886–8895. [Google Scholar]
- Wang, Y.; Huang, G.; Song, S.; Pan, X.; Xia, Y.; Wu, C. Regularizing deep networks with semantic data augmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3733–3748. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Liu, Y.; Yuan, J.; Wang, S.; Wang, Z.; Wang, W. Inter-class and inter-domain semantic augmentation for domain generalization. IEEE Trans. Image Process. 2024, 33, 1338–1347. [Google Scholar] [CrossRef]
- Zhou, K.; Yang, Y.; Qiao, Y.; Xiang, T. Domain generalization with mixstyle. arXiv 2021, arXiv:2104.02008. [Google Scholar]
- Kang, J.; Lee, S.; Kim, N.; Kwak, S. Style neophile: Constantly seeking novel styles for domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 7130–7140. [Google Scholar]
- Li, X.; Dai, Y.; Ge, Y.; Liu, J.; Shan, Y.; Duan, L. Uncertainty Modeling for Out-of-Distribution Generalization. In Proceedings of the International Conference on Learning Representations, Online, 25–29 April 2022; pp. 2000–2009. [Google Scholar]
- Zhang, Z.; Wang, B.; Jha, D.; Demir, U.; Bagci, U. Domain generalization with correlated style uncertainty. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 2000–2009. [Google Scholar]
- Wang, H.; Wu, X.; Huang, Z.; Xing, E.P. High-frequency component helps explain the generalization of convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8681–8691. [Google Scholar]
- Wang, J.; Du, R.; Chang, D.; Liang, K.; Ma, Z. Domain generalization via frequency-domain-based feature disentanglement and interaction. In Proceedings of the 30th ACM International Conference on Multimedia, Lisbon, Portugal, 10–14 October 2022; pp. 4821–4829. [Google Scholar]
- Guo, J.; Wang, N.; Qi, L.; Shi, Y. Aloft: A lightweight mlp-like architecture with dynamic low-frequency transform for domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–24 June 2023; pp. 24132–24141. [Google Scholar]
- Wang, C.; Zhang, Z.; Zhou, Z. Domain Feature Perturbation for Domain Generalization. In ECAI 2024; IOS Press: Amsterdam, The Netherlands, 2024; pp. 2532–2539. [Google Scholar]
- Kim, T.; Han, B. Randomized adversarial style perturbations for domain generalization. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 2317–2325. [Google Scholar]
- Zhang, Z.; Li, Y.; Shin, B.S. Learning generalizable visual representation via adaptive spectral random convolution for medical image segmentation. Comput. Biol. Med. 2023, 167, 107580. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, Y.; Qiu, R.; Huang, Z.; Baktashmotlagh, M. Learning to diversify for single domain generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 834–843. [Google Scholar]
- Zhang, W.; Ragab, M.; Sagarna, R. Robust domain-free domain generalization with class-aware alignment. In Proceedings of the ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; IEEE: New York, NY, USA, 2021; pp. 2870–2874. [Google Scholar]
- Smilkov, D.; Thorat, N.; Kim, B.; Viégas, F.; Wattenberg, M. Smoothgrad: Removing noise by adding noise. arXiv 2017, arXiv:1706.03825. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar]
- Brock, A.; Donahue, J.; Simonyan, K. Large Scale GAN Training for High Fidelity Natural Image Synthesis. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Bai, H.; Yang, C.; Xu, Y.; Chan, S.H.G.; Zhou, B. Improving out-of-distribution robustness of classifiers via generative interpolation. arXiv 2023, arXiv:2307.12219. [Google Scholar]
- Rumelhart, D.E.; McClelland, J.L.; Group, P.R. Parallel Distributed Processing, Volume 1: Explorations in the Microstructure of Cognition: Foundations; The MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Zhou, K.; Yang, Y.; Hospedales, T.; Xiang, T. Learning to generate novel domains for domain generalization. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XVI 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 561–578. [Google Scholar]
- Xia, H.; Jing, T.; Ding, Z. Generative inference network for imbalanced domain generalization. IEEE Trans. Image Process. 2023, 32, 1694–1704. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. Adv. Neural Inf. Process. Syst. 2013, 26. [Google Scholar]
- Wang, Y.; Li, H.; Cheng, H.; Wen, B.; Chau, L.P.; Kot, A.C. Variational disentanglement for domain generalization. arXiv 2021, arXiv:2109.05826. [Google Scholar]
- Zhang, Y.; Li, M.; Li, R.; Jia, K.; Zhang, L. Exact feature distribution matching for arbitrary style transfer and domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8025–8035. [Google Scholar]
- Zhang, Z.; Yang, S.; Dang, Q.; Jiang, T.; Liu, Q.; Wang, C.; Gu, L. Improving diversity and invariance for single domain generalization. Inf. Sci. 2025, 692, 121656. [Google Scholar] [CrossRef]
- Wang, Y.; Qi, L.; Shi, Y.; Gao, Y. Feature-based style randomization for domain generalization. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 5495–5509. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Truong, T.D.; Li, X.; Raj, B.; Cothren, J.; Luu, K. ED-SAM: An Efficient Diffusion Sampling Approach to Domain Generalization in Vision-Language Foundation Models. arXiv 2024, arXiv:2406.01432. [Google Scholar]
- Hemati, S.; Beitollahi, M.; Estiri, A.H.; Omari, B.A.; Lamghari, S.; Khalil, Y.H.; Chen, X.; Zhang, G. Beyond Loss Functions: Exploring Data-Centric Approaches with Diffusion Model for Domain Generalization. Trans. Mach. Learn. Res. 2024. [Google Scholar]
- Niemeijer, J.; Schwonberg, M.; Termöhlen, J.A.; Schmidt, N.M.; Fingscheidt, T. Generalization by adaptation: Diffusion-based domain extension for domain-generalized semantic segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 2830–2840. [Google Scholar]
- Noori, M.; Cheraghalikhani, M.; Bahri, A.; Hakim, G.A.V.; Osowiechi, D.; Ayed, I.B.; Desrosiers, C. TFS-ViT: Token-level feature stylization for domain generalization. Pattern Recognit. 2024, 149, 110213. [Google Scholar] [CrossRef]
- Chen, G.; Peng, P.; Ma, L.; Li, J.; Du, L.; Tian, Y. Amplitude-phase recombination: Rethinking robustness of convolutional neural networks in frequency domain. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 458–467. [Google Scholar]
- Zhao, D.; Qi, L.; Shi, X.; Shi, Y.; Geng, X. A Novel Cross-Perturbation for Single Domain Generalization. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 10903–10916. [Google Scholar] [CrossRef]
- Jackson, P.T.; Abarghouei, A.A.; Bonner, S.; Breckon, T.P.; Obara, B. Style augmentation: Data augmentation via style randomization. In Proceedings of the CVPR Workshops, Long Beach, CA, USA, 16–20 June 2019; Volume 6, pp. 10–11. [Google Scholar]
- Liu, C.; Cao, Y.; Su, X.; Zhu, H. Universal Frequency Domain Perturbation for Single-Source Domain Generalization. In Proceedings of the 32nd ACM International Conference on Multimedia, Melbourne, VIC, Australia, 28 October–1 November 2024; pp. 6250–6259. [Google Scholar]
- Li, D.; Yang, Y.; Song, Y.Z.; Hospedales, T.M. Deeper, broader and artier domain generalization. In Proceedings of the IEEE International Conference on COMPUTER Vision, Venice, Italy, 22–29 October 2017; pp. 5542–5550. [Google Scholar]
- Venkateswara, H.; Eusebio, J.; Chakraborty, S.; Panchanathan, S. Deep hashing network for unsupervised domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5018–5027. [Google Scholar]
- Guo, S.; Ji, K. Random color transformation for single domain generalized retinal image segmentation. Eng. Appl. Artif. Intell. 2024, 136, 108907. [Google Scholar] [CrossRef]
- Zhong, Z.; Zhao, Y.; Lee, G.H.; Sebe, N. Adversarial style augmentation for domain generalized urban-scene segmentation. Adv. Neural Inf. Process. Syst. 2022, 35, 338–350. [Google Scholar]
- Ilse, M.; Tomczak, J.M.; Louizos, C.; Welling, M. Diva: Domain invariant variational autoencoders. In Proceedings of the Medical Imaging with Deep Learning, Montreal, QC, Canada, 6–8 July 2020; pp. 322–348. [Google Scholar]
- Zhou, K.; Yang, Y.; Hospedales, T.; Xiang, T. Deep domain-adversarial image generation for domain generalisation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 13025–13032. [Google Scholar]
- Guo, J.; Qi, L.; Shi, Y.; Gao, Y. START: A Generalized State Space Model with Saliency-Driven Token-Aware Transformation. arXiv 2024, arXiv:2410.16020. [Google Scholar]
- Udupa, S.; Gurunath, P.; Sikdar, A.; Sundaram, S. MRFP: Learning Generalizable Semantic Segmentation from Sim-2-Real with Multi-Resolution Feature Perturbation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 5904–5914. [Google Scholar]
- Zhang, S.; Zhang, L.; Liu, Z.Y. Frequency-based pseudo-domain generation for domain generalizable object detection. Neurocomputing 2023, 542, 126265. [Google Scholar] [CrossRef]
- Lee, S.; Seong, H.; Lee, S.; Kim, E. Wildnet: Learning domain generalized semantic segmentation from the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 9926–9936. [Google Scholar]
- Zhang, Z.; Li, Y.; Shin, B.S. Generalizable Polyp Segmentation via Randomized Global Illumination Augmentation. IEEE J. Biomed. Health Inform. 2024, 28, 2138–2151. [Google Scholar] [CrossRef]
- Xu, Z.; Tang, J.; Qi, C.; Yao, D.; Liu, C.; Zhan, Y.; Lukasiewicz, T. Cross-domain attention-guided generative data augmentation for medical image analysis with limited data. Comput. Biol. Med. 2024, 168, 107744. [Google Scholar] [CrossRef]
- Xue, J.; Li, Y.; Li, Z.; Cui, Y.; Zhang, S.; Wang, S. A Cross-Domain Generative Data Augmentation Framework for Aspect-Based Sentiment Analysis. Electronics 2023, 12, 2949. [Google Scholar] [CrossRef]
- Taheri, A.; Zamanifar, A.; Farhadi, A. Enhancing aspect-based sentiment analysis using data augmentation based on back-translation. Int. J. Data Sci. Anal. 2024, 2024, 1–26. [Google Scholar] [CrossRef]
- Niu, C.; Wang, X.; Cheng, X.; Song, J.; Zhang, T. Enhancing Dialogue State Tracking Models through LLM-backed User-Agents Simulation. arXiv 2024, arXiv:2405.13037. [Google Scholar]
- Fang, Y.; Wang, W.; Dong, L.; Gao, S.; Lai, H.; Yu, Z. Decoupling-Enhanced Vietnamese Speech Recognition Accent Adaptation Supervised by Prosodic Domain Information. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; pp. 1–8. [Google Scholar]
- Wang, H.; Jin, Z.; Geng, M.; Hu, S.; Li, G.; Wang, T.; Xu, H.; Liu, X. Enhancing Pre-trained ASR System Fine-tuning for Dysarthric Speech Recognition using Adversarial Data Augmentation. In Proceedings of the ICASSP 2024–2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 12311–12315. [Google Scholar]
- Jin, Z.; Xie, X.; Wang, T.; Geng, M.; Deng, J.; Li, G.; Hu, S.; Liu, X. Towards Automatic Data Augmentation for Disordered Speech Recognition. In Proceedings of the ICASSP 2024–2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 10626–10630. [Google Scholar]
- Tobin, J.; Fong, R.; Ray, A.; Schneider, J.; Zaremba, W.; Abbeel, P. Domain randomization for transferring deep neural networks from simulation to the real world. In Proceedings of the 2017 IEEE/RSJ international conference on intelligent robots and systems (IROS), Vancouver, BC, Canada, 24–18 September 2017; pp. 23–30. [Google Scholar]
- Niu, H.; Chen, Q.; Liu, T.; Li, J.; Zhou, G.; Zhang, Y.; Hu, J.; Zhan, X. xTED: Cross-Domain Adaptation via Diffusion-Based Trajectory Editing. arXiv 2024, arXiv:2409.08687. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Mane, D.; Vasudevan, V.; Le, Q.V. Autoaugment: Learning augmentation strategies from data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 113–123. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. Lora: Low-rank adaptation of large language models. ICLR 2022, 1, 3. [Google Scholar]
- Zhu, R.; Zhang, Z.; Liang, S.; Liu, Z.; Xu, C. Learning to transform dynamically for better adversarial transferability. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 24273–24283. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 3–7 May 2021. [Google Scholar]
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision mamba: Efficient visual representation learning with bidirectional state space model. arXiv 2024, arXiv:2401.09417. [Google Scholar]
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mai, J.; Gao, C.; Bao, J. Domain Generalization Through Data Augmentation: A Survey of Methods, Applications, and Challenges. Mathematics 2025, 13, 824. https://doi.org/10.3390/math13050824
Mai J, Gao C, Bao J. Domain Generalization Through Data Augmentation: A Survey of Methods, Applications, and Challenges. Mathematics. 2025; 13(5):824. https://doi.org/10.3390/math13050824
Chicago/Turabian StyleMai, Junjie, Chongzhi Gao, and Jun Bao. 2025. "Domain Generalization Through Data Augmentation: A Survey of Methods, Applications, and Challenges" Mathematics 13, no. 5: 824. https://doi.org/10.3390/math13050824
APA StyleMai, J., Gao, C., & Bao, J. (2025). Domain Generalization Through Data Augmentation: A Survey of Methods, Applications, and Challenges. Mathematics, 13(5), 824. https://doi.org/10.3390/math13050824






