Construction of a Hybrid Class of Special Polynomials: Fubini–Bell-Based Appell Polynomials and Their Properties
Abstract
1. Introduction and Preliminaries
2. Fubini–Bell-Based Appell Polynomials
3. Symmetry Identities
4. Determinant Representation
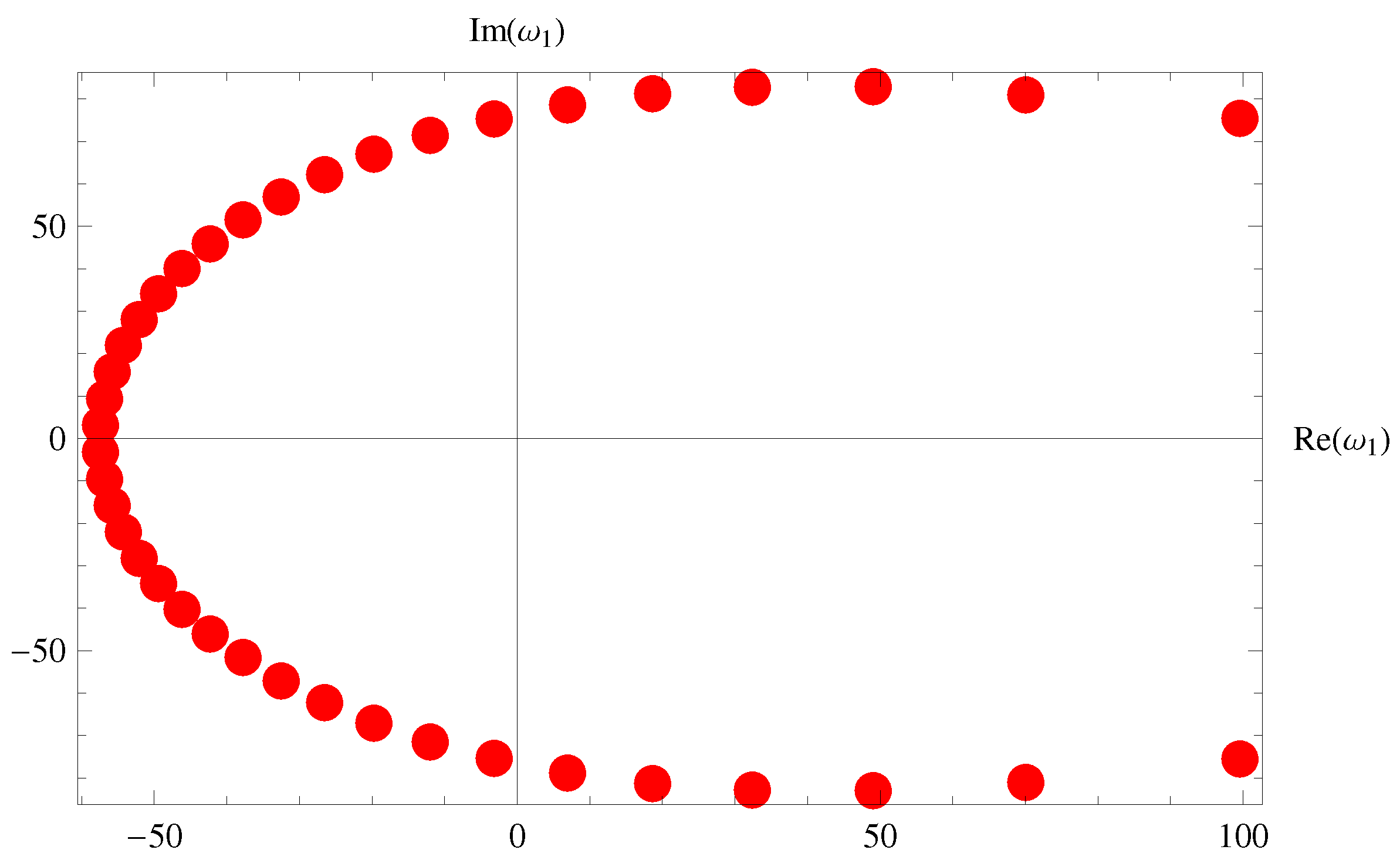
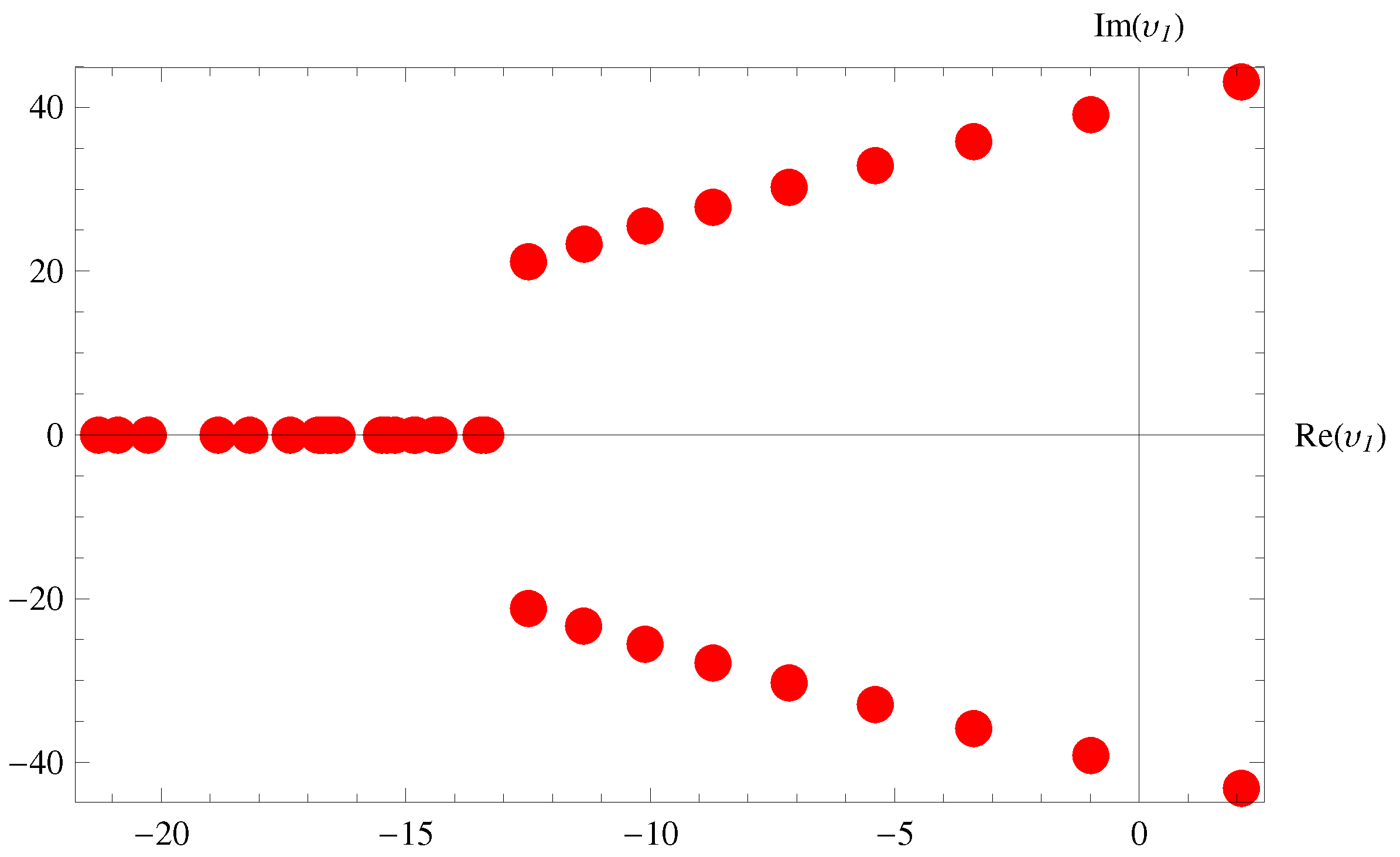
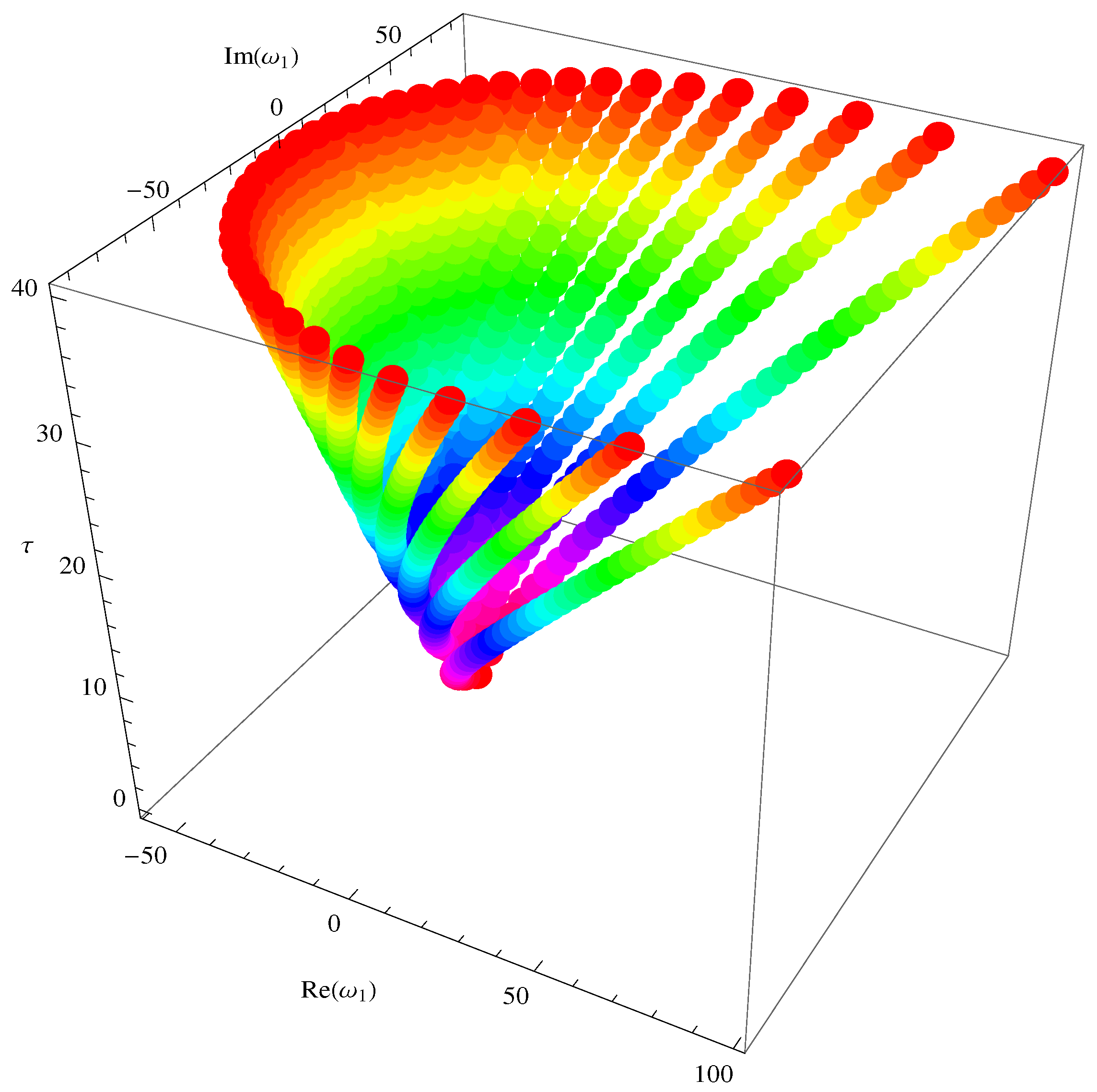
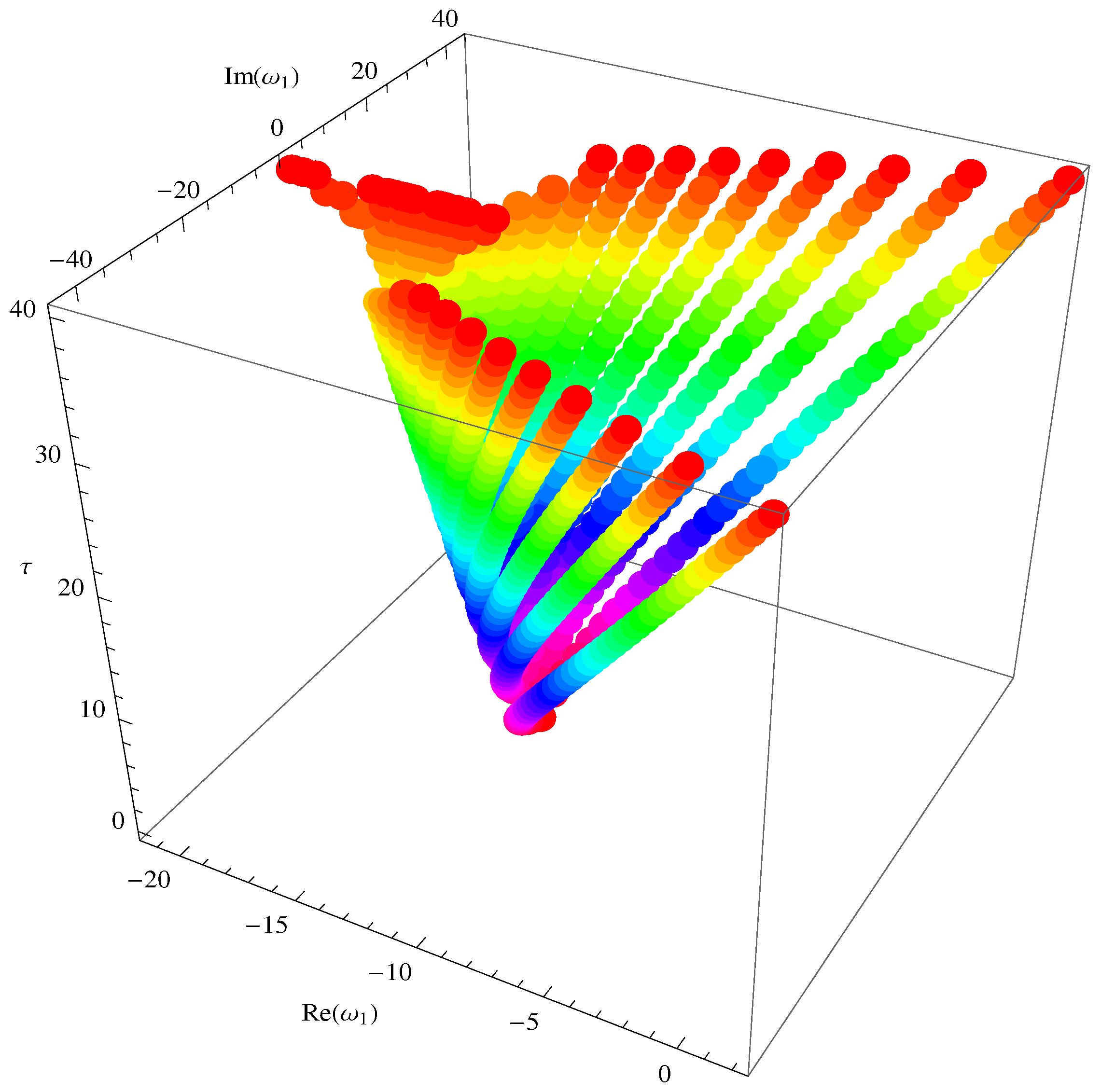
5. Special Members and Graphical Representations
5.1. Fubini–Bell-Based Bernoulli Polynomials
5.2. Fubini–Bell-Based Euler Polynomials
- For , the FBAP (19) reduce to the Fubini–Bell-based Genocchi polynomials, which are expressed as
- For , the FBAP (19) reduce to the Fubini–Bell-based Stirling polynomials, which are expressed as
- For , the FBAP (19) reduce to the Fubini–Bell-based Apostol-type polynomials, which are defined by
- For , the FBAP (19) reduce to the Fubini–Bell-based Apostol–Bernoulli polynomials, which are defined by
- For , the FBAP (19) reduce to the Fubini–Bell-based Apostol–Euler polynomials, which are defined by
- For , the FBAP (19) reduce to the Fubini–Bell-based Apostol–Genocchi polynomials, which are defined by
- For , the FBAP (19) reduce to the Fubini–Bell-based Apostol-type Forbenius–Euler polynomials, which are defined by
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kargin, L. Some formulae for products of geometric polynomials with applications. J. Integer Seq. 2017, 20, 15. [Google Scholar]
- Duran, U.; Acikgoz, M. Truncated Fubini polynomials. Mathematics 2019, 7, 431. [Google Scholar] [CrossRef]
- Kim, D.S.; Kim, T.; Jang, G.-W. A note on degenerate Fubini polynomials. Proc. Jangjeon Math. Soc. 2017, 20, 521–531. [Google Scholar]
- Kim, D.S.; Kim, T.; Kwon, H.I.; Park, J.W. Two variable higher-order Fubini polynomials. J. Korean Math. Soc. 2018, 55, 975–986. [Google Scholar] [CrossRef]
- Kilar, N.; Simsek, Y. A new family of Fubini type numbers and polynomials associated with Apostol-Bernoulli numbers and polynomials. J. Korean Math. Soc. 2017, 54, 1605–1621. [Google Scholar]
- Su, D.D.; He, Y. Some identities for the two variable Fubini polynomials. Mathematics 2019, 7, 115. [Google Scholar] [CrossRef]
- Benbernou, S.; Gala, S.; Ragusa, M.A. On the regularity criteria for the 3D magnetohydrodynamic equations via two components in terms of BMO space. Math. Methods Appl. Sci. 2014, 37, 2320–2325. [Google Scholar] [CrossRef]
- Boas, R.B.; Buck, R.C. Polynomial Expansions of Analytic Functions; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sándor, J.; Crstici, B. Handbook of Number Theory; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; Volume II. [Google Scholar]
- Duran, U.; Araci, S.; Acikgoz, M. Bell-based Bernoulli polynomials with applications. Axioms 2021, 10, 29. [Google Scholar] [CrossRef]
- Duran, U.; Acikgoz, M. Bell-based Genocchi polynomials. NTMSCI 2021, 9, 50–55. [Google Scholar] [CrossRef]
- Carlitz, L. Some remarks on the Bell numbers. Fibonacci Quart. 1980, 18, 66–73. [Google Scholar] [CrossRef]
- Al-Jawfi, R.A.; Muhyi, A.; Al-shameri, W.F.H. On generalized class of Bell polynomials associated with geometric applications. Axioms 2024, 13, 73. [Google Scholar] [CrossRef]
- Costabile, F.A.; Khan, S.; Ali, H. A Study of the q-Truncated Exponential–Appell Polynomials. Mathematics 2024, 12, 3862. [Google Scholar] [CrossRef]
- Muhyi, A.; Araci, S. A note on q-Fubini-Appell polynomials and related properties. J. Funct. Spaces 2022, 2021, 3805809. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Özarslan, M.A.; Yılmaz, B. Some families of differential equations associated with the Hermite-based Appell polynomials and other classes of Hermite-based polynomials. Filomat 2014, 28, 695–708. [Google Scholar] [CrossRef]
- Özat, Z.; Özarslan, M.A.; Çekim, B. On Bell based Appell polynomials. Turk. J. Math. 2023, 47, 1099–1128. [Google Scholar] [CrossRef]
- Avram, F.; Taqqu, M.S. Noncentral limit theorems and Appell polynomials. Ann. Probab. 1987, 15, 767–775. [Google Scholar] [CrossRef]
- Andrews, L.C. Special Functions for Engineers and Applied Mathematics; Macmillan Publishing Company: New York, NY, USA, 1985. [Google Scholar]
- Srivastava, H.M.; Manocha, H.L. A Treatise on Generating Functions; Halsted Press-Ellis Horwood Limited-John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Rainville, E.D. Special Functions; Chelsea Publishing Co.: Bronx, NY, USA, 1971. [Google Scholar]
- Lu, D.Q.; Luo, Q.M. Some properties of the generalized Apostol type polynomials. Bound. Value Probl. 2013, 2013, 64. [Google Scholar] [CrossRef]
- Kurt, B.; Simsek, Y. On the generalized Apostol-type Frobenius-Euler polynomials. Adv. Differ. Equ. 2013, 2013, 1–9. [Google Scholar] [CrossRef]
- Costabile, F.A.; Dell’Accio, F.; Gualtieri, M.I. A new approach to Bernoulli polynomials. Rend. Mat. Appl. 2006, 26, 1–12. [Google Scholar]
- Costabile, F.A.; Longo, E. A determinantal approach to Appell polynomials. J. Comput. Appl. Math. 2010, 234, 1528–1542. [Google Scholar] [CrossRef]
- Costabile, F.A.; Longo, E. An algebraic approach to Sheffer polynomial sequences. Integral Transforms Spec. Funct. 2013, 25, 295–311. [Google Scholar] [CrossRef]
- Cocolicchio, D.; Dattoli, G.; Srivastava, H.M. (Eds.) Advanced Special Functions and Applications; Aracne Editrice: Rome, Italy, 2000. [Google Scholar]
- Muhyi, A. A new class of Gould-Hopper-Eulerian-type polynomials. Appl. Math. Sci. Eng. 2022, 30, 283–306. [Google Scholar] [CrossRef]
- Ramírez, W.; Cesarano, C.; Wani, S.A.; Yousef, S.; Bedoya, D. About properties and the monomiality principle of Bell-based Apostol-Bernoulli-type polynomials. Carpathian Math. Publ. 2024, 16, 379–390. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Srivastava, R.; Muhyi, A.; Yasmin, G.; Islahi, H.; Araci, S. Construction of a new family of Fubini-type polynomials and its applications. Adv. Differ. Equ. 2021, 2021, 1–25. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Araci, S.; Khan, W.A.; Acikgoz, M. A note on the truncated-exponential based Apostol-type polynomials. Symmetry 2019, 11, 538. [Google Scholar] [CrossRef]
- Yasmin, G.; Muhyi, A. Extended forms of Legendre-Gould-Hopper-Appell polynomials. Adv. Stud. Contemp. Math. 2019, 29, 489–504. [Google Scholar]
- Masjed-Jamei, M.; Beyki, M.R.; Koepf, W. A new type of Euler polynomials and numbers. Mediterr. J. Math. 2018, 15, 138. [Google Scholar] [CrossRef]
- Steffensen, J.F. The poweriod, an extension of the mathematical notion of power. Acta Math. 1941, 73, 333–366. [Google Scholar] [CrossRef]
- Khan, N.; Husain, S. Analysis of Bell based Euler polynomials and their application. Int. J. Appl. Comput. Math. 2021, 7, 195. [Google Scholar] [CrossRef]
- Lyapin, A.P.; Akhtamova, S.S. Recurrence relations for the sections of the generating series of the solution to the multidimensional difference equation. Vestn. Udmurtsk. Univ. Mat. Mekh. 2021, 31, 414–423. [Google Scholar] [CrossRef]
- Leinartas, E.; Shishkina, O. The Euler-Maclaurin Formula in the Problem of Summation over Lattice Points of a Simplex. J. Sib. Fed. Univ. Math. Phys. 2022, 15, 108–113. [Google Scholar] [CrossRef]
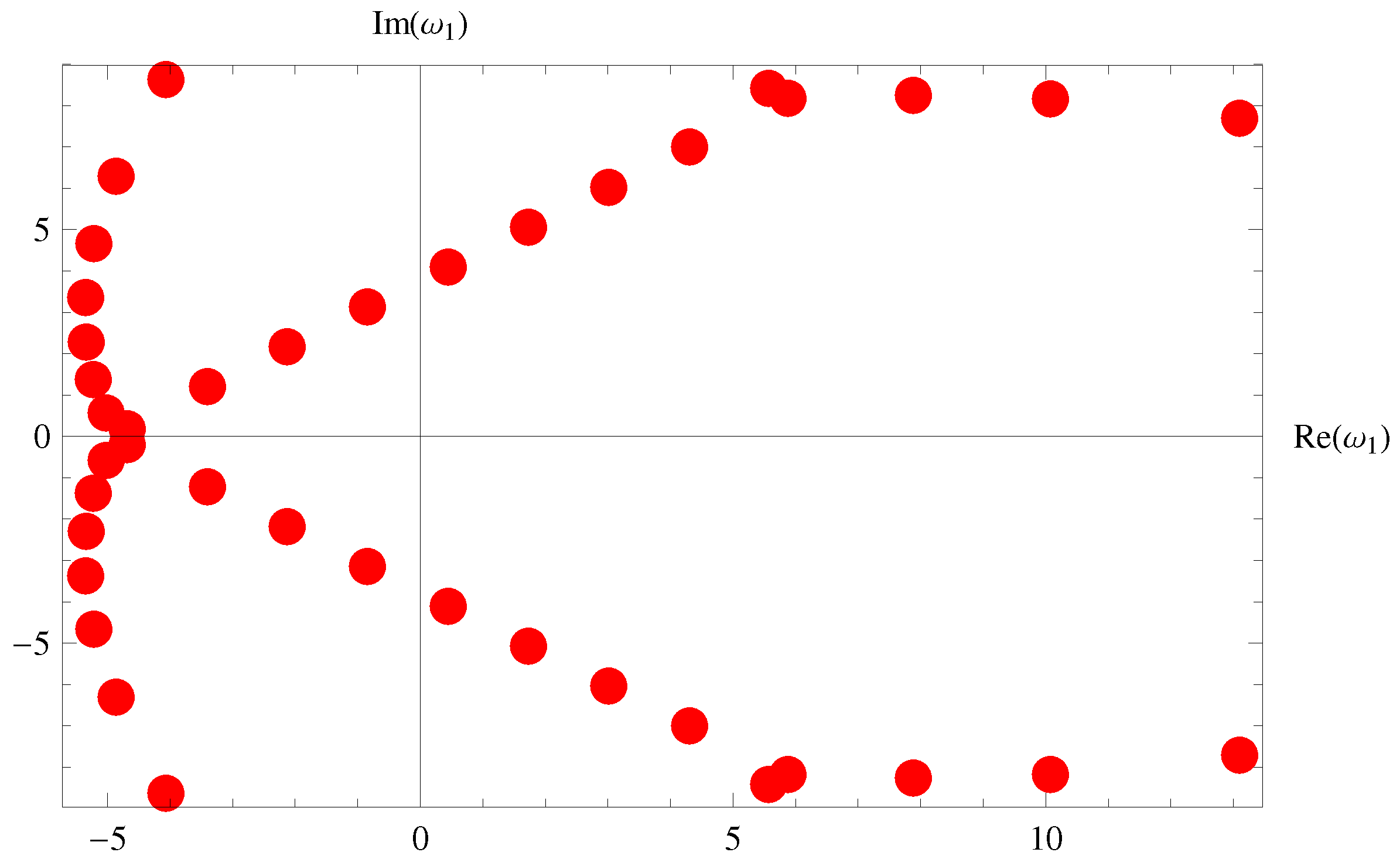

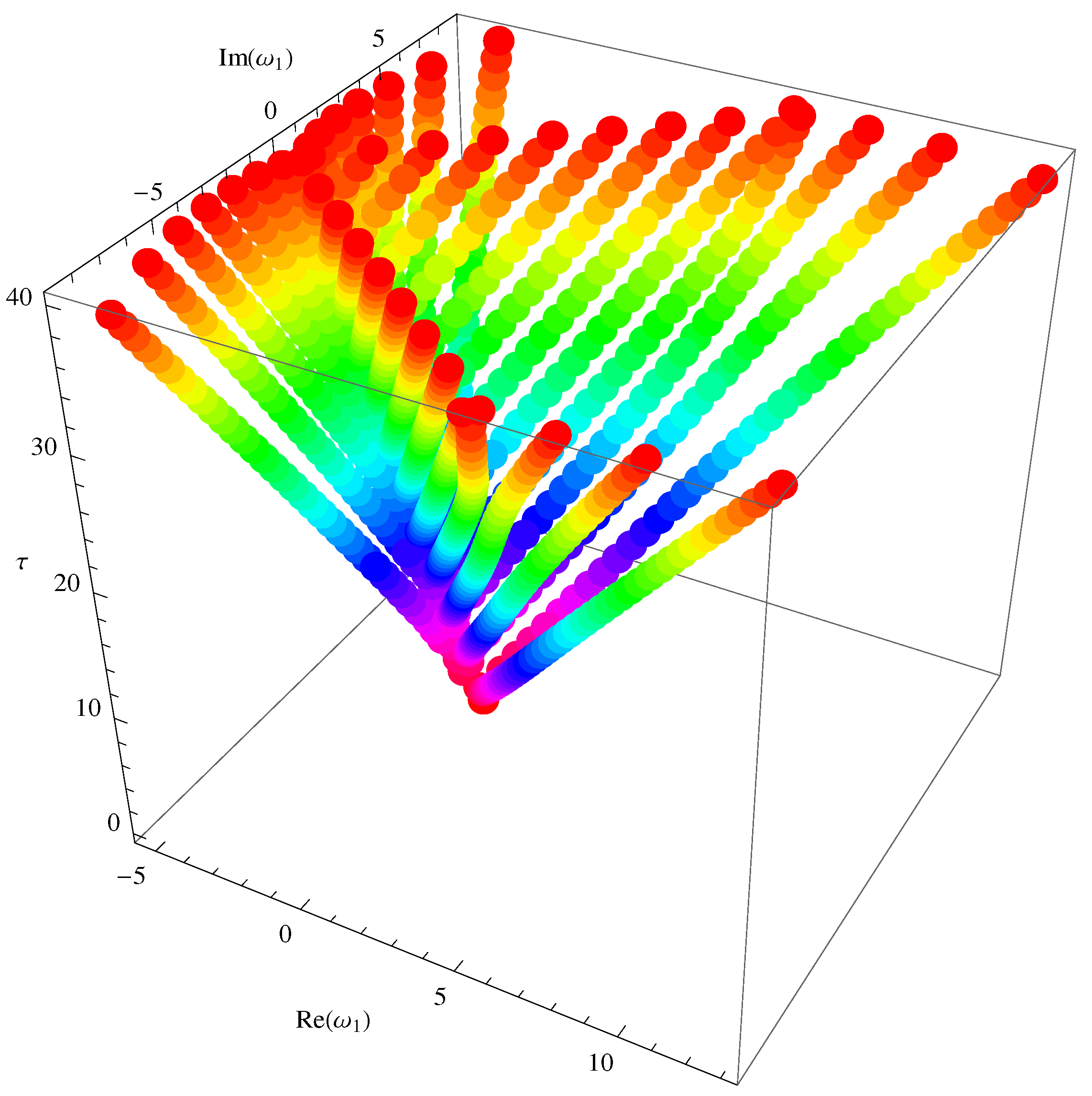

| S. No. | Generating Functions | Polynomials | |
|---|---|---|---|
| I. | The Bernoulli polynomials [21] | ||
| II. | The Euler polynomials [21] | ||
| III. | The Genocchi polynomials [21] | ||
| IV. | The Stirling polynomials [10] | ||
| V. | The Apostol type polynomials [22] | ||
| VI. | The Apostol–Bernoulli polynomials [23] | ||
| VII. | The Apostol–Euler polynomials [23] | ||
| VIII. | The Apostol–Genocchi polynomials [23] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madani, Y.A.; Muhyi, A.; Aldwoah, K.; Touati, A.; Mohamed, K.S.; Egami, R.H. Construction of a Hybrid Class of Special Polynomials: Fubini–Bell-Based Appell Polynomials and Their Properties. Mathematics 2025, 13, 1009. https://doi.org/10.3390/math13061009
Madani YA, Muhyi A, Aldwoah K, Touati A, Mohamed KS, Egami RH. Construction of a Hybrid Class of Special Polynomials: Fubini–Bell-Based Appell Polynomials and Their Properties. Mathematics. 2025; 13(6):1009. https://doi.org/10.3390/math13061009
Chicago/Turabian StyleMadani, Yasir A., Abdulghani Muhyi, Khaled Aldwoah, Amel Touati, Khidir Shaib Mohamed, and Ria H. Egami. 2025. "Construction of a Hybrid Class of Special Polynomials: Fubini–Bell-Based Appell Polynomials and Their Properties" Mathematics 13, no. 6: 1009. https://doi.org/10.3390/math13061009
APA StyleMadani, Y. A., Muhyi, A., Aldwoah, K., Touati, A., Mohamed, K. S., & Egami, R. H. (2025). Construction of a Hybrid Class of Special Polynomials: Fubini–Bell-Based Appell Polynomials and Their Properties. Mathematics, 13(6), 1009. https://doi.org/10.3390/math13061009








