Research on the Mechanism of Social Emotion Formation in Public Emergencies Based on the DeGroot Model
Abstract
1. Introduction
2. Literature Review
2.1. Social Emotions
2.2. Social Network DeGroot Model
2.3. Other Opinion Dynamics Models
2.4. Group Decision-Making Theory
3. Research Methodology
3.1. Trust Adjustment Method Based on the “Homogeneous Attraction Effect”
3.2. Clustering Method Based on Emotional Identification and Trust Segmentation
| Algorithm 1: Clustering Method Based on Similarity–Trust Scores Among Users |
| Objective: To partition users into multiple groups such that the intra-group similarity–trust scores are maximized. |
| Input: Similarity–trust score matrix , clustering threshold , and minimum group size . |
| Output: Clustered groups . |
| Step 1: Construct the trust homogeneity score matrix and its thresholded matrix , where elements greater than or equal to the clustering threshold are assigned a value of 1, and elements smaller than the clustering threshold are set to 0. |
| Step 2: For each decision-maker , calculate the number of non-zero elements in the -th column of the matrix , which represents the number of associated decision-makers whose trust homogeneity score is above the clustering threshold . Sort the decision-makers based on this number, forming a sorted set of decision-makers , where . Initialize the group index , where represents the -th group, and set = 1. |
| Step 3: Select the first decision-maker from the sorted set and assign it to group , and update the sorted set , so . |
| Step 4: For each decision-maker in the sorted set , if it satisfies with at least one decision-maker in the current group and has not been assigned to another group, then assign to group . Update and continue checking the remaining unassigned decision-makers. |
| Step 5: If there are still unassigned decision-makers within the current group , continue assigning them based on the above criteria. If a decision-maker does not meet the clustering conditions with any existing group members but belongs to a group that is too small , then find the existing group with the highest similarity to and directly merge into . |
| Step 6: If all decision-makers have been successfully classified, output the final number of groups and terminate the clustering process. Otherwise, increment the group index , select the next unassigned decision-maker as the starting member of a new group, and repeat steps 3–5 until all decision-makers have been clustered. |
| Algorithm 2: Determination of the Optimal Clustering Threshold |
| Objective: To determine the optimal clustering threshold that maximizes intra-group similarity across different clustering thresholds. |
| Input: The similarity–trust score matrix and the convergence threshold . |
| Output: The optimal clustering threshold and the corresponding internal cohesion score. |
| Step 1: Initialize , , and . |
| Step 2: Randomly generate three initial clustering thresholds , , and , and ensuring they satisfy . |
| Step 3: Input , , , and into Algorithm 1 to obtain the clustering results under these thresholds. |
| Step 4: Compute the average internal cohesion scores of the clustering results obtained under the thresholds , , and using Equations (4) and (5). Denote these scores as , , and , respectively. Let . If , , and set the corresponding threshold as the current optimal clustering threshold for . |
| Step 5: If , then set and . If , then set and . If , then set and . If , proceed to step 6; otherwise, return to step 2. |
| Step 6: Output the optimal clustering threshold . |
3.3. The Process of Reaching Group Consensus
3.4. Large-Scale Group Emotion Consensus Decision-Making Method Based on the Social Network DeGroot Model
| Algorithm 3: Group Consensus and Feedback Mechanism Based on the Social Network DeGroot Model |
| Input: A set of user preference matrices and a set of confidence vectors . |
| Output: A ranking of alternatives that meet the consensus criteria. |
| Step 1: Construct the users’ emotional information matrix , and the trust matrix , representing trust relationships among users. |
| Step 2: Adjust the trust relationships among users using the trust adjustment method based on the “similarity–attraction principle” from Algorithm 1, obtaining the adjusted trust matrix . |
| Step 3: Apply the clustering method from Algorithm 2, which considers emotional similarity and trust relationships, to partition the users into groups . |
| Step 4: Identify the top 10% of users based on the number of comments (interaction frequency) within the entire user population. These users will be selected as opinion leaders. For each group, assign the opinion leaders . |
| Step 5: Compute the aggregate preference values for the alternative options based on Equations (6)–(8), forming the set . |
| Step 6: Measure the consensus level among groups by calculating preference similarity. Compute the group consensus level CL based on Equations (9)–(11). If the consensus level exceeds the predefined threshold, proceed to step 8; otherwise, return to step 7 for further feedback adjustment. |
| Step 7: Use Equation (12) to obtain updated group preference values that satisfy the consensus level requirement. |
| Step 8: Based on the updated aggregate preference values and Equation (13), generate the ranking vector for the alternatives and output the final decision results. |
4. Case Study
4.1. Data Collection and Processing
4.2. Case Consensus Results
4.3. Case Simulation
5. Discussion
- (1)
- The formation of social emotions is a dynamic and multifaceted process influenced by multiple factors and stages, including the characteristics of the triggering event, individual cognitive processes, initial emotional states, interpersonal trust relationships, and group interactions. Fundamentally, this process represents a progressive consensus-building mechanism in emotional preferences among individuals, shaped by external stimuli, information inputs, and internal adjustments, ultimately leading to widespread emotional convergence. Key input variables in the social emotion formation process include event attributes, individual cognitive responses, pre-existing emotional states, and established trust relationships among users. As an event unfolds, trust relationships dynamically evolve based on emotional similarity, influencing group identity and collective emotional alignment. Opinion leaders play a pivotal role in shaping social emotions by guiding cluster formation and consensus adjustment processes, thereby amplifying specific emotional tendencies within the group. During crises, official responses, authoritative information, and media narratives exert significant influence over the trajectory of emotional evolution. Ultimately, through repeated communication and iterative interactions, social emotions emerge, culminating in a highly cohesive emotional state at the collective level.
- (2)
- User engagement and participation serve as critical determinants in the evolution of social emotion formation. Findings indicate that heightened public interest in an event correlates with increased user involvement, leading to more extensive discussions and contributing to the complexity of emotional dissemination. While highly salient events tend to accelerate the initial spread of emotions, the larger participant base and diverse viewpoints prolong the iterative processes required for emotional consensus, thereby extending the event’s duration and slowing the overall progression of social emotion formation. This underscores the necessity of implementing phased intervention strategies tailored to different event types and dynamically regulating user engagement levels to steer social emotions toward a more constructive trajectory.
- (3)
- Empirical results underscore the essential role of opinion leaders in shaping and facilitating social emotion formation. Opinion leaders with high levels of influence tend to retain their prominence and distinct emotional stances throughout the iterative emotional adjustment process. Their emotional orientations remain largely preserved and significantly impact the emotional adaptation of other users. This influence fosters emotional coherence and stability across successive iterations of social emotion formation. Furthermore, opinion leaders serve as crucial connectors across different social groups, acting as key facilitators in achieving group consensus. However, an excessive number of opinion leaders may introduce competition and fragmentation in emotional dissemination, whereas an insufficient number may hinder the effective guidance of collective emotions. Consequently, optimizing the identification, distribution, and influence of opinion leaders is imperative for ensuring the orderly and constructive evolution of social emotions.
- (4)
- Trust relationships among users play a fundamental role in emotional dissemination and formation. The study results indicate that high levels of trust significantly enhance coordination and mutual understanding among individuals, expediting the attainment of emotional consensus and contributing to the stability and persistence of social emotions. Simulation results further suggest that dynamically adjusting trust relationships aligns more closely with real-world social emotion formation processes, making emotional dissemination more flexible and adaptive while guiding emotions toward a more positive and authoritative direction. These findings emphasize the importance of strategically structuring and optimizing trust networks in emotional dissemination, which can serve as an effective mechanism for mitigating the accumulation of negative emotions within groups and fostering the constructive development of social emotions.
- (5)
- Further analysis reveals that emotional similarity among users and individual cognitive ability function as key drivers of emotional consensus during the dissemination and formation of social emotions. Emotional similarity reinforces users’ sense of group identity, facilitating deeper consensus integration throughout the dissemination process. This finding not only highlights the significance of trust relationships and opinion leaders but also elucidates the structural and interactive dynamics governing social emotion evolution. Moreover, cognitive ability determines individuals’ sensitivity and discernment in processing emotional information, directly influencing the efficiency and effectiveness of emotional dissemination. Collectively, these insights underscore the intricate interplay of cognitive and relational factors in shaping the consensus-building processes that underlie social emotion formation.
6. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Wang, J.; Yang, Y.; Chen, W. Chinese social mentality survey report. Democr. Sci. 2007, 19, 40–44. [Google Scholar]
- Yao, S.; Gu, M. A Consensus Model for Group Decision Making under the Influence of Empathy. Chin. J. Manag. Sci. 2021, 29, 203–214. [Google Scholar]
- Chu, J.; Lu, Y.; Wang, Y. A Large-Group Consensus Decision-Making Model in Social Networks Considering Non-Cooperative Behaviors. J. Syst. Sci. Math. Sci. 2023, 43, 961–981. [Google Scholar]
- Li, S.; Rodr Guez, R.M.; Wei, C. Managing manipulative and non-cooperative behaviors in large scale group decision making based on a WeChat-like interaction network. Inf. Fusion 2021, 75, 1–15. [Google Scholar]
- Chen, X.; Zhang, W.; Xu, H. Large group decision-making method based on hesitation and consistency under social network context. Syst. Eng.-Theory Pract. 2020, 40, 1178–1192. [Google Scholar]
- Liu, Y.; Li, Y.; Liang, H.; Dong, Y. Strategic experts’ weight manipulation in 2-rank consensus reaching in group decision making. Expert Syst. Appl. 2023, 216, 119432. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, W.; Dong, Y. The classification-based consensus model with minimum violations in heterogeneous group decision making. Syst. Eng.-Theory Pract. 2022, 42, 1378–1390. [Google Scholar]
- Tu, J.; Wu, Z. H-rank consensus models for fuzzy preference relations considering eliminating rank violations. IEEE Trans. Fuzzy Syst. 2021, 30, 2004–2018. [Google Scholar] [CrossRef]
- Li, S.; Wei, C. A two-stage dynamic influence model-achieving decision-making consensus within large scale groups operating with incomplete information. Knowl.-Based Syst. 2020, 189, 105132. [Google Scholar] [CrossRef]
- Wang, J. Social Emotions in the Perspective of Social Mentality. J. Yunnan Norm. Univ. (Humanit. Soc. Sci. Ed.) 2013, 45, 55–63. [Google Scholar]
- Wang, J. The Theory of Social Mentality; Social Sciences Academic Press: Beijing, China, 2014. [Google Scholar]
- Zhu, L.; Chen, X. Negative social emotions and their governance of major public health security incidents. J. Chongqing Univ. (Soc. Sci. Ed.) 2023, 29, 295–306. [Google Scholar]
- Zhu, D.; Wang, G. Influencing Factors and Mechanism of Netizens’ Social Emotions in Emergencies—Qualitative Comparative Analysis of Multiple Cases Based on Ternary Interactive Determinism (QCA). J. Intell. 2020, 39, 95–104. [Google Scholar]
- Zeng, X. A survey on Social Mood of Urban Residents in Hainan Under the Back Ground of “Encouraging People to Stay Put during the Spring Festival”. J. Wuhan Eng. Inst. 2021, 33, 56–59+74. [Google Scholar]
- Zion, S.R.; Louis, K.; Horii, R.; Leibowitz, K.; Healthcote, L.C.; Crum, A.J. Making sense of a pandemic: Mindsets influence emotions, behaviors, health, and wellbeing during the COVID-19 pandemic. Soc. Sci. Med. 2022, 301, 301114889. [Google Scholar] [CrossRef]
- Morse, C.R.; Volkman, J.E. An Examination into the Dyadic Effects of Mood in Social Interactions. Commun. Res. Rep. 2010, 27, 330–342. [Google Scholar] [CrossRef]
- Coviello, L.; Sohn, Y.; Kramer, A.D.; Marlow, C.; Franceschetti, M.; Christakis, N.A.; Fowler, J.H. Detecting Emotional Contagion in Massive Social Networks. PLoS ONE 2014, 9, e90315. [Google Scholar] [CrossRef]
- Boykov, V.E. Boomerang of Social Mood. Sociol. Abstr. 1998, 25, 87–90. [Google Scholar]
- Nofsinger, R.J. Social mood: The stock market and political cycle. J. Socio-Econ. 2007, 36, 734–744. [Google Scholar] [CrossRef]
- Woo, H.; Cho, Y.; Shim, E.; Lee, K.; Song, G. Public Trauma after the Sewol Ferry Disaster: The Role of Social Media in Understanding the Public Mood. Int. J. Environ. Res. Public Health 2015, 12, 10974–10983. [Google Scholar] [CrossRef]
- Hatfield, E.; Cacioppo, J.; Rapson, R.L. Emotional Contagion; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Zhang, B.; Zhang, Q. Research on the Law and Governance of Negative Emotional Contagion of Network Virtual Community in Major Public Emergencies: Enlightenment from Prevention and Control Measures to COVID-19. J. Intell. 2020, 39, 121–128. [Google Scholar]
- Liu, Z.; Zhang, T.; Lan, Q. An Extended SISa Model for Sentiment Contagion. Discret. Dyn. Nat. Soc. 2014, 2014, 262384. [Google Scholar] [CrossRef]
- Song, Z.; Shi, R.; Jia, J.; Wang, J. Sentiment contagion based on the modified SOSa-SPSa model. Comput. Math. Methods Med. 2016, 2016, 9682538. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Zhou, H.; Chen, W. Addition of an emotionally stable node in the SOSa-SPSa model for group emotional contagion of panic in public health emergency: Implications for epidemic emergency responses. Int. J. Environ. Res. Public Health 2020, 17, 5044. [Google Scholar] [CrossRef]
- Li, J.; Li, H. The Generation and Governance of Social Emotion in Online Public Opinion—Rethink from the Perspective of Information Asymmetry. J. Northeast Norm. Univ. (Philos. Soc. Sci.) 2019, 77–84. [Google Scholar]
- Jin, X.; Shi, X. On the Cultivation of University Students’ Healthy Social Emotion. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 6767–6773. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H. Propagation of social emotion in cyber space based on cognitive social psychology. IEEE Access 2016, 5, 1005–1012. [Google Scholar] [CrossRef]
- Cao, S. The Generation Logic and Governance Dimension of Network Political Emotion in the New Era. J. Intell. 2019, 38, 106–111. [Google Scholar]
- Degroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Dong, Y.; Ding, Z.; Martinez, L.; Herrera, F. Managing consensus based on leadership in opinion dynamics. Inf. Sci. 2017, 397, 187–205. [Google Scholar] [CrossRef]
- Zhou, J.L.; Chen, J.A. A consensus model to manage minority opinions and noncooperative behaviors in large group decision making with probabilistic linguistic term sets. IEEE Trans. Fuzzy Syst. 2020, 29, 1667–1681. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, J.; Chiclana, F.; Fujita, H.; Herrera-Viedma, E. A dynamic feedback mechanism with attitudinal consensus threshold for minimum adjustment cost in group decision making. IEEE Trans. Fuzzy Syst. 2021, 30, 1287–1301. [Google Scholar] [CrossRef]
- Long, J.; Liang, H.; Gao, L.; Dong, Y. Consensus reaching with two-stage minimum adjustments in multi-attribute group decision making: A method based on preference-approval structure and prospect theory. Comput. Ind. Eng. 2021, 158, 107349. [Google Scholar] [CrossRef]
- Wu, X.; Liao, H. A consensus-based probabilistic linguistic gained and lost dominance score method. Eur. J. Oper. Res. 2019, 272, 1017–1027. [Google Scholar] [CrossRef]
- Cheng, D.; Yuan, Y.; Wu, Y.; Cheng, F. Maximum satisfaction consensus with budget constraints considering individual tolerance and compromise limit behaviors. Eur. J. Oper. Res. 2022, 297, 221–238. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.; Gao, Y. Consensus reaching for group decision making with multi-granular unbalanced linguistic information: A bounded confidence and minimum adjustment-based approach. Inf. Fusion 2021, 74, 96–110. [Google Scholar] [CrossRef]
- Cheng, X.; Cheng, D.; Zhao, Y.; Luo, J. Research on the Low-carbon Supplier Selection Approach Based on the Consensus Decision Making. Oper. Res. Manag. Sci. 2012, 21, 68–73. [Google Scholar]
- Zha, Q.; Dong, Y.; Chiclana, F.; Herrera-Viedma, E. Consensus reaching in multiple attribute group decision making: A multi-stage optimization feedback mechanism with individual bounded confidences. IEEE Trans. Fuzzy Syst. 2021, 30, 3333–3346. [Google Scholar] [CrossRef]
- Zhou, X.; Ji, F.; Wang, L.; Ma, Y.; Fujita, H. Particle swarm optimization for trust relationship based social network group decision making under a probabilistic linguistic environment. Knowl.-Based Syst. 2020, 200, 105999. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, X.; Qin, J.; Zhou, L. Multi-criteria group decision-making for portfolio allocation with consensus reaching process under interval type-2 fuzzy environment. Inf. Sci. 2021, 570, 668–688. [Google Scholar] [CrossRef]
- Clifford, P.; Sudbury, A. A model for spatial conflict. Biometrika 1973, 60, 581–588. [Google Scholar] [CrossRef]
- Galam, S. Majority rule, hierarchical structures, and democratic totalitarianism: A statistical approach. J. Math. Psychol. 1986, 30, 426–434. [Google Scholar] [CrossRef]
- Sznajd-Weron, K.; Sznajd, J. Opinion evolution in closed community. Int. J. Mod. Phys. C 2000, 11, 1157–1165. [Google Scholar] [CrossRef]
- Friedkin, N.E.; Johnsen, E.C. Social influence and opinions. J. Math. Sociol. 1990, 15, 193–206. [Google Scholar] [CrossRef]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing beliefs among interacting agents. Adv. Complex Syst. 2000, 3, 87–98. [Google Scholar] [CrossRef]
- Rainer, H.; Krause, U. Opinion dynamics and bounded confidence: Models, analysis and simulation. J. Artif. Soc. Soc. Simul. 2002, 5, 1–33. [Google Scholar]
- Martins, A.C. Continuous opinions and discrete actions in opinion dynamics problems. Int. J. Mod. Phys. C 2008, 19, 617–624. [Google Scholar] [CrossRef]
- Dong, Y.; Ding, Z.; Chiclana, F.; Herrera-Viedma, E. Dynamics of public opinions in an online and offline social network. IEEE Trans. Big Data 2017, 7, 610–618. [Google Scholar] [CrossRef]
- Li, Q.; Du, Y.; Li, Z.; Hu, J.; Hu, R.; Lv, B.; Jia, P. HK–SEIR model of public opinion evolution based on communication factors. Eng. Appl. Artif. Intell. 2021, 100, 104192. [Google Scholar] [CrossRef]
- Dong, X.; Lian, Y.; Tang, X.; Liu, Y. The damped oscillator model (DOM) and its application in the prediction of emotion development of online public opinions. Expert Syst. Appl. 2020, 148, 113268. [Google Scholar] [CrossRef]
- Li, K.; Liang, H.; Kou, G.; Dong, Y. Opinion dynamics model based on the cognitive dissonance: An agent-based simulation. Inf. Fusion 2020, 56, 1–14. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Lin, M.-J. Group Decision Making Under Multiple Criteria: Methods and Applications; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Zhu, K.; Qu, S.; Ji, Y.; Ma, Y. Distributionally Robust Chance Constrained Maximum Expert Consensus Model with Incomplete Information on Uncertain Cost. Group Decis. Negot. 2024, 1–41. [Google Scholar] [CrossRef]
- Byrne, D. Attitudes and attraction. In Advances in Experimental Social Psychology; Elsevier: Amsterdam, The Netherlands, 1969; pp. 35–89. [Google Scholar]
- Xing, Y.; Wu, J.; Chiclana, F.; Liang, C.; Yager, R.R. An incentive mechanism-based minimum adjustment consensus model under dynamic trust relationship. IEEE Trans. Cybern. 2024, 54, 3666–3678. [Google Scholar] [CrossRef]
- Wu, D.; Si, S.; Wu, S.; Wang, R. Dynamic trust relationships aware data privacy protection in mobile crowd-sensing. IEEE Internet Things J. 2017, 5, 2958–2970. [Google Scholar] [CrossRef]
- Xiong, K.; Dong, Y.; Zha, Q. A large-scale consensus model to manage non-cooperative behaviors in group decision making: A perspective based on historical data. Expert Syst. Appl. 2023, 214, 119163. [Google Scholar] [CrossRef]
- Feng, J.; Yao, Z. What Factors Affect Purchase Intention in Social Commerce:Based on Strong and Weak Relationship Theory. Manag. Rev. 2015, 27, 99–109. [Google Scholar]

| 20.4414 | 36.2455 | 31.3199 | 39.8975 | 33.1443 | 19.7588 | 39.6924 |
| 0.9599 | 0.9576 | 0.9619 | 0.9693 | 0.9622 | 0.9340 | 0.9686 |
| Group | Opinion Leaders |
|---|---|
| 2.8819 | 2.1424 | 4.2014 | 3.6528 | 4.3403 | 3.2708 | 4.0104 |
| 3.4706 | 2.6765 | 4.0882 | 3.0294 | 4.0882 | 3.0588 | 4.0882 |
| 2.7778 | 2.6667 | 4.3333 | 3.2222 | 4.3333 | 2.8333 | 4.3333 |
| 3.5833 | 1.4167 | 4.2500 | 2.9167 | 4.2500 | 3.8333 | 4.2500 |
| 2.9999 | 1.8334 | 4.1666 | 4.1666 | 4.1666 | 3.0001 | 4.1666 |
| 0.8434 | 0.8258 | 0.9588 | 0.8740 | 0.9581 | 0.8580 | 0.9595 |
| Group | High | Medium | Low |
|---|---|---|---|
| Entry probability | 0.2 | 0.1 | 0.1 |
| Exit probability | 0.3 | 0.3 | 0.4 |
| Number of clusters | 43 | 38 | 33 |
| Number of iterations | 34 | 31 | 29 |
| Alternative emotion ranking | |||
| Iterative process diagram |  | 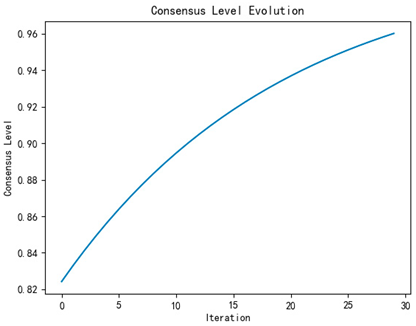 | 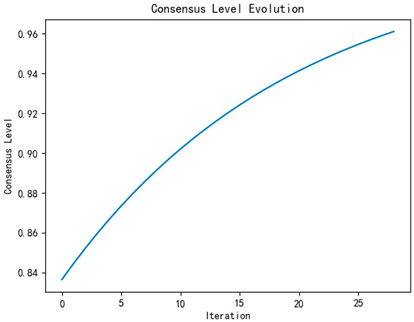 |
| Group | High | Medium | Low |
|---|---|---|---|
| Parameter setting | 30 | 20 | 10 |
| Number of clusters | 43 | 43 | 43 |
| Number of iterations | 34 | 35 | 33 |
| Alternative emotion ranking | |||
| Iterative process diagram | 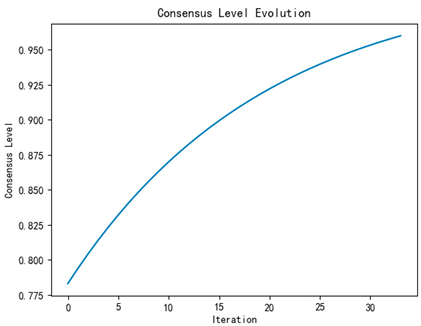 | 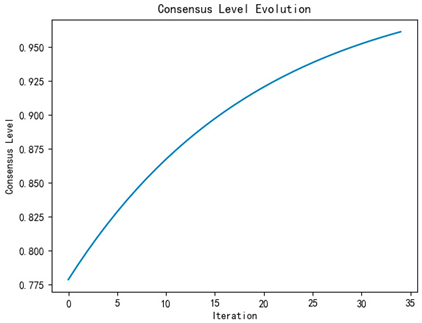 |  |
| Group | High | Medium | Low |
|---|---|---|---|
| Inter-group trust probability | 50 | 30 | 10 |
| Intra-group trust probability | 40 | 40 | 40 |
| Number of clusters | 43 | 43 | 43 |
| Number of iterations | 32 | 33 | 34 |
| Alternative emotion ranking | |||
| Iterative process diagram |  | 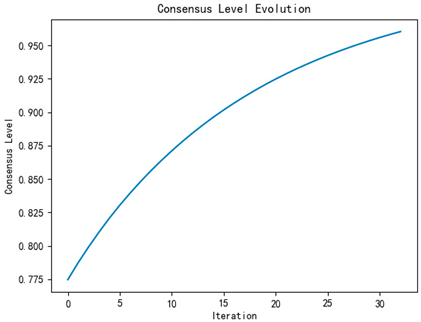 | 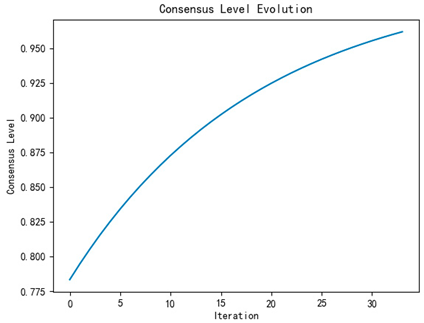 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Liu, Y.; Liu, T.; Chen, Y. Research on the Mechanism of Social Emotion Formation in Public Emergencies Based on the DeGroot Model. Mathematics 2025, 13, 904. https://doi.org/10.3390/math13060904
Yan X, Liu Y, Liu T, Chen Y. Research on the Mechanism of Social Emotion Formation in Public Emergencies Based on the DeGroot Model. Mathematics. 2025; 13(6):904. https://doi.org/10.3390/math13060904
Chicago/Turabian StyleYan, Xiaohan, Yi Liu, Tiezhong Liu, and Yan Chen. 2025. "Research on the Mechanism of Social Emotion Formation in Public Emergencies Based on the DeGroot Model" Mathematics 13, no. 6: 904. https://doi.org/10.3390/math13060904
APA StyleYan, X., Liu, Y., Liu, T., & Chen, Y. (2025). Research on the Mechanism of Social Emotion Formation in Public Emergencies Based on the DeGroot Model. Mathematics, 13(6), 904. https://doi.org/10.3390/math13060904






