Ruled Surfaces and Their Geometric Invariants via the Orthogonal Modified Frame in Minkowski 3-Space

Abstract

Ruled surfaces in Minkowski 3-space play a crucial role in differential geometry and have significant applications in physics and engineering. This study explores the fundamental properties of ruled surfaces via orthogonal modified frame in Minkowski space ${\mathrm{E}}_1^3$, focusing on their minimality, developability, and curvature characteristics. We examine the necessary and sufficient conditions for a ruled surface to be minimal, considering the mean curvature and its implications. Furthermore, we analyze the developability of such surfaces, determining the conditions under which they can be locally unfolded onto a plane without distortion. The Gaussian and mean curvatures of ruled surfaces in Minkowski space are computed and discussed, providing insights into their geometric behavior. Special attention is given to spacelike, timelike, and lightlike rulings, highlighting their unique characteristics. This research contributes to the broader understanding of the geometric properties of ruled surfaces within the framework of Minkowski geometry.

1. Introduction

The requirement that there is at least one straight line, known as a ruling, that lies wholly on the surface through each point on the surface defines ruled surfaces, a fundamental class of surfaces in differential geometry. These surfaces’ straightforward geometric structure and simplicity of creation make them useful in physics, engineering, and architecture. Compared to their Euclidean counterparts, governed surfaces in Minkowski 3-space $E_1^3$ have special geometric features, especially when categorized according to spacelike, timelike, or lightlike rulings.

In the parametric representation of a ruled surface, denoted as $\Lambda (\sigma ,\upsilon )=\vartheta \left(\sigma \right)+\upsilon U\left(\sigma \right)$, the base curve $\vartheta \left(\sigma \right)$ describes the shape of the surface, while the director vector $U\left(\sigma \right)$ determines the direction of the rulings. We can convey the points on the surface using two parameters $\sigma$ and $\upsilon$ owing to this representation; see [1,2].

The study of null geodesics, which characterize the motions of light beams in curved space–time, naturally involves ruled surfaces. For instance, governed surfaces made up of families of null geodesics can be thought of as light cones, which determine the causal structure of space–time (see [3]).

Ruled surfaces are used to explain wavefronts moving through gravitational fields in general relativity and optics. Due to the curvature of space–time, these wavefronts frequently create cusps and caustics, which are crucial for gravitational lensing effects (see [4]). Since the paths of charged particles frequently form helical or conical ruled surfaces in space–time diagrams, ruled surfaces may be used to examine the motion of charged particles in electromagnetic fields (see [5]). Also, since null geodesics establish the border between parts of space–time that can communicate with infinity and those that cannot, the event horizon of a revolving black hole (such as a Kerr black hole) is composed of ruled surfaces (see [6]).

Observing the behaviors of the ruled surfaces under Lorentz transformations, the orthogonal modified frame (OMF) provides a sophisticated geometric and algebraic framework, which modifies the Lorentz group for ruled surfaces in ${\mathrm{E}}_1^3$. Because traditional Frenet–Serret frames frequently falter in degenerate situations, such lightlike decisions, the OMF is a more reliable and flexible instrument. We may create frame-adaptive Lorentz transformations using an OMF that maintain the core geometric characteristics of ruled surfaces, such as their causal nature (spacelike, timelike, or lightlike). Specifically, the ruling structure can be preserved while applying modified Lorentz boosts and rotations to spacelike and timelike governed surfaces. It is necessary to perform certain null rotations (parabolic Lorentz transformations) for lightlike ruled surfaces in order to preserve the causal nature of the ruling. Since ruled surfaces are commonly seen in shock wavefronts, string theory, and relativistic kinematics, this method has obvious uses in relativity, differential geometry, and wave propagation in spacetime. This version of the Lorentz group preserves the basic structure of the governed surface while expanding our knowledge of symmetry transformations in ${\mathrm{E}}_1^3$.

Analyzing ruled surfaces’ curvature characteristics, minimality requirements, and developability is a crucial part of the study process. In [7,8], Struik and Eisenhart have performed classical studies on ruled surfaces, establishing basic conclusions in Euclidean and Lorentzian geometry. These investigations have been expanded to Minkowski space due to developments in contemporary differential geometry, where the behavior of ruled surfaces under various frame structures has emerged as a key field of study. In recent times, there has been a particular focus on the orthogonal modified frame with $\kappa \ne 0$ and $\tau \ne 0$ of a space curve in Minkowski 3-space. This framework involves studying curves in a three-dimensional space with specific curvature and torsion properties. Researchers have made notable contributions to this area, as referenced in works such as [9,10,11,12,13,14,15,16,17]. The purpose of this work is to use an orthogonal modified frame to investigate the geometric characteristics of ruled surfaces in Minkowski 3-space. We advance our knowledge of these surfaces and their uses in Lorentzian geometry by investigating the requirements for minimality, developability, and curvature properties. The results of this study give a wider view of the function of modified frame structures in differential geometry by comparing them with previous findings.

2. Preliminaries

The definition of the Lorentzian product in ${\mathrm{E}}_1^3$ is

$$\mathfrak{L}=d{\sigma }_1^2+d{\sigma }_2^2-d{\sigma }_3^2,$$

where $({\sigma }_1,{\sigma }_2,{\sigma }_3)$ is the coordinate system of ${\mathrm{E}}_1^3$. The characteristics of an arbitrary $\upsilon \in {\mathrm{E}}_1^3$ vector are as follows: Null if $\mathfrak{L}(\upsilon ,\upsilon )=0$ and $\upsilon \ne 0$, spacelike if $\mathfrak{L}(\upsilon ,\upsilon )>0$ or $\upsilon =0$, and timelike if $\mathfrak{L}(\upsilon ,\upsilon )<0$. Likewise, if a curve $\phi =\phi \left(\varrho \right)$ has a ${\phi }^{\prime }\left(\varrho \right)$ that is spacelike, timelike, or null, then it can also be spacelike, timelike, or null [18,19].

Let $\vartheta =\vartheta \left(\sigma \right)$ be a spacelike curve in ${\mathrm{E}}_1^3$. Let $\{t,n,b\}$ denote the moving Frenet frame of $\vartheta$, then $\{t,n,b\}$ satisfying [2,18,19]:

$$\begin{array}{cc}\hfill & \dot{t}\left(\sigma \right)=\kappa \left(\sigma \right)n\left(\sigma \right),\hfill \\ & \dot{n}\left(\sigma \right)=-\epsilon \kappa \left(\sigma \right)t\left(\sigma \right)+\tau \left(\sigma \right)b\left(\sigma \right),\hfill \\ & \dot{b}\left(\sigma \right)=\tau \left(\sigma \right)n\left(\sigma \right),\hfill \end{array}$$

(1)

where $\left(·={\displaystyle \frac{d}{d\sigma }}\right)$, $\mathfrak{L}(t,t)=1$, $\mathfrak{L}(n,n)=\epsilon$, $\mathfrak{L}(b,b)=-\epsilon$, and $\mathfrak{L}(t,n)=\mathfrak{L}(t,b)=(n,b)=0$. When $\epsilon =1$, $\vartheta \left(\sigma \right)$ is first kind spacelike and when $\epsilon =-1$, $\vartheta \left(\sigma \right)$ is second kind spacelike.

Assume that $\vartheta \left(\sigma \right)$ is an analytic curve with discrete zero points in ${\mathrm{E}}_1^3$. The orthogonal modified frames are provided under the assumption that $\kappa \left(\sigma \right)$ is not identically zero as [9,10,11]:

$$\begin{array}{cc}\hfill & \dot{T}\left(\sigma \right)=N\left(\sigma \right),\hfill \\ & \dot{N}\left(\sigma \right)=--\epsilon {\kappa }^2\left(\sigma \right)T\left(\sigma \right)+\left({\displaystyle \frac{\dot{\kappa }\left(\sigma \right)}{\kappa \left(\sigma \right)}}\right)N\left(\sigma \right)+\tau \left(\sigma \right)B\left(\sigma \right),\hfill \\ & \dot{B}\left(\sigma \right)=\tau \left(\sigma \right)N\left(\sigma \right)+\left({\displaystyle \frac{\dot{\kappa }\left(\sigma \right)}{\kappa \left(\sigma \right)}}\right)B\left(\sigma \right),\hfill \end{array}$$

(2)

where $\mathfrak{L}(T,T)=1$, $\mathfrak{L}(N,N)=\epsilon {\kappa }^2$, $\mathfrak{L}(B,B)=-\epsilon {\kappa }^2$, $\mathfrak{L}(T,B)=0$, $\mathfrak{L}(N,B)=0$, and $\mathfrak{L}(T,N)=0$.

A ruled surface $\Lambda$ in ${\mathrm{E}}_1^3$ can be represented as

$$\Lambda (\sigma ,\upsilon )=\vartheta \left(\sigma \right)+\upsilon \ell \left(\sigma \right),$$

(3)

where $\vartheta \left(\sigma \right)$ is base curve and $\ell \left(\sigma \right)$ is director. The unit normal vector field $\mathcal{N}$ on $\Lambda$ can be defined by [19]

$$N_{\Lambda }={\displaystyle \frac{{\Lambda }_{\sigma }\times {\Lambda }_{\upsilon }}{\parallel {\Lambda }_{\sigma }\times {\Lambda }_{\upsilon }\parallel }},$$

where ${\Lambda }_{\sigma }={\displaystyle \frac{\partial \Lambda }{\partial \sigma }}$ and ${\Lambda }_{\upsilon }={\displaystyle \frac{\partial \Lambda }{\partial \upsilon }}$. These are the first and second fundamental forms of $\Lambda$, respectively,

$$I:E=\parallel {\Lambda }_{\sigma }{\parallel }^2,F=\mathfrak{L}({\Lambda }_{\sigma },{\Lambda }_{\upsilon }),G={\parallel {\Lambda }_{\upsilon }\parallel }^2,$$

$$II:e=\mathfrak{L}({\Lambda }_{\sigma \sigma },N_{\Lambda }),f=\mathfrak{L}({\Lambda }_{\sigma \upsilon },N_{\Lambda }),g=\mathfrak{L}({\Lambda }_{\upsilon \upsilon },N_{\Lambda }).$$

The Gaussian and mean curvatures of $\Lambda$, respectively, are given by [19]

$$\begin{array}{cc}& K_{\Lambda }={\displaystyle \frac{eg-f^2}{EG-F^2}},\hfill \\ & H_{\Lambda }={\displaystyle \frac{Eg+Ge-2Ff}{2(EG-F^2)}}.\hfill \end{array}$$

Proposition 1

([20,21]). A ruled surface Λ is developable if and only if $K_{\Lambda }=0$, and minimal if and only if $H_{\Lambda }=0$.

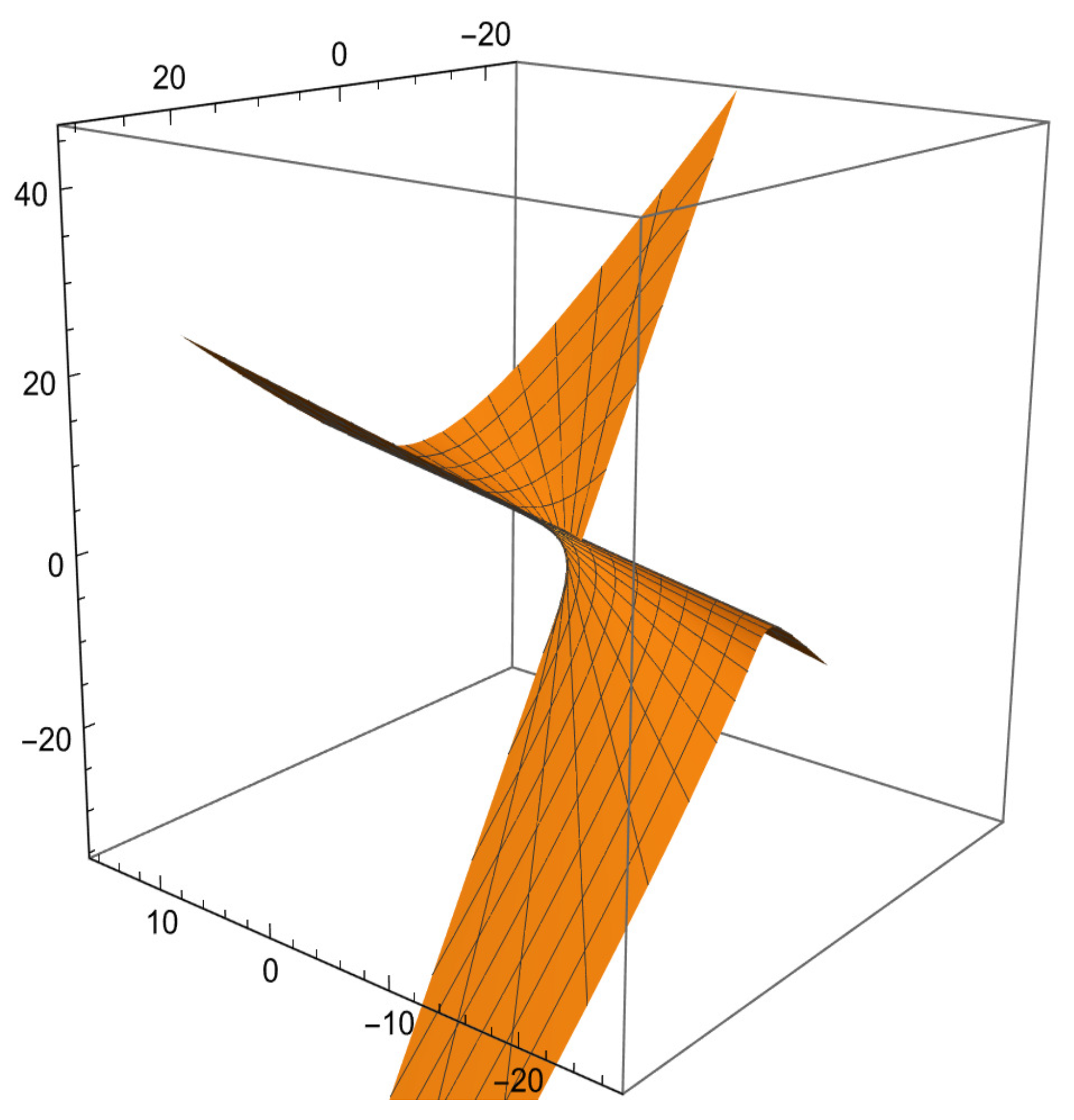
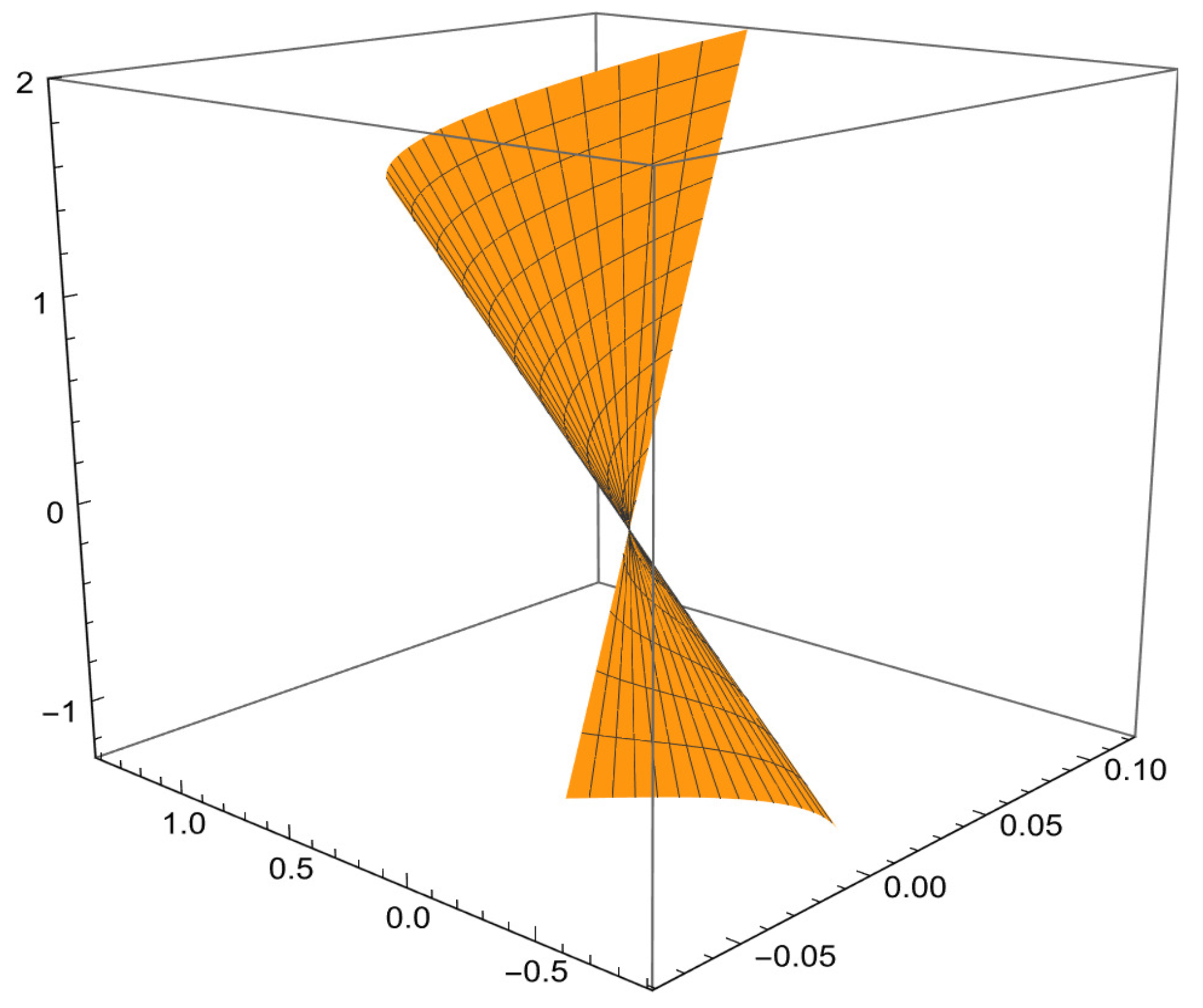
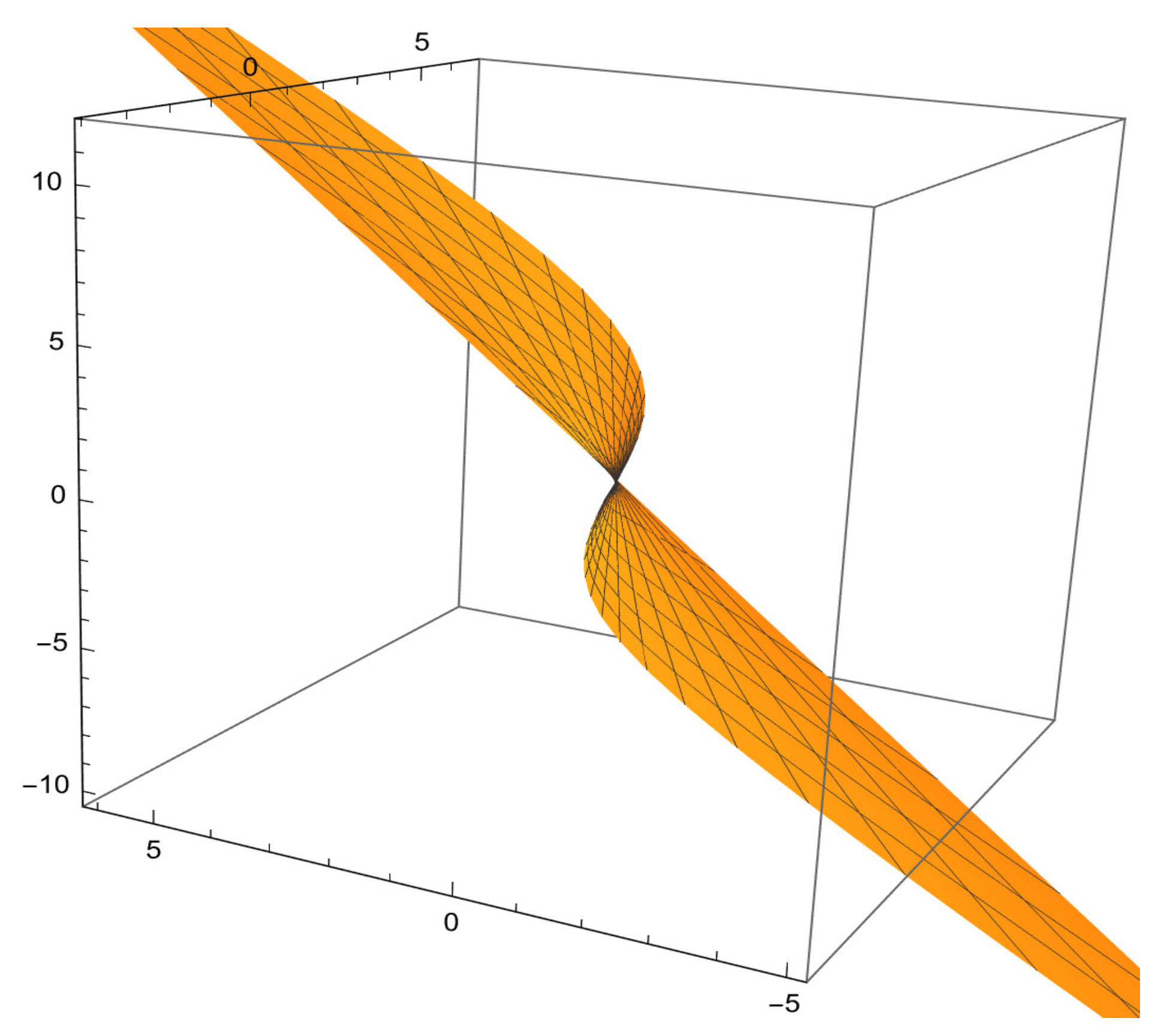
3. Characteristics of Ruled Surfaces via Orthogonal Modified Frame

We derive descriptions of the minimal and developable ruled surfaces from the orthogonal modified frame in ${\mathrm{E}}_1^3$.

The representation of a ruled surface for a regular spacelike curve $\beta =\beta \left(\sigma \right)$ via orthogonal modified frame in ${\mathrm{E}}_1^3$ is handed as

$$\Gamma (\sigma ,\upsilon )=\beta \left(\sigma \right)+\upsilon \ell \left(\sigma \right),$$

(4)

for $\beta \left(\sigma \right)$ the base curve and $\ell \left(\sigma \right)$ the director curve such that $\parallel \ell \left(\sigma \right)\parallel =1$. Then, we can write (4) in the form

$$\Gamma (\sigma ,\upsilon )=\beta \left(\sigma \right)+\upsilon \left[r_{1}T\left(\sigma \right)+r_{2}N\left(\sigma \right)+r_{3}B\left(\sigma \right)\right],r_1^2+\epsilon {\kappa }^2(r_2^2-r_3^2)=1.$$

(5)

Based on (5), the equations of I’s components and the unit normal vector field basic form of $\Gamma$ are as follows:

$$\begin{array}{cc}\hfill & E_{\Gamma }={(1-\epsilon \upsilon r_2{\kappa }^2)}^2+\epsilon {\upsilon }^2{\kappa }^2\left[{\left(r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right)}^2-{\left(r_2\tau +r_3\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\right)}^2\right],\hfill \\ & F_{\Gamma }=r_1(1-\epsilon \upsilon r_2{\kappa }^2)+\epsilon {\upsilon }^2{\kappa }^2\left[r_2\left(r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right)-r_3\left(r_2\tau +r_3\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\right)\right],\hfill \\ & G_{\Gamma }=1,\hfill \end{array}$$

(6)

$$N_{\Gamma }={\displaystyle \frac{{\alpha }_{1}T\left(\sigma \right)+{\alpha }_{2}N\left(\sigma \right)+{\alpha }_{3}B\left(\sigma \right)}{\sqrt{{\alpha }_1^2+\epsilon {\kappa }^2({\alpha }_2^2-{\alpha }_3^2)}}},$$

(7)

where

$$\begin{array}{cc}\hfill & {\alpha }_1=\upsilon r_3\left[r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right]-\upsilon r_2\left[r_2\tau +r_3\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\right],\hfill \\ & {\alpha }_2=\upsilon r_1\left[r_2\tau +r_3\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\right]-r_3(1-\epsilon \upsilon r_2{\kappa }^2),\hfill \\ & {\alpha }_3=\upsilon r_1\left[r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right]-r_2(1-\epsilon \upsilon r_2{\kappa }^2).\hfill \end{array}$$

(8)

The features of $\Gamma$’s second fundamental form are as follows:

$$\begin{array}{cc}\hfill & e_{\Gamma }={\displaystyle \frac{{\alpha }_1{\delta }_1+\epsilon {\kappa }^2({\alpha }_2{\delta }_2-{\alpha }_3{\delta }_3)}{\sqrt{{\alpha }_1^2+\epsilon {\kappa }^2({\alpha }_2^2-{\alpha }_3^2)}}},\hfill \\ & f_{\Gamma }={\displaystyle \frac{-\epsilon {\alpha }_1{r}_2{\kappa }^2+\epsilon {\kappa }^2\left[{\alpha }_2\left(r_1+r_2\left(\frac{\dot{\kappa }}{\kappa }\right)+r_3\tau \right)-{\alpha }_3\left(r_2\tau +r_3\left(\frac{\dot{\kappa }}{\kappa }\right)\right)\right]}{\sqrt{{\alpha }_1^2+\epsilon {\kappa }^2({\alpha }_2^2-{\alpha }_3^2)}}},\hfill \\ & g_{\Gamma }=0,\hfill \end{array}$$

(9)

where

$$\begin{array}{cc}\hfill & {\delta }_1=-\epsilon \upsilon \left\{2r_2\dot{\kappa }+\kappa \left[r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right]\right\},\hfill \\ & {\delta }_2=1-\epsilon \upsilon r_2{\kappa }^2+\upsilon \left\{r_3\dot{\tau }+r_2{\displaystyle \frac{d}{d\sigma }}\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\left[r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right]+\tau \left[r_2\tau +r_3\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\right]\right\},\hfill \\ & {\delta }_3=\upsilon \left\{r_2\dot{\tau }+r_3{\displaystyle \frac{d}{d\sigma }}\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+\tau \left[r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right]+\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\left[r_2\tau +r_3\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\right]\right\}.\hfill \end{array}$$

(10)

Through using above-mentioned information, the Gaussian and mean curvatures are calculated based on the following:

$$K_{\Gamma }=-{\displaystyle \frac{{\left\{-\epsilon {\alpha }_1{r}_2{\kappa }^2+\epsilon {\kappa }^2\left[{\alpha }_2\left(r_1+r_2\left(\frac{\dot{\kappa }}{\kappa }\right)+r_3\tau \right)-{\alpha }_3\left(r_2\tau +r_3\left(\frac{\dot{\kappa }}{\kappa }\right)\right)\right]\right\}}^2}{\Delta \left[{\alpha }_1^2+\epsilon {\kappa }^2({\alpha }_2^2-{\alpha }_3^2)\right])}},$$

(11)

$$\begin{array}{cc}& H_{\Gamma }={\displaystyle \frac{1}{2\Delta \sqrt{{\alpha }_1^2+\epsilon {\kappa }^2({\alpha }_2^2-{\alpha }_3^2)}}}\{{\alpha }_1{\delta }_1+\epsilon {\kappa }^2({\alpha }_2{\delta }_2-{\alpha }_3{\delta }_3)-2[r_1(1-\epsilon \upsilon r_2{\kappa }^2)\hfill \\ & +\epsilon {\upsilon }^2{\kappa }^2\left[r_2\left(r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right)-r_3\left(r_2\tau +r_3\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\right)\right]\left]\right[-\epsilon {\alpha }_1{r}_2{\kappa }^2\hfill \\ & +\epsilon {\kappa }^2\left[{\alpha }_2\left(r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right)-{\alpha }_3\left(r_2\tau +r_3\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\right)\right]\left]\right\},\hfill \end{array}$$

(12)

where

$$\begin{array}{cc}\hfill \Delta & ={(1-\epsilon \upsilon r_2{\kappa }^2)}^2+\epsilon {\upsilon }^2{\kappa }^2\left[{\left(r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right)}^2-{\left(r_2\tau +r_3\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\right)}^2\right]-\{r_1(1-\epsilon \upsilon r_2{\kappa }^2)\hfill \\ & +\epsilon {\upsilon }^2{\kappa }^2\left[r_2\left(r_1+r_2\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)+r_3\tau \right)-r_3\left(r_2\tau +r_3\left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)\right)\right]{\}}^2.\hfill \end{array}$$

As a result of the preceding findings, we can deduce the the next theorems.

Theorem 1.

At the point $(\sigma ,0)$, the ruled surface (5) via orthogonal modified frame fulfills the following requirements:

1. 

The surface is developable if and only if $\tau ={\displaystyle \frac{r_1{r}_3}{r_2^2-r_3^2}}$ .

2. 

The surface is minimal if and only if $\tau ={\displaystyle \frac{r_3(1-2r_1^2)}{2r_1(r_2^2-r_3^2)}}$ .

Case 1.

At $r_1=0$, the ruled surface (5) has to have the specific traits:

$$\begin{array}{cc}& K_{\Gamma }=-{\displaystyle \frac{\epsilon {\kappa }^2\left\{r_3\left[r_2\left(\frac{\dot{\kappa }}{\kappa }\right)+r_3\tau \right]-r_2\left[r_2\tau +r_3\left(\frac{\dot{\kappa }}{\kappa }\right)\right]\right\}}{r_2^2-r_3^2}},\hfill \\ & H_{\Gamma }=-{\displaystyle \frac{\epsilon r_3\kappa }{2\sqrt{\epsilon (r_2^2-r_3^2)}}}.\hfill \end{array}$$

(13)

Corollary 1.

At the point $(\sigma ,0)$, the ruled surface (5) via orthogonal modified frame with $r_1=0$ is developable if $\tau =0$.

Case 2.

For $\epsilon =1$ at $r_2=0$, the ruled surface (5) has to have the specific traits:

$$\begin{array}{cc}& K_{\Gamma }=-{\displaystyle \frac{{\kappa }^2(r_1+r_3\tau )}{r_3(r_1^2-1)}},\hfill \\ & H_{\Gamma }=-{\displaystyle \frac{\kappa \left[1-2r_1(r_1+r_3\tau )\right]}{2\sqrt{r_1^2-1)}}}.\hfill \end{array}$$

(14)

Corollary 2.

For $\epsilon =1$ and at the point $(\sigma ,0)$, the ruled surface (5) via orthogonal modified frame with $r_2=0$ is as follows:

1. 

Developable if only and only if $\tau =-\left({\displaystyle \frac{r_1}{r_3}}\right)$ .

2. 

Minimal if only and only if $\tau ={\displaystyle \frac{1-2r_1^2}{2r_1{r}_3}}$ .

Case 3.

For $\epsilon =-1$ at $r_3=0$, the ruled surface (5) has to have the specific traits:

$$\begin{array}{cc}& K_{\Gamma }={\displaystyle \frac{r_2^2\tau {\kappa }^2}{1-r_1^2}},H_{\Gamma }={\displaystyle \frac{r_1{r}_2\tau \kappa }{1-r_1^2}}.\hfill \end{array}$$

(15)

Corollary 3.

For $\epsilon =-1$ and at the point $(\sigma ,0)$, the ruled surface (5) via orthogonal modified frame with $r_2=0$ is an $(H_{\Gamma },K_{\Gamma })$-linear Weingarten surface if only and only if $\beta \left(\sigma \right)$ is a W-curve.

Case 4.

For $\epsilon =1$ at $r_1=r_2=0$, the ruled surface (5) has to have the specific traits:

$$\begin{array}{cc}& K_{\Gamma }=-\tau {\kappa }^2,H_{\Gamma }=-r_3\kappa .\hfill \end{array}$$

(16)

Corollary 4.

For $\epsilon =1$ and at the point $(\sigma ,0)$, the ruled surface (5) via orthogonal modified frame with $r_1=r_2=0$ is as follows:

1. 

Developable if only and only if $\tau =0$ .

2. 

An $(H_{\Gamma },K_{\Gamma })$-linear Weingarten surface if only and only if $\beta \left(\sigma \right)$ is a W-curve.

Case 5.

For $\epsilon =-1$ at $r_1=r_3=0$, the ruled surface (5) has to have the specific traits:

$$K_{\Gamma }=\tau {\kappa }^2,H_{\Gamma }=0.$$

(17)

Corollary 5.

For $\epsilon =-1$ and during the point $(\sigma ,0)$, the ruled surface (5) via orthogonal modified frame with $r_1=r_3=0$ is as follows:

1. 

A minimal surface.

2. 

Developable if only and only if $\tau =0$ .

3. 

An $(H_{\Gamma },K_{\Gamma })$-linear Weingarten surface if only and only if $\beta \left(\sigma \right)$ is a W-curve.

Example 1.

For $\epsilon =-1$, let $\beta \left(\sigma \right)=\left({\displaystyle \frac{\sqrt{3}\sigma }{2}},sinh\left({\displaystyle \frac{\sigma }{2}}\right),cosh\left({\displaystyle \frac{\sigma }{2}}\right)\right)$ be a spacelike curve in ${\mathrm{E}}_1^3$. It is simple to demonstrate the Frenet invariants as follows:

$$\begin{array}{cc}& t\left(\sigma \right)=\left({\displaystyle \frac{\sqrt{3}}{2}},{\displaystyle \frac{1}{2}}cosh\left({\displaystyle \frac{\sigma }{2}}\right),{\displaystyle \frac{1}{2}}sinh\left({\displaystyle \frac{\sigma }{2}}\right)\right),\hfill \\ & n\left(\sigma \right)=\left(0,sinh\left({\displaystyle \frac{\sigma }{2}}\right),cosh\left({\displaystyle \frac{\sigma }{2}}\right)\right),\hfill \\ & b\left(\sigma \right)=\left({\displaystyle \frac{1}{2}},-{\displaystyle \frac{\sqrt{3}}{2}}cosh\left({\displaystyle \frac{\sigma }{2}}\right),-{\displaystyle \frac{\sqrt{3}}{2}}sinh\left({\displaystyle \frac{\sigma }{2}}\right)\right),\hfill \\ & \kappa ={\displaystyle \frac{1}{4}},\tau =-{\displaystyle \frac{\sqrt{3}}{4}}.\hfill \end{array}$$

Then, the orthogonal modified frames are

$$\begin{array}{cc}& T\left(\sigma \right)=\left({\displaystyle \frac{\sqrt{3}}{2}},{\displaystyle \frac{1}{2}}cosh\left({\displaystyle \frac{\sigma }{2}}\right),{\displaystyle \frac{1}{2}}sinh\left({\displaystyle \frac{\sigma }{2}}\right)\right),\hfill \\ & N\left(\sigma \right)=\left(0,{\displaystyle \frac{1}{4}}sinh\left({\displaystyle \frac{\sigma }{2}}\right),{\displaystyle \frac{1}{4}}cosh\left({\displaystyle \frac{\sigma }{2}}\right)\right),\hfill \\ & B\left(\sigma \right)=\left({\displaystyle \frac{1}{8}},-{\displaystyle \frac{\sqrt{3}}{8}}cosh\left({\displaystyle \frac{\sigma }{2}}\right),-{\displaystyle \frac{\sqrt{3}}{8}}sinh\left({\displaystyle \frac{\sigma }{2}}\right)\right).\hfill \end{array}$$

Taking $r_1={\displaystyle \frac{3}{2\sqrt{2}}}$, $r_2=\sqrt{3}$, and $r_3=1$, the ruled surfaces via Frenet frame and orthogonal modified frame are then computed as follows (see Figure 1 and Figure 2):

$$\begin{array}{cc}& {\Gamma }_1(\sigma ,\upsilon )=(3\sigma +(2\sqrt{3}+\sqrt{2})\upsilon ,(\upsilon +1)sinh\left({\displaystyle \frac{\sigma }{2}}\right)+\left({\displaystyle \frac{(2-\sqrt{6})\upsilon }{2\sqrt{3}}}\right)cosh\left({\displaystyle \frac{\sigma }{2}}\right)\hfill \\ & ,\left({\displaystyle \frac{(2-\sqrt{6})\upsilon }{2\sqrt{3}}}\right)sinh\left({\displaystyle \frac{\sigma }{2}}\right)+(\upsilon +1)cosh\left({\displaystyle \frac{\sigma }{2}}\right)),\hfill \\ & {\Gamma }_2(\sigma ,\upsilon )=({\displaystyle \frac{1}{8\sqrt{2}}}\left[4\sqrt{6}\sigma +(\sqrt{2}+6\sqrt{3})\upsilon \right],\left({\displaystyle \frac{(4+\sqrt{3}\upsilon )}{4}}\right)sinh\left({\displaystyle \frac{\sigma }{2}}\right)+\left({\displaystyle \frac{(6-\sqrt{6})\upsilon }{8\sqrt{2}}}\right)cosh\left({\displaystyle \frac{\sigma }{2}}\right)\hfill \\ & ,\left({\displaystyle \frac{(6-\sqrt{6})\upsilon }{8\sqrt{2}}}\right)sinh\left({\displaystyle \frac{\sigma }{2}}\right)+\left({\displaystyle \frac{(4+\sqrt{3}\upsilon )}{4}}\right)cosh\left({\displaystyle \frac{\sigma }{2}}\right))\hfill \end{array}$$

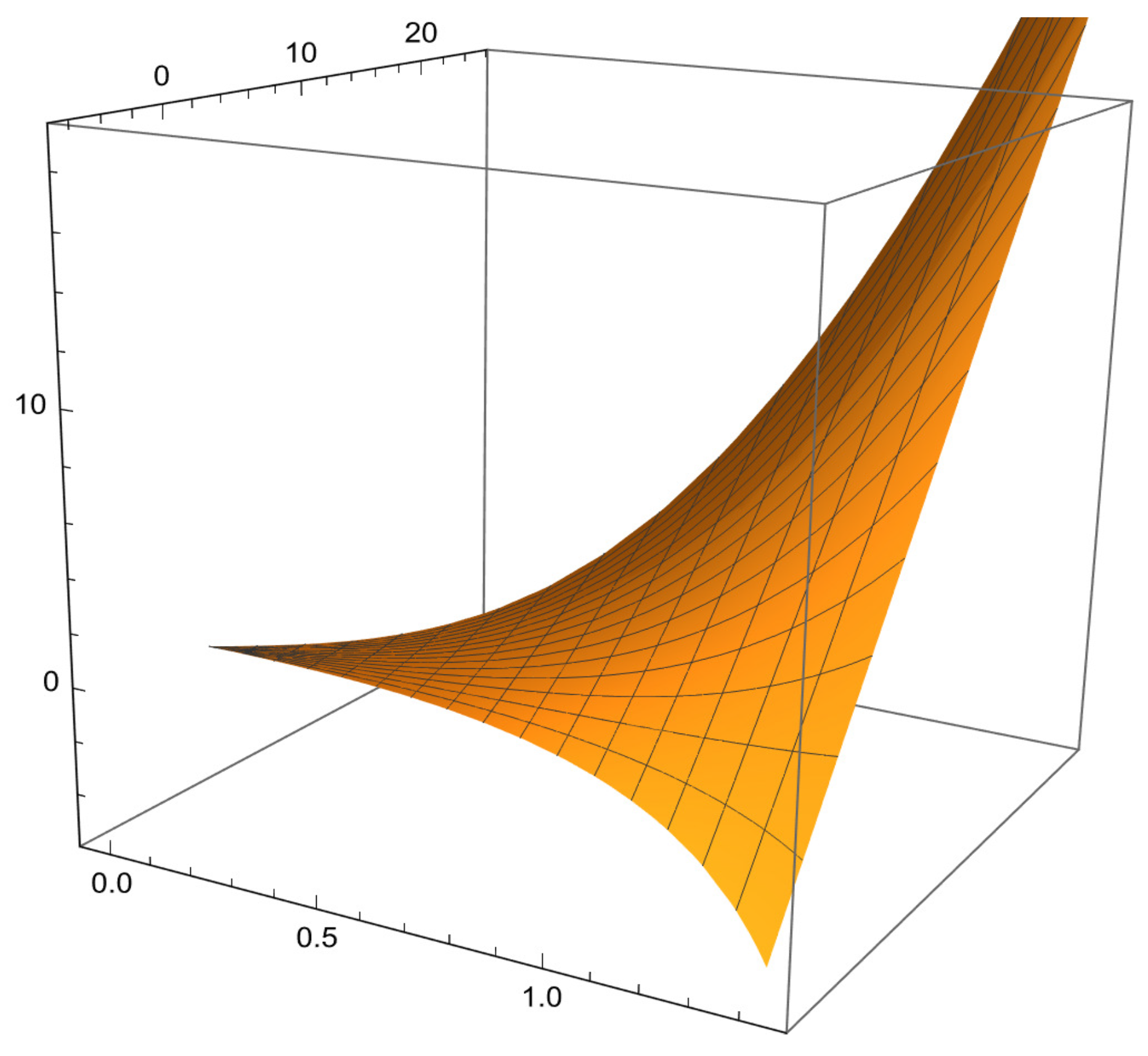
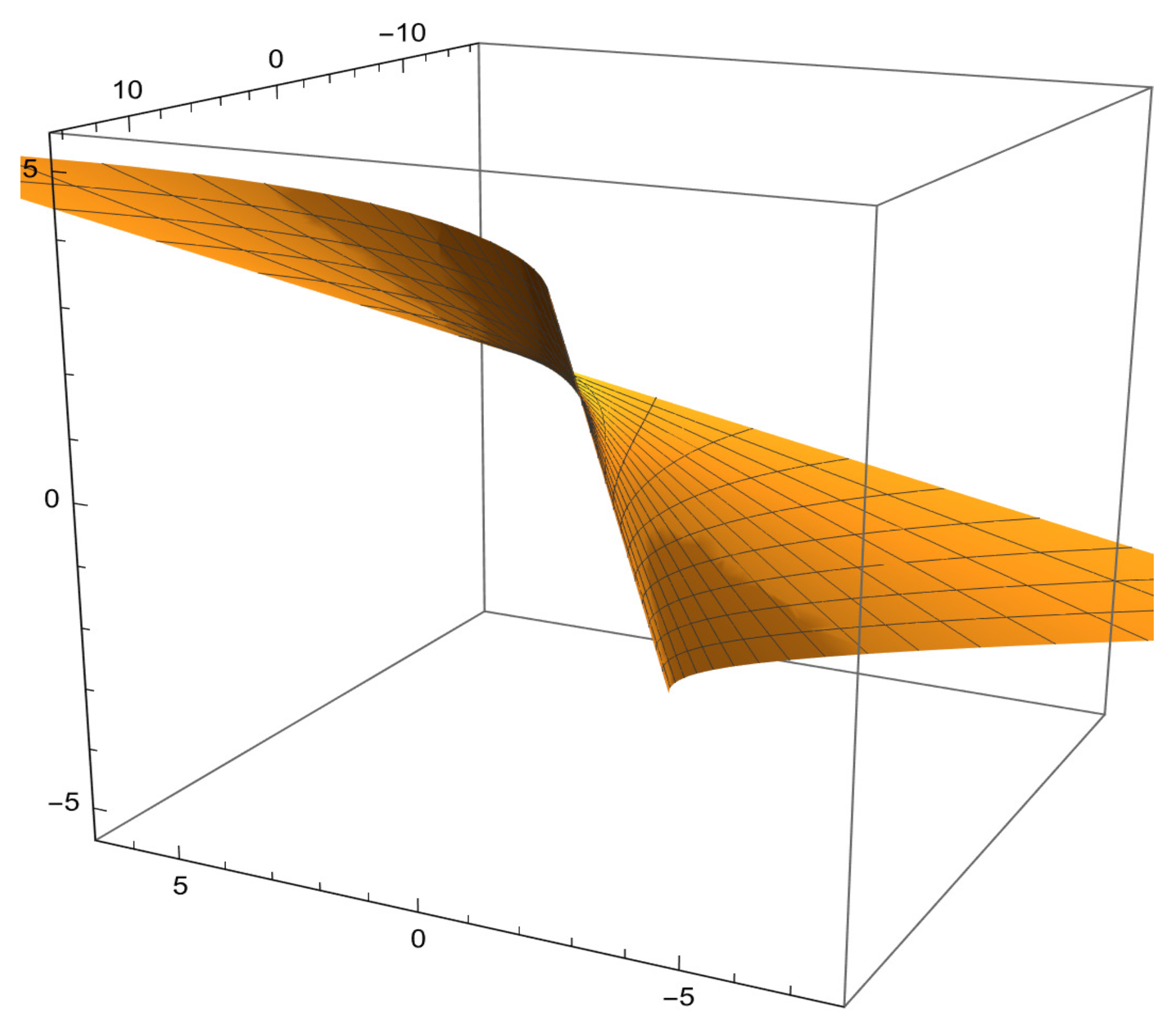
4. Evolutionary Characteristics of Spectacular Ruled Surfaces via Orthogonal Modified Frame

Within this section, we investigate the T-, N-, and B-ruled surfaces along an analytic space curve using orthogonal modified frames. If the $\beta \left(\sigma \right)$ and $\ell \left(\sigma \right)$ curves do, in fact, transit in time t, the ruled surface (4) looks like this:

$$\Gamma (\sigma ,\upsilon ,t)=\beta (\sigma ,t)+\upsilon \ell (\sigma ,t).$$

(18)

4.1. T-Ruled Surface via Orthogonal Modified Frame

For $\epsilon =-1$, the tangent-ruled surface is generated by the motion of the tangent vector $T\left(\sigma \right)$ of $\beta \left(\sigma \right)$, and its equation is represented by

$$\Psi (\sigma ,\upsilon ,t)=\beta (\sigma ,t)+\upsilon T(\sigma ,t).$$

(19)

The $\Psi$’s partial differentiations are

$$\begin{array}{cc}\hfill & {\Psi }_{\sigma }=T\left(\sigma \right)+\upsilon N\left(\sigma \right),\hfill \\ & {\Psi }_{\upsilon }=T\left(\sigma \right).\hfill \end{array}$$

(20)

Using (20), in reality, we may obtain the $I_{\Psi }$’quantities and the $\Psi$ unit normal vector field as follows:

$$\begin{array}{cc}\hfill & E_{\Psi }=1-{\upsilon }^2{\kappa }^2,\hfill \\ & F_{\Psi }=1,\hfill \\ & G_{\Psi }=1,\hfill \end{array}$$

(21)

$$N_{\Psi }={\displaystyle \frac{B\left(\sigma \right)}{\kappa }}.$$

(22)

Differentiating (20) in relation to $\sigma$ and $\upsilon$, respectively, and using (22), the $I{I}_{\Psi }$’quantities of $\Psi$ are

$$\begin{array}{cc}\hfill & e_{\Psi }=\upsilon \tau \kappa ,\hfill \\ & f_{\Psi }=0,\hfill \\ & g_{\Psi }=0.\hfill \end{array}$$

(23)

Then, $K_{\Psi }$ and $H_{\Psi }$ of a T-ruled surface $\Psi$ are

$$\begin{array}{cc}& K_{\Psi }=0,H_{\Psi }=-{\displaystyle \frac{\tau }{2\upsilon \kappa }}.\hfill \end{array}$$

(24)

Corollary 6.

For $\epsilon =-1$, the T-ruled surface (19) via an orthogonal modified frame is as follows:

1. 

A developable surface.

2. 

Minimal if only and only if $\tau =0$ .

3. 

An $(H_{\Psi },K_{\Psi })$-linear Weingarten surface if only and only if $\beta \left(\sigma \right)$ is a helix.

4.2. N-Ruled Surface via Orthogonal Modified Frame

The formula for the normal-ruled surface produced by the movement of the normal vector $N\left(\sigma \right)$ of $\beta \left(\sigma \right)$ is shown by

$$\Omega (\sigma ,\upsilon ,t)=\beta (\sigma ,t)+\upsilon N(\sigma ,t).$$

(25)

The $\Omega$’s velocity vectors are

$$\begin{array}{cc}\hfill & {\Omega }_{\sigma }=\left[1-\epsilon \upsilon {\kappa }^2\right]T\left(\sigma \right)+\upsilon \left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)N\left(\sigma \right)+\upsilon \tau B\left(\sigma \right),\hfill \\ & {\Omega }_{\upsilon }=N\left(\sigma \right).\hfill \end{array}$$

(26)

Using (26), we could really obtain the $\Omega$’s quantities of $I_{\Omega }$ and $N_{\Omega }$ as follows:

$$\begin{array}{cc}\hfill & E_{\Omega }={\left(1-\epsilon \upsilon {\kappa }^2\right)}^2+\epsilon {\upsilon }^2\left({\dot{\kappa }}^2-{\tau }^2{\kappa }^2\right),\hfill \\ & F_{\Omega }=\epsilon \upsilon \kappa \dot{\kappa },\hfill \\ & G_{\Omega }=\epsilon {\kappa }^2,\hfill \end{array}$$

(27)

$$N_{\Omega }={\displaystyle \frac{-\upsilon \tau T\left(\sigma \right)+(\epsilon \upsilon {\kappa }^2-1)B\left(\sigma \right)}{\sqrt{{\tau }^2{\kappa }^2-\epsilon {\kappa }^2{(\epsilon \upsilon {\kappa }^2-1)}^2}}}.$$

(28)

Differentiating (26) in relation to $\sigma$ and $\upsilon$, respectively, and using (28), the $\Omega$’s quantities of $I{I}_{\Omega }$ are

$$\begin{array}{cc}\hfill & e_{\Omega }={\displaystyle \frac{\epsilon \upsilon \kappa \left[3\upsilon \tau \dot{\kappa }-(\epsilon \upsilon {\kappa }^2-1)(\dot{\tau }\kappa +2\tau \dot{\kappa })\right]}{\sqrt{{\tau }^2{\kappa }^2-\epsilon {\kappa }^2{(\epsilon \upsilon {\kappa }^2-1)}^2}}},\hfill \\ & f_{\Omega }={\displaystyle \frac{\tau {\kappa }^2\left[\epsilon (\upsilon +1)-\upsilon {\kappa }^2\right]}{\sqrt{{\tau }^2{\kappa }^2-\epsilon {\kappa }^2{(\epsilon \upsilon {\kappa }^2-1)}^2}}},\hfill \\ & g_{\Omega }=0.\hfill \end{array}$$

(29)

Then, $K_{\Omega }$ and $H_{\Omega }$ of an N-ruled surface $\Omega$ are

$$\begin{array}{cc}& K_{\Omega }={\displaystyle \frac{{\tau }^2{\kappa }^2{\left[\epsilon (\upsilon +1)-\upsilon {\kappa }^2\right]}^2}{\left[\epsilon {(1-\epsilon \upsilon {\kappa }^2)}^2-{\upsilon }^2{\tau }^2{\kappa }^2\right]\left[{\tau }^2{\kappa }^2-\epsilon {\kappa }^2{(\epsilon \upsilon {\kappa }^2-1)}^2\right]}},\hfill \\ & H_{\Omega }={\displaystyle \frac{\upsilon \kappa \left[3\upsilon \tau \dot{\kappa }-(\epsilon \upsilon {\kappa }^2-1)(\dot{\tau }\kappa +2\tau \dot{\kappa })-2\epsilon \tau \dot{\kappa }[\epsilon (\upsilon +1)-\upsilon {\kappa }^2]\right]}{2\left[\epsilon {(1-\epsilon \upsilon {\kappa }^2)}^2-{\upsilon }^2{\tau }^2{\kappa }^2\right]\sqrt{{\tau }^2{\kappa }^2-\epsilon {\kappa }^2{(\epsilon \upsilon {\kappa }^2-1)}^2}}}.\hfill \end{array}$$

(30)

Corollary 7.

The N-ruled surface (25) via an orthogonal modified frame is as follows:

1. 

A developable surface iff $\tau =0$.

2. 

Minimal if only and only if

$$3\upsilon \tau \dot{\kappa }-(\epsilon \upsilon {\kappa }^2-1)(\dot{\tau }\kappa +2\tau \dot{\kappa })-2\epsilon \tau \dot{\kappa }[\epsilon (\upsilon +1)-\upsilon {\kappa }^2]=0.$$

4.3. B-Ruled Surface via Orthogonal Modified Frame

The binormal-ruled surface is generated by the motion of the binormal vector $B\left(\sigma \right)$ of $\beta \left(\sigma \right)$, and its equation is represented by

$$\Phi (\sigma ,\upsilon ,t)=\beta (\sigma ,t)+\upsilon B(\sigma ,t).$$

(31)

The $\Phi$’s velocity vectors are

$$\begin{array}{cc}\hfill & {\Phi }_{\sigma }=T\left(\sigma \right)+\left(\upsilon \tau \right)N\left(\sigma \right)+\upsilon \left({\displaystyle \frac{\dot{\kappa }}{\kappa }}\right)B\left(\sigma \right),\hfill \\ & {\Phi }_{\upsilon }=B\left(\sigma \right).\hfill \end{array}$$

(32)

Using (32), we could really obtain the $\Phi$’s quantities of $I_{\Phi }$ and $N_{\Phi }$ as follows:

$$\begin{array}{cc}\hfill & E_{\Phi }=1+\epsilon {\upsilon }^2\left[{\tau }^2{\kappa }^2-{\dot{\kappa }}^2\right],\hfill \\ & F_{\Phi }=-\epsilon \upsilon \kappa \dot{\kappa },\hfill \\ & G_{\Phi }=-\epsilon {\kappa }^2,\hfill \end{array}$$

(33)

$$N_{\Phi }={\displaystyle \frac{\upsilon \tau T\left(\sigma \right)-N\left(\sigma \right)}{\sqrt{\epsilon {\kappa }^2+{\upsilon }^2{\tau }^2}}}.$$

(34)

Differentiating (32) in relation to $\sigma$ and $\upsilon$, respectively, and using (34), the $\Phi$’s quantities of $I{I}_{\Phi }$ are

$$\begin{array}{cc}\hfill & e_{\Phi }=-{\displaystyle \frac{\epsilon \kappa \left[{\upsilon }^2{\tau }^2\kappa +2\upsilon \tau \dot{\kappa }+\kappa (1+\upsilon \dot{\tau })\right]}{\sqrt{\epsilon {\kappa }^2+{\upsilon }^2{\tau }^2}}},\hfill \\ & f_{\Phi }=-{\displaystyle \frac{\epsilon \tau {\kappa }^2}{\sqrt{\epsilon {\kappa }^2+{\upsilon }^2{\tau }^2}}},\hfill \\ & g_{\Phi }=0.\hfill \end{array}$$

(35)

Then, $K_{\Phi }$ and $H_{\Phi }$ of a B-ruled surface $\Phi$ are

$$\begin{array}{cc}& K_{\Phi }={\displaystyle \frac{{\tau }^2{\kappa }^2}{\left[\epsilon +{\upsilon }^2{\tau }^2{\kappa }^2\right]\left[\epsilon {\kappa }^2+{\upsilon }^2{\tau }^2\right]}},\hfill \\ & H_{\Phi }=-{\displaystyle \frac{{\kappa }^2\left[\upsilon \dot{\tau }+{\upsilon }^2{\tau }^2+1\right]}{2\left[\epsilon +{\upsilon }^2{\tau }^2{\kappa }^2\right]\sqrt{\epsilon {\kappa }^2+{\upsilon }^2{\tau }^2}}}.\hfill \end{array}$$

(36)

Corollary 8.

The B-ruled surface (31) via orthogonal modified frame is as follows:

1. 

A developable surface iff $\tau =0$.

2. 

Minimal if only and only if $\upsilon \dot{\tau }+{\upsilon }^2{\tau }^2+1=0$.

Example 2.

For $\epsilon =1$, let $\beta \left(\sigma \right)=\left({\displaystyle \sqrt{2}\sigma ,{\int }_0^{\sigma }sinh\left(\frac{\pi t^2}{2}\right)dt,{\int }_0^{\sigma }cosh\left(\frac{\pi t^2}{2}\right)dt}\right)$ be a spacelike curve in ${\mathrm{E}}_1^3$. It is simple to demonstrate the Frenet invariants as follows:

$$\begin{array}{cc}& t\left(\sigma \right)=\left(\sqrt{2},sinh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right),cosh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)\right),\hfill \\ & n\left(\sigma \right)=\left(0,\left({\displaystyle \frac{\sigma }{\left|\sigma \right|}}\right)cosh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right),\left({\displaystyle \frac{\sigma }{\left|\sigma \right|}}\right)sinh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)\right),\hfill \\ & b\left(\sigma \right)=\left(-{\displaystyle \frac{\sigma }{\left|\sigma \right|}},-\left({\displaystyle \frac{\sqrt{2}\sigma }{\left|\sigma \right|}}\right)sinh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right),-\left({\displaystyle \frac{\sqrt{2}\sigma }{\left|\sigma \right|}}\right)cosh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)\right),\hfill \\ & \kappa =\pi \left|\sigma \right|,\tau =\sqrt{2}\pi \sigma .\hfill \end{array}$$

Then, the orthogonal modified frames are

$$\begin{array}{cc}& T\left(\sigma \right)=\left(\sqrt{2},sinh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right),cosh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)\right),\hfill \\ & N\left(\sigma \right)=\left(0,\pi \sigma cosh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right),\pi \sigma sinh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)\right),\hfill \\ & B\left(\sigma \right)=\left(-\pi \sigma ,-\sqrt{2}\pi \sigma sinh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right),-\sqrt{2}\pi \sigma cosh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)\right).\hfill \end{array}$$

The T-ruled surface via an orthogonal modified frame is computed as follows (see Figure 3):

$$\begin{array}{cc}\hfill \Psi (\sigma ,\upsilon ,t)& {\displaystyle =(\sqrt{2}\left(\sigma +\upsilon \right),{\int }_0^{\sigma }sinh\left(\frac{\pi t^2}{2}\right)dt+\upsilon sinh\left(\frac{\pi {\sigma }^2}{2}\right),{\int }_0^{\sigma }cosh\left(\frac{\pi t^2}{2}\right)dt}\hfill \\ & +\upsilon cosh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)).\hfill \end{array}$$

The N-ruled surfaces via Frenet frame and orthogonal modified frame are then computed as (see Figure 4 and Figure 5).

$$\begin{array}{cc}& {\displaystyle {\Omega }_1(\sigma ,\upsilon ,t)=(\sqrt{2}\sigma ,{\int }_0^{\sigma }sinh\left(\frac{\pi t^2}{2}\right)dt+\left(\frac{\upsilon \sigma }{\left|\sigma \right|}\right)cosh\left(\frac{\pi {\sigma }^2}{2}\right),{\int }_0^{\sigma }cosh\left(\frac{\pi t^2}{2}\right)dt}\hfill \\ & +\left({\displaystyle \frac{\upsilon \sigma }{\left|\sigma \right|}}\right)sinh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)),\hfill \\ & {\displaystyle {\Omega }_2(\sigma ,\upsilon ,t)=(\sqrt{2}\sigma ,{\int }_0^{\sigma }sinh\left(\frac{\pi t^2}{2}\right)dt+\pi \upsilon \sigma cosh\left(\frac{\pi {\sigma }^2}{2}\right),{\int }_0^{\sigma }cosh\left(\frac{\pi t^2}{2}\right)dt}\hfill \\ & +\pi \upsilon \sigma sinh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)).\hfill \end{array}$$

The B-ruled surfaces via Frenet frame and orthogonal modified frame are then computed as follows (see Figure 6 and Figure 7):

$$\begin{array}{cc}& {\displaystyle {\Phi }_1(\sigma ,\upsilon ,t)=(\sqrt{2}\sigma -\frac{\upsilon \sigma }{\left|\sigma \right|},{\int }_0^{\sigma }sinh\left(\frac{\pi t^2}{2}\right)dt-\left(\frac{\sqrt{2}\upsilon \sigma }{\left|\sigma \right|}\right)sinh\left(\frac{\pi {\sigma }^2}{2}\right),{\int }_0^{\sigma }cosh\left(\frac{\pi t^2}{2}\right)dt}\hfill \\ & -\left({\displaystyle \frac{\sqrt{2}\upsilon \sigma }{\left|\sigma \right|}}\right)cosh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)),\hfill \\ & {\displaystyle {\Phi }_2(\sigma ,\upsilon ,t)=(\sqrt{2}\sigma -\upsilon \sigma ,{\int }_0^{\sigma }sinh\left(\frac{\pi t^2}{2}\right)dt-\sqrt{2}\upsilon \sigma sinh\left(\frac{\pi {\sigma }^2}{2}\right),{\int }_0^{\sigma }cosh\left(\frac{\pi t^2}{2}\right)dt}\hfill \\ & -\sqrt{2}\upsilon \sigma cosh\left({\displaystyle \frac{\pi {\sigma }^2}{2}}\right)).\hfill \end{array}$$

5. Conclusions

In this work, we used an orthogonal modified frame to investigate the geometric features of ruled surfaces in Minkowski 3-space ${\mathrm{E}}_1^3$. The research emphasized the influence of spacelike rulingson the behavior of these surfaces by concentrating on important features like minimality, developability, and curvature attributes. According to our research, ruled surfaces may be studied more methodically and effectively by using an orthogonal modified frame, which also offers fresh perspectives on the curvature requirements and categorization of these surfaces. In order to better comprehend minimum ruled surfaces in Lorentzian geometry, the requirements for these surfaces were investigated, and the connections between Gaussian and mean curvature were developed. We illustrate the benefits of using modified frames to analyze the geometric features of ruled surfaces by contrasting our findings with those of previous research. These results may have use in differential geometry, mathematical physics, and relativity, where Minkowski space is essential. By examining higher-dimensional governed surfaces or their dynamic behaviors under other geometric flows, further study might be built on this work. This work lays the groundwork for future investigations into ruled surfaces in the Minkowski framework, improving our theoretical knowledge of them and their possible uses in a range of scientific domains.