Modeling Information Diffusion on Social Media: The Role of the Saturation Effect
Abstract
:1. Introduction
2. Datasets
- Fridays for future: An international student-led movement advocating for urgent measures to combat global warming and climate change. The collected data are temporarily situated in the week of September 2019, when this movement prompted several global climate strikes.
- 2019 Spanish general elections: These elections took place on 10 November, the second time that year due to the failure to establish a government. The data comprise the discussion on this topic that occurred two days prior, on 8 November.
- 2020 United States elections: This case study is based on a conversation that took place two days before the elections held on 3 November 2020.
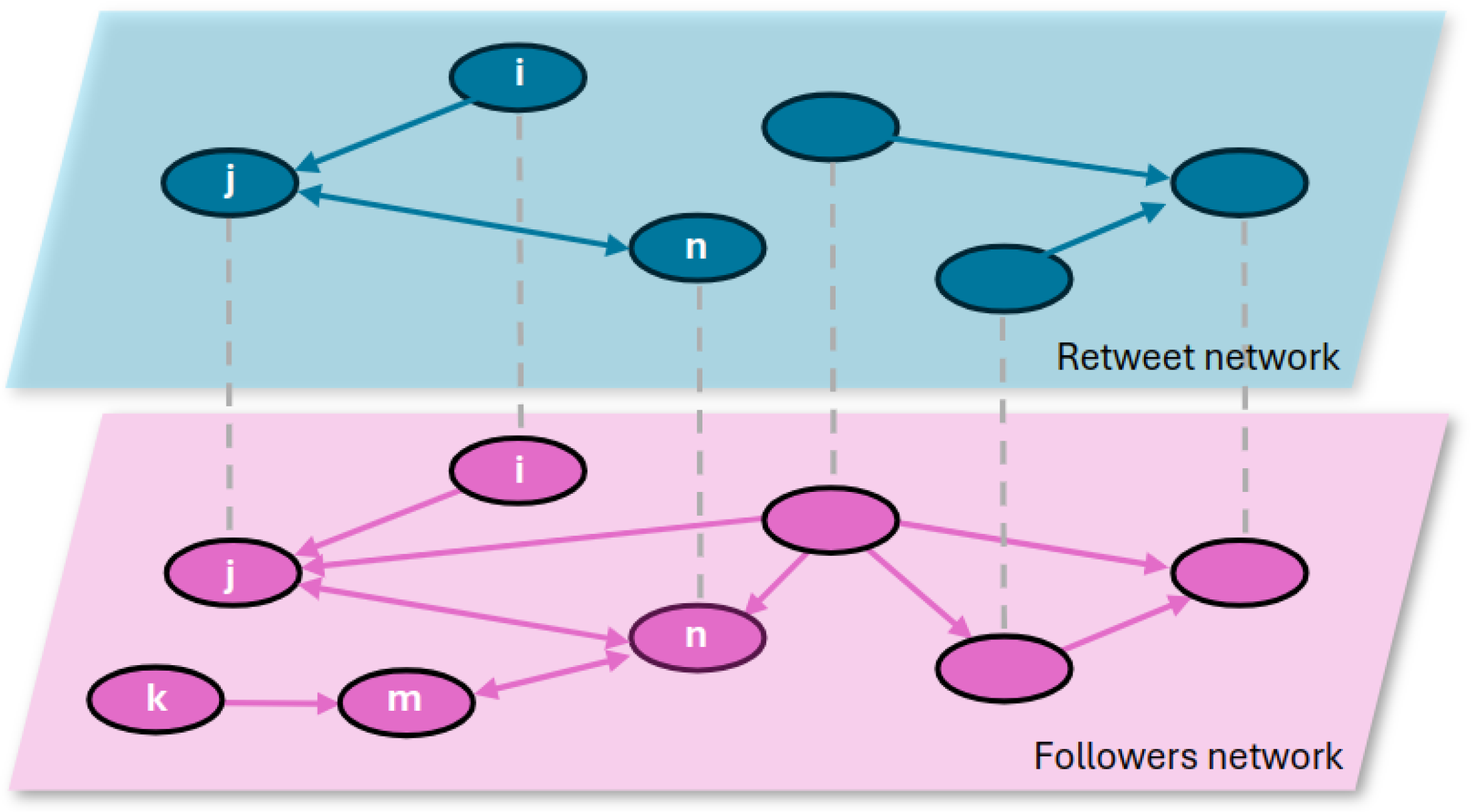
2.1. Model Diffusion Data
2.2. Data for the Temporal Analysis
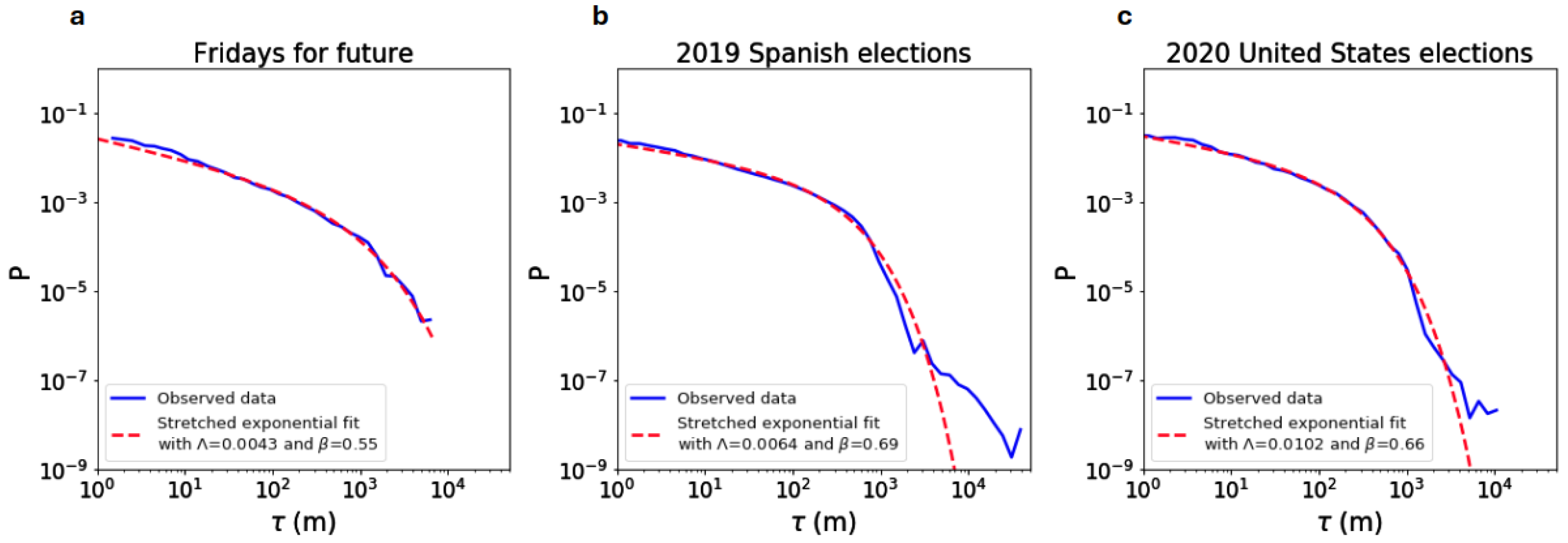
3. Results and Discussion
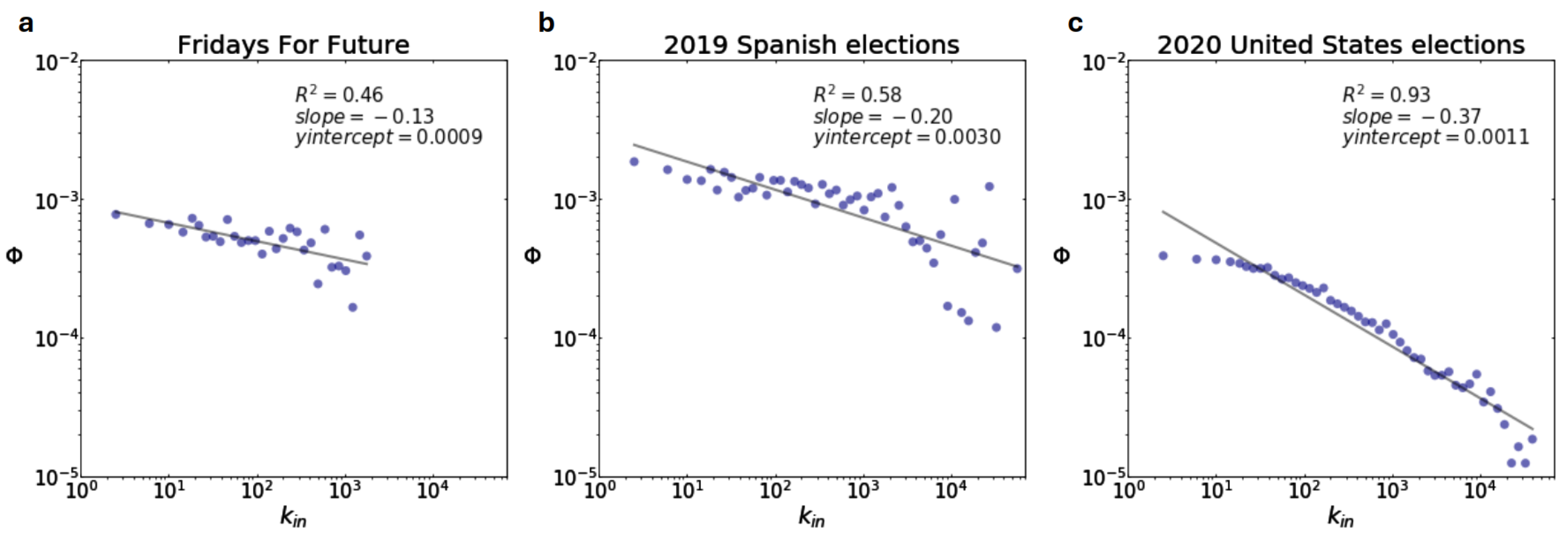
3.1. Diffusion Model
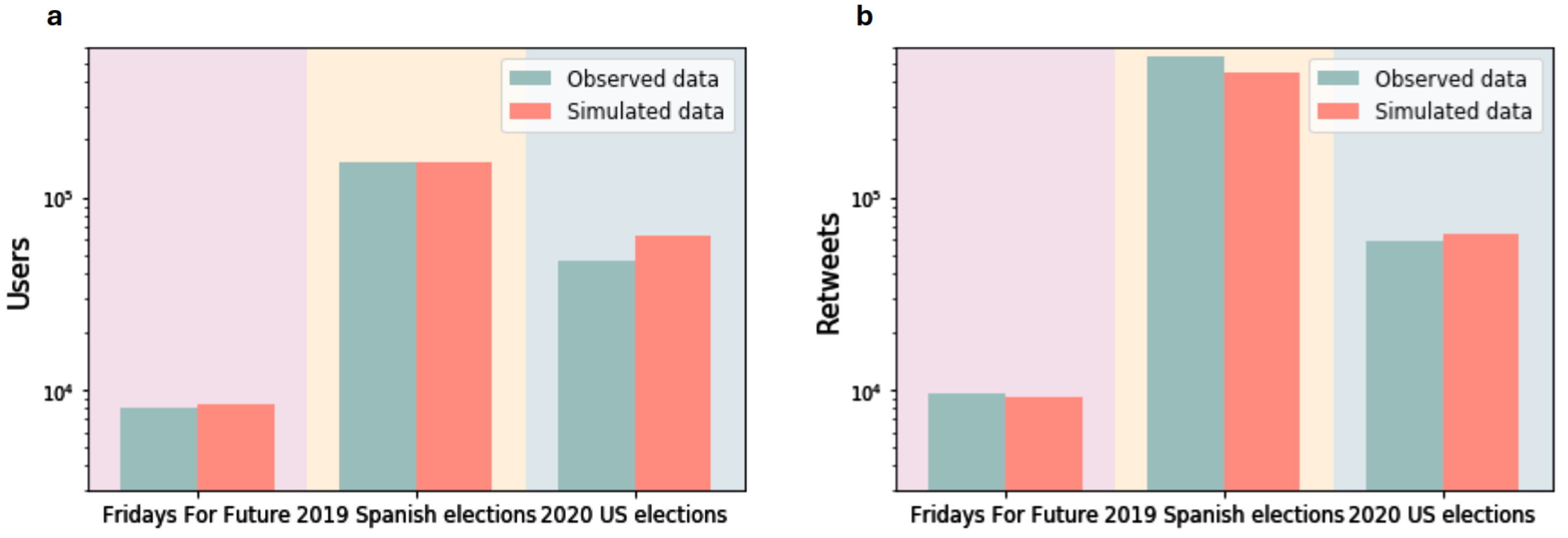
Model Verification
3.2. Temporal Behavior
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Simulation Algorithm
- Initialization: Each tweet is simulated individually, starting from the real original tweets author’s. The process involves simulating the diffusion trees of these tweets separately to construct the complete retweet network.
- Diffusion Process: To simulate the diffusion tree of a tweet, it is necessary to determine its Observers, i.e., those who can potentially see it. To begin with, all followers of the tweet’s author are considered Observers. For each Observer, a random probability value between 0 and 1 is generated. This probability is compared to the retweet ratio defined by the model parameter, which depends on the Observer’s , as well as on the parameters c and for each experimental case. is the number of users the Observer follows, so we calculate it with their out-degree in the follower network. If the generated random probability is less than the retweet ratio, the Observer retweets the tweet, becoming a Spreader.
- Iterative Expansion: After going through all the followers of the original author, the diffusion process is extended to the followers of the newly designated Spreaders. This iterative procedure continues, with each new set of Spreaders contributing to the expansion of the retweet network, until no additional Spreaders are identified.
- Completion: This simulation process is repeated for each original tweet, progressively constructing the entire simulated retweet network. By aggregating the results from all individual tweet simulations, the final network is assembled.
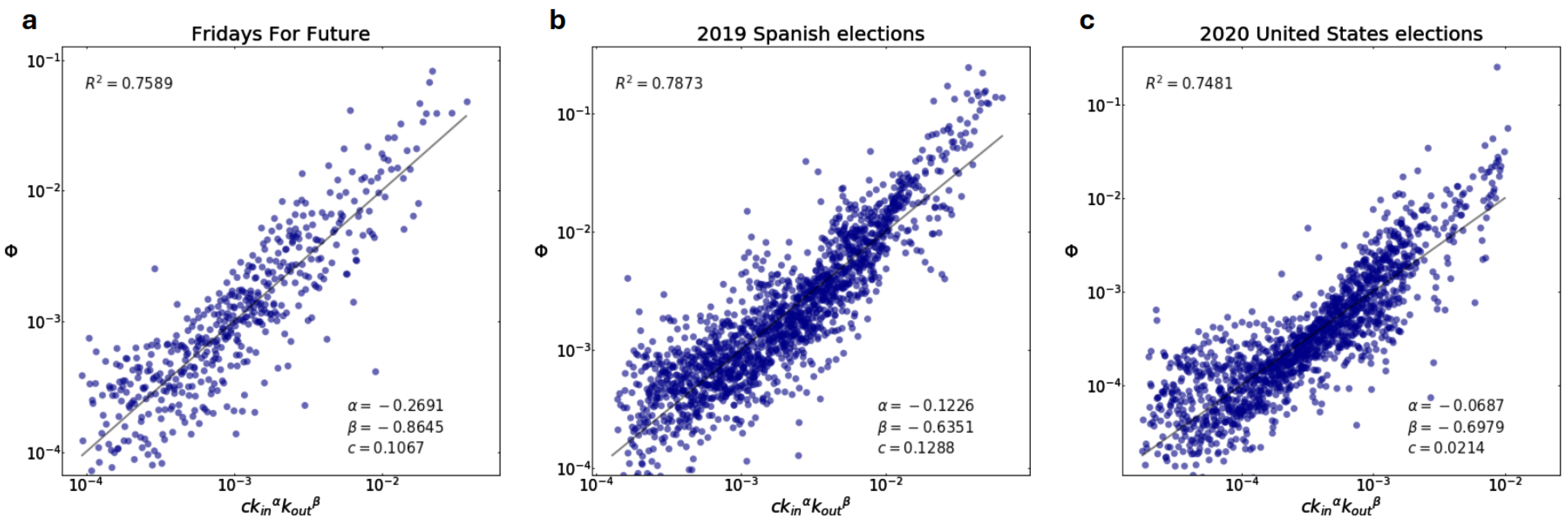
Appendix B. Predictive Ability of Different Diffusion Models

References
- Castells, M. Networks of Outrage And Hope: Social Movements in the Internet Age; John Wiley & Sons: London, UK, 2015. [Google Scholar]
- Shirky, C. Here Comes Everybody: The Power of Organizing Without Organizations; Alien Lane: New York, NY, USA, 2008. [Google Scholar]
- Bennett, W.L.; Segerberg, A. The Logic of Connective Action: Digital Media and the Personalization of Contentious Politics. Inf. Commun. Soc. 2012, 15, 739–768. [Google Scholar] [CrossRef]
- Meraz, S.; Papacharissi, Z. Networked Gatekeeping and Networked Framing on #Egypt. Int. J. Press. 2013, 18, 138–166. [Google Scholar]
- Lupia, A.; Sin, G. Which Public Goods Are Endangered? How Evolving Communication Technologies Affect the Logic of Collective Action. Public Choice 2003, 117, 315–331. [Google Scholar] [CrossRef]
- Duguay, S. “He has a way gayer Facebook than I do”: Investigating Sexual Identity Disclosure and Context Collapse on a Social Networking Site. New Media Soc. 2016, 18, 891–907. [Google Scholar] [CrossRef]
- Dynel, M. “I has seen image macros!” Advice Animals Memes as Visual-Verbal Jokes. Int. J. Commun. 2016, 10, 29. [Google Scholar]
- Eppler, M.J.; Mengis, J. The Concept of Information Overload: A Review of Literature from Organization Science, Accounting, Marketing, MIS, and Related Disciplines. In Kommunikationsmanagement im Wandel: Beiträge aus 10 Jahren Mcminstitute; Springer: Berlin, Germany, 2008; pp. 271–305. [Google Scholar]
- Chua, A.Y.K.; Chang, V. Information Overload: How it Affects Social Media Engagement and Well-Being. Comput. Hum. Behav. 2016, 65, 356–363. [Google Scholar]
- Dhir, A.; Kaur, P.; Chen, S. Social Media Fatigue and Information Overload: Understanding the Effects on User Behavior and Mental Health. Int. J. Inf. Manag. 2018, 40, 101–110. [Google Scholar]
- Arnold, M.; Goldschmitt, M.; Rigotti, T. Dealing with Information Overload: A Comprehensive Review. Front. Psychol. 2023, 14, 1122200. [Google Scholar] [CrossRef]
- Alfasi, Y. Attachment Style and Social Media Fatigue: The Role of Usage-Related Stressors, Self-Esteem, and Self-Concept Clarity. Cyberpsychology J. Psychosoc. Res. Cyberspace 2022, 16, 2. [Google Scholar] [CrossRef]
- Przybylski, A.K.; Murayama, K.; DeHaan, C.R.; Gladwell, V. Fear of Missing Out: A Cognitive and Emotional Analysis of Social Media Use. Comput. Hum. Behav. 2013, 29, 1841–1848. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, P.; Shi, L.; Gong, J. A Survey of Information Dissemination Model, Datasets, and Insight. Mathematics 2023, 11, 3707. [Google Scholar] [CrossRef]
- Zhang, X.; Akhter, S.; Nassani, A.A.; Haffar, M. Impact of News Overload on Social Media News Curation: Mediating Role of News Avoidance. Front. Psychol. 2022, 13, 865246. [Google Scholar] [CrossRef] [PubMed]
- Earle, M.; Hodson, G. News Media Impact on Sociopolitical Attitudes. PLoS ONE 2022, 17, e0264031. [Google Scholar] [CrossRef]
- Harlow, S.; Brown, D.K.; Salaverría, R.; García-Perdomo, V. Is the Whole World Watching? Building a Typology of Protest Coverage on Social Media from Around the World. Journal. Stud. 2020, 21, 1590–1608. [Google Scholar] [CrossRef]
- Borondo, J.; Morales, A.J.; Benito, R.M.; Losada, J.C. Multiple Leaders on a Multilayer Social Media. Chaos Solitons Fractals 2015, 72, 90–98. [Google Scholar] [CrossRef]
- Wang, Y.-Q.; Yang, X.-Y.; Han, Y.-L.; Wang, X.-A. Rumor Spreading Model with Trust Mechanism in Complex Social Networks. Commun. Theor. Phys. 2013, 59, 510. [Google Scholar] [CrossRef]
- Jin, F.; Dougherty, E.; Saraf, P.; Cao, Y.; Ramakrishnan, N. Epidemiological Modeling of News and Rumors on Twitter. In Proceedings of the 2013 International Conference on Advances in Social Networks Analysis and Mining, Niagara Falls, ON, Canada, 25–28 August 2013; pp. 739–744. [Google Scholar]
- Morales, A.J.; Borondo, J.; Losada, J.C.; Benito, R.M. Efficiency of Human Activity on Information Spreading on Twitter. Soc. Netw. 2014, 39, 1–11. [Google Scholar] [CrossRef]
- Goel, S.; Anderson, A.; Hofman, J.; Watts, D.J. The Structural Virality of Online Diffusion. Manag. Sci. 2016, 62, 180–196. [Google Scholar] [CrossRef]
- Weng, L.; Menczer, F.; Ahn, Y.-Y. Virality Prediction and Community Structure in Social Networks. Sci. Rep. 2013, 3, 1–6. [Google Scholar] [CrossRef]
- Bakshy, E.; Hofman, J.M.; Mason, W.A.; Watts, D.J. Everyone’s an Influencer: Quantifying Influence on Twitter. In Proceedings of the Fourth ACM International Conference on Web Search and Data Mining, Hong Kong, China, 9–12 February 2011; pp. 65–74. [Google Scholar]
- Centola, D. The Spread of Behavior in an Online Social Network Experiment. Science 2010, 329, 1194–1197. [Google Scholar] [CrossRef]
- Bawden, D.; Robinson, L. The Dark Side of Information: Overload, Anxiety and Other Paradoxes and Pathologies. J. Inf. Sci. 2009, 35, 180–191. [Google Scholar] [CrossRef]
- Roetzel, P.G. Information Overload in the Information Age: A Review of the Literature from Business Administration, Business Psychology, and Related Disciplines with a Bibliometric Approach and Framework Development. Bus. Res. 2019, 12, 479–522. [Google Scholar] [CrossRef]
- Barabási, A.-L. The Origin of Bursts and Heavy Tails in Human Dynamics. Nature 2005, 435, 207–211. [Google Scholar] [CrossRef]
- Iribarren, J.L.; Moro, E. Impact of Human Activity Patterns on the Dynamics of Information Diffusion. Phys. Rev. Lett. 2009, 103, 038702. [Google Scholar] [CrossRef]
- Akbarpour, M.; Jackson, M.O. Diffusion in Networks and the Virtue of Burstiness. Proc. Natl. Acad. Sci. USA 2018, 115, E6996–E7004. [Google Scholar] [CrossRef]
- Karsai, M.; Kivelä, M.; Pan, R.K.; Kaski, K.; Kertész, J.; Barabási, A.L.; Saramäki, J. Small but Slow World: How Network Topology and Burstiness Slow Down Spreading. Phys. Rev. E 2011, 83, 025102. [Google Scholar] [CrossRef]
- Pei, S.; Muchnik, L.; Tang, S.; Zheng, Z.; Makse, H.A. Exploring the Complex Pattern of Information Spreading in Online Blog Communities. PLoS ONE 2015, 10, e0126894. [Google Scholar] [CrossRef]
- Zhou, B.; Pei, S.; Muchnik, L.; Meng, X.; Xu, X.; Sela, A.; Havlin, S.; Stanley, H.E. Realistic Modelling of Information Spread Using Peer-to-Peer Diffusion Patterns. Nat. Hum. Behav. 2020, 4, 1198–1207. [Google Scholar]
- Barabási, A.-L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar]
- Newman, M.E.J. Power Laws, Pareto Distributions and Zipf’s Law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar]
- Cha, M.; Haddadi, H.; Benevenuto, F.; Gummadi, K. Measuring User Influence in Twitter: The Million Follower Fallacy. In Proceedings of the International AAAI Conference on Web and Social Media, Washington, DC, USA, 23–26 May 2010; Volume 4, pp. 10–17. [Google Scholar]
- Kwak, H.; Lee, C.; Park, H.; Moon, S. What Is Twitter, a Social Network or a News Media? In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 591–600. [Google Scholar]
- Alstott, J.; Bullmore, E.; Plenz, D. Powerlaw: A Python Package for Analysis of Heavy-Tailed Distributions. PLoS ONE 2014, 9, e85777. [Google Scholar] [CrossRef] [PubMed]
- Vuong, Q.H. Likelihood Ratio Tests for Model Selection and Non-Nested Hypotheses. Econom. J. Econom. Soc. 1989, 57, 307–333. [Google Scholar] [CrossRef]
- Anderson, D.; Burnham, K. Model Selection and Multi-Model Inference, 2nd ed.; Springer: New York, NY, USA, 2004; Volume 63, p. 10. [Google Scholar]
- Bollen, J.; Gonçalves, B.; Ruan, G.; Mao, H. Happiness Is Assortative in Online Social Networks. Artif. Life 2011, 17, 237–251. [Google Scholar] [CrossRef] [PubMed]
- Sweller, J. Cognitive Load During Problem Solving: Effects on Learning. Cogn. Sci. 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Hargittai, E.; Hsieh, Y.P. Succinct Survey Measures of Web-Use Skills. Soc. Sci. Comput. Rev. 2012, 30, 95–107. [Google Scholar] [CrossRef]
- Vosoughi, S.; Roy, D.; Aral, S. The Spread of True and False News Online. Science 2018, 359, 1146–1151. [Google Scholar] [CrossRef]
- Colleoni, E.; Rozza, A.; Arvidsson, A. Echo Chamber or Public Sphere? Predicting Political Orientation and Measuring Political Homophily in Twitter Using Big Data. J. Commun. 2014, 64, 317–332. [Google Scholar] [CrossRef]
- Friggeri, A.; Adamic, L.; Eckles, D.; Cheng, J. Rumor Cascades. In Proceedings of the International AAAI Conference on Web and Social Media, Ann Arbor, MI, USA, 1–4 June 2014; Volume 8, pp. 101–110. [Google Scholar]
- Cinelli, M.; Quattrociocchi, W.; Galeazzi, A.; Valensise, C.M.; Brugnoli, E.; Schmidt, A.L.; Zola, P.; Zollo, F.; Scala, A. The COVID-19 Social Media Infodemic. Sci. Rep. 2020, 10, 16598. [Google Scholar] [CrossRef]



| Case Study | # Links in the Followers Network | # Users in the Followers Network | # Weighted Links in the Retweet Network | # Users in the Retweet Network | Time Interval |
|---|---|---|---|---|---|
| Fridays for future | 2,041,083 | 44,541 | 9580 | 7958 | 24/09/20 09:00– 28/09/20 09:00 |
| 2019 Spanish elections | 48,928,270 | 233,503 | 537,715 | 152,170 | 08/11/19 00:00– 08/11/19 23:59 |
| 2020 United States elections | 93,892,405 | 358,001 | 59,101 | 46,838 | 01/11/20 00:00– 01/11/20 23:59 |
| Case Study | # Original Tweets | # Retweets | Time Interval of the Retweets Considered |
|---|---|---|---|
| Fridays for future | 3071 | 9580 | 24/09/20 09:00–28/09/20 09:00 |
| 2019 Spanish elections | 46,625 | 537,715 | 08/11/19 00:00–08/11/19 23:59 |
| 2020 United States elections | 10,974 | 59,101 | 01/11/20 00:00–01/11/20 23:59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atienza-Barthelemy, J.; Losada, J.C.; Benito, R.M. Modeling Information Diffusion on Social Media: The Role of the Saturation Effect. Mathematics 2025, 13, 963. https://doi.org/10.3390/math13060963
Atienza-Barthelemy J, Losada JC, Benito RM. Modeling Information Diffusion on Social Media: The Role of the Saturation Effect. Mathematics. 2025; 13(6):963. https://doi.org/10.3390/math13060963
Chicago/Turabian StyleAtienza-Barthelemy, Julia, Juan C. Losada, and Rosa M. Benito. 2025. "Modeling Information Diffusion on Social Media: The Role of the Saturation Effect" Mathematics 13, no. 6: 963. https://doi.org/10.3390/math13060963
APA StyleAtienza-Barthelemy, J., Losada, J. C., & Benito, R. M. (2025). Modeling Information Diffusion on Social Media: The Role of the Saturation Effect. Mathematics, 13(6), 963. https://doi.org/10.3390/math13060963








