Abstract
Network flow task management involves the efficient allocation and scheduling of data flow tasks within dynamic satellite networks, aiming to effectively address frequent changes in network topology and dynamic traffic fluctuations. Existing research primarily emphasizes traffic prediction and scheduling using spatiotemporal models and machine learning. However, these approaches often depend on extensive historical data for training, making real-time adaptation to rapidly changing network topologies and traffic patterns challenging in dynamic satellite environments. Additionally, their high computational complexity and slow convergence rates hinder their efficiency in large-scale networks. To address these issues, this paper proposes a collaborative optimization framework based on Coding Multi-Path Theory (CMPT). The framework utilizes a Nash bargaining game model to simulate resource competition among the different participants, ensuring fair resource distribution and load balancing. It also integrates real-time network state monitoring with optimization algorithms, within a multi-path scheduling strategy, enabling the dynamic selection of optimal transmission paths to accommodate frequent network topology changes and traffic variations. Experimental results indicate that the proposed method reduced resource allocation task execution time by at least 18.03% compared to traditional methods and enhanced task scheduling efficiency by at least 14.01%. Although CMPT exhibited a slightly higher task latency on certain small-scale datasets compared to some baseline algorithms, its performance remains exceptional in large-scale and high-dimensional scenarios.
MSC:
37N40; 68U35; 68M10
1. Introduction
Spatial Information Networks (SINs), including satellite platforms, ground stations, and other communication nodes, provide worldwide coverage and real-time information transmission services. Compared with traditional terrestrial communication systems, the advantages of satellite networks lie in their ability to efficiently and flexibly handle complex communication needs on a global scale, break through geographic constraints, and provide continuous and reliable communication safeguards in unexpected situations of extreme weather or natural disasters. Satellite networks will play an increasingly important role in the future development of 6G and next-generation communication technologies, and they will function alongside terrestrial networks to build a smarter and faster global communications infrastructure [1,2].
Although satellite information networks have demonstrated advantages in providing global coverage and real-time information transmission, there are still many challenges in adapting data transmission to rapidly changing network conditions in highly dynamic and uncertain environments [3]. Factors such as the high mobility of satellites, orbital changes, and fluctuations in the quality of communication links make routing design particularly complex [4]. Real-time sensing and adjustment of data transmission methods, to ensure efficient system operation and prevent resource wastage, have become core issues in current research. Furthermore, with the rapid advancement in multi-antenna satellite communication systems, effective calibration techniques for onboard wide-band RF antennas become critical for maintaining system accuracy and reliability [5]. Excessive resource waste not only diminishes a system’s overall effectiveness but may also lead to significant increases in operational costs and latency in critical tasks [6].
To address the challenges of resource allocation and task scheduling in highly dynamic and uncertain environments, researchers have primarily employed spatial-temporal models and machine learning methods for traffic prediction and scheduling. However, these approaches often rely on extensive historical data for training, making it difficult to adapt in real-time to frequent changes in network topology and traffic fluctuations. Additionally, their high computational complexity and slow convergence rates limit their efficiency in large-scale satellite networks. Excessive resource wastage not only diminishes the overall effectiveness of a system, but also leads to significant increases in operational costs and latency in critical tasks. Therefore, there is an urgent need for an innovative solution that can achieve maximum resource utilization and system stability in large-scale and high-dimensional environments.
This paper propose a novel adaptive dynamic resource allocation method for satellite networks, designed to maximize resource utilization and ensure system stability in large-scale and high-dimensional environments. Building on the limitations of existing approaches that rely heavily on historical data and face high computational demands, our method models the competitive interactions among network participants to achieve fair and efficient resource distribution. By continuously monitoring network conditions and dynamically adjusting resource allocations, the proposed framework effectively responds to frequent changes in network topology and fluctuating traffic demands. This strategy addresses real-time adaptability and resource optimization challenges, thereby minimizing resource wastage and enhancing satellite networks’ overall robustness and reliability.
In this paper, our main contributions are as follows:
- We propose a novel resource allocation framework based on cooperative game theory, to address the complex challenges of resource scarcity and interference constraints in satellite networks. This approach leverages Nash bargaining and Lagrangian multiplier methods to ensure efficient and fair resource distribution, effectively optimizing network performance in dynamic and competitive environments.
- We introduce an adaptive dynamic resource allocation method that combines network coding and multi-path transmission strategies. Supported by Software-Defined Networking (SDN) for domain partitioning, this method enhances the system’s adaptability and performance in highly dynamic and heterogeneous satellite network environments by efficiently balancing loads and minimizing latency.
- We propose a fair resource allocation strategy based on the Shapley value, integrating Pareto optimality and Nash equilibrium principles. This approach ensures global resource allocation optimality, achieving fairness and efficiency across the network, even in scenarios with fluctuating resource demands and varying network conditions.
- To validate the effectiveness of the proposed CMPT method, we conducted experiments on multiple satellite network simulation datasets using the Common-computing Simulation Tool Kit (CSTK) simulation platform. Our experiments, comparing CMPT with four baseline algorithms across four different satellite network datasets, demonstrated that CMPT outperformed existing methods in terms of resource allocation, computational complexity, and task scheduling efficiency.
2. Related Work
With the growing demand for efficient traffic scheduling and topology adjustment in satellite networks, existing research primarily encompasses protocol stack optimization, optimization algorithms, spatiotemporal models, machine learning, game theory, and multipath transmission. Although these methods have made progress in improving network latency, throughput, and resource utilization efficiency, they still face challenges such as insufficient adaptability, high computational complexity, and slow convergence rates in large-scale dynamic environments. Spatiotemporal models and machine learning rely heavily on extensive historical data, making real-time responses to rapidly changing network conditions difficult. Game theory and multipath transmission perform well for resource competition and network reliability, but still encounter high computational complexity and load-balancing issues in large-scale networks. Other approaches, such as congestion control, bandwidth allocation, and fault tolerance mechanisms, are effective in specific scenarios but must deal with the complexities and management overhead brought about by network interruptions, link failures, and rapidly changing demands in practical applications. Therefore, there is an urgent need for an innovative solution that can achieve maximum resource utilization and system stability in large-scale, high-dimensional environments, thereby comprehensively enhancing the performance and reliability of dynamic satellite networks.
2.1. Protocol Stack and Optimization Algorithms for Traffic Scheduling and Topology Adjustment
As the demand for efficient traffic scheduling and topology adjustment in satellite networks continues to grow, combining protocol stack optimization with optimization algorithms has proven to be an effective approach for enhancing network performance. Protocol stack optimization improves network latency and throughput by refining transport layer protocols and enabling multi-protocol cooperation, while optimization algorithms address resource allocation and network topology problems through mathematical modeling and problem-solving techniques. For instance, studies have demonstrated that modified transport layer control protocols, such as the Transmission Control Protocol (TCP), integrated with congestion control and traffic scheduling strategies, can significantly reduce data transmission latency and enhance throughput in high-latency environments [7,8,9]. In particular, Goswami and Shahane [8] highlighted how optimizing the TCP protocol effectively reduced latency and improved overall network performance. Similarly, network topology optimization methods based on graph theory and optimization algorithms, including integer and linear programming, have been widely applied in satellite networks to enhance resource allocation efficiency and minimize latency [10,11,12]. For example, Zhong et al. [10] demonstrated how linear programming techniques were employed to develop optimized resource allocation strategies. In addition, heuristic and metaheuristic algorithms, such as genetic algorithms and particle swarm optimization, have been incorporated to dynamically adjust resource allocation strategies, further reducing latency and improving network reliability [13,14,15]. For example, Mirmohseni et al. [15] described the design of novel congestion control algorithms to tackle challenges arising from link failures.
Despite these advancements, these methods often overlook the complex interactions between protocol layers. In dynamic environments, the performance of protocol stacks remains suboptimal, particularly under conditions of frequent topology changes and fluctuating traffic demands.
2.2. Spatiotemporal Models and Machine Learning for Traffic Prediction and Scheduling
To address the challenges of latency variability and bandwidth fluctuations in satellite networks, spatiotemporal models and machine-learning-based methods have become key research directions. Spatiotemporal models integrate the temporal and spatial characteristics of networks, enabling dynamic resource allocation adjustments to changing conditions. Machine learning approaches analyze historical data to predict future traffic demands, optimizing scheduling and resource management [16,17,18]. For instance, Liu et al. [16] employed spatiotemporal data fusion techniques to achieve precise traffic predictions, significantly enhancing resource allocation. Advanced techniques like deep learning and reinforcement learning have shown substantial improvements in network throughput and latency reduction. For example, Bhattacharyya et al. [19] demonstrated that reinforcement learning can dynamically optimize resource scheduling, greatly reducing latency. Similarly, Deep Neural Networks (DNN) and Long Short-Term Memory (LSTM) networks have been applied to model traffic fluctuations, enabling dynamic bandwidth allocation [20,21,22]. In [21], LSTM networks effectively captured traffic patterns, supporting real-time optimization. Reinforcement learning has also been used for real-time traffic distribution and scheduling, with [23] showcasing significant gains in network utilization through cross-path distribution.
Despite these advances, machine learning and spatiotemporal models heavily rely on historical data, limiting their real-time adaptability. Their generalization and responsiveness to sudden traffic changes remain critical challenges. Innovative approaches are needed to address these bottlenecks, ensuring both predictive accuracy and adaptability in dynamic satellite network environments.
2.3. Game Theory and Multipath Transmission for Network Resource Management
In satellite networks, in addition to protocol stack optimization, optimization algorithms, and machine learning approaches, game theory and multipath transmission techniques are widely utilized to enhance resource allocation and network reliability. Game-theoretic models typically simulate the interactions among multiple participants (e.g., satellites or users) to derive optimal resource allocation strategies [24,25]. For example, in [24], researchers developed a Nash-equilibrium-based model to address resource competition, achieving significant improvements in utilization efficiency and fairness. Such models effectively resolve resource conflicts in competitive environments, while optimizing overall network performance. Simultaneously, multipath transmission has emerged as a key technology for improving network fault tolerance. Multipath traffic scheduling algorithms mitigate the impact of single-path failures on performance by dynamically routing traffic through multiple paths [26,27,28]. For instance, in [26], a dynamic multipath routing algorithm was introduced, leveraging real-time network conditions to minimize packet loss and latency. Furthermore, multipath scheduling approaches actively select the optimal paths, to improve reliability and efficiency under varying network loads [29,30,31]. As an example, Zhang et al. [29] proposed a task-aware multipath scheduling framework that exploits path diversity, ensuring high reliability and reduced latency even in scenarios with significant traffic variability. These advancements collectively demonstrate the potential of game theory and multipath transmission in addressing the challenges of dynamic satellite network environments.
However, game theory and multipath transmission methods face challenges in large-scale networks, often suffering from high computational complexity and slow convergence speeds. Additionally, balancing load among multiple paths and ensuring efficient scheduling under rapid topology changes remain significant challenges for effective resource management.
2.4. Discussion on Unclassified Research Methods
Beyond the methods discussed above, additional research has explored alternative techniques to address traffic scheduling and resource allocation challenges in satellite networks. Studies on congestion control and bandwidth allocation have leveraged intelligent algorithms to dynamically reallocate resources, reducing congestion and enhancing data transmission efficiency [32,33,34]. For example, Usama et al. [32] introduced a congestion-aware bandwidth management system that reallocates resources in real time based on traffic conditions, significantly alleviating peak-load congestion. Dynamic bandwidth allocation methods emphasize load balancing to optimize throughput and reduce latency by adapting resource distribution [35,36,37]. For instance, Wang et al. [35] proposed a machine-learning-based approach to predict bandwidth demands and optimize node-level allocation, achieving improved efficiency and latency reduction. Fault tolerance mechanisms address network interruptions and link failures through redundancy and proactive designs to ensure seamless traffic scheduling [38,39,40]. Peng et al. [38] developed a proactive redundancy algorithm that pre-computes alternative paths, enabling uninterrupted rerouting and enhancing network resilience. By transforming the non-linear differential equations governing the system’s motion into a non-linear programming problem through direct collocation, they minimized the link rates during optimal re-orientations.
While these methods provide effective solutions, they face limitations for practical applications. Handling network interruptions often requires additional resources, increasing complexity and management overhead, while load-balancing strategies struggle to adapt to sudden demand fluctuations, limiting their real-time responsiveness.
Existing research on satellite network resource allocation and traffic scheduling has provided valuable insights but remains constrained by challenges such as poor adaptability and high computational complexity in dynamic environments. These limitations highlight the need for a paradigm shift in addressing resource competition, real-time scheduling, and network reliability. To overcome these gaps, this paper rethinks the problem from a collaborative optimization perspective, focusing on balancing fairness and efficiency, while dynamically adapting to fluctuating network conditions. By leveraging cooperative strategies and iterative refinement based on real-time feedback, this study seeks to enhance resource allocation and scheduling decisions, ensuring scalability and robustness in complex satellite network environments.
3. Problem Definition and Formulation
3.1. System Model
The proposed satellite network comprises three primary components: satellite nodes, ground stations, and user terminals. Each satellite node i is characterized by its resource vector , where denotes the computational capacity, represents the available bandwidth, and signifies the storage capacity.
The network topology is encapsulated by the adjacency matrix , where each element defines the connection attributes between satellite nodes i and j. Specifically, denotes the bandwidth and denotes the latency between node i and node j, respectively.
The satellite network employs a SDN controller to enable centralized management and dynamic resource scheduling. Acting as the global coordination center, the SDN controller continuously monitors the resource status of satellite nodes—including the computing capacity , bandwidth , and storage —as well as link parameters such as transmission delay and bandwidth , along with task queue information. Its core functions encompass dynamic domain clustering, multi-path optimization, and resource reallocation. Specifically, each satellite node periodically reports its local resource utilization, link reliability (Equation (32)), and task execution status to the SDN controller via dedicated control channels. The controller aggregates this global information and updates the real-time network topology graph . Based on the current network state, the controller performs dynamic domain clustering by optimizing the utility function as defined in Equation (30), determining the affiliation of nodes to logical domains . The clustering process minimizes the weighted objective to balance intra-domain link reliability and overall network overhead, ensuring proximity-based cooperation among nodes, while reducing signaling costs. Subsequently, for each task j, the controller dynamically selects the optimal path from the available path set based on real-time link conditions and node workloads, considering the path reliability (Equation (33)). The path assignment is then disseminated to the corresponding satellite nodes through the binary variable (Equation (2)). During task execution, if a resource overload () or link failures are detected, the controller triggers Nash bargaining models (Algorithm 1) and Lagrangian optimization (Algorithm 2) to adjust the resource allocation and update the task matrix T, ensuring all system constraints (Equations (3)–(9)) are satisfied. Through this mechanism, the SDN controller achieves real-time adaptation of the network topology and efficient resource scheduling, significantly enhancing the robustness and task execution efficiency of the satellite network in dynamic environments.
Data transmission initiates from user terminals, traverses through ground stations, and culminates in task requests directed to the satellite nodes. Task allocation is modeled by the matrix , where represents the quantity of resources allocated to task j by satellite node i. To ensure the physical realizability of resource allocation variables, this paper imposes the non-negativity assumption:
A multi-path scheduling strategy facilitates parallel data transmission across multiple pathways, mitigating packet loss and reducing latency. Formally, for each task j, a possible path represents a potential transmission route that can be used to transmit data from the source to the destination in the network. The set consists of all such feasible paths that can support the transmission of task j’s data under the current network conditions. Here, k denotes the path index within the set . Each path is characterized by various network parameters, including but not limited to bandwidth, latency, and network load. These parameters are critical in determining the suitability of a path for transmitting the task data.
The number of available paths for task j is denoted by k, and the selection of specific paths is modeled using binary variables . The binary variable is defined as
where represents a potential transmission route that can be used to transmit data from the source to the destination in the network.
Thus, the set of possible paths encompasses all paths that meet the network’s resource requirements (e.g., available bandwidth, latency tolerance, etc.) and are considered viable for transmission at any given time. The multi-path scheduling strategy utilizes these possible paths to dynamically allocate transmission tasks across multiple routes, helping to mitigate issues such as packet loss, congestion, and latency, thereby improving the overall network efficiency.
Resource allocation and scheduling are thus formulated as an optimization problem that assigns tasks to paths, while considering resource constraints and network performance metrics.
Resource competition among satellite nodes is modeled using game-theoretic principles. Each satellite node i possesses a utility function that depends on its resource allocation strategy and its interactions with other nodes. The objective for each node is to determine the optimal strategy that maximizes , leading to a game equilibrium (e.g., Nash equilibrium) that guides an equitable and efficient resource distribution. This equilibrium ensures optimal resource utilization and load balancing across the network.
Formally, for each satellite node i, the resource vector is , and the resource demand for each task j is . Task j necessitates data transmission through the network, with path selection governed by the multi-path scheduling strategy. Due to the inherent dynamics in network topology and traffic loads, resource allocation strategies must be adaptable in real time, to optimize network utility.
3.2. Constraints
In the optimization of resource allocation and task scheduling in satellite networks, several constraints must be considered to ensure the feasibility and practicality of the optimization solutions. These constraints are classified into resource constraints, task constraints, latency constraints, computational complexity constraints, path selection constraints, and connectivity constraints, to account for the practical needs and limitations in the optimization process.
3.2.1. Resource Constraints
Resource constraints reflect the limitations of resources at each node in the satellite network. In each time period, the total resource usage at a satellite node must not exceed its maximum resource capacity. For each satellite node i, its available resources must satisfy the following constraints:
where represents the resource allocation for task j at node i, and is the maximum resource capacity of satellite node i. This constraint ensures that the resources at each satellite node are not overloaded, preventing excessive resource allocation and maintaining network stability.
3.2.2. Task Constraints
Each task j must be completed within a certain time period, and the total resource demand for the task cannot exceed the total available resources of the satellite nodes. For task j, the total resource demand must satisfy the following condition:
where is the total resource requirement for task j. This constraint ensures that the resource requirements for each task are fully met and that there is no resource shortage during the allocation process.
3.2.3. Latency Constraints
To ensure real-time performance and timely completion of tasks, latency constraints cannot be ignored. The transmission latency for each task j must be less than or equal to the maximum acceptable latency for the task:
where represents the transmission latency for task j, and is the maximum acceptable latency for each task. This constraint ensures that the latency for each task does not exceed the acceptable range, maintaining the system’s efficiency and real-time responsiveness. In this study, the maximum acceptable latency is assumed to be the same for all tasks, simplifying the modeling process and ensuring system uniformity.
3.2.4. Computational Complexity Constraints
During the task allocation process, the change in computational complexity should be maintained within an acceptable range, to prevent an excessive computational burden. Specifically, for each task j and satellite node i, the change in computational complexity must adhere to the following constraint:
where and represent the original and adjusted resource allocations for task j at satellite node i, and is the maximum allowable change in computational complexity. This constraint ensures that the variation in computational resources during task scheduling does not exceed a certain threshold, helping to avoid an excessive computational burden and improving system stability and responsiveness.
3.2.5. Path Selection Constraints
In multi-path transmission, the path selection for each task must satisfy certain constraints to ensure efficient data transmission across the network. For each task j, the selected transmission path must adhere to the following constraint:
where is the set of available paths, and is the transmission path for task j. This constraint ensures that each task selects a valid transmission path, avoiding inconsistencies in path selection and facilitating path optimization and load balancing.
3.2.6. Connectivity Constraints
To ensure reliable data transmission and successful task completion, the nodes in the satellite network must maintain proper connectivity. For each task j, it must be guaranteed that a reachable path exists between its source node and destination node. This constraint can be expressed as
where and represent the source and destination nodes of task j, and represents the network graph, ensuring that a valid path exists between the source and destination nodes for each task.
3.2.7. Coupling Constraints Between Resource Allocation and Path Selection
To ensure logical consistency between satellite node resource allocation and path selection strategies, this paper introduces the following coupling constraint:
where denotes the indicator function that equals 1 if satellite node i belongs to path of task j, and 0 otherwise. represents the total available resource capacity of satellite node i. This constraint ensures system validity through dual mechanisms: First, resource allocation to node i is permitted only when i lies on an active path for task j, ensuring path–resource topological alignment. Meanwhile, the term enforces node capacity limits, while linearly coupling the resource allocation scale with path decisions via , preventing over-subscription and maintaining operational stability under dynamic conditions.
To facilitate a comprehensive understanding of the system model, we summarize the key variables and parameters in Table 1 and Table 2. This table provides detailed definitions and units for each variable, ensuring clarity and consistency throughout the analysis.

Table 1.
Variables defined in scenario.

Table 2.
Parameters List.
3.3. Problem Formulation and Objective Function
This section formulates the resource allocation and task scheduling problem as a multi-objective optimization problem in satellite networks. The goal is to maximize the total resource allocation of tasks across satellite nodes to enhance the network throughput, ensuring efficient data transmission within the network; simultaneously, by optimizing resource allocation and path selection, minimize task transmission latency to ensure timely completion of tasks; and reduce computational complexity by controlling the extent of resource adjustments, avoiding excessive computational burdens, and thereby improving system responsiveness, stability, and real-time performance. The following explains each part of the objective function and the meaning of the variables.
Network throughput represents the total amount of data successfully transmitted within the network, which depends on the resources allocated to each task at each satellite node. Let denote the resources allocated to task j at satellite node i. The network throughput is expressed as , where n is the number of satellite nodes, and m is the number of tasks. By maximizing this sum, the optimization goal is to increase the total data transmission, thereby improving the network throughput.
Computational complexity measures the computational load during the resource allocation process. Frequent adjustments in resource allocation lead to a higher computational complexity. This is quantified by the difference between the original resource allocation and the adjusted allocation , expressed as . The total transmission latency D for all tasks should be minimized, where represents the transmission latency for task j. The total latency can be formulated as .
The optimization problem aims to maximize network throughput, while minimizing both computational complexity and transmission latency. This is achieved by optimizing resource allocation and task scheduling to enhance the overall transmission capacity, reduce the computational load, and ensure timely task completion. The objective function is formulated as
s.t.
where , , and are weighting factors balancing the importance of throughput, latency, and computational complexity, respectively. represents all combinations of resource allocation, task scheduling, and path selection that satisfy the constraints.
Specifically, the definition of is
Here, represents the task–resource allocation matrix, represents the resource constraints at each satellite node, and represents the transmission path for each task.
For the variables in the objective function, represents the amount of resources allocated to task j at satellite node i. By maximizing the sum of resource allocations for all tasks at all nodes, i.e., , we aim to increase the overall throughput of the network (i.e., the total amount of data transmitted). The term quantifies the computational complexity due to resource allocation adjustments, while represents the total transmission latency across all tasks.
Theorem 1.
Proof.
We prove that the proposed optimization problem is NP-hard by reducing a well-known NP-hard problem, the Multipath Shortest Path Problem (MSPP), to our resource allocation and task scheduling problem.
The MSPP seeks to find k disjoint paths from source s to target t in a given directed graph , minimizing the total cost, defined as
where represents the cost associated with each edge in path . The total cost is the sum of individual edge costs over all selected paths.
The optimization problem for the MSPP can then be formulated as
s.t.
To demonstrate that our resource allocation and task scheduling problem is at least as hard as the MSPP, we map each path cost in the MSPP to the resource allocation cost in our model. We define the resource allocation decision variable for task j at node i and introduce a cost function for resource utilization:
where represents the cost of assigning resources at node i for task j. This function directly parallels the MSPP cost function, establishing an equivalence.
Since the MSPP is known to be NP-hard, and our problem generalizes the MSPP by introducing resource allocation dependencies, our problem is at least NP-hard. □
4. Methodology
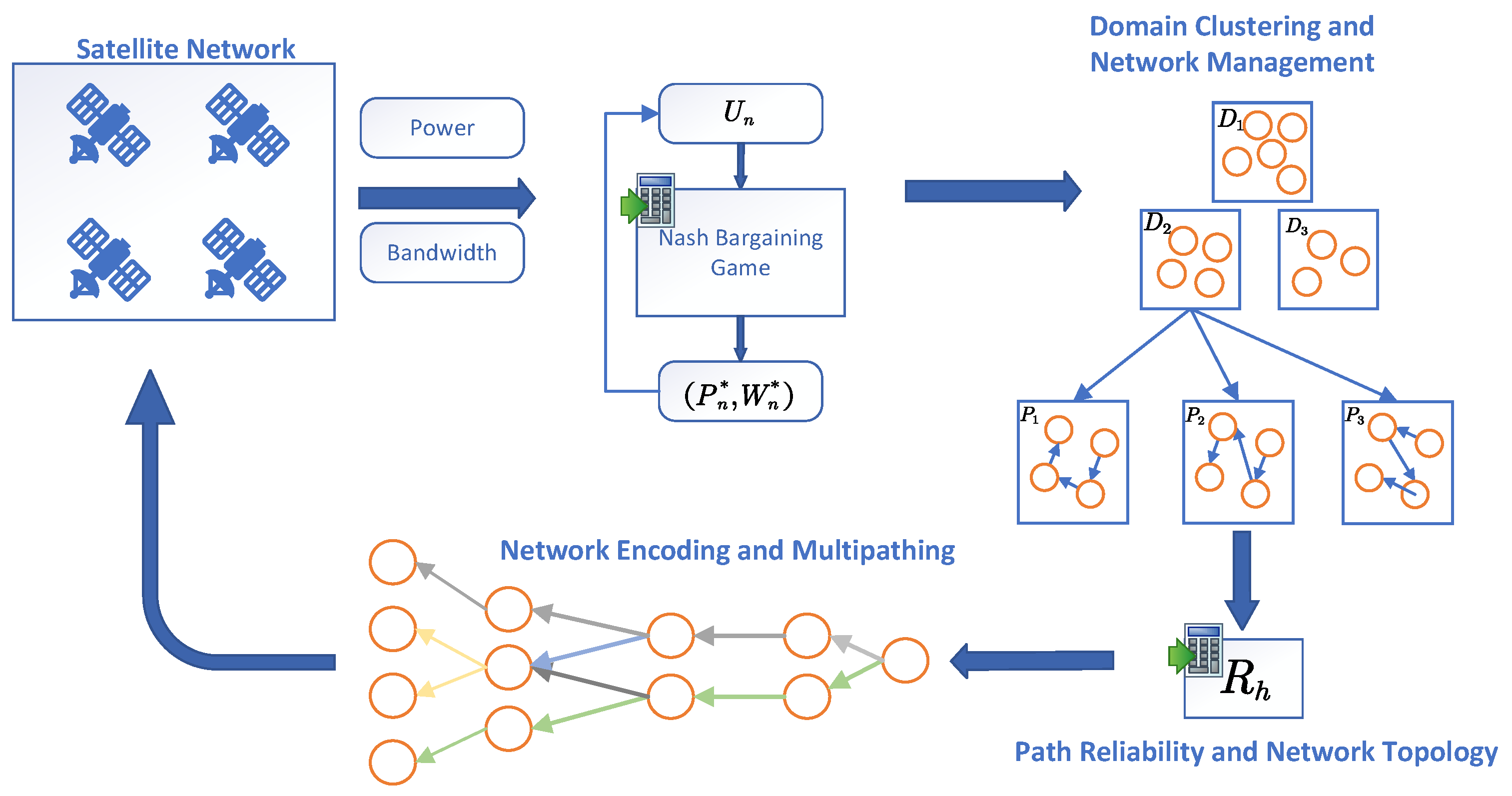
To address resource competition issues, the low allocation efficiency in satellite networks, and the lack of adaptability and real-time performance in dynamic environments, this paper proposes the Coding Multi-Path Theory (CMPT) method. CMPT employs a game-theoretic model with Nash bargaining mechanisms to simulate resource competition among satellites and users, ensuring efficient and fair resource distribution. It leverages the Lagrangian multiplier method to optimize resource allocation, while satisfying multiple constraints such as bandwidth, power, and interference, thereby achieving multi-path load balancing. Additionally, CMPT incorporates a multi-path scheduling strategy based on real-time network state monitoring to dynamically select optimal transmission paths, reducing packet loss and latency, and enhancing network reliability. By integrating Random Linear Network Coding (RLNC) and Software-Defined Networking (SDN)-based domain clustering, CMPT ensures robust data transmission and minimizes network control overhead. The proposed CMPT framework is illustrated in Figure 1, outlining the key steps, from dynamic network state monitoring, game-theoretic resource allocation and load balancing, and multi-path scheduling based on real-time conditions, to the execution of optimized scheduling and resource allocation decisions.
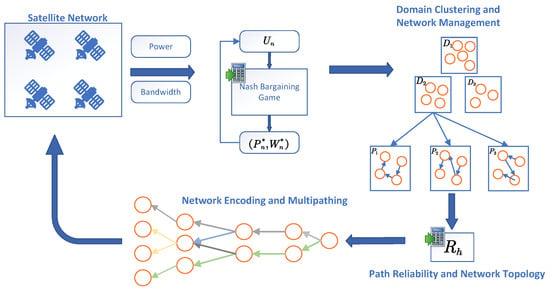
Figure 1.
Schematic diagram of main conception of CMPT.
4.1. Cooperative Resource Allocation Method Based on Nash Bargaining Game and Lagrangian Optimization
In satellite networks, due to the interdependence between nodes (satellites, ground stations, and user terminals) and the dynamic changes in the network environment, efficiently allocating limited resources (such as bandwidth and power) to optimize overall system performance becomes a critical issue. Traditional resource allocation methods often assume that nodes make independent decisions, but this non-cooperative strategy tends to lead to suboptimal global outcomes, resembling the “prisoner’s dilemma” in game theory. To overcome this problem, we propose a cooperative resource allocation model based on game theory, aiming to optimize resource configuration in cognitive satellite networks, particularly under resource constraints and interference limitations.
4.1.1. Definitions
First, we define the relevant concepts in the game model to mathematically model the resource allocation process:
- Network topology: Let the satellite network consist of N satellite nodes and M ground station nodes. Each node has certain resource demands and transmission capabilities.
- Utility function: For each node n, its utility function reflects the relationship between the resources allocated to the node and its performance. The utility function maximizes the node’s throughput, minimizes latency and energy consumption, and considers various resource constraints.
- Resource allocation: In the process of resource allocation, the power allocation and bandwidth allocation are distributed among the nodes based on the strategies defined in the game model.
- Cooperative game: Each node engages in cooperative behavior by sharing information and coordinating strategies to optimize the resource allocation of the overall system. This cooperative game facilitates information sharing and collaboration among nodes, aiming to enhance the overall utility.
4.1.2. Assumptions
In constructing the model, we make the following assumptions to simplify the analysis and ensure the feasibility of the resource allocation framework:
Assumption 1
(Information sharing). All nodes can share sufficient information, including utility functions, resource allocations, and environmental states. Specifically, each node’s utility function is known to all, and each node can observe the network’s current state, including interference levels and channel conditions .
This assumption simplifies the modeling process and ensures that the Nash bargaining solution can be computed globally. However, in large-scale satellite networks, full information sharing may not be realistic, due to communication delays and overhead. This implies potential scalability challenges when the network grows.
Assumption 2
(Interference model). The interference experienced by node n from node m is given by
where is the power allocated to node m, is the channel gain between nodes n and m, and is the distance between them.
This assumption models interference as distance-based attenuation, which is practical and widely used. It enables analytical tractability, but neglects complex factors like atmospheric conditions, multi-path fading, or directional antennas. This may lead to inaccuracies in environments with strong physical dynamics or non-line-of-sight scenarios.
Assumption 3.
The utility function of each node n incorporates the following interference:
where is a function depending on the power, bandwidth, and interference.
By explicitly modeling interference in the utility function, this assumption ensures that the resource allocation considers the mutual impact between nodes. This reflects realistic network competition but also increases model complexity. Any deviation from the assumed interference model could directly affect the fairness and efficiency of the Nash bargaining solution.
Assumption 4
(Bounded Rationality and Limited Knowledge). Satellite nodes and user terminals operate under bounded rationality, possessing limited knowledge about global channel states and external interference conditions. Each node makes decisions based on estimated local channel gains and interference levels , where estimation errors are bounded within known margins and , respectively. Nodes periodically communicate these estimated values to the SDN controller, which aggregates and utilizes this information in Nash bargaining equilibrium computations.
Based on Assumptions 3 and 4, we incorporate bounded rationality and limited knowledge, enhancing the realism and applicability of the proposed model, and enabling the Nash bargaining equilibrium to better reflect network behaviors under realistic operational conditions. Consequently, this refinement provides critical insights into equilibrium stability and robustness against channel variability and external interference, addressing key considerations for practical deployment scenarios.
4.1.3. Dynamic Adjustment Mechanism Based on Game Model
In this study, we adopt the Nash Bargaining Game (NBG) model for resource allocation in satellite networks, due to its ability to ensure fairness, adaptability, and efficiency in dynamic environments. Unlike traditional non-cooperative game models, which may lead to suboptimal global outcomes due to selfish decision-making by individual nodes, the NBG model guarantees a Pareto-optimal solution, while ensuring that each participant receives a utility greater than their disagreement point, thereby preventing unfair allocations. Additionally, NBG facilitates dynamic resource allocation by allowing adjustments in response to real-time changes in network topology, ensuring robustness under fluctuating resource constraints. From an optimization perspective, the convexity of the utility function within the NBG framework enables efficient problem-solving using Lagrangian multipliers and subgradient methods, leading to a globally optimal resource distribution. Under the assumptions stated above—including Assumption 4 regarding channel variability, external interference, and limited player knowledge—the Nash bargaining solution is shown to be stable and yields a fair and efficient resource allocation. In scenarios where these factors deviate significantly, adjustments to the disagreement point or utility estimation may be necessary. Given these advantages, the NBG model is particularly well-suited for our proposed collaborative multi-path resource allocation framework, providing a balance between fairness, efficiency, and computational feasibility in large-scale satellite networks.
Let there be K participants, where each node n’s utility function satisfies the following conditions:
- Individual rationality: For each node n, its utility cannot be lower than some minimum utility , i.e., .
- Feasibility: The solution to the utility function must lie within the utility space U.
- Pareto optimality: The resource allocation is Pareto optimal, meaning no node can increase its utility without making others worse off.
In the Nash bargaining game, the optimal solution can be obtained by maximizing the utility difference:
This formula maximizes the utility difference for each node, to ensure optimal resource allocation.
To further refine the resource allocation process, we introduce the following lemmas and theorems to support the mathematical derivation of our approach.
Lemma 1.
If the utility function for each node is concave with respect to resource allocation constraints, then the overall utility maximization problem is a convex optimization problem.
Proof.
The utility function of each node typically depends on the allocated power and bandwidth . To account for differences in satellite capacities, we normalize the utility by the total available resource capacity . Specifically, the normalized utility function is given as follows:
where represents the channel gain, is the power allocated to node n at frequency f and time slot t, and denotes the resource availability.
To determine the concavity of , we compute the second-order derivative of with respect to :
Since this second-order derivative is always non-positive, is a concave function with respect to .
Similarly, if is also concave with respect to (which is typically the case for resource allocation problems involving Shannon capacity-based utility functions), then each node’s utility function is concave.
Now, considering the overall utility maximization problem,
Since the sum of concave functions remains concave, and as the constraints are linear, the optimization problem remains a convex optimization problem. Thus, it can be efficiently solved using standard convex optimization methods. □
Theorem 2.
Given the interference constraints and power limitations, the system’s utility can be optimized using the Nash bargaining solution in the game, and the utility of each node will not be lower than its minimum utility.
Proof.
First, we assume that the total utility of the system is the sum of the utilities of all nodes. Each node n’s utility function is given by
According to Nash bargaining game theory, the total utility needs to be maximized, i.e., solving the following maximization problem to obtain the optimal solution:
This problem has constraints on power and bandwidth maximums (i.e., and ). By introducing Lagrange multipliers, we can transform this problem into a dual problem involving power and bandwidth constraints, as well as maximizing the utility function.
Consider the following optimization problem:
The Lagrangian function (25) converts the constrained optimization problem (24) into an unconstrained form by introducing dual variables and . Here, and penalize violations of the total power and bandwidth constraints.
By optimizing the Lagrange multipliers, we can find the optimal power and bandwidth allocation, proving that the game process can maximize the system’s total utility, while satisfying the minimum utility constraints of each node. □
To achieve a fair and efficient resource distribution among satellite nodes, the proposed CMPT framework integrates a Nash Bargaining Game model that simulates the resource competition between satellites and users. The detailed implementation of this game-theoretic resource allocation process is presented in Algorithm 1.
| Algorithm 1 Nash Bargaining Game for Resource Allocation (NBGRA) |
|
The algorithm input includes the number of satellite nodes N, the number of ground station nodes M, channel gains , power limits , and bandwidth limits , while the output consists of each satellite node’s optimal resource allocation . For each node n, the utility function is calculated based on power, bandwidth, and interference (Lines 1–2). Subsequently, for each time slot t and frequency f, the utility value in the current state is computed according to the defined utility function (Lines 3–5). After traversing all time slots and frequencies, the optimal resource allocation scheme is calculated based on the Nash bargaining solution formula (Line 8). Finally, each node’s optimal power and bandwidth allocation results are returned (Line 10).
Theorem 3.
By updating the Lagrange multipliers using the subgradient method, we can iteratively approach the optimal resource allocation strategy.
Proof.
In the game process, we need to optimize the Lagrangian function. The Lagrangian function is as follows:
where and are the Lagrange multipliers corresponding to the power and bandwidth constraints.
To solve this problem, we use the subgradient method to update the Lagrange multipliers. Specifically, in each iteration, we update the Lagrange multipliers based on the partial derivatives of the utility function with respect to power and bandwidth:
where is the learning rate, which controls the step size of the update. After each update, we can gradually converge to the optimal solution using the subgradient method, thereby obtaining the optimal resource allocation strategy. □
To further optimize resource allocation and ensure optimal power and bandwidth configurations under multiple constraints, we introduce an iterative resource allocation algorithm utilizing the Lagrangian multiplier method. The detailed implementation of this optimization process is presented in Algorithm 2.
| Algorithm 2 Iterative Resource Allocation Using Lagrange Multipliers (IRA-LM) |
|
The algorithm input includes the initial power and bandwidth allocation , and the output consists of the optimal power allocation and bandwidth allocation for each node. Initialize the Lagrange multipliers and (Line 1). Until the convergence condition is met, continuously perform the following steps (Line 2): Update the Lagrange multipliers based on predefined rules (line 3), then adjust the power and bandwidth allocations to optimize resource configuration (Line 4). Next, evaluate whether the current power and bandwidth allocations have reached the convergence criteria (Line 5). When the convergence condition is satisfied, terminate the iteration process and return the optimized power and bandwidth allocation results (Line 7).
4.2. Domain Clustering Based on Multi-Path Transmission
In satellite network resource allocation and task scheduling optimization, traditional methods often overlook the dynamic nature of the network topology and the complex interactions between nodes. Existing optimization methods mainly focus on static models or single-path resource allocation, lacking in-depth consideration of dynamic changes in network topology, node-to-node game behaviors, and multi-path transmission strategies. Therefore, this paper proposes an optimized method based on Network Coding (NC) and Multi-Path Transmission Strategies, and incorporates game theory and cluster head election techniques for improved performance, addressing the inadequacies of traditional methods in dynamic environments.
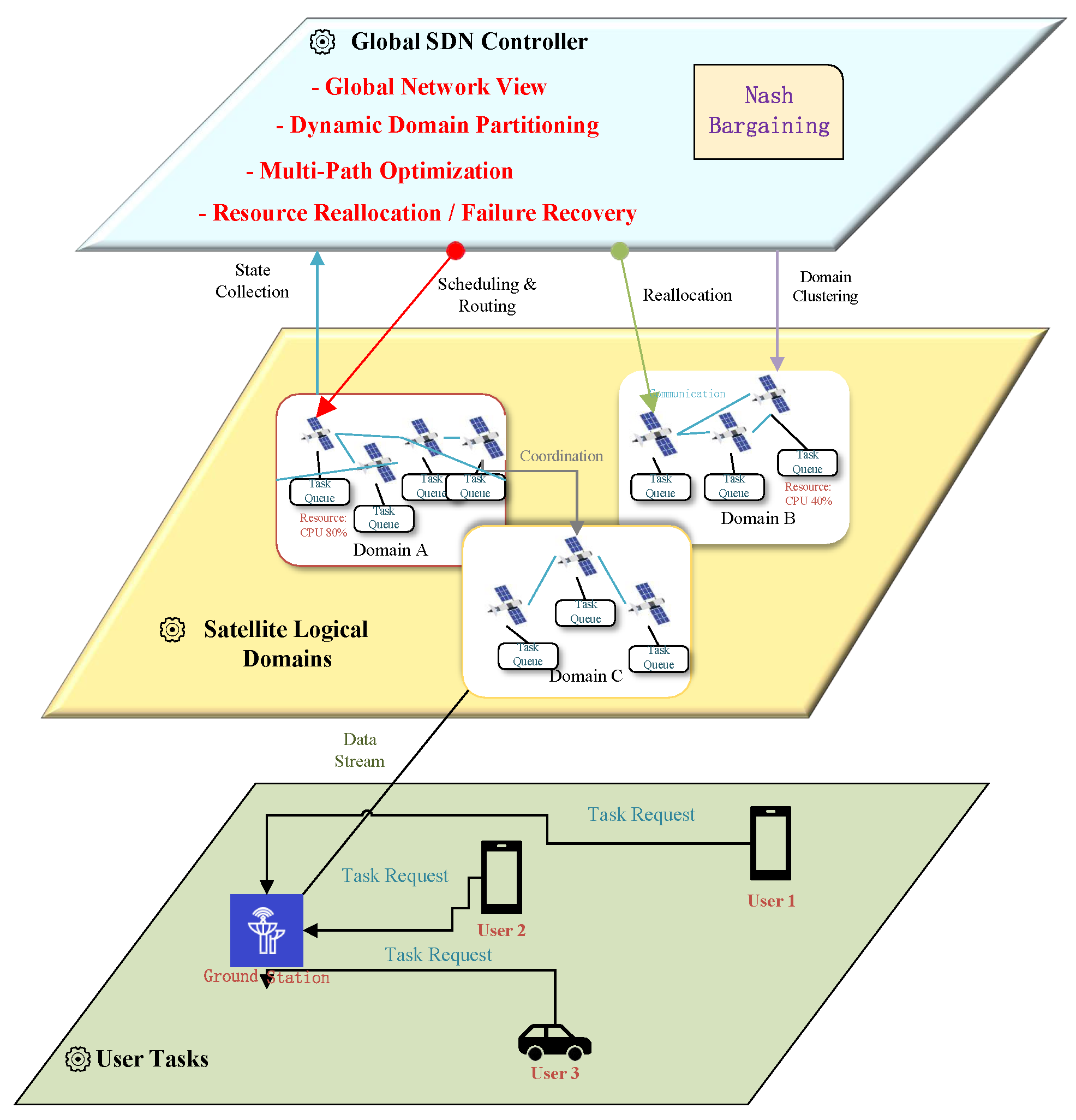
The Figure 2 illustrates the SDN-based domain clustering and collaborative scheduling framework for large-scale satellite networks. The global SDN controller gathers real-time state information from satellite nodes, performs dynamic domain partitioning, and optimizes multi-path scheduling. By integrating Nash bargaining game models and resource reallocation mechanisms, the framework ensures efficient resource utilization, fair task allocation, and rapid failure recovery. Tasks originating from ground users are distributed across multiple satellite logical domains, enhancing load balancing and system robustness in highly dynamic network environments.
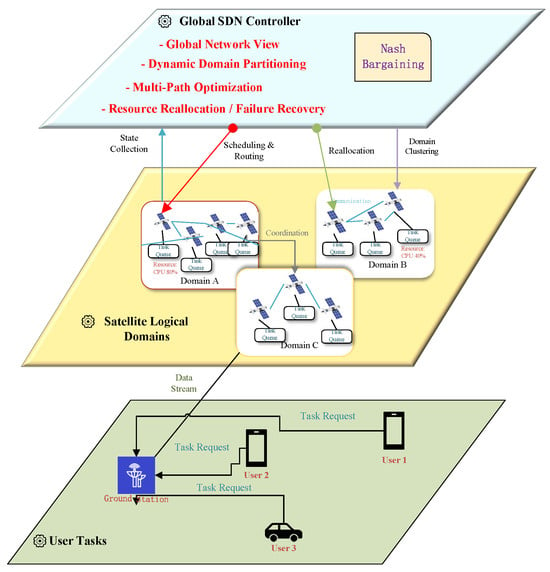
Figure 2.
SDN-based domain clustering and collaborative scheduling framework.
4.2.1. Domain Clustering and Network Management
In large-scale satellite networks, effectively managing resources and reducing network overhead is a critical problem. Existing methods often ignore changes in network topology and interdependencies between nodes, making them ill-suited for dynamic network environments. To address these challenges, our approach adopts an SDN-based domain clustering strategy. SDN enables centralized control and dynamic management, which is crucial for satellite networks characterized by frequently changing topologies and unstable connections. By partitioning the network into multiple logical domains (Domain Clusters, DCs), the SDN controller can obtain a global view of the network state, perform real-time resource scheduling, and optimize path selection. This centralized management significantly reduces the network control overhead, improves response times, and enhances overall network stability, while also facilitating rapid detection and mitigation of network anomalies. Accordingly, this paper proposes a domain clustering scheme based on a hierarchical control mechanism (SDN), which divides the satellite network into multiple logical domains, where the nodes within each domain coordinate and communicate with each other to efficiently manage inter-node communication and further reduce the control overhead.
Suppose there are N satellite nodes in the network, and each node can choose to join a different domain , where the link reliability represents the reliability of the link between nodes . This paper introduces a weighted objective function to optimize the node assignment strategy, to maximize the network’s reliability and overhead balance:
where R is the path reliability, is the total network overhead, is the maximum overhead standard, and is the weighting factor.
Regarding a performance comparison with other hierarchical clustering mechanisms, such as federated-learning-based adaptive clustering for resource allocation, our study specifically addresses the challenges of dynamically unstable network connections. Federated learning methods typically rely on stable communication links for consistent model aggregation and convergence. In our dynamic satellite network scenario, where connections are frequently disrupted, federated learning may suffer from discontinuous model updates, leading to unstable training outcomes and poor convergence. Additionally, the inherent lack of explainability in federated learning models further complicates real-time fault diagnosis and adjustment. In contrast, the SDN-based domain clustering approach leverages centralized control and real-time network state monitoring, making it more robust and efficient for resource allocation in such environments.
In the domain clustering process, the utility function of each node is used to describe its performance within the selected domain. For node i belonging to domain , the utility function can be defined as
where is the distance from node i to the center of its assigned domain, is the adjustment factor, and is the link reliability between node i and other nodes j in the domain. This utility function considers both the node’s distance and link reliability.
Theorem 4.
In dynamic satellite networks, the hierarchical control-based domain clustering method can effectively improve network reliability and performance in the context of multi-path transmission and cluster head election.
Proof.
To prove this theorem, we first calculate the utility function for each node i and optimize the node assignment according to the objective function. By introducing a weighted mechanism for the distance between nodes, we ensure that each node is assigned to the same domain as its neighboring nodes, thus reducing the control overhead across the entire network. Furthermore, through numerical simulations, we validate that this domain clustering method improves network reliability. Assume that there are N nodes in the network, and the reliability of each node is . After the domain division, the final reliability is given by the following formula:
The optimal network reliability is achieved by adjusting the weighting factor and the path assignment strategy. □
4.2.2. Network Topology and Path Reliability
Although the domain clustering method effectively improves network reliability, path selection randomness still exists, especially when the link reliability is unstable. Traditional methods often overlook the coupling effects between links. Therefore, accurately evaluating path reliability and making reasonable path selection decisions becomes the next key problem to address.
To this end, we introduce the conventional reliability and irregular reliability of the links, to model the link states. The link reliability considers the weighted combination of historical data and the current state:
where is the adjustment factor, and and represent the conventional and irregular reliability, respectively.
The path reliability is then represented as the product of the reliabilities of all links in the path:
Theorem 5.
Given the link reliability model, the reliability of a path is the product of the reliabilities of all the links in the path, and path selection can achieve optimality through dynamic adjustment.
Proof.
Suppose that all paths in the network consist of a series of links , and the reliability of each path can be calculated as the product of the reliabilities of the links in that path. Therefore, the path reliability is
To ensure optimal path selection, nodes need to select the path with the highest reliability. By comparing the reliability values of different paths, nodes will choose the path with the highest reliability for data transmission. Since the path reliability is the product of link reliabilities, optimizing this product value can adjust the path selection strategy. □
4.2.3. Network Coding and Multi-Path Transmission
While traditional path selection methods can optimize some paths, they still suffer from transmission bottlenecks, especially when link failures or losses occur. Therefore, we introduce Random Linear Network Coding (RLNC) to enhance network redundancy, ensuring data transmission, even when some paths experience packet loss.
Network coding allows data to be transmitted over multiple paths by performing linear combination of data packets at intermediate nodes, enhancing the network’s robustness. Suppose data packets are encoded into :
where are randomly generated coding coefficients.
Theorem 6
(Robustness under Non-Ideal Conditions). Assume that each individual link i in a transmission path has a success probability . For a given path P consisting of L links, the end-to-end success probability is
In a multi-path transmission scenario with K independent paths, let the overall probability that at least one path successfully delivers a coded packet be defined as
Suppose that the source data consist of m packets and that n coded packets are transmitted over the multi-path channels, with . With Random Linear Network Coding (RLNC), successful decoding is achieved if at least m linearly independent coded packets are received. Hence, the decoding condition is satisfied with high probability if
or equivalently,
Thus, as long as the aggregate multi-path reliability satisfies the above inequality, the proposed multi-path transmission strategy maintains its performance, even under non-ideal conditions.
Proof.
For each individual path , let the end-to-end success probability be
where is the number of links in the kth path and denotes the success probability of the ith link in that path.
For K independent paths, the probability that none of the paths delivers a successful packet is
Therefore, the probability that at least one path is successful is
Assuming n coded packets are transmitted, the expected number of successfully received packets is
Since RLNC allows successful decoding if at least m independent packets are received, a sufficient condition is
Rearranging this yields the condition
Thus, the proposed multi-path transmission strategy maintains its performance under non-ideal conditions if the overall multi-path reliability satisfies the above bound. □
In this paper, the encoding coefficients used in the network coding process are generated randomly, to improve the robustness and redundancy of the network. To ensure the rationality and stability of these encoding coefficients, the generation process follows the rules and parameters described below:
- The encoding coefficients are randomly generated within the range of using a uniform distribution. The generation method employs a standard pseudorandom number generator to guarantee the independence and randomness of the coefficients.
- To enhance the encoding efficiency and fault tolerance of the network, the generated encoding coefficients ensure independence, meaning that there is no correlation between the different encoding coefficients. Additionally, the distribution range of the encoding coefficients can be adaptively adjusted using a scaling factor. In particular, this scaling factor can help adjust the distribution characteristics of the encoding coefficients to suit different network topologies.
- The generation process involves extracting each encoding coefficient from a uniform distribution using a pseudorandom number generator, ensuring the randomness and independence of each coefficient, thereby guaranteeing the reliability and effectiveness of the network coding process.
Through these control measures, the generated encoding coefficients not only meet the requirements of randomness, but also ensure the stability and reliability of the network coding, thereby helping to enhance the redundancy and recovery capability during data transmission.
Theorem 7.
In multi-path transmission, combining network coding strategies can effectively improve data transmission reliability, especially in scenarios where multiple paths provide redundancy and can mitigate the impact of single link losses on the entire system.
Proof.
Network coding performs encoding combination of data packets over multiple paths, such that even if some links fail, data can still be transmitted successfully over other paths. Let data packets be encoded into , where each data packet is a linear combination of the original data packets, and the coding coefficients are randomly chosen. When some links in a path fail, redundant data packets from other paths can compensate for the lost information, ensuring reliable data transmission. This feature allows the network to recover data via alternate paths in the event of link failures. □
To facilitate efficient resource allocation, the CMPT framework includes a preprocessing step that calculates utility values, evaluates link and path reliabilities, and encodes data packets for transmission. The implementation of this preprocessing procedure is detailed in Algorithm 3.
The algorithm input includes the set of satellite nodes N, resource demands D, link reliability , interference coefficients , optimal power and bandwidth allocation , interference threshold , and signal-to-noise ratio threshold . The output consists of utility values U for each satellite node, link reliability values , path reliability values , and network-coded data packets . For each node i, each link , and each path , the utility value is first calculated based on the node’s utility function (Lines 1–2). Subsequently, node i is assigned to the corresponding domain based on its utility value (Line 3). Next, the link reliability is computed (Line 4) and the path reliability is determined, completing the traversal of all nodes, links, and paths (Line 5).
Following this, for each data packet , the data packets are encoded to generate network-coded data packets (Lines 7–8), and the encoded data packets are transmitted over multiple paths to achieve redundancy (Line 9). After the iterative process concludes, the computed utility values U, link reliabilities , path reliabilities , and encoded data packets are returned (Line 12).
| Algorithm 3 Preprocessing Framework for Resource Allocation and Reliability Optimization (PF-RARO) |
|
4.2.4. Nash Bargaining Game Model and Algorithm Optimization
This section introduces the MCGT-1 algorithm, which optimizes resource allocation in satellite networks through Nash bargaining games. The MCGT-1 algorithm aims to achieve a fair distribution among multiple satellite users through negotiation, while ensuring overall system utility. We derive the core mathematical model of the algorithm, presenting relevant theorems to ensure the rigor of the derivation process.
The utility function for user is defined as
where is the actual throughput, and is the minimum acceptable throughput. This difference represents the user’s utility. The objective is to optimize the overall network utility by selecting the optimal resource allocation strategy for each user.
Theorem 8.
Suppose U is a non-empty, bounded, convex, and closed set. Then, there exists a unique Nash bargaining solution that satisfies
Proof.
The goal of the Nash bargaining game is to maximize the product of the utilities of all participants, ensuring both fairness and efficiency in resource allocation. Formally, the optimization problem is defined as
where is the utility of the k-th user, and is their minimum utility requirement.
The system utility function is
To find the optimal utility , we take the natural logarithm of the utility function to simplify differentiation:
Differentiating with respect to and setting the derivative to zero for maximization, we obtain
This condition ensures that each user’s utility exceeds their minimum requirement, aligning with the feasibility of the solution.
Given that U is a non-empty, bounded, convex, and closed set, and the utility functions are concave, the optimization problem possesses a unique solution . This uniqueness arises from the strict concavity of the objective function, which guarantees that the maximum is attained at a single point within the feasible set.
Thus, the Nash bargaining solution is uniquely determined, ensuring an optimal and fair resource allocation among all participants. □
4.2.5. Cooperative Resource Allocation Game
Resource allocation in multi-user, multi-node satellite networks is formulated as a cooperative game to address resource competition and collaboration, ensuring fair and efficient distribution among users and nodes. The cooperative game model enhances the overall network utility by balancing global and individual optimality through shared resources.
Consider a cooperative game with N participants. The utility function for participant i is defined as
where is the power allocated to participant i, is the bandwidth allocated to participant i, is the signal-to-noise ratio (SNR) for participant i, and is the throughput for participant i.
The interference between participants i and j is denoted by . The resource allocation strategy aims to maximize the total network utility, while ensuring each participant’s utility meets a minimum required level:
s.t.
Revenue sharing is implemented using the Shapley value, to ensure a fair distribution of resources based on each participant’s contribution. The Shapley value is a widely recognized method for fair allocation in cooperative games, calculated as
where is the utility of coalition S, is the number of participants in coalition S, and is the Shapley value for participant i.
The Shapley value ensures that each participant receives a fair share of the total utility based on their marginal contribution to all possible coalitions.
4.2.6. Problem Modeling and Optimization Algorithm Design
We address the satellite network resource allocation optimization using the Lagrange multiplier method and dual problem solving. The approach involves decomposing the main problem into sub-problems and applying the Karush–Kuhn–Tucker (KKT) conditions to ensure feasibility and solvability.
The utility function for each user is defined as the difference between its transmitted throughput and the minimum required throughput:
where is the interference coefficient for user at frequency f and time t. is the power allocation for user at frequency f and time t. is the signal-to-noise ratio for user at frequency f and time t. is the minimum acceptable throughput for user .
The optimization objective is to maximize the total utility across all users:
s.t.
To solve the optimization problem, we formulate the Lagrangian:
where , , and are Lagrange multipliers corresponding to the interference threshold, maximum power limit, and signal-to-noise ratio constraints, respectively.
The dual problem is then formulated as
Applying the KKT conditions, we derive the necessary conditions for optimality:
- Primal Feasibility: All constraints must be satisfied.
- Dual Feasibility: The Lagrange multipliers must be non-negative, i.e., , .
- Stationarity: The gradient of the Lagrangian with respect to must be zero:
These conditions collectively ensure that the solution obtained is optimal under the given constraints.
In the optimization process, the Karush–Kuhn–Tucker (KKT) conditions are essential for identifying the optimal solution based on the given constraints. One situation arises when constraints are inactive, meaning that they do not affect the optimal solution. In such cases, the corresponding Lagrange multipliers are zero, i.e., . This typically occurs when resources, such as power or computational capacity, are abundant and far exceed the required demand. In such scenarios, the inactive constraints do not influence the optimization. We can adopt the approach of excluding these inactive constraints from the optimization process to enhance computational efficiency, focusing only on the active constraints that directly affect resource allocation.
Another situation arises when constraints are active, meaning that they are satisfied as equalities, i.e., , and the Lagrange multipliers associated with these constraints are strictly positive, i.e., . This occurs when resource limits, such as bandwidth or computational capacity, are fully utilized. In this case, the optimization adjusts resource allocation among the nodes to ensure that all active constraints are satisfied, while maximizing the overall performance. To handle this scenario, we can consider fine-tuning the Lagrange multipliers, allowing the optimization process to strike a balance between satisfying the constraints and maximizing system efficiency.
A third scenario arises when the optimization problem becomes infeasible due to conflicting constraints. This situation is characterized by for all i, where no feasible solution can simultaneously satisfy all constraints. This may happen when the required resources exceed the available capacity, such as when the demand for bandwidth or power exceeds the network’s capability. To address this, we can introduce slack variables that relax some of the constraints slightly, allowing minor violations. Additionally, we can incorporate a penalty function into the objective function to penalize these constraint violations. This approach would allow the optimization to converge to a feasible solution, even when the problem initially seems unsolvable, ensuring robustness in resource-tight conditions.
To achieve optimal resource allocation, the CMPT framework employs an algorithm that integrates Shapley-value-based resource distribution with Lagrangian multiplier optimization techniques. The detailed implementation of this optimized resource allocation process is presented in Algorithm 4.
The algorithm input includes the utility set , link reliabilities , path reliabilities , and network-coded data packets . The output consists of the optimal resource allocations , bandwidth allocations , and power distributions for each node. For each participant , the Shapley value is first calculated (Lines 1–2), followed by resource allocation based on the computed Shapley value (Line 3). After resource allocation for all participants is completed, the Lagrangian function is defined (Line 5), and the corresponding dual problem and KKT conditions are solved (Lines 6–7). Finally, the optimized resource allocation results , , and are returned (Line 8).
| Algorithm 4 Cooperative Resource Allocation with Shapley Value and Dual Optimization (CRA) |
|
This Algorithm 5 first receives the satellite node set N, task set T, network topology , and resource capacity R as input (Line 1), and then aims to output the task allocation A, power allocation P, and bandwidth allocation B (Line 2). It begins by preprocessing the network information and task requirements to compute the utility values U, link reliability matrix , path reliability , and the encoded data packets Y necessary for subsequent resource allocation (Line 2). The algorithm then performs domain clustering based on the network topology and clustering criteria, to divide all nodes into multiple sub-domains D (Line 4). For each domain in D, it approximates the local Shapley value to evaluate the fair contribution of each node within the domain, significantly reducing the computational complexity compared to global Shapley calculation (Lines 5–7). Next, it adjusts the resource utility through Nash bargaining optimization using the computed fairness factor and domain information D, to ensure fair and efficient resource allocation (Line 9). After that, the algorithm solves the dual optimization problem to obtain the final optimal power allocation and bandwidth allocation under system constraints (Line 11). Finally, it returns the optimized task allocation A, power allocation , and bandwidth allocation as the output (Line 12).
| Algorithm 5 CMPT: Fairness-Aware Resource Allocation with Local Shapley Approximation |
Require: Satellite node set N, task set T, network topology , resource capacity R Ensure: Task allocation A, power allocation P, bandwidth allocation B
|
5. Experimental Results
This study used the Common Satellite Tool Kit (CSTK) as the simulation environment to accurately model a dynamic satellite network scenario. To address the challenges of resource allocation and task scheduling under fluctuating network topologies and varying traffic demands, we developed specialized modules within the simulation system, including satellite orbit simulation, communication link management, and task scheduling mechanisms. Leveraging these modules, we constructed a series of comprehensive experiments that evaluated the performance of the proposed Coding Multi-Path Theory (CMPT) method against established comparative algorithms across different satellite configurations and task loads. The experimental setup encompassed diverse datasets, multiple satellite scales, and a range of task priorities, to thoroughly assess CMPT’s effectiveness and scalability in real-world dynamic network conditions.
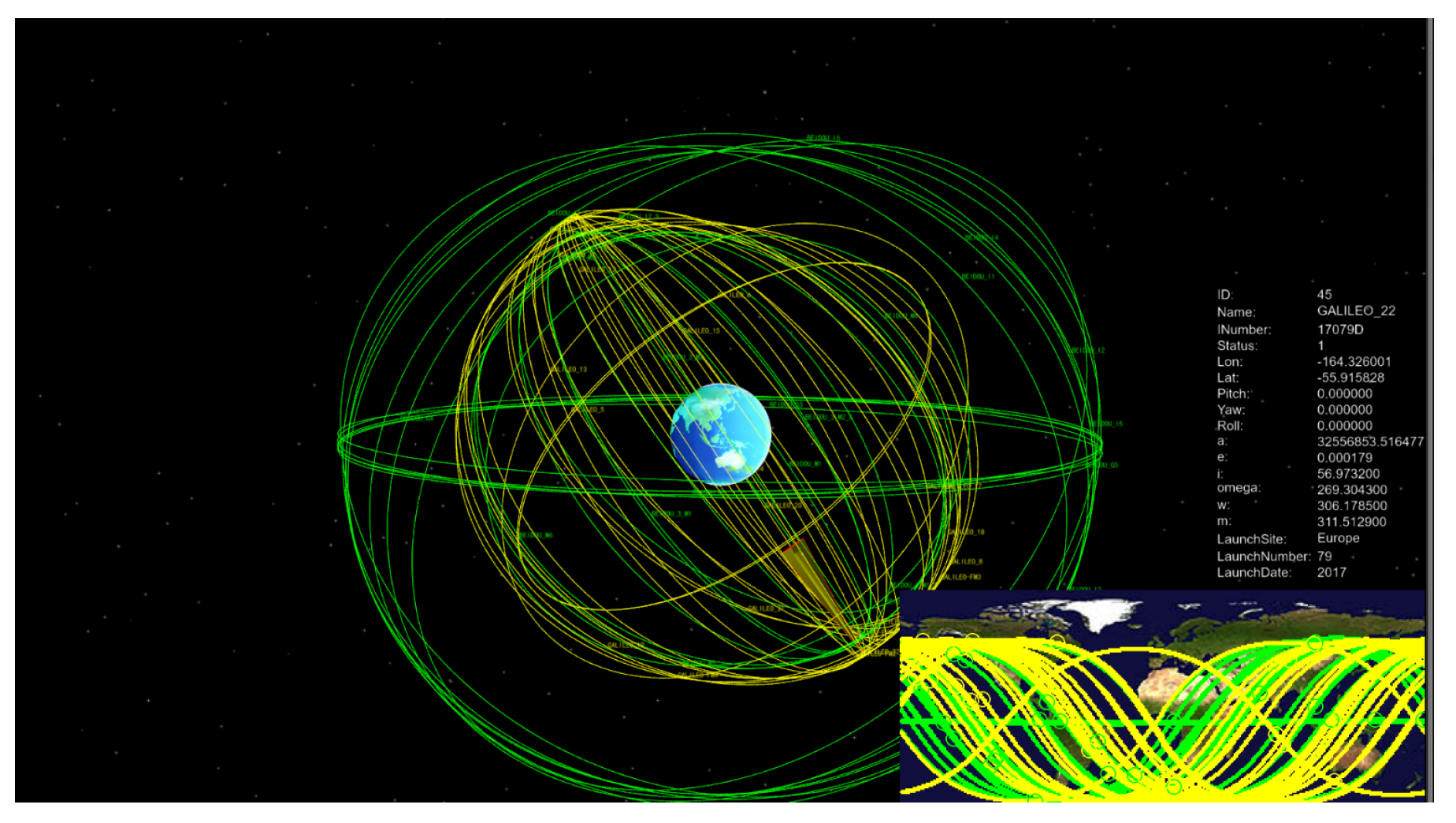
The basic simulation interface of CSTK is shown in Figure 3. The system integrates orbit dynamics modeling, link-state awareness, and task coordination scheduling. As illustrated, the platform features a central Earth model (blue sphere) surrounded by dynamically rendered satellite constellation trajectories (yellow/green orbital lines). The left panel provides real-time updates on satellite node states (e.g., ID, longitude, latitude, and attitude angles), while the bottom timeline synchronizes the simulation progress with real-world timestamps. Leveraging three-dimensional visualization and parameter-coupling mechanisms, the platform enables interpretable representation of dynamic network topologies (orbital period variations), quantitative monitoring of multi-path resource states (bandwidth/latency parameters embedded in satellite attribute panels), and spatiotemporal consistency verification of task scheduling processes (scenario-simulated time alignment).
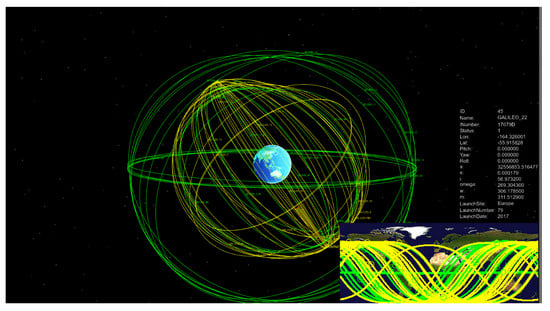
Figure 3.
Main simulation interface of the CSTK platform.
5.1. Dataset Details and Scenario Description
The dataset used in this study encompassed various parameters required for satellite network resource allocation and scheduling, specifically including each satellite node’s resource vector , corresponding to computational capacity , bandwidth and storage capacity . Here, represents the computational capacity of satellite node i and is a non-negative real number; denotes the bandwidth, also a non-negative real number; and indicates the storage capacity, similarly a non-negative real number. The network topology matrix describes the connection characteristics between nodes, where represents the bandwidth or latency between node i and node j, and is a non-negative real number.
The task allocation matrix represents the amount of resources allocated to task j at satellite node i, with each element being a non-negative real number. The resource demand vector for each task corresponds to the computational demand , bandwidth demand , and storage demand , all of which are non-negative real numbers. Additionally, the task transmission latency and the adjusted resource allocation are defined as non-negative real numbers, to ensure the rationality and feasibility of the scheduling process.
Satellite orbit parameters include the semi-major axis (semi_major_axis), eccentricity (eccentricity), inclination (inclination), argument of perigee (argument_of_perigee), longitude of ascending node (longitude_of_ascending_node), and mean anomaly (mean_anomaly). These parameters were obtained from the CelesTrak database and were used to define the satellites’ orbits, simulating their trajectories and communication windows. The semi-major axis typically ranges from 6000 km to 42,164 km for Low Earth Orbit (LEO) to Geostationary Orbit (GEO) satellites, the eccentricity ranges from 0 (circular orbit) to just below 1 (highly elliptical orbit), the inclination ranges from 0° to 180°, the argument of perigee ranges from 0° to 360°, the longitude of ascending node ranges from 0° to 360°, and the mean anomaly ranges from 0° to 360°. These orbital parameters are crucial for simulating the relative positions and communication conditions between satellites.
The Common Satellite Tool Kit (CSTK) simulation platform was utilized to emulate a realistic satellite network environment, supporting the simulation of various satellite configurations and task loads. CSTK provides modules for satellite orbits, communication links, and task scheduling, enabling precise simulation of communication windows (visibility_window) between satellites and ground stations. Using this platform, visibility windows for each task were calculated based on target region information and satellite orbit parameters. Additionally, CSTK generated a network graph that described the connection relationships between the source node (source_node_j) and destination node (destination_node_j) for each task j, ensuring that each task had a feasible transmission path (transmission_path_j belonging to available_paths).
The simulation scenarios encompassed a variety of satellite configurations and task loads, to evaluate the system performance under different conditions. The simulation time was defined by scenario_start_time and scenario_end_time, for example, from 3 September 2023, 00:00 UTC to 15 September 2023, 23:59 UTC. Task demand parameters included the task priority, data size, and execution time. These parameters were customized based on specific remote sensing task regions and user requirements. Task priority reflected the urgency of the task, the data size was set according to the scale and resolution requirements of the target area, and the execution time was determined by the complexity of the task and the resource allocation.
5.2. Comparative Algorithms
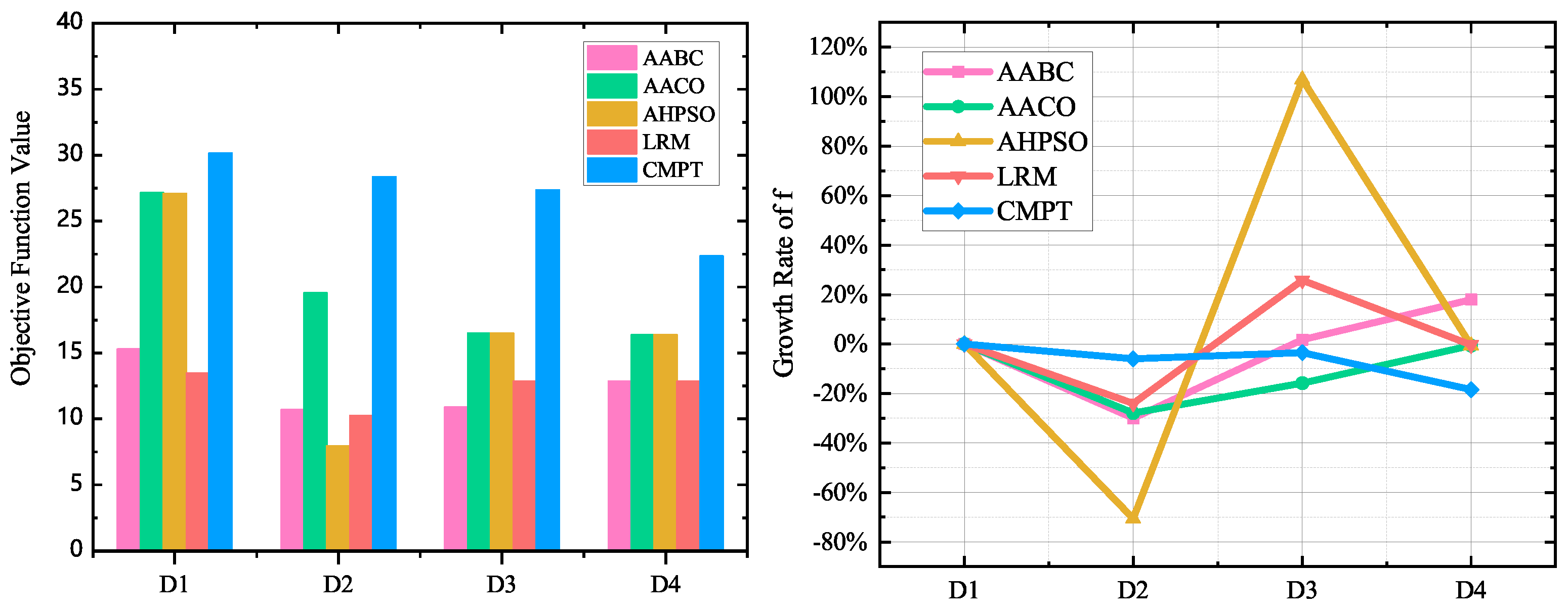
This study selected four representative algorithms for performance evaluation, each offering unique strengths in handling complex optimization tasks. The Adaptive Ant Colony Optimization Algorithm (AACO) [41], with a time complexity of , where T is the number of iterations, k is the number of ants, n is the number of nodes, and m is the number of edges, optimizes resource allocation through pheromone-based path selection. The Adaptive Ant Bee Colony Algorithm (AABC) [42] combines ant and bee colony behaviors for global and local optimization, exhibiting a time complexity of , where N is the population size, D is the problem dimension, and T is the number of iterations. The Improved Hybrid Particle Swarm Optimization Algorithm (AHPSO) [43], with a time complexity of , where n is the number of particles and T is the maximum number of iterations, integrates swarm intelligence and genetic operators for robust optimization. Lastly, the Linear Regression Model (LRM) [44], with a time complexity of , where k is the number of iterations, n is the subproblem size, and m is the number of constraints, provides a deterministic approach for optimizing resource allocation. These algorithms are well-suited to diverse resource scheduling tasks, balancing complexity with adaptability to dynamic environments.
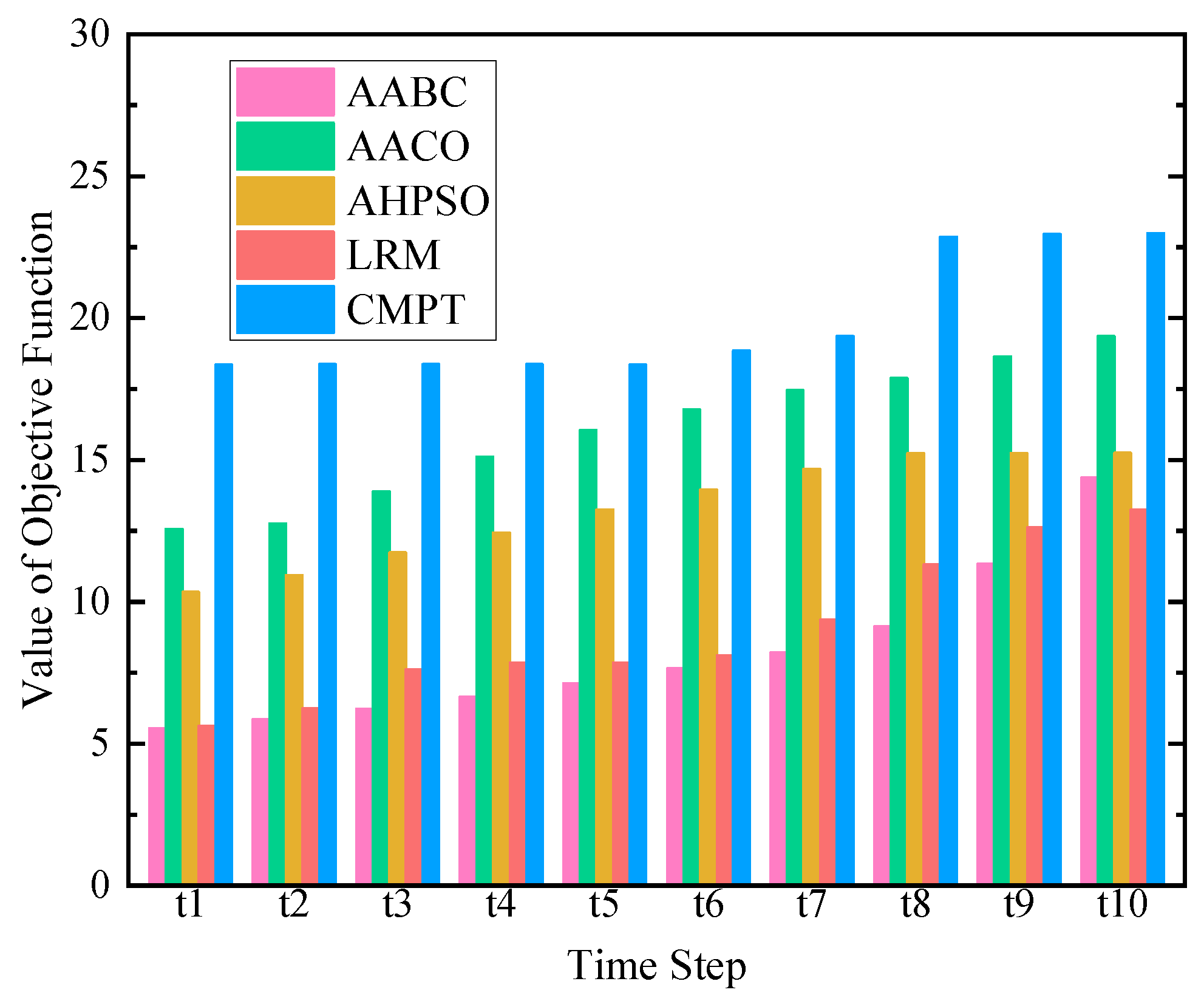
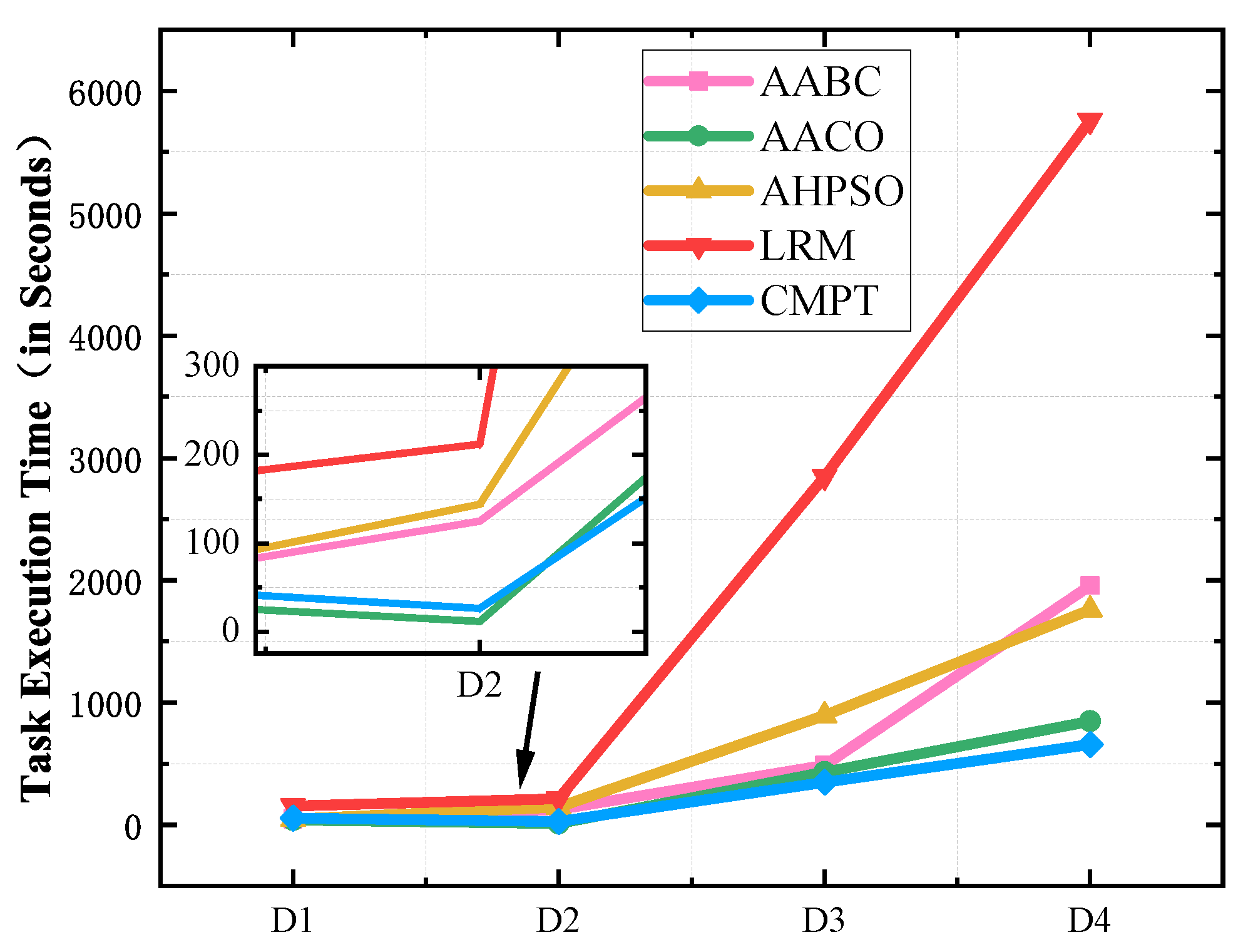
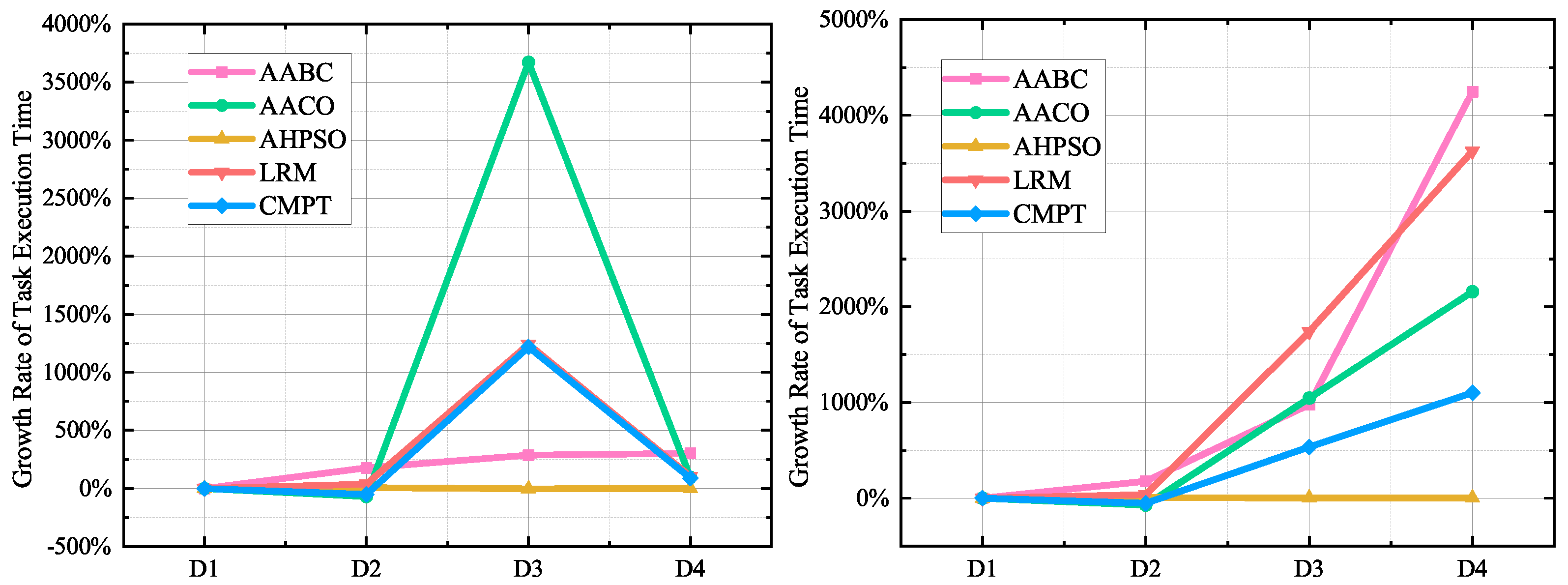
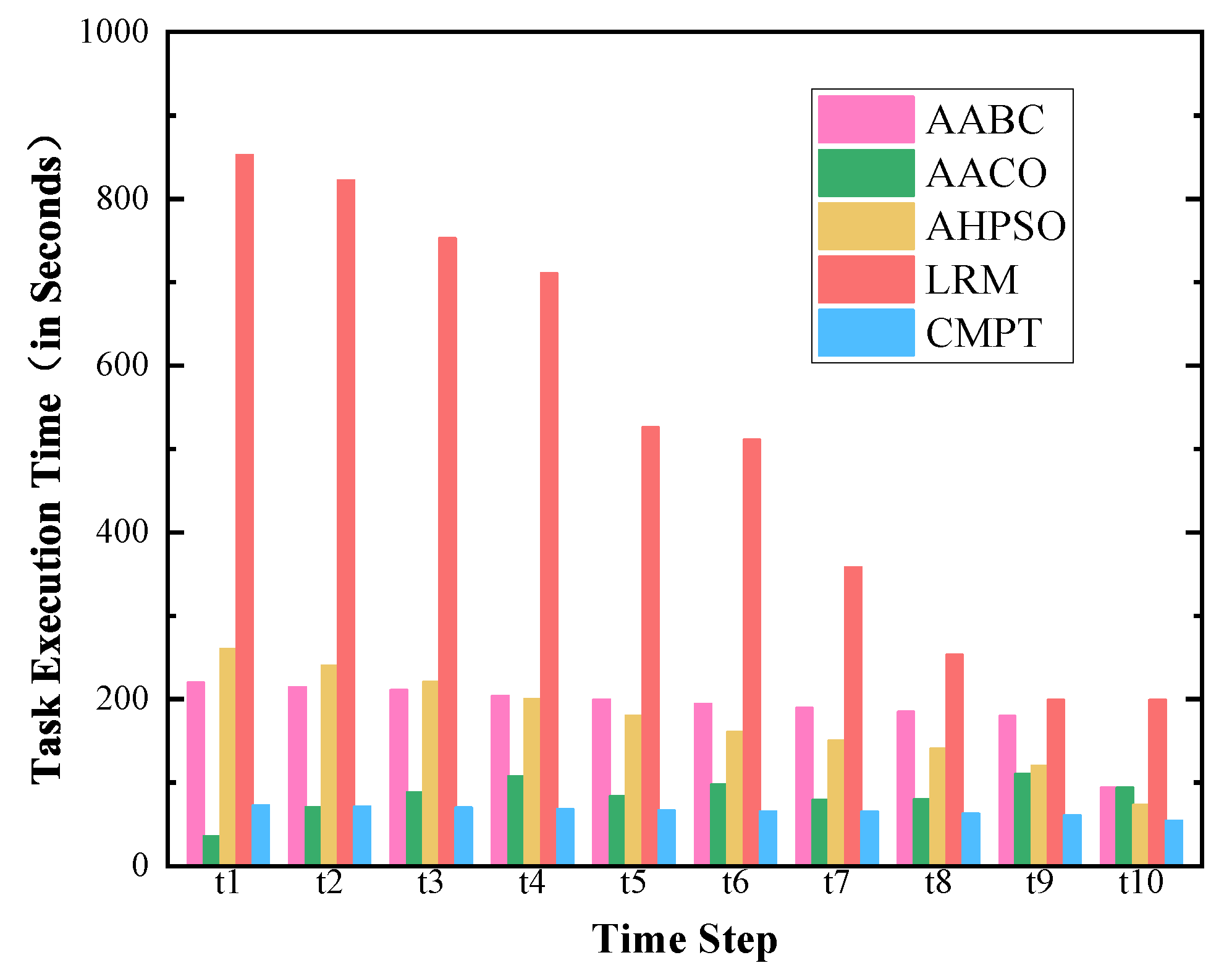
5.3. Evaluation Indicators
This study employed multiple indicators to comprehensively evaluate the performance of the proposed resource allocation and scheduling algorithms. The evaluation indicators included the objective function value, resource utilization rate, algorithm execution time, task execution time, and objective function value optimization rate.
The objective function value served as the core evaluation metric, reflecting the algorithm’s overall performance in optimizing network throughput and reducing computational complexity. Specifically, the objective function value measures the overall network efficiency by maximizing network throughput T and minimizing the difference in resource allocation adjustments .
Task execution time evaluated the time taken for each task from initiation to completion, including the total time for data transmission and processing, represented by the task transmission latency . This indicator reflected the system’s responsiveness and real-time performance in practical applications.
Through comprehensive analysis of these evaluation indicators, the study effectively measured the performance of the proposed algorithms in multi-satellite collaborative computing environments, ensuring their superiority in network throughput, resource utilization efficiency, and task execution efficiency.
5.4. Numerical Analysis
In the four experimental scenarios with different satellite scales (Table 3), CMPT demonstrated a significant advantage in terms of objective function values and growth rate stability, as shown in Figure 4. Across all datasets (D1 to D4), CMPT consistently achieved higher objective function values compared to the other algorithms, including AABC, AACO, AHPSO, and LRM, indicating its effectiveness in enhancing the network throughput and reducing computational complexity in resource allocation and task scheduling. This performance is attributed to its cooperative game-theoretic model and real-time resource allocation strategies, which balance global and local optimization, significantly improving resource utilization efficiency. Moreover, CMPT exhibited superior stability in the growth rate of objective function values across datasets, particularly for D2 and D3, where its growth rates remained consistent. In contrast, algorithms such as LRM experienced significant fluctuations, especially on D3. This stability underscores CMPT’s adaptability to diverse resource distributions and topological changes in dynamic satellite networks. By leveraging a Nash bargaining model, CMPT efficiently coordinates resource competition among nodes, ensuring balanced resource allocation and effective load balancing under multiple constraints.

Table 3.
Configuration of selected datasets.
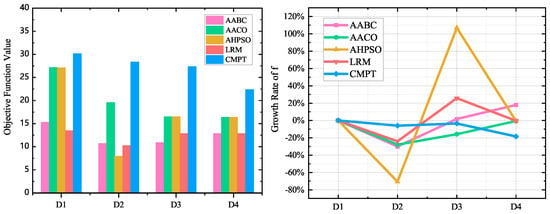
Figure 4.
Objective function values and growth rates of all algorithms.
Figure 5 and Table 4 illustrates the variation in objective function values for the different algorithms over the time steps. Throughout the entire time period, CMPT consistently maintained a significant performance advantage, with its objective function value steadily improving over time and surpassing those of AABC, AACO, AHPSO, and LRM. This superiority stems from the integration of Lagrangian dual optimization and multi-path scheduling strategies within CMPT, which enable fine-grained resource allocation and real-time feedback mechanisms in dynamic networks. This ensures system reliability and efficiency even in complex environments. In contrast, the other algorithms failed to simultaneously optimize resource utilization and scheduling performance under multiple constraints, resulting in inferior performance.
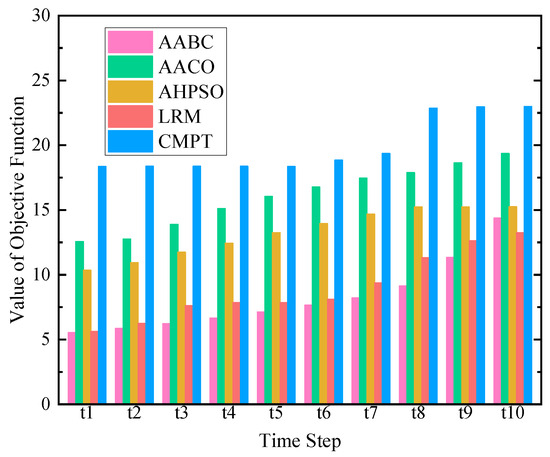
Figure 5.
Objective function values in 10 time steps.

Table 4.
Objective function values and optimization rates across four datasets.
In this study, the growth rate of the task execution time was calculated based on the variation in task execution time across consecutive time steps. Specifically, the growth rate between two consecutive time steps and was computed as the relative change in task execution time. The growth rate is defined by the following formula:
where and represent the task execution times at time steps and , respectively. This formula quantifies the relative change in task execution time between two consecutive time steps and is used to assess the rate of performance change over time.
As shown in Figure 6 and Table 5, CMPT exhibited clear advantages in task execution time across the four datasets (D1 to D4). Compared to AABC, AACO, AHPSO, and LRM, CMPT consistently achieved lower execution times, especially for datasets D3 and D4, where it demonstrated better scalability and stability. This performance was due to CMPT’s combination of Nash bargaining and Lagrangian dual optimization, which enables efficient resource scheduling and conflict mitigation, significantly reducing task execution time. In contrast, the other algorithms, particularly LRM, showed a substantial increase in execution time as the dataset size grew, highlighting their limited adaptability to large-scale and complex scenarios.
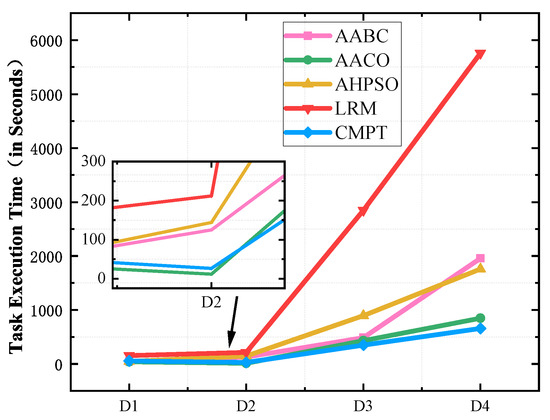
Figure 6.
Task execution time between algorithms across four datasets.

Table 5.
Task execution time(in seconds) across four datasets.
Figure 7 illustrates the growth rate of task execution time, where CMPT also demonstrated exceptional stability. While AHPSO achieved lower growth rates for D1 and D2, it exhibited a sharp increase in D3, reflecting significant fluctuations. In contrast, CMPT maintained consistently low and stable growth rates across all datasets, showcasing its strong adaptability to dynamic network environments. This stability is enabled by CMPT’s domain clustering management and multi-path transmission strategies, which optimize path selection and task allocation in real time, effectively reducing the latency caused by link failures or resource contention. On the other hand, AABC and LRM exhibited greater fluctuations, struggling to maintain consistency and control over growth rates.
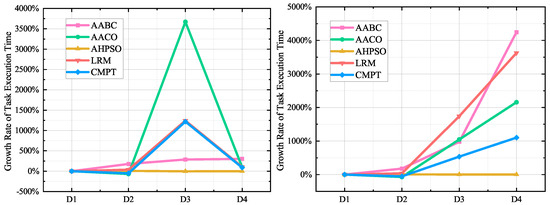
Figure 7.
Growth rate of task execution time across four datasets.
As shown in Figure 8, CMPT demonstrated sustained advantages in task execution time across the different time steps. From to , CMPT consistently outperformed the other algorithms, maintaining significantly lower execution times and showcasing superior real-time performance and efficiency. This is primarily attributed to its optimized multi-path scheduling strategy and real-time feedback mechanism, which dynamically adjust task paths to minimize resource waste and link latency. In contrast, AABC and LRM exhibited persistently higher task execution times throughout the time steps, further indicating their inefficiency in handling real-time scheduling tasks.
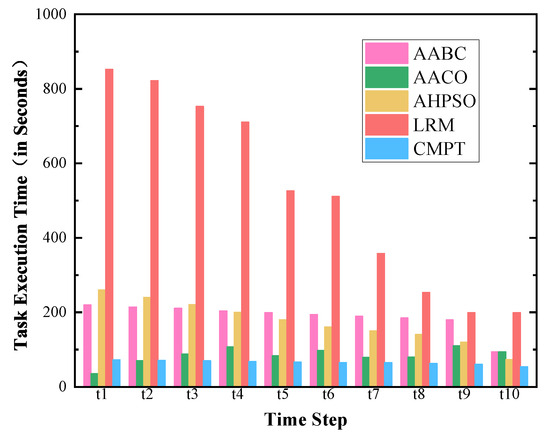
Figure 8.
Task execution time across discrete time steps.
5.5. Summary
The experimental results demonstrate that the Coding Multi-Path Theory (CMPT) method achieved high throughput efficiency, balanced resource utilization, and superior real-time performance in multi-satellite collaborative computing and dynamic network environments. Specifically, across the four datasets with varying numbers of satellites, CMPT attained an average objective function value of 27.56626, significantly outperforming baseline algorithms such as LRM (12.35987), AHPSO (16.48567), AABC (12.42628), and AACO (19.39466). Moreover, CMPT exhibited outstanding scalability and stability for task execution time, with an average execution time of 271.91026 units, markedly better than LRM (1743.62500), AHPSO (710.29763), AABC (652.25000), and AACO (331.35843). This superior performance is attributed to CMPT’s integration of Nash bargaining game and Lagrangian dual optimization, which ensures coordinated resource allocation and efficient load balancing, even under multiple interference constraints and large-scale task loads.
However, despite its advantages, CMPT also presents certain limitations. For instance, the algorithm’s computational complexity may increase with extremely large-scale networks or highly dynamic environments, potentially impacting its real-time responsiveness. Additionally, the reliance on accurate real-time network state monitoring necessitates robust data acquisition mechanisms, which might introduce additional overhead in practical deployments. Future work should focus on further optimizing the algorithm’s scalability and enhancing its adaptability to diverse and unpredictable network conditions, to fully realize its potential in satellite network resource scheduling and task allocation.
Overall, the experimental analysis validated the efficacy and feasibility of CMPT in optimizing resource allocation and task scheduling in satellite networks, showcasing its aptitude for comprehensively enhancing system performance and management efficiency.
6. Conclusions
This paper addressed the issues of low resource utilization and high system latency in dynamic satellite networks concerning resource allocation and task scheduling. We proposed a collaborative optimization framework based on game theory and multi-path transmission—CMPT. This method integrates a cooperative game model, Random Linear Network Coding (RLNC), Software-Defined Networking (SDN)-based domain clustering strategies, and the Lagrangian multiplier method, aiming to achieve fairness and efficiency in resource allocation. Despite a latency slightly higher than some comparative algorithms, its performance remains outstanding in large-scale and high-dimensional problems. Future research will focus on further optimizing the CMPT algorithm to significantly reduce task latency for small-scale datasets, extending the resource allocation.
The experimental results demonstrate that the CMPT algorithm reduced the resource allocation task execution time by at least 18.03% compared to traditional methods and improved task scheduling efficiency by at least 14.01%. Although on certain small-scale datasets, the task latency of CMPT was slightly higher than some comparative algorithms, future research will focus on adapting it to more complex and heterogeneous satellite network environments—including multiple types of satellite nodes and diversified task requirements—and explore the algorithm’s scalability and performance optimization for larger satellite constellations.
Author Contributions
Conceptualization, S.W.; methodology, S.W. and Y.W.; software, C.Z.; validation, Y.W. and C.Z.; formal analysis, S.W.; investigation, Y.W.; resources, S.W. and J.L.; data curation, Y.W.; writing original draft preparation, S.W.; writing review and editing, S.W. and C.Z.; visualization, Y.W. and C.Z.; supervision, L.L. and J.L.; project administration, J.L.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (Grant No. U2003208 and No. 61972398), the Science and Technology Plan of Hunan Province (Grant No. 2016TP1003), the Key Technology R&D Program of Hunan Province (Grant No. 2018GK2052), the Foundation for Equipment Procurement (Grant No. 6141A020227), and the Theory and Method of Multi-Satellite Collaborative Application Foundation (Grant No. 2019-JCJQ-ZD-342-00).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hong, E.K.; Lee, I.; Shim, B.; Ko, Y.C.; Kim, S.H.; Pack, S.; Lee, K.; Kim, S.; Kim, J.H.; Shin, Y.; et al. 6G R&D vision: Requirements and candidate technologies. J. Commun. Netw. 2022, 24, 232–245. [Google Scholar] [CrossRef]
- Bazzi, A.; Bomfin, R.; Mezzavilla, M.; Rangan, S.; Rappaport, T.; Chafii, M. Upper Mid-Band Spectrum for 6G: Vision, Opportunity and Challenges. arXiv 2025, arXiv:2502.17914. [Google Scholar]
- Lai, Z.; Li, H.; Wang, Y.; Wu, Q.; Deng, Y.; Liu, J.; Li, Y.; Wu, J. Achieving Resilient and Performance-Guaranteed Routing in Space-Terrestrial Integrated Networks. In Proceedings of the IEEE INFOCOM 2023—IEEE Conference on Computer Communications, New York, NY, USA, 17–20 May 2023; pp. 1–10. [Google Scholar] [CrossRef]
- Gounder, V.; Prakash, R.; Abu-Amara, H. Routing in LEO-based satellite networks. In Proceedings of the 1999 IEEE Emerging Technologies Symposium, Wireless Communications and Systems (IEEE Cat. No.99EX297), Richardson, TX, USA, 12–13 April 1999; pp. 22.1–22.6. [Google Scholar] [CrossRef]
- Bazzi, A.; Cottatellucci, L.; Slock, D. Blind on board wideband antenna RF calibration for multi-antenna satellites. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 6294–6298. [Google Scholar] [CrossRef]
- Alagoz, F.; Gur, G. Energy Efficiency and Satellite Networking: A Holistic Overview. Proc. IEEE 2011, 99, 1954–1979. [Google Scholar] [CrossRef]
- Polese, M.; Chiariotti, F.; Bonetto, E.; Rigotto, F.; Zanella, A.; Zorzi, M. A Survey on Recent Advances in Transport Layer Protocols. IEEE Commun. Surv. Tutor. 2019, 21, 3584–3608. [Google Scholar] [CrossRef]
- Goswami, C.; Shahane, R. Transport Control Protocol (TCP) enhancement over wireless environment: Issues and challenges. In Proceedings of the 2017 International Conference on Inventive Computing and Informatics (ICICI), Coimbatore, India, 23–24 November 2017; pp. 742–749. [Google Scholar] [CrossRef]
- Al-Saadi, R.; Armitage, G.; But, J.; Branch, P. A Survey of Delay-Based and Hybrid TCP Congestion Control Algorithms. IEEE Commun. Surv. Tutor. 2019, 21, 3609–3638. [Google Scholar] [CrossRef]
- Zhong, X.; Guo, N.; Li, A.; Gong, Y.; Wang, Y.; Wang, N.; Liu, L. Link Topology and Multi-Objective Mission Flow Optimization for Remote Sensing Satellites With Inter-Layer Links and Satellite-Ground Links. IEEE Trans. Veh. Technol. 2024, 73, 15621–15635. [Google Scholar] [CrossRef]
- Yuan, S.; Sun, Y.; Peng, M. Joint Network Function Placement and Routing Optimization in Dynamic Software-Defined Satellite-Terrestrial Integrated Networks. IEEE Trans. Wirel. Commun. 2024, 23, 5172–5186. [Google Scholar] [CrossRef]
- Guo, N.; Liu, L.; Zhong, X. Task-Aware Distributed Inter-Layer Topology Optimization Method in Resource-Limited LEO-LEO Satellite Networks. IEEE Trans. Wirel. Commun. 2024, 23, 3572–3585. [Google Scholar] [CrossRef]
- Hamdi, M.; Zaied, M. Resource allocation based on hybrid genetic algorithm and particle swarm optimization for D2D multicast communications. Appl. Soft Comput. 2019, 83, 105605. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Mirmohseni, S.M.; Javadpour, A.; Tang, C. LBPSGORA: Create load balancing with particle swarm genetic optimization algorithm to improve resource allocation and energy consumption in clouds networks. Math. Probl. Eng. 2021, 2021, 5575129. [Google Scholar] [CrossRef]
- Liu, S.; He, M.; Wu, Z.; Lu, P.; Gu, W. Spatial–temporal graph neural network traffic prediction based load balancing with reinforcement learning in cellular networks. Inf. Fusion 2024, 103, 102079. [Google Scholar] [CrossRef]
- Tamada, K.; Kawamoto, Y.; Kato, N. Bandwidth Usage Reduction by Traffic Prediction Using Transfer Learning in Satellite Communication Systems. IEEE Trans. Veh. Technol. 2024, 73, 7459–7463. [Google Scholar] [CrossRef]
- Jiang, W.; Mu, J.; Han, H.; Zhang, Y.; Huang, S. Federated Learning-Based Mobile Traffic Prediction in Satellite-Terrestrial Integrated Networks. Softw. Pract. Exp. 2024, 55, 613–628. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Nambiar, S.M.; Ojha, R.; Gyaneshwar, A.; Chadha, U.; Srinivasan, K. Machine Learning and Deep Learning powered satellite communications: Enabling technologies, applications, open challenges, and future research directions. Int. J. Satell. Commun. Netw. 2023, 41, 539–588. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.; Yu, P.; Yuan, X. Machine Learning with Adaptive Time Stepping for Dynamic Traffic Load Prediction in 6G Satellite Networks. Electronics 2023, 12, 4473. [Google Scholar] [CrossRef]
- Lapsiwala, P.B.; Vasava, P.B. Link handling for the atmospheric turbulence using LSTM neural networks in free space optical (FSO) communication. J. Opt. Commun. 2023, 45, s1805–s1816. [Google Scholar] [CrossRef]
- Deng, B.; Jiang, C.; Yao, H.; Guo, S.; Zhao, S. The Next Generation Heterogeneous Satellite Communication Networks: Integration of Resource Management and Deep Reinforcement Learning. IEEE Wirel. Commun. 2020, 27, 105–111. [Google Scholar] [CrossRef]
- Chinchali, S.; Hu, P.; Chu, T.; Sharma, M.; Bansal, M.; Misra, R.; Pavone, M.; Katti, S. Cellular network traffic scheduling with deep reinforcement learning. In Proceedings of the Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar] [CrossRef]
- Huang, J.; Xing, C.C.; Qian, Y.; Haas, Z.J. Resource Allocation for Multicell Device-to-Device Communications Underlaying 5G Networks: A Game-Theoretic Mechanism With Incomplete Information. IEEE Trans. Veh. Technol. 2018, 67, 2557–2570. [Google Scholar] [CrossRef]
- Khan, S.U.; Ahmad, I. A Cooperative Game Theoretical Technique for Joint Optimization of Energy Consumption and Response Time in Computational Grids. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 346–360. [Google Scholar] [CrossRef]
- Ahrar, E.M.; Nassiri, M.; Theoleyre, F. Multipath aware scheduling for high reliability and fault tolerance in low power industrial networks. J. Netw. Comput. Appl. 2019, 142, 25–36. [Google Scholar] [CrossRef]
- Cetinkaya, C. Improving the efficiency of multipath traffic via opportunistic traffic scheduling. Comput. Netw. 2007, 51, 2181–2197. [Google Scholar] [CrossRef]
- Radi, M.; Dezfouli, B.; Bakar, K.A.; Lee, M. Multipath routing in wireless sensor networks: Survey and research challenges. Sensors 2012, 12, 650–685. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Dong, P.; Yang, D.; Du, X.; Yu, C.; Zhang, H. TA2LS: A Traffic-Aware Multipath Scheduler for Cost-Effective QoE in Dynamic HetNets. IEEE Trans. Mob. Comput. 2024, 23, 13603–13620. [Google Scholar] [CrossRef]
- Aljubayri, M. Enhancements to the Multipath Transmission Control Protocol for Internet of Things Wireless Networks. Ph.D. Thesis, King’s College London, London, UK, 2022. [Google Scholar]
- Xu, C.; Zhao, J.; Muntean, G.M. Congestion Control Design for Multipath Transport Protocols: A Survey. IEEE Commun. Surv. Tutor. 2016, 18, 2948–2969. [Google Scholar] [CrossRef]
- Usama, M.; Ullah, U.; Muhammad, Z.; Bux, M.; Ullah, I.; Rouf, M.; Islam, T. Data traffic management in AI-IoT network to reduce congestion. In Artificial Intelligence for Intelligent Systems; CRC Press: Boca Raton, FL, USA, 2024; pp. 145–189. [Google Scholar]
- Jiang, X.; Wu, H.; Jiang, H.; Du, X.; Fang, J. CO-HCCA: Bandwidth Allocation Strategy in Internet of Vehicles with Dynamically Segmented Congestion Control. J. Commun. Inf. Netw. 2021, 6, 175–183. [Google Scholar] [CrossRef]
- Zhu, Y. Intelligent Congestion Control of Data Transmission in Low Earth Orbit Satellite Networks Based on Reinforcement Learning: Analysis and Optimization. Inf. Sci. 2024, 694, 121692. [Google Scholar] [CrossRef]
- Wang, F.; Yao, H.; Zhang, Q.; Wang, J.; Gao, R.; Guo, D.; Guizani, M. Dynamic Distributed Multi-Path Aided Load Balancing for Optical Data Center Networks. IEEE Trans. Netw. Serv. Manag. 2022, 19, 991–1005. [Google Scholar] [CrossRef]
- Xu, S.; Li, P.; Qi, F.; Guo, S.; Zhou, G.; Deng, W.; Li, Y. Load-Balancing and QoS Based Dynamic Resource Allocation Method for Smart Gird Fiber-Wireless Networks. Chin. J. Electron. 2019, 28, 1234–1243. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, R. Issues and challenges of load balancing techniques in cloud computing: A survey. ACM Comput. Surv. (CSUR) 2019, 51, 1–35. [Google Scholar] [CrossRef]
- Peng, G.; Wang, S.; Huang, T.; Li, F.; Zhao, K.; Huang, Y.; Xiong, Z. FastTS: Enabling Fault-Tolerant and Time-Sensitive Scheduling in Space-Terrestrial Integrated Networks. IEEE J. Sel. Areas Commun. 2024, 42, 3551–3565. [Google Scholar] [CrossRef]
- Zeng, G.; Zhan, Y.; Pan, X. Failure-Tolerant and Low-Latency Telecommand in Mega-Constellations: The Redundant Multi-Path Routing. IEEE Access 2021, 9, 34975–34985. [Google Scholar] [CrossRef]
- Mamun, M.A.A.; Li, M.; Pramanik, B.K. Development of Delay-Tolerant Networking Protocols for Reliable Data Transmission in Space Networks: A Simulation-Based Approach. IEEE Access 2024, 12, 178642–178658. [Google Scholar] [CrossRef]
- Sahu, C.; Parhi, D.R.; Kumar, P.B. An Approach to Optimize the Path of Humanoids using Adaptive Ant Colony Optimization. J. Bionic Eng. 2018, 15, 623–635. [Google Scholar] [CrossRef]
- Yurtkuran, A.; Emel, E. An adaptive artificial bee colony algorithm for global optimization. Appl. Math. Comput. 2015, 271, 1004–1023. [Google Scholar] [CrossRef]
- Arif, S.M.; Hussain, A.; Lie, T.T.; Ahsan, S.M.; Khan, H.A. Analytical Hybrid Particle Swarm Optimization Algorithm for Optimal Siting and Sizing of Distributed Generation in Smart Grid. J. Mod. Power Syst. Clean Energy 2020, 8, 1221–1230. [Google Scholar] [CrossRef]
- Wang, R.; Zhu, W.; Liu, G. Lagrange Relaxation Based Inter-satellite Links Scheduling for Satellite Networks. In Proceedings of the 6GN for Future Wireless Networks, Huizhou, China, 30–31 October 2021; Springer: Cham, Switzerland, 2022; pp. 3–15. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).