Mathematical Modeling of Economic Growth, Corruption, Employment and Inflation
Abstract
1. Introduction
2. The Proposed Mathematical Model
2.1. The Proposed Mathematical Model with Inflation
2.2. Positivity of the Model
3. Stability Analysis of the Model
3.1. Equilibrium Points
- The Trivial equilibrium point represents the complete absence of economic resources, corruption, unemployment, and inflation.
- The axial equilibrium point represents a state with no economic growth, no corruption, and no inflation with some unemployment level.
- The Axial equilibrium point depicts a state with maximum economic growth but without corruption, unemployment or inflation.
- The equilibrium point represents a state with maximum economic growth, no corruption, no inflation, and a specific unemployment level determined by job creation density and resource depletion rates.
- The interior equilibrium point with
- ,
- ,
- ,
- .
- The interior equilibrium point with
- ,
- ,
- ,
- ,
- .
3.2. Stability Analysis of Equilibrium Points
3.2.1. Stability Analysis of
3.2.2. Stability Analysis of
3.2.3. Stability Analysis of
- . This is always certain since .
- . Thus, this guarantees that .
- . If then one obtain that . If then .
3.2.4. Stability Analysis of
3.2.5. Stability Analysis of
- if that is, ,
- iforthat is,since ,
- ifthat is,,
- iforthat is,since .
- (a)
- Fixed parameters values for and kept free.
- (b)
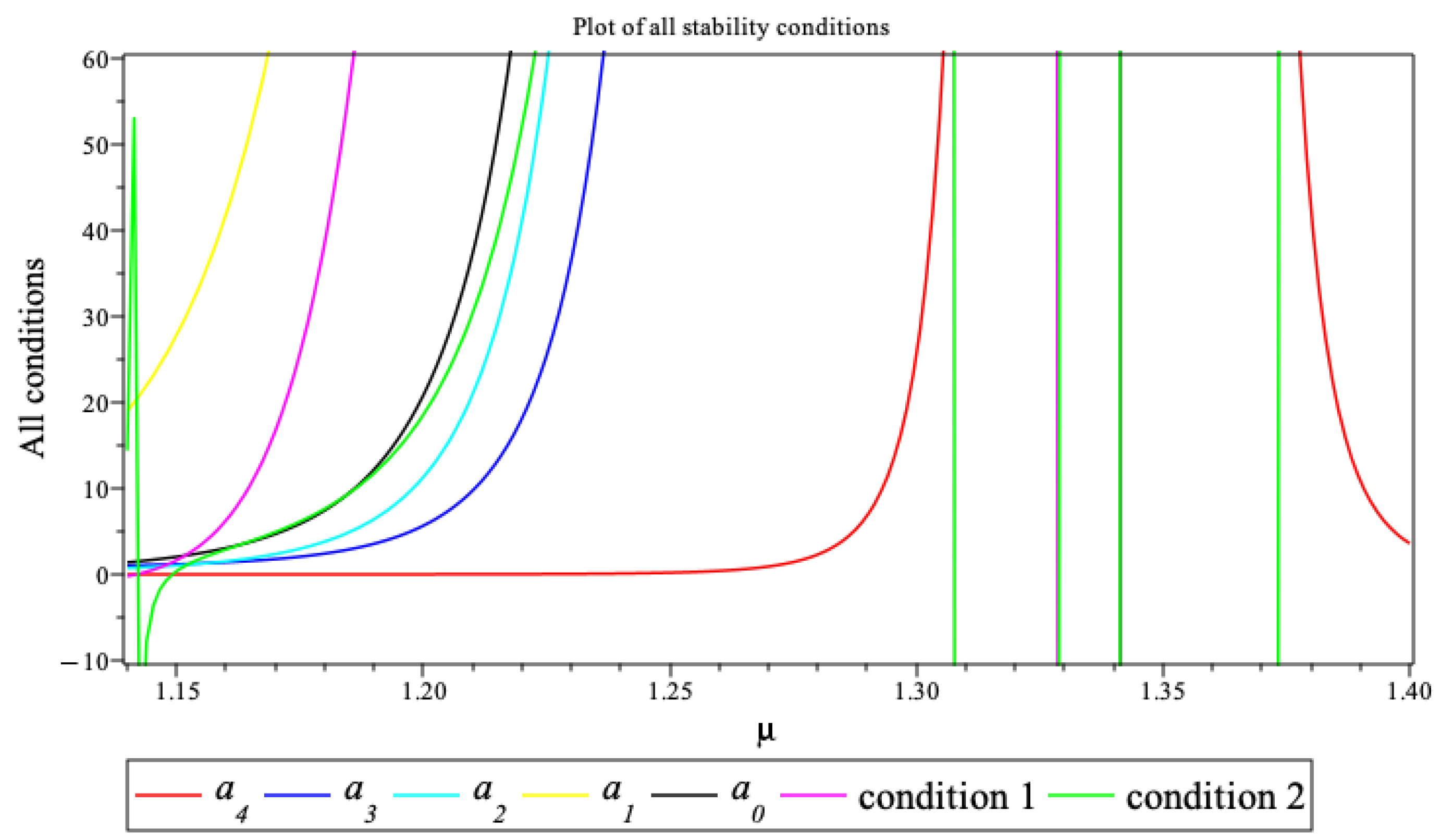
- The Jacobian (4) was evaluated at the equilibrium point and the corresponding characteristic polynomial was analyzed using the Routh–Hurwitz stability criteria to ascertain the interval for where the stability criteria is satisfied.
- (c)
- Find the Routh–Hurwitz stability criteria in terms of by using the polynomial . In this case, the Routh–Hurwitz stability criteria requires
- for .
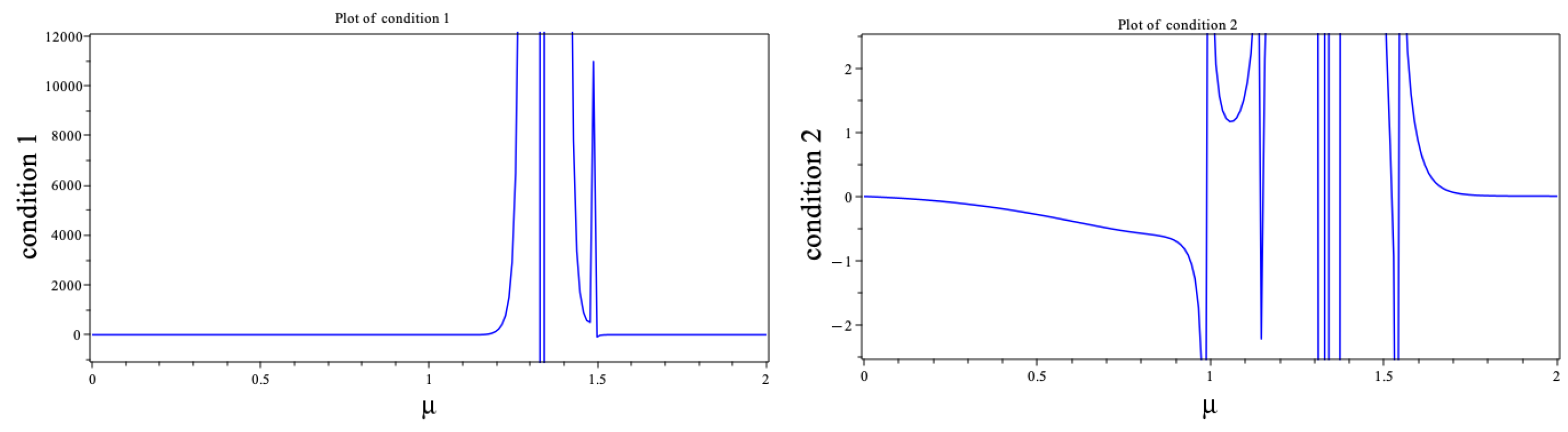
- Condition 1: .
- Condition 2: .
- (d)
- The stability conditions are visualized by plots due to the complexity of the conditions.
3.2.6. Stability Analysis of
- if that is, .
- iforthat is,since .
- ifthat is,.
- iforthat is,since .
4. Numerical Results
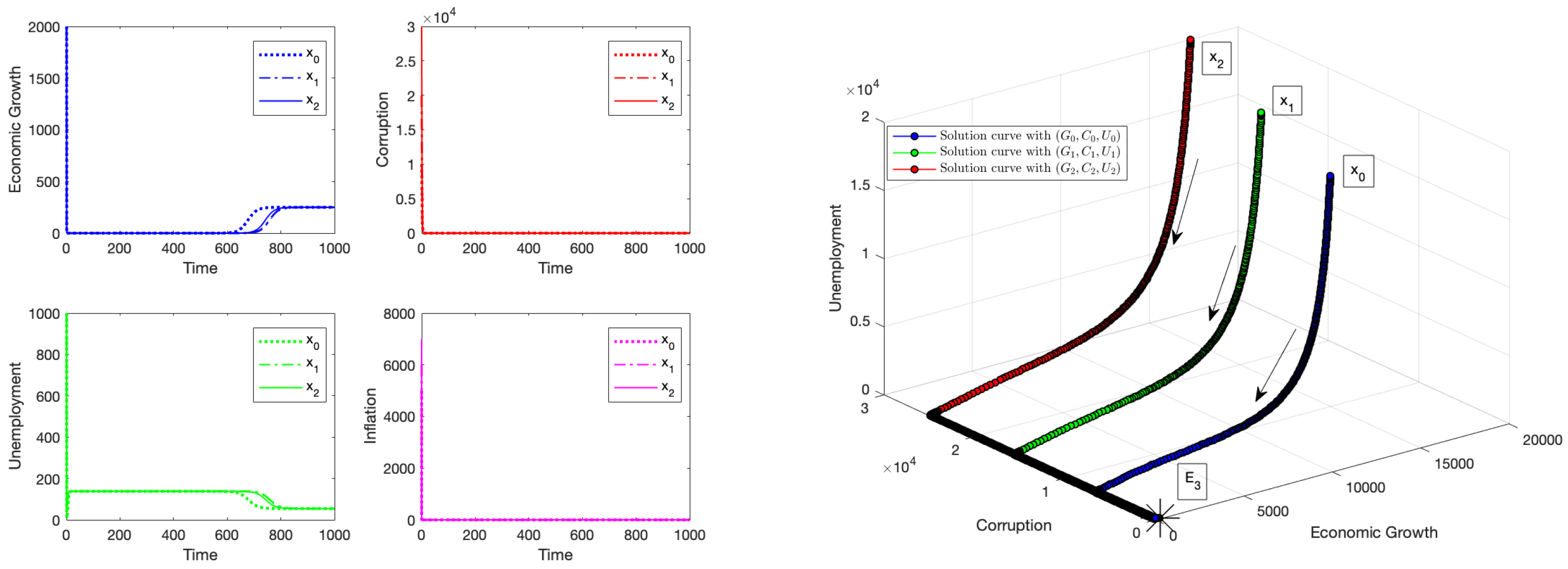
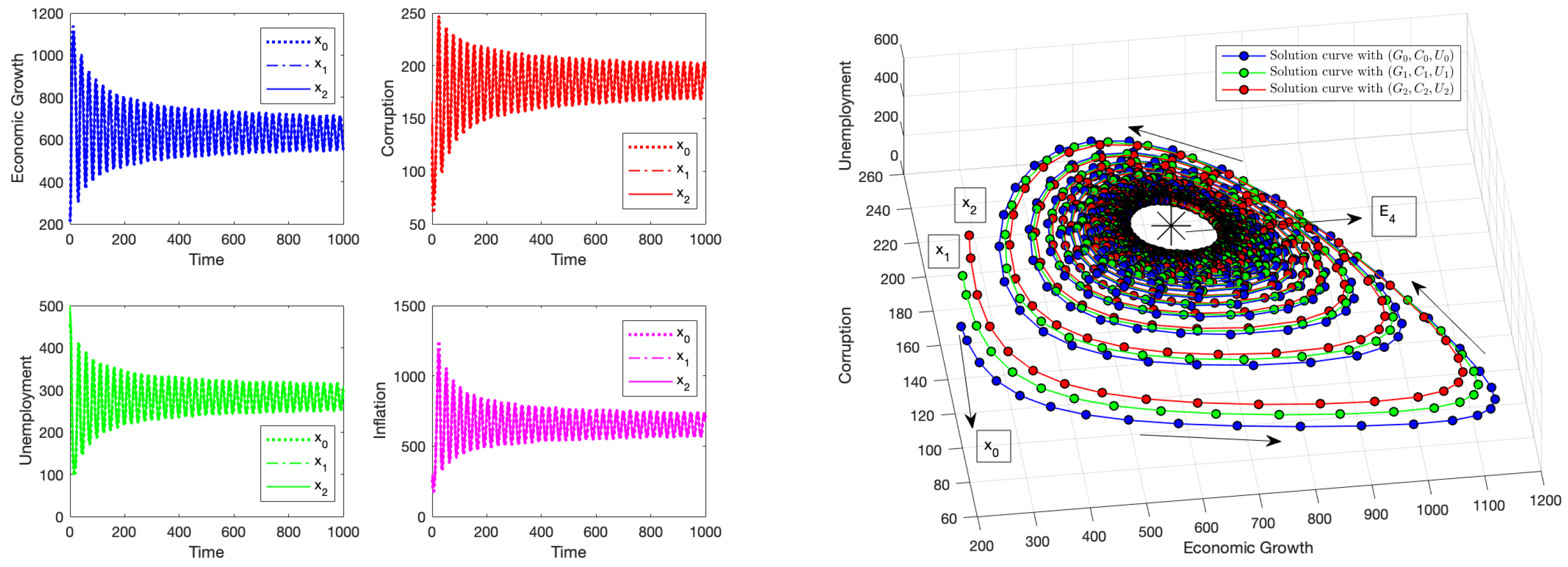
4.1. Numerical Simulation: Instability of the Equilibrium Point
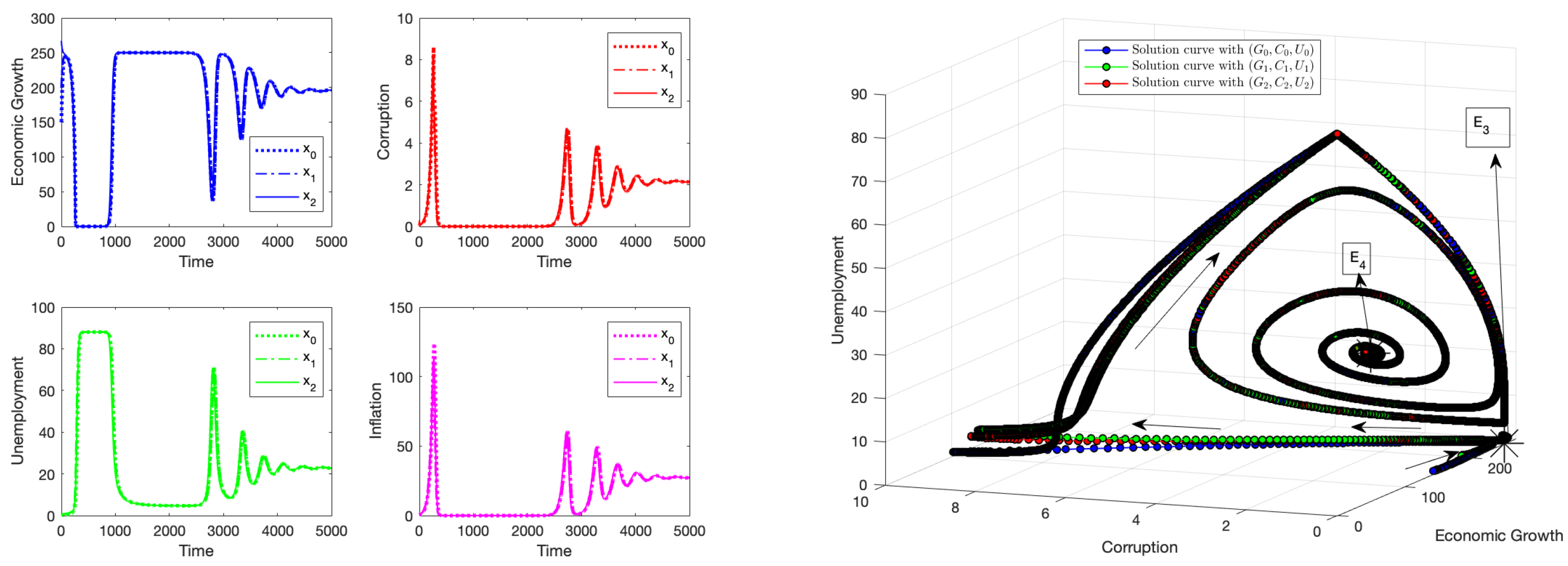
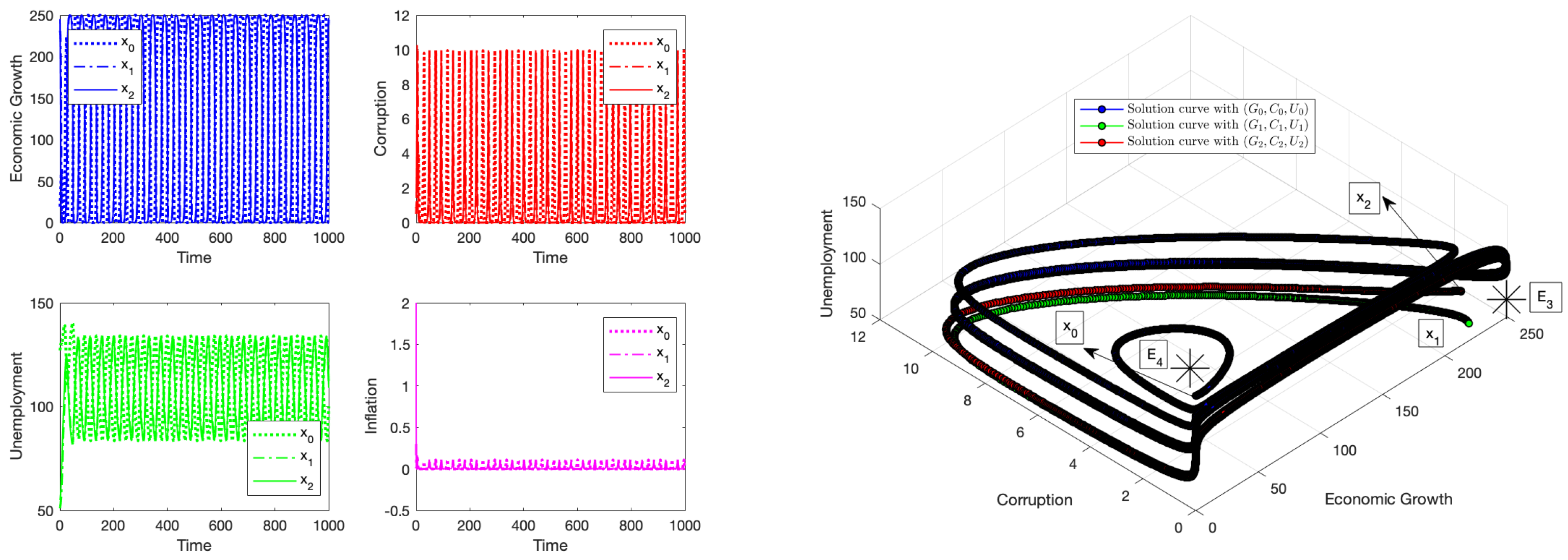
4.2. Numerical Simulation: Instability of the Equilibrium Point
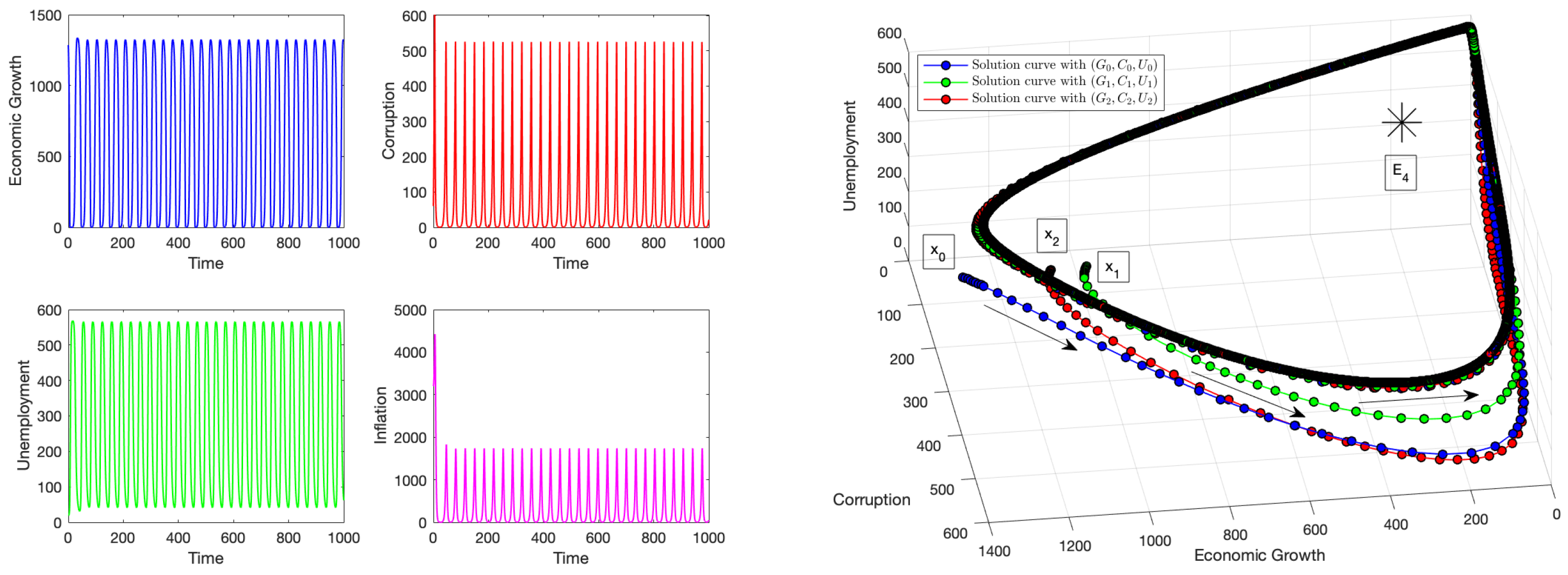
4.3. Numerical Simulation: Instability of the Equilibrium Point
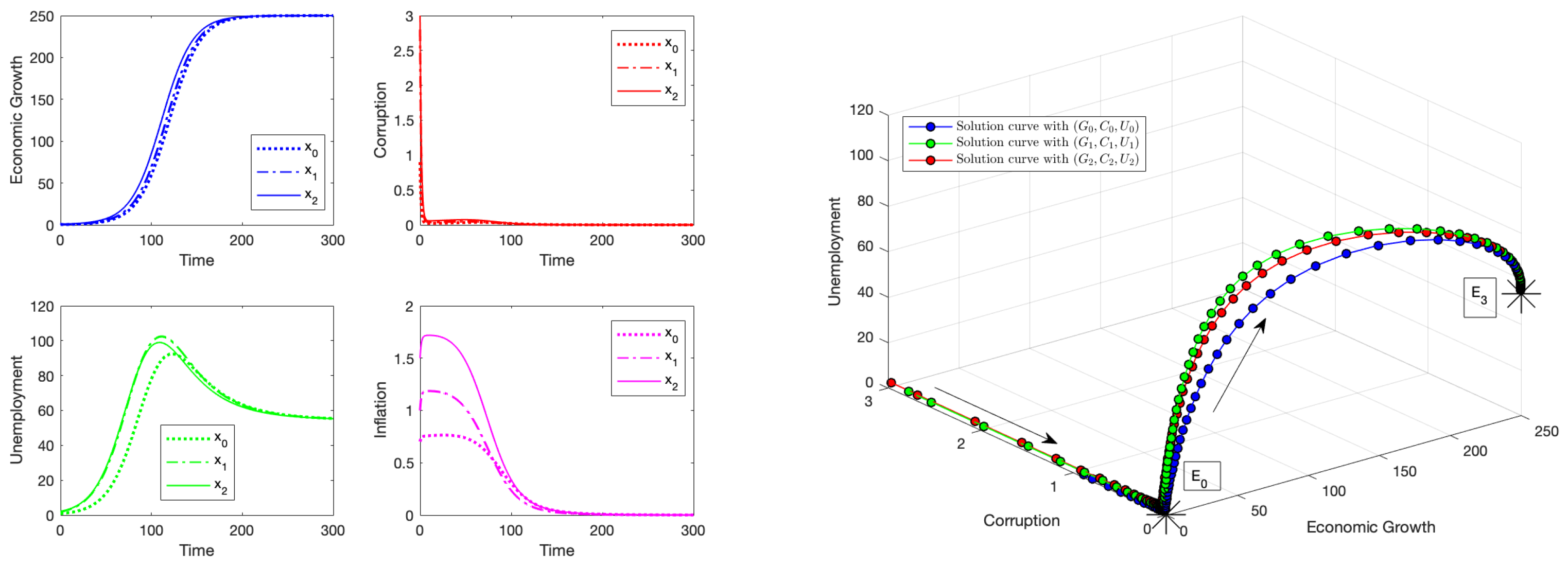
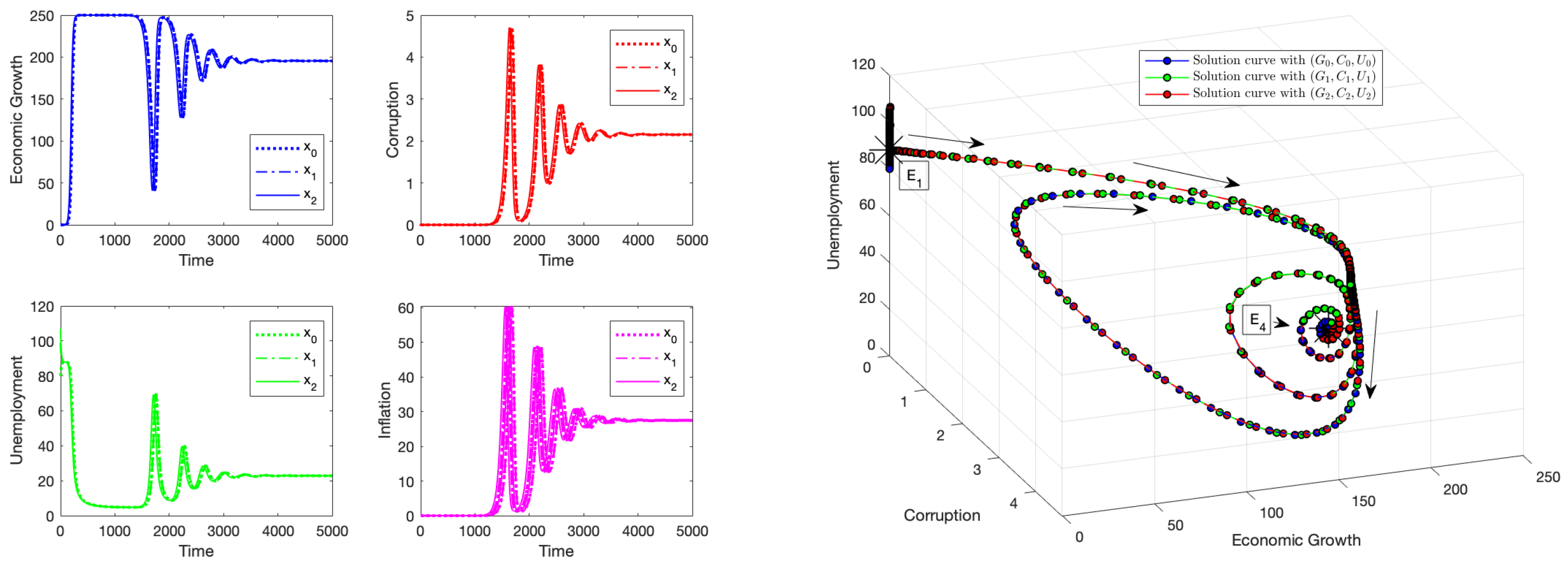
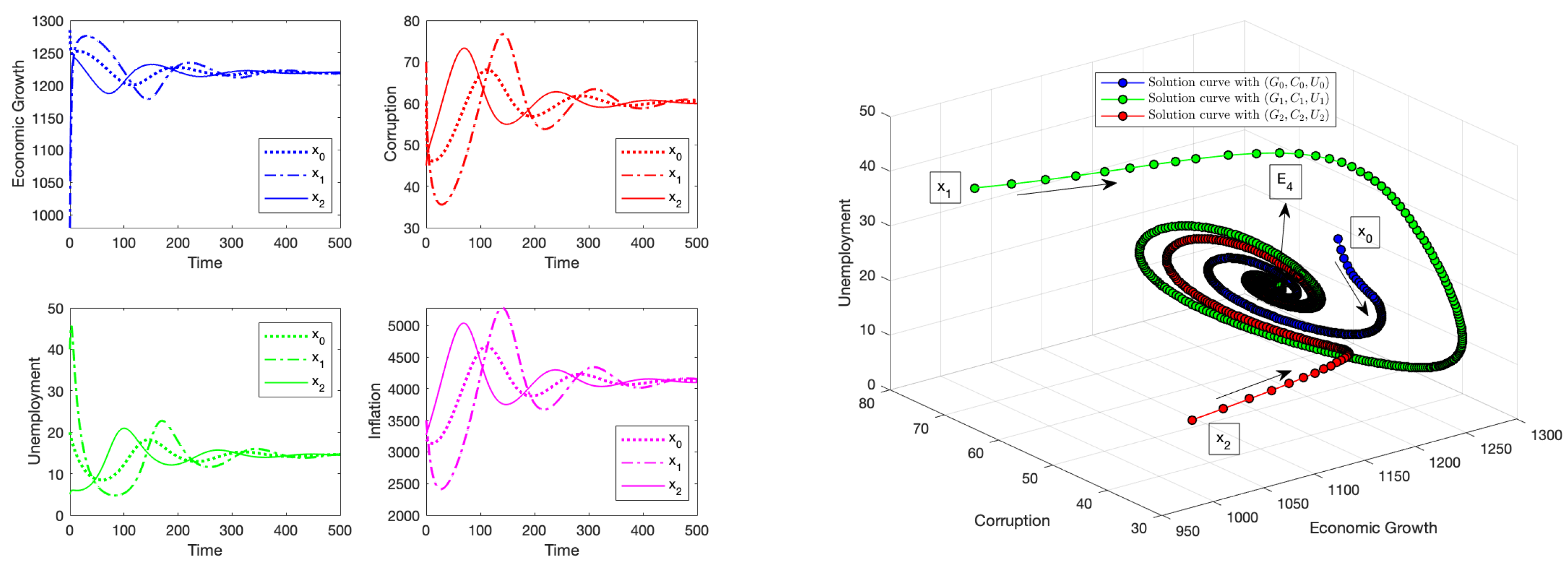
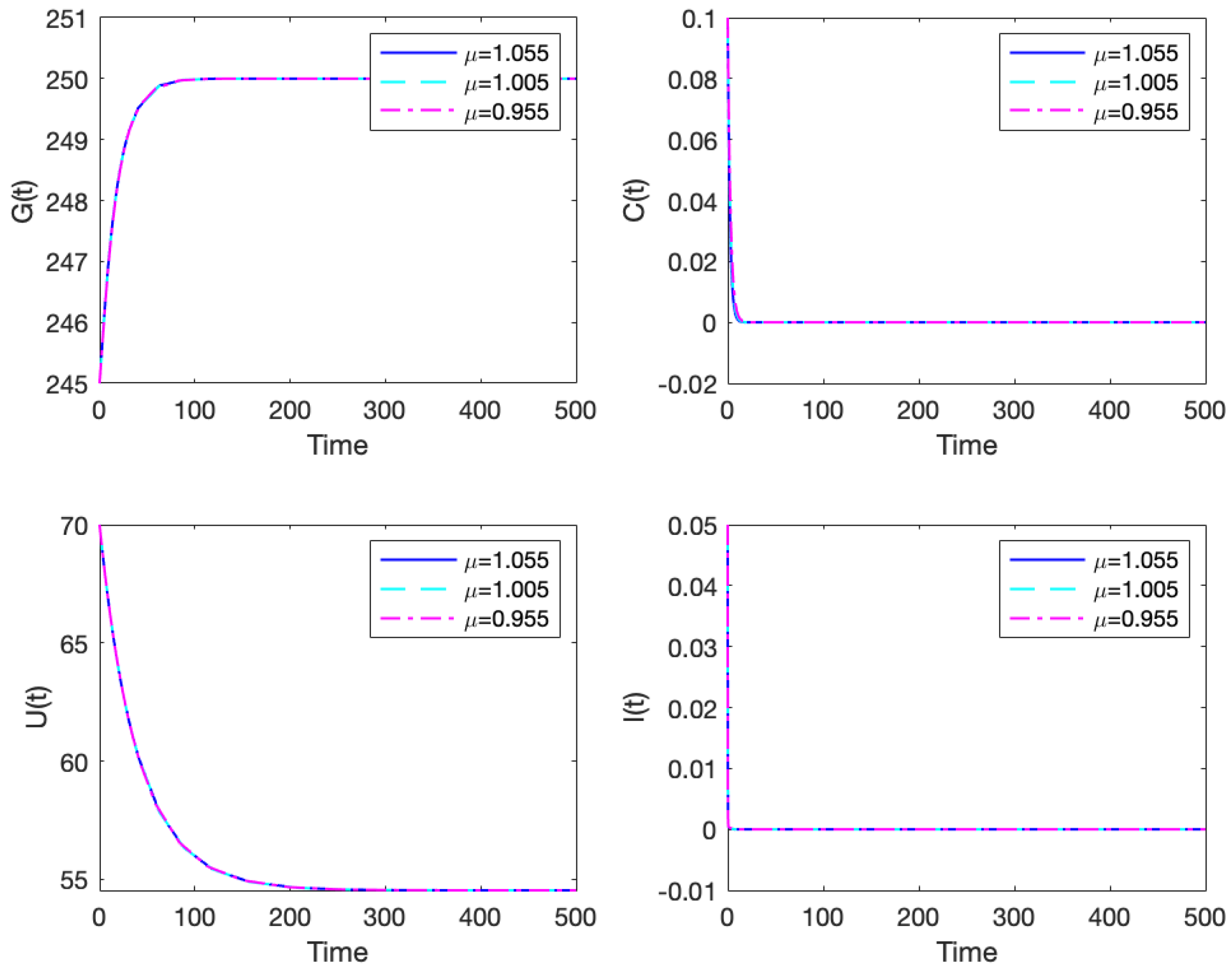
4.4. Numerical Results Related to the Stability of Equilibrium Point
4.5. Numerical Results Related to the Stability of Equilibrium Point
5. Sensitivity Analysis
5.1. Sensitivity Analysis for
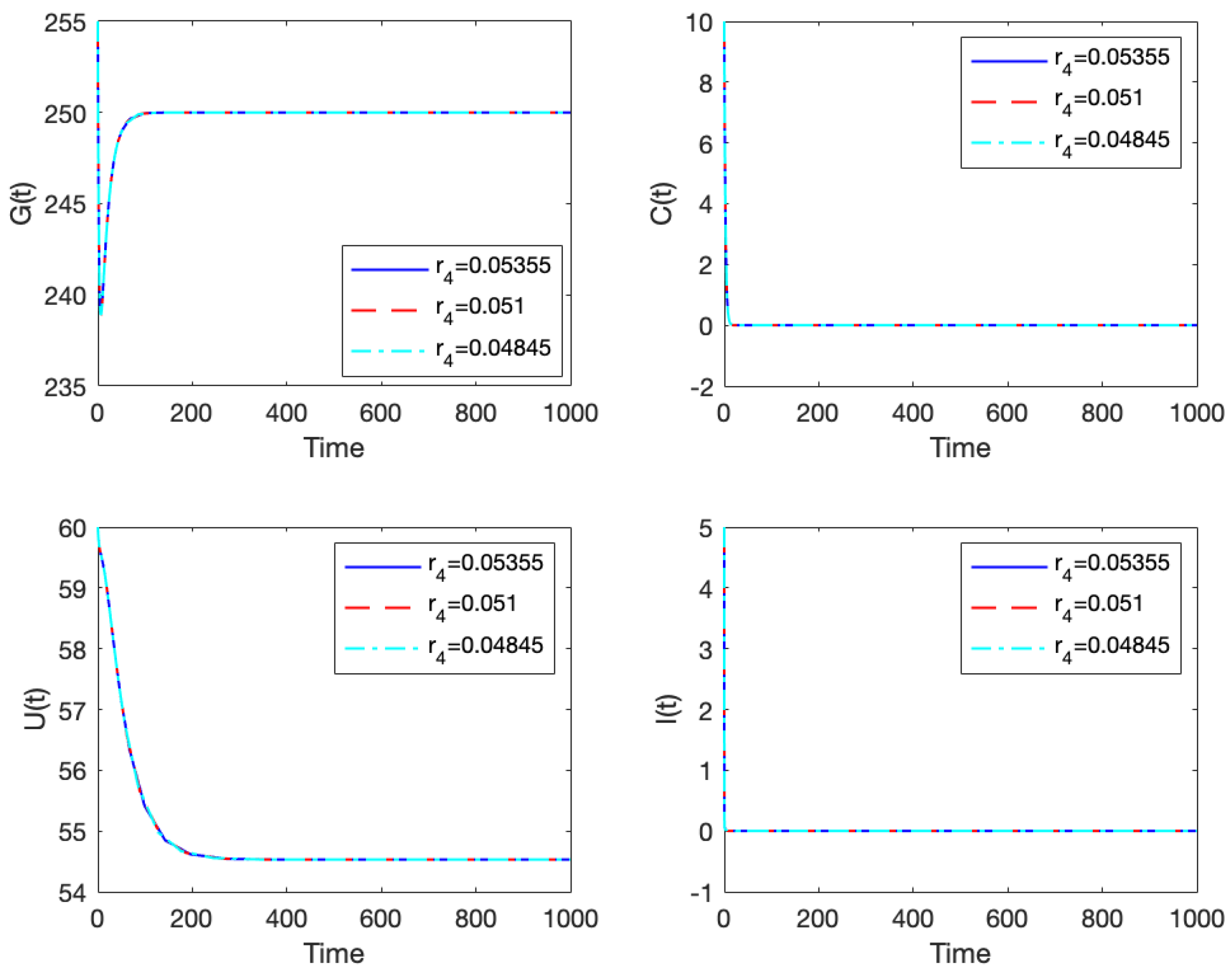
- Effects of Inflation using parameters and hEconomically and socially, an increase or decrease in inflation affects economic growth, corruption, and unemployment, and it is crucial to study how the increase or decrease in inflation affects these state variables. When a nation sets up adequate policies to curb inflation, it helps the general welfare. These policies are factors that decrease inflation through the parameters h and . We will study this effect using and h with a increase and decrease. First, we use the parameter values , and . Figure 11 and Figure 12 show the effect of the variation of the parameters and h on the dynamics of system (2), respectively. It can be observed that variations of to parameters and h do not produce a notable change in the output of system (2). This means that, for the economy to experience a significant reduction in inflation, higher inflation curtailment factors should be enforced. That is, huge increases in the factors that curb inflation are critical in ensuring noteworthy and positive outcomes.
- Effects of corruption using parameter
5.2. Sensitivity Analysis for
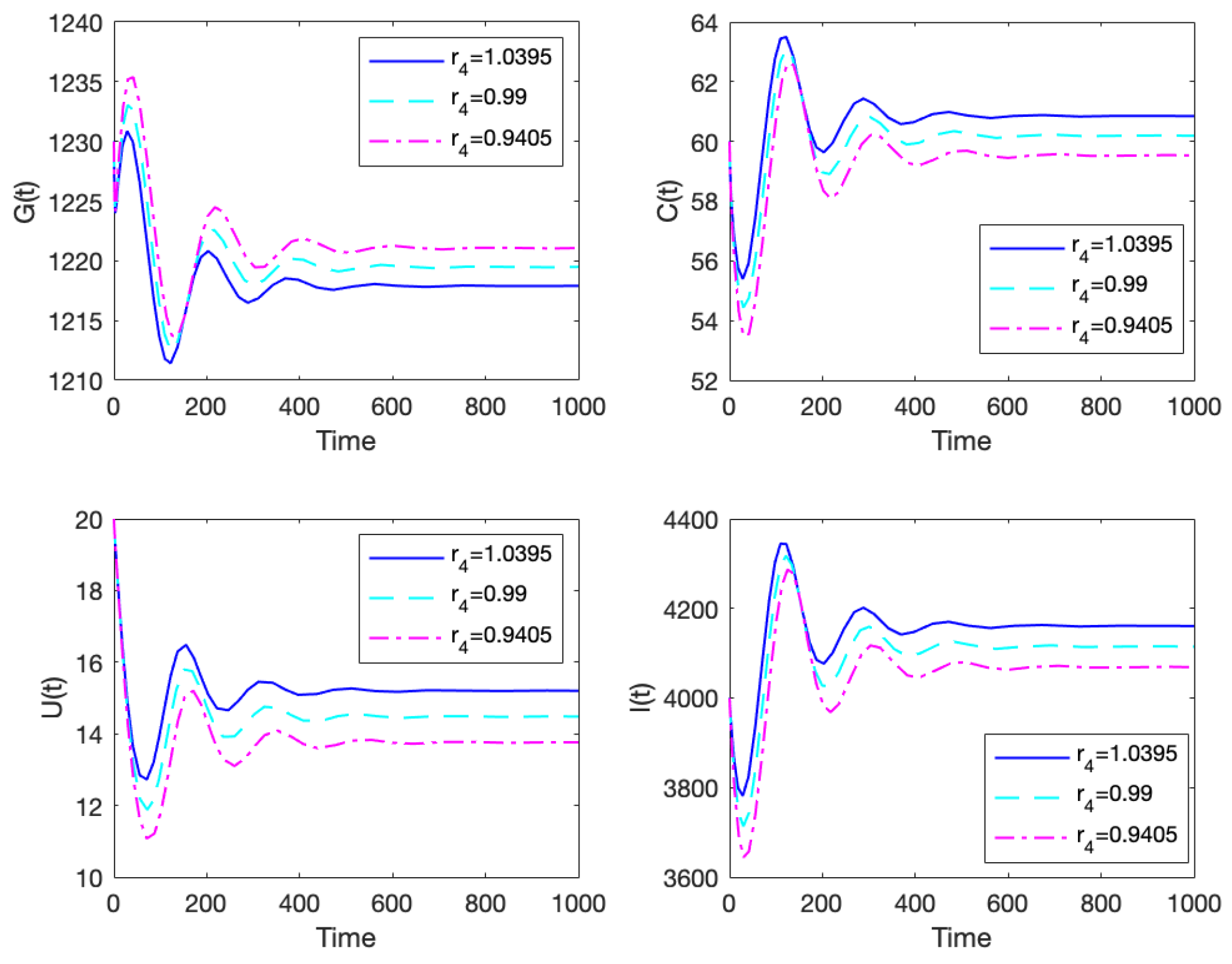
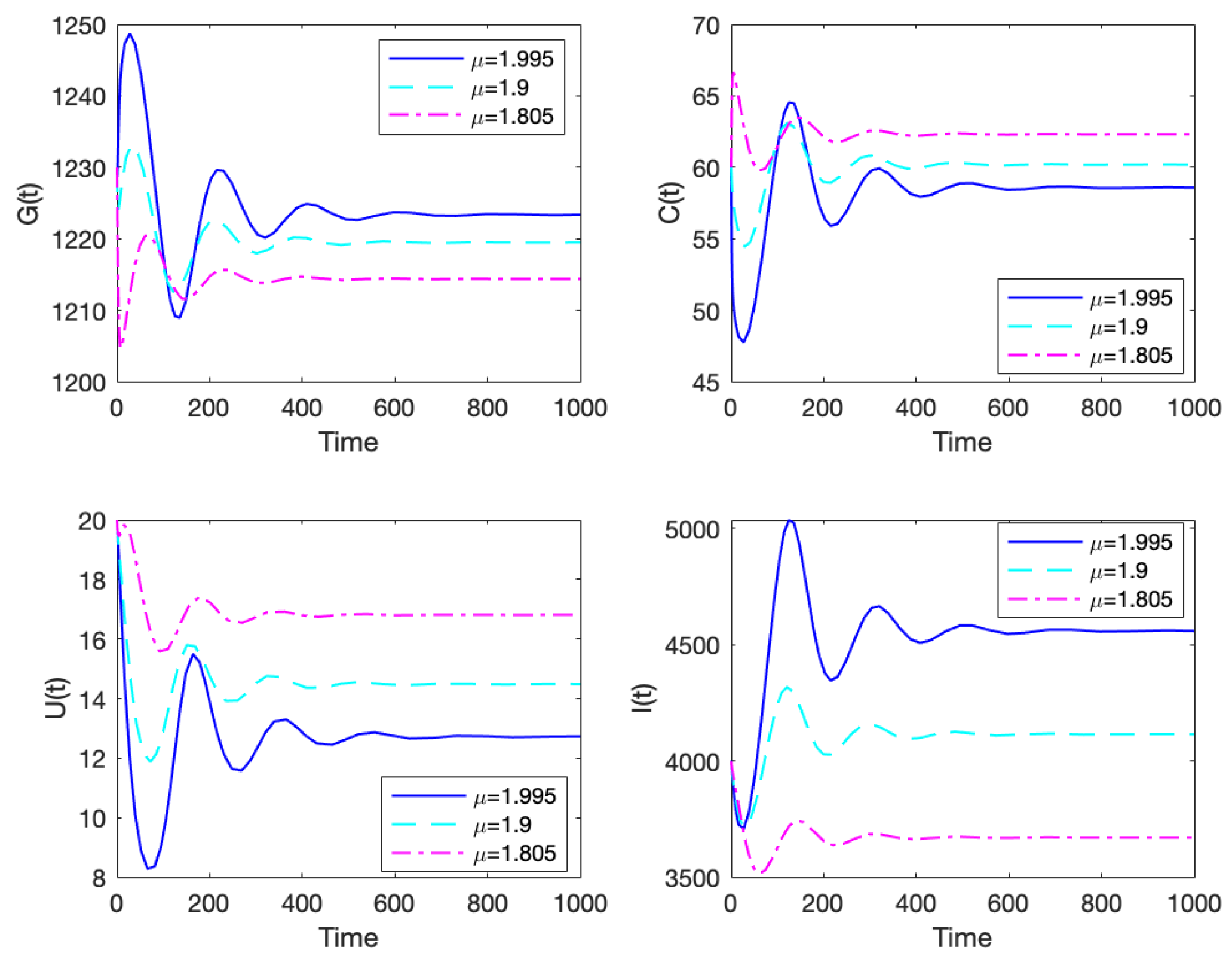
- Effects of Inflation using parameters and hThis section is devoted to the sensitivity analysis of system (2) for the equilibrium point by varying the input in key parameters of the model. The control of inflation has been the top game for policymakers, especially in recent times. Striving to keep the inflation rate at the required level that promotes economic growth is paramount in any nation’s economy. Research has shown that there can be no positive outcome for economic growth and employment if a nation’s economy is run on high inflation [86]. We use the parameter values are used with a variation for . Figure 14 shows that even a little variation in produces a significant change in the system. As increases, inflation, corruption, and unemployment increase while economic growth reduces and vice versa. This is a typical scenario seen in several economies around the world. When the cost of goods and services increases, many companies struggle to stay in business, and a direct implication of this is laying off employees, increasing the unemployment rate. Again, these high rates will reduce the demand for goods and services, leading to a reduction in the labor force.Next, we investigate the inflation parameter h (factors that directly decrease inflation) using the parameter values with a variation for h. Figure 15 shows a significant change in the outcome when varying h. As h increases (increase in the factors that directly curb inflation), economic growth improves, corruption and unemployment decline, and vice versa. Thus, for any ideal economic scenario, policymakers should focus on keeping inflation levels in check by establishing and enforcing factors like decreased government spending and money supply, monetary and fiscal policies. For instance, in the USA, the Federal Reserve adjusts the rates in order to control inflation [87,88].
- Effects of Corruption using the parameterThe parameter represents factors that directly reduce corruption, and it is a crucial parameter to study any economic scenario close to . Economically and socially, corruption plays a role in the progression or the retrogression of a nation’s economy [89,90]. If there are more factors enforced to curb corruption, a nation’s economic growth will flourish, which in turn aids in the reduction in unemployment, corruption, and inflation rates [89]. We use the parameter values , with a variation for . Figure 16 shows the impact caused by a variation of . The system is sensitive to corruption. It tells us that, when there are more factors that aid in corruption reduction, economic growth blossoms, unemployment reduces, inflation increases, and vice versa. Reduced corruption can sometimes lead to a temporary increase in inflation because when a government becomes less corrupt, it often needs to implement new policies and procedures to manage the economy more efficiently, which can disrupt existing market dynamics and lead to short-term price fluctuations, particularly if the government is also trying to increase transparency in pricing mechanisms. Socioeconomic relationships are sometimes not always black and white since there are other sub-socioeconomic phenomena all interwoven in a nation’s economy [91].
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
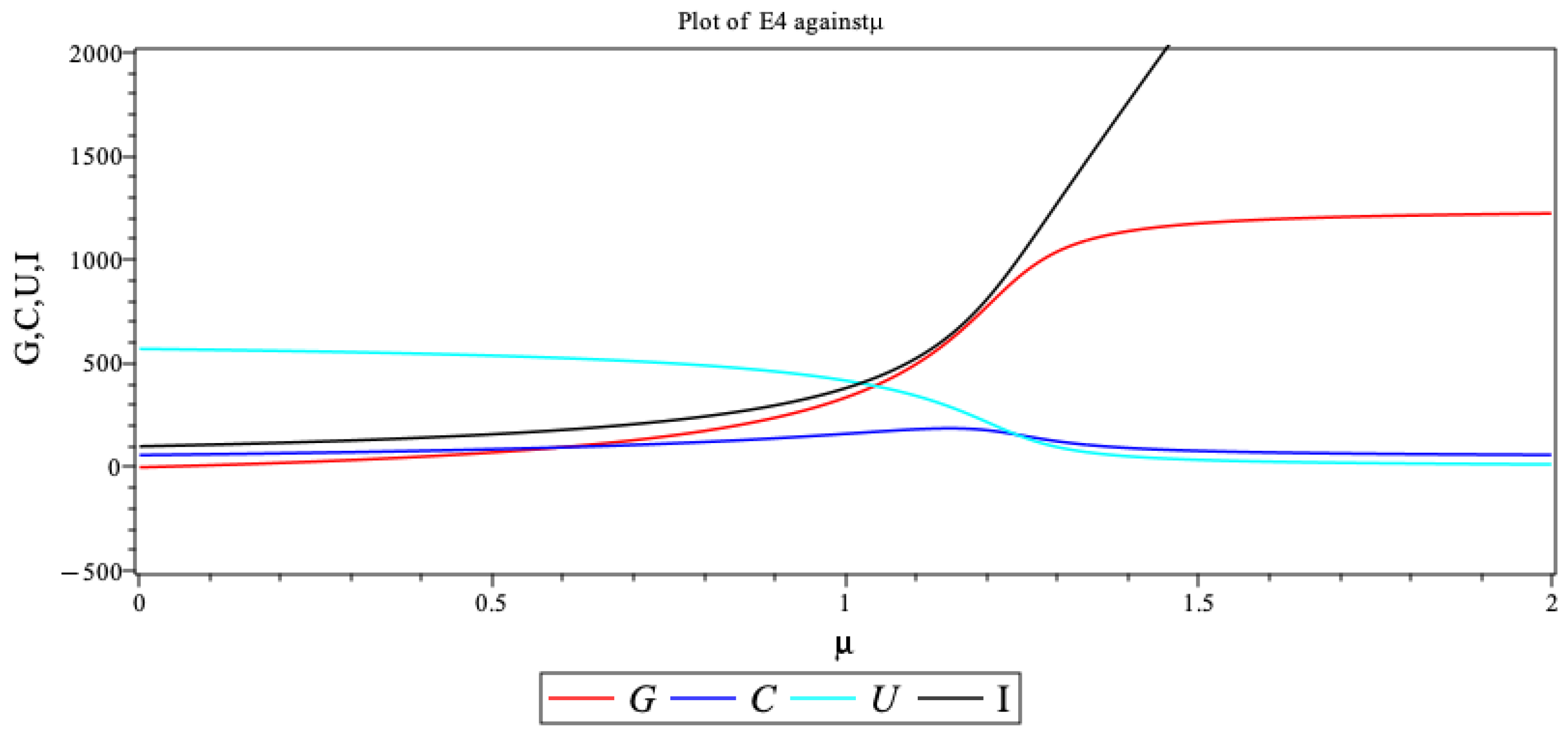

- for
- condition 1:
- condition 2:


References
- De la Fuente, A.; De La Fuente, A. Mathematical Methods and Models for Economists; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Gandolfo, G. Economic Dynamics: Methods and Models; Elsevier: Amsterdam, The Netherlands, 1971; Volume 16. [Google Scholar]
- Hritonenko, N.; Yatsenko, Y. Mathematical Modeling in Economics, Ecology and the Environment; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Morgan, M.S.; Knuuttila, T. Models and modelling in economics. Philos. Econ. 2012, 13, 49–87. [Google Scholar]
- Radzicki, M.J. System dynamics and its contribution to economics and economic modeling. In System Dynamics: Theory and Applications; Springer: New York, NY, USA, 2020; pp. 401–415. [Google Scholar]
- Zhang, W.B. Differential Equations, Bifurcations and Chaos in Economics; World Scientific Publishing Company: Singapore, 2005; Volume 68. [Google Scholar]
- Katsouleas, G.; Chalikias, M.; Skordoulis, M.; Sidiropoulos, G. A Differential Equations Analysis of Stock Prices. In Proceedings of the Economic and Financial Challenges for Eastern Europe: Proceedings of the 9th International Conference on the Economies of the Balkan and Eastern European Countries in the Changing World (EBEEC); Springer: Berlin/Heidelberg, Germany, 2019; pp. 361–365. [Google Scholar]
- Arbex, M.; Perobelli, F.S. Solow meets Leontief: Economic growth and energy consumption. Energy Econ. 2010, 32, 43–53. [Google Scholar] [CrossRef]
- Boyko, A.; Kukartsev, V.; Tynchenko, V.; Eremeev, D.; Kukartsev, A.; Tynchenko, S. Simulation-dynamic model of long-term economic growth using Solow model. J. Phys. Conf. Ser. 2019, 1353, 012138. [Google Scholar]
- Brock, W.A.; Taylor, M.S. The green Solow model. J. Econ. Growth 2010, 15, 127–153. [Google Scholar]
- Solow, R.M. Technical progress, capital formation, and economic growth. Am. Econ. Rev. 1962, 52, 76–86. [Google Scholar]
- Burger, M.; Caffarelli, L.; Markowich, P.A. Partial differential equation models in the socio-economic sciences. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2014, 372, 20130406. [Google Scholar]
- González-Parra, G.; Chen-Charpentier, B.; Arenas, A.J.; Díaz-Rodríguez, M. Mathematical modeling of physical capital diffusion using a spatial Solow model: Application to smuggling in Venezuela. Economies 2022, 10, 164. [Google Scholar] [CrossRef]
- Puu, T.; Puu, T. Nonlinear Economic Dynamics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Reinecke, J.; Schmidt, P.; Weick, S. Dynamic modeling with structural equations and stochastic differential equations: Applications with the German Socio-Economic Panel. Qual. Quant. 2005, 39, 483–506. [Google Scholar]
- Buedo-Fernández, S.; Liz, E. On the stability properties of a delay differential neoclassical model of economic growth. Electron. J. Qual. Theory Differ. Equ. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Erman, S. Stability Analysis of Some Dynamic Economic Systems Modeled by State-Dependent Delay Differential Equations. In Global Approaches in Financial Economics, Banking, and Finance; Dincer, H., Hacioglu, Ü., Yüksel, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 227–240. [Google Scholar] [CrossRef]
- Krawiec, A.; Szydłowski, M. Economic growth cycles driven by investment delay. Econ. Model. 2017, 67, 175–183. [Google Scholar]
- Matsumoto, A.; Szidarovszky, F. Delay differential nonlinear economic models. In Nonlinear Dynamics in Economics, Finance and Social Sciences: Essays in Honour of John Barkley Rosser Jr; Springer: Berlin/Heidelberg, Germany, 2009; pp. 195–214. [Google Scholar]
- Ruzgas, T.; Jankauskienė, I.; Zajančkauskas, A.; Lukauskas, M.; Bazilevičius, M.; Kaluževičiūtė, R.; Arnastauskaitė, J. Solving Linear and Nonlinear Delayed Differential Equations Using the Lambert W Function for Economic and Biological Problems. Mathematics 2024, 12, 2760. [Google Scholar] [CrossRef]
- Segura, J.; Franco, D.; Perán, J. Long-run economic growth in the delay spatial Solow model. Spat. Econ. Anal. 2023, 18, 158–172. [Google Scholar]
- Özbay, H.; Sağlam, H.Ç.; Yüksel, M.K. Hopf cycles in one-sector optimal growth models with time delay. Macroecon. Dyn. 2017, 21, 1887–1901. [Google Scholar]
- Aniţa, S.; Arnăutu, V.; Capasso, V. An Introduction to Optimal Control Problems in Life Sciences and Economics: From Mathematical Models to Numerical Simulation with MATLAB; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Chukwu, E. Control of nonlinear delay differential equations in W2 (1) with economic applications. Appl. Math. Comput. 1997, 85, 17–59. [Google Scholar]
- De Feo, F.; Federico, S.; Świech, A. Optimal control of stochastic delay differential equations and applications to path-dependent financial and economic models. SIAM J. Control Optim. 2024, 62, 1490–1520. [Google Scholar]
- Halanay, A.; Samuel, J. Differential Equations, Discrete Systems and Control: Economic Models; Springer Science & Business Media: Berlin, Germany, 2013; Volume 3. [Google Scholar]
- Kiselev, Y.N.; Orlov, M. Optimal resource allocation program in a two-sector economic model with a Cobb-Douglas production function. Differ. Equ. 2010, 46, 1750–1766. [Google Scholar]
- Babakordi, F.; Allahviranloo, T.; Shahriari, M.; Catak, M. Fuzzy Laplace transform method for a fractional fuzzy economic model based on market equilibrium. Inf. Sci. 2024, 665, 120308. [Google Scholar]
- Chen-Charpentier, B.; González-Parra, G.; Arenas, A.J. Fractional order financial models for awareness and trial advertising decisions. Comput. Econ. 2016, 48, 555–568. [Google Scholar]
- Johansyah, M.D.; Supriatna, A.K.; Rusyaman, E.; Saputra, J. Application of fractional differential equation in economic growth model: A systematic review approach. AIMS Math. 2021, 6, 10266–10280. [Google Scholar]
- Škovránek, T.; Podlubny, I.; Petráš, I. Modeling of the national economies in state-space: A fractional calculus approach. Econ. Model. 2012, 29, 1322–1327. [Google Scholar]
- Al-Hdaibat, B. Computational Dynamical Systems Analysis: Bogdanov-Takens Points and an Economic Model. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2015. [Google Scholar]
- Manfredi, P.; Fanti, L. Cycles in dynamic economic modelling. Econ. Model. 2004, 21, 573–594. [Google Scholar]
- Pribylova, L. Bifurcation routes to chaos in an extended Van der Pol’s equation applied to economic models. Electron. J. Differ. Equ. (EJDE) 2009, 2009, 1–21. [Google Scholar]
- Dockner, E.J.; Feichtinger, G. On the optimality of limit cycles in dynamic economic systems. J. Econ. 1991, 53, 31–50. [Google Scholar]
- Feichtinger, G. Limit cycles in dynamic economic systems. Ann. Oper. Res. 1992, 37, 313–344. [Google Scholar]
- Feichtinger, G.; Novak, A.; Wirl, F. Limit cycles in intertemporal adjustment models: Theory and applications. J. Econ. Dyn. Control 1994, 18, 353–380. [Google Scholar]
- Kryuchkov, V.; Solomonovich, M.; Anton, C. Moving limit cycles model of an economic system. In Proceedings of the Numerical Analysis and Its Applications: 6th International Conference, NAA 2016, Lozenetz, Bulgaria, 15–22 June 2016; Revised Selected Papers 6. Springer: Berlin/Heidelberg, Germany, 2017; pp. 456–463. [Google Scholar]
- Markakis, M.; Douris, P. Stability and analytical approximation of limit cycles in Hopf bifurcations of four-dimensional economic models. Appl. Math. Sci. 2014, 8, 3697–3990. [Google Scholar]
- Araujo, R.A.; Flaschel, P.; Moreira, H.N. Limit cycles in a model of supply-side liquidity/profit-rate in the presence of a Phillips curve. Economia 2020, 21, 145–159. [Google Scholar]
- Asada, T.; Demetrian, M.; Zimka, R. The stability of normal equilibrium point and the existence of limit cycles in a simple Keynesian macrodynamic model of monetary policy. In Essays in Economic Dynamics: Theory, Simulation Analysis, and Methodological Study; Springer: Singapore, 2016; pp. 145–162. [Google Scholar]
- Bazán Navarro, C.E.; Benazic Tomé, R.M. Structural Stability Analysis in a Dynamic IS-LM-AS Macroeconomic Model with Inflation Expectations. Int. J. Differ. Equ. 2022, 2022, 5026061. [Google Scholar]
- Ifeacho, O.; González-Parra, G. Hopf Bifurcations in a Mathematical Model for Economic Growth, Corruption, and Unemployment: Computation of Economic Limit Cycles. Axioms 2025, 14, 173. [Google Scholar] [CrossRef]
- Çalış, Y.; Demirci, A.; Özemir, C. Hopf bifurcation of a financial dynamical system with delay. Math. Comput. Simul. 2022, 201, 343–361. [Google Scholar]
- Baráková, L. Asymptotic Behaviour and Hopf Bifurcation of a Three-Dimensional Nonlinear Autonomous System. Georgian Math. J. 2002, 9, 207–226. [Google Scholar]
- Marsden, J.E.; McCracken, M. The Hopf Bifurcation and Its Applications; Springer Science & Business Media: Berlin, Germany, 2012; Volume 19. [Google Scholar]
- Harari, G.; Monteiro, L. Bifurcations in a Model of Criminal Organizations and a Corrupt Judiciary. Entropy 2024, 26, 906. [Google Scholar] [CrossRef] [PubMed]
- Callen, T. Gross Domestic Product: An Economy’s All; International Monetary Fund: Washington, DC, USA, 2012. [Google Scholar]
- McCusker, J.J. Estimating early American gross domestic product. Hist. Methods J. Quant. Interdiscip. Hist. 2000, 33, 155–162. [Google Scholar]
- Tacchella, A.; Mazzilli, D.; Pietronero, L. A dynamical systems approach to gross domestic product forecasting. Nat. Phys. 2018, 14, 861–865. [Google Scholar] [CrossRef]
- Makinde, O.S.; Adepetun, A.O.; Oseni, B.M. Modeling the gross domestic product of Nigeria from 1985 to 2018. Commun. Stat. Case Stud. Data Anal. Appl. 2020, 6, 353–363. [Google Scholar]
- Mimkes, J. Stokes integral of economic growth: Calculus and the Solow model. Phys. Stat. Mech. Its Appl. 2010, 389, 1665–1676. [Google Scholar]
- Eggoh, J.C.; Khan, M. On the nonlinear relationship between inflation and economic growth. Res. Econ. 2014, 68, 133–143. [Google Scholar] [CrossRef]
- Onwuemeka, I.O.; Obiukwu, S.I.; Kelechi Chibueze3 Okeke, Q. Is there a Trade-Off between Inflation and Unemployment: The Case of Nigeria. Int. J. Res. Innov. Soc. Sci. 2024, 8, 2606–2620. [Google Scholar]
- Pittaluga, G.B.; Seghezza, E.; Morelli, P. The political economy of hyperinflation in Venezuela. Public Choice 2021, 186, 337–350. [Google Scholar] [CrossRef]
- Restuccia, D. The monetary and fiscal history of Venezuela: 1960–2016. In University of Chicago, Becker Friedman Institute for Economics Working Paper; University of Chicago: Chicago, IL, USA, 2018. [Google Scholar]
- Belda Mullor, G. Citizens’ Attitude towards Political Corruption and the Impact of Social Media. Ph.D. Thesis, Universitat Jaume I, Castellón de la Plana, Spain, 2018. [Google Scholar]
- Okoye, R. Nigeria has lost 400 bn oil revenue to corruption since Independence–Ezekwesili. Dly. Post Newsp. 2012, 31, 2012. [Google Scholar]
- Sassi, S.; Gasmi, A. The Dynamic Relationship Between Corruption—Inflation: Evidence from Panel Vector Autoregression. Jpn. Econ. Rev. 2017, 68, 458–469. [Google Scholar]
- Al-Marhubi, F.A. Corruption and inflation. Econ. Lett. 2000, 66, 199–202. [Google Scholar]
- Aloke, S.N. Analyzing Corruption Dynamics and Control Measures in Nigeria: A Mathematical Model. Asian J. Pure Appl. Math. 2023, 5, 493–511. [Google Scholar]
- Delgadillo-Alemán, S.E.; Kú-Carrillo, R.A.; Torres-Nájera, A. A Corruption Impunity Model Considering Anticorruption Policies. Math. Comput. Appl. 2024, 29, 81. [Google Scholar] [CrossRef]
- Gutema, T.W.; Wedajo, A.G.; Koya, P.R. A mathematical analysis of the corruption dynamics model with optimal control strategy. Front. Appl. Math. Stat. 2024, 10, 1387147. [Google Scholar]
- Stepantsov, M. Simulation of the “Power–Society–Economics” System with Elements of Corruption Based on Cellular Automata. Math. Model. Comput. Simulations 2018, 10, 249–254. [Google Scholar]
- Teklu, S.W. Insight into the optimal control strategies on corruption dynamics using fractional order derivatives. Sci. Afr. 2024, 23, e02069. [Google Scholar]
- Dritsaki, C.; Dritsaki, M. Phillips curve inflation and unemployment: An empirical research for Greece. Int. J. Comput. Econ. Econom. 2013, 3, 27–42. [Google Scholar]
- Ho, S.Y.; Iyke, B.N. Unemployment and inflation: Evidence of a nonlinear Phillips curve in the Eurozone. J. Dev. Areas 2019, 53, 4. [Google Scholar]
- Ormerod, P.; Rosewell, B.; Phelps, P. Inflation/unemployment regimes and the instability of the Phillips curve. Appl. Econ. 2013, 45, 1519–1531. [Google Scholar]
- Ravenna, F.; Walsh, C.E. Vacancies, unemployment, and the Phillips curve. Eur. Econ. Rev. 2008, 52, 1494–1521. [Google Scholar] [CrossRef]
- Flaschel, P.; Landesmann, M. Mathematical Economics and the Dynamics of Capitalism: Goodwin’s Legacy Continued; Routledge: London, UK, 2016. [Google Scholar]
- Gómez, M.; Irewole, O.E. Economic growth, inflation and unemployment in Africa: An autoregressive distributed lag bounds testing approach, 1991–2019. Afr. J. Econ. Manag. Stud. 2023, 15, 318–330. [Google Scholar] [CrossRef]
- Mamo, D.K.; Ayele, E.A.; Teklu, S.W. Modelling and Analysis of the Impact of Corruption on Economic Growth and Unemployment. Proc. Oper. Res. Forum. 2024, 5, 36. [Google Scholar] [CrossRef]
- Ardjouni, A.; Djoudi, A. Existence and positivity of solutions for a totally nonlinear neutral periodic differential equation. Miskolc Math. Notes 2013, 14, 757–768. [Google Scholar] [CrossRef]
- Ito, T. A note on the positivity constraint in Olech’s theorem. J. Econ. Theory 1978, 17, 312–318. [Google Scholar] [CrossRef]
- Mehdizadeh Khalsaraei, M.; Shokri, A.; Ramos, H.; Mohammadnia, Z.; Khakzad, P. A positivity-preserving improved nonstandard finite difference method to solve the Black-Scholes equation. Mathematics 2022, 10, 1846. [Google Scholar] [CrossRef]
- Blanes, S.; Iserles, A.; Macnamara, S. Positivity-preserving methods for ordinary differential equations. ESAIM Math. Model. Numer. Anal. 2022, 56, 1843–1870. [Google Scholar] [CrossRef]
- González-Parra, G.; Arenasm, A.J.; Chen-Charpentier, B.M. Positive numerical solution for a nonarbitrage liquidity model using nonstandard finite difference schemes. Numer. Methods Partial. Differ. Equ. 2014, 30, 210–221. [Google Scholar] [CrossRef]
- Hoang, M.T. Positivity and boundedness preserving nonstandard finite difference schemes for solving Volterra’s population growth model. Math. Comput. Simul. 2022, 199, 359–373. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer Science & Business Media: Berlin, Germany, 2013; Volume 42. [Google Scholar]
- Hirsch, M.W.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Anagnost, J.J.; Desoer, C.A. An elementary proof of the Routh-Hurwitz stability criterion. Circuits Syst. Signal Process. 1991, 10, 101–114. [Google Scholar]
- Labonte, M. Unemployment and inflation: Implications for policymaking. Congr. Res. Serv. 2016. [Google Scholar]
- Holzman, F.D. Inflation: Cost-push and demand-pull. Am. Econ. Rev. 1960, 50, 20–42. [Google Scholar]
- Bosi, S.; Desmarchelier, D. Local bifurcations of three and four-dimensional systems: A tractable characterization with economic applications. Math. Soc. Sci. 2019, 97, 38–50. [Google Scholar]
- Moza, G.; Rocşoreanu, C.; Sterpu, M.; Oliveira, R. Stability and bifurcation analysis of a four-dimensional economic model. Carpathian J. Math. 2024, 40, 139–153. [Google Scholar]
- Pollin, R.; Zhu, A. Inflation and economic growth: A cross-country non-linear analysis. In Beyond Inflation Targeting; Edward Elgar Publishing: Cheltenham, UK, 2009. [Google Scholar]
- Ireland, P.N. Interest rates, inflation, and Federal Reserve policy since 1980. J. Money Credit. Bank. 2000, 32, 417–434. [Google Scholar]
- Surico, P. The Fed’s monetary policy rule and US inflation: The case of asymmetric preferences. J. Econ. Dyn. Control 2007, 31, 305–324. [Google Scholar]
- Acemoglu, D.; Verdier, T. Property rights, corruption and the allocation of talent: A general equilibrium approach. Econ. J. 1998, 108, 1381–1403. [Google Scholar]
- Acemoglu, D.; Robinson, J.A. Why Nations Fail: The Origins of Power, Prosperity, and Poverty; Crown Currency: New York, NY, USA, 2013. [Google Scholar]
- Ogbeidi, M.M. Political leadership and corruption in Nigeria since 1960: A socio-economic analysis. J. Niger. Stud. 2012, 1, 2. [Google Scholar]
- Anyanwu, J.C. Factors affecting economic growth in Africa: Are there any lessons from China? Afr. Dev. Rev. 2014, 26, 468–493. [Google Scholar]
- Jong-A-Pin, R. On the measurement of political instability and its impact on economic growth. Eur. J. Political Econ. 2009, 25, 15–29. [Google Scholar]
- Batrancea, L.M.; Balcı, M.A.; Akgüller, Ö.; Gaban, L. What drives economic growth across European countries? A multimodal approach. Mathematics 2022, 10, 3660. [Google Scholar] [CrossRef]
- Cornwell, C.; Trumbull, W.N. Estimating the economic model of crime with panel data. Rev. Econ. Stat. 1994, 76, 360–366. [Google Scholar]
- González-Parra, G.; Chen-Charpentier, B.; Kojouharov, H.V. Mathematical modeling of crime as a social epidemic. J. Interdiscip. Math. 2018, 21, 623–643. [Google Scholar]
- Halkos, G.E.; Tzeremes, N.G. Corruption and economic efficiency: Panel data evidence. Glob. Econ. Rev. 2010, 39, 441–454. [Google Scholar]
- Langseth, P. Measuring corruption. In Measuring Corruption; Routledge: London, UK, 2016; pp. 7–44. [Google Scholar]
- Pozsgai-Alvarez, J. Three-Dimensional Corruption Metrics: A Proposal for Integrating Frequency, Cost, and Significance. Soc. Indic. Res. 2024, 1–24. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ifeacho, O.; González-Parra, G. Mathematical Modeling of Economic Growth, Corruption, Employment and Inflation. Mathematics 2025, 13, 1102. https://doi.org/10.3390/math13071102
Ifeacho O, González-Parra G. Mathematical Modeling of Economic Growth, Corruption, Employment and Inflation. Mathematics. 2025; 13(7):1102. https://doi.org/10.3390/math13071102
Chicago/Turabian StyleIfeacho, Ogochukwu, and Gilberto González-Parra. 2025. "Mathematical Modeling of Economic Growth, Corruption, Employment and Inflation" Mathematics 13, no. 7: 1102. https://doi.org/10.3390/math13071102
APA StyleIfeacho, O., & González-Parra, G. (2025). Mathematical Modeling of Economic Growth, Corruption, Employment and Inflation. Mathematics, 13(7), 1102. https://doi.org/10.3390/math13071102






