Accuracy Comparison of Machine Learning Algorithms on World Happiness Index Data
Abstract
1. Introduction
2. Literature Review
3. Method
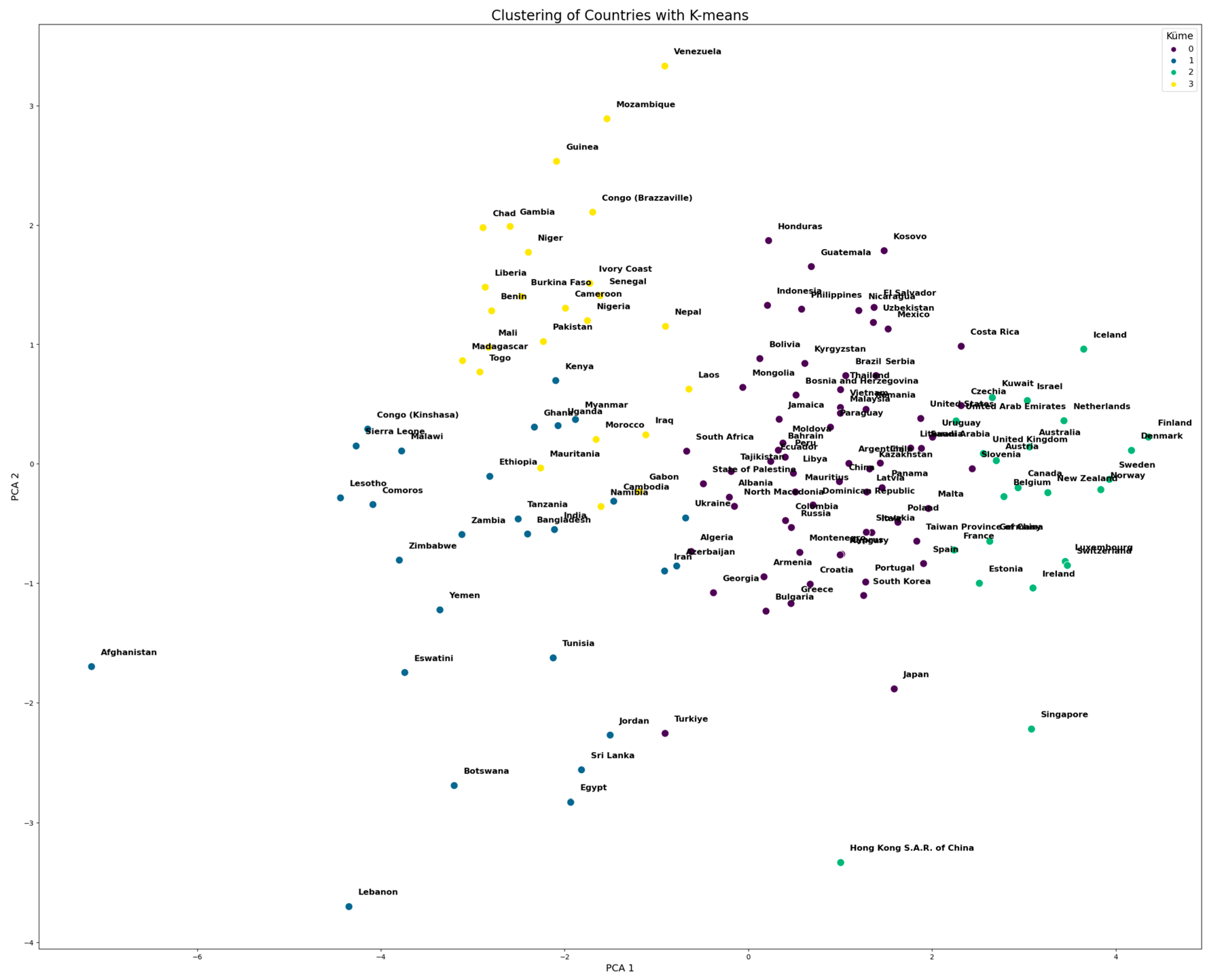
3.1. K-Means
3.2. Logistic Regression
3.3. Decision Tree
3.4. Support Vector Machines
3.5. Random Forest
3.6. Artificial Neural Network
3.7. XGBoost
3.8. Principal Component Analysis
4. Dataset
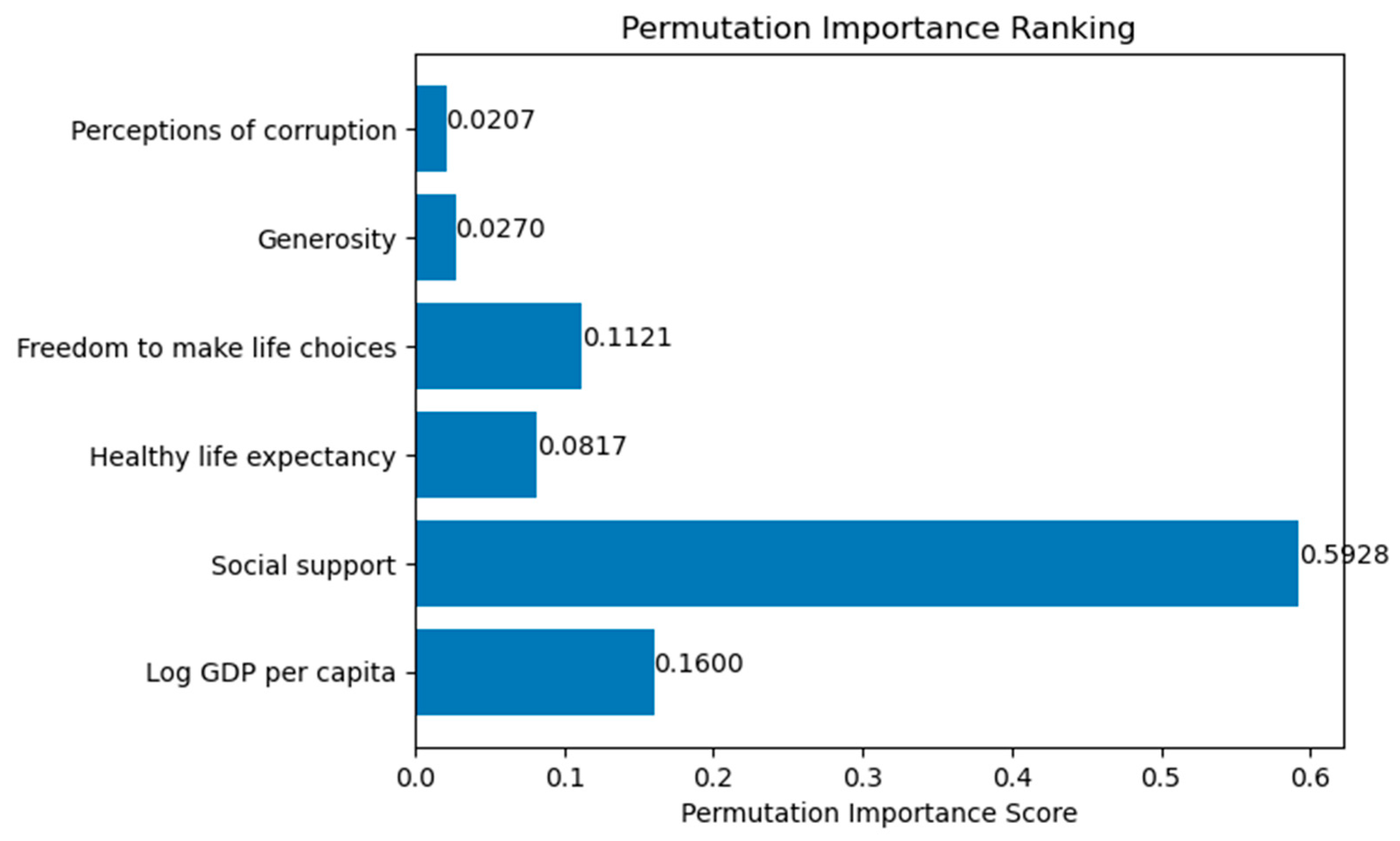
5. Analysis Results and Findings
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lakócai, C. How Sustainable Is Happiness? An Enquiry about the Sustainability and Wellbeing Performance of Societies. Int. J. Sustain. Dev. World Ecol. 2023, 30, 420–427. [Google Scholar] [CrossRef]
- Glatzer, W. Worldwide Indicators for Quality of Life: The Ten Leading Countries in the View of the Peoples and the Measurements of Experts around 2020. SCIREA J. Sociol. 2023, 7, 368–383. [Google Scholar] [CrossRef]
- Jannani, A.; Sael, N.; Benabbou, F. Machine Learning for the Analysis of Quality of Life Using the World Happiness Index and Human Development Indicators. Math. Model. Comput. 2023, 10, 534–546. [Google Scholar] [CrossRef]
- Du, L.; Liang, Y.; Ahmad, M.I.; Zhou, P. K-Means Clustering Based on Chebyshev Polynomial Graph Filtering. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; IEEE: New York, NY, USA, 2024; pp. 7175–7179. [Google Scholar]
- Spowart, S. A Path to Happiness. In Happiness and Wellness—Biopsychosocial and Anthropological Perspectives; IntechOpen: London, UK, 2023. [Google Scholar]
- Lomas, T. Happiness; The MIT Press: Cambridge, MA, USA, 2023; ISBN 9780262370837. [Google Scholar]
- Ağralı Ermiş, S.; Dereceli, E. The Effect of the Life Satisfaction of Individuals Over 65 Years on Their Happiness. Turk. J. Sport Exerc. 2023, 25, 310–318. [Google Scholar] [CrossRef]
- Tipi, R.; Şahin, H.; Doğru, Ş.; Zengin Bintaş, G.Ç. A Comparative Evalution on the Prediction Performance of Regression Algorithms in Machine Learning for Die Design Cost Estimation. Electron. Lett. Sci. Eng. 2023, 19, 48–62. [Google Scholar]
- Dünder, M.; Dünder, E. Comparison of Machine Learning Algorithms in the Presence of Class Imbalance in Categorical Data: An Application on Student Success. J. Digit. Technol. Educ. 2024, 3, 28–38. [Google Scholar]
- Dixit, S.; Chaudhary, M.; Sahni, N. Network Learning Approaches to Study World Happiness. arXiv 2020, arXiv:2007.09181. [Google Scholar]
- Chen, S.; Yang, M.; Lin, Y. Predicting Happiness Levels of European Immigrants and Natives: An Application of Artificial Neural Network and Ordinal Logistic Regression. Front. Psychol. 2022, 13, 1012796. [Google Scholar] [CrossRef]
- Khder, M.; Sayf, M.; Fujo, S. Analysis of World Happiness Report Dataset Using Machine Learning Approaches. Int. J. Adv. Soft Comput. Its Appl. 2022, 14, 15–34. [Google Scholar] [CrossRef]
- Zhang, Y. Analyze and Predict the 2022 World Happiness Report Based on the Past Year’s Dataset. J. Comput. Sci. 2023, 19, 483–492. [Google Scholar] [CrossRef]
- Timmapuram, M.; Ramdas, R.; Vutkur, S.R.; Mali, Y.R.; Vasanth, K. Understanding the Regional Differences in World Happiness Index Using Machine Learning. In Proceedings of the 2023 International Conference on Innovative Computing, Intelligent Communication and Smart Electrical Systems (ICSES), Chennai, India, 14–15 December 2023; IEEE: New York, NY, USA, 2023; pp. 1–9. [Google Scholar]
- Liu, A.; Zhang, Y. Happiness Index Prediction Using Machine Learning Algorithms. Appl. Comput. Eng. 2023, 5, 386–389. [Google Scholar] [CrossRef]
- Sihombing, P.R.; Budiantono, S.; Arsani, A.M.; Aritonang, T.M.; Kurniawan, M.A. Comparison of Regression Analysis with Machine Learning Supervised Predictive Model Techniques. J. Ekon. Dan Stat. Indones. 2023, 3, 113–118. [Google Scholar] [CrossRef]
- Akanbi, K.; Jones, Y.; Oluwadare, S.; Nti, I.K. Predicting Happiness Index Using Machine Learning. In Proceedings of the 2024 IEEE 3rd International Conference on Computing and Machine Intelligence (ICMI), Mt Pleasant, MI, USA, 13–14 April 2024; IEEE: New York, NY, USA, 2024; pp. 1–5. [Google Scholar]
- Jaiswal, R.; Gupta, S. Money Talks, Happiness Walks: Dissecting the Secrets of Global Bliss with Machine Learning. J. Chin. Econ. Bus. Stud. 2024, 22, 111–158. [Google Scholar] [CrossRef]
- Airlangga, G.; Liu, A. A Hybrid Gradient Boosting and Neural Network Model for Predicting Urban Happiness: Integrating Ensemble Learning with Deep Representation for Enhanced Accuracy. Mach. Learn. Knowl. Extr. 2025, 7, 4. [Google Scholar] [CrossRef]
- Rusdiana, L.; Hardita, V.C. Algoritma K-Means Dalam Pengelompokan Surat Keluar Pada Program Studi Teknik Informatika STMIK Palangkaraya. J. Saıntekom 2023, 13, 55–66. [Google Scholar] [CrossRef]
- Paratama, M.A.Y.; Hidayah, A.R.; Avini, T. Clusterıng K-Means Untuk Analısıs Pola Persebaran Bencana Alam Dı Indonesıa. J. Inform. Dan Tekonologi Komput. (JITEK) 2023, 3, 108–114. [Google Scholar] [CrossRef]
- Cui, J.; Liu, J.; Liao, Z. Research on K-Means Clustering Algorithm and Its Implementation. In Proceedings of the 2nd International Conference on Computer Science and Electronics Engineering (ICCSEE 2013), Hangzhou, China, 22–23 March 2013; Atlantis Press: Paris, France, 2013. [Google Scholar]
- Wu, B. K-Means Clustering Algorithm and Python Implementation. In Proceedings of the 2021 IEEE International Conference on Computer Science, Artificial Intelligence and Electronic Engineering (CSAIEE), Virtual Conference, 20–22 August 2021; IEEE: New York, NY, USA, 2021; pp. 55–59. [Google Scholar]
- Zhao, Y.; Zhou, X. K-Means Clustering Algorithm and Its Improvement Research. J. Phys. Conf. Ser. 2021, 1873, 012074. [Google Scholar] [CrossRef]
- Kamgar-Parsi, B.; Kamgar-Parsi, B. Penalized K-Means Algorithms for Finding the Number of Clusters. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; IEEE: New York, NY, USA, 2021; pp. 969–974. [Google Scholar]
- Sirikayon, C.; Thammano, A. Deterministic Initialization of K-Means Clustering by Data Distribution Guide. In Proceedings of the 2022 Joint International Conference on Digital Arts, Media and Technology with ECTI Northern Section Conference on Electrical, Electronics, Computer and Telecommunications Engineering (ECTI DAMT & NCON), Chiang Rai, Thailand, 26–28 January 2022; IEEE: New York, NY, USA, 2022; pp. 279–284. [Google Scholar]
- Thulasidas, M. A Quality Metric for K-Means Clustering. In Proceedings of the 2018 14th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Huangshan, China, 28–30 July 2018; IEEE: New York, NY, USA, 2018; pp. 752–757. [Google Scholar]
- Dong, Q.; Chen, X.; Huang, B. Logistic Regression. Data Anal. Pavement Eng. 2024, 141–152. [Google Scholar] [CrossRef]
- Kravets, P.; Pasichnyk, V.; Prodaniuk, M. Mathematical Model of Logistic Regression for Binary Classification. Part 1. Regression Models of Data Generalization. Vìsnik Nacìonalʹnogo unìversitetu “Lʹvìvsʹka polìtehnìka”. Serìâ Ìnformacìjnì sistemi ta merežì 2024, 15, 290–321. [Google Scholar] [CrossRef]
- Ma, Q. Recent Applications and Perspectives of Logistic Regression Modelling in Healthcare. Theor. Nat. Sci. 2024, 36, 185–190. [Google Scholar] [CrossRef]
- Zaidi, A.; Al Luhayb, A.S.M. Two Statistical Approaches to Justify the Use of the Logistic Function in Binary Logistic Regression. Math. Probl. Eng. 2023, 2023, 5525675. [Google Scholar] [CrossRef]
- Zaidi, A. Mathematical Justification on the Origin of the Sigmoid in Logistic Regression. Cent. Eur. Manag. J. 2022, 30, 1327–1337. [Google Scholar] [CrossRef]
- Kawano, S.; Konishi, S. Nonlinear Logistic Discrimination via Regularized Gaussian Basis Expansions. Commun. Stat. Simul. Comput. 2009, 38, 1414–1425. [Google Scholar] [CrossRef]
- Thierry, D. Logistic Regression, Neural Networks and Dempster–Shafer Theory: A New Perspective. Knowl. Based Syst. 2019, 176, 54–67. [Google Scholar] [CrossRef]
- Yuen, J.; Twengström, E.; Sigvald, R. Calibration and Verification of Risk Algorithms Using Logistic Regression. Eur. J. Plant Pathol. 1996, 102, 847–854. [Google Scholar] [CrossRef]
- Bokov, A.; Antonenko, S. Application of Logistic Regression Equation Analysis Using Derivatives for Optimal Cutoff Discriminative Criterion Estimation. Ann. Math. Phys. 2020, 3, 032–035. [Google Scholar] [CrossRef]
- Grace, A.L.; Thenmozhi, M. Optimizing Logistics with Regularization Techniques: A Comparative Study. In Proceedings of the 2023 IEEE World Conference on Applied Intelligence and Computing (AIC), Sonbhadra, India, 29–30 July 2023; IEEE: New York, NY, USA, 2023; pp. 338–344. [Google Scholar]
- Reznychenko, T.; Uglickich, E.; Nagy, I. Accuracy Comparison of Logistic Regression, Random Forest, and Neural Networks Applied to Real MaaS Data. In Proceedings of the 2024 Smart City Symposium Prague (SCSP), Prague, Czech Republic, 23–24 May 2024; IEEE: New York, NY, USA, 2024; pp. 1–5. [Google Scholar]
- Xu, C.; Peng, Z.; Jing, W. Sparse Kernel Logistic Regression Based on L 1/2 Regularization. Sci. China Inf. Sci. 2013, 56, 1–16. [Google Scholar] [CrossRef][Green Version]
- Huang, H.-H.; Liu, X.-Y.; Liang, Y. Feature Selection and Cancer Classification via Sparse Logistic Regression with the Hybrid L1/2 +2 Regularization. PLoS ONE 2016, 11, e0149675. [Google Scholar] [CrossRef]
- Hsieh, W.W. Decision Trees, Random Forests and Boosting. In Introduction to Environmental Data Science; Cambridge University Press: Cambridge, UK, 2023; pp. 473–493. [Google Scholar]
- Chopra, D.; Khurana, R. Decision Trees. In Introduction to Machine Learning with Python; Bentham Science Publishers: Sharjah, United Arab Emirates, 2023; pp. 74–82. [Google Scholar]
- Lai, Y. Research on the Application of Decision Tree in Mobile Marketing. In Frontier Computing; Springer: Singapore, 2023; pp. 1488–1495. [Google Scholar]
- Zhao, X.; Nie, X. Splitting Choice and Computational Complexity Analysis of Decision Trees. Entropy 2021, 23, 1241. [Google Scholar] [CrossRef]
- Tangirala, S. Evaluating the Impact of GINI Index and Information Gain on Classification Using Decision Tree Classifier Algorithm. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 612–619. [Google Scholar] [CrossRef]
- Sharma, N.; Iqbal, S.I.M. Applying Decision Tree Algorithm Classification and Regression Tree (CART) Algorithm to Gini Techniques Binary Splits. Int. J. Eng. Adv. Technol. 2023, 12, 77–81. [Google Scholar] [CrossRef]
- Aaboub, F.; Chamlal, H.; Ouaderhman, T. Statistical Analysis of Various Splitting Criteria for Decision Trees. J. Algorithm. Comput. Technol. 2023, 17, 1–13. [Google Scholar] [CrossRef]
- Pathan, S.; Sharma, S.K. Design an Optimal Decision Tree Based Algorithm to Improve Model Prediction Performance. Int. J. Recent Innov. Trends Comput. Commun. 2023, 11, 127–133. [Google Scholar] [CrossRef]
- Disha, R.A.; Waheed, S. Performance Analysis of Machine Learning Models for Intrusion Detection System Using Gini Impurity-Based Weighted Random Forest (GIWRF) Feature Selection Technique. Cybersecurity 2022, 5, 1. [Google Scholar] [CrossRef]
- Chandra, B.; Paul Varghese, P. Fuzzifying Gini Index Based Decision Trees. Expert Syst. Appl. 2009, 36, 8549–8559. [Google Scholar] [CrossRef]
- Zeng, G. On Impurity Functions in Decision Trees. Commun. Stat. Theory Methods 2025, 54, 701–719. [Google Scholar] [CrossRef]
- Khanduja, D.K.; Kaur, S. The Categorization of Documents Using Support Vector Machines. Int. J. Sci. Res. Comput. Sci. Eng. 2023, 11, 1–12. [Google Scholar] [CrossRef]
- Ramadani, K.; Erda, G.E.G. World Greenhouse Gas Emission Classification Using Support Vector Machine (SVM) Method. Parameter J. Stat. 2024, 4, 1–8. [Google Scholar] [CrossRef]
- Ananda, J.S.; Fendriani, Y.; Pebralia, J. Classification Analysis Of Brain Tumor Dissease In Radiographic Images Using Support Vector Machines (SVM) With Python. J. Online Phys. 2024, 9, 110–115. [Google Scholar] [CrossRef]
- Wang, Q. Support Vector Machine Algorithm in Machine Learning. In Proceedings of the 2022 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 24–26 June 2022; IEEE: New York, NY, USA, 2022; pp. 750–756. [Google Scholar]
- Dabas, A. Application of Support Vector Machines in Machine Learning. 2024. Available online: https://d197for5662m48.cloudfront.net/documents/publicationstatus/216532/preprint_pdf/0712c8e4f08648a45d2de5c43f47e9e6.pdf (accessed on 10 February 2025).
- Li, H. Support Vector Machine. In Machine Learning Methods; Springer Nature: Singapore, 2024; pp. 127–177. [Google Scholar]
- Huang, C.; Zhang, R.; Zhang, J.; Guo, X.; Wei, P.; Wang, L.; Huang, P.; Li, W.; Wang, Y. A Novel Method for Fatigue Design of FRP-Strengthened RC Beams Based on Machine Learning. Compos. Struct. 2025, 359, 118867. [Google Scholar] [CrossRef]
- Tarigan, A.; Agushinta, D.; Suhendra, A.; Budiman, F. Determination of SVM-RBF Kernel Space Parameter to Optimize Accuracy Value of Indonesian Batik Images Classification. J. Comput. Sci. 2017, 13, 590–599. [Google Scholar] [CrossRef][Green Version]
- Wainer, J.; Fonseca, P. How to Tune the RBF SVM Hyperparameters? An Empirical Evaluation of 18 Search Algorithms. Artif. Intell. Rev. 2021, 54, 4771–4797. [Google Scholar] [CrossRef]
- Aiman Ngadilan, M.A.; Ismail, N.; Rahiman, M.H.F.; Taib, M.N.; Mohd Ali, N.A.; Tajuddin, S.N. Radial Basis Function (RBF) Tuned Kernel Parameter of Agarwood Oil Compound for Quality Classification Using Support Vector Machine (SVM). In Proceedings of the 2018 9th IEEE Control and System Graduate Research Colloquium (ICSGRC), Shah Alam, Malaysia, 3–4 August 2018; IEEE: New York, NY, USA, 2018; pp. 64–68. [Google Scholar]
- Maindola, M.; Al-Fatlawy, R.R.; Kumar, R.; Boob, N.S.; Sreeja, S.P.; Sirisha, N.; Srivastava, A. Utilizing Random Forests for High-Accuracy Classification in Medical Diagnostics. In Proceedings of the 2024 7th International Conference on Contemporary Computing and Informatics (IC3I), Greater Noida, India, 18–20 September 2024; IEEE: New York, NY, USA, 2024; pp. 1679–1685. [Google Scholar]
- Zhu, J.; Zhang, A.; Zheng, H. Research on Predictive Model Based on Ensemble Learning. Highlights Sci. Eng. Technol. 2023, 57, 311–319. [Google Scholar] [CrossRef]
- Gu, Q.; Tian, J.; Li, X.; Jiang, S. A Novel Random Forest Integrated Model for Imbalanced Data Classification Problem. Knowl. Based Syst. 2022, 250, 109050. [Google Scholar] [CrossRef]
- Ignatenko, V.; Surkov, A.; Koltcov, S. Random Forests with Parametric Entropy-Based Information Gains for Classification and Regression Problems. PeerJ Comput. Sci. 2024, 10, e1775. [Google Scholar] [CrossRef]
- Salman, H.A.; Kalakech, A.; Steiti, A. Random Forest Algorithm Overview. Babylon. J. Mach. Learn. 2024, 2024, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Tarchoune, I.; Djebbar, A.; Merouani, H.F. Improving Random Forest with Pre-Pruning Technique for Binary Classification. All Sci. Abstr. 2023, 1, 11. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, X.; Bai, K.; Zhang, R. A New Random Forest Ensemble of Intuitionistic Fuzzy Decision Trees. IEEE Trans. Fuzzy Syst. 2023, 31, 1729–1741. [Google Scholar] [CrossRef]
- Aryan Rose, A.R. How Do Artificial Neural Networks Work. J. Adv. Sci. Technol. 2024, 20, 172–177. [Google Scholar] [CrossRef]
- Hussain, N.Y. Deep Learning Architectures Enabling Sophisticated Feature Extraction and Representation for Complex Data Analysis. Int. J. Innov. Sci. Res. Technol. (IJISRT) 2024, 9, 2290–2300. [Google Scholar] [CrossRef]
- Kalita, J.K.; Bhattacharyya, D.K.; Roy, S. Artificial Neural Networks. In Fundamentals of Data Science; Elsevier: Amsterdam, The Netherlands, 2024; pp. 121–160. [Google Scholar]
- Piña, O.C.; Villegas-Jimenéz, A.A.; Aguilar-Canto, F.; Gambino, O.J.; Calvo, H. Neuroscience-Informed Interpretability of Intermediate Layers in Artificial Neural Networks. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; IEEE: New York, NY, USA, 2024; pp. 1–8. [Google Scholar]
- Wang, L.; Fu, K. Artificial Neural Networks. In Wiley Encyclopedia of Computer Science and Engineering; Wiley: Hoboken, NJ, USA, 2009; pp. 181–188. [Google Scholar]
- Schonlau, M. Neural Networks; Springer Nature: Singapore, 2023; pp. 285–322. [Google Scholar]
- Dutta, S.; Adhikary, S. Evolutionary Swarming Particles To Speedup Neural Network Parametric Weights Updates. In Proceedings of the 2023 9th International Conference on Smart Computing and Communications (ICSCC), Kochi, Kerala, India, 17–19 August 2023; IEEE: New York, NY, USA, 2023; pp. 413–418. [Google Scholar]
- Yang, L. Theoretical Analysis of Adam Optimizer in the Presence of Gradient Skewness. Int. J. Appl. Sci. 2024, 7, 27. [Google Scholar] [CrossRef]
- Lei, X.; Liu, J.; Ye, X. Research on Network Traffic Anomaly Detection Technology Based on XGBoost. In Proceedings of the International Conference on Algorithms, High Performance Computing, and Artificial Intelligence (AHPCAI 2024), Zhengzhou, China, 21–23 June 2024; Loskot, P., Hu, L., Eds.; SPIE: Bellingham, WA, USA, 2024; p. 69. [Google Scholar]
- Pang, Y.; Wang, X.; Tang, Y.; Gu, G.; Chen, J.; Yang, B.; Ning, L.; Bao, C.; Zhou, S.; Cao, X.; et al. A Traffic Accident Early Warning Model Based on XGBOOST. In Proceedings of the Fourth International Conference on Advanced Algorithms and Neural Networks (AANN 2024), Qingdao, China, 9–11 August 2024; Lu, Q., Zhang, W., Eds.; SPIE: Bellingham, WA, USA, 2024; p. 120. [Google Scholar]
- Rani, R.; Gill, K.S.; Upadhyay, D.; Devliyal, S. XGBoost-Driven Insights: Enhancing Chronic Kidney Disease Detection. In Proceedings of the 2024 5th International Conference on Smart Electronics and Communication (ICOSEC), Trichy, India, 18–20 September 2024; IEEE: New York, NY, USA, 2024; pp. 1131–1134. [Google Scholar]
- Murdiansyah, D.T. Prediksi Stroke Menggunakan Extreme Gradient Boosting. J. Inform. Dan Komput. JIKO 2024, 8, 419. [Google Scholar] [CrossRef]
- Chimphlee, W.; Chimphlee, S. Hyperparameters Optimization XGBoost for Network Intrusion Detection Using CSE-CIC-IDS 2018 Dataset. IAES Int. J. Artif. Intell. IJ-AI 2024, 13, 817. [Google Scholar] [CrossRef]
- Ryu, S.-E.; Shin, D.-H.; Chung, K. Prediction Model of Dementia Risk Based on XGBoost Using Derived Variable Extraction and Hyper Parameter Optimization. IEEE Access 2020, 8, 177708–177720. [Google Scholar] [CrossRef]
- Wen, H.; Hu, J.; Zhang, J.; Xiang, X.; Liao, M. Rockfall Susceptibility Mapping Using XGBoost Model by Hybrid Optimized Factor Screening and Hyperparameter. Geocarto Int. 2022, 37, 16872–16899. [Google Scholar] [CrossRef]
- Ghatasheh, N.; Altaharwa, I.; Aldebei, K. Modified Genetic Algorithm for Feature Selection and Hyper Parameter Optimization: Case of XGBoost in Spam Prediction. IEEE Access 2022, 10, 84365–84383. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, S. A Mobile Package Recommendation Method Based on Grid Search Combined with XGBoost Model. In Proceedings of the Sixth International Conference on Advanced Electronic Materials, Computers, and Software Engineering (AEMCSE 2023), Shenyang, China, 21–23 April 2023; Yang, L., Tan, W., Eds.; SPIE: Bellingham, WA, USA, 2023; p. 51. [Google Scholar]
- Matsumoto, N.; Okada, M.; Sugase-Miyamoto, Y.; Yamane, S.; Kawano, K. Population Dynamics of Face-Responsive Neurons in the Inferior Temporal Cortex. Cereb. Cortex 2005, 15, 1103–1112. [Google Scholar] [CrossRef]
- Çelik, S.; Cömertler, N. K-Means Kümeleme ve Diskriminant Analizi Ile Ülkelerin Mutluluk Hallerinin İncelenmesi. J. Curr. Res. Bus. Econ. 2021, 11, 15–38. [Google Scholar] [CrossRef]
- Wicaksono, A.P.; Widjaja, S.; Nugroho, M.F.; Putri, C.P. Elbow and Silhouette Methods for K Value Analysis of Ticket Sales Grouping on K-Means. SISTEMASI 2024, 13, 28. [Google Scholar] [CrossRef]
- Maulana, I.; Roestam, R. Optimizing KNN Algorithm Using Elbow Method for Predicting Voter Participation Using Fixed Voter List Data (DPT). J. Sos. Teknol. 2024, 4, 441–451. [Google Scholar] [CrossRef]
- Chanchí, G.; Barrera, D.; Barreto, S. Proposal of a Mathematical and Computational Method for Determining the Optimal Number of Clusters in the K-Means Algorithm. Preprints 2024. [Google Scholar] [CrossRef]
- Zamri, N.; Bakar, N.A.A.; Aziz, A.Z.A.; Madi, E.N.; Ramli, R.A.; Si, S.M.M.M.; Koon, C.S. Development of Fuzzy C-Means with Fuzzy Chebyshev for Genomic Clustering Solutions Addressing Cancer Issues. Procedia Comput. Sci. 2024, 237, 937–944. [Google Scholar] [CrossRef]



| Authors | Methodology | Findings | Contributions |
|---|---|---|---|
| Dixit et al. (2020) [10] | -Predictive Modelling using General Regression Neural Networks (GRNNs). -Bayesian Networks (BNs) with manual discretization scheme. | The paper demonstrates that General Regression Neural Networks (GRNNs) outperform other state-of-the-art predictive models when applied to the historical happiness index data of 156 nations, showcasing their effectiveness in predicting world happiness based on various influential features. | -Developed predictive models for world happiness using GRNNs. -Established causal links through Bayesian Network analysis. |
| Chen, et al. (2022) [11] | -Ordinal Logistic Regression (OLR). -Artificial Neural Network (ANN). | The paper reports overall accuracies of over 80% for both Ordinal Logistic Regression and Artificial Neural Network models in predicting happiness levels among European immigrants and natives, indicating the effective performance of these machine learning techniques in this context. | -Investigates happiness factors for immigrants and natives. -Demonstrates machine learning’s effectiveness in predicting happiness levels. |
| Khder et al. (2022) [12] | -Supervised machine learning approaches (Neural Network, OneR). -Ensemble of randomized regression trees (random neural forests). | The study evaluated the accuracy of machine learning algorithms, achieving 0.9239 accuracy with the Neural Network model. The OneR model also demonstrated sufficient accuracy, indicating the effective classification of happiness scores based on the World Happiness Report dataset. | -Identified critical variables for life happiness score using machine learning. -Highlighted GDP per Capita and Health Life Expectancy as key indicators. |
| Jannani et al. (2023) [3] | -Statistical techniques: Pearson correlation, principal component analysis. -Machine learning algorithms: Random Forest regression, XGBoost regression, Decision Tree regression. | The random forest regression achieved the highest accuracy with an score of 0.93667, followed by XGBoost regression and Decision Tree regression. Performance metrics included a mean squared error of 0.0033048 and a root mean squared error of 0.05748. | -Identified key factors affecting happiness internationally. -Highlighted the significance of economic indicators in happiness prediction. |
| Zhang (2023) [13] | -Linear regression models used to predict happiness scores in 2022. -Preliminary exploratory data analysis conducted to select appropriate variables. | The study utilized linear regression for predicting happiness scores, achieving a Root Mean Square Error (RMSE) of 0.236 and Mean Squared Error (MSE) of 0.056 for 2022. Other machine learning algorithms were mentioned but not specifically compared. | -Analyzing and predicting the 2022 World Happiness Report based on past data. -Presenting two linear regression models to predict happiness scores. |
| Timmapuram et al. (2023) [14] | -Regression and Decision Trees for prediction models. -Support Vector Regression (SVR) for QoL indicator prediction. | The study employed regression techniques with an R-squared value of 0.7867 and a Root Mean Square Error (RMSE) of 0.4797. Support Vector Regression (SVR) was identified as the best approach for predicting the Quality of Life indicator for 2023. | -Identifies key factors influencing national happiness levels. -Develops predictive models for happiness scores using machine learning. |
| Liu and Zhang (2023) [15] | -Support Vector Machine (SVM). -Naive Bayes. | The study found that the Support Vector Machine (SVM) achieved an accuracy of 92%, while the Naive Bayes algorithm reached 87% when predicting the happiness index, indicating SVM’s superior performance in analyzing world happiness index data. | -Used SVM and Naive Bayes for happiness index prediction -Economic and medical factors most affect happiness |
| Sihombing et al. (2023) [16] | -Regression trees, Random Forests, Support Vector Regression (SVR). -SVR model outperformed others in error and values. | The study compares regression models, including regression trees, random forests, and Support Vector Regression (SVR), on happiness index data. SVR demonstrated the lowest error values (MSE, RMSE, MAE) and the highest , indicating it as the most accurate model. | -Determines factors contributing to people’s happiness. -Compares regression models using machine learning techniques. |
| Akanbi et al. (2024) [17] | -Random Forest, XGBoost, Lasso Regressor. -Machine learning methods used for predicting happiness index. | XGBoost achieved the highest accuracy with an R-squared of 85.03% and MSE of 0.0032. Random Forest followed with 83.68% and 0.0035, while Lasso Regressor obtained 80.61% and 0.0041 in accuracy on the happiness index data. | -Predicts happiness index using machine learning models. -Evaluates model performance with R-squared and Mean Square Error. |
| Jaiswal and Gupta (2024) [18] | -Constructed a model using machine learning techniques. -Employed Random Forest for accuracy in predictions. | The study found that the Random Forest algorithm achieved an accuracy rate of 92.2709, outperforming other machine learning models in predicting happiness based on various constructs, highlighting its effectiveness in analyzing World Happiness Index data. | -Constructs a model for predicting happiness using machine learning. -Highlights GDP per capita’s impact on national happiness levels. |
| Airlangga and Liu (2025) [19] | -Hybrid model combining gradient boosting machine and Neural Network. -Evaluated against various baseline machine learning and deep learning models. | The hybrid GBM + NN model outperformed various baseline algorithms, achieving the lowest RMSE of 0.3332, an R2 of 0.9673, and a MAPE of 7.0082%, demonstrating superior accuracy in predicting urban happiness compared to traditional machine learning models. | -Hybrid model combines GBM and NN for urban happiness prediction. -Achieved superior performance and actionable insights for urban planners. |
| Number of Clusters | Cluster Size |
|---|---|
| 0 | 47 |
| 1 | 41 |
| 2 | 19 |
| 3 | 36 |
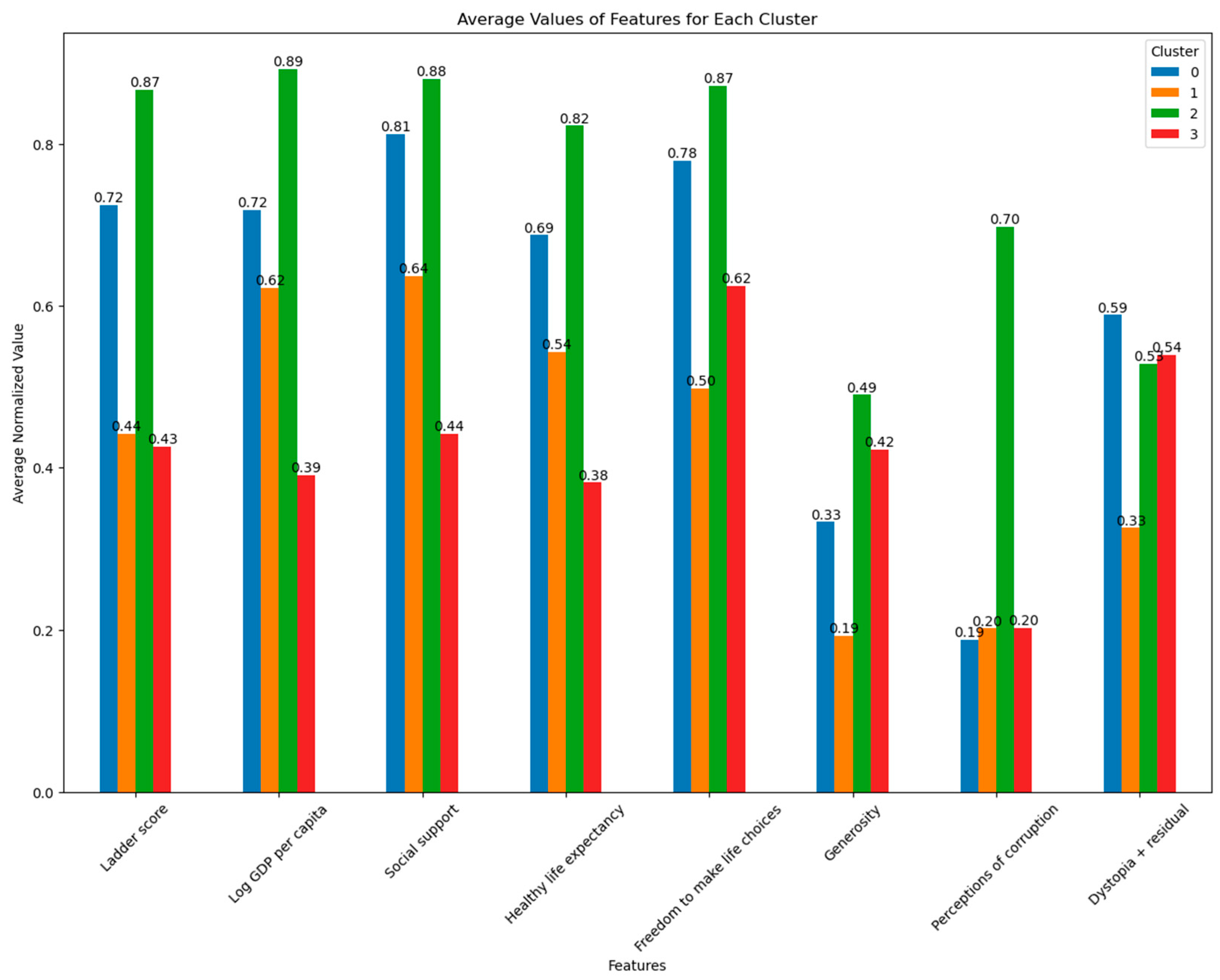
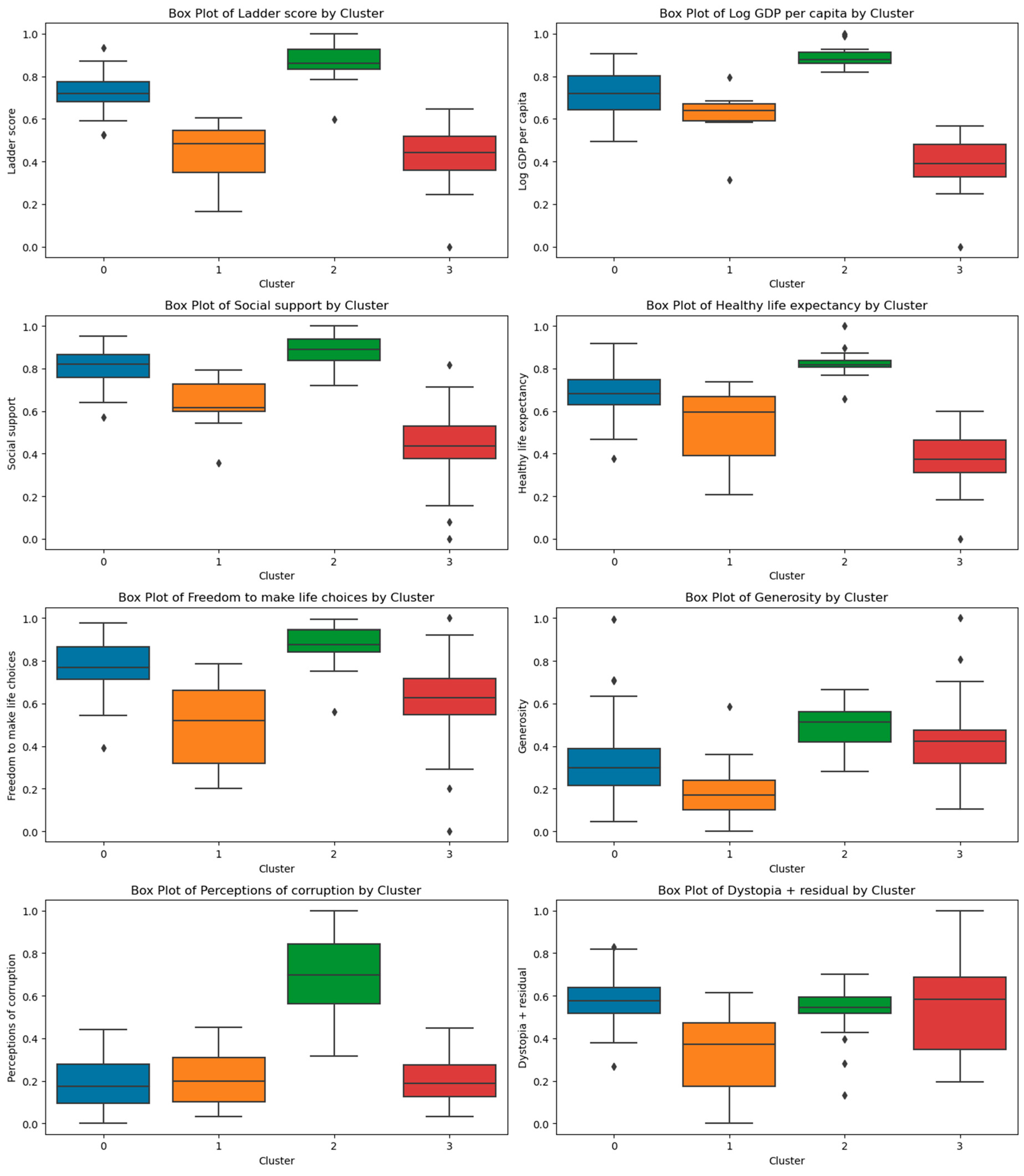
| Cluster | Mean | |||||||
|---|---|---|---|---|---|---|---|---|
| Ladder Score | Log GDP Per Capita | Social Support | Healthy Life Expectancy | Freedom to Make Life Choices | Generosity | Perceptions of Corruption | Dystopia + Residual | |
| 0 | 0.724 | 0.718 | 0.812 | 0.687 | 0.779 | 0.333 | 0.187 | 0.589 |
| 1 | 0.442 | 0.623 | 0.637 | 0.543 | 0.498 | 0.192 | 0.202 | 0.326 |
| 2 | 0.867 | 0.893 | 0.880 | 0.822 | 0.871 | 0.490 | 0.698 | 0.528 |
| 3 | 0.426 | 0.391 | 0.442 | 0.382 | 0.625 | 0.423 | 0.202 | 0.539 |
| Cluster | Standard Deviation | |||||||
| Ladder Score | Log GDP Per Capita | Social Support | Healthy Life Expectancy | Freedom to Make Life Choices | Generosity | Perceptions of Corruption | Dystopia + Residual | |
| 0 | 0.079 | 0.100 | 0.083 | 0.101 | 0.120 | 0.178 | 0.115 | 0.112 |
| 1 | 0.133 | 0.098 | 0.105 | 0.168 | 0.192 | 0.147 | 0.124 | 0.203 |
| 2 | 0.085 | 0.050 | 0.076 | 0.061 | 0.095 | 0.104 | 0.184 | 0.132 |
| 3 | 0.124 | 0.111 | 0.162 | 0.117 | 0.191 | 0.164 | 0.098 | 0.204 |
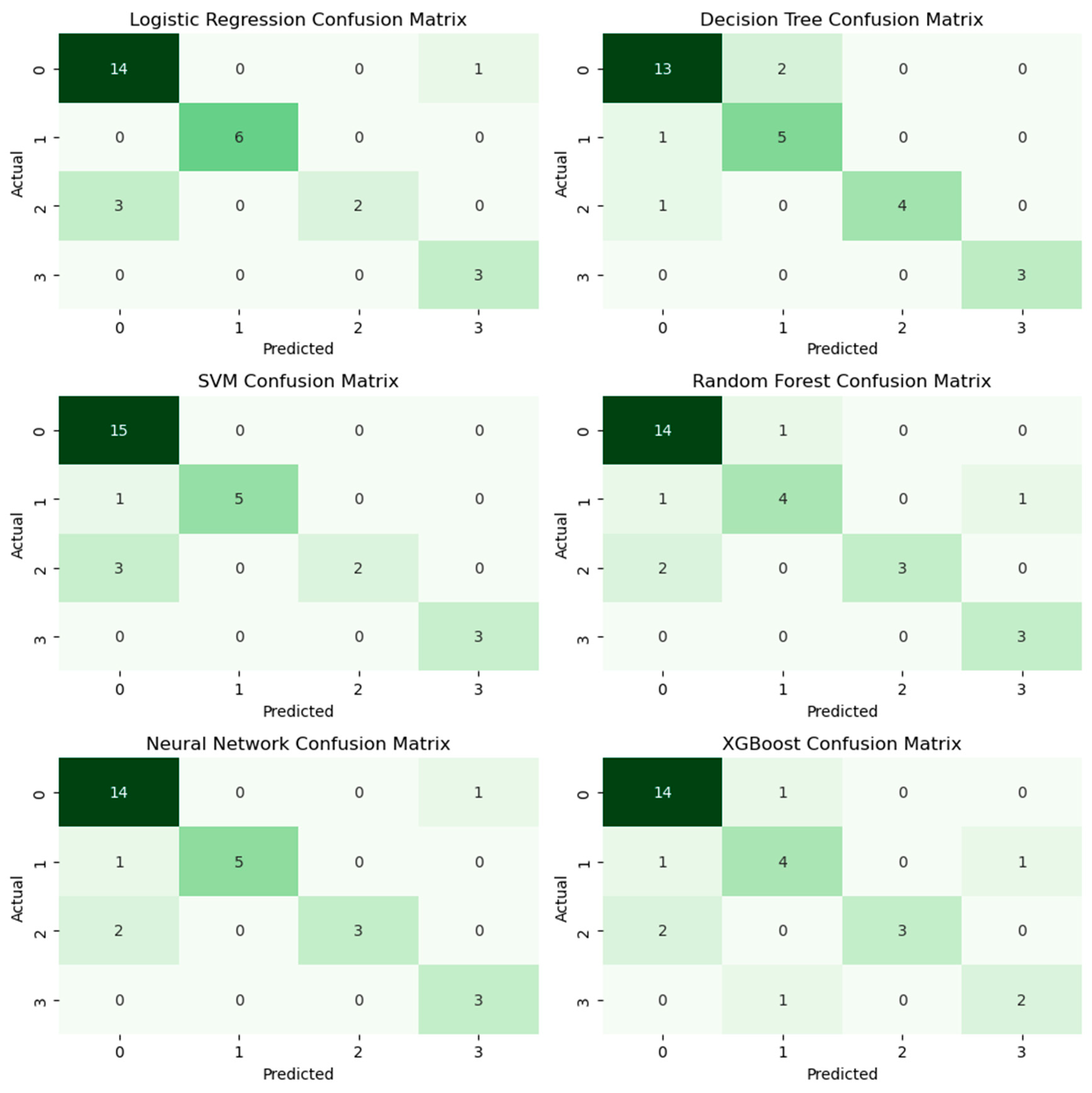
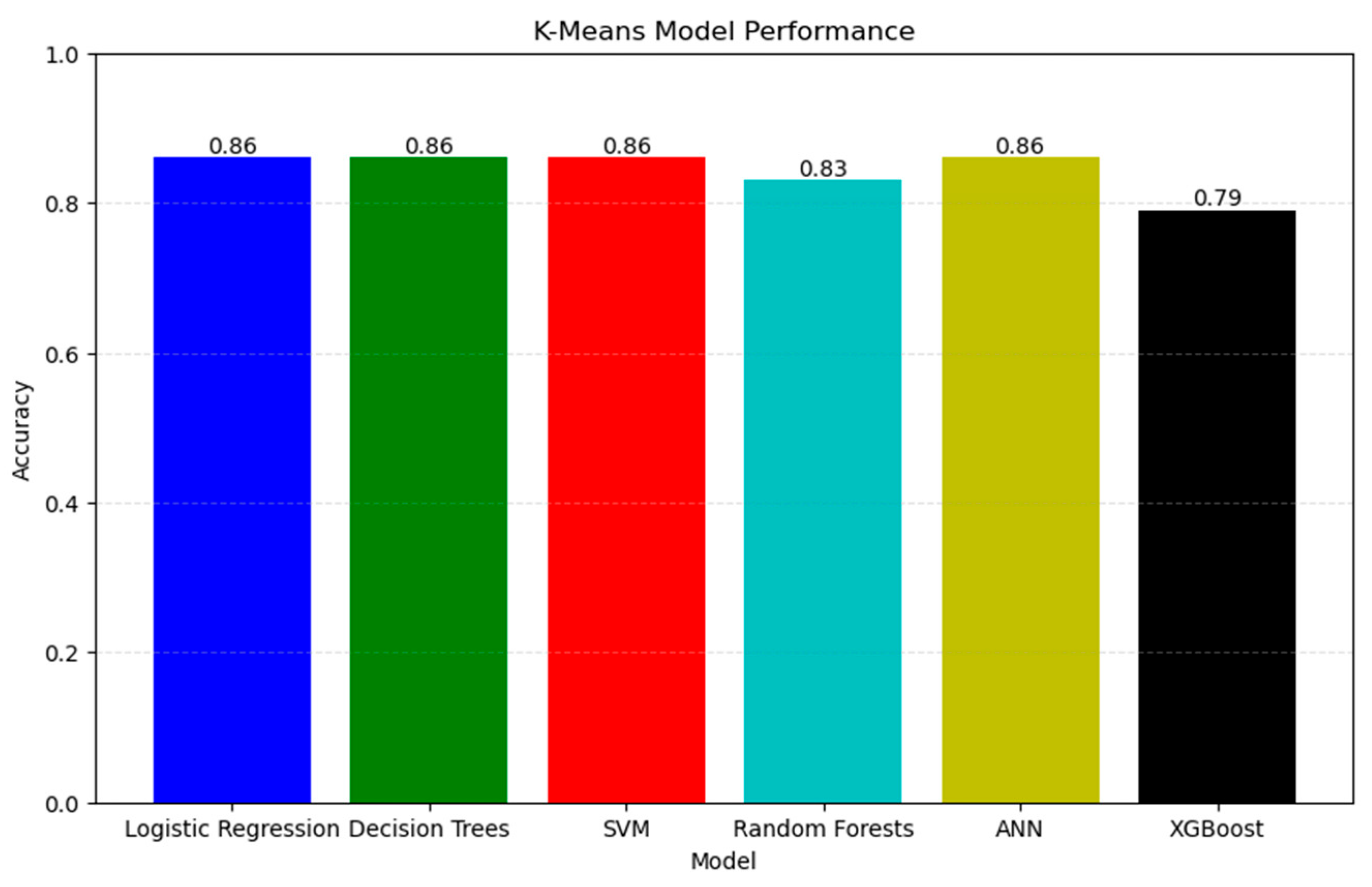
| Logistic Regression Accuracy: 0.8620689655172413 | ||||
| Logistic Regression Classification Report: | ||||
| precision | recall | f1-score | Support | |
| Cluster | ||||
| 0 | 0.82 | 0.93 | 0.87 | 15 |
| 1 | 1.00 | 1.00 | 1.00 | 6 |
| 2 | 1.00 | 0.40 | 0.57 | 5 |
| 3 | 0.75 | 1.00 | 0.86 | 3 |
| accuracy | 0.86 | 29 | ||
| macro avg | 0.89 | 0.83 | 0.83 | 29 |
| weighted avg | 0.88 | 0.86 | 0.85 | 29 |
| Decision Tree Accuracy: 0.8620689655172413 | ||||
| Decision Tree Classification Report: | ||||
| precision | recall | f1-score | Support | |
| Cluster | ||||
| 0 | 0.87 | 0.87 | 0.87 | 15 |
| 1 | 0.71 | 0.83 | 0.77 | 6 |
| 2 | 1.00 | 0.80 | 0.89 | 5 |
| 3 | 1.00 | 1.00 | 1.00 | 3 |
| accuracy | 0.86 | 29 | ||
| macro avg | 0.90 | 0.88 | 0.88 | 29 |
| weighted avg | 0.87 | 0.86 | 0.86 | 29 |
| SVM Accuracy: 0.8620689655172413 | ||||
| SVM Classification Report: | ||||
| precision | recall | f1-score | Support | |
| Cluster | ||||
| 0 | 0.79 | 1.00 | 0.88 | 15 |
| 1 | 1.00 | 0.83 | 0.91 | 6 |
| 2 | 1.00 | 0.40 | 0.57 | 5 |
| 3 | 1.00 | 1.00 | 1.00 | 3 |
| accuracy | 0.86 | 29 | ||
| macro avg | 0.95 | 0.81 | 0.84 | 29 |
| weighted avg | 0.89 | 0.86 | 0.85 | 29 |
| Random Forest Accuracy: 0.8275862068965517 | ||||
| Random Forest Accuracy: 0.8275862068965517 | ||||
| precision | recall | f1-score | support | |
| Cluster | ||||
| 0 | 0.82 | 0.93 | 0.87 | 15 |
| 1 | 0.80 | 0.67 | 0.73 | 6 |
| 2 | 1.00 | 0.60 | 0.75 | 5 |
| 3 | 0.75 | 1.00 | 0.86 | 3 |
| accuracy | 0.83 | 29 | ||
| macro avg | 0.84 | 0.80 | 0.80 | 29 |
| weighted avg | 0.84 | 0.83 | 0.82 | 29 |
| Neural Network Accuracy: 0.8620689655172413 | ||||
| Neural Network Classification Report: | ||||
| precision | recall | f1-score | support | |
| Cluster | ||||
| 0 | 0.82 | 0.93 | 0.87 | 15 |
| 1 | 1.00 | 0.83 | 0.91 | 6 |
| 2 | 1.00 | 0.60 | 0.75 | 5 |
| 3 | 0.75 | 1.00 | 0.86 | 3 |
| accuracy | 0.86 | 29 | ||
| macro avg | 0.89 | 0.84 | 0.85 | 29 |
| weighted avg | 0.88 | 0.86 | 0.86 | 29 |
| XGBoost Accuracy: 0.7931034482758621 | ||||
| XGBoost Classification Report: | ||||
| precision | recall | f1-score | support | |
| Cluster | ||||
| 0 | 0.82 | 0.93 | 0.87 | 15 |
| 1 | 0.67 | 0.67 | 0.67 | 6 |
| 2 | 1.00 | 0.60 | 0.75 | 5 |
| 3 | 0.67 | 0.67 | 0.67 | 3 |
| accuracy | 0.79 | 29 | ||
| macro avg | 0.79 | 0.72 | 0.74 | 29 |
| weighted avg | 0.81 | 0.79 | 0.79 | 29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çelik, S.; Doğanlı, B.; Şaşmaz, M.Ü.; Akkucuk, U. Accuracy Comparison of Machine Learning Algorithms on World Happiness Index Data. Mathematics 2025, 13, 1176. https://doi.org/10.3390/math13071176
Çelik S, Doğanlı B, Şaşmaz MÜ, Akkucuk U. Accuracy Comparison of Machine Learning Algorithms on World Happiness Index Data. Mathematics. 2025; 13(7):1176. https://doi.org/10.3390/math13071176
Chicago/Turabian StyleÇelik, Sadullah, Bilge Doğanlı, Mahmut Ünsal Şaşmaz, and Ulas Akkucuk. 2025. "Accuracy Comparison of Machine Learning Algorithms on World Happiness Index Data" Mathematics 13, no. 7: 1176. https://doi.org/10.3390/math13071176
APA StyleÇelik, S., Doğanlı, B., Şaşmaz, M. Ü., & Akkucuk, U. (2025). Accuracy Comparison of Machine Learning Algorithms on World Happiness Index Data. Mathematics, 13(7), 1176. https://doi.org/10.3390/math13071176







