Numerical Simulation of the Entrance Length in a Laminar Pipe Flow at Low Reynolds Numbers
Abstract
1. Introduction
2. Governing Equations and Methods
2.1. Governing Equations
2.2. Geometry and Boundary Conditions
2.3. Numerical Method
3. Results
3.1. Grid Independence Verification
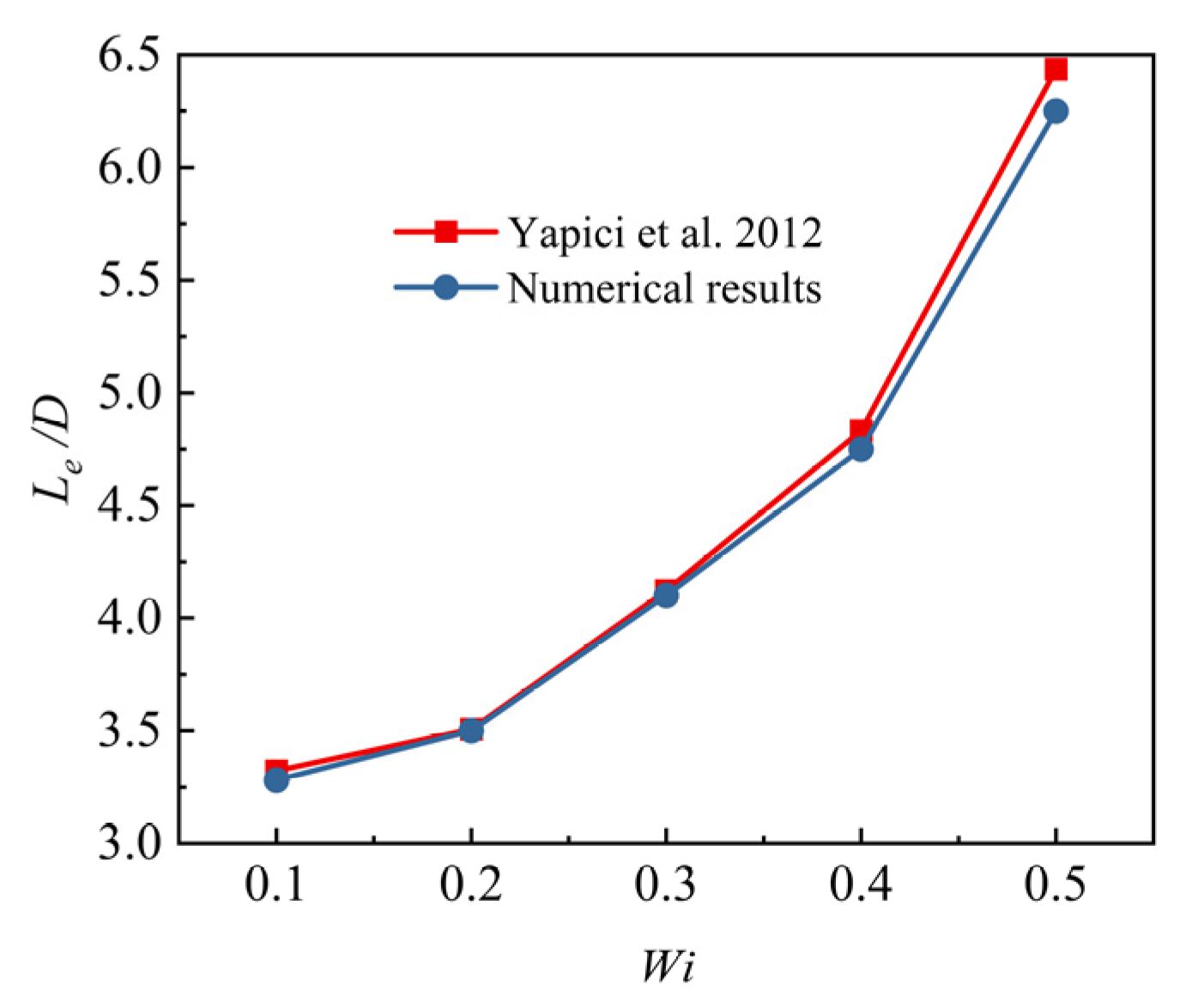
3.2. Accuracy Verification
3.3. Lower Reynolds Number
3.4. Influence of Dimensionless Entrance Length and Friction Factor
3.4.1. Reynolds Number
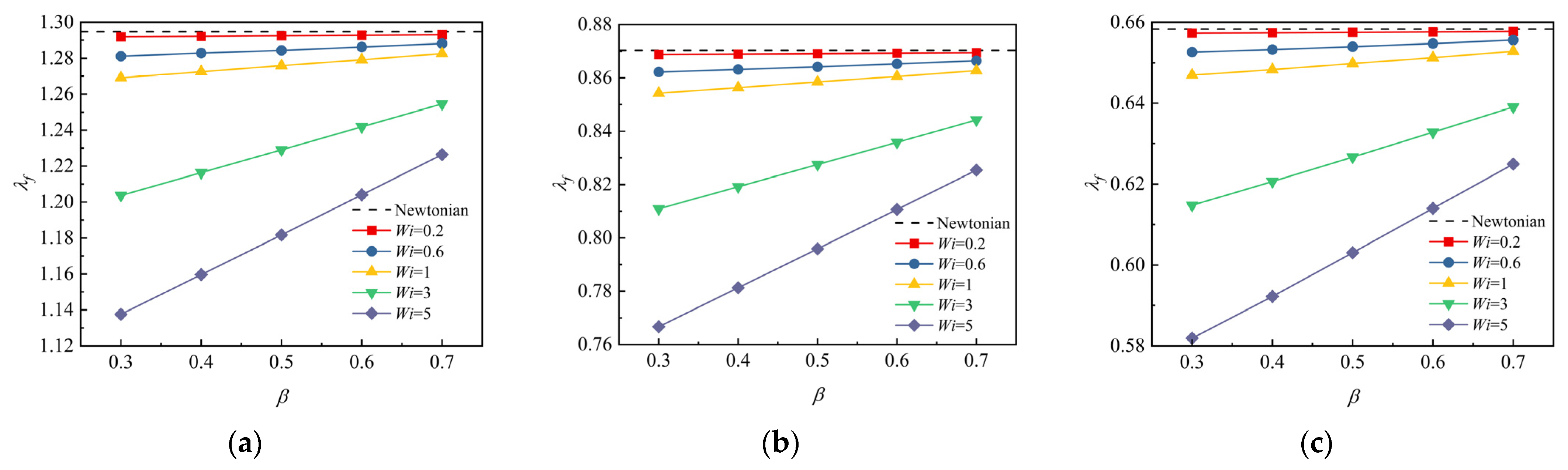
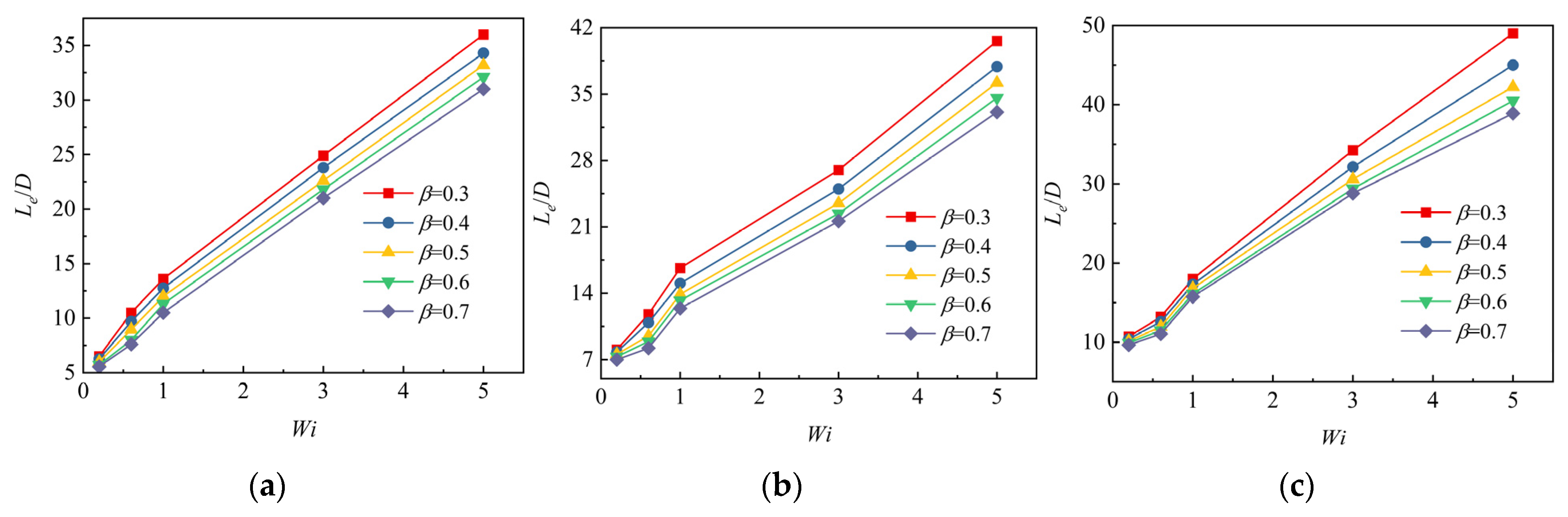
3.4.2. Solvent Viscosity Ratio
3.4.3. Weissenberg Numbers
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | PBiCG | Preconditioned Bi-conjugate Gradient | |
| PTT | Phan-Thien–Tanner | ||
| Bi | Bingham number | SIMPLE | Semi-Implicit Method for Pressure Linked Equations |
| C | Conformation tensor | ||
| D | Diameter | SIMPLER | Semi-Implicit Method for Pressure Linked Equations Revised |
| g | Gravitational acceleration | ||
| hf | Friction head loss | Greek letters | |
| l | Characteristic length | β | Solvent viscosity ratio |
| L | Length | δ | Boundary layer thickness |
| Le | Entrance length | η | Viscosity |
| M | Mesh | λ | Relaxation time |
| n | Exponential | λf | Friction factor |
| p | Pressure | ρ | Density |
| R | Eigenvector matrix | τ | Stress tensor |
| Re | Reynolds number | Δ | Change symbol |
| ReL | Lower Reynolds number | Λ | Diagonal matrix composed of eigenvalues |
| S | Logarithm of conformation tensor | Ω | Anti-symmetry matrix |
| t | Time | ||
| u | Velocity vector | Superscripts | |
| V | Average velocity | ∇ | Gradient |
| Wi | Weissenberg number | T | Transposition |
| Abbreviations | Subscripts | ||
| CUBISTA | Convergent and Universally Bounded Interpolation Scheme for Treatment of Advection | f | Friction |
| i | ith segment | ||
| l | Characteristic length | ||
| DILU | Diagonal-based Incomplete LU | L | Low |
| gPTT | Generalized Phan-Thien Tanner | s | Solvent |
| log | Logarithm | p | Polymer |
| LCR | Log-Conformation Representation | 0 | Zero-shear rate |
References
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C. Dynamics of Polymeric Liquids; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1987. [Google Scholar]
- Langhaar, H. Steady Flow in the Transition Length of a Straight Tube. J. Appl. Mech. 1942, 9, A55–A58. [Google Scholar] [CrossRef]
- Campbell, W.D.; Slattery, J.C. Flow in the Entrance of a Tube. J. Basic Eng. 1963, 85, 41–45. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Lin, S.H.; Lundgren, T.S. Flow Development in the Hydrodynamic Entrance Region of Tubes and Ducts. Phys. Fluids 1964, 7, 338–347. [Google Scholar] [CrossRef]
- Friedmann, M.; Gillis, J.; Liron, N. Laminar flow in a pipe at low and moderate Reynolds numbers. Appl. Sci. Res. 1968, 19, 426–438. [Google Scholar] [CrossRef]
- Na, Y.; Yoo, J.Y. A finite volume technique to simulate the flow of a viscoelastic fluid. Comput. Mech. 1991, 8, 43–55. [Google Scholar] [CrossRef]
- Alves, M.A.; Oliveira, P.J.; Pinho, F.T. Benchmark solutions for the flow of Oldroyd-B and PTT fluids in planar contractions. J. Non-Newton. Fluid Mech. 2003, 110, 45–75. [Google Scholar] [CrossRef]
- Durst, F.; Ray, S.; Unsal, B. The Development Lengths of Laminar Pipe and Channel Flows. J. Fluids Eng. 2005, 127, 1154–1160. [Google Scholar] [CrossRef]
- Poole, R.J.; Ridley, B.S. Development-Length Requirements for Fully Developed Laminar Pipe Flow of Inelastic Non-Newtonian Liquids. J. Fluids Eng. 2007, 129, 1281–1287. [Google Scholar] [CrossRef]
- Yapici, K.; Karasozen, B.; Uludag, Y. Numerical Analysis of Viscoelastic Fluids in Steady Pressure-Driven Channel Flow. J. Fluids Eng. 2012, 134, 051206. [Google Scholar] [CrossRef]
- Bertoco, J.; Leiva, R.T.; Ferrás, L.L. Development Length of Fluids Modelled by the gPTT Constitutive Differential Equation. Appl. Sci. 2021, 11, 10352. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sharifpur, M.; Abd, E.M. Mathematical Correlation Study of Nanofluid Flow Merging Points in Entrance Regions. Mathematics 2022, 10, 4148. [Google Scholar] [CrossRef]
- Lavrov, A. Precision calculation of the entrance length for laminar flow of Bingham fluid between parallel plates with yield number from 0 to 1000. Chem. Eng. Sci. 2024, 297, 120292. [Google Scholar] [CrossRef]
- Chen, R.Y. Flow in the Entrance Region at Low Reynolds Numbers. J. Fluids Eng. 1973, 95, 153–158. [Google Scholar] [CrossRef]
- Everts, M.; Meyer, J.P. Laminar hydrodynamic and thermal entrance lengths for simultaneously hydrodynamically and thermally developing forced and mixed convective flows in horizontal tubes. Exp. Therm. Fluid Sci. 2020, 18, 11015. [Google Scholar] [CrossRef]
- Favero, J.L.; Secchi, A.R.; Cardozo, N.S.M.; Jasak, H. Viscoelastic flow analysis using the software OpenFOAM and differential constitutive equations. J. Non-Newton. Fluid Mech. 2010, 165, 23–24. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M.A. Stabilization of an open-source finite-volume solver for viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2017, 239, 85–104. [Google Scholar] [CrossRef]
- Fattal, R.; Kupferman, R. Constitutive laws for the matrix-logarithm of the conformation tensor. J. Non-Newton. Fluid Mech. 2004, 123, 281–285. [Google Scholar] [CrossRef]
- Fattal, R.; Kupferman, R. Time-dependent simulation of viscoelastic flows at high Weissenberg number using the log-conformation representation. J. Non-Newton. Fluid Mech. 2005, 126, 23–37. [Google Scholar] [CrossRef]
- Hulsen, M.A.; Fattal, R.; Kupferman, R. Flow of viscoelastic fluids past a cylinder at high Weissenberg number: Stabilized simulations using matrix logarithms. J. Non-Newton. Fluid Mech. 2005, 127, 27–39. [Google Scholar] [CrossRef]
- Afonso, A.; Oliveira, P.; Pinho, F. The log-conformation tensor approach in the finite-volume method framework. J. Non-Newton. Fluid Mech. 2009, 157, 55–65. [Google Scholar] [CrossRef]
- King, J.R.; Lind, S.J. High Weissenberg number simulations with incompressible Smoothed Particle Hydrodynamics and the log-conformation formulation. J. Non-Newton. Fluid Mech. 2021, 293, 104556. [Google Scholar] [CrossRef]
- Rath, S.; Mahapatra, B. Low Reynolds Number Pulsatile Flow of a Viscoelastic Fluid Through a Channel: Effects of Fluid Rheology and Pulsation Parameters. J. Fluids Eng. 2022, 144, 021201. [Google Scholar] [CrossRef]
- Chen, X.; Marschall, H.; Schäfer, M. A comparison of stabilisation approaches for finite-volume simulation of viscoelastic fluid flow. Int. J. Comput. Fluid Dyn. 2013, 27, 229–250. [Google Scholar] [CrossRef]
- Habla, F.; Tan, M.W.; Haßlberger, J.; Hinrichsen, O. Numerical simulation of the viscoelastic flow in a three-dimensional lid-driven cavity using the log-conformation reformulation in OpenFOAM®. J. Non-Newton. Fluid Mech. 2014, 212, 47–62. [Google Scholar] [CrossRef]
- Mohanty, P.K.; Bharti, R.P.; Sahu, A.K. CFD analysis of the influence of solvent viscosity ratio on the creeping flow of viscoelastic fluid over a channel- confined circular cylinder. Phys. Fluids 2024, 36, 073103. [Google Scholar] [CrossRef]
- Alves, M.A.; Oliveira, P.J.; Pinho, F.T. Numerical Methods for Viscoelastic Fluid Flows. Annu. Rev. Fluid Mech. 2020, 53, 509–541. [Google Scholar] [CrossRef]

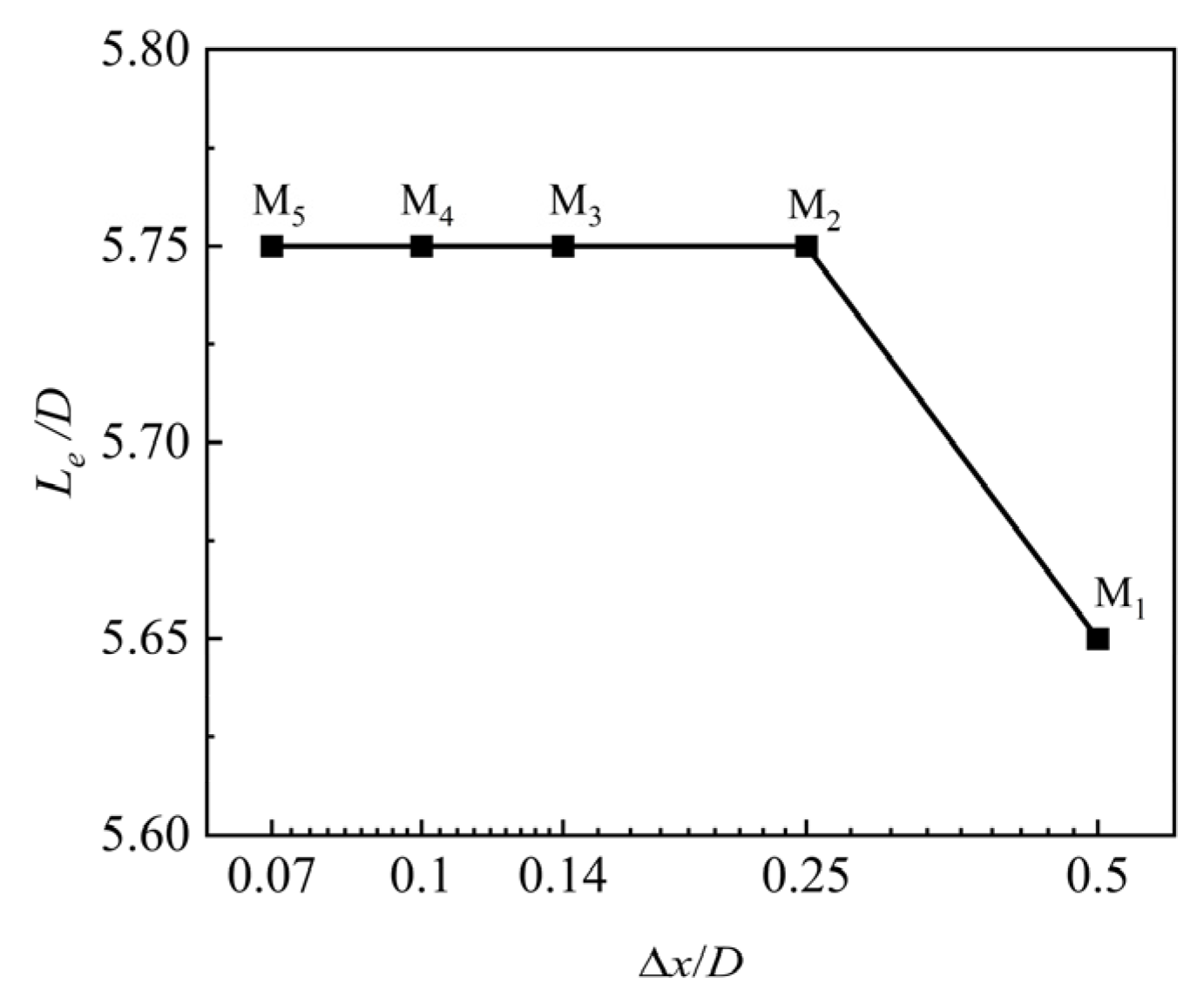






| Mesh | Number of Nodes | Δx/D | Δy/D |
|---|---|---|---|
| M1 | 100 × 5 | 0.5 | 0.1 |
| M2 | 200 × 10 | 0.25 | 0.05 |
| M3 | 350 × 15 | 0.1429 | 0.0333 |
| M4 | 500 × 20 | 0.1 | 0.025 |
| M5 | 700 × 30 | 0.0714 | 0.0167 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, X.; Wang, Q.; Ke, L. Numerical Simulation of the Entrance Length in a Laminar Pipe Flow at Low Reynolds Numbers. Mathematics 2025, 13, 1234. https://doi.org/10.3390/math13081234
Qi X, Wang Q, Ke L. Numerical Simulation of the Entrance Length in a Laminar Pipe Flow at Low Reynolds Numbers. Mathematics. 2025; 13(8):1234. https://doi.org/10.3390/math13081234
Chicago/Turabian StyleQi, Xiaoli, Qikun Wang, and Lingjie Ke. 2025. "Numerical Simulation of the Entrance Length in a Laminar Pipe Flow at Low Reynolds Numbers" Mathematics 13, no. 8: 1234. https://doi.org/10.3390/math13081234
APA StyleQi, X., Wang, Q., & Ke, L. (2025). Numerical Simulation of the Entrance Length in a Laminar Pipe Flow at Low Reynolds Numbers. Mathematics, 13(8), 1234. https://doi.org/10.3390/math13081234





