A 2.5D Generalized Finite Difference Method for Elastic Wave Propagation Problems
Abstract
:1. Introduction
2. Elastic Wave Propagation Problems
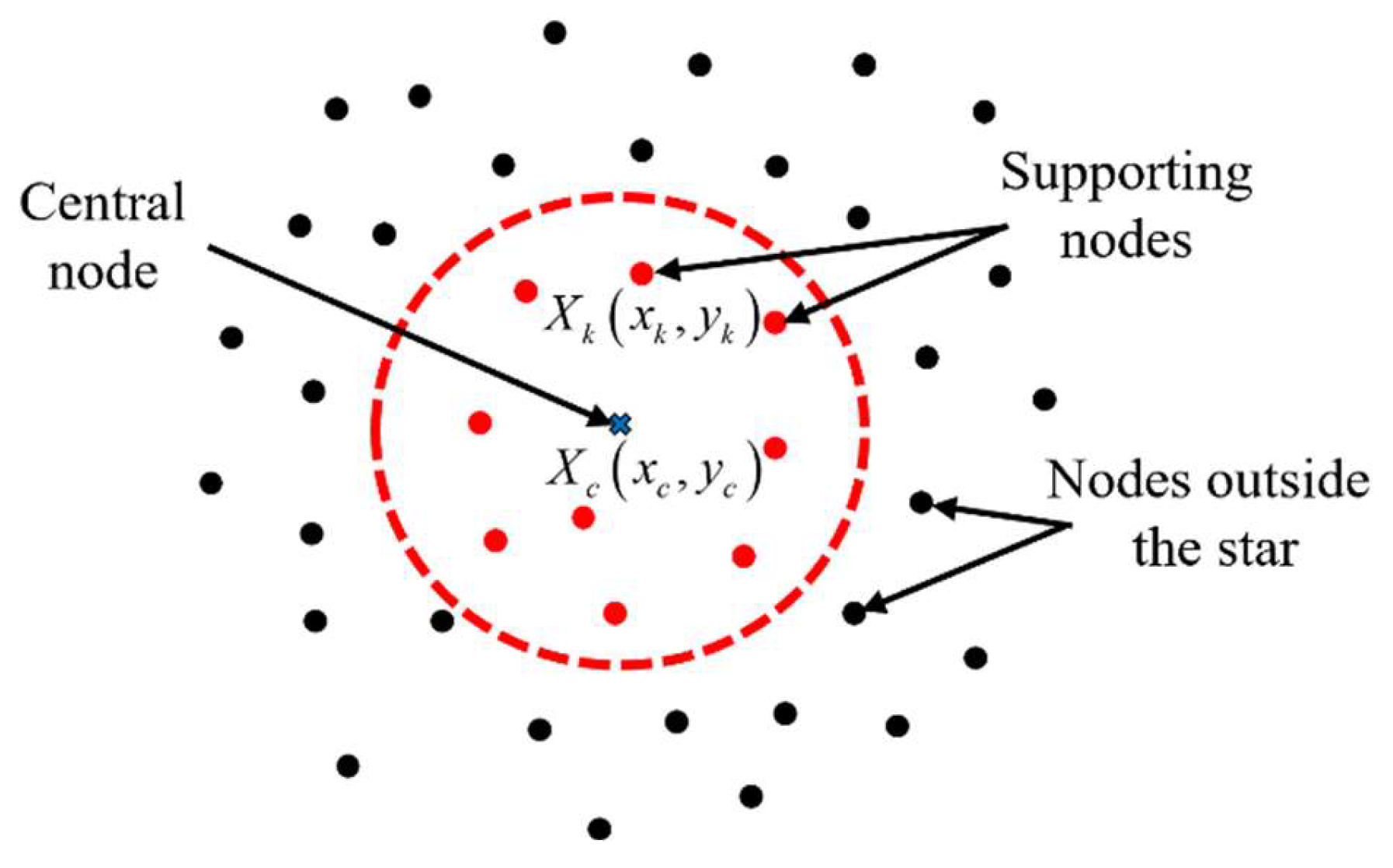
3. 2.5D GFDM for Elastic Wave Propagation Problems
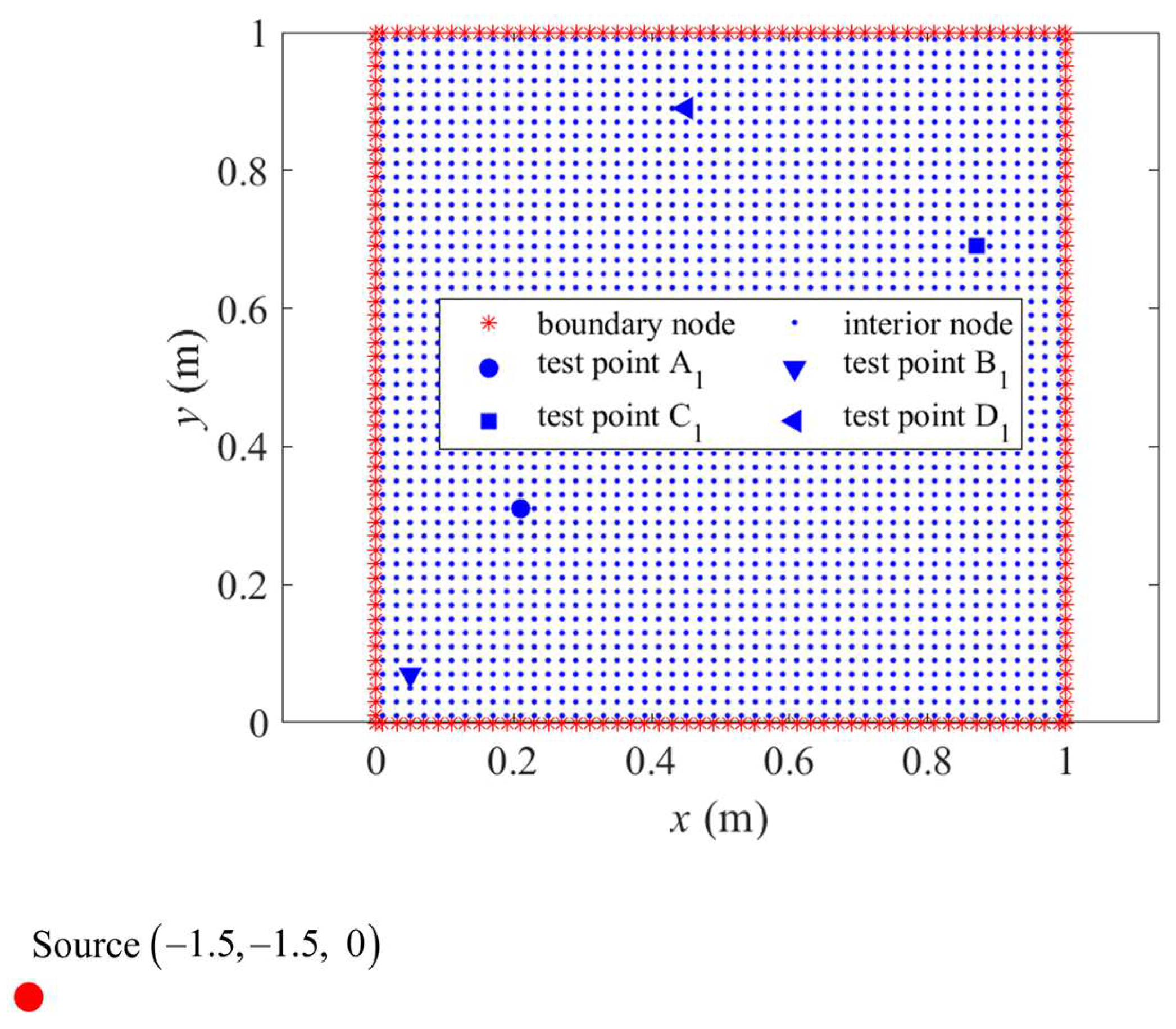
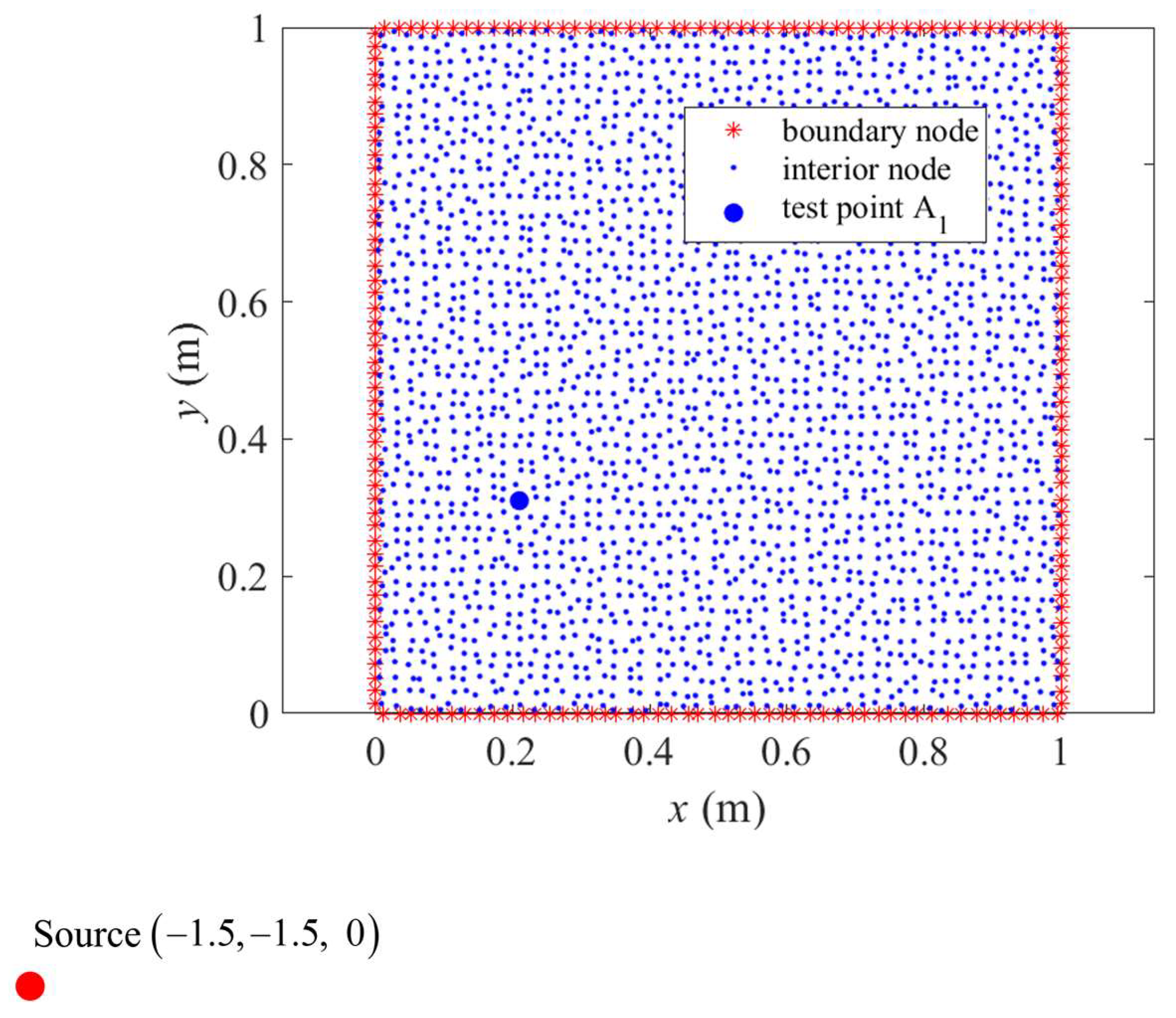
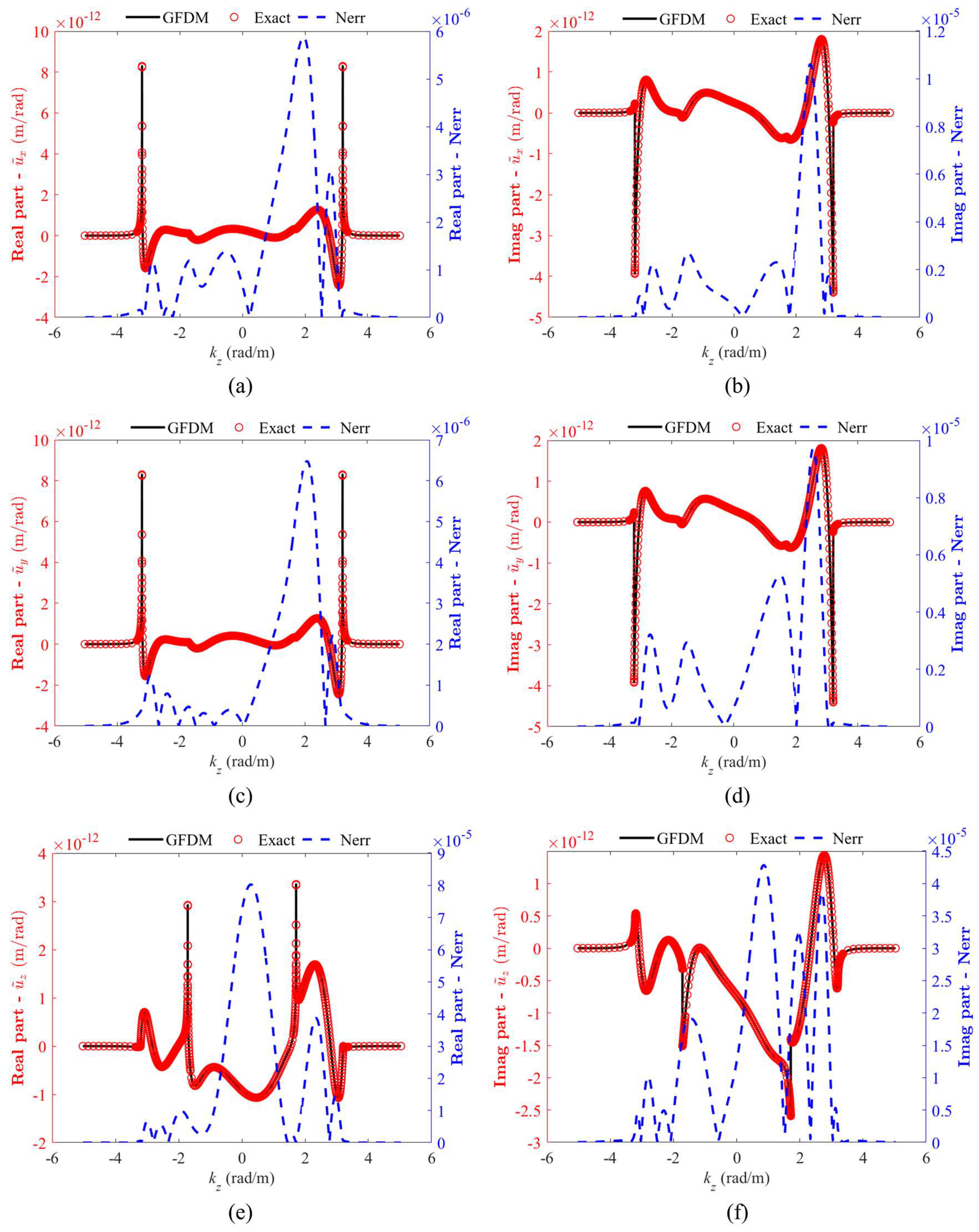
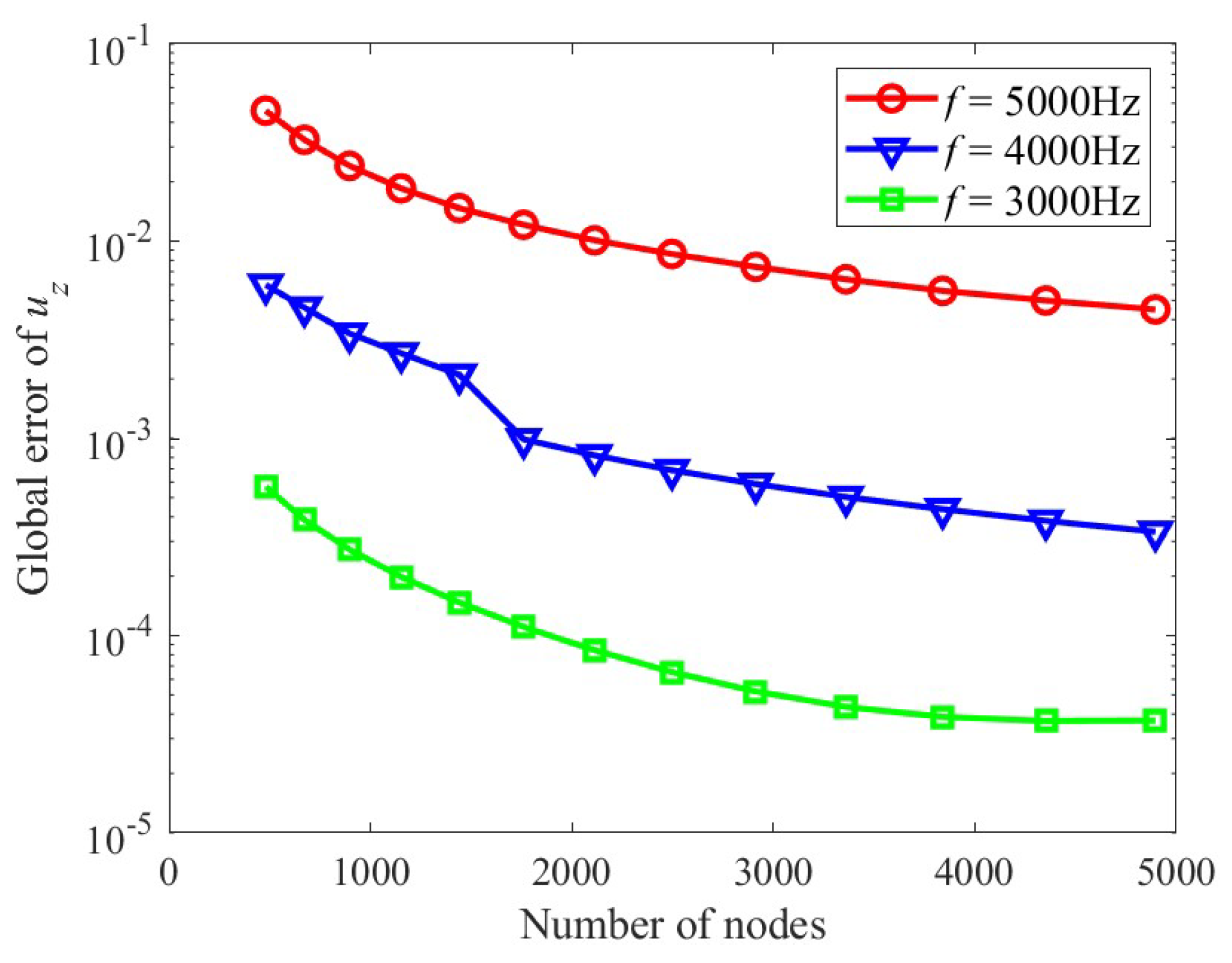
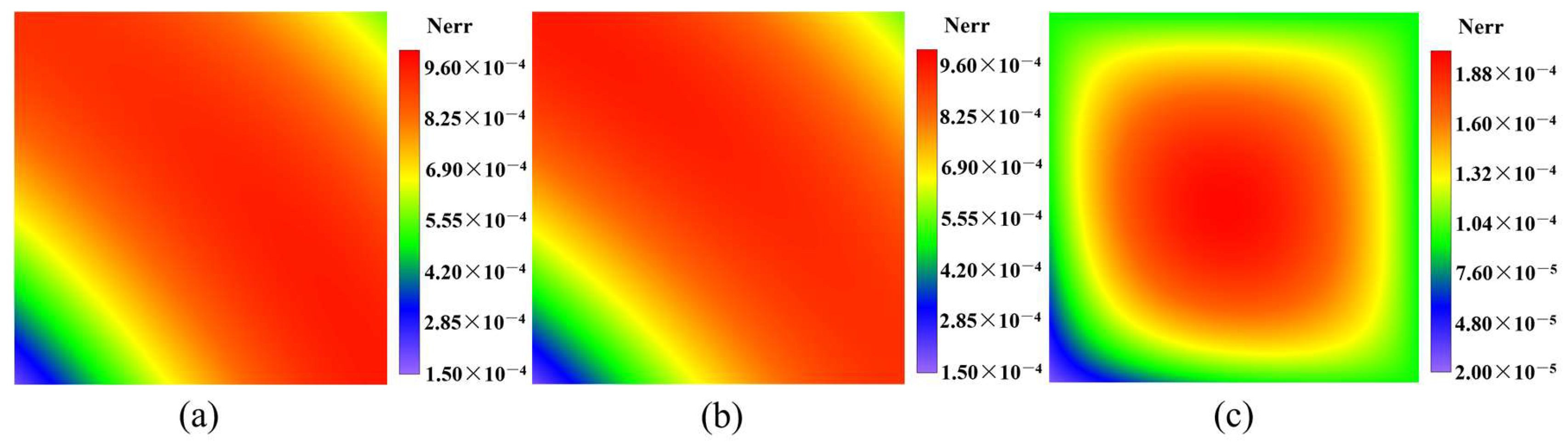
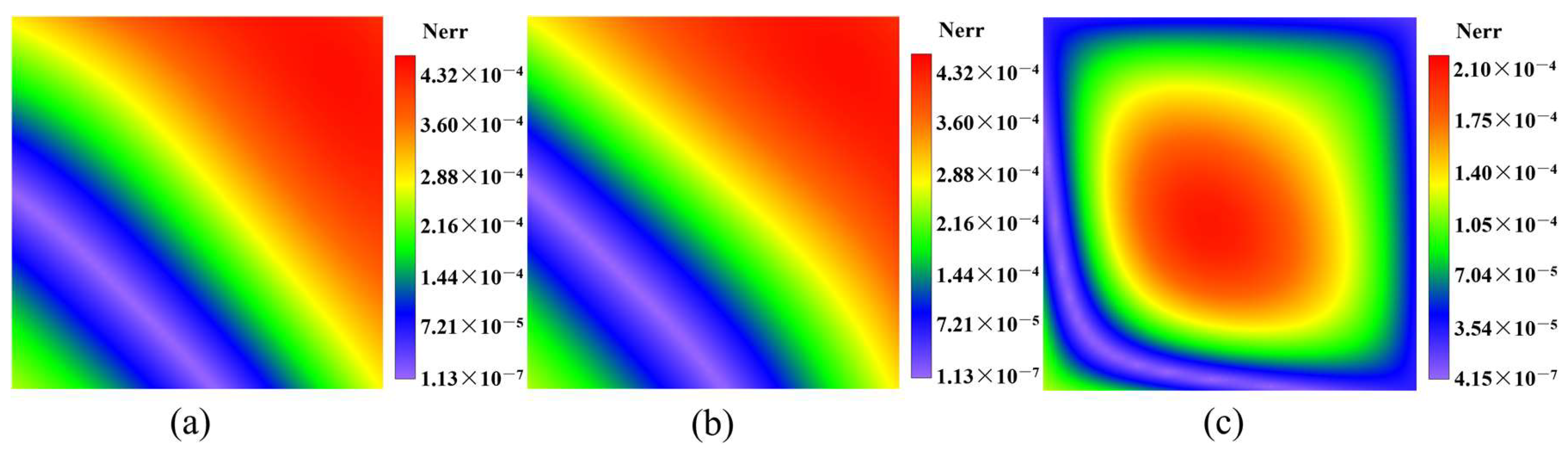
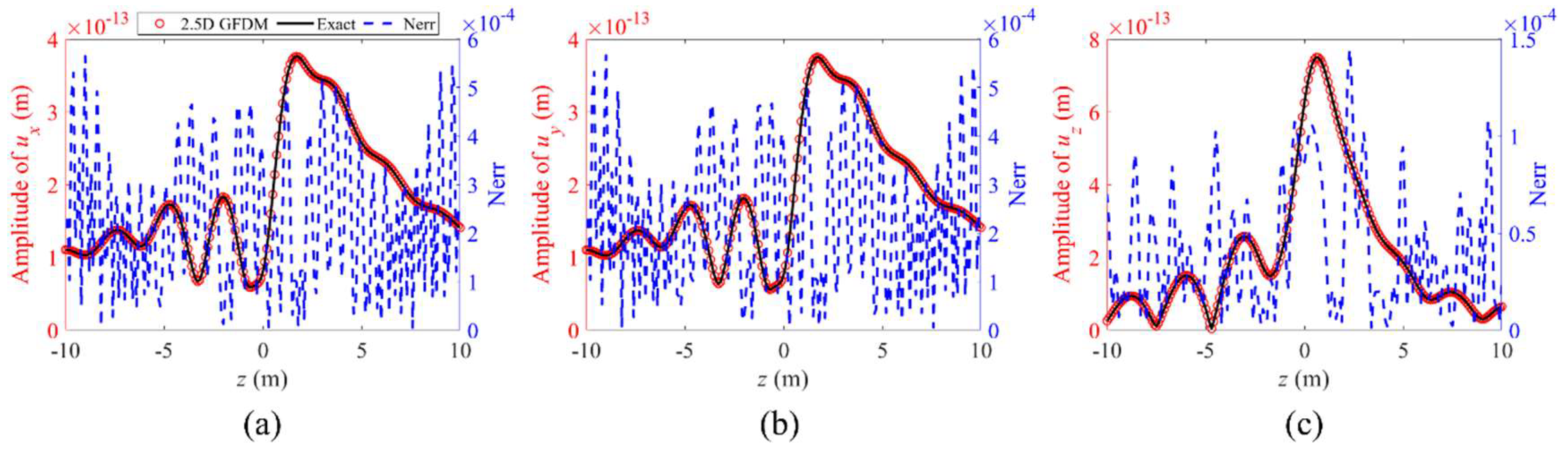
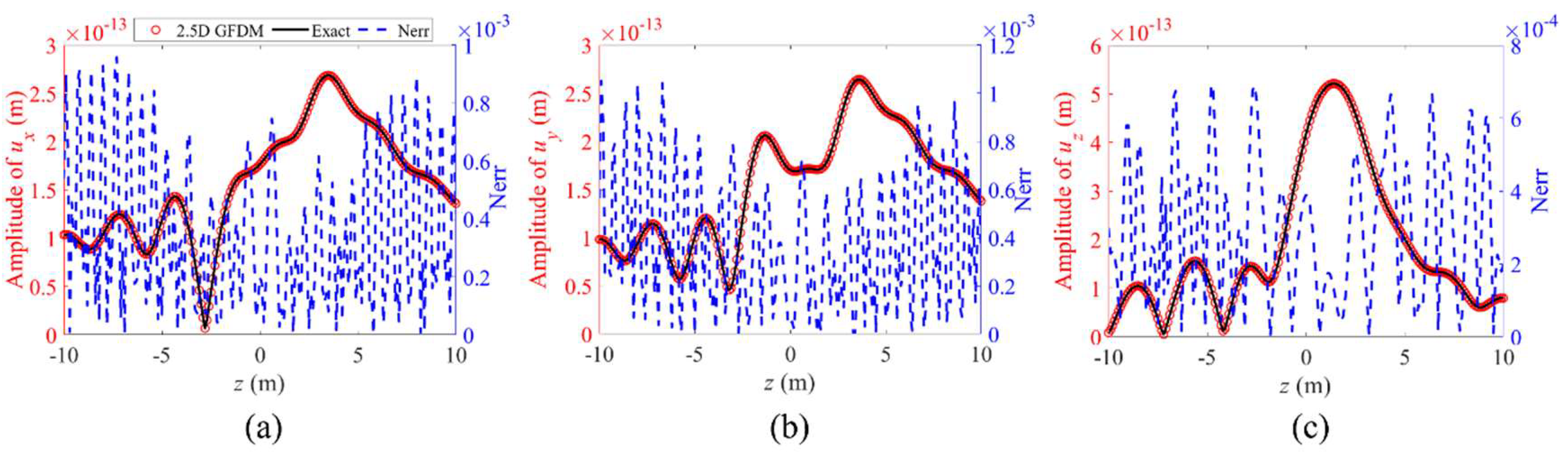
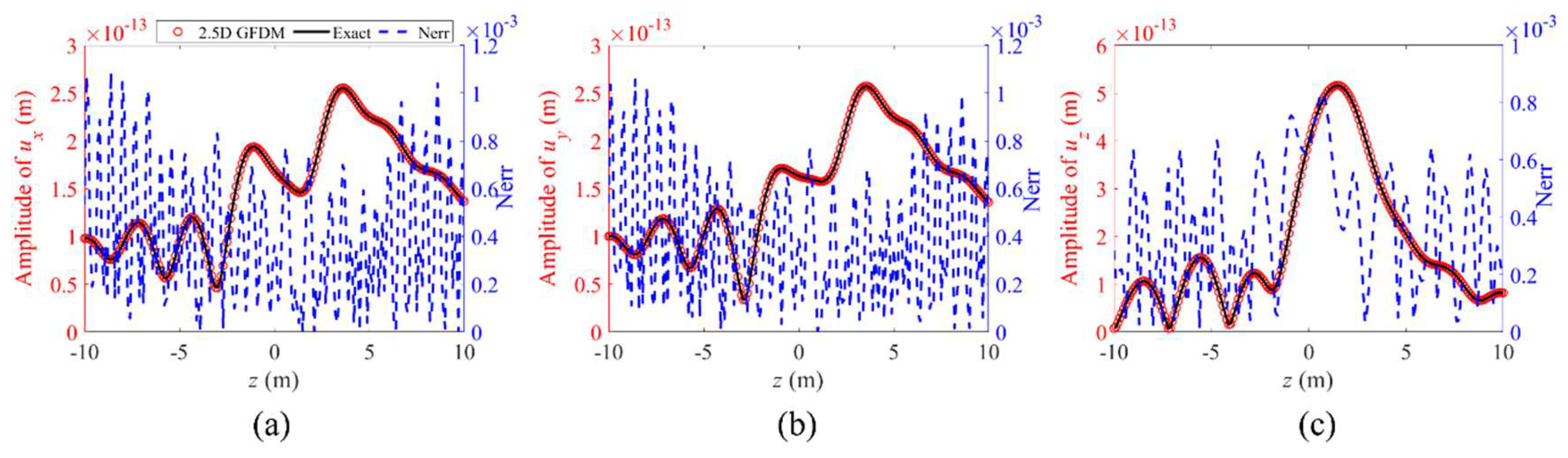
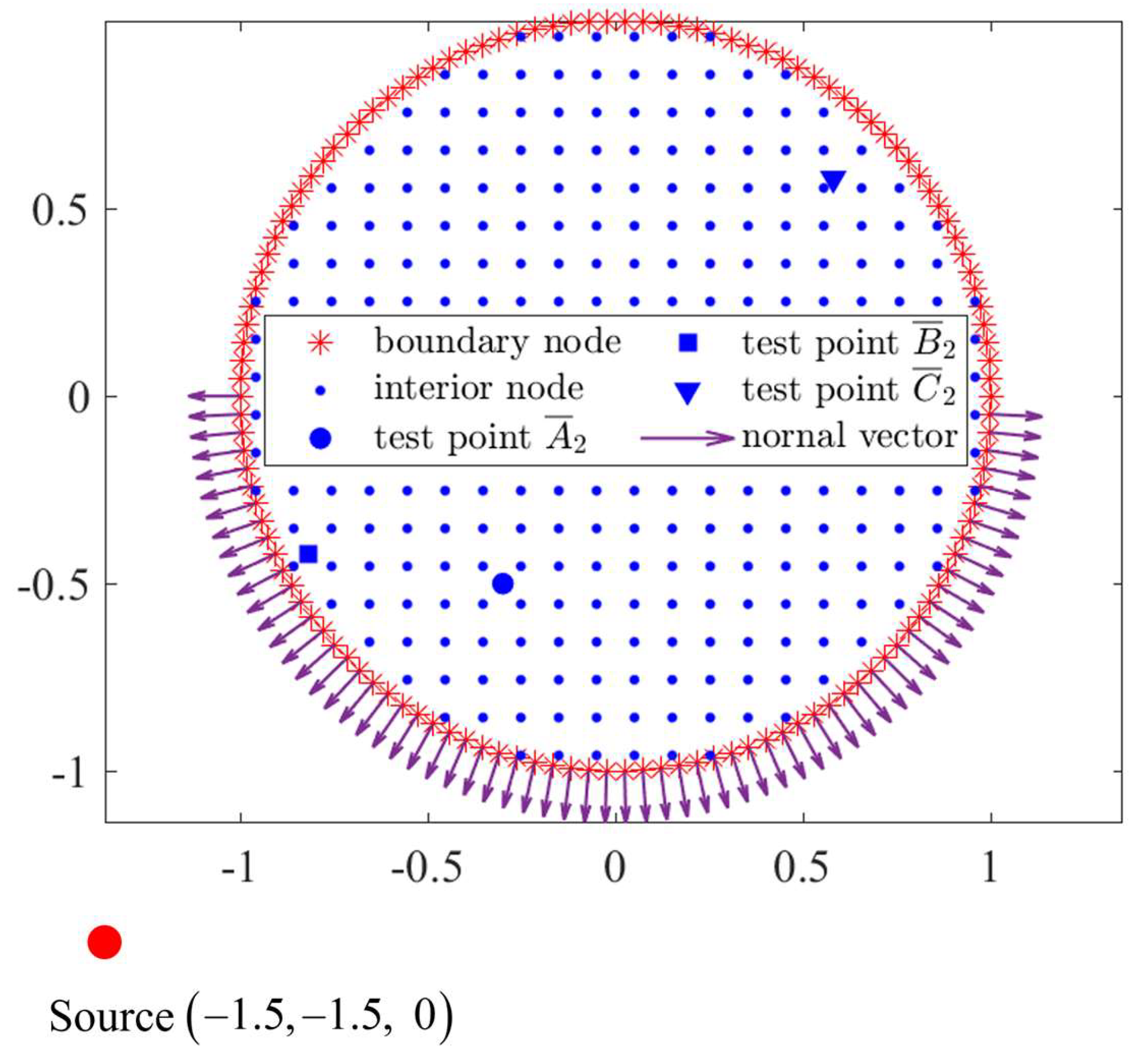
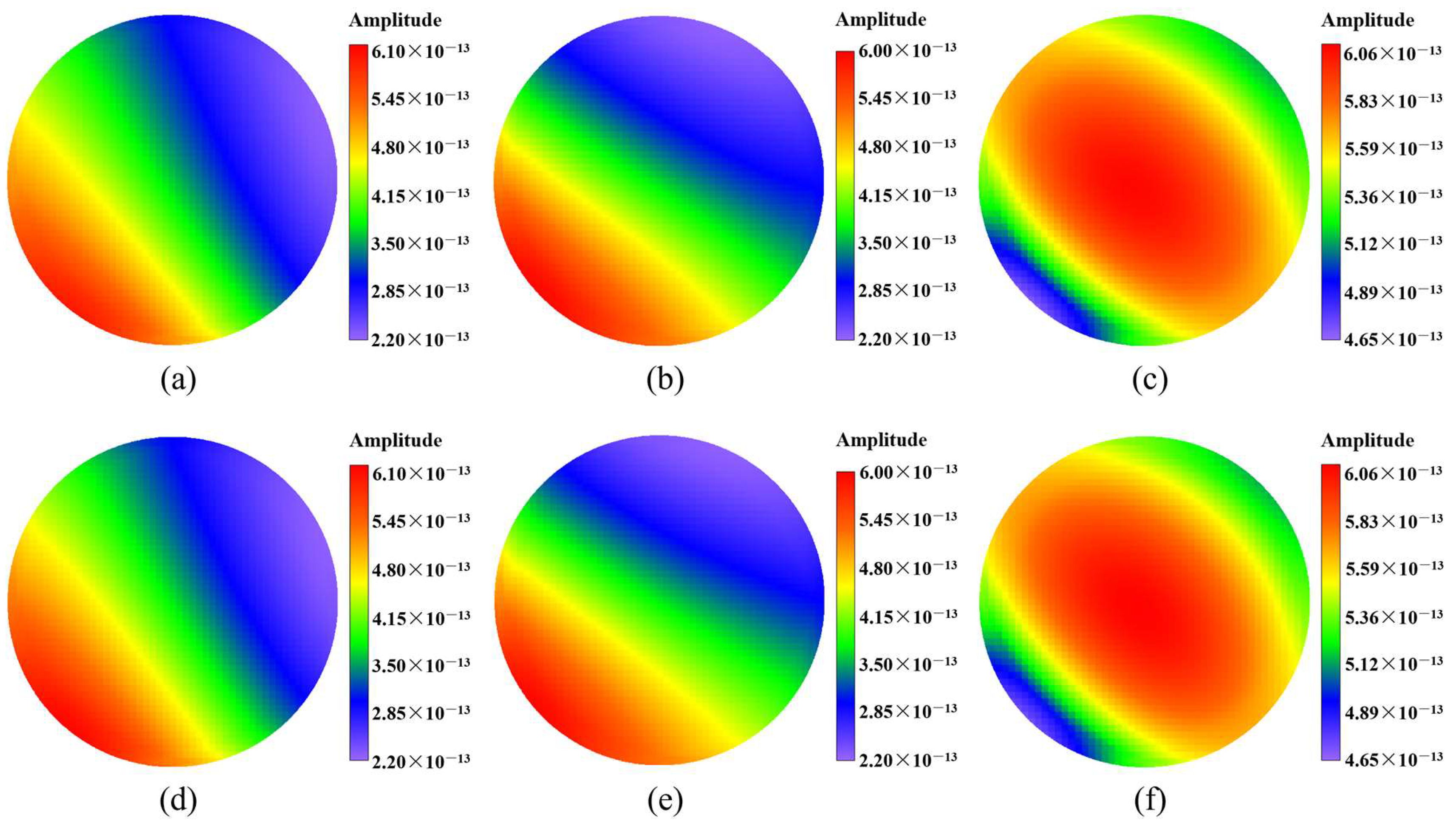
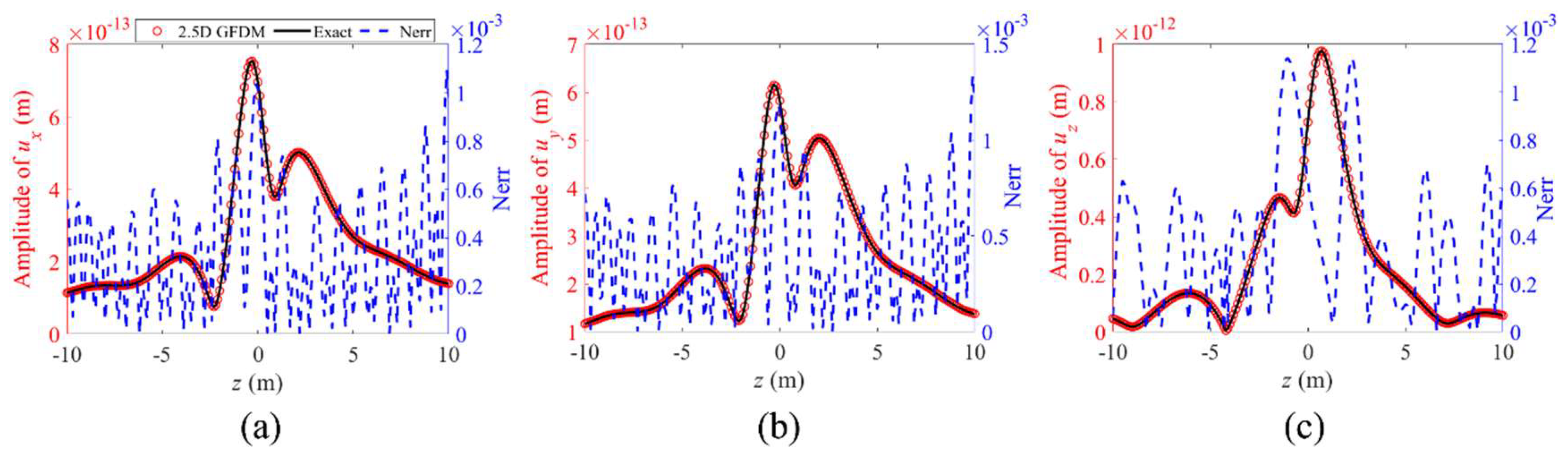
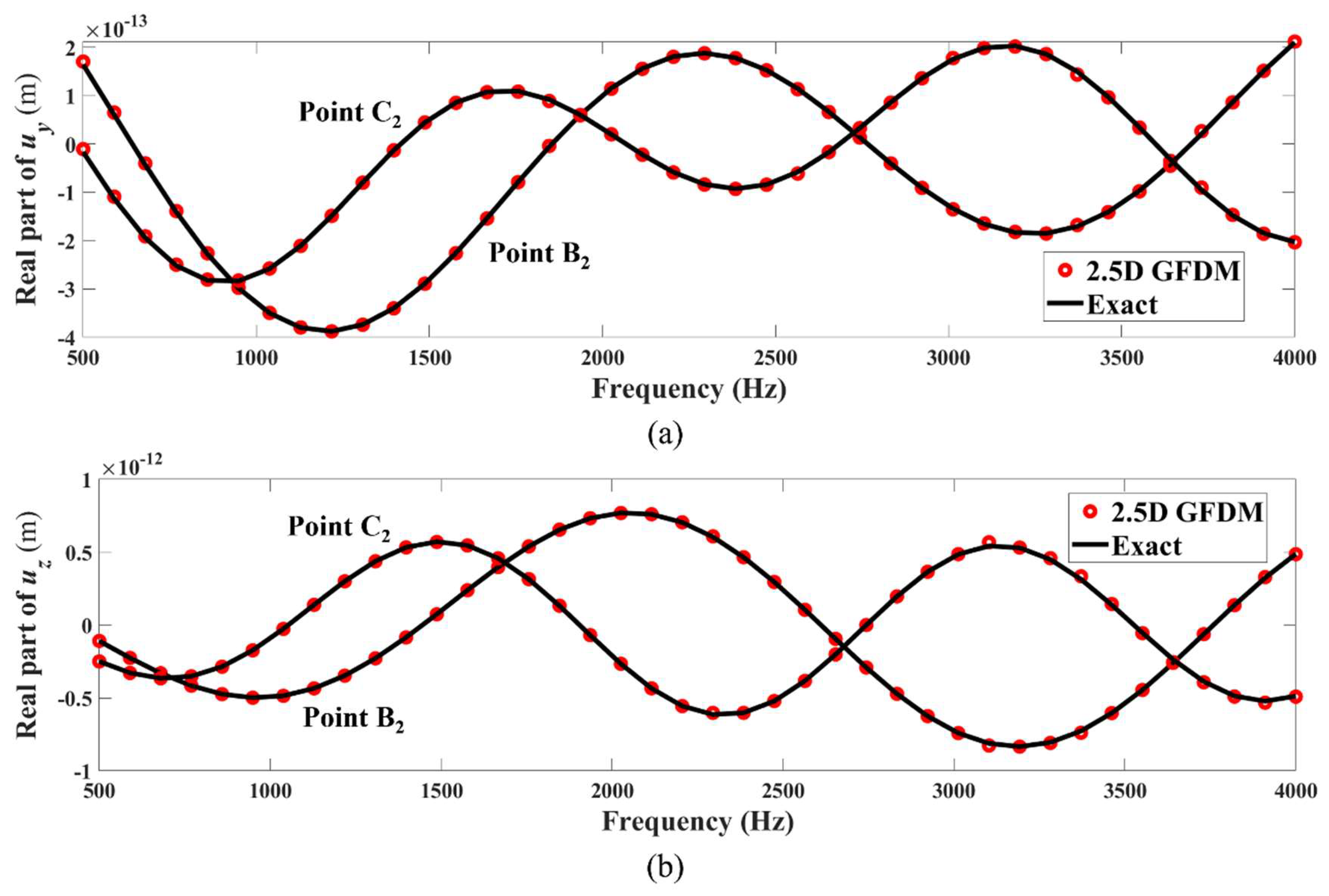
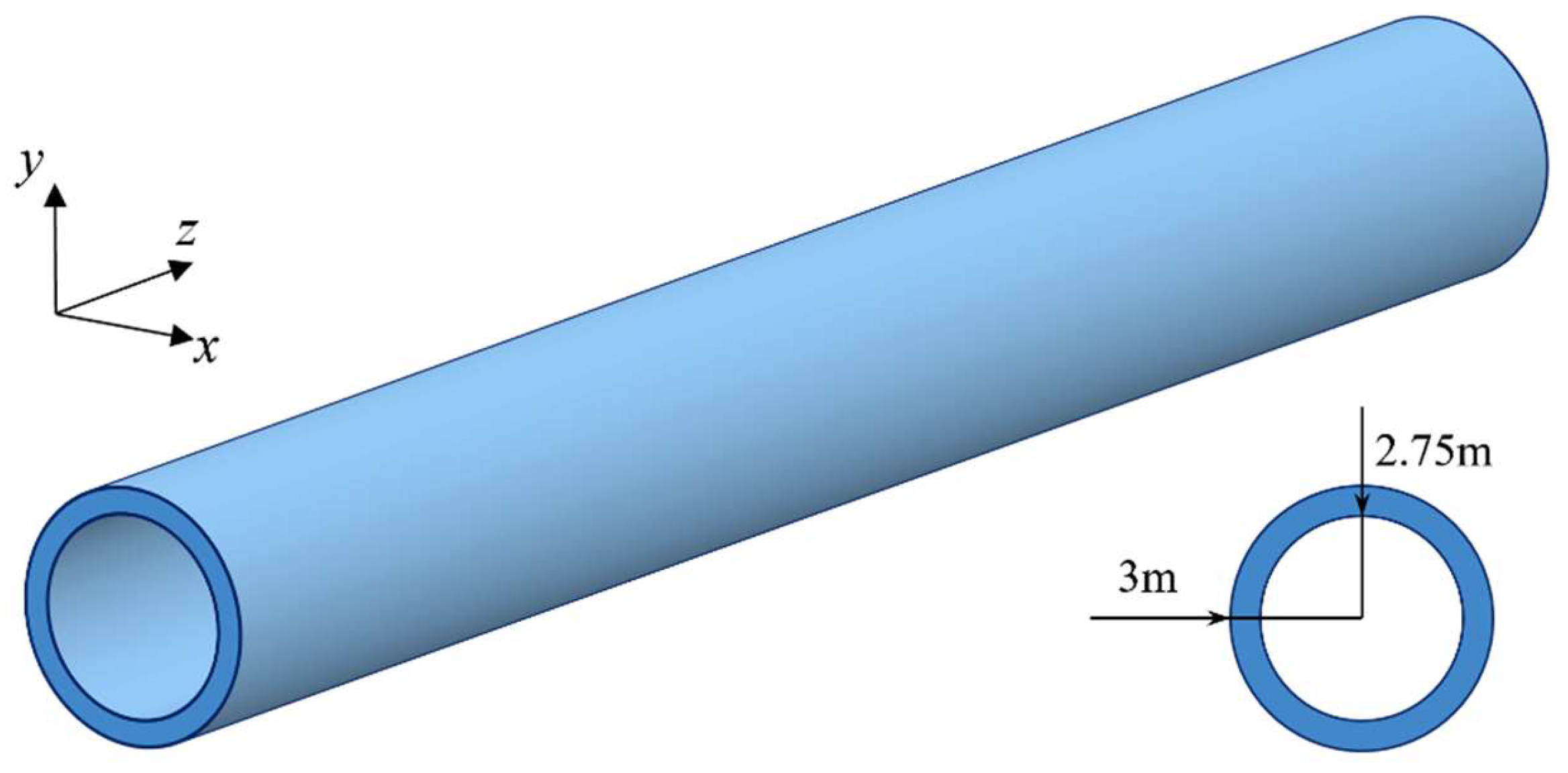
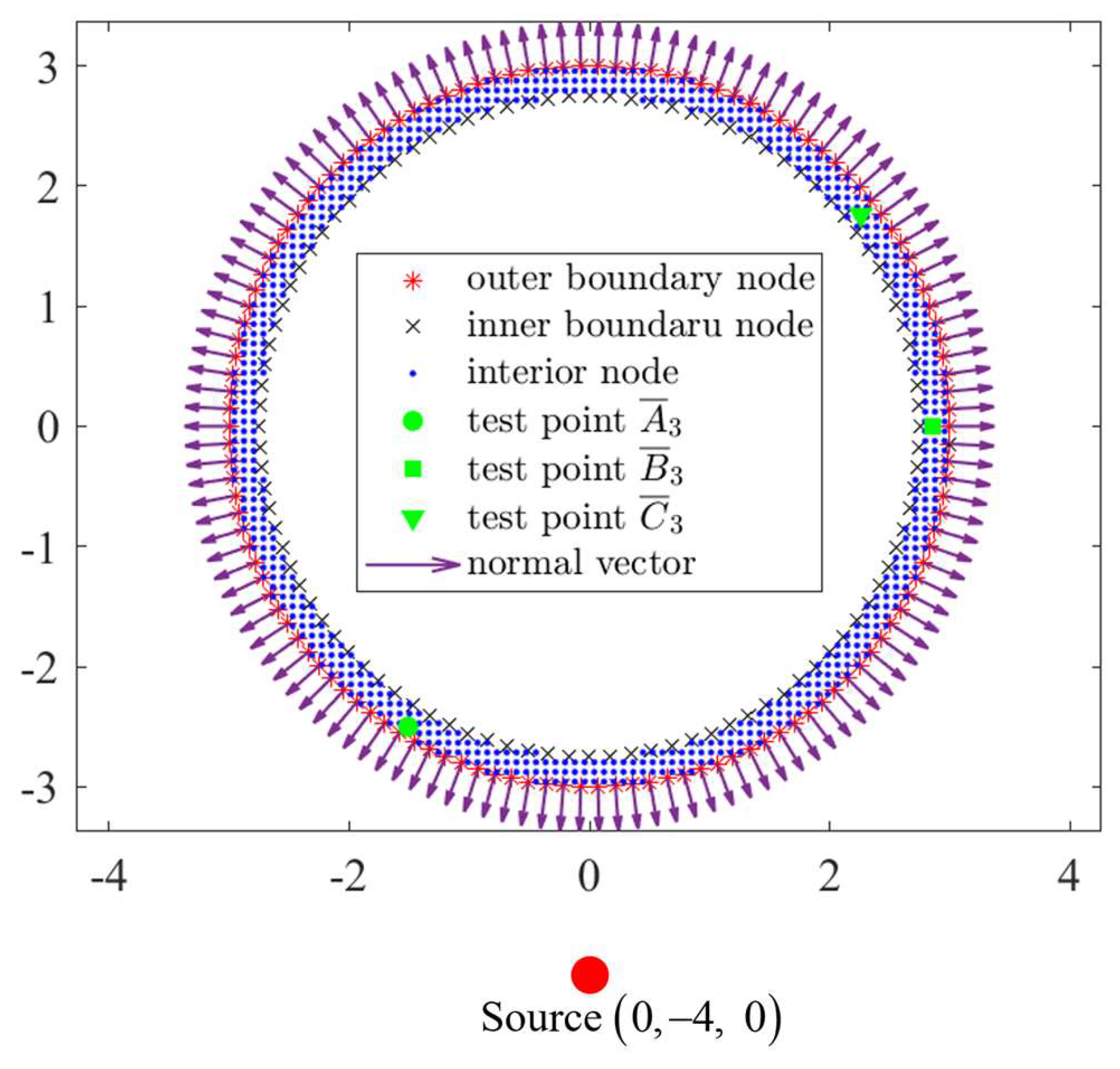
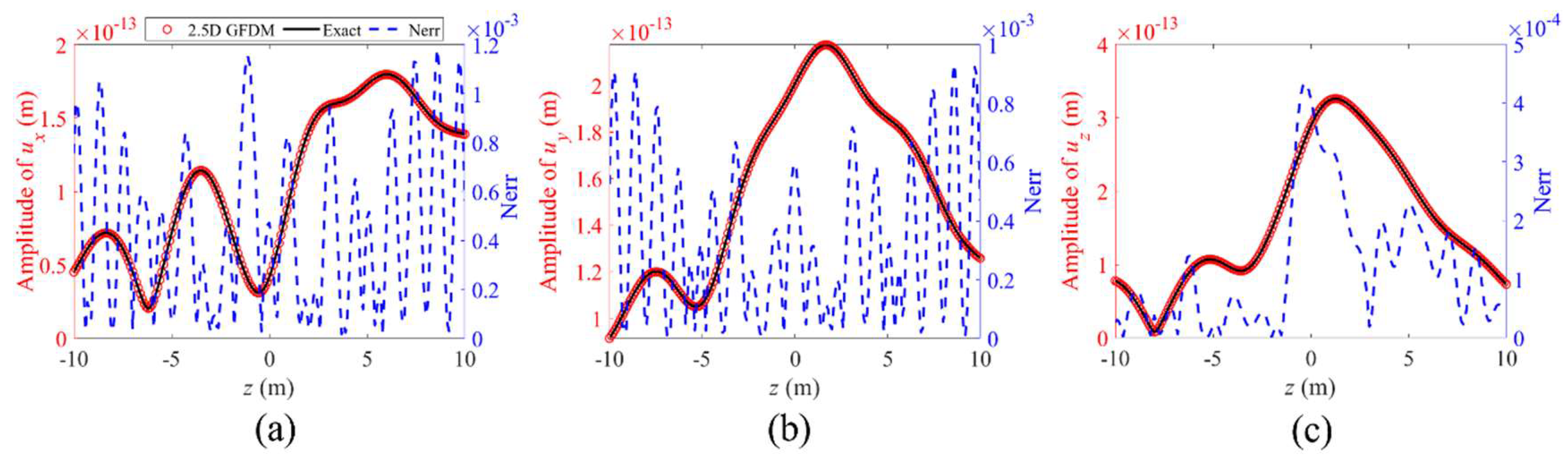
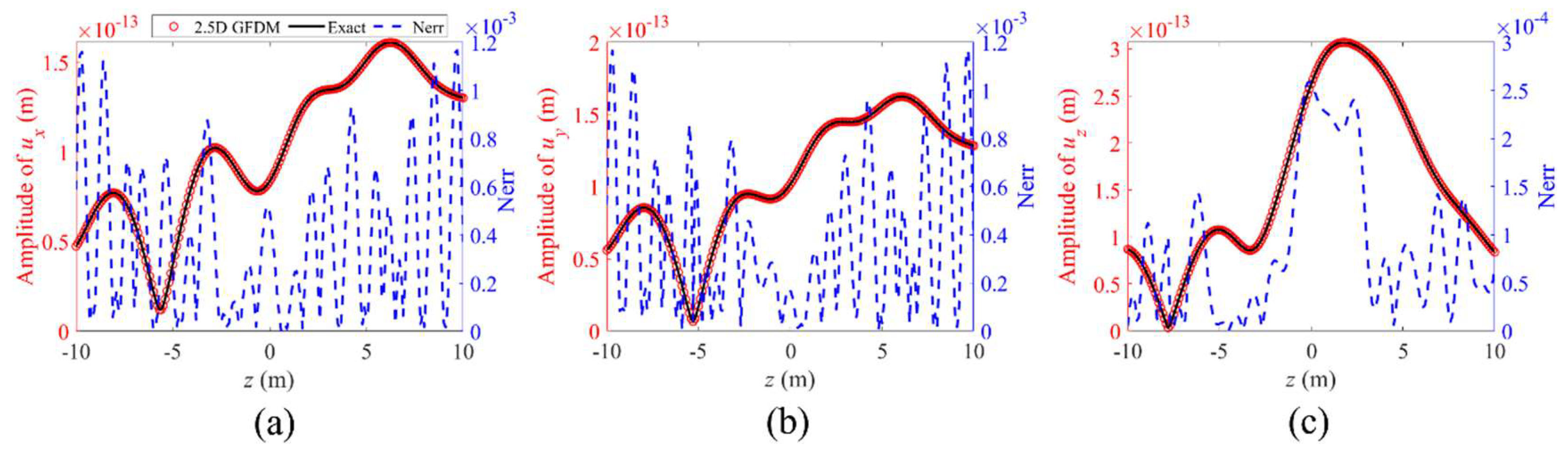
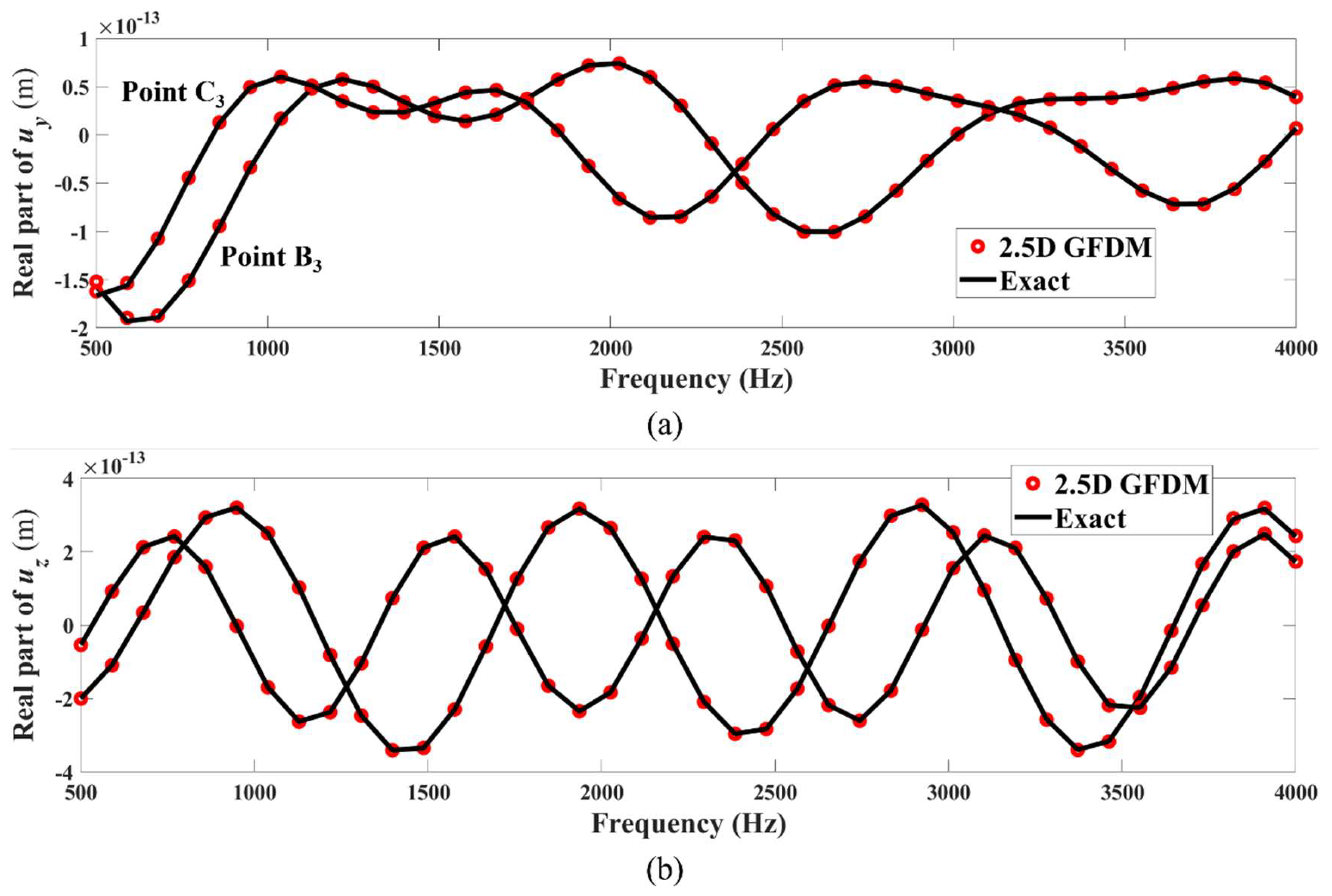
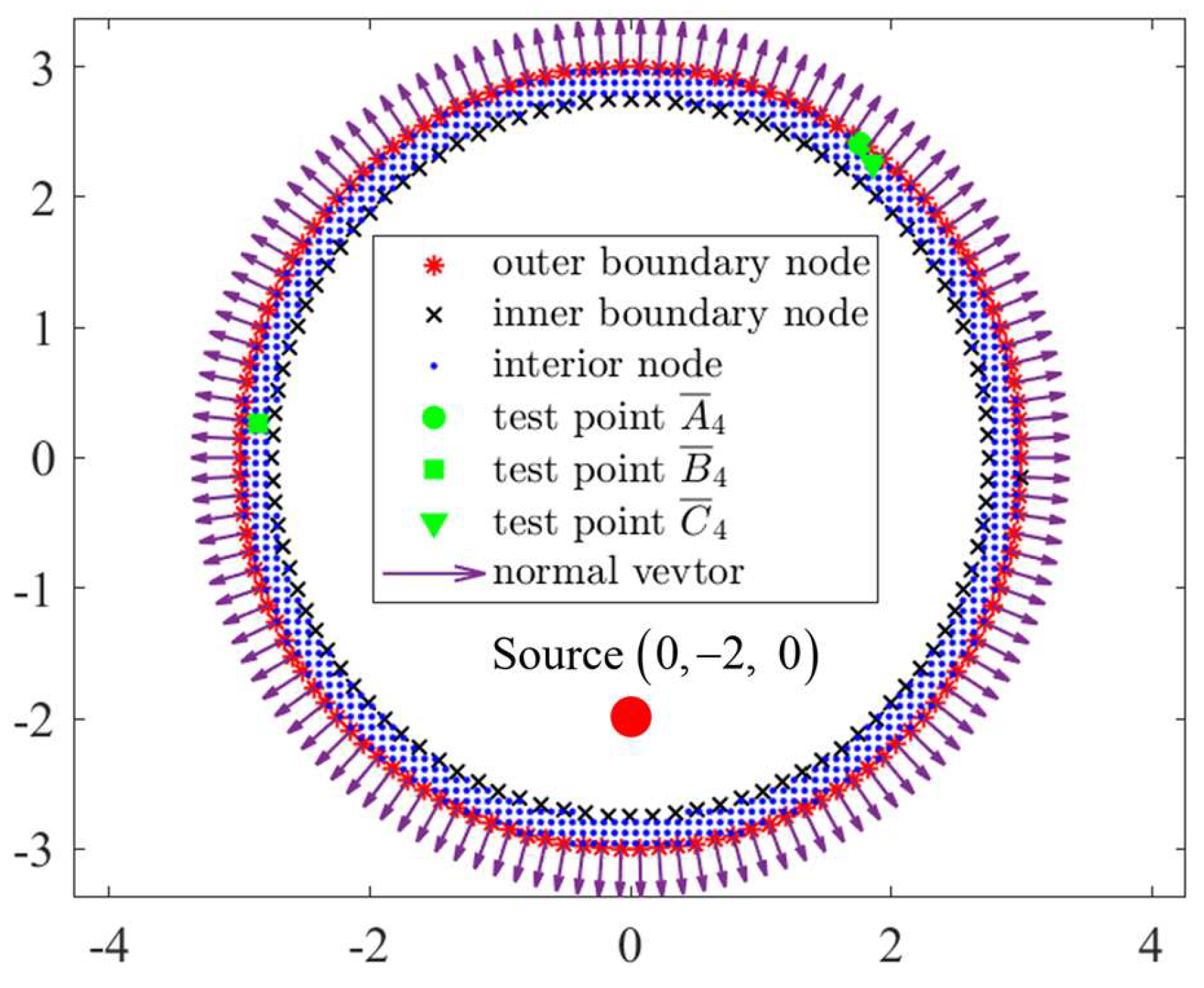
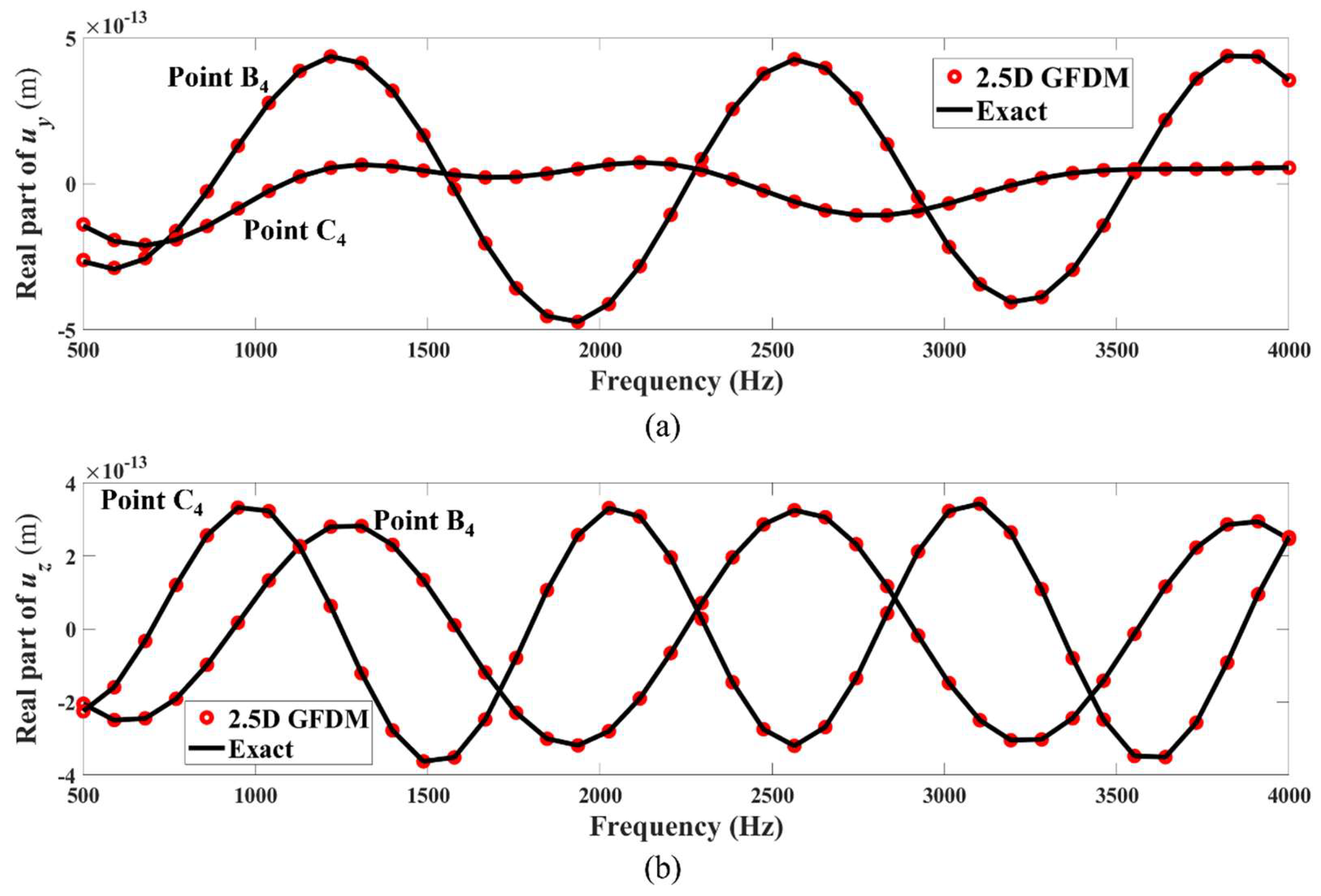
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bao, H.; Bielak, J.; Ghattas, O.; Kallivokas, L.F.; O’Hallaron, D.R.; Shewchuk, J.R.; Xu, J. Large-scale simulation of elastic wave propagation in heterogeneous media on parallel computers. Comput. Methods Appl. Mech. Eng. 1998, 152, 85–102. [Google Scholar] [CrossRef]
- Ureña, F.; Benito, J.J.; Salete, E.; Gavete, L. A note on the application of the generalized finite difference method to seismic wave propagation in 2D. J. Comput. Appl. Math. 2012, 236, 3016–3025. [Google Scholar] [CrossRef]
- Benito, J.; Ureña, F.; Salete, E.; Muelas, A.; Gavete, L.; Galindo, R. Wave propagation in soils problems using the Generalized Finite Difference Method. Soil Dyn. Earthq. Eng. 2015, 79, 190–198. [Google Scholar] [CrossRef]
- Salete, E.; Benito, J.J.; Ureña, F.; Gavete, L.; Ureña, M.; García, A. Stability of perfectly matched layer regions in generalized finite difference method for wave problems. J. Comput. Appl. Math. 2017, 312, 231–239. [Google Scholar] [CrossRef]
- Qu, W.; Gu, Y.; Fan, C.-M. A stable numerical framework for long-time dynamic crack analysis. Int. J. Solids Struct. 2024, 293, 112768. [Google Scholar] [CrossRef]
- Moser, F.; Jacobs, L.J.; Qu, J. Modeling elastic wave propagation in waveguides with the finite element method. Ndt E Int. 1999, 32, 225–234. [Google Scholar] [CrossRef]
- Serón, F.; Sanz, F.; Kindelan, M.; Badal, J. Finite-element method for elastic wave propagation. Commun. Appl. Numer. Methods 1990, 6, 359–368. [Google Scholar] [CrossRef]
- Fu, Z.; Xi, Q.; Li, Y.; Huang, H.; Rabczuk, T. Hybrid FEM–SBM solver for structural vibration induced underwater acoustic radiation in shallow marine environment. Comput. Methods Appl. Mech. Eng. 2020, 369, 113236. [Google Scholar] [CrossRef]
- Li, Y.; Dang, S.; Li, W.; Chai, Y. Free and forced vibration analysis of two-dimensional linear elastic solids using the finite element methods enriched by interpolation cover functions. Mathematics 2022, 10, 456. [Google Scholar] [CrossRef]
- Jianfeng, Z. Quadrangle-grid velocity-stress finite-difference method for elastic-wave-propagation simulation. Geophys. J. Int. 1997, 131, 127–134. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Chen, X. Three-dimensional elastic wave numerical modelling in the presence of surface topography by a collocated-grid finite-difference method on curvilinear grids. Geophys. J. Int. 2012, 190, 358–378. [Google Scholar] [CrossRef]
- Beskos, D.E. Boundary element methods in dynamic analysis. Appl. Mech. Rev. 1987, 40, 1–23. [Google Scholar] [CrossRef]
- Liu, Y.; Rizzo, F. Hypersingular boundary integral equations for radiation and scattering of elastic waves in three dimensions. Comput. Methods Appl. Mech. Eng. 1993, 107, 131–144. [Google Scholar] [CrossRef]
- Zou, M.-s.; Wu, Y.-s.; Liu, Y.-m.; Lin, C.-g. A three-dimensional hydroelasticity theory for ship structures in acoustic field of shallow sea. J. Hydrodyn. Ser. B 2013, 25, 929–937. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, L.; Liang, J.; Zhou, Y. An indirect boundary element method to model the 3-D scattering of elastic waves in a fluid-saturated poroelastic half-space. Eng. Anal. Bound. Elem. 2016, 66, 91–108. [Google Scholar] [CrossRef]
- Perrey-Debain, E.; Trevelyan, J.; Bettess, P. Plane wave interpolation in direct collocation boundary element method for radiation and wave scattering: Numerical aspects and applications. J. Sound Vib. 2003, 261, 839–858. [Google Scholar] [CrossRef]
- De Basabe, J.D.; Sen, M.K. A comparison of finite-difference and spectral-element methods for elastic wave propagation in media with a fluid-solid interface. Geophys. J. Int. 2015, 200, 278–298. [Google Scholar] [CrossRef]
- Deckers, E.; Jonckheere, S.; Van Belle, L.; Claeys, C.; Desmet, W. Prediction of transmission, reflection and absorption coefficients of periodic structures using a hybrid wave based–finite element unit cell method. J. Comput. Phys. 2018, 356, 282–302. [Google Scholar] [CrossRef]
- Moldovan, I.D.; de Freitas, J.A.T. Hybrid-Trefftz finite element models for bounded and unbounded elastodynamic problems. In Proceedings of III European Conference on Computational Mechanics: Solids, Structures and Coupled Problems in Engineering: Book of Abstracts; Springer: Dordrecht, The Netherlands, 2006; p. 400. [Google Scholar]
- de Freitas, J.T. Hybrid finite element formulations for elastodynamic analysis in the frequency domain. Int. J. Solids Struct. 1999, 36, 1883–1923. [Google Scholar] [CrossRef]
- Qin, Q.-H. Trefftz Finite Element Method and Its Applications. Appl. Mech. Rev. 2005, 58, 316–337. [Google Scholar] [CrossRef]
- Fu, Z.-J.; Xi, Q.; Gu, Y.; Li, J.; Qu, W.; Sun, L.; Wei, X.; Wang, F.; Lin, J.; Li, W.; et al. Singular boundary method: A review and computer implementation aspects. Eng. Anal. Bound. Elem. 2023, 147, 231–266. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, W.; He, X.-Q. Singular boundary method for steady-state heat conduction in three dimensional general anisotropic media. Int. J. Heat Mass Transf. 2012, 55, 4837–4848. [Google Scholar] [CrossRef]
- Liu, H.; Wang, F. A novel semi-analytical meshless method for the thickness optimization of porous material distributed on sound barriers. Appl. Math. Lett. 2024, 147, 108844. [Google Scholar] [CrossRef]
- Wang, F.; Chen, W.; Tadeu, A.; Correia, C.G. Singular boundary method for transient convection–diffusion problems with time-dependent fundamental solution. Int. J. Heat Mass Transf. 2017, 114, 1126–1134. [Google Scholar] [CrossRef]
- Liu, Q.; Šarler, B. Non-singular method of fundamental solutions for two-dimensional isotropic elasticity problems. Comput. Model. Eng. Sci. 2013, 91, 235–266. [Google Scholar]
- Lan, L.; Zhou, Z.; Liu, H.; Wei, X.; Wang, F. An ACA-BM-SBM for 2D acoustic sensitivity analysis. AIMS Math. 2024, 9, 1939–1958. [Google Scholar] [CrossRef]
- Fan, C.-M.; Chien, C.-S.; Chan, H.-F.; Chiu, C.-L. The local RBF collocation method for solving the double-diffusive natural convection in fluid-saturated porous media. Int. J. Heat Mass Transf. 2013, 57, 500–503. [Google Scholar] [CrossRef]
- Fu, Z.-J.; Chen, W.; Yang, H.-T. Boundary particle method for Laplace transformed time fractional diffusion equations. J. Comput. Phys. 2013, 235, 52–66. [Google Scholar] [CrossRef]
- Fan, C.; Liu, Y.; Chan, H.; Hsiao, S. Solutions of boundary detection problem for modified Helmholtz equation by Trefftz method. Inverse Probl. Sci. Eng. 2014, 22, 267–281. [Google Scholar] [CrossRef]
- Liu, C.-S.; Kuo, C.-L.; Jhao, W.-S. The multiple-scale polynomial Trefftz method for solving inverse heat conduction problems. Int. J. Heat Mass Transf. 2016, 95, 936–943. [Google Scholar] [CrossRef]
- Ju, B.; Gu, Y.; Wang, R. An enriched radial integration method for evaluating domain integrals in transient boundary element analysis. Appl. Math. Lett. 2024, 153, 109067. [Google Scholar] [CrossRef]
- Wang, F.; Wang, C.; Chen, Z. Local knot method for 2D and 3D convection-diffusion-reaction equations in arbitrary domains. Appl. Math. Lett. 2020, 105, 106308. [Google Scholar] [CrossRef]
- Qiu, X.; Yue, X. Solving time fractional partial differential equations with variable coefficients using a spatio-temporal meshless method. AIMS Math 2024, 9, 27150–27166. [Google Scholar] [CrossRef]
- Chen, C.-S.; Fan, C.-M.; Wen, P. The method of approximate particular solutions for solving elliptic problems with variable coefficients. Int. J. Comput. Methods 2011, 8, 545–559. [Google Scholar] [CrossRef]
- Chen, C.-S.; Fan, C.-M.; Wen, P. The method of approximate particular solutions for solving certain partial differential equations. Numer. Methods Partial Differ. Equ. 2012, 28, 506–522. [Google Scholar] [CrossRef]
- Benito, J.; Urena, F.; Gavete, L. Influence of several factors in the generalized finite difference method. Appl. Math. Model. 2001, 25, 1039–1053. [Google Scholar] [CrossRef]
- Gavete, L.; Gavete, M.; Benito, J. Improvements of generalized finite difference method and comparison with other meshless method. Appl. Math. Model. 2003, 27, 831–847. [Google Scholar] [CrossRef]
- Prieto, F.U.; Muñoz, J.J.B.; Corvinos, L.G. Application of the generalized finite difference method to solve the advection–diffusion equation. J. Comput. Appl. Math. 2011, 235, 1849–1855. [Google Scholar] [CrossRef]
- Chan, H.-F.; Fan, C.-M.; Kuo, C.-W. Generalized finite difference method for solving two-dimensional non-linear obstacle problems. Eng. Anal. Bound. Elem. 2013, 37, 1189–1196. [Google Scholar] [CrossRef]
- Li, P.-W.; Fan, C.-M.; Chen, C.-Y.; Ku, C.-Y. Generalized finite difference method for numerical solutions of density-driven groundwater flows. Comput. Model. Eng. Sci. 2014, 101, 319–350. [Google Scholar]
- Hosseini, S.M. Shock-induced two dimensional coupled non-Fickian diffusion–elasticity analysis using meshless generalized finite difference (GFD) method. Eng. Anal. Bound. Elem. 2015, 61, 232–240. [Google Scholar] [CrossRef]
- Gavete, L.; Ureña, F.; Benito, J.J.; García, A.; Ureña, M.; Salete, E. Solving second order non-linear elliptic partial differential equations using generalized finite difference method. J. Comput. Appl. Math. 2017, 318, 378–387. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, L.; Chen, W.; Zhang, C.; He, X. Application of the meshless generalized finite difference method to inverse heat source problems. Int. J. Heat Mass Transf. 2017, 108, 721–729. [Google Scholar] [CrossRef]
- Hua, Q.; Gu, Y.; Qu, W.; Chen, W.; Zhang, C. A meshless generalized finite difference method for inverse Cauchy problems associated with three-dimensional inhomogeneous Helmholtz-type equations. Eng. Anal. Bound. Elem. 2017, 82, 162–171. [Google Scholar] [CrossRef]
- Sun, W.; Qu, W.; Gu, Y.; Zhao, S. Three-dimensional elastodynamic analysis employing the generalized finite difference method with arbitrary-order accuracy. Comput. Math. Appl. 2024, 174, 151–166. [Google Scholar] [CrossRef]
- Zhang, F.; Li, P.-W.; Gu, Y.; Fan, C.-M. A space-time generalized finite difference scheme for long wave propagation based on high-order Korteweg-de Vries type equations. Math. Comput. Simul. 2025, 228, 298–312. [Google Scholar] [CrossRef]
- Orkisz, J. Meshless finite difference method I. Basic approach. In Proceedings of the IACM-Fourth World Congress in Computational Mechanics, Buenos Aires, Argentina, 29 June–2 July 1998. [Google Scholar]
- Li, P.-W.; Chen, W.; Fu, Z.-J.; Fan, C.-M. Generalized finite difference method for solving the double-diffusive natural convection in fluid-saturated porous media. Eng. Anal. Bound. Elem. 2018, 95, 175–186. [Google Scholar] [CrossRef]
- Song, L.; Li, P.-W.; Gu, Y.; Fan, C.-M. Generalized finite difference method for solving stationary 2D and 3D Stokes equations with a mixed boundary condition. Comput. Math. Appl. 2020, 80, 1726–1743. [Google Scholar] [CrossRef]
- Suchde, P.; Kuhnert, J. A meshfree generalized finite difference method for surface PDEs. Comput. Math. Appl. 2019, 78, 2789–2805. [Google Scholar] [CrossRef]
- Ureña, F.; Salete, E.; Benito, J.J.; Gavete, L. Solving third-and fourth-order partial differential equations using GFDM: Application to solve problems of plates. Int. J. Comput. Math. 2012, 89, 366–376. [Google Scholar] [CrossRef]
- Gu, Y.; Qu, W.; Chen, W.; Song, L.; Zhang, C. The generalized finite difference method for long-time dynamic modeling of three-dimensional coupled thermoelasticity problems. J. Comput. Phys. 2019, 384, 42–59. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, C.; Ouyang, H.; Yan, Q.; Yu, W. 2.5 D modelling of wave propagation in longitudinally curved viscoelastic structure using a coupled FEM-PML approach. Eng. Struct. 2021, 226, 111337. [Google Scholar] [CrossRef]
- Sun, L.; Wei, X.; Chen, B. A meshless singular boundary method for elastic wave propagation in 2D partially saturated poroelastic media. Eng. Anal. Bound. Elem. 2020, 113, 82–98. [Google Scholar] [CrossRef]
- Wei, X.; Liu, D.; Luo, W.; Chen, S.; Sun, L. A half-space singular boundary method for predicting ground-borne vibrations. Appl. Math. Model. 2022, 111, 630–643. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, W.; Fu, Z.-J.; Zhang, B. The singular boundary method: Mathematical background and application in orthotropic elastic problems. Eng. Anal. Bound. Elem. 2014, 44, 152–160. [Google Scholar] [CrossRef]
- Liravi, H.; Arcos, R.; Clot, A.; Conto, K.F.; Romeu, J. A 2.5 D coupled FEM–SBM methodology for soil–structure dynamic interaction problems. Eng. Struct. 2022, 250, 113371. [Google Scholar] [CrossRef]
- Liravi, H.; Clot, A.; Arcos, R.; Fakhraei, J.; Godinho, L.; Conto, K.F.; Romeu, J. A 2.5 D hybrid SBM-MFS methodology for elastic wave propagation problems. J. Sound Vib. 2024, 586, 118501. [Google Scholar] [CrossRef]
- Sun, L.; Fu, Z.; Chen, Z. A localized collocation solver based on fundamental solutions for 3D time harmonic elastic wave propagation analysis. Appl. Math. Comput. 2023, 439, 127600. [Google Scholar] [CrossRef]
- Aubry, D.; Clouteau, D.; Bonnet, G. Modelling of wave propagation due to fixed or mobile dynamic sources. In Proceedings of the Workshop Wave ’94, Wave Propagation and Reduction of Vibrations, Ruhr-Universität Bochum, Germany, 8 December 1994; pp. 109–121. [Google Scholar]
- Sheng, X.; Jones, C.; Petyt, M. Ground vibration generated by a harmonic load acting on a railway track. J. Sound Vib. 1999, 225, 3–28. [Google Scholar] [CrossRef]
- Sheng, X.-Z.; Jones, C.; Petyt, M. Ground vibration generated by a load moving along a railway track. J. Sound Vib. 1999, 228, 129–156. [Google Scholar] [CrossRef]
- Zeng, S.; Chen, F.; Li, D.; Chen, J.; Chen, J. A novel 2.5 D finite difference scheme for simulations of resistivity logging in anisotropic media. J. Appl. Geophys. 2018, 150, 144–152. [Google Scholar] [CrossRef]
- Suchde, P. Particle-based adaptive coupling of 3D and 2D fluid flow models. Comput. Methods Appl. Mech. Eng. 2024, 429, 117199. [Google Scholar] [CrossRef]
- Yang, S.-b.; Zhou, B.; Bai, C.-y. A generalized 2.5-D time-domain seismic wave equation to accommodate various elastic media and boundary conditions. Pure Appl. Geophys. 2021, 178, 2999–3025. [Google Scholar] [CrossRef]
- Amado-Mendes, P.; Costa, P.A.; Godinho, L.M.; Lopes, P. 2.5 D MFS–FEM model for the prediction of vibrations due to underground railway traffic. Eng. Struct. 2015, 104, 141–154. [Google Scholar] [CrossRef]
- Tadeu, A.J.; Kausel, E. Green’s functions for two-and-a-half-dimensional elastodynamic problems. J. Eng. Mech. 2000, 126, 1093–1097. [Google Scholar] [CrossRef]
- Xing, Y.; Song, L.; He, X.; Qiu, C. A generalized finite difference method for solving elliptic interface problems. Math. Comput. Simul. 2020, 178, 109–124. [Google Scholar] [CrossRef]
- Lin, J.; Chen, W.; Sun, L. Simulation of elastic wave propagation in layered materials by the method of fundamental solutions. Eng. Anal. Bound. Elem. 2015, 57, 88–95. [Google Scholar] [CrossRef]









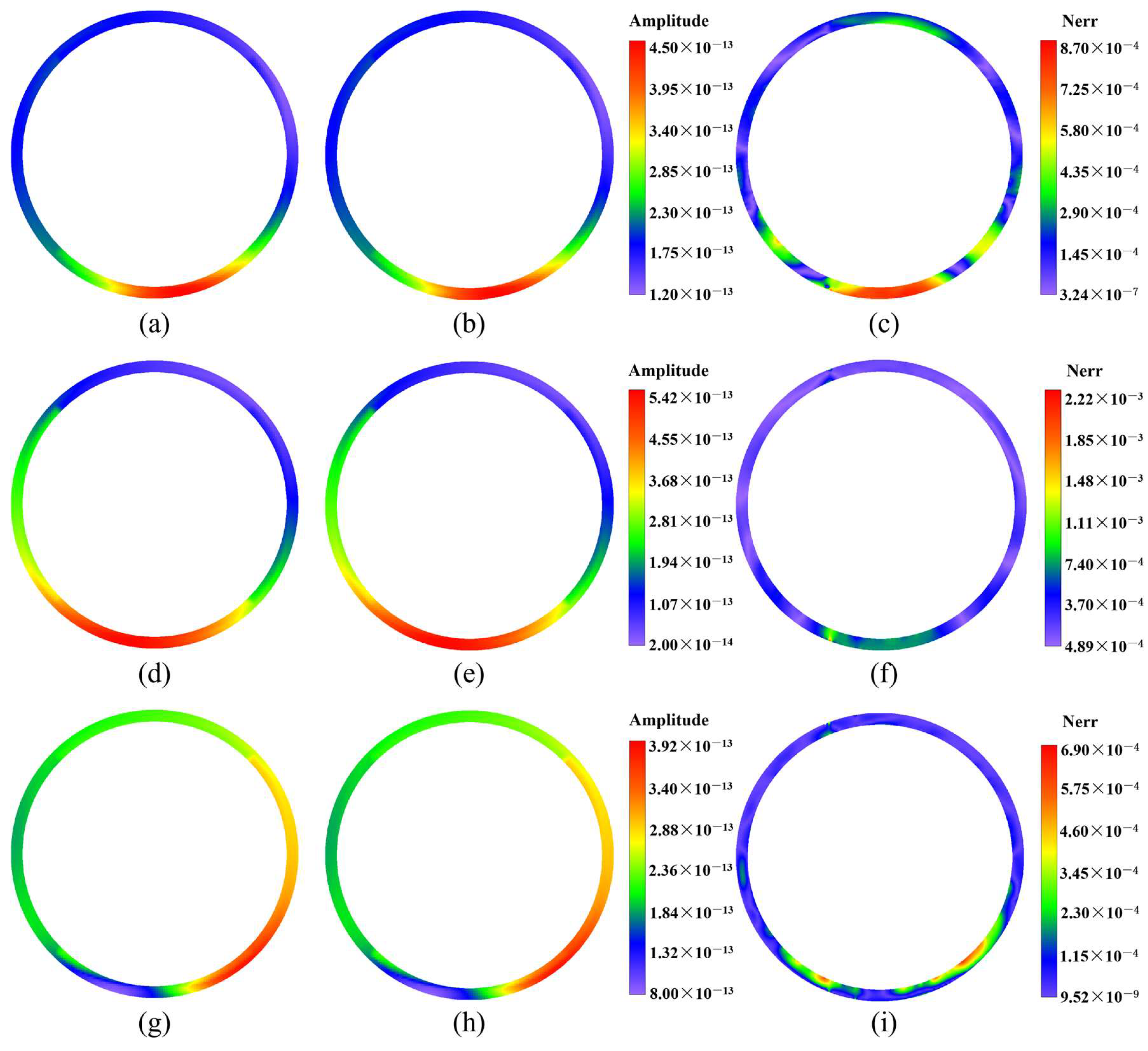
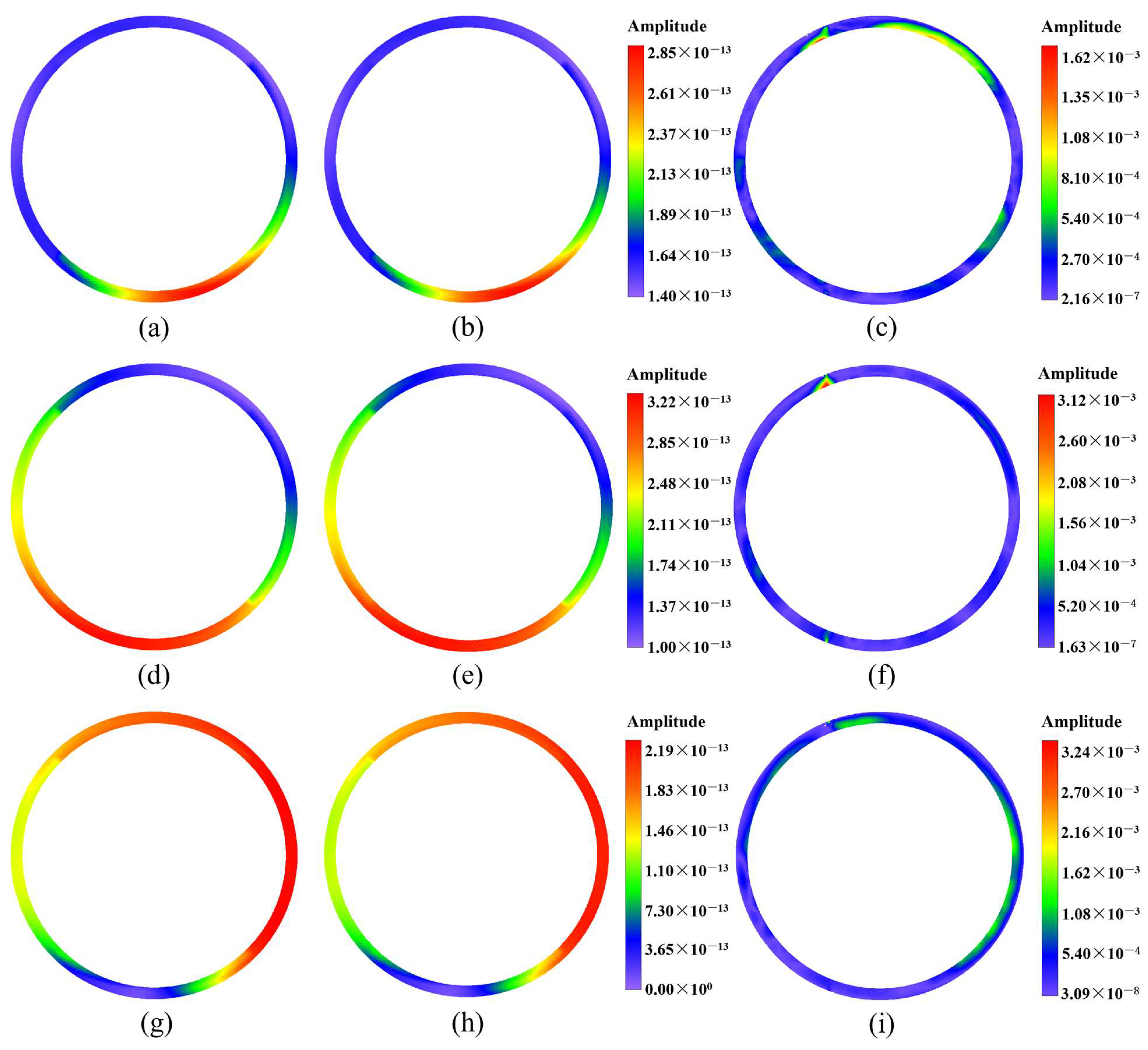
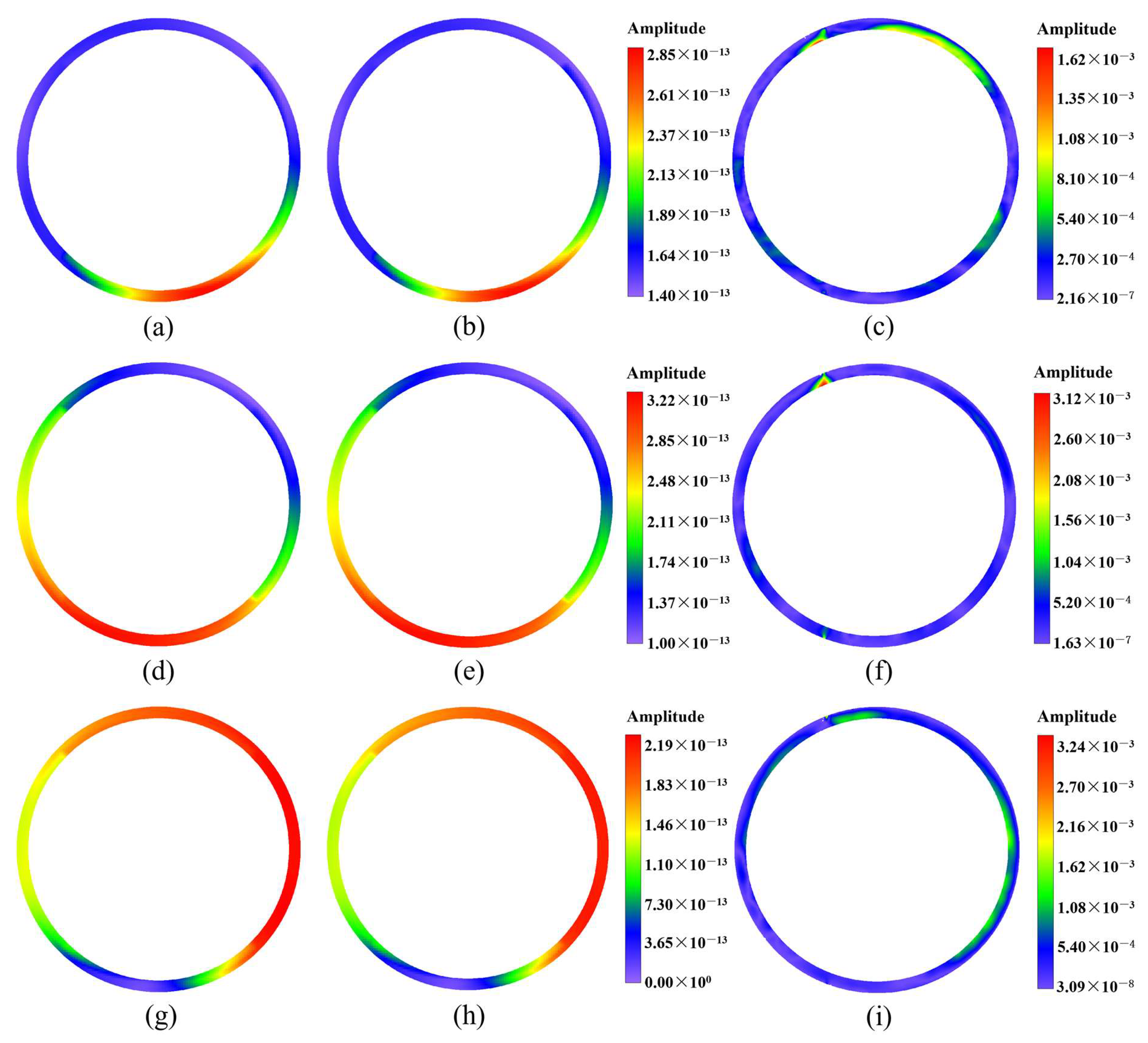
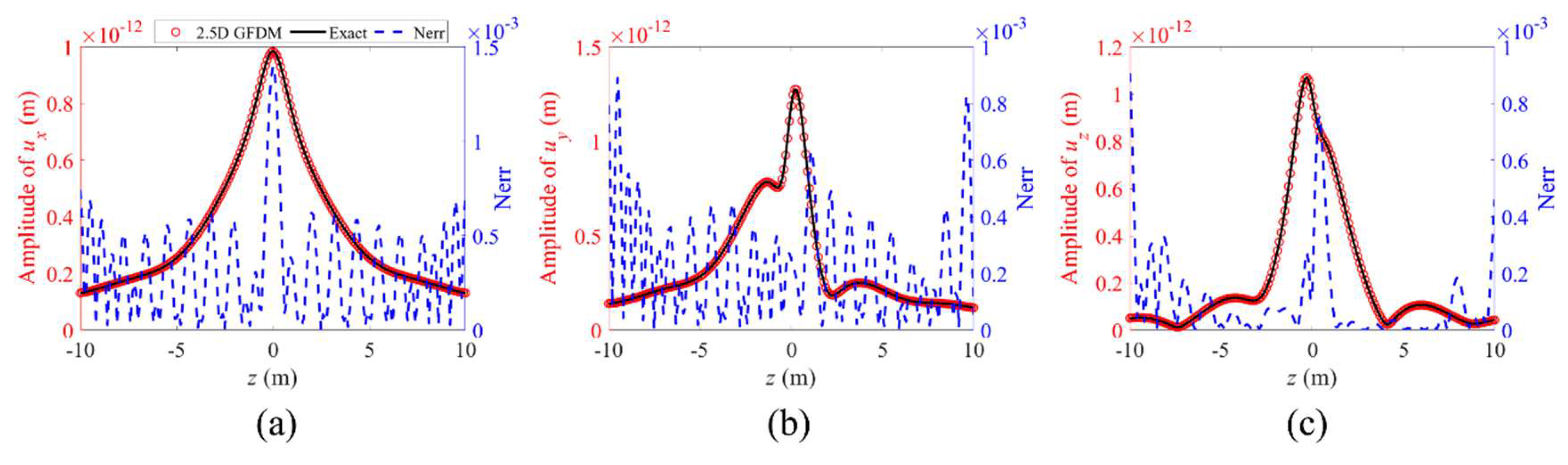

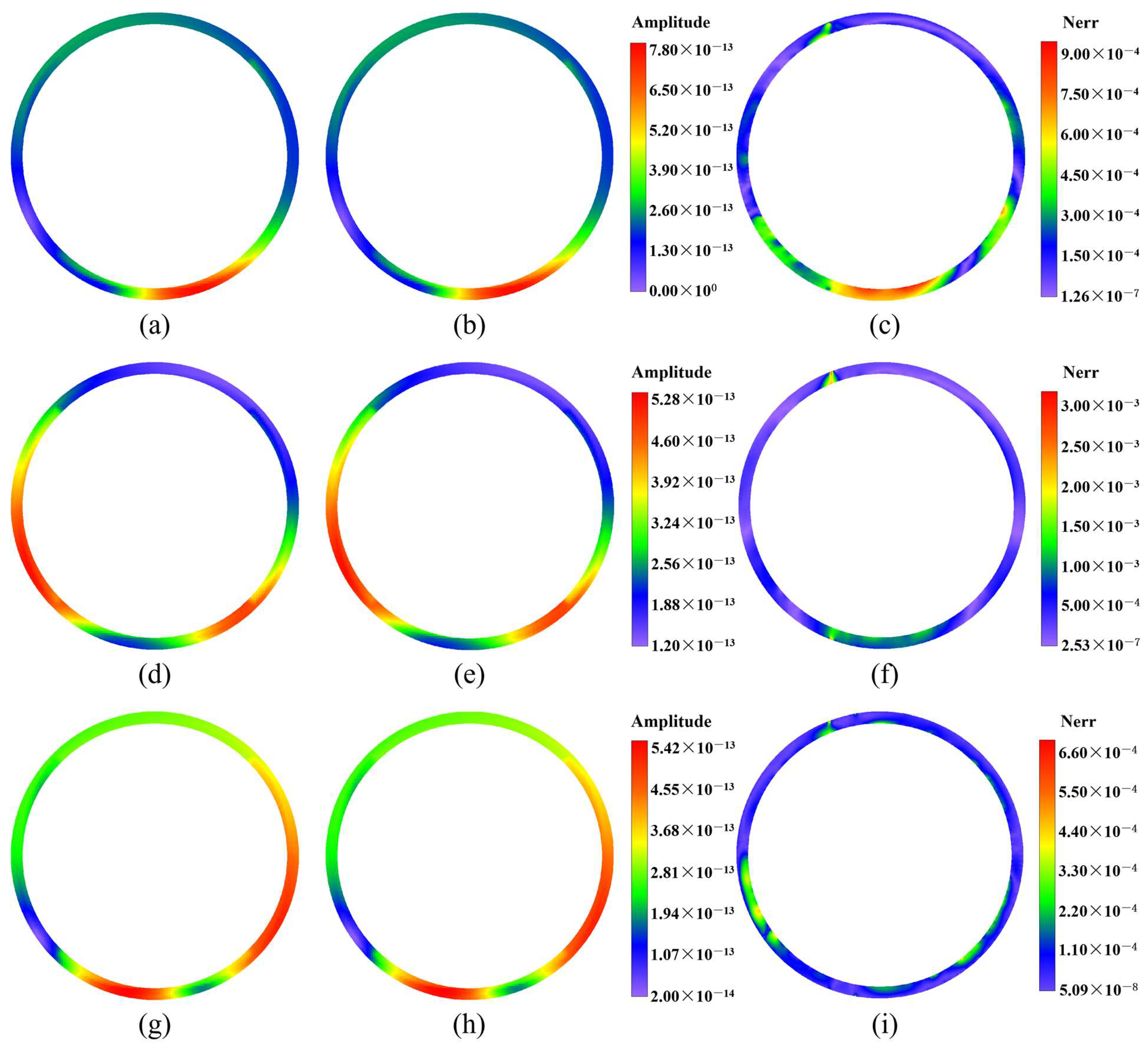


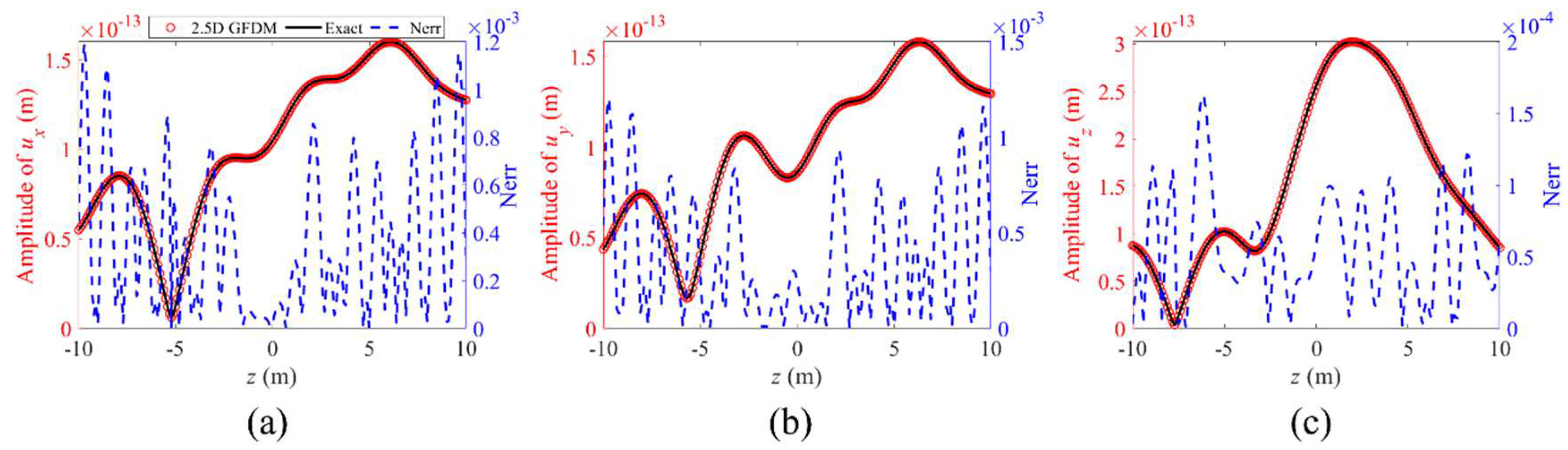
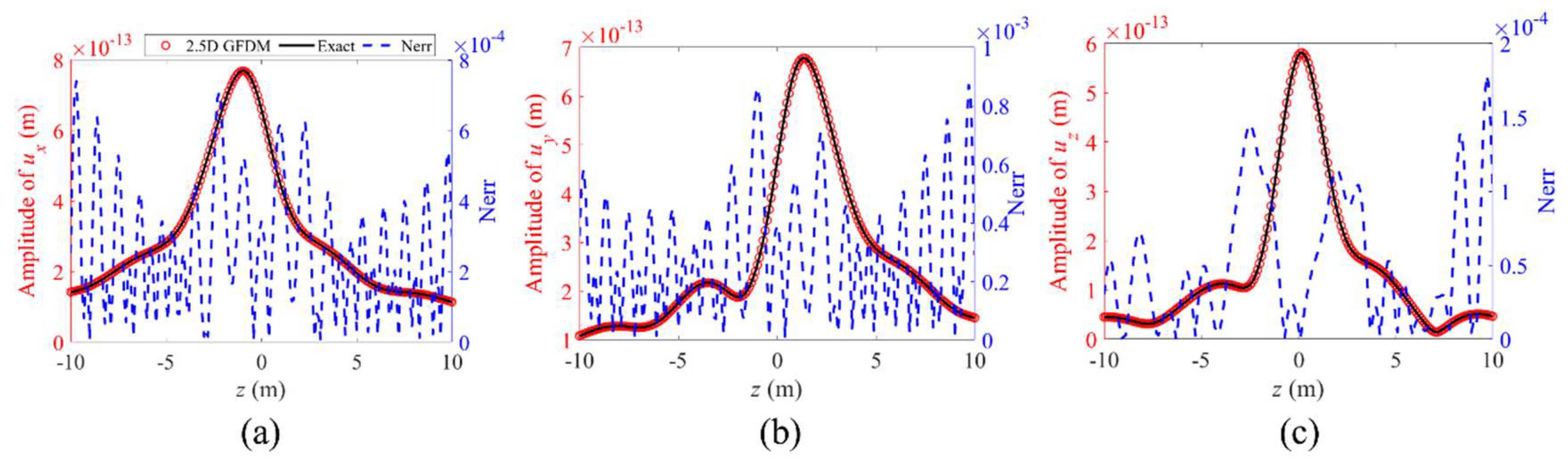
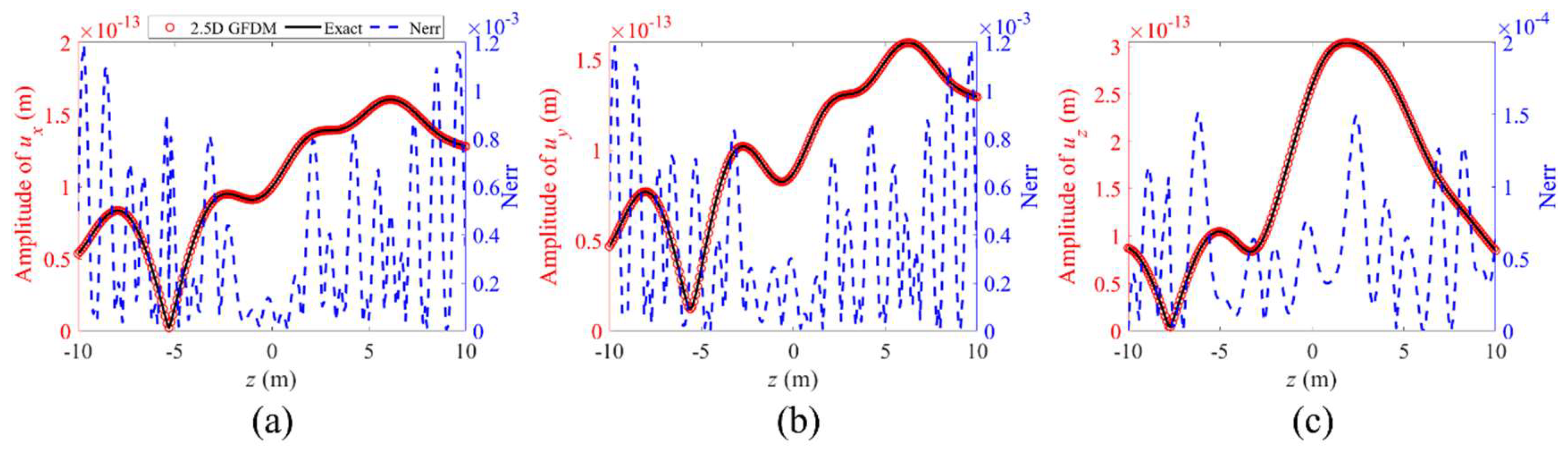

| Number of Nodes | Global Errors | |
|---|---|---|
| Uniform Distribution | Non-Uniform Distribution | |
| 1020 | 2.3220 × 10−4 | 3.1495 × 10−4 |
| 1365 | 1.5837 × 10−4 | 1.9652 × 10−4 |
| 1760 | 1.1066 × 10−4 | 1.5055 × 10−4 |
| Frequency | Number of m | Global Errors | Time |
|---|---|---|---|
| 3000 Hz | 12 | 3.3319 × 10−4 | 316 s |
| 18 | 4.0470 × 10−4 | 330 s | |
| 25 | 6.0844 × 10−4 | 342 s | |
| 4000 Hz | 12 | 1.2688 × 10−3 | 320 s |
| 18 | 1.6112 × 10−3 | 331 s | |
| 25 | 2.4420 × 10−3 | 358 s |
| Frequency | 2.5D GFDM | 3D FEM-PML | ||||
|---|---|---|---|---|---|---|
| Number of Nodes | Global Errors | Time | Number of Units | Global Errors | Time | |
| 3000 Hz | 1020 | 8.9959 × 10−4 | 46 s | 187,322 | 2.4157 × 10−3 | 52 s |
| 4000 Hz | 2205 | 1.5428 × 10−4 | 243 s | 784,280 | 5.7978 × 10−2 | 378 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.; Wang, F.; Yue, X.; Qiu, L.; Sun, L. A 2.5D Generalized Finite Difference Method for Elastic Wave Propagation Problems. Mathematics 2025, 13, 1249. https://doi.org/10.3390/math13081249
Chang H, Wang F, Yue X, Qiu L, Sun L. A 2.5D Generalized Finite Difference Method for Elastic Wave Propagation Problems. Mathematics. 2025; 13(8):1249. https://doi.org/10.3390/math13081249
Chicago/Turabian StyleChang, Hao, Fajie Wang, Xingxing Yue, Lin Qiu, and Linlin Sun. 2025. "A 2.5D Generalized Finite Difference Method for Elastic Wave Propagation Problems" Mathematics 13, no. 8: 1249. https://doi.org/10.3390/math13081249
APA StyleChang, H., Wang, F., Yue, X., Qiu, L., & Sun, L. (2025). A 2.5D Generalized Finite Difference Method for Elastic Wave Propagation Problems. Mathematics, 13(8), 1249. https://doi.org/10.3390/math13081249







