Robustness and Efficiency Considerations When Testing Process Reliability with a Limit of Detection
Abstract
:1. Introduction
2. Background on Methods
3. Inference Under Model Misspecification
- solves
- and
- ;
- ;
- ;
- .
4. A Piecewise-Constant Hazard-Based Model
- is the “cumulative hazard”;
- is the “time at risk” in over the interval .
4.1. Maximum Likelihood Estimation
4.2. Profile Likelihood Ratio Test
- Write where : lettingwe have , soHence, continuing from the likelihood function (7) above, we have
- Compute the profile likelihood estimate : We can optimize the log-likelihoodnumerically for a given value of to get .
- Under , we havewhere and are the (non-profile) MLEs derived in Section 4.1, and . Thus, a profile likelihood interval for is given bywhere is the quantile of .
- Reject if falls outside the profile likelihood interval computed in step (3). This constitutes a hypothesis test at significance level .
5. Empirical Studies
5.1. Bias, Power, Robustness, and Efficiency
5.2. Model Selection
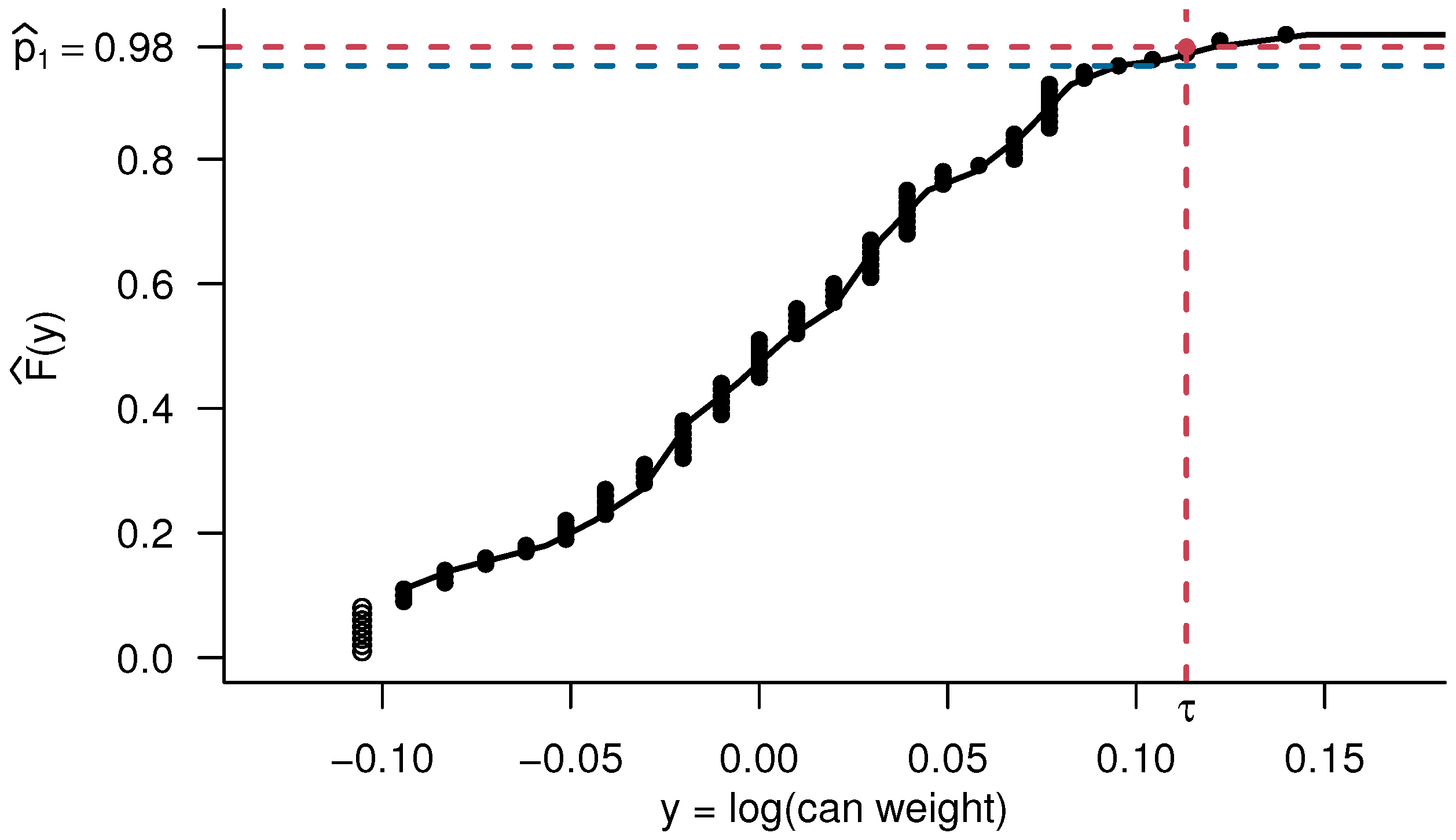
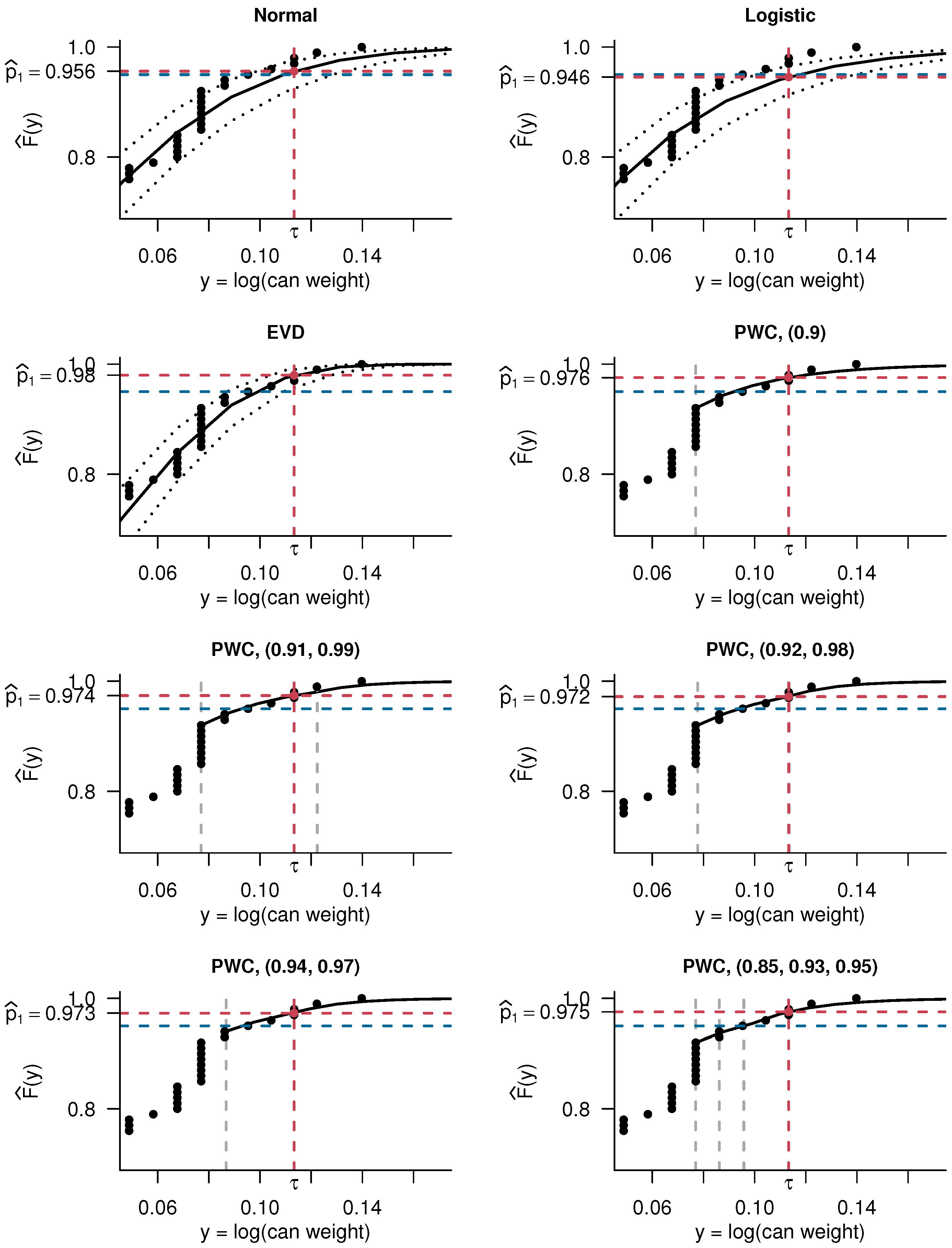
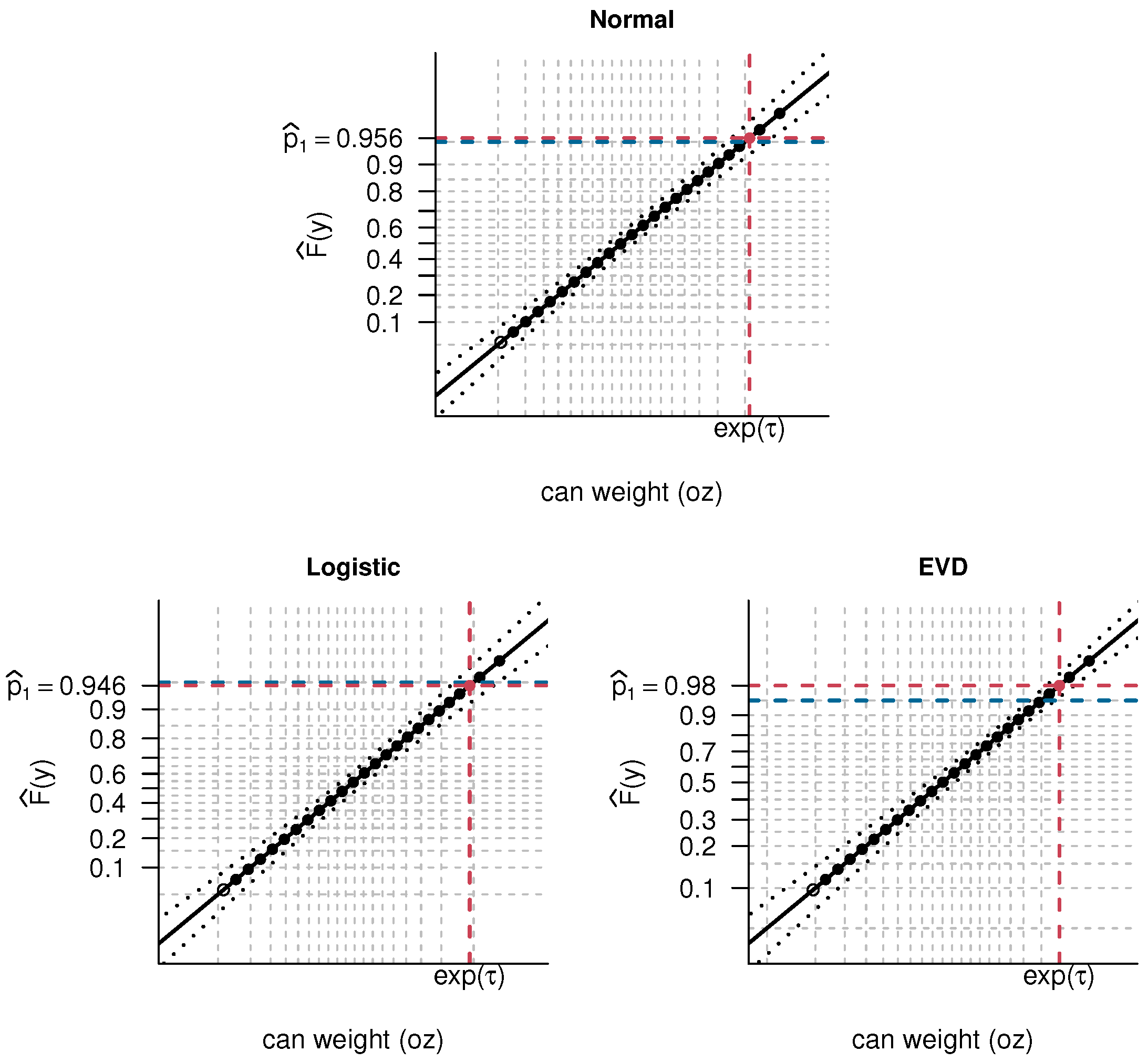
6. Application
- is one of the models considered in the simulation study of Section 5.1;
- is an adaptation of another model from the simulation study, with the middle cut-point adjusted upward to ensure that each interval of the resulting model strictly contains at least one observation;
- is suggested by the simulation from Section 5.2;
- and are the models that are, respectively, the closest to and farthest from demonstrating reliability from a grid search of two-cut-point models whose first cut-point is in and whose second cut-point is in .
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Parameter Estimands in Misspecified Location-Scale Models with Left-Censored Data
Appendix B. Robust Asymptotic Variance of Parameter Estimators in Misspecified Location-Scale Models with Left-Censored Data
Appendix C. Assumed Asymptotic Variance of Parameter Estimators in Misspecified Location-Scale Models with Left-Censored Data
Appendix D. Testing Goodness of Fit Under LLD
| Left-Censoring Rate | n | Data-Generation Model | ||
|---|---|---|---|---|
| Normal | Logistic | Extreme Value | ||
| 0% | 20 | 0.048 | 0.116 | 0.332 |
| 40 | 0.056 | 0.182 | 0.582 | |
| 60 | 0.056 | 0.215 | 0.768 | |
| 80 | 0.058 | 0.238 | 0.879 | |
| 10% | 20 | 0.047 | 0.117 | 0.124 |
| 40 | 0.056 | 0.160 | 0.224 | |
| 60 | 0.056 | 0.209 | 0.346 | |
| 80 | 0.050 | 0.229 | 0.491 | |
| 25% | 20 | 0.047 | 0.112 | 0.080 |
| 40 | 0.060 | 0.164 | 0.124 | |
| 60 | 0.059 | 0.222 | 0.180 | |
| 80 | 0.056 | 0.252 | 0.264 | |
References
- United States Food and Drug Administration. Considerations for the Development of Dried Plasma Products Intended for Transfusion: Guidance for Industry; Docket Number FDA-2018-D-3759; United States Food and Drug Administration: Silver Spring, MD, USA, 2019. Available online: https://www.fda.gov/regulatory-information/search-fda-guidance-documents/considerations-development-dried-plasma-products-intended-transfusion (accessed on 17 October 2024).
- United States Food and Drug Administration. Submission and Review of Sterility Information in Premarket Notification (510(k)) Submissions for Devices Labeled as Sterile: Guidance for Industry and Food and Drug Administration Staff; Docket Number FDA-2008-D-0611; United States Food and Drug Administration: Silver Spring, MD, USA, 2024. Available online: https://www.fda.gov/regulatory-information/search-fda-guidance-documents/submission-and-review-sterility-information-premarket-notification-510k-submissions-devices-labeled (accessed on 17 October 2024).
- United States Food and Drug Administration. Approaches to Establish Thresholds for Major Food Allergens and for Gluten in Food; United States Food and Drug Administration: Silver Spring, MD, USA, 2006. Available online: https://www.fda.gov/food/food-labeling-nutrition/approaches-establish-thresholds-major-food-allergens-and-gluten-food (accessed on 17 October 2024).
- Government of Ontario. R.R.O. 1990, Reg. 347: General—Waste Management. In Environmental Protection Act; Government of Ontario: Toronto, ON, Canada, 2024. Available online: https://www.ontario.ca/laws/regulation/900347 (accessed on 17 October 2024).
- Newman, M.C.; Dixon, P.M.; Looney, B.B.; Pinder, J.E., III. Estimating Mean and Variance for Environmental Samples with Below Detection Limit Observations. JAWRA J. Am. Water Resour. Assoc. 1989, 25, 905–916. [Google Scholar] [CrossRef]
- Helsel, D.R. Much Ado About Next to Nothing: Incorporating Nondetects in Science. Ann. Occup. Hyg. 2010, 54, 257–262. [Google Scholar] [CrossRef] [PubMed]
- Hwang, M.; Lee, S.C.; Park, J.-H.; Choi, J.; Lee, H.-J. Statistical methods for handling nondetected results in food chemical monitoring data to improve food risk assessments. Food Sci. Nutr. 2023, 11, 5223–5235. [Google Scholar] [CrossRef] [PubMed]
- Gilliom, R.J.; Helsel, D.R. Estimation of Distributional Parameters for Censored Trace Level Water Quality Data: 1. Estimation Techniques. Water Resour. Res. 1986, 22, 135–146. [Google Scholar] [CrossRef]
- Helsel, D.R.; Cohn, T.A. Estimation of Descriptive Statistics for Multiply Censored Water Quality Data. Water Resour. Res. 1988, 24, 1997–2004. [Google Scholar] [CrossRef]
- Farewell, V.T. Some comments on analysis techniques for censored water quality data. Environ. Monit. Assess. 1989, 13, 285–294. [Google Scholar] [CrossRef]
- Shumway, R.H.; Azari, R.S.; Kayhanian, M. Statistical Approaches to Estimating Mean Water Quality Concentrations with Detection Limits. Environ. Sci. Technol. 2002, 36, 3345–3353. [Google Scholar] [CrossRef]
- Antweiler, R.C.; Taylor, H.E. Evaluation of statistical treatments of left-censored environmental data using coincident uncensored data sets: I. Summary statistics. Environ. Sci. Technol. 2008, 42, 3732–3738. [Google Scholar] [CrossRef]
- Shoari, N.; Dubé, J.-S.; Chenouri, S. On the use of the substitution method in left-censored environmental data. Hum. Ecol. Risk Assess. Int. J. 2015, 22, 435–446. [Google Scholar] [CrossRef]
- Tekindal, M.A.; Erdoğan, B.D.; Yavuz, Y. Evaluating Left-Censored Data Through Substitution, Parametric, Semi-parametric, and Nonparametric Methods: A Simulation Study. Interdiscip. Sci. Comput. Life Sci. 2017, 9, 153–172. [Google Scholar] [CrossRef]
- Kaplan, E.L.; Meier, P. Nonparametric Estimation from Incomplete Observations. J. Am. Stat. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Sprott, D.A. Statistical Inference in Science; Springer: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Huynh, T.; Quick, H.; Ramachandran, G.; Banerjee, S.; Stenzel, M.; Sandler, D.P.; Engel, L.S.; Kwok, R.K.; Blair, A.; Stewart, P.A. A Comparison of the β-Substitution Method and a Bayesian Method for Analyzing Left-Censored Data. Ann. Occup. Hyg. 2016, 60, 56–73. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Therneau, T.M.; Grambsch, P.M. Modeling Survival Data: Extending the Cox Model; Springer: New York, NY, USA, 2000. [Google Scholar]
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Duxbury: Pacific Grove, CA, USA, 2002. [Google Scholar]
- White, H. Maximum likelihood estimation of misspecified models. Econometrica 1982, 50, 1–25. [Google Scholar] [CrossRef]
- Gourieroux, C.; Monfort, A.; Trognon, A. Pseudo Maximum Likelihood Methods: Theory. Econometrica 1984, 52, 681–700. [Google Scholar] [CrossRef]
- Qin, J.; Lawless, J. Empirical Likelihood and General Estimating Equations. Ann. Stat. 1994, 22, 300–325. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Francia, R.S. An Approximate Analysis of Variance Test for Normality. J. Am. Stat. Assoc. 1972, 67, 215–216. [Google Scholar] [CrossRef]
- Berry, G.; Armitage, P. Mid-P confidence intervals: A brief review. J. R. Stat. Soc. Ser. D Stat. 1995, 44, 417–423. [Google Scholar] [CrossRef]
- Lawless, J.F.; Zhan, M. Analysis of interval-grouped recurrent event data using piecewise-constant rate functions. Can. J. Stat. 1998, 26, 549–565. [Google Scholar] [CrossRef]
- SAS Institute Inc. Reading Spec Limits from an Input Data Set; SAS Institute Inc.: Cary, NC, USA, n.d.; Available online: https://documentation.sas.com/doc/en/pgmsascdc/9.4_3.4/qcug/qcug_code_capspec2.htm (accessed on 11 January 2025).
- Fauvernier, M.; Remontet, L.; Uhry, Z.; Bossard, N.; Roche, L. survPen: An R package for hazard and excess hazard modelling with multidimensional penalized splines. J. Open Source Softw. 2019, 4, 1434. [Google Scholar] [CrossRef]
- Wigle, A.; Béliveau, A.; Blackmore, D.; Lapeyre, P.; Osadetz, K.; Lemieux, C.; Daun, K.J. Estimation and Applications of Uncertainty in Methane Emissions Quantification Technologies: A Bayesian Approach. ACS ES T Air 2024, 1, 1000–1014. [Google Scholar] [CrossRef]
- Arjas, E.; Gasbarra, D. Nonparametric Bayesian Inference from Right Censored Survival Data, Using the Gibbs Sampler. Stat. Sin. 1994, 4, 505–524. [Google Scholar]
- Ghosh, J.K.; Delampady, M.; Samanta, T. An Introduction to Bayesian Analysis: Theory and Methods, 1st ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Millard, S.P. EnvStats: An R Package for Environmental Statistics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Blom, G. Statistical Estimates and Transformed Beta-Variables; John Wiley & Sons: Hoboken, NJ, USA, 1958. [Google Scholar]
- Weisberg, S.; Bingham, C. An Approximate Analysis of Variance Test for Non-Normality Suitable for Machine Calculation. Technometrics 1975, 17, 133–134. [Google Scholar] [CrossRef]
- Royston, P. A Toolkit for Testing for Non-Normality in Complete and Censored Samples. J. R. Stat. Soc. Ser. D Stat. 1993, 42, 37–43. [Google Scholar] [CrossRef]
- Verrill, S.; Johnson, R.A. Tables and Large-Sample Distribution Theory for Censored-Data Correlation Statistics for Testing Normality. J. Am. Stat. Assoc. 1988, 83, 1192–1197. [Google Scholar] [CrossRef]

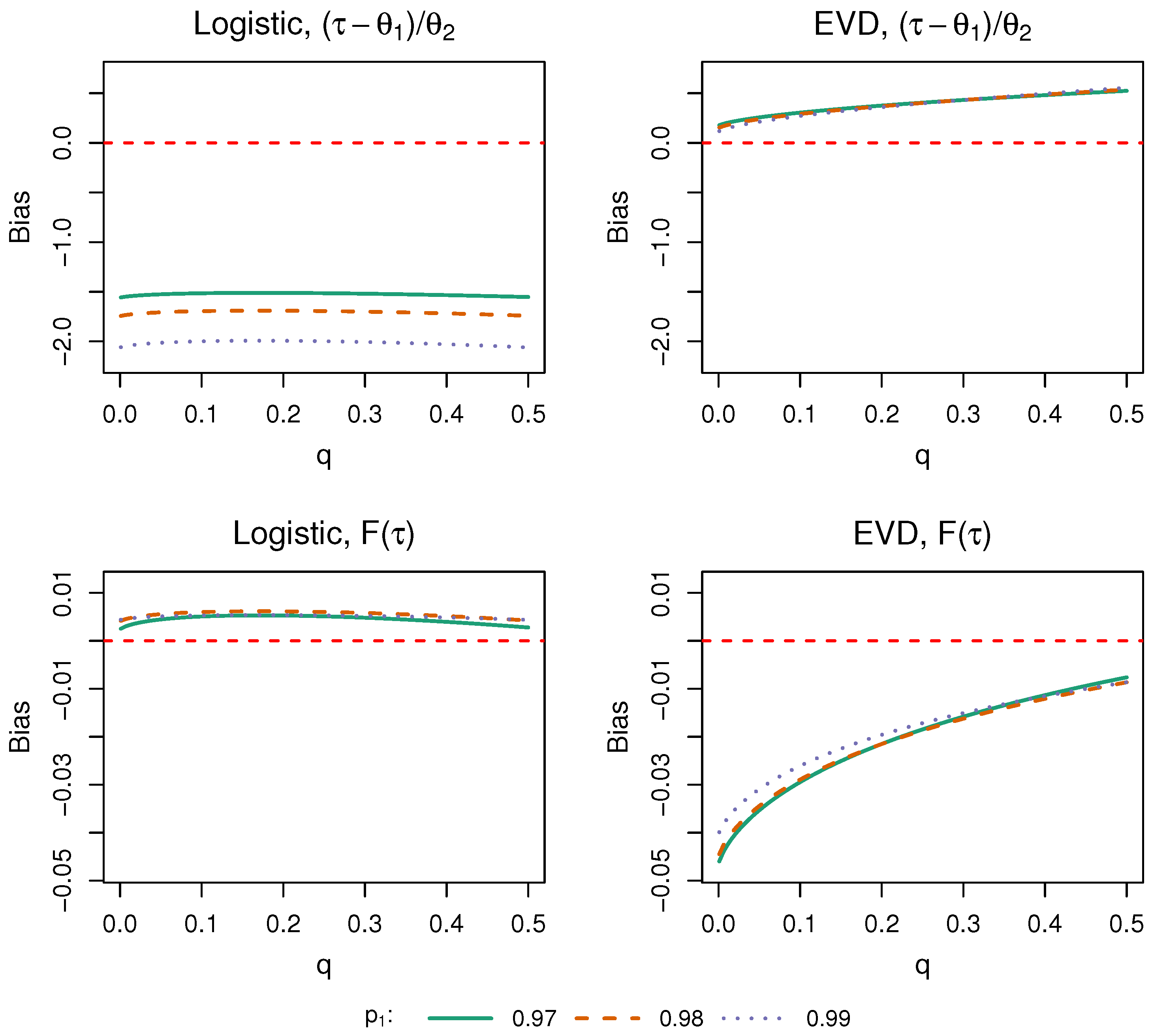

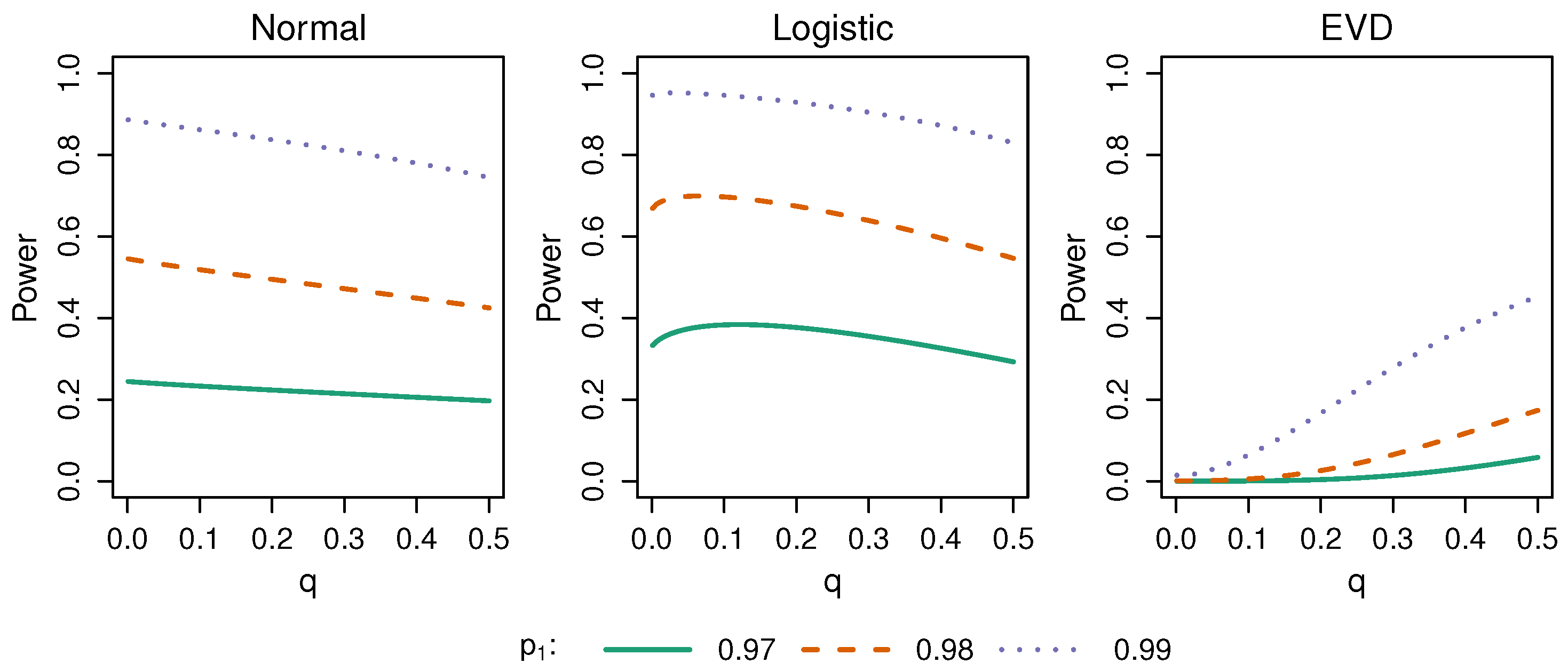
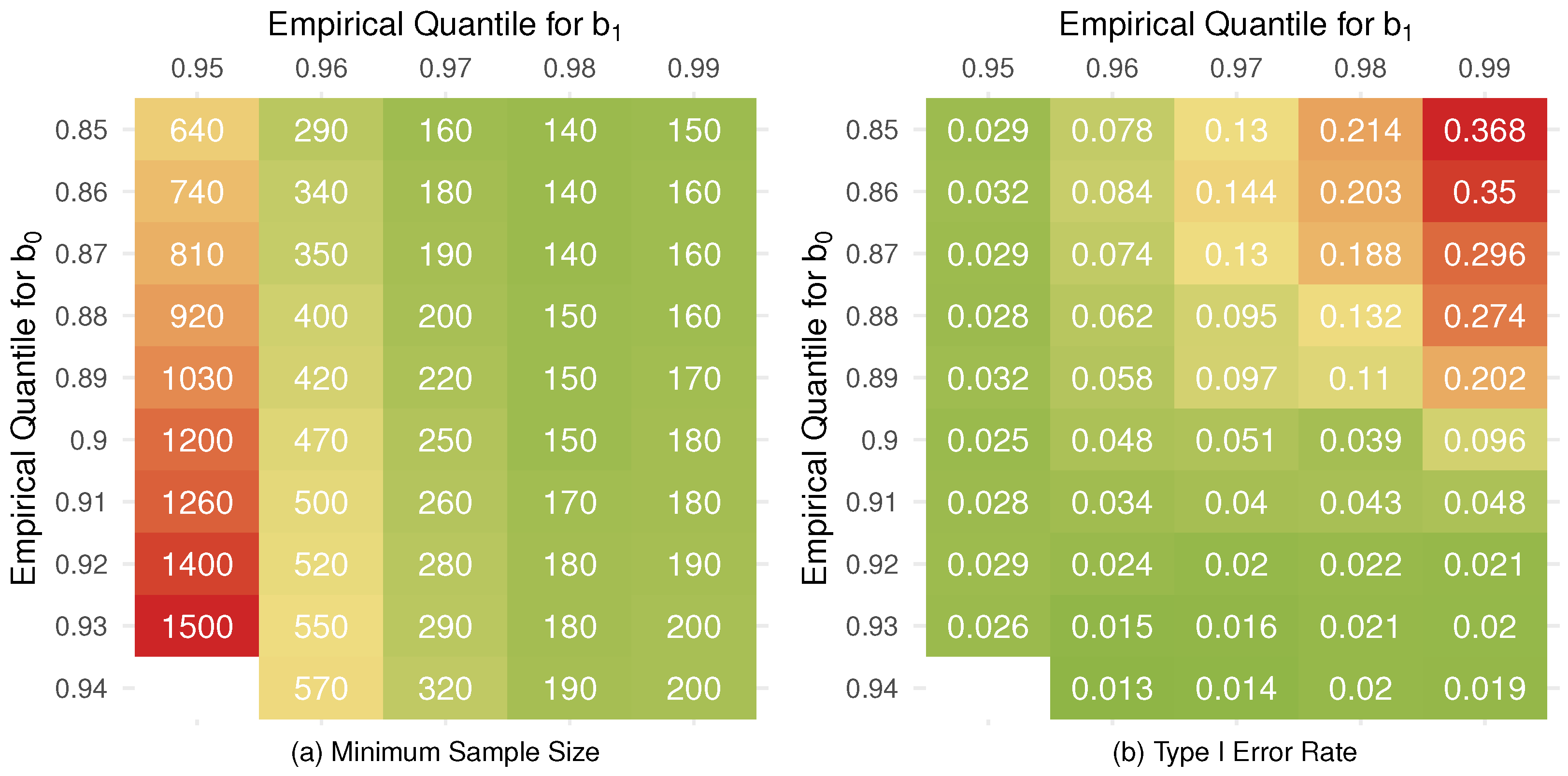
| Data-Generating Model | n | Normal | Piecewise-Constant 1 | Exact Test | |||
|---|---|---|---|---|---|---|---|
| 0.95 | Normal | 20 | 0.949 | 0.957 | 0.955 | 0.949 | |
| 40 | 0.950 | 0.951 | 0.951 | 0.950 | 0.949 | ||
| 60 | 0.950 | 0.949 | 0.950 | 0.946 | 0.949 | ||
| 80 | 0.949 | 0.947 | 0.950 | 0.947 | 0.949 | ||
| Logistic | 20 | 0.951 | 0.953 | 0.955 | 0.950 | ||
| 40 | 0.950 | 0.943 | 0.949 | 0.945 | 0.949 | ||
| 60 | 0.951 | 0.938 | 0.948 | 0.940 | 0.950 | ||
| 80 | 0.951 | 0.935 | 0.947 | 0.941 | 0.950 | ||
| Extreme Value | 20 | 0.925 | 0.959 | 0.957 | 0.951 | ||
| 40 | 0.923 | 0.954 | 0.952 | 0.952 | 0.950 | ||
| 60 | 0.923 | 0.952 | 0.951 | 0.948 | 0.949 | ||
| 80 | 0.923 | 0.952 | 0.951 | 0.949 | 0.949 | ||
| 0.97 | Normal | 20 | 0.968 | 0.972 | 0.972 | 0.969 | |
| 40 | 0.969 | 0.970 | 0.970 | 0.970 | 0.969 | ||
| 60 | 0.969 | 0.969 | 0.969 | 0.968 | 0.969 | ||
| 80 | 0.969 | 0.968 | 0.969 | 0.968 | 0.969 | ||
| Logistic | 20 | 0.973 | 0.969 | 0.973 | 0.970 | ||
| 40 | 0.973 | 0.962 | 0.968 | 0.966 | 0.969 | ||
| 60 | 0.974 | 0.958 | 0.966 | 0.961 | 0.969 | ||
| 80 | 0.974 | 0.956 | 0.965 | 0.960 | 0.970 | ||
| Extreme Value | 20 | 0.942 | 0.974 | 0.974 | 0.970 | ||
| 40 | 0.941 | 0.972 | 0.971 | 0.972 | 0.969 | ||
| 60 | 0.941 | 0.971 | 0.970 | 0.971 | 0.969 | ||
| 80 | 0.941 | 0.971 | 0.970 | 0.971 | 0.969 | ||
| 0.99 | Normal | 20 | 0.988 | 0.990 | 0.990 | 0.990 | |
| 40 | 0.989 | 0.990 | 0.989 | 0.990 | 0.990 | ||
| 60 | 0.989 | 0.990 | 0.989 | 0.991 | 0.990 | ||
| 80 | 0.989 | 0.990 | 0.989 | 0.990 | 0.989 | ||
| Logistic | 20 | 0.993 | 0.989 | 0.991 | 0.990 | ||
| 40 | 0.994 | 0.987 | 0.989 | 0.988 | 0.990 | ||
| 60 | 0.994 | 0.986 | 0.988 | 0.987 | 0.990 | ||
| 80 | 0.995 | 0.986 | 0.987 | 0.986 | 0.990 | ||
| Extreme Value | 20 | 0.964 | 0.989 | 0.990 | 0.991 | ||
| 40 | 0.964 | 0.989 | 0.990 | 0.990 | 0.990 | ||
| 60 | 0.964 | 0.989 | 0.990 | 0.991 | 0.990 | ||
| 80 | 0.964 | 0.990 | 0.990 | 0.990 | 0.990 | ||
| Data-Generating Model | n | Normal | Piecewise-Constant 1 | Exact Test | ||||
|---|---|---|---|---|---|---|---|---|
| p-Value | mid-p | |||||||
| 0.95 | Normal | 20 | 0.039 | 0.035 | 0.015 | 0.000 | 0.000 | |
| 40 | 0.029 | 0.031 | 0.042 | 0.048 | 0.000 | 0.000 | ||
| 60 | 0.031 | 0.026 | 0.035 | 0.053 | 0.000 | 0.045 | ||
| 80 | 0.026 | 0.023 | 0.032 | 0.037 | 0.020 | 0.020 | ||
| Logistic | 20 | 0.048 | 0.059 | 0.017 | 0.000 | 0.000 | ||
| 40 | 0.049 | 0.047 | 0.044 | 0.056 | 0.000 | 0.000 | ||
| 60 | 0.050 | 0.042 | 0.042 | 0.058 | 0.000 | 0.050 | ||
| 80 | 0.058 | 0.028 | 0.030 | 0.033 | 0.021 | 0.021 | ||
| Extreme Value | 20 | 0.002 | 0.027 | 0.018 | 0.000 | 0.000 | ||
| 40 | 0.000 | 0.022 | 0.030 | 0.039 | 0.000 | 0.000 | ||
| 60 | 0.001 | 0.023 | 0.029 | 0.044 | 0.000 | 0.048 | ||
| 80 | 0.000 | 0.019 | 0.029 | 0.034 | 0.017 | 0.017 | ||
| 0.97 | Normal | 20 | 0.100 | 0.072 | 0.032 | 0.000 | 0.000 | |
| 40 | 0.124 | 0.087 | 0.077 | 0.090 | 0.000 | 0.000 | ||
| 60 | 0.177 | 0.113 | 0.085 | 0.137 | 0.000 | 0.153 | ||
| 80 | 0.225 | 0.125 | 0.111 | 0.128 | 0.090 | 0.090 | ||
| Logistic | 20 | 0.167 | 0.132 | 0.037 | 0.000 | 0.000 | ||
| 40 | 0.241 | 0.169 | 0.110 | 0.159 | 0.000 | 0.000 | ||
| 60 | 0.340 | 0.155 | 0.119 | 0.166 | 0.000 | 0.164 | ||
| 80 | 0.405 | 0.154 | 0.120 | 0.144 | 0.093 | 0.093 | ||
| Extreme Value | 20 | 0.005 | 0.059 | 0.023 | 0.000 | 0.000 | ||
| 40 | 0.003 | 0.064 | 0.062 | 0.080 | 0.000 | 0.000 | ||
| 60 | 0.002 | 0.089 | 0.076 | 0.129 | 0.000 | 0.156 | ||
| 80 | 0.000 | 0.108 | 0.098 | 0.116 | 0.078 | 0.078 | ||
| 0.99 | Normal | 20 | 0.355 | 0.192 | 0.055 | 0.000 | 0.000 | |
| 40 | 0.639 | 0.374 | 0.253 | 0.364 | 0.000 | 0.000 | ||
| 60 | 0.848 | 0.524 | 0.406 | 0.557 | 0.000 | 0.538 | ||
| 80 | 0.924 | 0.620 | 0.524 | 0.604 | 0.429 | 0.429 | ||
| Logistic | 20 | 0.583 | 0.339 | 0.112 | 0.000 | 0.000 | ||
| 40 | 0.846 | 0.539 | 0.383 | 0.486 | 0.000 | 0.000 | ||
| 60 | 0.958 | 0.603 | 0.474 | 0.580 | 0.000 | 0.538 | ||
| 80 | 0.989 | 0.648 | 0.541 | 0.608 | 0.448 | 0.448 | ||
| Extreme Value | 20 | 0.029 | 0.132 | 0.044 | 0.000 | 0.000 | ||
| 40 | 0.035 | 0.273 | 0.200 | 0.277 | 0.000 | 0.000 | ||
| 60 | 0.048 | 0.435 | 0.364 | 0.515 | 0.000 | 0.557 | ||
| 80 | 0.072 | 0.590 | 0.542 | 0.603 | 0.459 | 0.459 | ||
| Model 1 | Confidence/Likelihood Interval 2 | |
|---|---|---|
| Normal | 0.961 | |
| Logistic | 0.951 | |
| Extreme Value | 0.982 | |
| 0.976 | ||
| 0.974 | ||
| 0.972 | ||
| 0.973 | ||
| 0.975 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bumbulis, L.S.; Cook, R.J. Robustness and Efficiency Considerations When Testing Process Reliability with a Limit of Detection. Mathematics 2025, 13, 1274. https://doi.org/10.3390/math13081274
Bumbulis LS, Cook RJ. Robustness and Efficiency Considerations When Testing Process Reliability with a Limit of Detection. Mathematics. 2025; 13(8):1274. https://doi.org/10.3390/math13081274
Chicago/Turabian StyleBumbulis, Laura S., and Richard J. Cook. 2025. "Robustness and Efficiency Considerations When Testing Process Reliability with a Limit of Detection" Mathematics 13, no. 8: 1274. https://doi.org/10.3390/math13081274
APA StyleBumbulis, L. S., & Cook, R. J. (2025). Robustness and Efficiency Considerations When Testing Process Reliability with a Limit of Detection. Mathematics, 13(8), 1274. https://doi.org/10.3390/math13081274






