Federated-Learning-Based Strategy for Enhancing Orbit Prediction of Satellites
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description
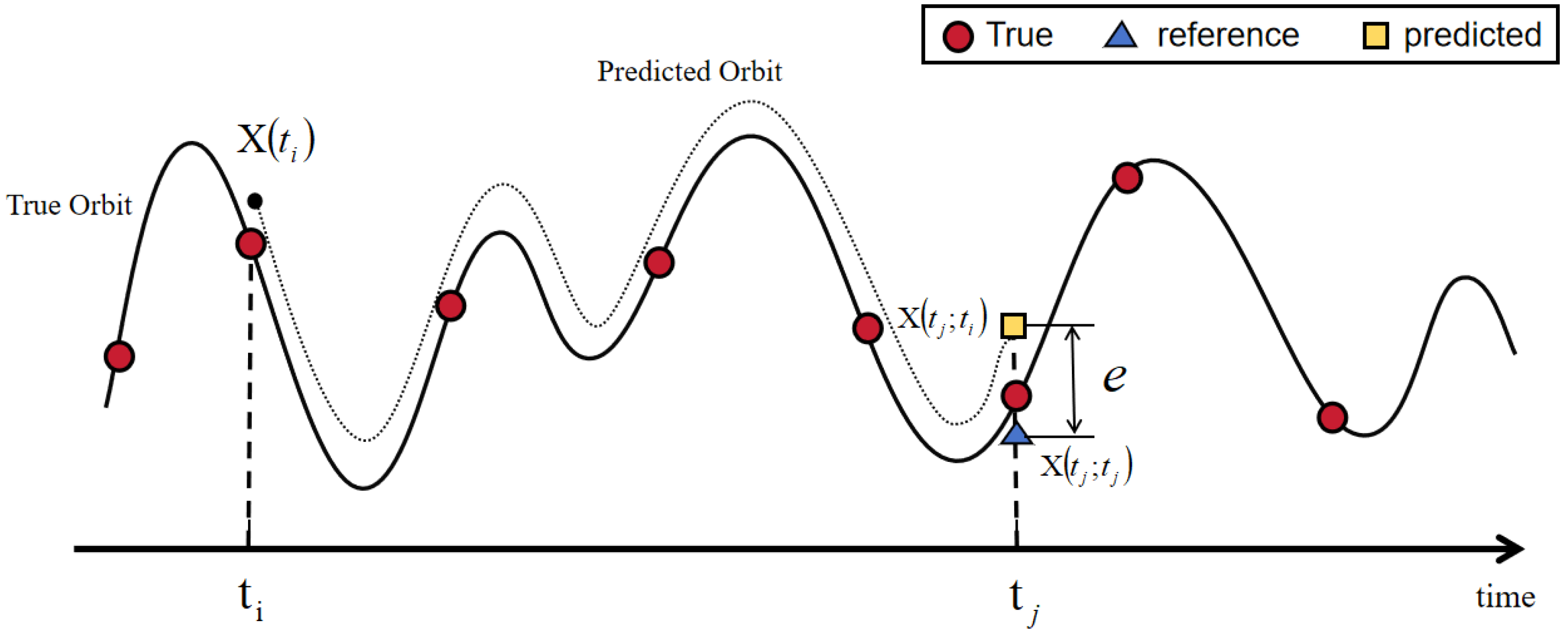
- indicates the difference between the start time and the end time;
- denotes the initial position vector in ECI coordinates with three directions, ;
- denotes the initial velocity vector in ECI coordinates with three directions, ;
- denotes the predicted position vector of j obtained based on i, which can also be expressed as ;
- denotes the predicted velocity vector of j obtained based on i, which can also be expressed as ;
- represents the damping coefficient, taking into account the effect of atmospheric drag effect.
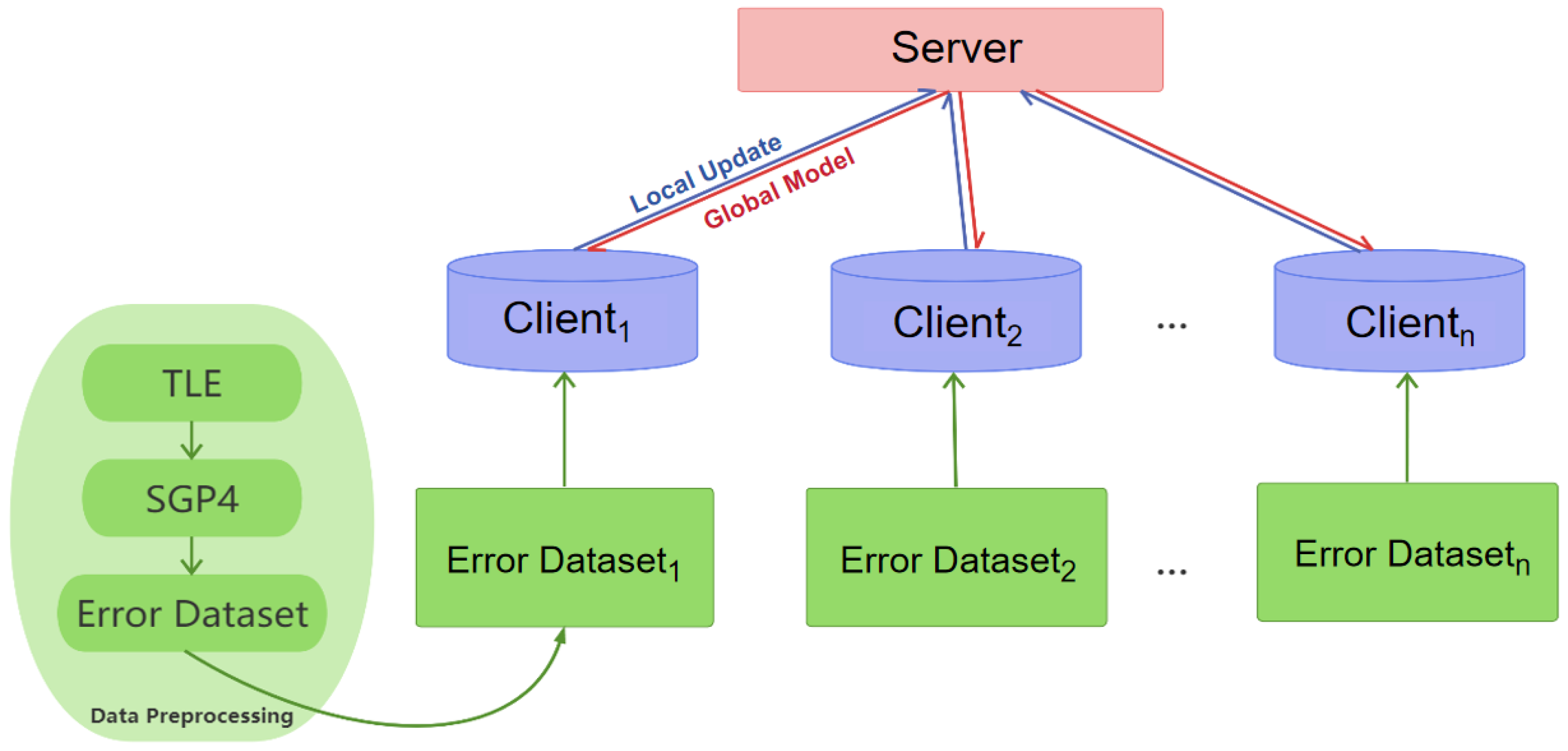
2.2. Method
3. Results
3.1. Experimental Evaluation Metrics
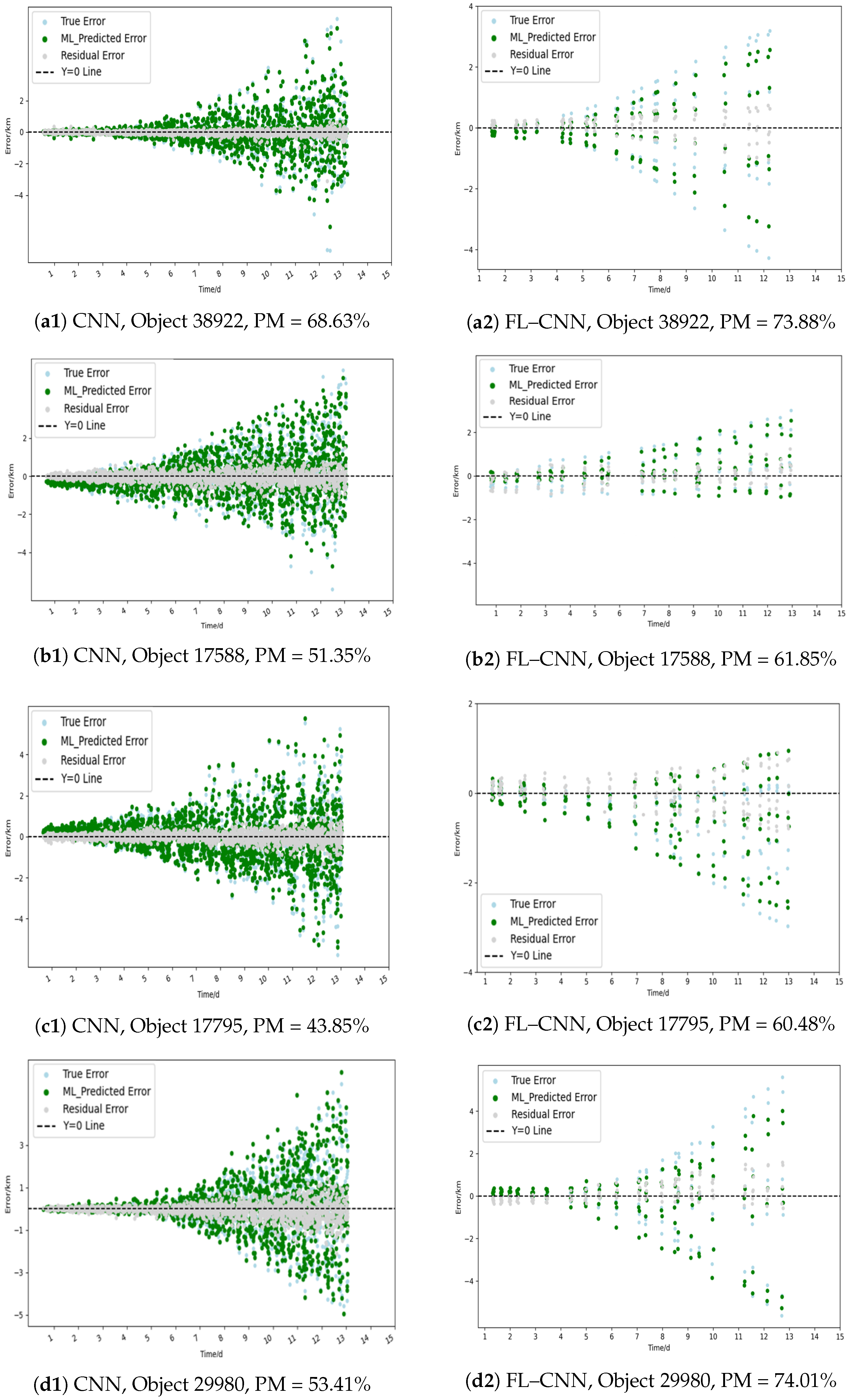
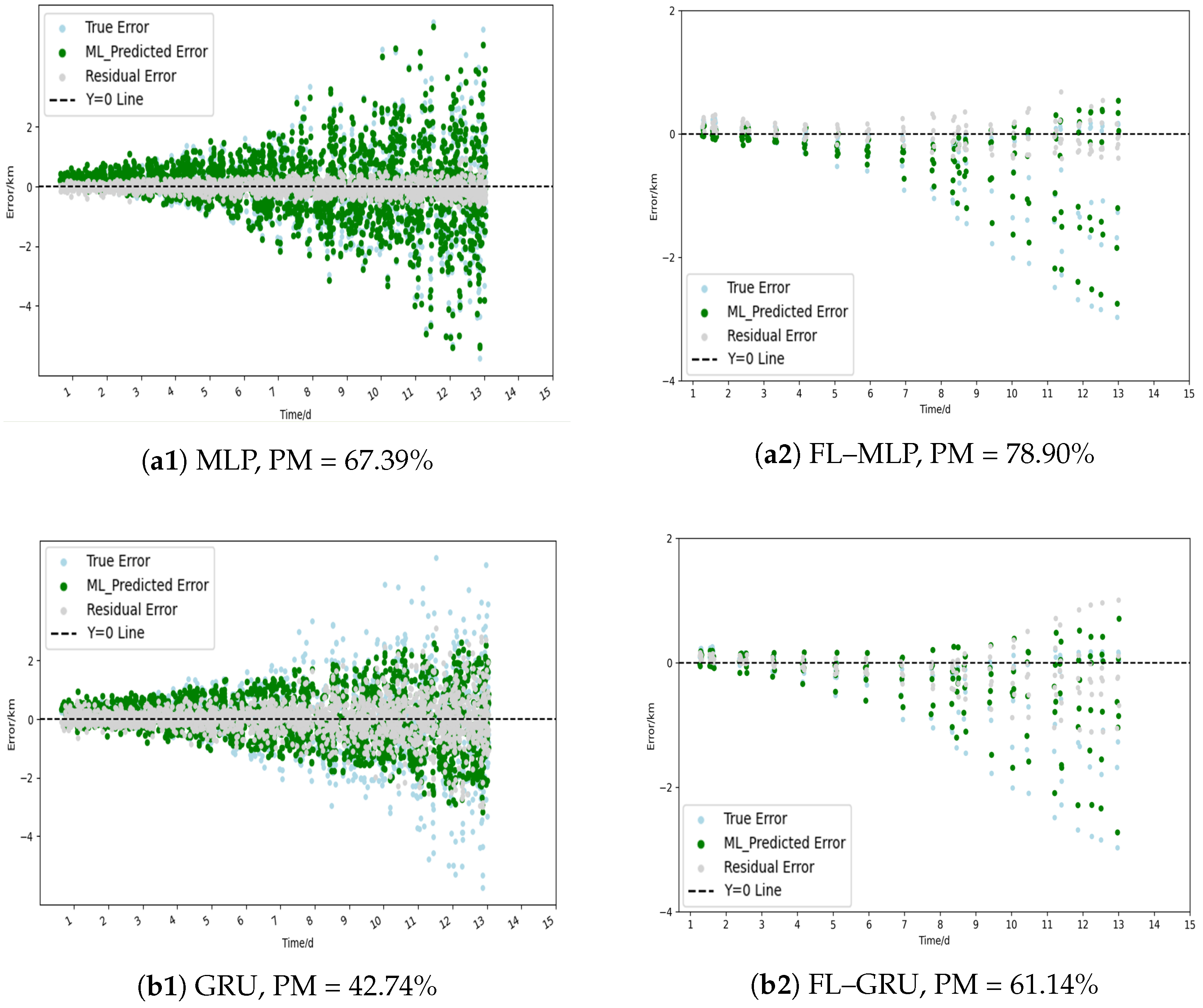
3.2. Performance Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RSO | Resident Space Object |
| SSA | Space Situational Awareness |
| TLE | Two-Line Element |
| SGP4 | Simplified General Perturbations 4 |
| GBDT | Gradient-Enhanced Decision Trees |
| CNN | Convolutional Neural Networks |
| ISL | Inter-Satellite Link |
| ML | Machine Learning |
| DL | Deep Learning |
| SGD | Stochastic Gradient Descent |
| PM | Performance Metric |
| MLP | Multi-Layer Perceptron |
| LSTM | Long Short-Term Memory |
| RNN | Recurrent Neural Network |
| GRU | Gated Recurrent Unit |
| NORAD | North American Aerospace Defense Command |
| MSE | Mean Squared Error |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
| MAPE | Mean Absolute Percentage Error |
References
- Kelso, T. Iridium 33/Cosmos 2251 Collision. 2012. Available online: http://celestrak.com/events/collision/ (accessed on 15 February 2017).
- Montenbruck, O. Numerical integration methods for orbital motion. Celest. Mech. Dyn. Astron. 1992, 53, 59–69. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Jiang, K.; Li, W.; Zhao, Q.; Fang, R.; Wei, N.; Mu, R. Improving Precise Orbit Determination of LEO Satellites Using Enhanced Solar Radiation Pressure Modeling. Space Weather 2023, 21, e2022SW003292. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X. Machine Learning Approach to Improve Satellite Orbit Prediction Accuracy Using Publicly Available Data. J. Astronaut. Sci. 2020, 67, 762–793. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X. Improving orbit prediction accuracy through supervised machine learning. Adv. Space Res. 2018, 61, 2628–2646. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Huang, J.; Sang, J. Improved orbit predictions using two-line elements through error pattern mining and transferring. Acta Astronaut. 2021, 188, 405–415. [Google Scholar] [CrossRef]
- Ferrer, E.; Ruiz-De-Azua, J.A.; Betorz, F.; Escrig, J. Inter-Satellite Link Prediction with Supervised Learning Based on Kepler and SGP4 Orbits. Int. J. Comput. Intell. Syst. 2024, 17, 217. [Google Scholar] [CrossRef]
- Li, W.; Tao, Y.; Deng, H. Improved Orbit Prediction Method Based on Two-Line Elements with Dynamic Loss Function. EasyChair Prepr. 2025, 15676. [Google Scholar]
- Chen, X.; Wang, H.; Lu, S.; Yan, R. ALC-PFL: Bearing remaining useful life prediction method based on personalized federated learning. Chin. J. Sci. Instrum. 2023, 44, 69–78. [Google Scholar]
- McMahan, H.B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (AISTATS 2016), Cadiz, Spain, 9–11 May 2016; pp. 1273–1282. [Google Scholar]
- Zhang, R.; Wang, H.; Li, B.; Cheng, X.; Yang, L. A Survey on Federated Learning in Intelligent Transportation Systems. arXiv 2024, arXiv:2403.07444. [Google Scholar] [CrossRef]
- Pruckovskaja, V.; Weissenfeld, A.; Heistracher, C.; Graser, A.; Kafka, J.; Leputsch, P.; Schall, D.; Kemnitz, J. Federated Learning for Predictive Maintenance and Quality Inspection in Industrial Applications. In Proceedings of the 2023 Prognostics and Health Management Conference (PHM), Salt Lake City, UT, USA, 28 October–2 November 2023; pp. 312–317. [Google Scholar]
- Teo, Z.L.; Jin, L.; Liu, N.; Li, S.; Miao, D.; Zhang, X.; Ng, W.Y.; Tan, T.F.; Lee, D.M.; Chua, K.J.; et al. Federated machine learning in healthcare: A systematic review on clinical applications and technical architecture. Cell Rep. Med. 2024, 5, 101419. [Google Scholar] [CrossRef] [PubMed]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.B.; Cormode, G.; Cummings, R.; et al. Advances and Open Problems in Federated Learning. Found. Trends Mach. Learn. 2019, 14, 1–210. [Google Scholar] [CrossRef]
- Yang, T.; Andrew, G.; Eichner, H.; Sun, H.; Li, W.; Kong, N.; Ramage, D.; Beaufays, F. Applied federated learning: Improving google keyboard query suggestions. arXiv 2018, arXiv:1812.02903. [Google Scholar]
- Zhao, L.; Geng, S.; Tang, X.; Hawbani, A.; Sun, Y.; Xu, L.; Tarchi, D. ALANINE: A Novel Decentralized Personalized Federated Learning For Heterogeneous LEO Satellite Constellation. arXiv 2024, arXiv:2411.07752. [Google Scholar] [CrossRef]
- Vallado, D.A. Fundamentals of Astrodynamics and Applications, 2nd ed.; Microcosm Press: Torrance, CA, USA, 2001. [Google Scholar]
- Levit, C.; Marshall, W. Improved orbit predictions using two-line elements. Adv. Space Res. 2011, 47, 1107–1115. [Google Scholar] [CrossRef]
- Chambers, J. Graphical Methods for Data Analysis: 0; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wang, J.; Kong, L.; Huang, Z.; Chen, L.; Liu, Y.; He, A.; Xiao, J. Research review of federated learning algorithms. Big Data Res. 2020, 6, 2020055. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Y.; Zhang, H. Recent Advances in Stochastic Gradient Descent in Deep Learning. Mathematics 2023, 11, 682. [Google Scholar] [CrossRef]
- Huang, W.; Ye, M.; Shi, Z.; Wan, G.; Li, H.; Du, B.; Yang, Q. Federated Learning for Generalization, Robustness, Fairness: A Survey and Benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 46, 9387–9406. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Kuang, K.; Liu, Y.; Chen, L.; Lu, J.; Shao, Y.; Wu, F.; Wu, C.; Xiao, J. Towards Multi-level Fairness and Robustness on Federated Learning. In Proceedings of the ICML 2022 Workshop on Spurious Correlations, Invariance and Stability, Baltimore, MD, USA, 22 July 2022. [Google Scholar]

| NORAD ID | Object Type | Year | Eccentricity | Inclination [deg] | Period [min] | Perigee [km] |
|---|---|---|---|---|---|---|
| 17717 | DEBRIS | 1970 | 0.9786 | 99.98 | 712 | 600 |
| 17795 | DEBRIS | 1982 | 0.1059 | 65.84 | 1084 | 989 |
| 17806 | DEBRIS | 1982 | 0.1043 | 65.83 | 1005 | 919 |
| 17588 | ROCKET BODY | 1987 | 0.1147 | 82.57 | 1471 | 1410 |
| 23233 | PAYLOAD | 1994 | 0.1017 | 98.83 | 847 | 832 |
| 30035 | DEBRIS | 1999 | 0.1003 | 99.36 | 853 | 689 |
| 29980 | DEBRIS | 1999 | 0.1025 | 98.57 | 940 | 811 |
| 45863 | PAYLOAD | 2020 | 0.0011 | 0.06 | 35,800 | 35,773 |
| 38922 | DEBRIS | 2012 | 0.1227 | 50.05 | 3340 | 260 |
| NORAD ID | ||||||
|---|---|---|---|---|---|---|
| CNN | FL–CNN | CNN | FL–CNN | CNN | FL–CNN | |
| 29980 | 50.45 | 74.26 | 68.33 | 80.43 | 53.41 | 85.72 |
| 17588 | 62.00 | 62.13 | 51.00 | 61.85 | 90.00 | 76.82 |
| 17795 | 65.54 | 65.82 | 65.38 | 44.21 | 83.90 | 85.39 |
| 38922 | 64.22 | 80.74 | 73.24 | 75.10 | 68.81 | 74.91 |
| Direction | NORAD ID | 29980 | 17588 | 17795 | 38922 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | ||||||||||
| N | MLP/FL–MLP | 43.95 | 83.32 | 55.05 | 59.38 | 67.39 | 78.90 | 74.05 | 77.23 | |
| RNN/FL–RNN | 20.41 | 68.18 | 61.00 | 51.17 | 58.50 | 65.78 | 66.24 | 68.98 | ||
| GRU/FL–GRU | 22.50 | 23.54 | 31.29 | 45.85 | 42.74 | 61.14 | 9.68 | 81.58 | ||
| LSTM/FL–LSTM | 19.24 | 61.51 | 53.01 | 61.15 | 45.70 | 58.31 | 72.01 | 63.60 | ||
| Trans/FL–Trans | 35.60 | 62.79 | 49.40 | 45.62 | 41.73 | 77.35 | 40.49 | 52.27 | ||
| W | MLP/FL–MLP | 41.69 | 72.37 | 89.76 | 49.47 | 68.47 | 79.40 | 77.07 | 79.59 | |
| RNN/FL–RNN | 15.09 | 69.12 | 62.78 | 48.82 | 75.98 | 67.95 | 62.50 | 65.94 | ||
| GRU/FL–GRU | 29.98 | 74.83 | 61.71 | 66.15 | 34.70 | 76.72 | 11.49 | 75.53 | ||
| LSTM/FL–LSTM | 34.38 | 72.11 | 77.09 | 43.31 | 76.68 | 80.52 | 67.06 | 81.78 | ||
| Trans/FL–Trans | 39.97 | 70.11 | 70.25 | 45.52 | 64.28 | 47.72 | 44.17 | 52.20 | ||
| U | MLP/FL–MLP | 45.68 | 88.33 | 68.95 | 55.93 | 72.00 | 50.97 | 68.73 | 75.86 | |
| RNN/FL–RNN | 23.15 | 69.94 | 60.35 | 71.76 | 53.08 | 74.35 | 67.41 | 70.18 | ||
| GRU/FL–GRU | 24.03 | 28.85 | 41.82 | 68.86 | 23.26 | 86.19 | 32.36 | 84.55 | ||
| LSTM/FL–LSTM | 34.43 | 46.18 | 60.68 | 53.44 | 52.85 | 67.59 | 72.77 | 58.93 | ||
| Trans/FL–Trans | 38.46 | 54.86 | 53.91 | 54.15 | 28.65 | 58.48 | 36.78 | 68.05 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Li, W.; Zhao, Q.; Chi, H. Federated-Learning-Based Strategy for Enhancing Orbit Prediction of Satellites. Mathematics 2025, 13, 1312. https://doi.org/10.3390/math13081312
Tang J, Li W, Zhao Q, Chi H. Federated-Learning-Based Strategy for Enhancing Orbit Prediction of Satellites. Mathematics. 2025; 13(8):1312. https://doi.org/10.3390/math13081312
Chicago/Turabian StyleTang, Jiayi, Wenxin Li, Qinchen Zhao, and Hongmei Chi. 2025. "Federated-Learning-Based Strategy for Enhancing Orbit Prediction of Satellites" Mathematics 13, no. 8: 1312. https://doi.org/10.3390/math13081312
APA StyleTang, J., Li, W., Zhao, Q., & Chi, H. (2025). Federated-Learning-Based Strategy for Enhancing Orbit Prediction of Satellites. Mathematics, 13(8), 1312. https://doi.org/10.3390/math13081312






