Multi-Condition Rolling Bearing Fault Denoising Method and Application Based on RIME-VMD
Abstract
:1. Introduction
- (1)
- Taking the multi-condition rolling bearing signal as the research object, a method for rolling bearing signal decomposition based on VMD is proposed. The signal decomposition problem is constructed as a variational problem to optimize the central frequency of each modal function, so as to achieve the purpose of signal decomposition and realize the separation of effective components and noise in the signal.
- (2)
- The RIME algorithm is used to optimize VMD parameters, and power spectrum entropy and the kurtosis value are introduced to establish a fitness function in order to obtain the best combination of VMD parameters, so as to realize the noise reduction in a multi-working condition rolling bearing fault signal and effectively retain the fault signal.
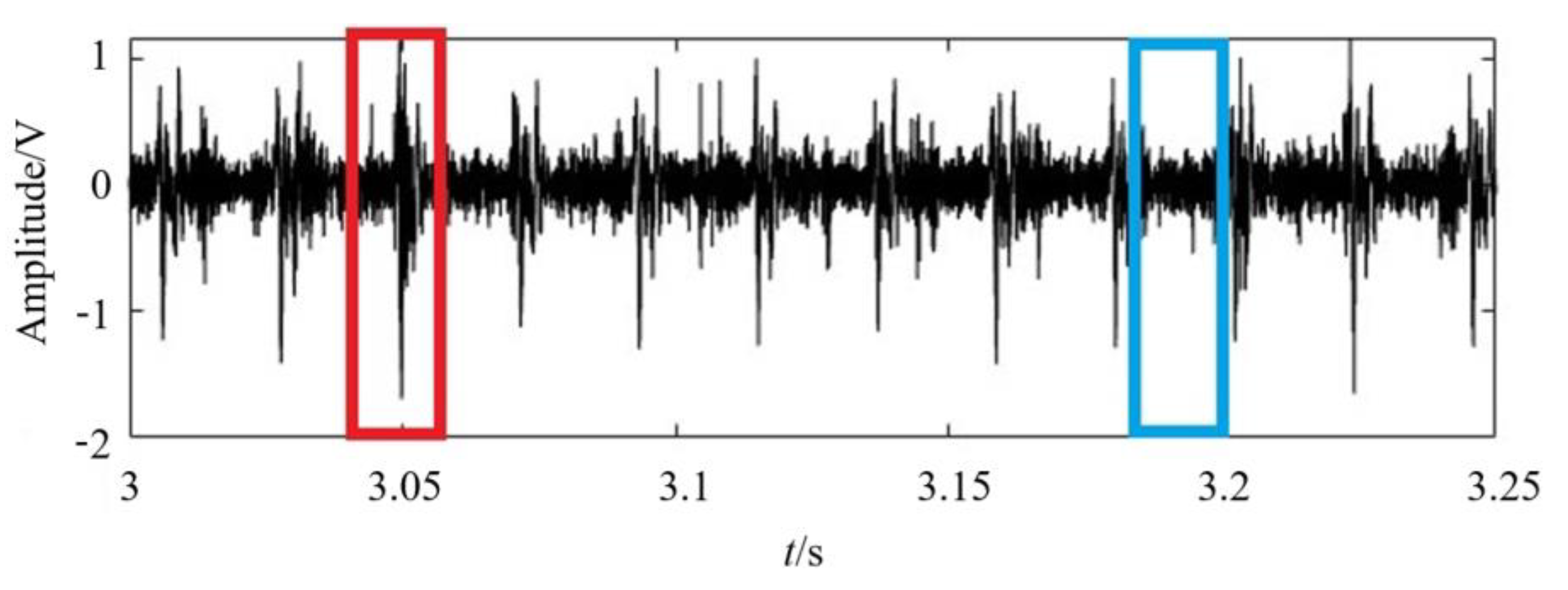
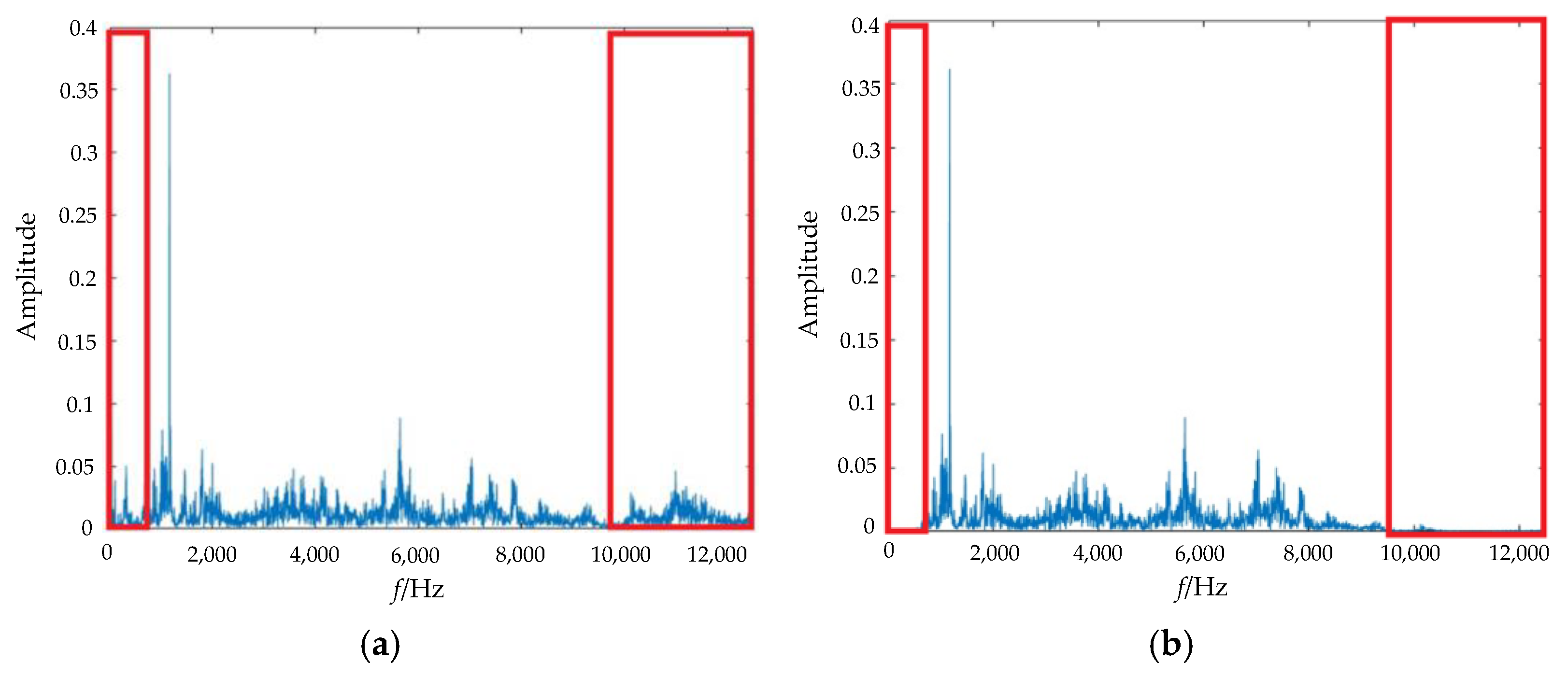
2. The Noise Analysis of Rolling Bearing Signal
3. Basic Theory
3.1. Variational Mode Decomposition
3.2. Frost and Ice Algorithm
3.3. Fitness Function
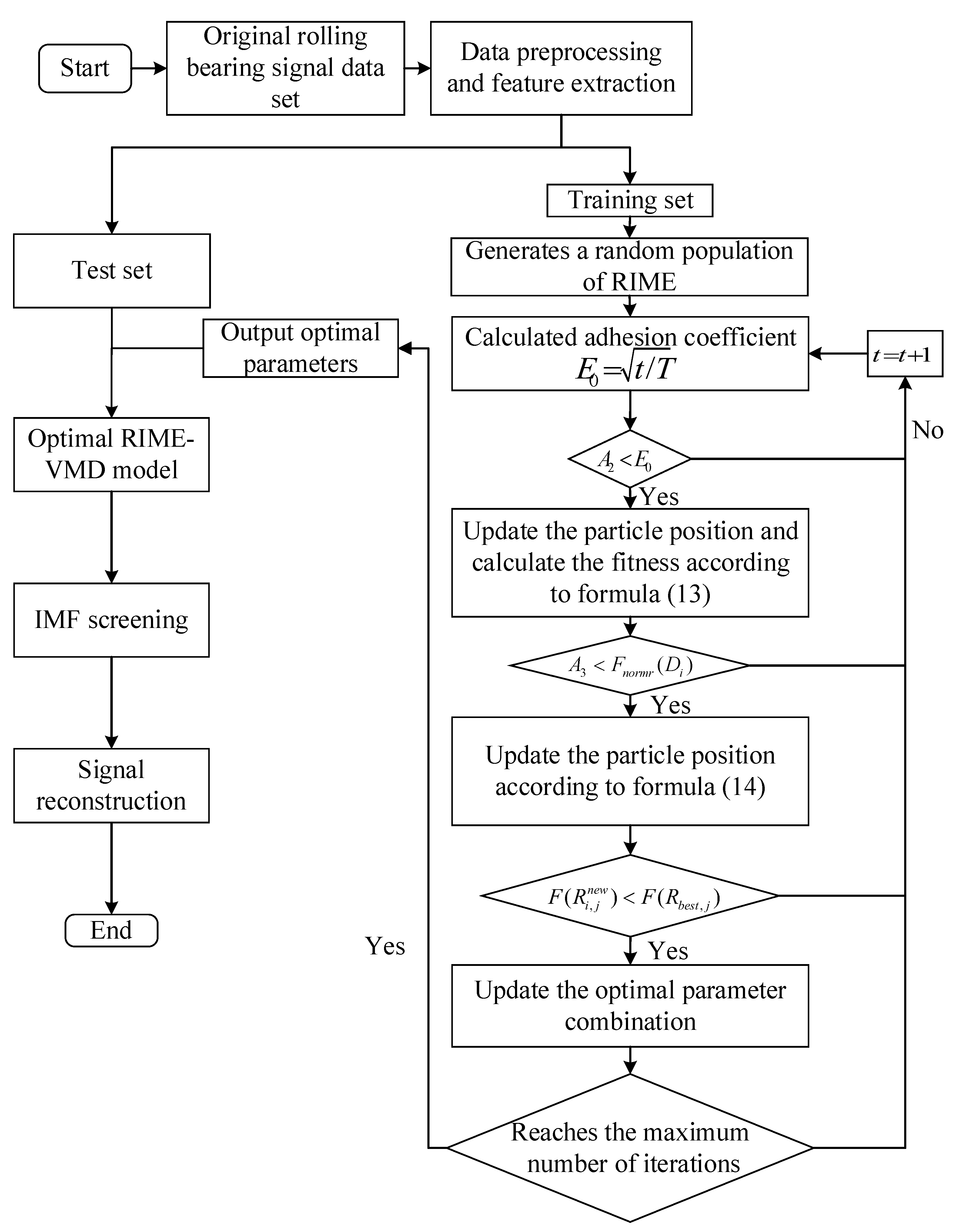
4. Multi-Condition Rolling Bearing Fault Denoising Method Based on RIME-VMD
- (1)
- The rolling bearing signal is obtained and then put into the RIME initialization port, and the ranges of VMD key parameter combination and relevant parameters in RIME are solved. These parameters include the maximum number of iterations, spatial dimensions, and so on.
- (2)
- According to the obtained parameters, the signal is decomposed by using VMD, and eigenmode functions (IMFs) from low frequency to high frequency are obtained. The fitness function value of each iteration is solved, and then the current minimum fitness function value and the corresponding local optimal solution are constantly updated and saved.
- (3)
- According to Formula (14), the algorithm is updated and iterated continuously until the stopping condition is reached or the maximum number of iterations is met. Currently, the parameter combination corresponding to the lowest fitness function value is the optimal parameter combination.
- (4)
- The VMD decomposition of the rolling bearing signal is performed using the optimal parameter combination to obtain the components, and the envelope entropy and kurtosis values corresponding to each component are calculated. The components with large kurtosis and small envelope entropy are selected as the effective components with a high correlation degree and more characteristics of the target signal, and the effective components are decomposed again by VMD. After reconstruction, the optimal component IMF representing the characteristics of the target signal is generated, which is the effective fault frequency component signal of the rolling bearing signal extracted by RIME-VMD.
| Algorithm 1. Pseudo-Code of RIME-VMD |
| 1: Initialize frost body population R 2: Obtain the current optimal parameter combination and its optimal fitness functionss 3: While 4: The adhesion coefficient is 5: If 6: Update the parameter combination agent location by soft RIME search policy 7: End if 8: If 9: Cross-update between parameter combination agents via the hard RIME mechanism 10: End if 11: If 12: Select the optimal solution parameter combination and its optimal fitness function and use the positive greedy selection mechanism to replace the sub-optimal solution 13: 14: End While |
5. Experiment and Analysis
5.1. Experimental Dataset and Evaluation Index Settings
5.2. Experimental Environment and Parameter Configuration
5.3. Ablation Experiment
5.4. Sensitivity Analysis of RIME Parameters Affecting the Denoising Performance
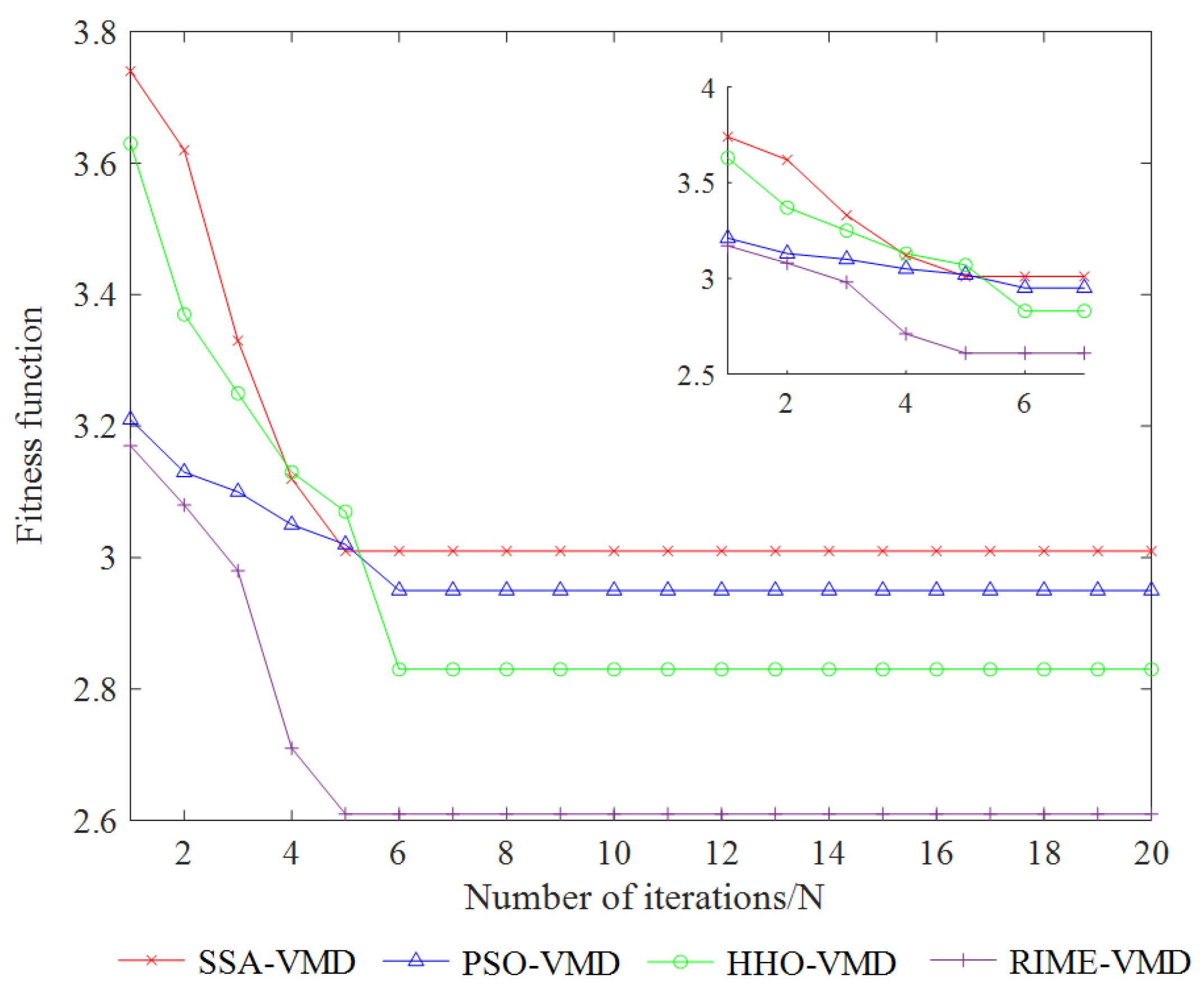
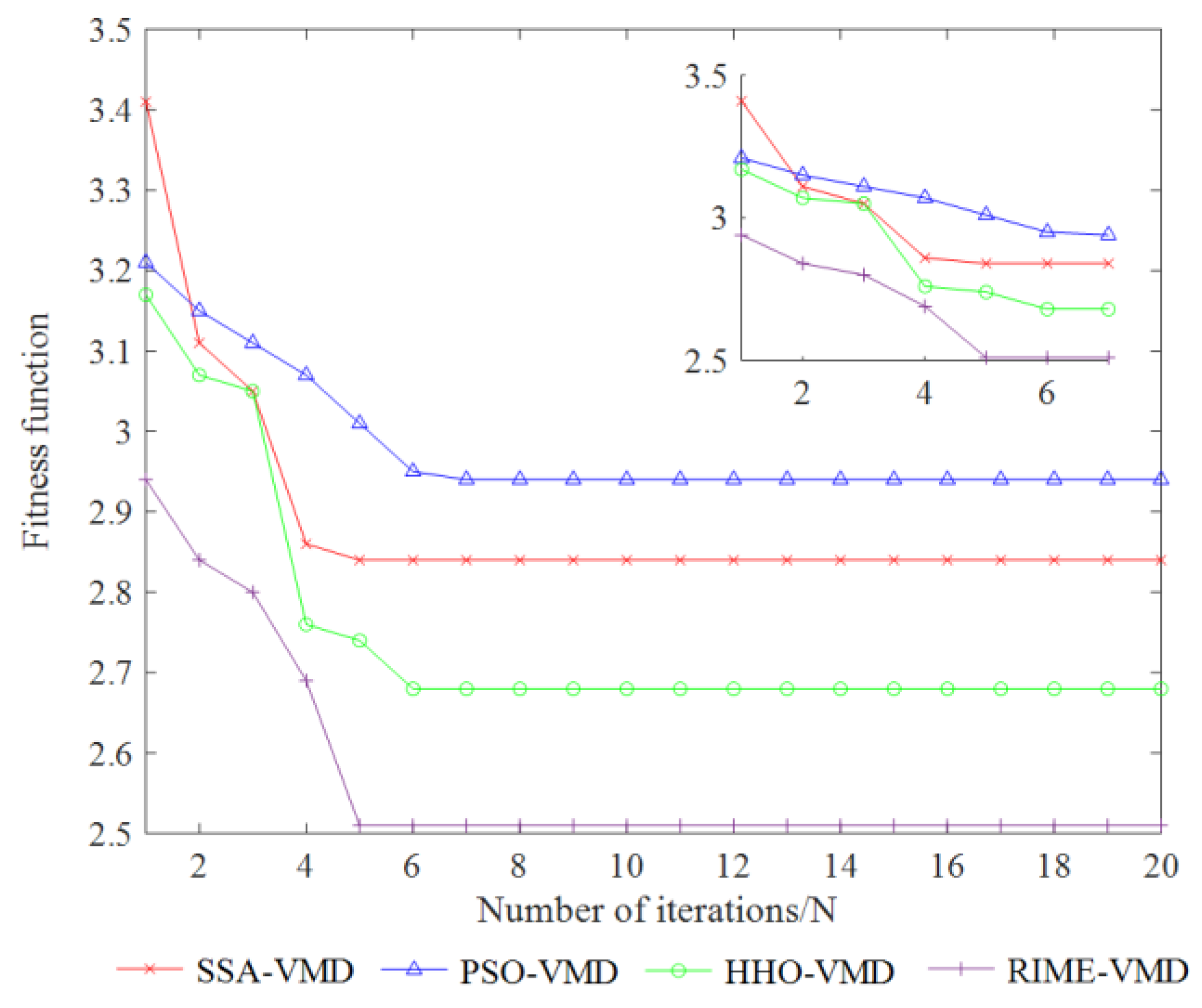
5.5. Comparative Experimental Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Li, H.; Zhang, W.; Chen, Y. Adaptive modal total variational mode decomposition method and its performance evaluation. J. Vib. Shock 2023, 42, 251–262. [Google Scholar]
- Phan, V.; Vo, C.; Dao, H.; Ahn, K. Robust fault-tolerant control of an electro-hydraulic actuator with a novel nonlinear unknown input observer. IEEE Access 2021, 9, 30750–30760. [Google Scholar] [CrossRef]
- Burda, E.; Zusman, G.; Naumenko, A. An overview of vibration analysis techniques for the fault diagnostics of rolling bearings in machinery. Shock Vib. 2022, 2022, 6136231. [Google Scholar] [CrossRef]
- Liu, J.; Shao, Y. Overview of dynamic modelling and analysis of rolling element bearings with localized and distributed faults. Nonlinear Dyn. 2018, 93, 1765–1798. [Google Scholar] [CrossRef]
- Xie, C.; Wang, X.; Xiao, F.; Peng, C.; Mei, Y.; Liu, P. Review of bearing fault modes and fault diagnosis methods. Comput. Meas. Control 2024, 1–11. [Google Scholar]
- Zhang, Y.; Zhang, T.; Ge, P.; Wang, C.; Wang, Y. Review on intelligent fault diagnosis of motor bearings. Mech. Electr. Eng. Technol. 2024, 53, 1–6. [Google Scholar]
- Liu, Z.; Yu, H.; Miao, X. RMCW: An improved residual network with multi-channel weighting for machinery fault diagnosis. IEEE Access 2023, 11, 124472–124483. [Google Scholar] [CrossRef]
- Smith, W.; Randall, R. Rolling element bearing diagnostics using the case western reserve university data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar]
- Ding, J.; Huang, L.; Li, X. GMPSO-VMD Algorithm and its application to rolling bearing fault feature extraction. Sensors 2020, 20, 1946. [Google Scholar] [CrossRef]
- Xiao, F.; Yang, D.; Wang, Y. VMD-based denoising methods for surface electromyography signals. J. Neural Eng. 2019, 16, 056017. [Google Scholar] [CrossRef]
- Bian, J.; Jing, L.; Liu, Y. Application of entropy theory in bearing fault diagnosis. J. Dalian Polytech. Univ. 2024, 43, 300–306. [Google Scholar]
- Gu, J.; Peng, Y. An improved complementary ensemble empirical mode decomposition method and its application in rolling bearing fault diagnosis. Digit. Signal Process. 2021, 113, 103050. [Google Scholar] [CrossRef]
- Zhou, J.; Xiao, M.; Ji, G. Rolling Bearing Fault Diagnosis Based on WGWOA-VMD-SVM. Sensors 2022, 22, 6281. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Peng, Z.; Zhou, P. Review of Signal Decomposition Theory and Its Applications in Machine Fault Diagnosis. J. Mech. Eng. 2020, 56, 91–107. [Google Scholar]
- Fan, H.; Xu, H.; Fan, W.; Chen, B.; Li, Q.; Zhang, T.; Cao, X.; Zhang, X. Cloud–edge collaborative intelligent fault diagnosis of rotor-bearing system: Methodology and experiment. IEEE Sens. J. 2025, 25, 5044–5059. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X. An equivalent target plate damage probability calculation mathematics model and damage evaluation method. Def. Technol. 2024, 41, 82–103. [Google Scholar] [CrossRef]
- Sun, M.; Li, Z.; Li, Z.; Li, Q.; Liu, Y.; Wang, J. A noise attenuation method for weak seismic signals based on compressed sensing and CEEMD. IEEE Access 2020, 8, 71951–71964. [Google Scholar] [CrossRef]
- Liu, F.; Gao, J.; Liu, H. The feature extraction and diagnosis of rolling bearing based on CEEMD and LDWPSO-PNN. IEEE Access 2020, 8, 19810–19819. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Kang, W. A testing and data processing method of projectile explosion position based on three UAVs’ visual spatial constrain mechanism. Expert Syst. Appl. 2025, 265, 125984. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Gao, J. A projectile signal recognize algorithm using variational mode decomposition and wavelet mode maximum fusion in sky screen sensor and its application. IEEE Sens. J. 2024, 24, 40648–40658. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, Y.; Chen, J. Noise reduction based on a CEEMD-WPT crack acoustic emission datase. Appl. Sci. 2023, 13, 10274. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Chen, Q. An optimized VMD method and its applications in bearing fault diagnosis. Measurement 2020, 166, 108185. [Google Scholar] [CrossRef]
- Cui, H.; Guan, Y.; Chen, H. Rolling element fault diagnosis based on VMD and sensitivity MCKD. IEEE Access 2021, 9, 120297–120308. [Google Scholar] [CrossRef]
- Quan, Y.; Yu, M.; Wang, W.; Wei, L. Short-term wind speed prediction based on fractal optimization of VMD-GA-BP. Acta Energiae Solaris Sin. 2023, 44, 436–446. [Google Scholar]
- Jiang, L.; Lu, X.; Wang, J.; Yu, M. Feature parameters extraction method of gear based on PSO-VMD. Manuf. Technol. Mach. Tool 2017, 11, 65–71. [Google Scholar]
- Chen, W.; Li, J.; Zhang, W. Rolling bearing fault diagnosis based on VMD hybrid domain feature and SSA-SVM. Mach. Tool Hydraul. 2022, 50, 159–164. [Google Scholar]
- Zhong, X.; Zhao, Y.; Hu, J. Application of total variation denoising based on particle swarm optimization in bearing fault diagnosis. Machinery 2020, 47, 1–5+21. [Google Scholar]
- Chen, C.; Zhou, L.; Yang, L. Axle box bearing fault diagnosis based on average autocorrelation and optimized VMD. J. Vib. Meas. Diagn. 2023, 43, 231–239+405. [Google Scholar]
- Qin, Y.; Li, G.; Qi, J.; Wang, J. Fault diagnosis of transverse damper for high-speed trains based on RIME-VMD. J. Railw. Sci. Eng. 2024, 46, 761. [Google Scholar]
- Li, H.; Li, M.; Ma, Y.; Zheng, Y.; Li, S. A variational mode decomposition projectile signal processing algorithm of infrared sky screen velocity measurement system and detection mathematical model of detection screen. Optik 2023, 287, 171077. [Google Scholar] [CrossRef]
- Lei, Y.; Han, T.; Wang, B.; Li, N.; Yan, T.; Yang, J. XJTU-SY Rolling element bearing accelerated life test datasets: A tutorial. J. Mech. Eng. 2019, 55, 1–6. [Google Scholar]
- Wang, M.; Wang, W.; Zhang, Y. An integrated method based on sparrow search algorithm improved variational mode decomposition and support vector machine for fault diagnosis of rolling bearing. J. Vib. Eng. Technol. 2022, 10, 2893–2904. [Google Scholar] [CrossRef]
- Mao, M.; Chang, J.; Wang, Z. Research on VMD-based adaptive TDLAS signal denoising method. Photonics 2023, 10, 674. [Google Scholar] [CrossRef]
- Zhang, B.; Su, Y.; Jiang, Y. Bearing fault diagnosis based on improved variational mode decomposition and optimized stacked denoising autoencoder. Comput. Integr. Manuf. Syst. 2024, 30, 1408–1421. [Google Scholar]


| Signal Decomposition and Reconstruction Method | RMSE | RC | SNR/dB | NCC | Kurtosis |
|---|---|---|---|---|---|
| VMD | 0.482 | 0.9213 | 11.56 | 0.813 | 4.978 |
| RIME-VMD | 0.047 | 0.9849 | 13.32 | 0.984 | 5.682 |
| NO. | Particle Population/N | Number of Iterations/T | RMSE | RC | SNR/dB | NCC | Kurtosis | Computation Time/s |
|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 30 | 0.473 | 0.918 | 8.31 | 0.773 | 4.978 | 61.34 |
| 2 | 30 | 50 | 0.154 | 0.982 | 12.51 | 0.954 | 5.682 | 150.68 |
| 3 | 50 | 100 | 0.132 | 0.985 | 12.17 | 0.912 | 5.311 | 319.91 |
| Working Condition | Signal Decomposition and Reconstruction Method | RMSE | RC | SNR | NCC | Kurtosis |
|---|---|---|---|---|---|---|
| Rotational speed: 2100/(r/min) Radial force: 12/KN | SSA-VMD | 0.585 | 0.881 | 11.56 | 0.784 | 5.81 |
| PSO-VMD | 0.426 | 0.935 | 10.77 | 0.792 | 5.53 | |
| HHO-VMD | 0.107 | 0.908 | 9.20 | 0.761 | 5.01 | |
| RIME-VMD | 0.067 | 0.991 | 13.29 | 0.845 | 5.92 |
| Working Condition | Signal Decomposition and Reconstruction Method | RMSE | RC | SNR | NCC | Kurtosis |
|---|---|---|---|---|---|---|
| Rotational speed: 2100/(r/min) Radial force: 12/KN | SSA-VMD | 0.677 | 0.923 | 9.56 | 0.657 | 5.32 |
| PSO-VMD | 0.421 | 0.918 | 9.98 | 0.778 | 5.11 | |
| HHO-VMD | 0.302 | 0.852 | 8.78 | 0.721 | 5.54 | |
| RIME-VMD | 0.071 | 0.984 | 12.95 | 0.821 | 5.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Liu, X.; Li, H. Multi-Condition Rolling Bearing Fault Denoising Method and Application Based on RIME-VMD. Mathematics 2025, 13, 1348. https://doi.org/10.3390/math13081348
Zhao X, Liu X, Li H. Multi-Condition Rolling Bearing Fault Denoising Method and Application Based on RIME-VMD. Mathematics. 2025; 13(8):1348. https://doi.org/10.3390/math13081348
Chicago/Turabian StyleZhao, Xin, Xuebin Liu, and Hanshan Li. 2025. "Multi-Condition Rolling Bearing Fault Denoising Method and Application Based on RIME-VMD" Mathematics 13, no. 8: 1348. https://doi.org/10.3390/math13081348
APA StyleZhao, X., Liu, X., & Li, H. (2025). Multi-Condition Rolling Bearing Fault Denoising Method and Application Based on RIME-VMD. Mathematics, 13(8), 1348. https://doi.org/10.3390/math13081348






