Blood Flow Simulation in Bifurcating Arteries: A Multiscale Approach After Fenestrated and Branched Endovascular Aneurysm Repair
Abstract
1. Introduction
2. Mathematical Formulation
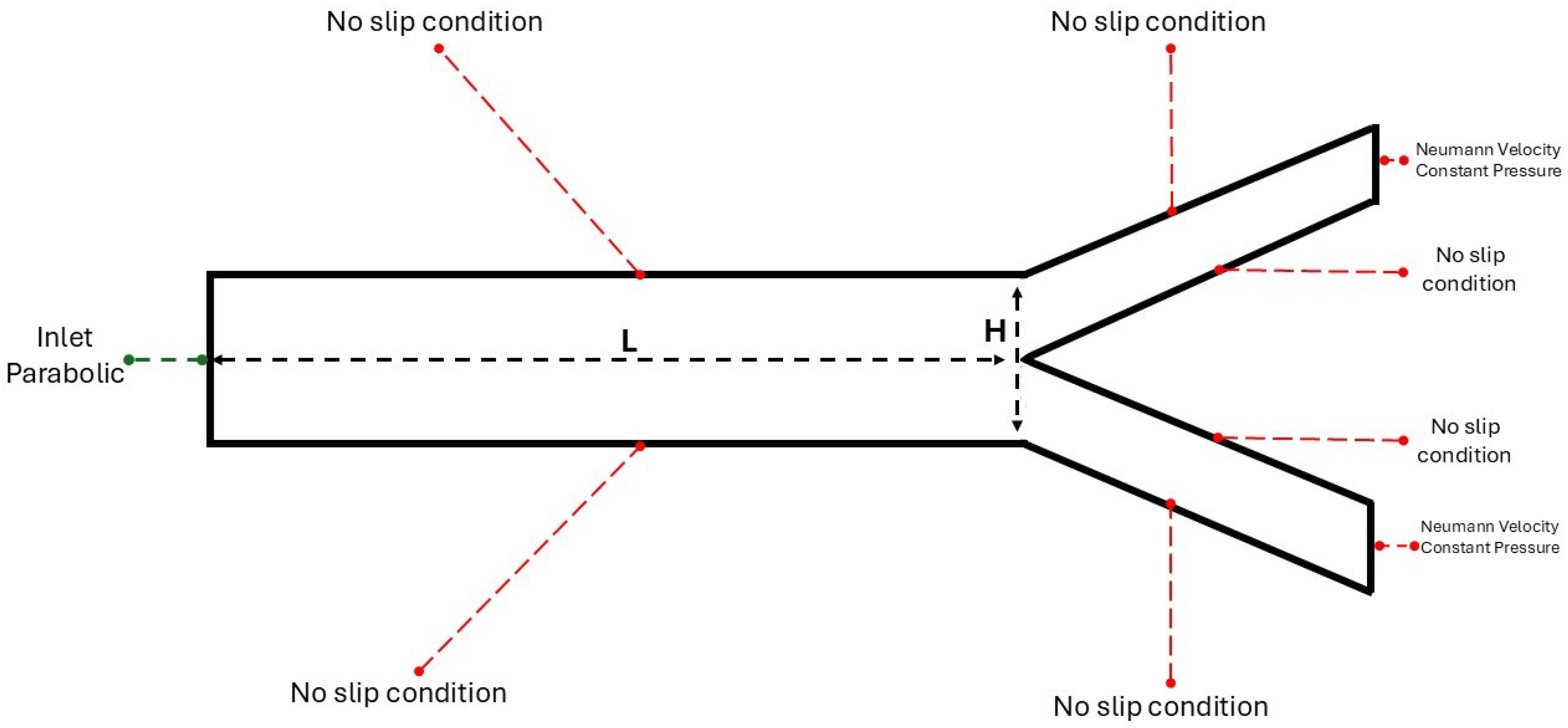
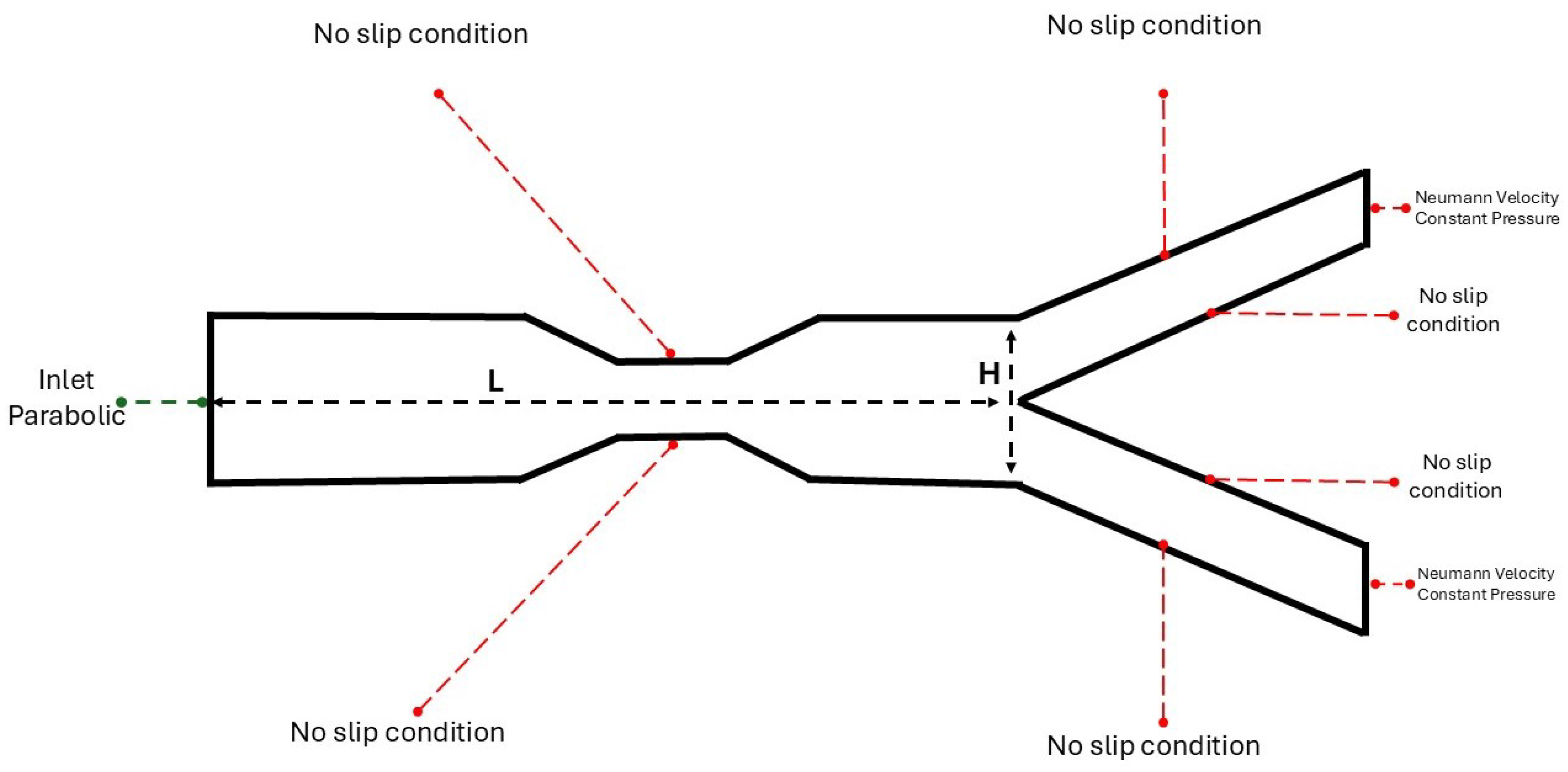
2.1. The 2D Study
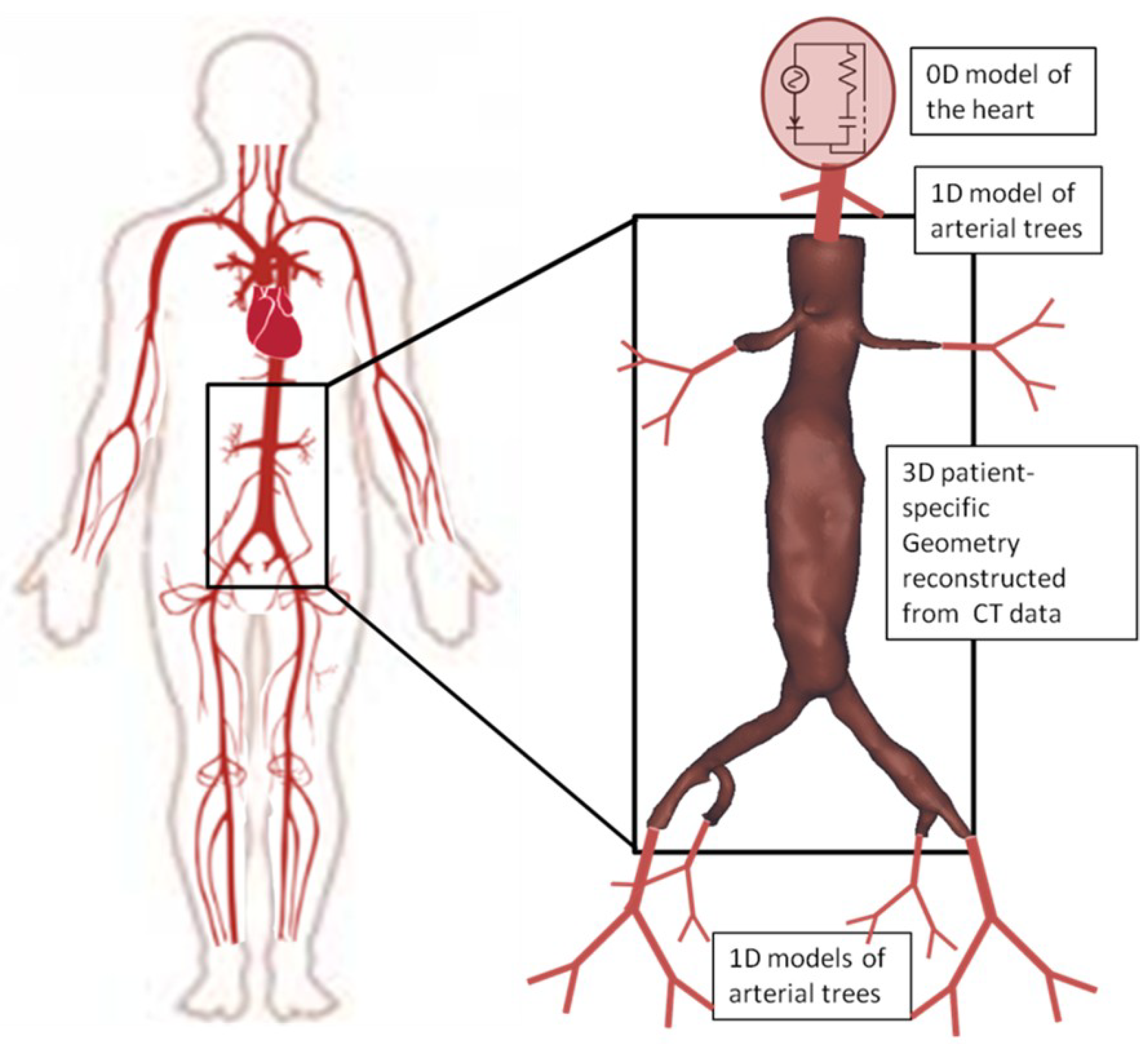
2.2. The 3D Study
3. Results
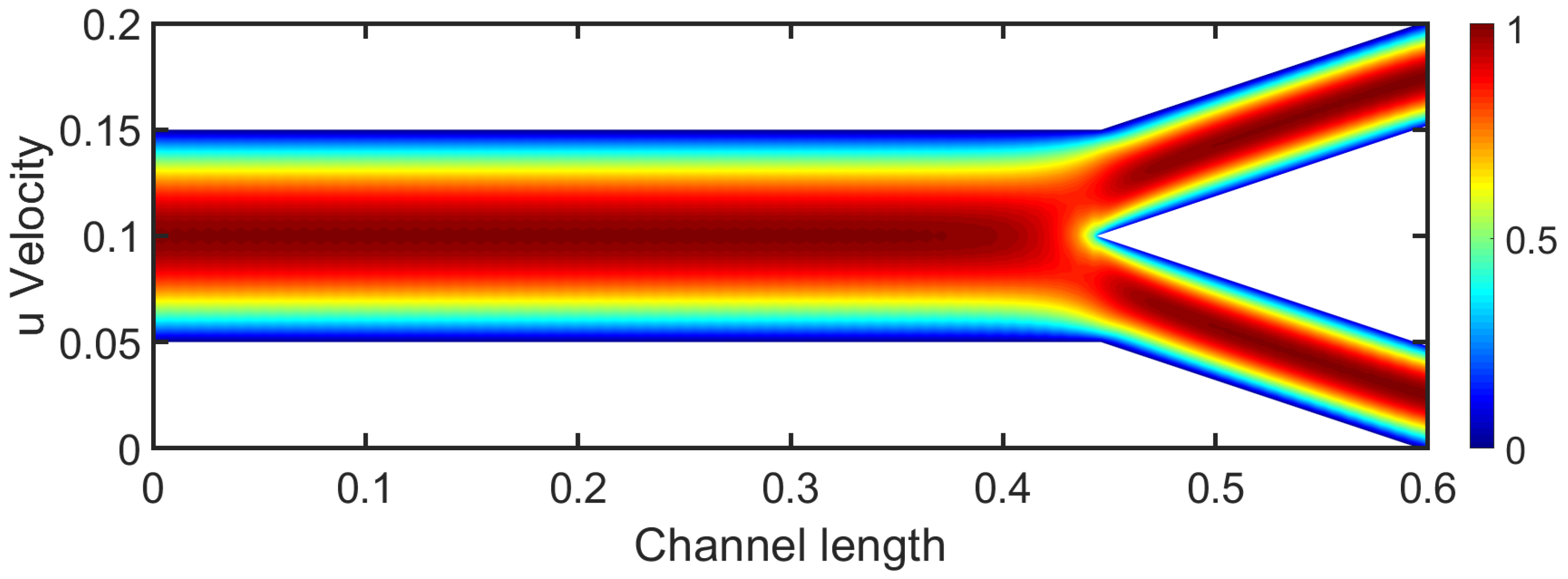
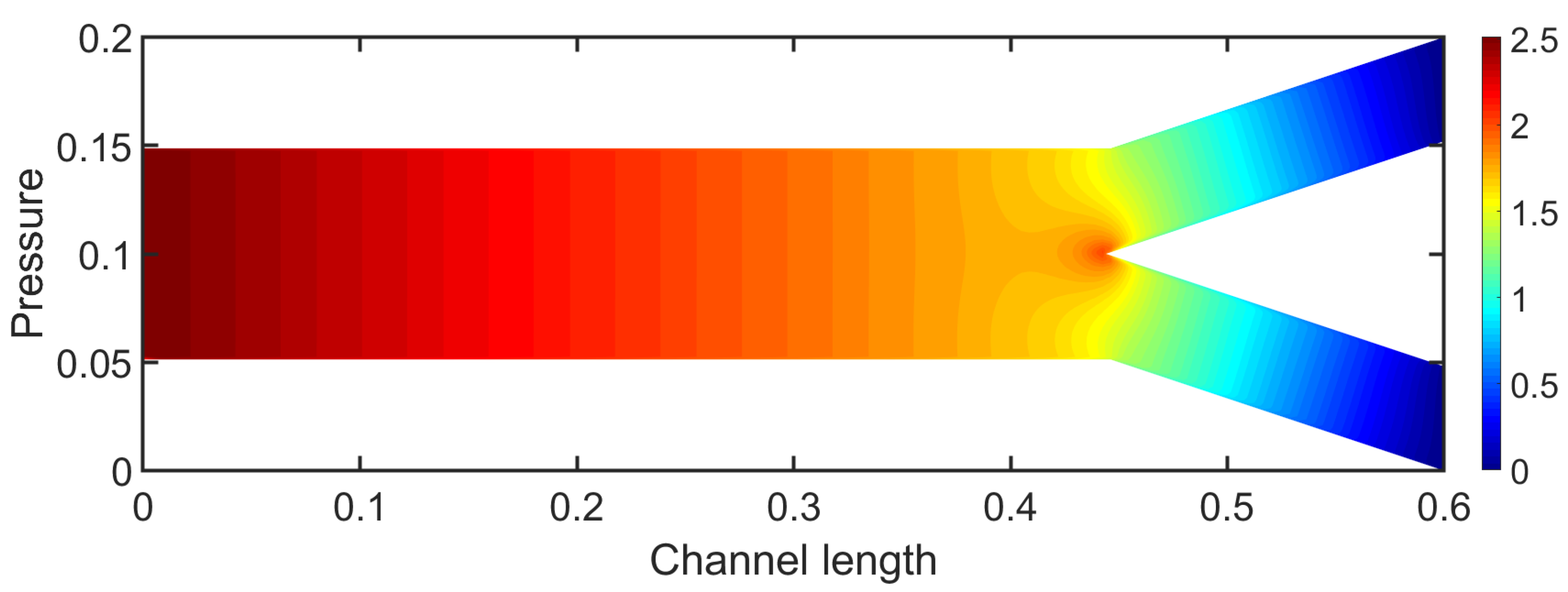
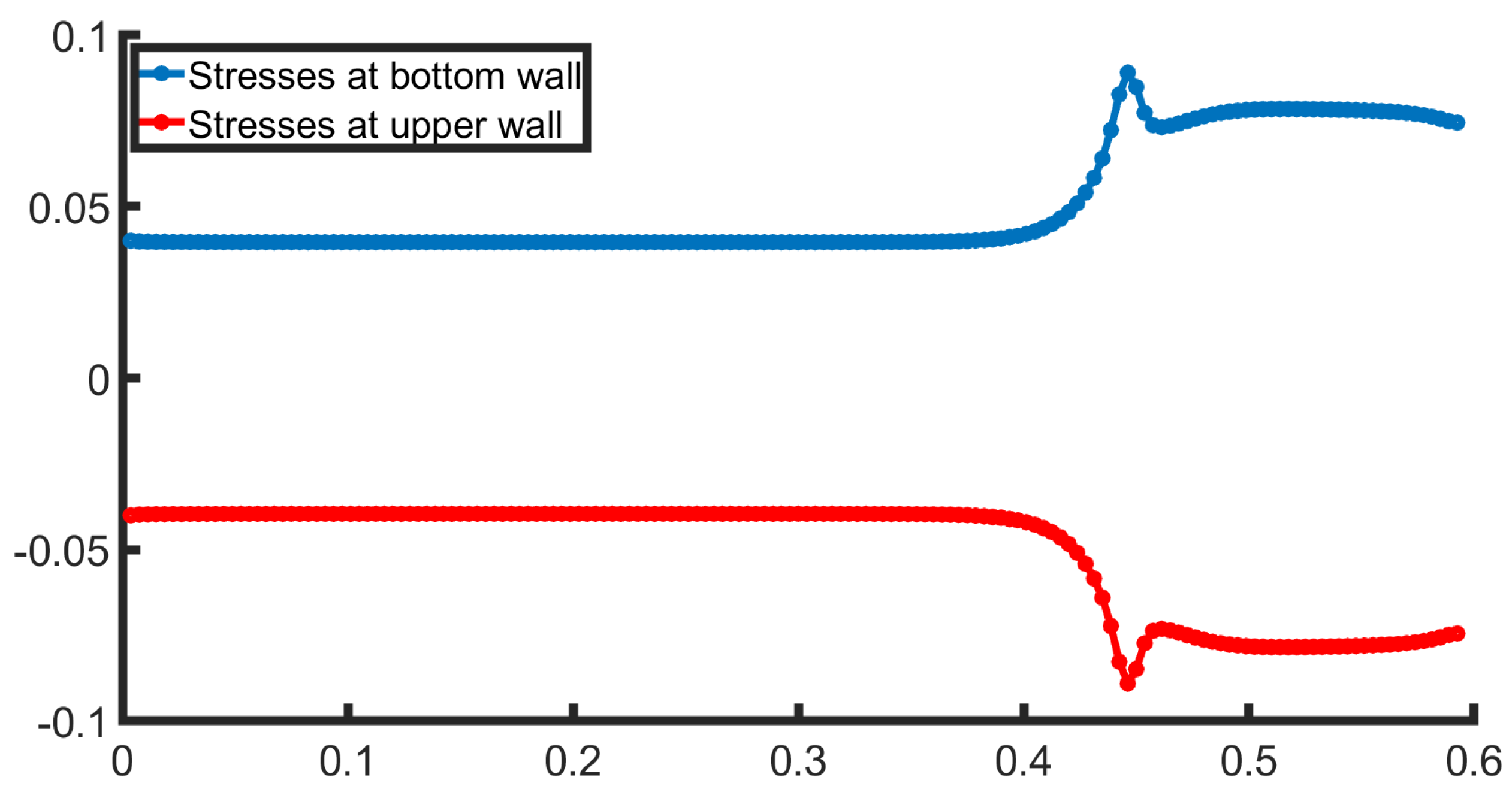
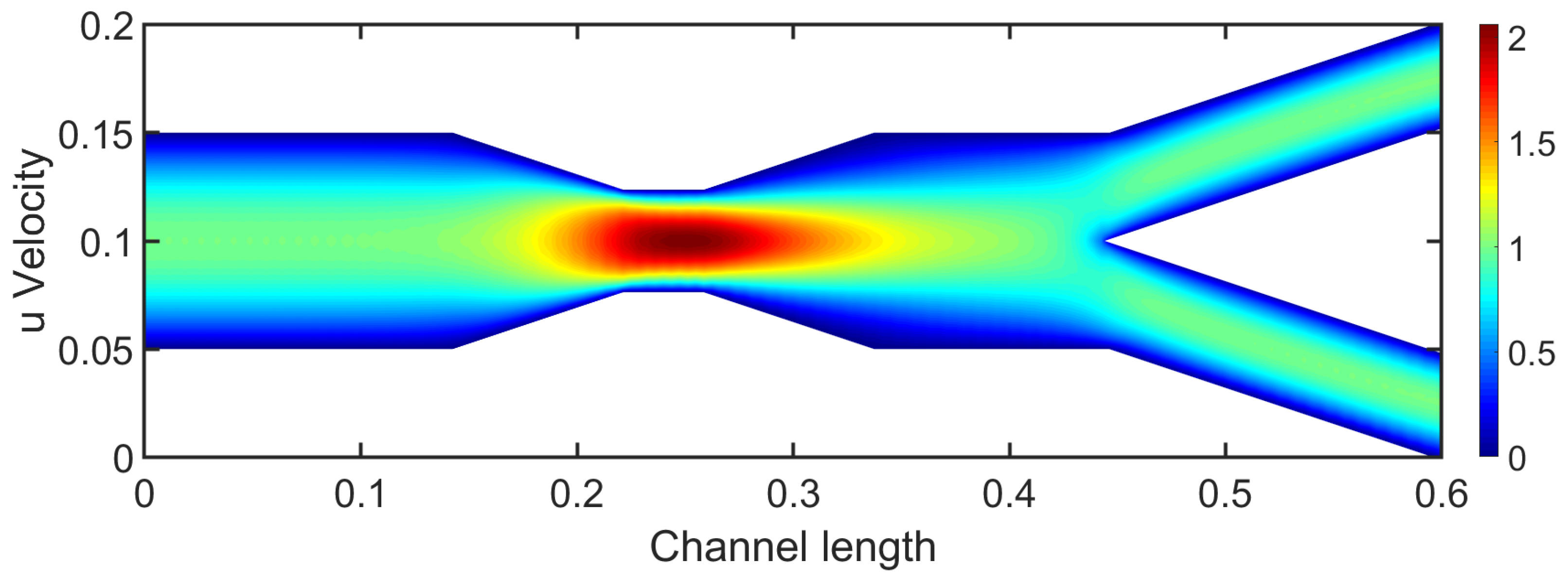
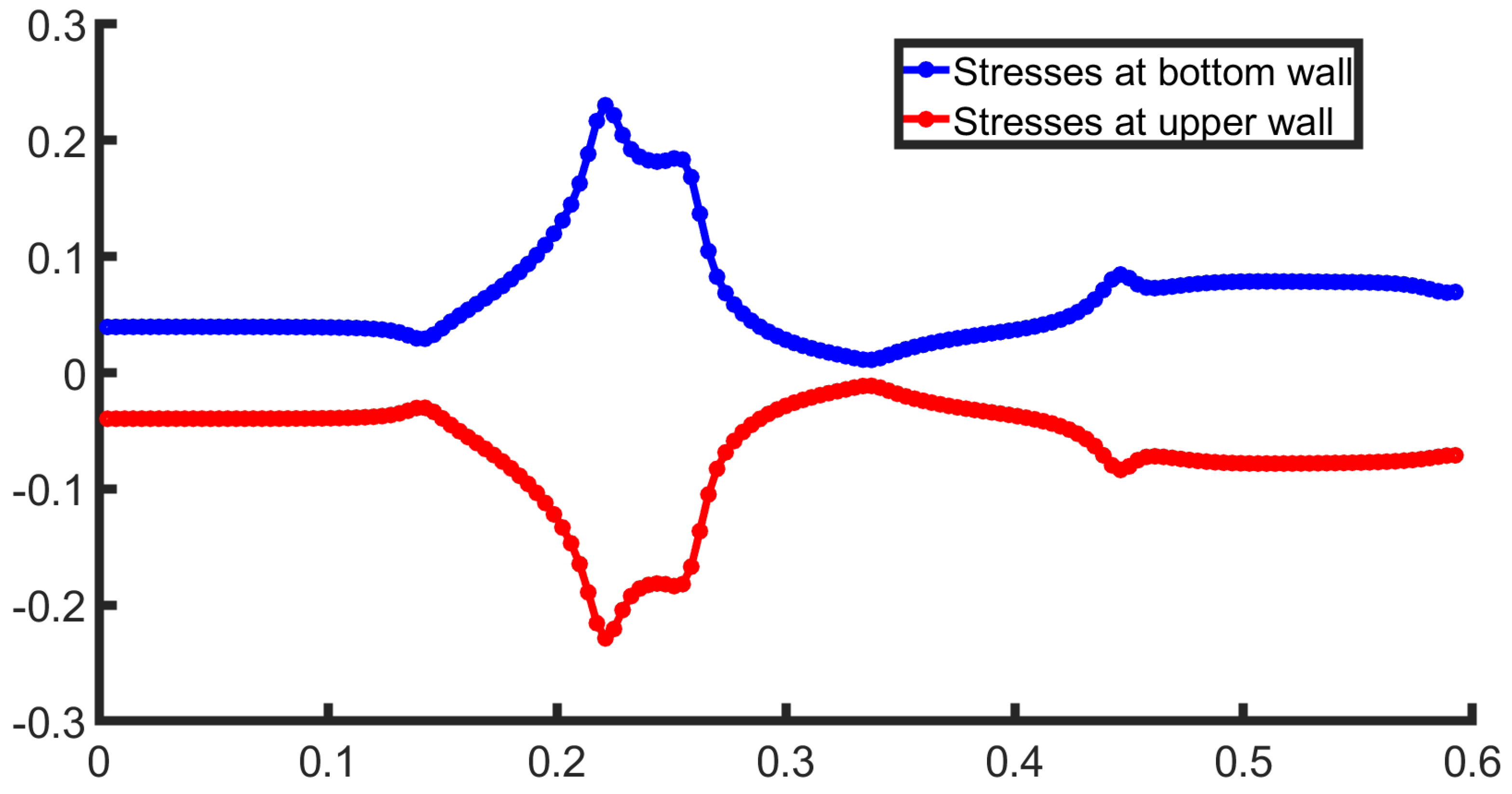
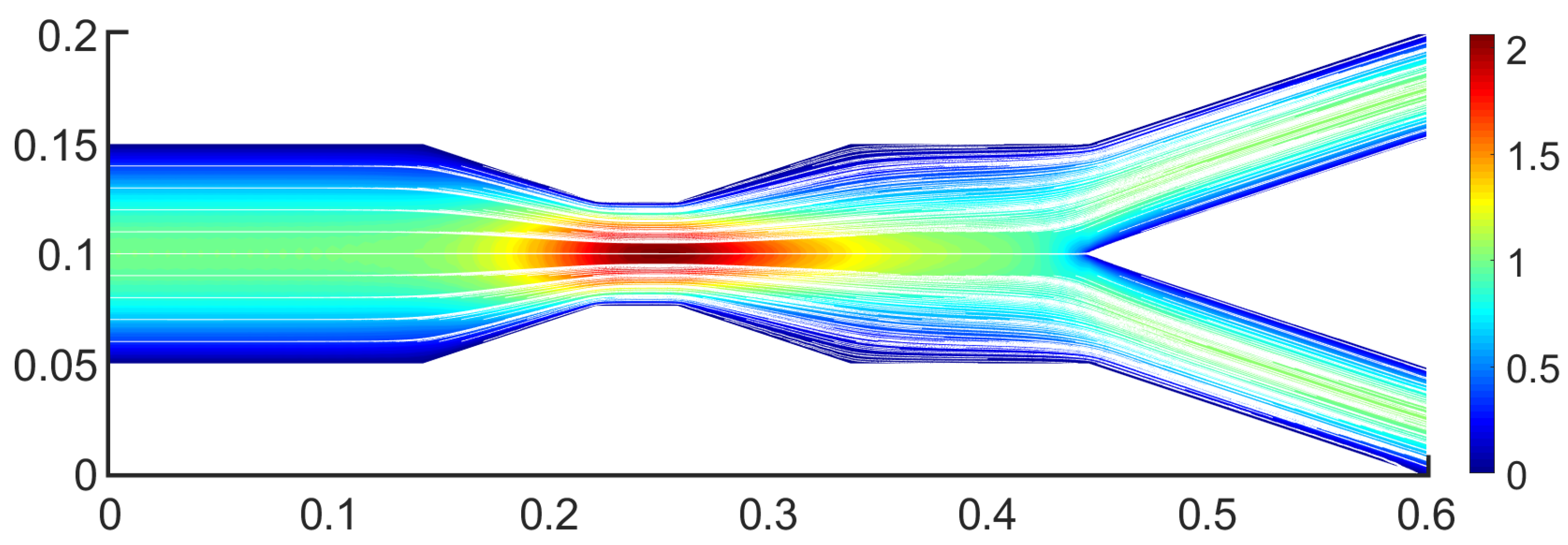
3.1. Two-Dimensional Bifurcation Results
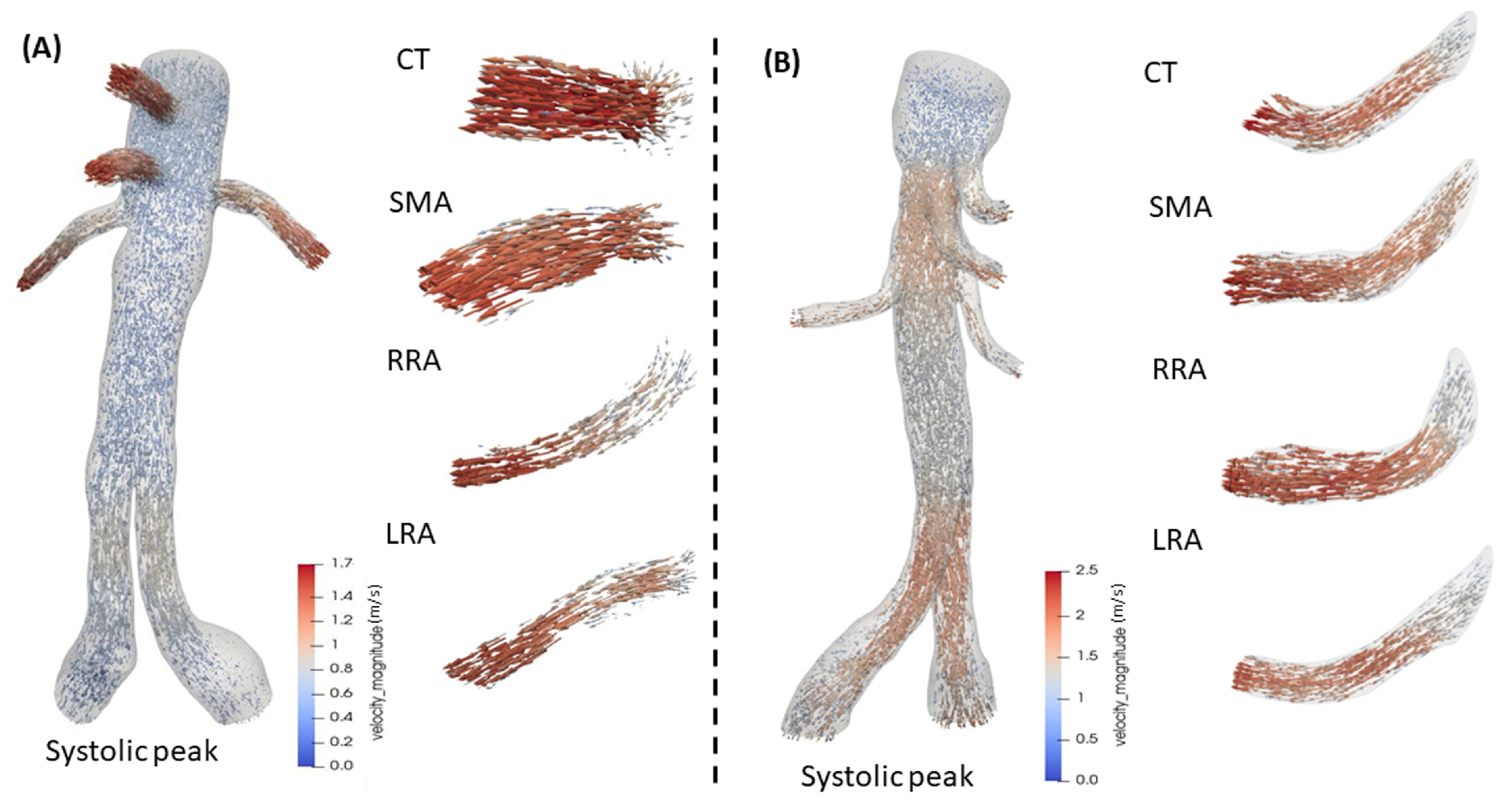
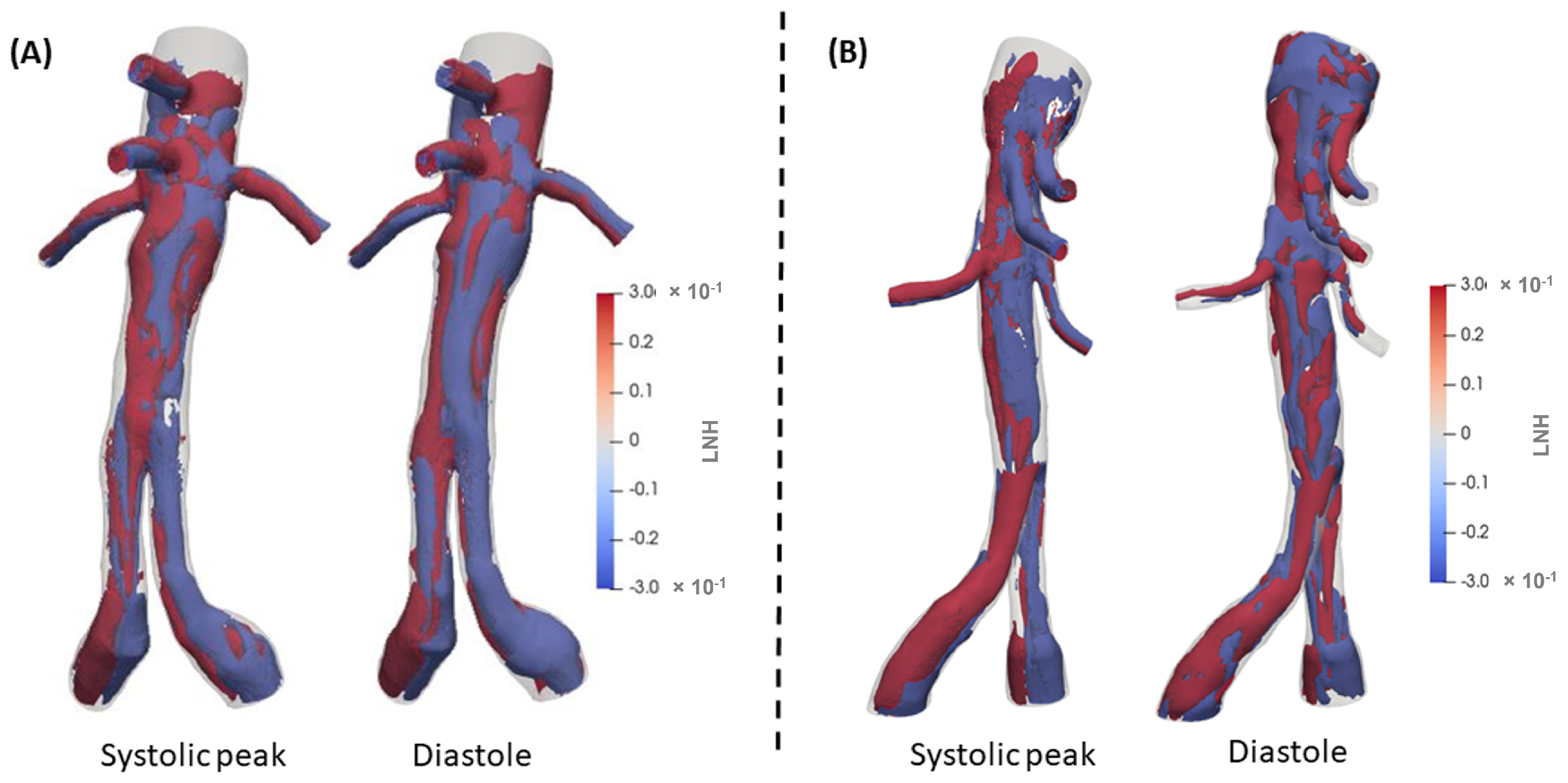
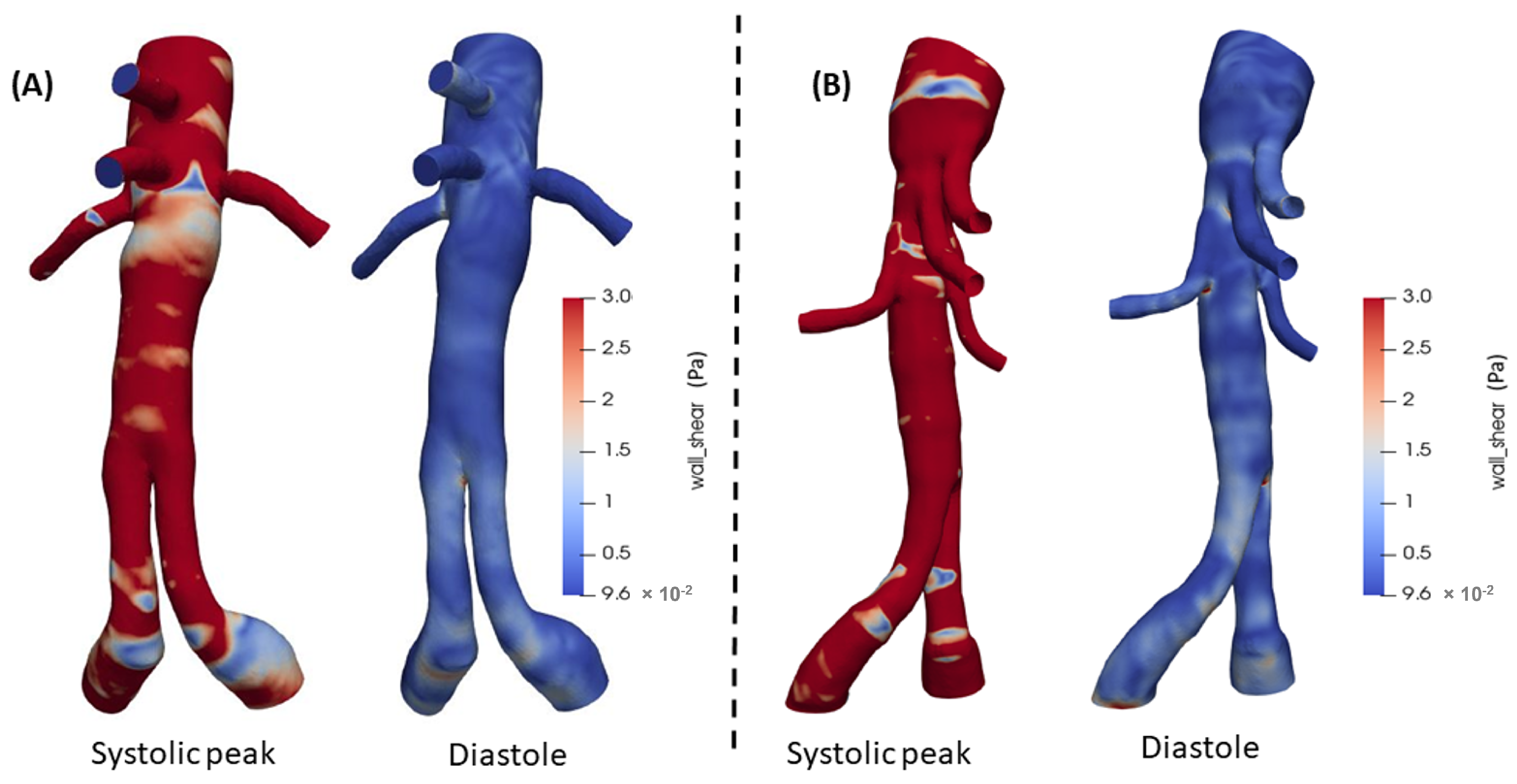
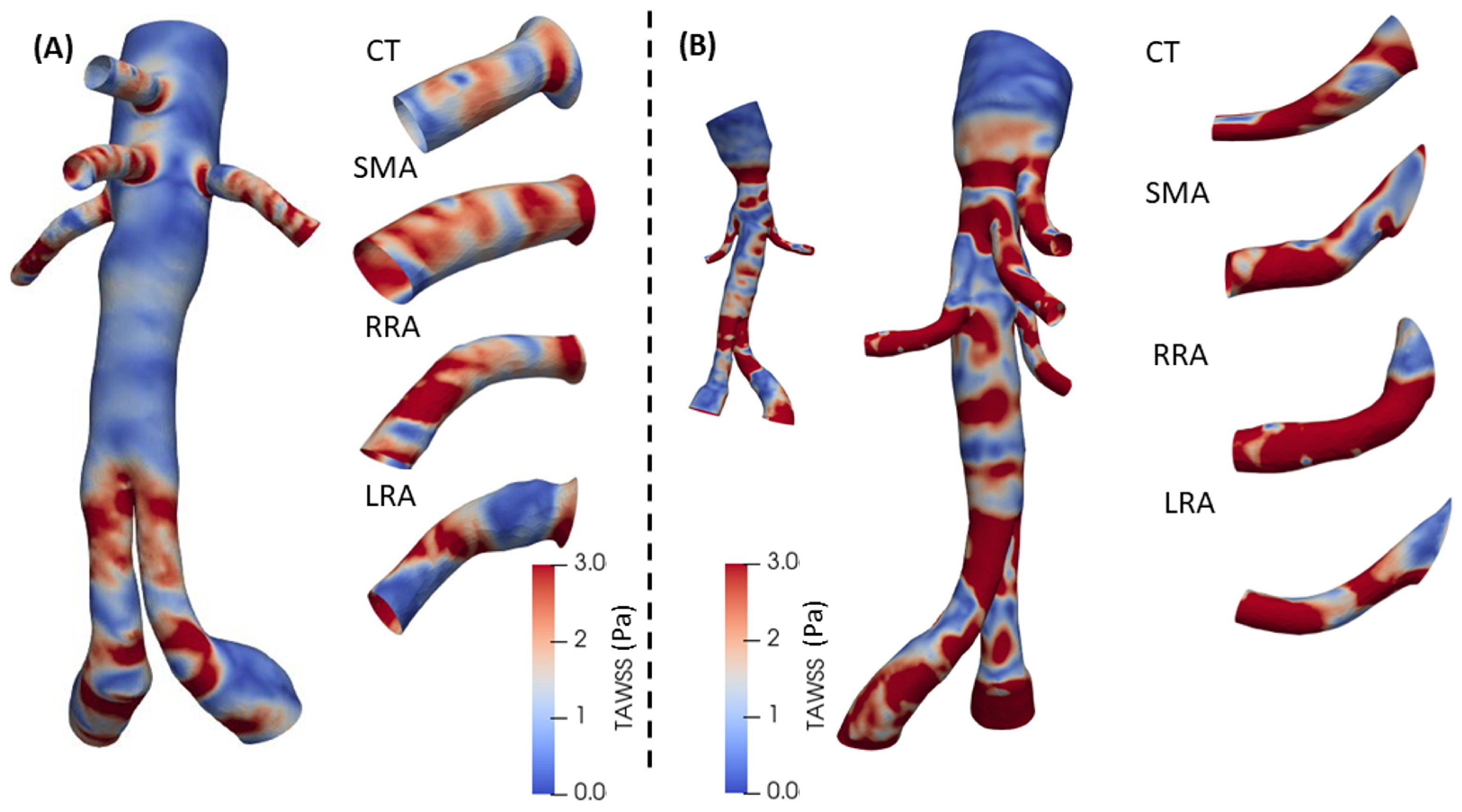
3.2. 3D Multiscale Patient-Specific Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pedley, T.J.; Schroter, R.C.; Sudlow, M.F. Flow and Pressure Drop in Systems of Repeatedly Branching Tubes. J. Fluid Mech. 1971, 46, 365–383. [Google Scholar] [CrossRef]
- Pradhan, K.; Guha, A. Fluid Dynamics of a Bifurcation. Int. J. Heat Fluid Flow 2019, 80, 108483. [Google Scholar] [CrossRef]
- De Wilde, D.; Trachet, B.; Debusschere, N.; Iannaccone, F.; Swillens, A.; Degroote, J.; Vierendeels, J.; De Meyer, G.R.Y.; Segers, P. Assessment of Shear Stress Related Parameters in the Carotid Bifurcation Using Mouse-Specific FSI Simulations. J. Biomech. 2016, 49, 2135–2142. [Google Scholar] [CrossRef] [PubMed]
- Lewandowska, N.; Micker, M.; Ciałkowski, M.; Warot, M.; Chęciński, M. Numerical Study of Carotid Bifurcation Angle Effect in Blood Flow Disorders. In New Developments on Computational Methods and Imaging in Biomechanics and Biomedical Engineering; Tavares, J.M.R.S., Fernandes, P.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Ahmed, H.; Podder, C. Hemodynamical Behavior Analysis of Anemic, Diabetic, and Healthy Blood Flow in the Carotid Artery. Heliyon 2024, 10, e26622. [Google Scholar] [CrossRef] [PubMed]
- García, J.; Manuel, F.; Doce, Y.; Castro, F.; Fernández, J.A. Pulsatile Flow in Coronary Bifurcations for Different Stenting Techniques. In Proceedings of the 10th World Congress on Computational Mechanics, São Paulo, Brazil, 8–13 July 2012; pp. 1382–1394. [Google Scholar] [CrossRef][Green Version]
- Younis, H.F.; Kaazempur-Mofrad, M.R.; Chan, R.C.; Isasi, A.G.; Hinton, D.P.; Chau, A.H.; Kim, L.A.; Kamm, R.D. Hemodynamics and Wall Mechanics in Human Carotid Bifurcation and its Consequences for Atherogenesis: Investigation of Inter-Individual Variation. Biomech. Model. Mechanobiol. 2004, 3, 17–32. [Google Scholar] [CrossRef]
- Guha, A.; Pradhan, K. Secondary motion in 3D branching networks. Phys. Fluids 2017, 29, 063602. [Google Scholar] [CrossRef]
- Wilquem, F.; Degrez, G. Numerical Modeling of Steady Inspiratory Airflow Through a Three-Generation Model of the Human Central Airways. J. Biomech. Eng. 1997, 119, 59–65. [Google Scholar] [CrossRef]
- Comer, J.K.; Kleinstreuer, C.; Kim, C.S. Flow Structures and Particle Deposition Patterns in Double-Bifurcation Airway Models. Part 2. Aerosol Transport and Aeposition. J. Fluid Mech. 2001, 435, 55–80. [Google Scholar] [CrossRef]
- Liu, Y.; So, R.M.C.; Zhang, C.H. Modeling the Bifurcating Flow in a Human Lung Airway. J. Biomech. 2002, 35, 465–473. [Google Scholar] [CrossRef]
- Fresconi, F.E.; Prasad, A.K. Secondary Velocity Fields in the Conducting Airways of the Human Lung. J. Biomech. Eng. 2007, 129, 722–732. [Google Scholar] [CrossRef]
- Malatos, S.; Fazzini, L.; Raptis, A.; Nana, P.; Kouvelos, G.; Tasso, P.; Gallo, D.; Morbiducci, U.; Xenos, M.A.; Giannoukas, A.; et al. Evaluation of Hemodynamic Properties After Chimney and Fenestrated Endovascular Aneurysm Repair. Ann. Vasc. Surg. 2024, 104, 237–247. [Google Scholar] [CrossRef] [PubMed]
- Tran, K.; Deslarzes-Dubuis, C.; DeGlise, S.; Kaladji, A.; Yang, W.; Marsden, A.L.; Lee, J.T. Patient-Specific Computational Flow Simulation Reveals Significant Differences in Paravisceral Aortic Hemodynamics between Fenestrated and Branched Endovascular Aneurysm Repair. JVS-Vasc. Sci. 2023, 5, 100183. [Google Scholar] [CrossRef] [PubMed]
- Malatos, S.; Raptis, A.; Xenos, M.A.; Kouvelos, G.; Giannoukas, A.; Verhoeven, E.L. A multiscale model for hemodynamic properties’ prediction after fenestrated endovascular aneurysm repair. A pilot study. Hell. Vasc. J. 2019, 1, 73–79. [Google Scholar]
- Kandail, H.S.; Hamady, M.; Xu, X.Y. Hemodynamic Functions of Fenestrated Stent Graft under Resting, Hypertension, and Exercise Conditions. Front. Surg. 2016, 3, 35. [Google Scholar] [CrossRef]
- Suess, T.; Anderson, J.; Danielson, L.; Pohlson, K.; Remund, T.; Blears, E.; Gent, S.; Kelly, P. Examination of near-wall hemodynamic parameters in the renal bridging stent of various stent graft configurations for repairing visceral branched aortic aneurysms. J. Vasc. Surg. 2015, 64, 788–796. [Google Scholar] [CrossRef] [PubMed]
- Ricotta, J.J.; Oderich, G.S. Fenestrated and branched stent grafts. Perspect. Vasc. Surg. Endovasc. Ther. 2008, 202, 174–187; discussion 188–189. [Google Scholar] [CrossRef]
- Verhoeven, E.L.; Vourliotakis, G.; Bos, W.T.; Tielliu, I.F.; Zeebregts, C.J.; Prins, T.R.; Bracale, U.M.; van den Dungen, J.J. Fenestrated stent grafting for short-necked and juxtarenal abdominal aortic aneurysm: An 8-year single-centre experience. Eur. J. Vasc. Endovasc. Surg. 2010, 39, 529–536. [Google Scholar] [CrossRef]
- Verhoeven, E.L.; Tielliu, I.F.; Bos, W.T.; Zeebregts, C.J. Present and future of branched stent grafts in thoraco-abdominal aortic aneurysm repair: A single-centre experience. Eur. J. Vasc. Endovasc. Surg. 2009, 38, 155–161. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Olufsen, M.S.; Peskin, C.S.; Kim, W.Y.; Pedersen, E.M.; Nadim, A.; Larsen, J. Numerical Simulation and Experimental Validation of Blood Flow in Arteries with Structured-Tree Outflow Conditions. Ann. Biomed. Eng. 2000, 28, 1281–1299. [Google Scholar] [CrossRef]
- Stergiopulos, N.; Young, D.F.; Rogge, T.R. Computer Simulation of Arterial Flow with Applications to Arterial and Aortic Stenoses. J. Biomech. 1992, 25, 1477–1488. [Google Scholar] [CrossRef]
- Reymond, P.; Merenda, F.; Perren, F.; Rüfenacht, D.; Stergiopulos, N. Validation of a one-dimensional model of the systemic arterial tree. Am. J. Physiol. Heart Circ. Physiol. 2009, 297, H208–H222. [Google Scholar] [CrossRef] [PubMed]
- Morbiducci, U.; Ponzini, R.; Gallo, D.; Bignardi, C.; Rizzo, G. Inflow boundary conditions for image-based computational hemodynamics: Impact of idealized versus measured velocity profiles in the human aorta. J. Biomech. 2013, 46, 102–109. [Google Scholar] [CrossRef]
- Van de Vosse, F.N.; Stergiopulos, N. Pulse Wave Propagation in the Arterial Tree. Annu. Rev. Fluid Mech. 2011, 43, 467–499. [Google Scholar] [CrossRef]
- Morbiducci, U.; Ponzini, R.; Rizzo, G.; Cadioli, M.; Esposito, A.; De Cobelli, F.; Del Maschio, A.; Montevecchi, F.M.; Redaelli, A. In vivo quantification of helical blood flow in human aorta by time-resolved 3D cine phase contrast magnetic resonance imaging. Ann. Biomed. Eng. 2009, 37, 516–531. [Google Scholar] [CrossRef] [PubMed]
- Morbiducci, U.; Ponzini, R.; Grigioni, M.; Redaelli, A. Helical flow as fluid dynamic signature for atherogenesis risk in aortocoronary bypass. A numeric study. J. Biomech. 2007, 40, 519–534. [Google Scholar] [CrossRef]
- Gallo, D.; Steinman, D.A.; Bijari, P.B.; Morbiducci, U. Helical flow in carotid bifurcation as surrogate marker of exposure to disturbed shear. J. Biomech. 2012, 45, 2398–2404. [Google Scholar] [CrossRef] [PubMed]
- Gallo, D.; Bijari, P.B.; Morbiducci, U.; Qiao, Y.; Xie, Y.J.; Etesami, M.; Habets, D.; Lakatta, E.G.; Wasserman, B.A.; Steinman, D.A. Segment-specific associations between local hemodynamic and imaging markers of early atherosclerosis at the carotid artery: An in vivo human study. J. R. Soc. 2018, 15, 20180352. [Google Scholar] [CrossRef]
- Donas, K.P.; Torsello, G.B.; Piccoli, G.; Pitoulias, G.A.; Torsello, G.F.; Bisdas, T.; Austermann, M.; Gasparini, D. The PROTAGORAS study to evaluate the performance of the Endurant stent graft for patients with pararenal pathologic processes treated by the chimney/snorkel endovascular technique. J. Vasc. Surg. 2016, 63, 1–7. [Google Scholar] [CrossRef]
- Ullery, B.W.; Tran, K.; Itoga, N.K.; Dalman, R.L.; Lee, J.T. Natural history of gutter-related type Ia endoleaks after snorkel/chimney endovascular aneurysm repair. J. Vasc. Surg. 2017, 65, 981–990. [Google Scholar] [CrossRef]
- Raptis, A.; Xenos, M.; Georgakarakos, E.; Kouvelos, G.; Giannoukas, A.; Labropoulos, N.; Matsagkas, M. Comparison of physiological and post-endovascular aneurysm repair infrarenal blood flow. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 242–249. [Google Scholar] [CrossRef]
- Chrimatopoulos, G.; Tzirtzilakis, E.E.; Xenos, M.A. Magnetohydrodynamic and Ferrohydrodynamic Fluid Flow Using the Finite Volume Method. Fluids 2023, 9, 5. [Google Scholar] [CrossRef]
- Tasso, P.; Raptis, A.; Matsagkas, M.; Rizzini, M.L.; Gallo, D.; Xenos, M.; Morbiducci, U. Abdominal Aortic Aneurysm Endovascular Repair: Profiling Postimplantation Morphometry and Hemodynamics With Image-Based Computational Fluid Dynamics. J. Biomech. Eng. 2018, 140, 111003. [Google Scholar] [CrossRef] [PubMed]

| FEVAR | BEVAR | FEVAR | BEVAR | FEVAR | BEVAR | |
|---|---|---|---|---|---|---|
| SMA | SMA | RRA | RRA | LRA | LRA | |
| TAWSS-Mean (Pa) | ||||||
| Patient 1 | 2.0107 | 3.3955 | 1.8828 | 4.5400 | 1.7417 | 2.8088 |
| Patient 2 | 2.4245 | 2.5005 | 2.7188 | 3.0423 | 2.8505 | 2.2069 |
| Patient 3 | 2.6683 | 3.0862 | 2.3013 | 3.8802 | 2.0257 | 2.1344 |
| Average | 2.3668 | 2.9941 | 2.3019 | 3.9660 | 2.2059 | 2.3831 |
| Flow Rate-Mean (mL/s) | ||||||
| Patient 1 | 1.20 | 1.89 | 7.77 | 8.79 | 4.91 | 7.35 |
| Patient 2 | 4.53 | 5.57 | 5.77 | 6.88 | 4.76 | 4.14 |
| Patient 3 | 6.20 | 7.68 | 5.15 | 6.44 | 3.48 | 5.27 |
| Average | 2.82 | 1.08 | 6.23 | 7.44 | 6.27 | 6.27 |
| Pressure-MAP (Pa) | ||||||
| Patient 1 | 12,448.00 | 13,042.20 | 12,458.97 | 12,881.43 | 12,125.09 | 12,397.97 |
| Patient 2 | 12,447.69 | 12,829.75 | 12,247.65 | 12,691.85 | 12,436.33 | 12,652.13 |
| Patient 3 | 12,446.99 | 12,390.30 | 12,275.51 | 12,198.13 | 12,907.63 | 12,758.13 |
| Average | 12,447.89 | 12,754.75 | 12,327.38 | 12,590.47 | 12,489.68 | 12,569.74 |
| WSS, peak systole (Pa) | ||||||
| Patient 1 | 15.7564 | 22.3136 | 15.1828 | 22.8823 | 13.0550 | 29.2930 |
| Patient 2 | 20.5820 | 23.3455 | 17.4531 | 16.1189 | 19.5660 | 19.9550 |
| Patient 3 | 23.3368 | 19.7350 | 18.6989 | 14.9496 | 25.6950 | 26.6720 |
| Average | 19.2211 | 23.3953 | 17.1111 | 18.9836 | 19.1054 | 24.0419 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katsoudas, S.; Malatos, S.; Raptis, A.; Matsagkas, M.; Giannoukas, A.; Xenos, M. Blood Flow Simulation in Bifurcating Arteries: A Multiscale Approach After Fenestrated and Branched Endovascular Aneurysm Repair. Mathematics 2025, 13, 1362. https://doi.org/10.3390/math13091362
Katsoudas S, Malatos S, Raptis A, Matsagkas M, Giannoukas A, Xenos M. Blood Flow Simulation in Bifurcating Arteries: A Multiscale Approach After Fenestrated and Branched Endovascular Aneurysm Repair. Mathematics. 2025; 13(9):1362. https://doi.org/10.3390/math13091362
Chicago/Turabian StyleKatsoudas, Spyridon, Stavros Malatos, Anastasios Raptis, Miltiadis Matsagkas, Athanasios Giannoukas, and Michalis Xenos. 2025. "Blood Flow Simulation in Bifurcating Arteries: A Multiscale Approach After Fenestrated and Branched Endovascular Aneurysm Repair" Mathematics 13, no. 9: 1362. https://doi.org/10.3390/math13091362
APA StyleKatsoudas, S., Malatos, S., Raptis, A., Matsagkas, M., Giannoukas, A., & Xenos, M. (2025). Blood Flow Simulation in Bifurcating Arteries: A Multiscale Approach After Fenestrated and Branched Endovascular Aneurysm Repair. Mathematics, 13(9), 1362. https://doi.org/10.3390/math13091362







