Reinforcement Learning for Mitigating Malware Propagation in Wireless Radar Sensor Networks with Channel Modeling
Abstract
1. Introduction
- 1.
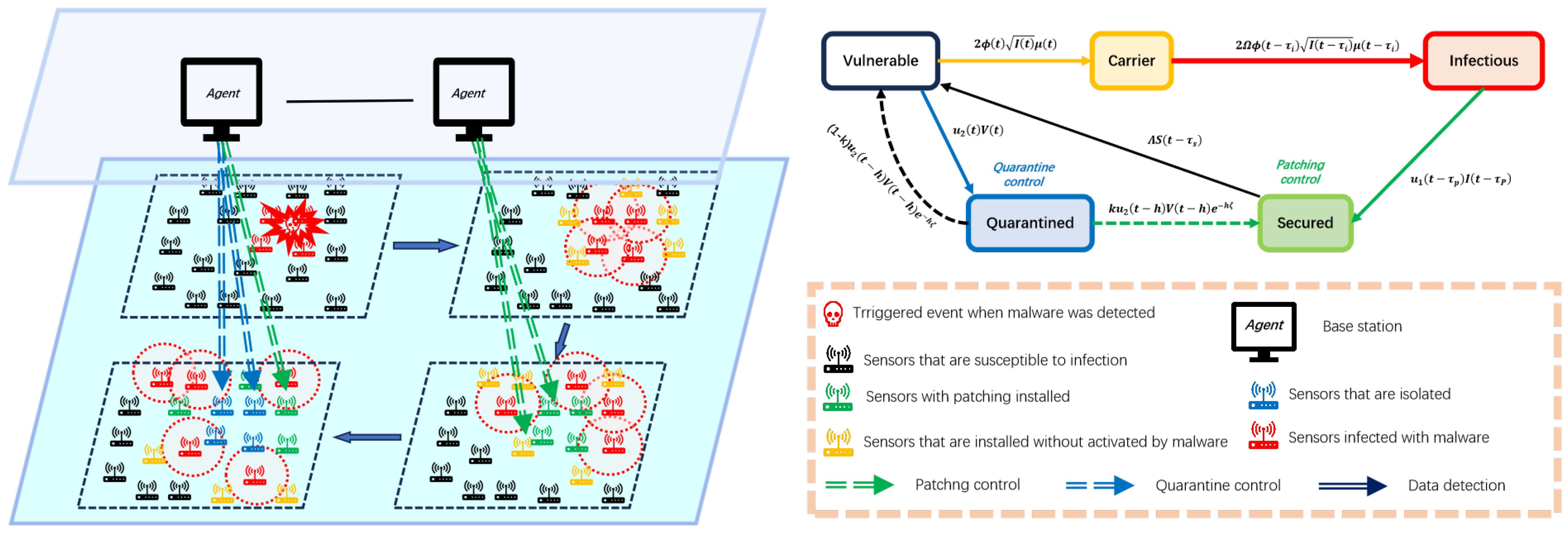
- A malware propagation model VCISQ is proposed, which incorporates Rayleigh fading, node density, and time delay to model malware propagation in WRSNs. Compared to other existing epidemic models, VCISQ accounts for additional critical factors influencing malware spread in WRSNs. This has to some extent improved the accuracy of depicting real scenes in WRSNs. To effectively combat malware propagation, hybrid patching and quarantine strategies are introduced. At the same time, the optimal control method under these strategies is derived. The optimal control outputs help preserve network integrity by protecting data transmission against malware interference, thereby enhancing the performance of WRSNs. Furthermore, the optimal control method provides a theoretical benchmark solution for static propagation models, offering a reference baseline for evaluating the performance of RL methods.
- 2.
- To achieve more practical and adaptive control schemes that can boost the performance of WRSNs, two novel model-free RL algorithms, PPO and MAPPO, are introduced for the first time to suppress malware propagation in WRSNs. PPO employs a clipping parameter to limit policy updates, minimizing the risks associated with sub-optimal control decisions. This not only enhances the efficiency of malware suppression but also improves the adaptability of the network to dynamic changes in the environment. In WRSNs, such adaptability is crucial for maintaining high-performance operation as environmental factors can vary rapidly. On the other hand, MAPPO leverages a Centralized Training, Decentralized Execution (CTDE) framework. This framework allows for more efficient learning and decision-making across multiple agents in the WRSN. As a result, it can better coordinate the actions of different nodes in the network, leading to more effective suppression of malware and ultimately enhancing the overall performance of WRSNs.
- 3.
- To validate the effectiveness of the proposed model and its associated control strategies in improving WRSN performance, this study compares the performance differences between the optimal control and RL algorithms under various scenarios. The experimental results indicate that both PPO and MAPPO algorithms demonstrate excellent adaptability when facing changes in environmental parameters. In WRSNs, environmental parameter changes can cause significant performance fluctuations. The ability of PPO and MAPPO to adapt well means that they can maintain stable and high-performance operation. Compared to traditional control strategies such as Deep Q-Network (DQN) [19] and Double Deep Q-Network (DDQN) [20], PPO and MAPPO are able to more precisely regulate information propagation. This precise regulation ensures that data are transmitted in an optimal manner, reducing the negative impact of malicious programs on network performance. As a result, WRSNs equipped with these algorithms can operate more efficiently and with higher reliability, thus significantly enhancing the overall performance of WRSNs.
2. Related Work
3. Model Establishment and Optimal Control Problem
3.1. The Number of Susceptible Neighboring Nodes with Rayleigh Fading
3.2. Contact Rate Between Neighboring Nodes
3.3. Malware Propagation Model
3.4. Optimal Control Problem
- (1)
- The adjoint equations are described aswhere is state nodes of the system (3), and is a characteristic function. More precisely, if and zero otherwise.
- (2)
- The boundary condition is given bywhere is a characteristic function.
- (3)
- The optimal control satisfies
4. Algorithm Implementation
4.1. PPO
4.1.1. Data Collecting
4.1.2. Training of Neural Networks
4.2. MAPPO
| Algorithm 1 MAPPO for WRSNs | |
| 1: | Initialize agents number M, Action (1, …, M) ∈ (0,1), episode length T, maximum training episodes L |
| 2: | Initialize each policy network and value network , memory buffer D, Set learning rate |
| 3: | for episode = 1, 2, …, L do |
| 4: | for t = 1, 2, …, T do |
| 5: | for u = 1, 2, …, M do |
| 6: | Agent u executes according to ; |
| 7: | Get the reward , and the next state ; |
| 8: | Store into D; |
| 9: | end for |
| 10: | end for |
| 11: | Get from D; |
| 12: | Compute ; |
| 13: | Compute advantages according to Equation (23); |
| 14: | Store data , into D; |
| 15: | for epoch = 1, 2, …, W do |
| 16: | Shuffle and renumber the data’s order; |
| 17: | for u = 1, 2, …, M do |
| 18: | for i = 0, 1, 2, …, T/B-1 do |
| 19: | Select B group of data ; |
| 20: | = |
| 21: | |
| 22: | Compute gradient according to Equation (25); |
| 23: | Compute gradient according to Equation (26); |
| 24: | Update agent u actor networks; |
| 25: | Update agent u critic networks; |
| 26: | end for |
| 27: | end for |
| 28: | end for |
| 29: | Empty memory buffer D for MAPPO |
| 30: | end for |
- (1)
- Decentralized execution (lines 4–10): In the process of decentralized execution, each agent and the environment execute forward propagation independently. At the current step size, each agent selects the optimal action based on the state values of each node and the current policy (line 6). It interacts with the corresponding environment to obtain the reward and the next state in the environment (line 7), and stores the current , , , in the data buffer (line 8). During this process, each agent is unaware of the information of other agents.
- (2)
- Centralized training process (lines 15–28): The policy network and the value network are optimized W times according to their respective loss functions and . To break the correlation between the data samples, the data samples are randomly shuffled and renumbered (line 16). Then, a small batch of data is sampled from the memory buffer D (lines 19–20). The policy network and the value network have the same structure and both use the Adam optimizer for gradient updates.
4.3. Complexity Analysis
5. Simulation Experiments
- 1.
- Impact of Removing Time Delay: We investigate the influence of time delay on system dynamics and control strategy (Theorem 2) performance, analyzing its sensitivity to model stability and control effectiveness.
- 2.
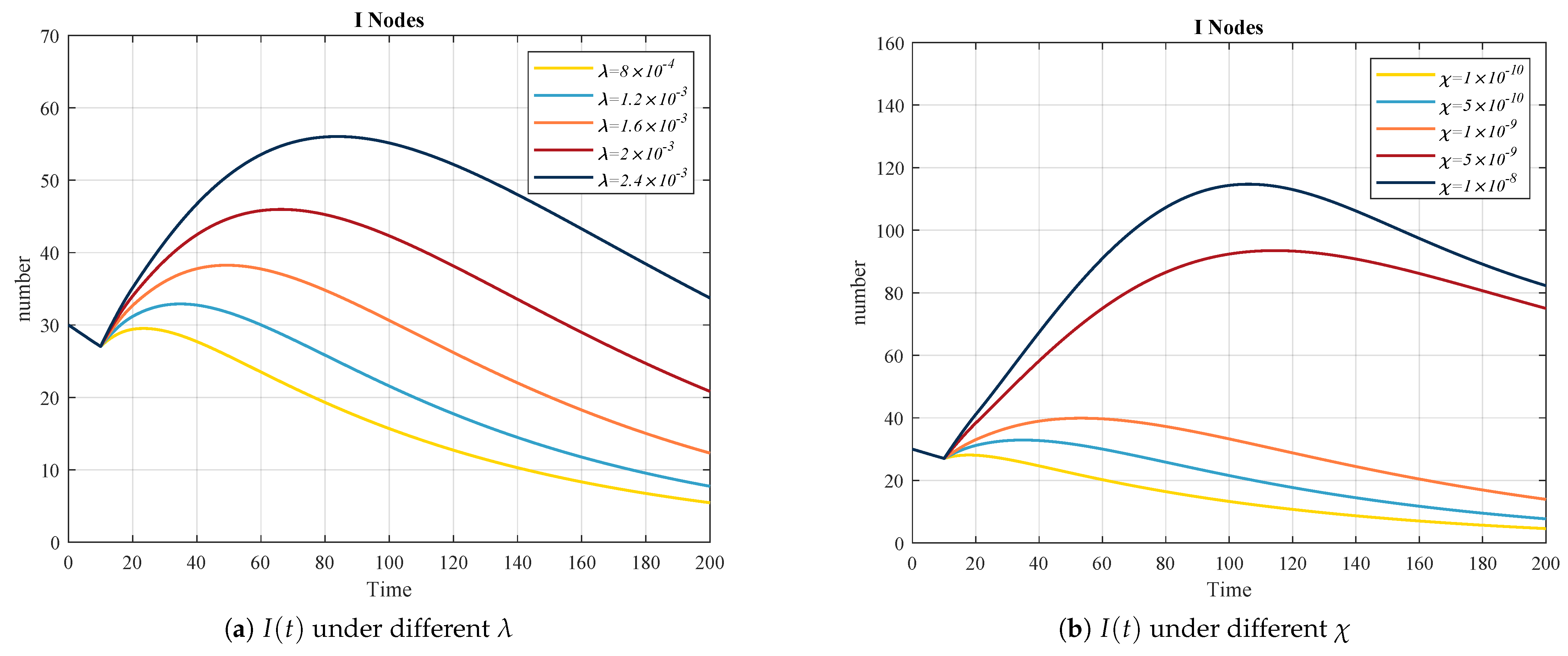
- Analysis of Node Density and Transmit Power Coefficient Impact on Epidemic Propagation Dynamics: The influence of different node density and transmit power coefficient on the VCISQ mathematical model are analyzed under constant control variables ( and ). Specifically, the changes in infected node I under different values of and are analyzed. This comparative experiment is added to demonstrate the rationality and effectiveness of the mathematical model.
- 3.
- Comparison of Costs Under Different Control Strategies: By comparing the performance of the hybrid control strategy (Theorem 2) with two single-control strategies (patching-only control in Theorem 3 and quarantine-only control in Theorem 4), we demonstrate the superiority of hybrid control in suppressing malware propagation and minimizing control costs.
- 4.
- Stability Analysis: We validate the stability and robustness of the model (Figure 1) under different parameter conditions by adjusting two key parameters (the density of total nodes and transmit power coefficient ).
- 5.
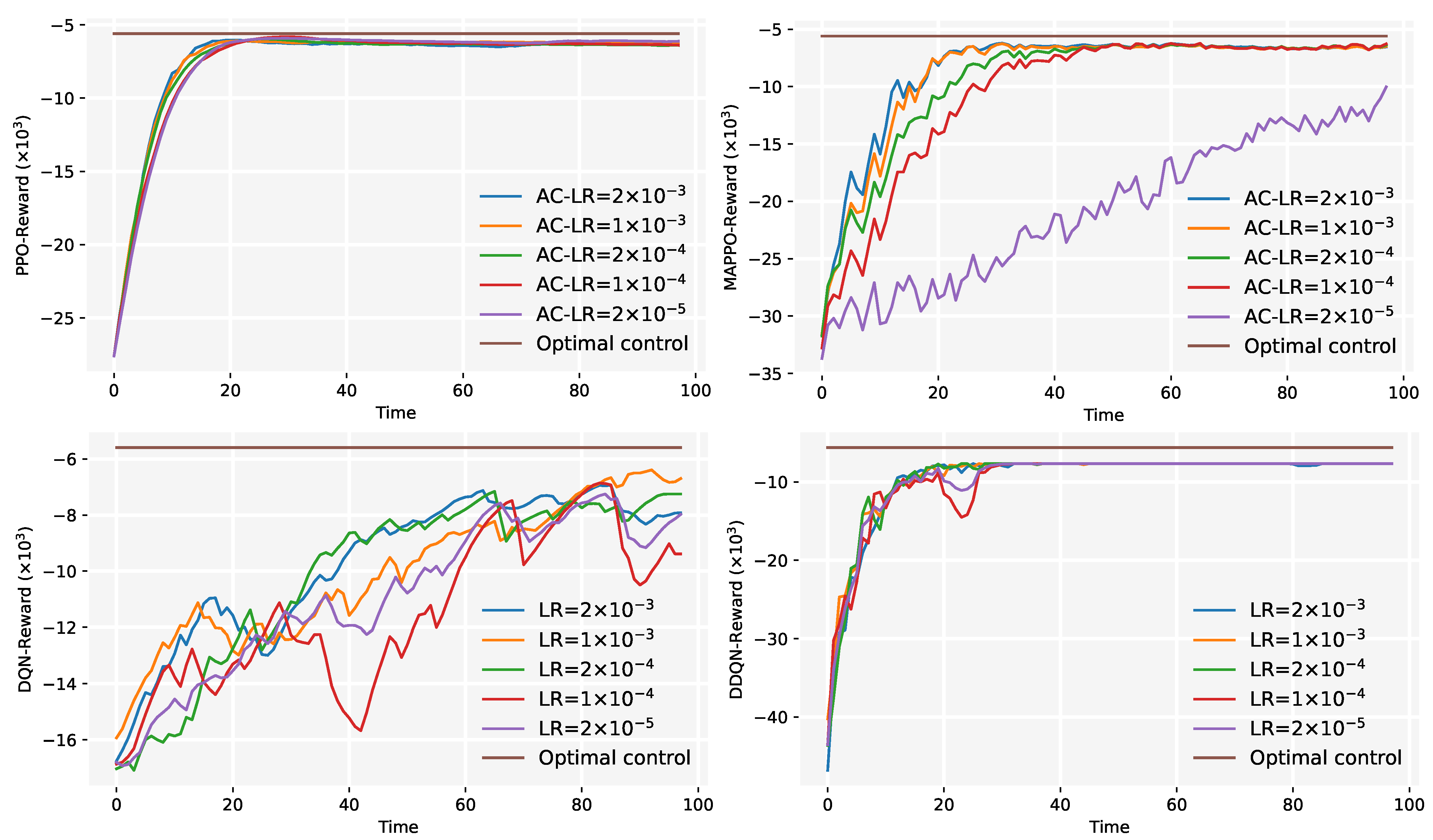
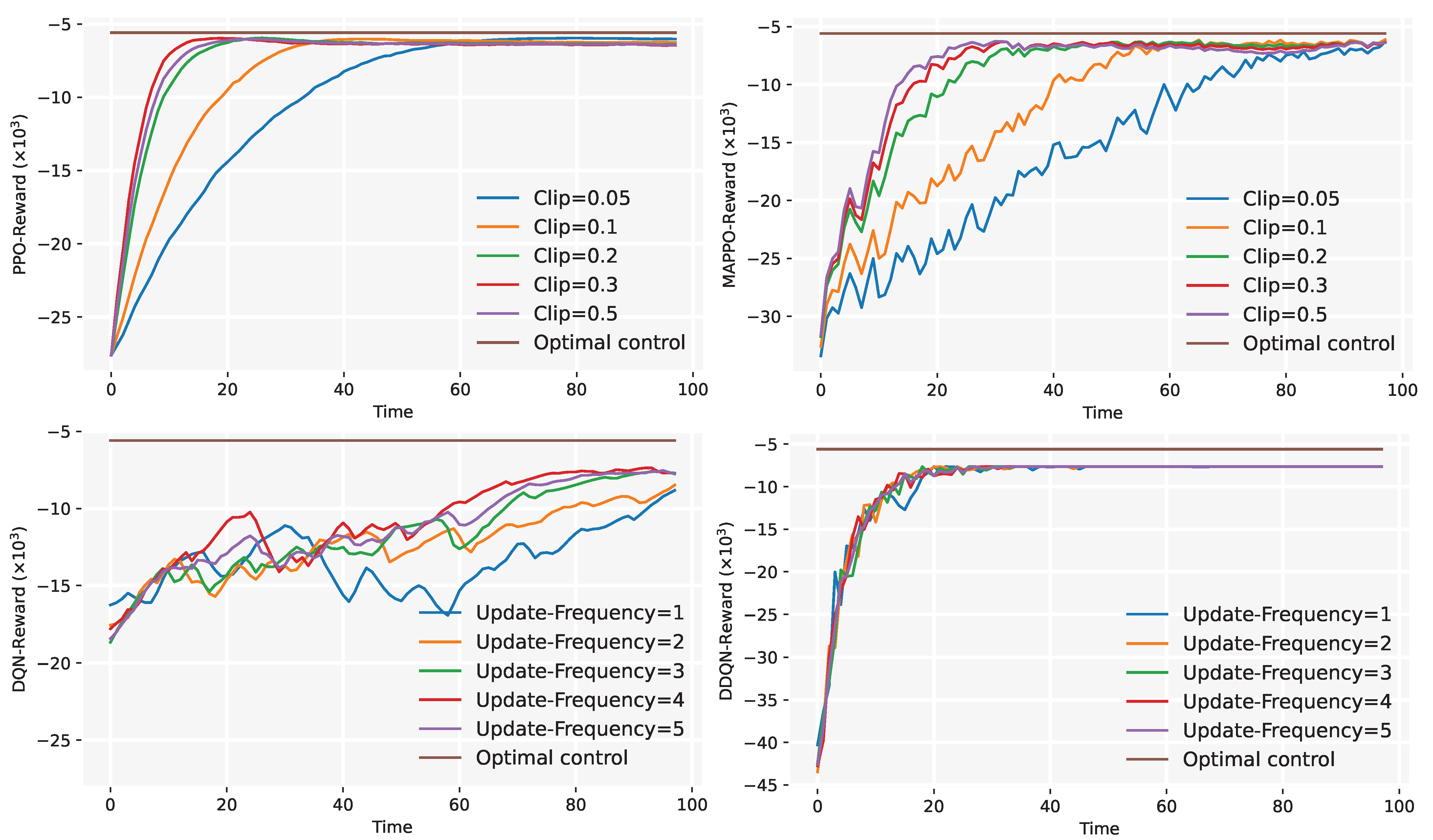
- Convergence Experiment: We analyze the convergence performance of PPO (Section 4.1) and MAPPO (Section 4.2) by varying algorithm hyperparameters, optimizing algorithm configurations to improve training efficiency.
- 6.
- Comparison Of Various Algorithms: We verify the significant advantages of PPO (Section 4.1) and MAPPO (Section 4.2) in control accuracy, learning capability, and adaptability by comparing traditional RL algorithms with optimal control in terms of cost.
5.1. Impact of Removing Time Delay
5.2. Analysis of Node Density and Transmit Power Coefficient Impact on Epidemic Propagation Dynamics
5.3. Comparison of Costs Under Different Control Strategies
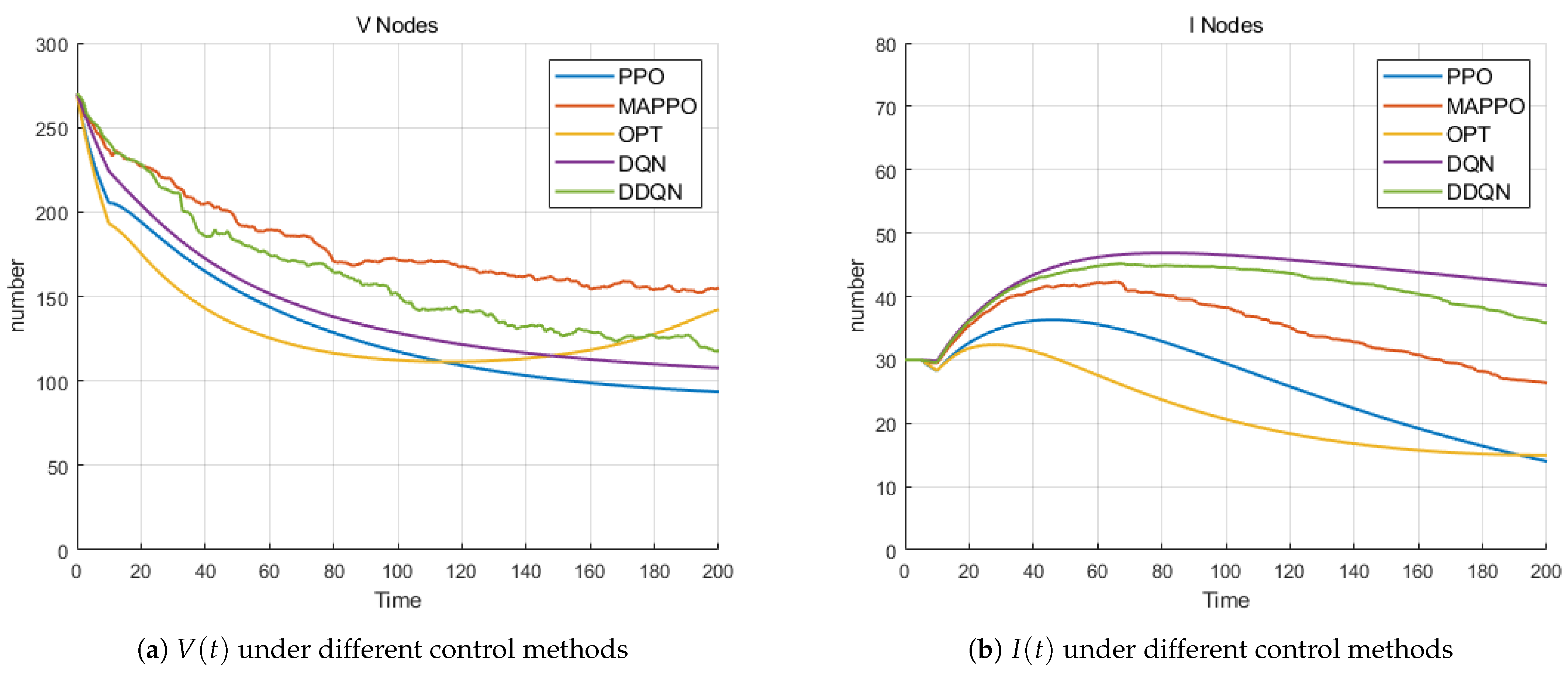
5.4. Stability Analysis
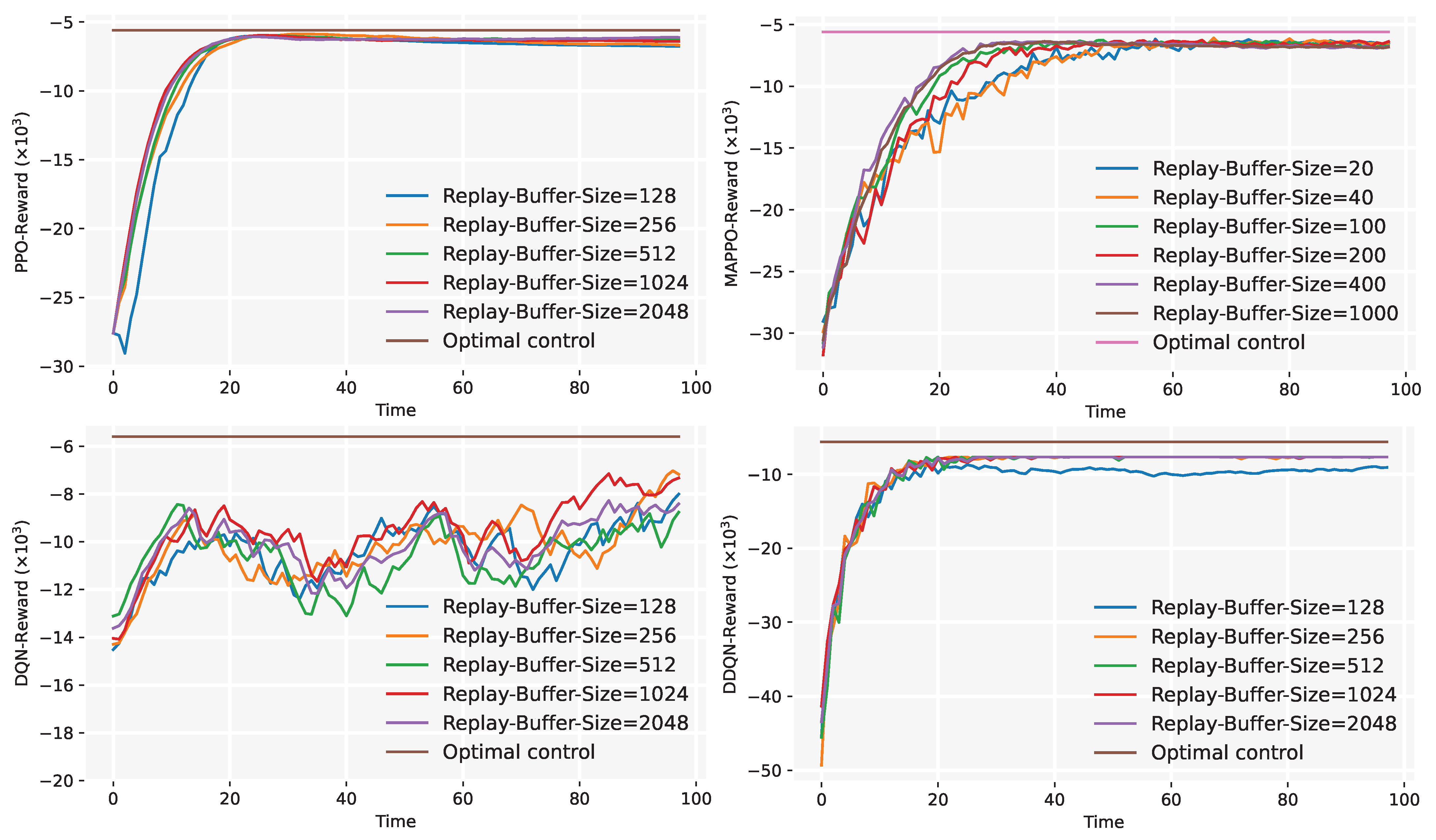
5.5. Convergence Experiment
5.6. Comparison of Various Algorithms
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akan, O.B.; Arik, M. Internet of Radars: Sensing versus Sending with Joint Radar-Communications. IEEE Commun. Mag. 2020, 58, 13–19. [Google Scholar] [CrossRef]
- Luo, F.; Bodanese, E.; Khan, S.; Wu, K. Spectro-Temporal Modeling for Human Activity Recognition Using a Radar Sensor Network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5103913. [Google Scholar] [CrossRef]
- Bartoletti, S.; Conti, A.; Giorgetti, A.; Win, M.Z. Sensor radar networks for indoor tracking. IEEE Wirel. Commun. Lett. 2014, 3, 157–160. [Google Scholar]
- Gulmezoglu, B.; Guldogan, M.B.; Gezici, S. Multiperson tracking with a network of ultrawideband radar sensors based on Gaussian mixture PHD filters. IEEE Sens. J. 2014, 15, 2227–2237. [Google Scholar] [CrossRef]
- Peng, H.; Wang, Y.; Chen, Z.; Lv, Z. Dynamic sensor speed measurement algorithm and influencing factors of traffic safety with wireless sensor network nodes and RFID. IEEE Sens. J. 2020, 21, 15679–15686. [Google Scholar] [CrossRef]
- Primeau, N.; Falcon, R.; Abielmona, R.; Petriu, E.M. A review of computational intelligence techniques in wireless sensor and actuator networks. IEEE Commun. Surv. Tutor. 2018, 20, 2822–2854. [Google Scholar] [CrossRef]
- Haghighi, M.S.; Wen, S.; Xiang, Y.; Quinn, B.; Zhou, W. On the race of worms and patches: Modeling the spread of information in wireless sensor networks. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2854–2865. [Google Scholar] [CrossRef]
- Liu, G.; Peng, Z.; Liang, Z.; Zhong, X.; Xia, X. Analysis and Control of Malware Mutation Model in Wireless Rechargeable Sensor Network with Charging Delay. Mathematics 2022, 10, 2376. [Google Scholar] [CrossRef]
- Liu, G.; Chen, J.; Liang, Z.; Peng, Z.; Li, J. Dynamical Analysis and Optimal Control for a SEIR Model Based on Virus Mutation in WSNs. Mathematics 2021, 9, 929. [Google Scholar] [CrossRef]
- Nwokoye, C.H.; Madhusudanan, V. Epidemic models of malicious-code propagation and control in wireless sensor networks: An indepth review. Wirel. Pers. Commun. 2022, 125, 1827–1856. [Google Scholar] [CrossRef]
- Peng, S.C. A survey on malware containment models in smartphones. Appl. Mech. Mater. 2013, 263, 3005–3011. [Google Scholar] [CrossRef]
- Guillén, J.H.; del Rey, A.M. A mathematical model for malware spread on WSNs with population dynamics. Phys. A Stat. Mech. Its Appl. 2020, 545, 123609. [Google Scholar] [CrossRef]
- Shen, S.; Li, H.; Han, R.; Vasilakos, A.V.; Wang, Y.; Cao, Q. Differential game-based strategies for preventing malware propagation in wireless sensor networks. IEEE Trans. Inf. Forensics Secur. 2014, 9, 1962–1973. [Google Scholar] [CrossRef]
- Bai, L.; Liu, J.; Han, R.; Zhang, W. Wireless radar sensor networks: Epidemiological modeling and optimization. IEEE J. Sel. Areas Commun. 2022, 40, 1993–2005. [Google Scholar] [CrossRef]
- Liu, X.; Yang, L. Stability analysis of an SEIQV epidemic model with saturated incidence rate. Nonlinear Anal. Real World Appl. 2012, 13, 2671–2679. [Google Scholar] [CrossRef]
- Sun, A.; Sun, C.; Du, J.; Wei, D. Optimizing Energy Efficiency in UAV-Assisted Wireless Sensor Networks with Reinforcement Learning PPO2 Algorithm. IEEE Sens. J. 2023, 23, 29705–29721. [Google Scholar] [CrossRef]
- Kuai, Z.; Wang, T.; Wang, S. Fair virtual network function mapping and scheduling using proximal policy optimization. IEEE Trans. Commun. 2022, 70, 7434–7445. [Google Scholar] [CrossRef]
- Xiao, J.; Chen, Z.; Sun, X.; Zhan, W.; Wang, X.; Chen, X. Online Multi-Agent Reinforcement Learning for Multiple Access in Wireless Networks. IEEE Commun. Lett. 2023, 27, 3250–3254. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Z.; Li, W.; Wang, Y.; Li, Y.; Sauer, D.U. Battery Thermal- and Health-Constrained Energy Management for Hybrid Electric Bus Based on Soft Actor-Critic DRL Algorithm. IEEE Trans. Ind. Inform. 2021, 17, 3751–3761. [Google Scholar] [CrossRef]
- Rakelly, K.; Zhou, A.; Finn, C.; Levine, S.; Quillen, D. Efficient off-policy meta-reinforcement learning via probabilistic context variables. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 5331–5340. [Google Scholar]
- Xiao, X.; Fu, P.; Dou, C.; Li, Q.; Hu, G.; Xia, S. Design and analysis of SEIQR worm propagation model in mobile internet. Commun. Nonlinear Sci. Numer. Simul. 2017, 43, 341–350. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, J.; Zhong, X.; Hu, X.; Liang, Z. Hybrid optimal control for malware propagation in UAV-WSN system: A stacking ensemble learning control algorithm. IEEE Internet Things J. 2024, 11, 36549–36568. [Google Scholar] [CrossRef]
- Keshri, N.; Mishra, B.K. Two time-delay dynamic model on the transmission of malicious signals in wireless sensor network. Chaos Solitons Fractals 2014, 68, 151–158. [Google Scholar] [CrossRef]
- Zhuang, Q.; Xiao, M.; Ding, J.; Yang, Q.; Cao, J.; Zheng, W.X. Spatiotemporal Evolution Control of Malicious Virus Propagation in Cyber Physical Systems Via PD Feedback Control. IEEE Trans. Control Netw. Syst. 2023, 11, 1562–1575. [Google Scholar] [CrossRef]
- Shen, S.; Xie, L.; Zhang, Y.; Wu, G.; Zhang, H.; Yu, S. Joint Differential Game and Double Deep Q-Networks for Suppressing Malware Spread in Industrial Internet of Things. IEEE Trans. Inf. Forensics Secur. 2023, 18, 5302–5315. [Google Scholar] [CrossRef]
- Zhong, X.; Yang, Y.; Deng, F.; Liu, G. Rumor Propagation Control With Anti-Rumor Mechanism and Intermittent Control Strategies. IEEE Trans. Comput. Soc. Syst. 2024, 11, 2397–2409. [Google Scholar] [CrossRef]
- Zhong, X.; Pang, B.; Deng, F.; Zhao, X. Hybrid stochastic control strategy by two-layer networks for dissipating urban traffic congestion. Sci. China Inf. Sci. 2024, 67, 140204. [Google Scholar] [CrossRef]
- Cui, S.; Dong, C.; Shen, M.; Liu, Y.; Jiang, B.; Lu, Z. CBSeq: A Channel-Level Behavior Sequence for Encrypted Malware Traffic Detection. IEEE Trans. Inf. Forensics Secur. 2023, 18, 5011–5025. [Google Scholar] [CrossRef]
- He, Y.; Kang, X.; Yan, Q.; Li, E. ResNeXt+: Attention Mechanisms Based on ResNeXt for Malware Detection and Classification. IEEE Trans. Inf. Forensics Secur. 2024, 19, 1142–1155. [Google Scholar] [CrossRef]
- Chen, X.; Hao, Z.; Li, L.; Cui, L.; Zhu, Y.; Ding, Z.; Liu, Y. CruParamer: Learning on Parameter-Augmented API Sequences for Malware Detection. IEEE Trans. Inf. Forensics Secur. 2022, 17, 788–803. [Google Scholar] [CrossRef]
- Tian, B.; Jiang, J.; He, Z.; Yuan, X.; Dong, L.; Sun, C. Functionality-Verification Attack Framework Based on Reinforcement Learning Against Static Malware Detectors. IEEE Trans. Inf. Forensics Secur. 2024, 19, 8500–8514. [Google Scholar] [CrossRef]
- Farooq, M.J.; Zhu, Q. Modeling, analysis, and mitigation of dynamic botnet formation in wireless IoT networks. IEEE Trans. Inf. Forensics Secur. 2019, 14, 2412–2426. [Google Scholar] [CrossRef]
- Gao, Q.; Zhuang, J. Stability analysis and control strategies for worm attack in mobile networks via a VEIQS propagation model. Appl. Math. Comput. 2020, 368, 124584. [Google Scholar] [CrossRef]
- Ding, L.; Hu, P.; Guan, Z.H.; Li, T. An efficient hybrid control strategy for restraining rumor spreading. IEEE Trans. Syst. Man, Cybern. Syst. 2020, 51, 6779–6791. [Google Scholar] [CrossRef]
- Liu, G.; Li, H.; Xiong, L.; Tan, Z.; Liang, Z.; Zhong, X. Fractional-Order Optimal Control and FIOV-MASAC Reinforcement Learning for Combating Malware Spread in Internet of Vehicles. IEEE Trans. Autom. Sci. Eng. 2025, 22, 10313–10332. [Google Scholar] [CrossRef]
- Gu, Y.; Guo, K.; Zhao, C.; Yu, X.; Guo, L. Fast Reactive Mechanism for Desired Trajectory Attacks on Unmanned Aerial Vehicles. IEEE Trans. Ind. Inform. 2023, 19, 8976–8984. [Google Scholar] [CrossRef]
- Han, S.; Zhao, H.; Li, X.; Yu, J.; Liu, Z.; Yan, L.; Zhang, T. Joint Multiple Resources Allocation for Underwater Acoustic Cooperative Communication in Time-Varying IoUT Systems: A Double Closed-Loop Adversarial Bandit Approach. IEEE Internet Things J. 2024, 11, 2573–2587. [Google Scholar] [CrossRef]
- Heidari, A.; Jamali, M.A.J. Internet of Things intrusion detection systems: A comprehensive review and future directions. Clust. Comput. 2023, 26, 3753–3780. [Google Scholar] [CrossRef]
- Chai, Y.; Wang, Y. Optimal Control of Information Diffusion in Temporal Networks. IEEE Trans. Netw. Serv. Manag. 2023, 20, 104–119. [Google Scholar] [CrossRef]
- Tayseer Jafar, M.; Yang, L.X.; Li, G.; Zhu, Q.; Gan, C. Minimizing Malware Propagation in Internet of Things Networks: An Optimal Control Using Feedback Loop Approach. IEEE Trans. Inf. Forensics Secur. 2024, 19, 9682–9697. [Google Scholar] [CrossRef]
- Liu, G.; Tan, Z.; Liang, Z.; Chen, H.; Zhong, X. Fractional Optimal Control for Malware Propagation in Internet of Underwater Things. IEEE Internet Things J. 2024, 11, 11632–11651. [Google Scholar] [CrossRef]
- Shen, S.; Cai, C.; Shen, Y.; Wu, X.; Ke, W.; Yu, S. Joint Mean-Field Game and Multiagent Asynchronous Advantage Actor-Critic for Edge Intelligence-Based IoT Malware Propagation Defense. IEEE Trans. Dependable Secur. Comput. 2025, preprints. [Google Scholar] [CrossRef]
- Lee, J.; Cheng, Y.; Niyato, D.; Guan, Y.L.; González, D. Intelligent resource allocation in joint radar-communication with graph neural networks. IEEE Trans. Veh. Technol. 2022, 71, 11120–11135. [Google Scholar] [CrossRef]
- Thornton, C.E.; Kozy, M.A.; Buehrer, R.M.; Martone, A.F.; Sherbondy, K.D. Deep reinforcement learning control for radar detection and tracking in congested spectral environments. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 1335–1349. [Google Scholar] [CrossRef]
- Guo, J.; Jafarkhani, H. Sensor deployment with limited communication range in homogeneous and heterogeneous wireless sensor networks. IEEE Trans. Wirel. Commun. 2016, 15, 6771–6784. [Google Scholar] [CrossRef]
- Guo, J.; Li, M.; Guo, Z.; She, Z. Reinforcement Learning-Based 3-D Sliding Mode Interception Guidance via Proximal Policy Optimization. IEEE J. Miniaturization Air Space Syst. 2023, 4, 423–430. [Google Scholar] [CrossRef]
- Wang, H.; Hao, J.; Wu, W.; Jiang, A.; Mao, K.; Xia, Y. A New AGV Path Planning Method Based On PPO Algorithm. In Proceedings of the 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 3760–3765. [Google Scholar] [CrossRef]
- Kang, H.; Chang, X.; Mišić, J.; Mišić, V.B.; Fan, J.; Liu, Y. Cooperative UAV Resource Allocation and Task Offloading in Hierarchical Aerial Computing Systems: A MAPPO-Based Approach. IEEE Internet Things J. 2023, 10, 10497–10509. [Google Scholar] [CrossRef]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of ppo in cooperative multi-agent games. Adv. Neural Inf. Process. Syst. 2022, 35, 24611–24624. [Google Scholar]
- Cui, J.; Liu, Y.; Nallanathan, A. Multi-agent reinforcement learning-based resource allocation for UAV networks. IEEE Trans. Wirel. Commun. 2019, 19, 729–743. [Google Scholar] [CrossRef]
- Jafar, M.T.; Yang, L.X.; Li, G. An innovative practical roadmap for optimal control strategies in malware propagation through the integration of RL with MPC. Comput. Secur. 2025, 148, 104186. [Google Scholar] [CrossRef]
- Ren, Y.; Sun, Y.; Peng, M. Deep Reinforcement Learning Based Computation Offloading in Fog Enabled Industrial Internet of Things. IEEE Trans. Ind. Inform. 2021, 17, 4978–4987. [Google Scholar] [CrossRef]
- Wu, P.; Tian, L.; Zhang, Q.; Mao, B.; Chen, W. MARRGM: Learning Framework for Multi-Agent Reinforcement Learning via Reinforcement Recommendation and Group Modification. IEEE Robot. Autom. Lett. 2024, 9, 5385–5392. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, C.; Tang, R.; Zhang, W.; He, X.; Yu, Y. Large-Scale Interactive Recommendation with Tree-Structured Reinforcement Learning. IEEE Trans. Knowl. Data Eng. 2023, 35, 4018–4032. [Google Scholar] [CrossRef]
- Yang, M.; Wang, Y.; Yu, Y.; Zhou, M.; U, L.H. MixLight: Mixed-Agent Cooperative Reinforcement Learning for Traffic Light Control. IEEE Trans. Ind. Inform. 2024, 20, 2653–2661. [Google Scholar] [CrossRef]
- Kassab, R.; Destounis, A.; Tsilimantos, D.; Debbah, M. Multi-Agent Deep Stochastic Policy Gradient for Event Based Dynamic Spectrum Access. In Proceedings of the 2020 IEEE 31st Annual International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, 31 August–3 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, Y.; Yu, J.; Headley, W.; Buehrer, R. Deep Reinforcement Learning for Dynamic Spectrum Access in Wireless Networks. In Proceedings of the MILCOM 2018–2018 IEEE Military Communications Conference (MILCOM), Los Angeles, CA, USA, 29–31 October 2018; pp. 207–212. [Google Scholar] [CrossRef]
- Han, M.; Sun, X.; Zhan, W.; Gao, Y.; Jiang, Y. Multi-Agent Reinforcement Learning Based Uplink OFDMA for IEEE 802.11ax Networks. IEEE Trans. Wirel. Commun. 2024, 23, 8868–8882. [Google Scholar] [CrossRef]





| Study | Main Research | Characteristics of Model Construction | Control Method | Optimal Control | RL Algorithms | |||
|---|---|---|---|---|---|---|---|---|
| Epidemic | Channel | Time Delay | Quarantine | Patching | ||||
| Shen et al. [13] | Optimized control | ✔ | ✘ | ✘ | ✘ | ✘ | ✔ | ✘ |
| Sun et al. [16] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ | ✘ |
| Kuai et al. [17] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ (PPO) |
| Xiao et al. [18] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ |
| Zhuang et al. [24] | Optimized control | ✔ | ✘ | ✔ | ✘ | ✔ | ✘ | ✘ |
| Farooq and Zhu [32] | Optimized control | ✘ | ✘ | ✘ | ✔ | ✘ | ✔ | ✘ |
| Lee et al. [43] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ |
| Thornton et al. [44] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ |
| Guo and Jafarkhani [45] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ |
| Guo et al. [46] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ (PPO) |
| Wang et al. [47] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ (PPO) |
| Kang et al. [48] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ (MAPPO) |
| Yu et al. [49] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ (MARL) |
| Cui et al. [50] | Optimized control | ✘ | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ (MAPPO) |
| Jafar et al. [51] | Optimized control | ✔ | ✘ | ✘ | ✘ | ✘ | ✔ | ✔ |
| Proposed framework | Optimized control | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ (PPO/MAPPO) |
| Parameters | Description |
|---|---|
| N | Number of wireless radar sensors |
| The number of neighbors of a I-node that can be infected | |
| Real-time contact rate | |
| a | Slide length of the target square area |
| The density of total nodes | |
| q | The communication difference coefficient between ideal and reality |
| Signal-to-noise threshold | |
| Density of total nodes | |
| The number of nodes around any node that can receive information | |
| Transmit power coefficient | |
| Malware installation success rate | |
| Malware installation delay | |
| Patch installation delay | |
| Patch failure delay | |
| Patch failure rate | |
| Quarantine rate | |
| Background noise power | |
| Quarantine retention exponent | |
| Path loss exponent | |
| h | Quarantine failure delay |
| t | Working cycle |
| T | Maximum number of episodes |
| Parameters | Values | |
|---|---|---|
| WRSNs | Number of wireless radar sensors N | 300 |
| Slide length of the target square area a | 500 m | |
| The density of total nodes | ||
| The communication difference coefficient between ideal and reality q | ||
| Signal-to-noise threshold | 3 dB | |
| Transmit power coefficient | ||
| Malware installation success rate | 0.8 | |
| Malware installation delay | 1 | |
| Patch installation delay | 0.5 | |
| Patch failure delay | 2 | |
| Patch failure rate | 0.05 | |
| Quarantine rate | 0.5 | |
| Background noise power | −60 dBm | |
| Quarantine retention exponent | 0.05 | |
| Path loss exponent | 4 | |
| Quarantine failure delay h | 1 | |
| The weighted cost parameter for V-nodes | 300 | |
| The weighted cost parameter for I-nodes | 900 | |
| The weighted cost parameter for Q-nodes | 300 | |
| The weighted cost of patching-control | 12 | |
| The weighted cost of quarantine-control | 12 | |
| PPO | AC network learning rate | |
| Clipping parameter | 0.2 | |
| Experience buffer sizes | 1024 | |
| Batch size | 64 | |
| Value discount factor | 0.99 | |
| Entropy coefficient of the policy | 0.01 | |
| MAPPO | AC network learning rate | |
| Clipping parameter | 0.2 | |
| Experience buffer sizes | 200 | |
| Batch size | 200 | |
| Value discount factor | 0.99 | |
| Entropy coefficient of the policy | 0.01 | |
| DQN | Learning rate | |
| Update frequency | 4 | |
| Experience buffer sizes | 1024 | |
| Batch size | 64 | |
| Value discount factor | 0.99 | |
| DDQN | Learning rate | |
| Update frequency | 4 | |
| Experience buffer sizes | 1024 | |
| Batch size | 64 | |
| Value discount factor | 0.99 |
| Control | Total Value | Optimal | PPO | MAPPO | DQN | DDQN |
|---|---|---|---|---|---|---|
| Case | ||||||
| Theorem 2: The Hybrid Optimal Control (Patching-control and Quarantine- control ) | = 8 , = 5 | 5461.56 | 5780.12 | 6075.45 | 7554.78 | 7372.23 |
| = 1.2 , = 5 | 5595.64 | 5955.67 | 6456.52 | 7197.03 | 7145.24 | |
| = 1.6 , = 5 | 5768.76 | 6107.56 | 6876.89 | 7398.34 | 7111.67 | |
| = 2 , = 5 | 5969.37 | 6356.90 | 6991.15 | 8804.48 | 7575.72 | |
| = 2.4 , = 5 | 6175.36 | 6601.59 | 7382.83 | 8894.17 | 7537.42 | |
| = 1.2 , = 1 | 5384.65 | 5671.98 | 5945.31 | 6682.54 | 7687.87 | |
| = 1.2 , = 5 | 5595.64 | 5955.67 | 6456.52 | 7197.03 | 7145.24 | |
| = 1.2 , = 1 | 5815.20 | 6250.53 | 6724.76 | 7101.99 | 7603.14 | |
| = 1.2 , = 5 | 6653.47 | 7288.70 | 7930.25 | 8329.58 | 8026.81 | |
| = 1.2 , = 1 | 6805.33 | 7762.66 | 8251.92 | 8438.19 | 7949.44 | |
| Theorem 3: Single Control (Patching-control ) = 0.1 | = 8 , = 5 | 5488.77 | 5866.91 | 5945.22 | 6384.55 | 7657.46 |
| = 1.2 , = 5 | 5626.74 | 6019.01 | 6183.70 | 6514.57 | 7605.31 | |
| = 1.6 , = 5 | 5811.79 | 6247.24 | 6548.57 | 6840.80 | 7539.13 | |
| = 2 , = 5 | 6033.49 | 6433.73 | 6935.26 | 7368.60 | 7464.84 | |
| = 2.4 , = 5 | 6262.18 | 6721.43 | 7290.69 | 7612.93 | 7384.16 | |
| = 1.2 , = 1 | 5422.41 | 5802.64 | 5852.97 | 6253.30 | 7434.63 | |
| = 1.2 , = 5 | 5626.74 | 6019.01 | 6183.70 | 6514.57 | 7605.31 | |
| = 1.2 , = 1 | 5862.66 | 6254.96 | 6634.21 | 6973.52 | 7521.75 | |
| = 1.2 , = 5 | 6790.98 | 7246.29 | 8149.71 | 8614.75 | 8642.31 | |
| = 1.2 , = 1 | 6937.94 | 7477.61 | 8374.90 | 8887.46 | 8981.14 | |
| Theorem 4: Single Control (Quarantine-control ) = 0.1 | = 8 , = 5 | 5680.24 | 5811.79 | 6006.21 | 6375.27 | 5991.35 |
| = 1.2 , = 5 | 5776.77 | 5930.91 | 6154.30 | 6554.67 | 6211.14 | |
| = 1.6 , = 5 | 5910.32 | 6078.84 | 6348.24 | 6605.91 | 6940.35 | |
| = 2 , = 5 | 6083.10 | 6256.74 | 6609.28 | 6885.77 | 6977.84 | |
| = 2.4 , = 5 | 6278.38 | 6538.30 | 6876.93 | 6957.14 | 7018.47 | |
| = 1.2 , = 1 | 5635.31 | 5750.58 | 5952.34 | 6452.54 | 5992.79 | |
| = 1.2 , = 5 | 5776.77 | 5930.91 | 6154.30 | 6554.67 | 6211.14 | |
| = 1.2 , = 1 | 5949.41 | 6153.15 | 6408.25 | 6314.20 | 6253.04 | |
| = 1.2 , = 5 | 6825.21 | 7350.12 | 7734.18 | 7874.58 | 7843.41 | |
| = 1.2 , = 1 | 7064.30 | 7480.24 | 8094.19 | 8534.73 | 8204.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Li, H.; Xiong, L.; Chen, Y.; Wang, A.; Shen, D. Reinforcement Learning for Mitigating Malware Propagation in Wireless Radar Sensor Networks with Channel Modeling. Mathematics 2025, 13, 1397. https://doi.org/10.3390/math13091397
Liu G, Li H, Xiong L, Chen Y, Wang A, Shen D. Reinforcement Learning for Mitigating Malware Propagation in Wireless Radar Sensor Networks with Channel Modeling. Mathematics. 2025; 13(9):1397. https://doi.org/10.3390/math13091397
Chicago/Turabian StyleLiu, Guiyun, Hao Li, Lihao Xiong, Yiduan Chen, Aojing Wang, and Dongze Shen. 2025. "Reinforcement Learning for Mitigating Malware Propagation in Wireless Radar Sensor Networks with Channel Modeling" Mathematics 13, no. 9: 1397. https://doi.org/10.3390/math13091397
APA StyleLiu, G., Li, H., Xiong, L., Chen, Y., Wang, A., & Shen, D. (2025). Reinforcement Learning for Mitigating Malware Propagation in Wireless Radar Sensor Networks with Channel Modeling. Mathematics, 13(9), 1397. https://doi.org/10.3390/math13091397








