Measurement Uncertainty for Finite Quantum Observables

Abstract

Measurement uncertainty relations are lower bounds on the errors of any approximate joint measurement of two or more quantum observables. The aim of this paper is to provide methods to compute optimal bounds of this type. The basic method is semidefinite programming, which we apply to arbitrary finite collections of projective observables on a finite dimensional Hilbert space. The quantification of errors is based on an arbitrary cost function, which assigns a penalty to getting result x rather than y, for any pair $(x,y)$. This induces a notion of optimal transport cost for a pair of probability distributions, and we include an Appendix with a short summary of optimal transport theory as needed in our context. There are then different ways to form an overall figure of merit from the comparison of distributions. We consider three, which are related to different physical testing scenarios. The most thorough test compares the transport distances between the marginals of a joint measurement and the reference observables for every input state. Less demanding is a test just on the states for which a “true value” is known in the sense that the reference observable yields a definite outcome. Finally, we can measure a deviation as a single expectation value by comparing the two observables on the two parts of a maximally-entangled state. All three error quantities have the property that they vanish if and only if the tested observable is equal to the reference. The theory is illustrated with some characteristic examples.

1. Introduction

Measurement uncertainty relations are quantitative expressions of complementarity. As Bohr often emphasized, the predictions of quantum theory are always relative to some definite experimental arrangement, and these settings often exclude each other. In particular, one has to make a choice of measuring devices, and typically, quantum observables cannot be measured simultaneously. This often used term is actually misleading, because time has nothing to do with it. For a better formulation, recall that quantum experiments are always statistical, so the predictions refer to the frequency with which one will see certain outcomes when the whole experiment is repeated very often. Therefore, the issue is not simultaneous measurement of two observables, but joint measurement in the same shot. That is, a device R is a joint measurement of observable A with outcomes $x\in X$ and observable B with outcomes $y\in Y$, if it produces outcomes of the form $(x,y)$ in such a way that if we ignore outcome y, the statistics of the x outcomes is always (i.e., for every input state) the same as obtained with a measurement of A and symmetrically for ignoring x and comparing to B. It is in this sense that non-commuting projection-valued observables fail to be jointly measurable.

However, this is not the end of the story. One is often interested in approximate joint measurements. One such instance is Heisenberg’s famous γ-ray microscope [1], in which a particle’s position is measured by probing it with light of some wavelength λ, which from the outset sets a scale for the accuracy of this position measurement. Naturally, the particle’s momentum is changed by the Compton scattering, so if we make a momentum measurement on the particles after the interaction, we will find a different distribution from what would have been obtained directly. Note that in this experiment, we get from every particle a position value and a momentum value. Moreover, errors can be quantified by comparing the respective distributions with some ideal reference: the accuracy of the microscope position measurement is judged by the degree of agreement between the distribution obtained and the one an ideal position measurement would give. Similarly, the disturbance of momentum is judged by comparing a directly measured distribution with the one after the interaction. 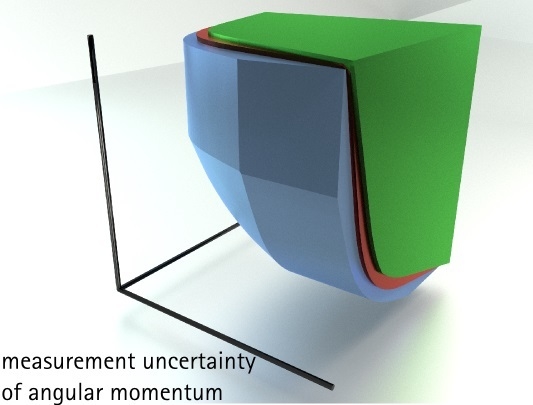The same is true for the uncontrollable disturbance of momentum. This refers to a scenario where we do not just measure momentum after the interaction, but try to build a device that recovers the momentum in an optimal way, by making an arbitrary measurement on the particle after the interaction, utilizing everything that is known about the microscope, correcting all known systematic errors and even using the outcome of the position measurement. The only requirement is that at the end of the experiment, for each individual shot, some value of momentum must come out. Even then it is impossible to always reproduce the pre-microscope distribution of momentum. The tradeoff between accuracy and disturbance is quantified by a measurement uncertainty relation. Since it simply quantifies the impossibility of a joint exact measurement, it simultaneously gives bounds on how an approximate momentum measurement irretrievably disturbs position. The basic setup is shown in Figure 1.

Note that in this description of errors, we did not ever bring in a comparison with some hypothetical “true value”. Indeed, it was noted already by Kennard [2] that such comparisons are problematic in quantum mechanics. Even if one is willing to feign hypotheses about the true value of position, as some hidden variable theorists will, an operational criterion for agreement will always have to be based on statistical criteria, i.e., the comparison of distributions. Another fundamental feature of this view of errors is that it provides a figure of merit for the comparison of two devices, typically some ideal reference observable and an approximate version of it. An “accuracy” ε in this sense is a promise that no matter which input state is chosen, the distributions will not deviate by more than ε. Such a promise does not involve a particular state. This is in contrast to preparation uncertainty relations, which quantify the impossibility to find a state for which the distributions of two given observables (e.g., position and momentum) are both sharp.

Measurement uncertainty relations in the sense described here were first introduced for position and momentum in [3] and were initially largely ignored. A bit earlier, an attempt by Ozawa [4] to quantify error-disturbance tradeoffs with state dependent and somewhat unfortunately chosen [5] quantities had failed, partly for reasons already pointed out in [6]. When experiments confirmed some predictions of the Ozawa approach (including the failure of the error-disturbance tradeoff), a debate ensued [7,8,9,10]. Its unresolved part is whether a meaningful role for Ozawa’s definitions can be found.

Technically, the computation of measurement uncertainty remained hard, since there were no efficient methods to compute sharp bounds in generic cases. A direct computation along the lines of the definition is not feasible, since it involves three nested optimization problems. The only explicit solutions were for qubits [11,12,13], one case of angular momentum [14] and all cases with phase space symmetry [7,15,16], in which the high symmetry allows the reduction to preparation uncertainty as in [3,9]. The main aim of the current paper is to provide efficient algorithms for sharp measurement uncertainty relations of generic observables, even without any symmetry.

In order to do that, we restrict the setting in some ways, but allow maximal generality in others. We will restrict to finite dimensional systems and reference observables, which are projection valued and non-degenerate. Thus, each of the ideal observables will basically be given by an orthonormal basis in the same d-dimensional Hilbert space. The labels of this basis are the outcomes $x\in X$ of the measurement, where X is a set of d elements. We could choose all $X=\{1,\dots ,d\}$, but it will help to keep track of things using a separate set for each observable. Moreover, this includes the choice $X\subset \mathbb{R}$, the set of eigenvalues of some Hermitian operator. We allow not just two observables, but any finite number $n\ge 2$ of them. This makes some expressions easier to write down, since the sum of an expression involving observable A and an analogous one for observable B becomes an indexed sum. We also allow much generality in the way errors are quantified. In earlier works, we relied on two elements to be chosen for each observable, namely a metric D on the outcome set and an error exponent α, distinguishing, say, absolute ($\alpha =1$), root-mean-square ($\alpha =2$) and maximal ($\alpha =\infty$) deviations. Deviations were then averages of $D{(x,y)}^{\alpha }$. Here, we generalize further to an arbitrary cost function $c:X\times X\to \mathbb{R}$, which we take to be positive and zero exactly on the diagonal (e.g., $c(x,y)=D{(x,y)}^{\alpha }$), but not necessarily symmetric. Again, this generality comes mostly as a simplification of notation. For a reference observable A with outcome set X and an approximate version $A^{\prime }$ with the same outcome set, this defines an error $\epsilon \left(A_{}^{\prime }\right|A_{})$. Our aim is to provide algorithms for computing the uncertainty diagram associated with such data, of which Figure 2 gives an example. The given data for such a diagram are n projection valued observables $A_1,\dots ,A_n$, with outcome sets $X_i$, for each of which we are given also a cost function $c_i:X_i\times X_i\to \mathbb{R}$ for quantifying errors. An approximate joint measurement is then an observable R with outcome set $X_1\times \dots \times X_n$, and hence, with POVMelements $R(x_1,\dots ,x_n)$, where $x_i\in X_i$. By ignoring every output, but one, we get the n marginal observables:

$$A_i^{\prime }\left(x_i\right)=\sum _{x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n}R(x_1,\dots ,x_n)$$

(1)

and a corresponding tuple:

$$\overrightarrow{\epsilon }\left(R\right)=\left(\epsilon \left(A_1^{\prime }\right|A_1),\dots ,\epsilon \left(A_n^{\prime }\right|A_n)\right)$$

(2)

of errors. The set of such tuples, as R runs over all joint measurements, is the uncertainty region. The surface bounding this set from below describes the uncertainty tradeoffs. For $n=2$, we call it the tradeoff curve. Measurement uncertainty is the phenomenon that, for general reference observables $A_i$, the uncertainty region is bounded away from the origin. In principle, there are many ways to express this mathematically, from a complete characterization of the exact tradeoff curve, which is usually hard to get, to bounds that are simpler to state, but suboptimal. Linear bounds will play a special role in this paper.

We will consider three ways to build a single error quantity out of the comparison of distributions, denoted by ${\epsilon }_M\left(A_{}^{\prime }\right|A_{})$, ${\epsilon }_C\left(A_{}^{\prime }\right|A_{})$ and ${\epsilon }_E\left(A_{}^{\prime }\right|A_{})$. These will be defined in Section 2. For every choice of observables and cost functions, each will give an uncertainty region, denoted by ${\mathcal{U}}_M$, ${\mathcal{U}}_C$ and ${\mathcal{U}}_E$, respectively. Since they are all based on the same cost function c, they are directly comparable (see Figure 2). We show in Section 3 that the three regions are convex and hence characterized completely by linear bounds. In Section 4, we show how to calculate the optimal linear lower bounds by semidefinite programs. Finally, an Appendix collects the basic information on the beautiful theory of optimal transport, which is needed in Section 2.1 and Section 4.1.

2. Deviation Measures for Observables

Here, we define the measures we use to quantify how well an observable $A^{\prime }$ approximates a desired observable A. In this section, we do not use the marginal condition Equation (1), so $A^{\prime }$ is an arbitrary observable with the same outcome set X as A, i.e., we drop all indices i identifying the different observables. Our error quantities are operational in the sense that each is motivated by an experimental setup, which will in particular provide a natural way to measure them. All error definitions are based on the same cost function $c:X\times X\to \mathbb{R}$, where $c(x,y)$ is the “cost” of getting a result $x\in X$, when $y\in X$ would have been correct. The only assumptions are that $c(x,y)\ge 0$ with $c(x,y)=0$ iff $x=y$.

As described above, we consider a quantum system with Hilbert space ${\mathbb{C}}^d$. As a reference observable A, we allow any complete von Neumann measurement on this system, that is any observable whose set X of possible measurement outcomes has size $\left|X\right|=d$ and whose POVM elements $A\left(y\right)\in \mathcal{B}\left({\mathbb{C}}^d\right)$ ($y\in X$) are mutually orthogonal projectors of rank 1; we can then also write $A\left(y\right)=|{\varphi }_y\rangle \langle {\varphi }_y|$ with an orthonormal basis $\left\{{\varphi }_y\right\}$ of ${\mathbb{C}}^d$. For the approximating observable $A^{\prime }$, the POVM elements $A^{\prime }\left(x\right)$ (with $x\in X$) are arbitrary with $A^{\prime }\left(x\right)\ge 0$ and ${\sum }_{x\in X}A\left(x\right)=\mathrm{𝟙}$.

The comparison will be based on a comparison of output distributions, for which we use the following notations: given a quantum state ρ on this system, i.e., an operator with $\rho \ge 0$ and $tr\rho =1$, and an observable, such as A, we will denote the outcome distribution by $\rho A$, so $\left(\rho A\right)\left(y\right):=tr\left(\rho A_y\right)$. This is a probability distribution on the outcome set X and can be determined physically as the empirical outcome distribution after many experiments.

For comparing just two probability distributions $p:X\to {\mathbb{R}}_{+}$ and $q:X\to {\mathbb{R}}_{+}$, a canonical choice is the “minimum transport cost”:

$$\check{c}(p,q):=\underset{\gamma }{inf}\left\{\sum _{xy}c(x,y)\gamma (x,y)|\gamma \mathrm{couples}p\mathrm{to}q\right\}$$

(3)

where the infimum runs over the set of all couplings or “transport plans” $\gamma :X\times X\to {\mathbb{R}}_{+}$ of p to q, i.e., the set of all probability distributions γ satisfying the marginal conditions ${\sum }_y\gamma (x,y)=p\left(x\right)$ and ${\sum }_x\gamma (x,y)=q\left(y\right)$. The motivations for this notion and the methods to compute it efficiently are described in the Appendix. Since X is finite, the infimum is over a compact set, so it is always attained. Moreover, since we assumed $c\ge 0$ and $c(x,y)=0\iff x=y$, we also have $\check{c}(p,q)\ge 0$ with equality iff $p=q$. If one of the distributions, say q, is concentrated on a point $\tilde{y}$, only one coupling exists, namely $\gamma (x,y)=p\left(x\right){\delta }_{y\tilde{y}}$. In this case, we abbreviate $\check{c}(p,q)=\check{c}(p,\tilde{y})$, and get:

$$\check{c}(p,\tilde{y})=\sum _{x}p\left(x\right)c(x,\tilde{y})$$

(4)

i.e., the average cost of moving all of the points x distributed according to p to $\tilde{y}$.

2.1. Maximal Measurement Error ${\epsilon }_M\left(A_{}^{\prime }\right|A_{})$

The worst case error over all input states is:

$${\epsilon }_M\left(A_{}^{\prime }\right|A_{}):=\underset{\rho }{sup}\left\{\check{c}(\rho A^{\prime },\rho A)| \rho \text{quantum}\text{state}\text{on}{\mathbb{C}}^d\right\}$$

(5)

which we call the maximal error. Note that, like the cost function c and the transport costs $\check{c}$, the measure ${\epsilon }_M\left(A_{}^{\prime }\right|A_{})$ need not be symmetric in its arguments, which is sensible, as the reference and approximating observables have distinct roles. Similar definitions for the deviation of an approximating measurement from an ideal one have been made, for specific cost functions, in [7,9] and [14] before.

The definition Equation (5) makes sense even if the reference observable A is not a von Neumann measurement. Instead, the only requirement is that A and $A^{\prime }$ be general observables with the same (finite) outcome set X, not necessarily of size d. All of our results below that involve only the maximal measurement error immediately generalize to this case, as well.

One can see that it is expensive to determine the quantity ${\epsilon }_M\left(A_{}^{\prime }\right|A_{})$ experimentally according to the definition: one would have to measure and compare (see Figure 3) the outcome statistics $\rho A^{\prime }$ and $\rho A$ for all possible input states ρ, which form a continuous set. The following definition of observable deviation alleviates this burden.

2.2. Calibration Error ${\epsilon }_C\left(A_{}^{\prime }\right|A_{})$

Calibration (see Figure 4) is a process by which one tests a measuring device on inputs (or measured objects) for which the “true value” is known. Even in quantum mechanics, we can set this up by demanding that the measurement of the reference observable on the input state gives a sharp value y. In a general scenario with continuous outcomes, this can only be asked with a finite error δ, which goes to zero at the end [7], but in the present finite scenario, we can just demand $\left(\rho A\right)\left(y\right)=1$. Since, for every outcome y of a von Neumann measurement, there is only one state with this property (namely $\rho =|{\varphi }_y\rangle \langle {\varphi }_y|$), we can simplify even further, and define the calibration error by:

$${\epsilon }_C\left(A_{}^{\prime }\right|A_{}):=\underset{y,\rho }{sup}\left\{\check{c}(\rho A^{\prime },y)\right|tr\left(\rho A\left(y\right)\right)=1\}=\underset{y}{max}\sum _x\langle {\varphi }_y|A^{\prime }\left(x\right)|{\varphi }_y\rangle c(x,y)$$

(6)

Note that the calibration idea only makes sense when there are sufficiently many states for which the reference observable has deterministic outcomes, i.e., for projective observables A.

A closely related quantity has recently been proposed by Appleby [10]. It is formulated for real valued quantities with cost function $c(x,y)={(x-y)}^2$ and has the virtue that it can be expressed entirely in terms of first and second moments of the probability distributions involved. Therefore, for any ρ, let m and v be the mean and variance of $\rho A$ and $v^{\prime }$ the mean quadratic deviation of $\rho A^{\prime }$ from m. Then, Appleby defines:

$${\epsilon }_D\left(A_{}^{\prime }\right|A_{})=\underset{\rho }{sup}{(\sqrt{v^{\prime }}-\sqrt{v})}^2$$

(7)

Here, we added the square to make Appleby’s quantity comparable to our variance-like (rather than standard deviation-like) quantities and chose the letter D, because Appleby calls this the D-error. Since in the supremum, we have also the states for which A has a sharp distribution (i.e., $v=0$), we clearly have ${\epsilon }_D\left(A_{}^{\prime }\right|A_{})\ge {\epsilon }_C\left(A_{}^{\prime }\right|A_{})$. On the other hand, let $\mathrm{\Phi }\left(x\right)=t{(x-m)}^2$ and $\mathrm{\Psi }\left(y\right)=t/(1-t){(y-m)}^2$. Then, one easily checks that $\mathrm{\Phi }\left(x\right)-\mathrm{\Psi }\left(y\right)\le {(x-y)}^2$, so $(\mathrm{\Phi },\mathrm{\Psi })$ is a pricing scheme in the sense defined in the Appendix. Therefore:

$$\check{c}(\rho A^{\prime },\rho A)\ge \sum _x\left(\rho A^{\prime }\right)\left(x\right)\mathrm{\Phi }\left(x\right)-\sum _y\left(\rho A\right)\left(y\right)\mathrm{\Psi }\left(y\right)=t{v}^{\prime }-\frac{t}{1-t}v$$

(8)

Maximizing this expression over t gives exactly Equation (7). Therefore,

$${\epsilon }_C\left(A_{}^{\prime }\right|A_{})\le {\epsilon }_D\left(A_{}^{\prime }\right|A_{})\le {\epsilon }_M\left(A_{}^{\prime }\right|A_{}).$$

2.3. Entangled Reference Error ${\epsilon }_E\left(A_{}^{\prime }\right|A_{})$

In quantum information theory, a standard way of providing a reference state for later comparison is by applying a channel or observable to one half of a maximally-entangled system. Two observables would be compared by measuring them (or suitable modifications) on the two parts of a maximally-entangled system (see Figure 5). Let us denote the entangled vector by $\mathrm{\Omega }=d^{-1/2}{\sum }_k|kk\rangle$. Since later, we will look at several distinct reference observables, the basis kets $|k\rangle$ in this expression have no special relation to A or its eigenbasis ${\varphi }_y$. We denote by $X^{\mathsf{T}}$ the transpose of an operator X in the $|k\rangle$ basis, and by $A^{\mathsf{T}}$ the observable with POVM elements $A{\left(y\right)}^{\mathsf{T}}=|\overline{{\varphi }_y}\rangle \langle \overline{{\varphi }_y}|$, where $\overline{{\varphi }_y}$ is the complex conjugate of ${\varphi }_y$ in $|k\rangle$-basis. These transposes are needed due to the well-known relation $(X\otimes \mathrm{𝟙})\mathrm{\Omega }=(\mathrm{𝟙}\otimes X^{\mathsf{T}})\mathrm{\Omega }$. We now consider an experiment, in which $A^{\prime }$ is measured on the first part and $A^{\mathsf{T}}$ on the second part of the entangled system, so we get the outcome pair $(x,y)$ with probability:

$$p(x,y)=\langle \mathrm{\Omega }|A^{\prime }\left(x\right)\otimes A{\left(y\right)}^{\mathsf{T}}|\mathrm{\Omega }\rangle =\langle \mathrm{\Omega }|A^{\prime }\left(x\right)A\left(y\right)\otimes \mathrm{𝟙}|\mathrm{\Omega }\rangle =\frac{1}{d}tr\left(A^{\prime }\left(x\right)A\left(y\right)\right)$$

(9)

As A is a complete von Neumann measurement, this probability distribution is concentrated on the diagonal ($x=y$) iff $A^{\prime }=A$, i.e., there are no errors of $A^{\prime }$ relative to A. Averaging with the error costs, we get a quantity we call the entangled reference error:

$${\epsilon }_E\left(A_{}^{\prime }\right|A_{}):=\sum _{xy}\frac{1}{d}tr\left(A^{\prime }\left(x\right)A\left(y\right)\right)c(x,y)$$

(10)

Note that this quantity is measured as a single expectation value in the experiment with source Ω. Moreover, when we later want to measure different such deviations for the various marginals, the source and the tested joint measurement device can be kept fixed, and only the various reference observables $A_i^{\mathsf{T}}$ acting on the second part need to be adapted suitably.

2.4. Summary and Comparison

The quantities ${\epsilon }_M\left(A_{}^{\prime }\right|A_{})$, ${\epsilon }_C\left(A_{}^{\prime }\right|A_{})$ and ${\epsilon }_E\left(A_{}^{\prime }\right|A_{})$ constitute three different ways to quantify the deviation of an observable $A^{\prime }$ from a projective reference observable A. Nevertheless, they are all based on the same distance-like measure, the cost function c on the outcome set X. Therefore, it makes sense to compare them quantitatively. Indeed, they are ordered as follows:

$${\epsilon }_M\left(A_{}^{\prime }\right|A_{})\ge {\epsilon }_C\left(A_{}^{\prime }\right|A_{})\ge {\epsilon }_E\left(A_{}^{\prime }\right|A_{})$$

(11)

Here, the first inequality follows by restricting the supremum Equation (5) to states that are sharp for A and the second by noting that the Equation (6) is the maximum of a function of y, of which Equation (10) is the average.

Moreover, as we argued before in Equation (10), ${\epsilon }_E\left(A_{}^{\prime }\right|A_{})=0$ if and only if $A=A^{\prime }$, which is hence equivalent also to ${\epsilon }_M\left(A_{}^{\prime }\right|A_{})=0$ and ${\epsilon }_C\left(A_{}^{\prime }\right|A_{})=0$.

3. Convexity of Uncertainty Diagrams

For two observables $B_1$ and $B_2$ with the same outcome set, we can easily realize their mixture or convex combination $B=t{B}_1+(1-t)B_2$ by flipping a coin with probability t for heads in each instance and then apply $B_1$ when heads is up and $B_2$ otherwise. In terms of POVM elements, this reads $B\left(x\right)=t{B}_1\left(x\right)+(1-t)B_2\left(x\right)$. We show first that this mixing operation does not increase the error quantities from Section 2.

Lemma 1. 

For $L\in \{M,D,C,E\}$ the error quantity ${\epsilon }_L\left(B\right|A)$, is a convex function of B, i.e., for $B=t{B}_1+(1-t)B_2$ and $t\in [0,1]$:

$$\begin{array}{cc}\hfill {\epsilon }_L\left(B\right|A)& \le t{\epsilon }_L\left(B_1\right|A)+(1-t){\epsilon }_L\left(B_1\right|A)\hfill \end{array}$$

(12)

Proof. 

The basic fact used here is that the pointwise supremum of affine functions (i.e., those for which equality holds in the definition of a convex function) is convex. This is geometrically obvious and easily verified from the definitions. Hence, we only have to check that each of the error quantities is indeed represented as a supremum of functions, which are affine in the observable B.

For $L=E$, we even get an affine function, because Equation (10) is linear in $A^{\prime }$. For $L=C$, Equation (6) has the required form. For $L=M$, Equation (5) is a supremum, but the function $\check{c}$ is defined as an infimum. However, we can use the duality theory described in the Appendix to write it instead as a supremum over pricing schemes, of an expression that is just the expectation of $\mathrm{\Phi }\left(x\right)$ plus a constant and, therefore, an affine function. Finally, for Appleby’s case Equation (7), we get the same supremum, but over the subset of pricing schemes (the quadratic ones).  ☐

The convexity of the error quantities distinguishes measurement from preparation uncertainty. Indeed, the variances appearing in preparation uncertainty relations are typically concave functions, because they arise from minimizing the expectation of ${(x-m)}^2$ over m. Consequently, the preparation uncertainty regions may have gaps and non-trivial behavior on the side of large variances. The following proposition will show that measurement uncertainty regions are better behaved.

For every cost function c on a set X, we can define a “radius” ${\overline{c}}^{*}$, the largest transportation cost from the uniform distribution (the “center” of the set of probability distributions) and a “diameter” $c^{*}$, the largest transportation cost between any two distributions:

$${\overline{c}}^{*}=\underset{y}{max}\sum _{x}c(x,y)/d{c}^{*}=ma{x}_{xy}c(x,y)$$

(13)

Proposition 2. 

Let n observables $A_i$ and cost functions $c_i$ be given, and define $c_i^M=c_i^C=c_i^{*}$ and $c_i^E={\overline{c_i}}^{*}$. Then, for $L=\{M,C,E\}$, the uncertainty regions ${\mathcal{U}}_L$ is a convex set and has the following (monotonicity) property: when $\overrightarrow{x}=(x_1,\dots ,x_n)\in {\mathcal{U}}_L$ and $\overrightarrow{y}=(y_i,\dots ,y_n)\in {\mathbb{R}}^n$ are such that $x_i\le y_i\le c_i^L$, then $\overrightarrow{y}\in {\mathcal{U}}_L$.

Proof. 

Let us first clarify how to make the worst possible measurement B, according to the various error criteria, for which we go back to the setting of Section 2, with just one observable A and cost function c. In all cases, the worst measurement is one with constant and deterministic output, i.e., $B\left(x\right)={\delta }_{x^{*},x}\mathrm{𝟙}$. For $L=C$ and $L=M$, such a measurement will have ${\epsilon }_L\left(B\right|A)={max}_{y}c(x^{*},y)$, and we can choose $x^{*}$ to make this equal to $c^{*}=c^L$. For $L=E$, we get instead the average, which is maximized by ${\overline{c}}^{*}$.

We can now make a given joint measurement R worse by replacing it partly by a bad one, say for the first observable $A_1$. That is, we set, for $\lambda \in [0,1]$,

$$\tilde{R}(x_1,x_2,\dots ,x_n)=\lambda B_1\left(x_1\right)\sum _{y_1}R(y_1,x_2,\dots ,x_n)+(1-\lambda )R(x_1,x_2,\dots ,x_n)$$

(14)

Then, all marginals ${\tilde{A}}_i^{\prime }$ for $i\ne 1$ are unchanged, but ${\tilde{A}}_1^{\prime }\left(x_1\right)=\lambda B_1\left(x_1\right)+(1-\lambda )A^{\prime }\left(x_1\right)$. Now, as λ changes from zero to one, the point in the uncertainty diagram will move continuously in the first coordinate direction from $\overrightarrow{x}$ to the point in which the first coordinate is replaced by its maximum value (see Figure 6 (left)). Obviously, the same holds for every other coordinate direction, which proves the monotonicity statement of the proposition.

Let $R_1$ and $R_2$ be two observables, and let $R=\lambda R_1+(1-\lambda )R_2$ be their mixture. For proving the convexity of ${\mathcal{U}}_L$, we will have to show that every point on the line between ${\overrightarrow{\epsilon }}_L\left(R_1\right)$ and ${\overrightarrow{\epsilon }}_L\left(R_2\right)$ can be attained by a tuple of errors corresponding to some allowed observable (see Figure 6 (right)). Now, lemma 1 tells us that every component of ${\overrightarrow{\epsilon }}_L\left(R\right)$ is convex, which implies that ${\overrightarrow{\epsilon }}_L\left(R\right)\le \lambda {\overrightarrow{\epsilon }}_L\left(R_1\right)+(1-\lambda ){\overrightarrow{\epsilon }}_L\left(R_2\right)$. However, by monotonicity, this also means that $\lambda {\overrightarrow{\epsilon }}_L\left(R_1\right)+(1-\lambda )\overrightarrow{\epsilon }\left(R_2\right)$ is in ${\mathcal{U}}_L$ again, which shows the convexity of ${\mathcal{U}}_L$. ☐

Example: Phase Space Pairs

As is plainly visible from Figure 2, the three error criteria considered here usually give different results. However, under suitable circumstances, they all coincide. This is the case for conjugate pairs related by Fourier transform [15]. The techniques needed to show this are the same as for the standard position/momentum case [9,17] and, in addition, imply that the region for preparation uncertainty is also the same.

In the finite case, there is not much to choose: we have to start from a finite abelian group, which we think of as position space, and its dual group, which is then the analogue of momentum space. The unitary connecting the two observables is the finite Fourier associated with the group. The cost function needs to be translation invariant, i.e., $c(x,y)=c(x-y)$. Then, by an averaging argument, we find for all error measures that a covariant phase space observable minimizes measurement uncertainty (all three versions). The marginals of such an observable can be simulated by first doing the corresponding reference measurement and then adding some random noise. This implies [14] that ${\epsilon }_M\left(A_{}^{\prime }\right|A_{})={\epsilon }_C\left(A_{}^{\prime }\right|A_{})$. However, we know more about this noise: it is independent of the input state, so that the average and the maximum of the noise (as a function of the input) coincide, i.e., ${\epsilon }_C\left(A_{}^{\prime }\right|A_{})={\epsilon }_E\left(A_{}^{\prime }\right|A_{})$. Finally, we know that the noise of the position marginal is distributed according to the position distribution of a certain quantum state, which is, up to normalization and a unitary parity inversion, the POVM element of the covariant phase space observable at the origin. The same holds for the momentum noise. However, then the two noise quantities are exactly related like the position and momentum distributions of a state, and the tradeoff curve for that problem is exactly preparation uncertainty, with variance criteria based on the same cost function.

If we choose the discrete metric for c, the uncertainty region depends only on the number d of elements in the group we started from [15]. The largest ε for all quantities is the distance from a maximally-mixed state to any pure state, which is $\Delta =(1-1/d)$. The exact tradeoff curve is then an ellipse, touching the axes at the points $(0,\Delta )$ and $(\Delta ,0)$. The resulting family of curves, parameterized by d, is shown in Figure 7. In general, however, the tradeoff curve requires the solution of a non-trivial family of ground state problems and cannot be given in closed form. For bit strings of length n and the cost, some convex function of Hamming distance there is an expression for large n [15].

4. Computing Uncertainty Regions via Semidefinite Programming

We show here how the uncertainty regions, and therefore, optimal uncertainty relations, corresponding to each of the three error measures can actually be computed, for any given set of projective observables $A_1,\dots ,A_n$ and cost functions $c_1,\dots ,c_n$. Our algorithms will come in the form of semidefinite programs (SDPs) [18,19], facilitating efficient numerical computation of the uncertainty regions via the many existing program packages to solve SDPs. Moreover, the accuracy of such numerical results can be rigorously certified via the duality theory of SDPs. To obtain the illustrations in this paper, we used the CVX package [20,21] under MATLAB.

As all of our uncertainty regions ${\mathcal{U}}_L\subset {\mathbb{R}}^n$ (for $L=M,C,E$) are convex and closed (Section 3), they are completely characterized by their supporting hyperplanes (for a reference to convex geometry, see [22]). Due to the monotonicity property stated in Proposition 2, some of these hyperplanes just cut off the set parallel along the planes $x_i=c_i^L$. The only hyperplanes of interest are those with nonnegative normal vectors $\overrightarrow{w}=(w_1,\dots ,w_n)\in {\mathbb{R}}_{+}^n$ (see Figure 8). Each hyperplane is completely specified by its “offset” $b_L\left(\overrightarrow{w}\right)$ away from the origin, and this function determines ${\mathcal{U}}_L$:

$$\begin{array}{ccc}\hfill b_L\left(\overrightarrow{w}\right)& :=& inf\left\{\overrightarrow{w}·\overrightarrow{\epsilon }|\overrightarrow{\epsilon }\in {\mathcal{U}}_L\right\}\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill {\mathcal{U}}_L& =& \left\{\overrightarrow{\epsilon }\in {\mathbb{R}}^n|\forall \overrightarrow{w}\in {\mathbb{R}}_{+}^n\overrightarrow{w}·\overrightarrow{\epsilon }\ge b_L\left(\overrightarrow{w}\right)\right\}\hfill \end{array}$$

(16)

In fact, due to homogeneity $b_L\left(t\overrightarrow{w}\right)=t{b}_L\left(\overrightarrow{w}\right)$, we can restrict everywhere to the subset of vectors $\overrightarrow{w}\in {\mathbb{R}}_{+}^n$ that, for example, satisfy ${\sum }_i{w}_i=1$, suggesting an interpretation of the $w_i$ as weights of the different uncertainties ${\epsilon }_i$. Our algorithms will, besides evaluating $b_L\left(\overrightarrow{w}\right)$, also allow one to compute a (approximate) minimizer $\overrightarrow{\epsilon }$, so that one can plot the boundary of the uncertainty region ${\mathcal{U}}_L$ by sampling over $\overrightarrow{w}$, which is how the figures in this paper were obtained.

Let us further note that knowledge of $b_L\left(\overrightarrow{w}\right)$ for some $\overrightarrow{w}\in {\mathbb{R}}_{+}^n$ immediately yields a quantitative uncertainty relation: every error tuple $\overrightarrow{\epsilon }\in {\mathcal{U}}_L$ attainable via a joint measurement is constrained by the affine inequality $\overrightarrow{w}·\overrightarrow{\epsilon }\ge b_L\left(\overrightarrow{w}\right)$, meaning that some weighted average of the attainable error quantities ${\epsilon }_i$ cannot become too small. When $b_L\left(\overrightarrow{w}\right)>0$ is strictly positive, this excludes in particular the zero error point $\overrightarrow{\epsilon }=\overrightarrow{0}$. The obtained uncertainty relations are optimal in the sense that there exists $\overrightarrow{\epsilon }\in {\mathcal{U}}_L$, which attains strict equality $\overrightarrow{w}·\overrightarrow{\epsilon }=b_L\left(\overrightarrow{w}\right)$.

Having reduced the computation of an uncertainty region essentially to determining $b_L\left(\overrightarrow{w}\right)$ (possibly along with an optimizer $\overrightarrow{\epsilon }$), we now treat each case $L=M,C,E$ in turn.

4.1. Computing the Uncertainty Region ${\mathcal{U}}_M$

On the face of it, the computation of the offset $b_M\left(\overrightarrow{w}\right)$ looks daunting: expanding the definitions, we obtain:

$$\begin{array}{c}\hfill b_M\left(\overrightarrow{w}\right)=\underset{R}{inf}\sum _{i=1}^n{w}_i\underset{\rho }{sup}{\check{c}}_i(\rho A_i^{\prime },\rho A_i)\end{array}$$

(17)

where the infimum runs over all joint measurements R with outcome set $X_1\times \dots \times X_n$, inducing the marginal observables $A_i^{\prime }=A_i^{\prime }\left(R\right)$ according to Equation (1), and the supremum over all sets of n quantum states ${\rho }_1,\dots ,{\rho }_n$ and where the transport costs ${\check{c}}_i(p,q)$ are given as a further infimum Equation (3) over the couplings ${\gamma }_i$ of $p=\rho A_i^{\prime }$ and $q=\rho A_i$.

The first simplification is to replace the infimum over each coupling ${\gamma }_i$, via a dual representation of the transport costs, by a maximum over optimal pricing schemes $({\mathrm{\Phi }}_{\alpha },{\mathrm{\Psi }}_{\alpha })$, which are certain pairs of functions ${\mathrm{\Phi }}_{\alpha },{\mathrm{\Psi }}_{\alpha }:X_i\to \mathbb{R}$, where α runs over some finite label set ${\mathcal{S}}_i$. The characterization and computation of the pairs $({\mathrm{\Phi }}_{\alpha },{\mathrm{\Psi }}_{\alpha })$, which depend only on the chosen cost function $c_i$ on $X_i$, are described in the Appendix. The simplified expression for the optimal transport costs is then:

$${\check{c}}_i(p,q)=\underset{\alpha \in {\mathcal{S}}_i}{max}\sum _x{\mathrm{\Phi }}_{\alpha }\left(x\right)p\left(x\right)-\sum _y{\mathrm{\Psi }}_{\alpha }\left(y\right)q\left(y\right)$$

(18)

We can then continue our computation of $b_M\left(\overrightarrow{w}\right)$:

$$\begin{array}{cc}\hfill b_M\left(\overrightarrow{w}\right)& =\underset{R}{inf}\sum _i{w}_i\underset{\rho }{sup}\underset{\alpha \in {\mathcal{S}}_i}{max}\left(\sum _x{\mathrm{\Phi }}_{\alpha }\left(x\right)tr\left[\rho A_i^{\prime }\left(x\right)\right]-\sum _y{\mathrm{\Psi }}_{\alpha }\left(y\right)tr\left[\rho A_i\left(y\right)\right]\right)\hfill \end{array}$$

(19)

$$\begin{array}{cc}& =\underset{R}{inf}\sum _i{w}_i\underset{\alpha \in {\mathcal{S}}_i}{max}\underset{\rho }{sup}tr\left[\rho \left(\sum _x{\mathrm{\Phi }}_{\alpha }\left(x\right)A_i^{\prime }\left(x\right)-\sum _y{\mathrm{\Psi }}_{\alpha }\left(y\right)A_i\left(y\right)\right)\right]\hfill \end{array}$$

(20)

$$\begin{array}{cc}& =\underset{R}{inf}\sum _i{w}_i\underset{\alpha \in {\mathcal{S}}_i}{max}{\lambda }_{\max }\left(\sum _x{\mathrm{\Phi }}_{\alpha }\left(x\right)A_i^{\prime }\left(x\right)-\sum _y{\mathrm{\Psi }}_{\alpha }\left(y\right)A_i\left(y\right)\right)\hfill \end{array}$$

(21)

where ${\lambda }_{\max }\left(B_{i,\alpha }\right)$ denotes the maximum eigenvalue of a Hermitian operator $B_{i,\alpha }$. Note that ${\lambda }_{\max }\left(B_{i,\alpha }\right)=inf\left\{{\mu }_i\right|B_{i,\alpha }\le {\mu }_i\mathrm{𝟙}\}$, which one can also recognize as the dual formulation of the convex optimization ${sup}_{\rho }tr\left(\rho B_{i,\alpha }\right)$ over density matrices, so that:

$$\underset{\alpha \in {\mathcal{S}}_i}{max}{\lambda }_{\max }\left(B_{i,\alpha }\right)=inf\left\{{\mu }_i\right|\forall \alpha \in {\mathcal{S}}_i:B_{i,\alpha }\le {\mu }_i\mathrm{𝟙}\}$$

(22)

We obtain thus a single constrained minimization:

$$\begin{array}{c}\hfill b_M\left(\overrightarrow{w}\right)=\underset{R,\left\{{\mu }_i\right\}}{inf}\left\{\sum _i{w}_i{\mu }_i|\forall i\forall \alpha \in {\mathcal{S}}_i:\sum _x{\mathrm{\Phi }}_{\alpha }\left(x\right)A_i^{\prime }\left(x\right)-\sum _y{\mathrm{\Psi }}_{\alpha }\left(y\right)A_i\left(y\right)\le {\mu }_i\mathrm{𝟙}\right\}\end{array}$$

(23)

Making the constraints on the POVM elements $R(x_1,\dots ,x_n)$ of the joint observable R explicit and expressing the marginal observables $A_i^{\prime }=A_i^{\prime }\left(R\right)$ directly in terms of them by Equation (1), we finally obtain the following SDP representation for the quantity $b_M\left(\overrightarrow{w}\right)$:

$$\boxed{{\displaystyle \begin{array}{cc}& b_M\left(\overrightarrow{w}\right)=inf\sum _i{w}_i{\mu }_i\hfill \\ & \text{with}\text{real}\text{variables}{\mu }_i\text{and}d\times d-\text{matrix}\text{variables}R(x_1,\dots ,x_n)\text{subject}\text{to}\hfill \\ & \begin{array}{cc}\hfill {\mu }_i\mathrm{𝟙}& \ge \sum _{x_1,\dots ,x_n}{\mathrm{\Phi }}_{\alpha }\left(x_i\right)R(x_1,\dots ,x_n)-\sum _y{\mathrm{\Psi }}_{\alpha }\left(y\right)A\left(y\right)\forall i\forall \alpha \in {\mathcal{S}}_i\hfill \\ \hfill R(x_1,\dots ,x_n)& \ge 0\forall x_1,\dots ,x_n\hfill \\ \hfill \sum _{x_1,\dots ,x_n}R(x_1,\dots ,x_n)& =\mathrm{𝟙}.\hfill \end{array}\hfill \end{array}}}$$

(24)

The derivation above shows further that, when $w_i>0$, the ${\mu }_i$ attaining the infimum equals ${\mu }_i={sup}_{\rho }{\check{c}}_i(\rho A_i^{\prime },\rho A_i)={\epsilon }_M\left(A_i^{\prime }\right|A_i)$, where $A_i^{\prime }$ is the marginal coming from a corresponding optimal joint measurement $R(x_i,\dots ,x_n)$. Since numerical SDP solvers usually output an (approximate) optimal variable assignment, one obtains in this way directly a boundary point $\overrightarrow{\epsilon }=({\mu }_1,\dots ,{\mu }_n)$ of ${\mathcal{U}}_M$ when all $w_i$ are strictly positive. If $w_i=0$ vanishes, a corresponding boundary point $\overrightarrow{\epsilon }$ can be computed via ${\epsilon }_i={\epsilon }_M\left(A_i^{\prime }\right|A_i)={max}_{\alpha \in {\mathcal{S}}_i}{\lambda }_{\max }({\sum }_{x_1,\dots ,x_n}{\mathrm{\Phi }}_{\alpha }\left(x_i\right)R(x_1,\dots ,x_n)-{\sum }_y{\mathrm{\Psi }}_{\alpha }\left(y\right)A\left(y\right))$ from an optimal assignment for the POVM elements $R(x_1,\dots ,x_n)$.

For completeness, we also display the corresponding dual program [18] (note that strong duality holds and the optima of both the primal and the dual problem are attained):

$$\boxed{\begin{array}{c}\hfill {\displaystyle \begin{array}{cc}& b_M\left(\overrightarrow{w}\right)=suptr\left[C\right]-\sum _{i,\alpha }tr[D_{i,\alpha }\sum _y{\mathrm{\Psi }}_{\alpha }\left(y\right)A_i\left(y\right)]\hfill \\ & \text{with}d\times d-\text{matrix}\text{variables}C\text{and}{D}_{i,\alpha }\text{subject}\text{to}:\hfill \\ & \begin{array}{cc}\hfill C& \le \sum _{i,\alpha }{\mathrm{\Phi }}_{\alpha }\left(x_i\right)D_{i,\alpha }\forall x_1,\dots ,x_n\hfill \\ \hfill 0& \le D_{i,\alpha }\forall i\forall \alpha \in {\mathcal{S}}_i\hfill \\ \hfill w_i& =\sum _{\alpha }tr\left[D_{i,\alpha }\right]\forall i.\hfill \end{array}\hfill \end{array}}\end{array}}$$

(25)

4.2. Computing the Uncertainty Region ${\mathcal{U}}_C$

To compute the offset function $b_C\left(\overrightarrow{w}\right)$ for the calibration uncertainty region ${\mathcal{U}}_C$, we use the last form in Equation (6) and recall that the projectors onto the sharp eigenstates of $A_i$ (see Section 2.2) are exactly the POVM elements $A_i\left(x\right)$ for $x\in X_i$:

$$\begin{array}{cc}\hfill b_C\left(\overrightarrow{w}\right)& =\underset{R}{inf}\sum _i{w}_i\underset{y}{max}\sum _{x}tr\left[A_i^{\prime }\left(x\right)A_i\left(y\right)\right]c_i(x,y)\hfill \end{array}$$

(26)

$$\begin{array}{cc}& =\underset{R}{inf}\sum _i{w}_i\underset{\left\{{\lambda }_{i,y}\right\}}{sup}\sum _y{\lambda }_{i,y}\sum _{x}tr\left[A_i^{\prime }\left(x\right)A_i\left(y\right)\right]c_i(x,y)\hfill \end{array}$$

(27)

$$\begin{array}{cc}& =\underset{R}{inf}\underset{\left\{{\lambda }_{i,y}\right\}}{sup}\sum _{x_1,\dots ,x_n}tr\left[R(x_1,\dots ,x_n)\sum _{i,y}{w}_i{\lambda }_{i,y}{c}_i(x_i,y)A_i\left(y\right)\right]\hfill \end{array}$$

(28)

where again, the infimum runs over all joint measurements R, inducing the marginals $A_i^{\prime }$, and we have turned, for each $i=1,\dots ,n$, the maximum over y into a linear optimization over probabilities ${\lambda }_{i,y}\ge 0$ ($y=1,\dots ,d$) subject to the normalization constraint ${\sum }_y{\lambda }_{i,y}=1$. In the last step, we have made the $A_i^{\prime }$ explicit via Equation (1).

The first main step towards a tractable form is von Neumann’s minimax theorem [23,24]: as the sets of joint measurements R and of probabilities $\left\{{\lambda }_{i,y}\right\}$ are both convex and the optimization function is an affine function of R and, separately, also an affine function of the $\left\{{\lambda }_{i,y}\right\}$, we can interchange the infimum and the supremum:

$$\begin{array}{c}\hfill b_C\left(\overrightarrow{w}\right)=\underset{\left\{{\lambda }_{i,y}\right\}}{sup}\underset{R}{inf}\sum _{x_1,\dots ,x_n}tr\left[R(x_1,\dots ,x_n)\sum _{i,y}{w}_i{\lambda }_{i,y}{c}_i(x_i,y)A_i\left(y\right)\right]\end{array}$$

(29)

The second main step is to use SDP duality [19] to turn the constrained infimum over R into a supremum, abbreviating the POVM elements as $R(x_1,\dots ,x_n)=R_{\xi }$:

$$\begin{array}{c}\hfill \underset{\left\{R_{\xi }\right\}}{inf}\left\{\sum _{\xi }{R}_{\xi }{B}_{\xi }\right|R_{\xi }\ge 0\forall \xi ,\sum _{\xi }{R}_{\xi }=\mathrm{𝟙}\}=\underset{Y}{sup}\{tr\left[Y\right]|Y\le B_{\xi }\forall \xi \}\end{array}$$

(30)

which is very similar to a dual formulation often employed in optimal ambiguous state discrimination [25,26].

Putting everything together, we arrive at the following SDP representation for the offset quantity $b_C\left(\overrightarrow{w}\right)$:

$$\boxed{{\displaystyle \begin{array}{cc}& b_C\left(\overrightarrow{w}\right)=suptr\left[Y\right]\hfill \\ & \text{with}\text{real}\text{variables}{\lambda }_{i,y}\text{and}\text{a}d\times d-\text{matrix}\text{variable}Y\text{subject}\text{to}\hfill \\ & \begin{array}{cc}\hfill Y& \le \sum _{i,y}{w}_i{\lambda }_{i,y}{c}_i(x_i,y)A_i\left(y\right)\forall x_1,\dots ,x_n\hfill \\ \hfill {\lambda }_{i,y}& \ge 0\forall i\forall y\hfill \\ \hfill \sum _y{\lambda }_{i,y}& =1\forall i.\hfill \end{array}\hfill \end{array}}}$$

(31)

The dual SDP program reads (again, strong duality holds, and both optima are attained):

$$\boxed{{\displaystyle \begin{array}{cc}& b_C\left(\overrightarrow{w}\right)=inf\sum _i{w}_i{m}_i\hfill \\ & \text{with}\text{real}\text{variables}{m}_i\text{and}d\times d-\text{matrix}\text{variables}R(x_1,\dots ,x_n)\text{subject}\text{to}\hfill \\ & \begin{array}{cc}\hfill m_i& \ge \sum _{x_1,\dots ,x_n}tr[R(x_1,\dots ,x_n)A_i\left(y\right)]c_i(x_i,y)\forall i\forall y\hfill \\ \hfill R(x_1,\dots ,x_n)& \ge 0\forall x_1,\dots ,x_n\hfill \\ \hfill \sum _{x_1,\dots ,x_n}R(x_1,\dots ,x_n)& =\mathrm{𝟙}.\hfill \end{array}\hfill \end{array}}}$$

(32)

This dual version can immediately be recognized as a translation of Equation (26) into SDP form, via an alternative way of expressing the maximum over y (or via the linear programming dual of ${sup}_{\left\{{\lambda }_{i,y}\right\}}$ from Equation (28)).

To compute a boundary point $\overrightarrow{\epsilon }$ of ${\mathcal{U}}_C$ lying on the supporting hyperplane with normal vector $\overrightarrow{w}$, it is best to solve the dual SDP Equation (32) and to obtain $\overrightarrow{\epsilon }=(m_1,\dots ,m_n)$ from an (approximate) optimal assignment of the $m_i$. Again, this works when $w_i>0$, whereas otherwise, one can compute ${\epsilon }_i={max}_y{\sum }_{x_1,\dots ,x_n}tr\left[R(x_1,\dots ,x_n)A_i\left(y\right)\right]c_i(x_i,y)$ from an optimal assignment of the $R(x_1,\dots ,x_n)$. From many primal-dual numerical SDP solvers (such as CVX [20,21]), one can alternatively obtain optimal POVM elements $R(x_1,\dots ,x_n)$ also from solving the primal SDP Equation (31) as optimal dual variables corresponding to the constraints $Y\le \dots$ and compute $\overrightarrow{\epsilon }$ from there.

4.3. Computing the Uncertainty Region ${\mathcal{U}}_E$

As one can see by comparing the last expressions in the defining Equations (6) and (10), respectively, the evaluation of $b_E\left(\overrightarrow{w}\right)$ is quite similar to Equation (26), except that the maximum over y is replaced by a uniform average over y. This simply corresponds to fixing ${\lambda }_{i,y}=1/d$ for all $i,y$ in Equation (28), instead of taking the supremum. Therefore, the primal and dual SDPs for the offset $b_E\left(\overrightarrow{w}\right)$ are:

$$\boxed{{\displaystyle \begin{array}{cc}& b_E\left(\overrightarrow{w}\right)=sup\frac{1}{d}tr\left[Y\right]\hfill \\ & \text{with}\text{a}d\times d-\text{matrix}\text{variable}Y\text{subject}\text{to}\hfill \\ & \begin{array}{cc}\hfill Y& \le \sum _{i,y}{w}_i{c}_i(x_i,y)A_i\left(y\right)\forall x_1,\dots ,x_n.\hfill \end{array}\hfill \end{array}}}$$

(33)

and:

$$\boxed{{\displaystyle \begin{array}{cc}& b_E\left(\overrightarrow{w}\right)=inf\frac{1}{d}\sum _i\sum _y\sum _{x_1,\dots ,x_n}{w}_{i}tr[R(x_1,\dots ,x_n)A_i\left(y\right)]c_i(x_i,y)\hfill \\ & \text{with}d\times d-\text{matrix}\text{variables}R(x_1,\dots ,x_n)\text{subject}\text{to}\hfill \\ & \begin{array}{cc}\hfill R(x_1,\dots ,x_n)& \ge 0\forall x_1,\dots ,x_n\hfill \\ \hfill \sum _{x_1,\dots ,x_n}R(x_1,\dots ,x_n)& =\mathrm{𝟙}.\hfill \end{array}\hfill \end{array}}}$$

(34)

The computation of a corresponding boundary point $\overrightarrow{\epsilon }\in {\mathcal{U}}_E$ is similar as above.

5. Conclusions

We have provided efficient methods for computing optimal measurement uncertainty bounds in the case of finite observables. The extension to infinite dimensional and unbounded observables would be very interesting. The SDP formulation is also a powerful tool for deriving further analytic statements. This process has only just begun.