Geometric Construction of Some Lehmer Means
Abstract
:1. Introduction
| M1 | Internality: | |
| M2 | Symmetry: | |
| M3 | Homogeneity: | |
| M4 | Isotonicity: | if and then |
| M5 | Equality: | if then |
| M6 | Power size: | when |
| M7 | Infinite power: | and |
2. Geometric Constructions of Some Lehmer Mean of Two Variables
2.1. Geometric Construction of and
2.2. Construction of and
3. Further Results and Remarks
3.1. On the Geometric Construction of Lehmer Means for Any Number of Variables
3.1.1. Power and
3.1.2. Power
3.2. Geometric Construction of All Lehmer Means of Two Variables with Integer Power k and , Where m Is an Integer
3.3. Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hischer, H. Fundamentale Ideen und Historische Verankerungen—Dargerstellt am Beispiel der Mittelwertbildung. Math. Didactica 1998, 21, 3–21. [Google Scholar]
- Hischer, H. Viertausend Jahre Mittelwertbildung—Eine Fundamentale Idee der Mathematik und didactische Implikationen. Math. Didactica 2002, 25, 3–51. [Google Scholar]
- Hischer, H.; Lambert, A. Was ist ein numerischer Mittelwert? Math. Didactica 2003, 17, 3–42. [Google Scholar]
- Bullen, P.S.; Mitrinovic, D.S.; Vasic, P.M. Means and Their Inequalities; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Niculescu, C.; Persson, L.E. Convex Functions and Their Applications. A Contemporary Approach, Second Edition, CMS Books in Mathematics; Springer: Berlin, Germany, 2018. [Google Scholar]
- Faradj, M.K. Which Mean do You Mean? An Exposition on Means. Master’s Thesis, Department of Mathematics, Louisiana State University, Baton Rouge, LA, USA, 2004. [Google Scholar]
- Hardy, G.H.; Littlewood, J.E.; Polya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1934. [Google Scholar]
- Sykora, S. Mathematical Means and Averages: Basic Properties; Stan’s Library: Castano Primo, Italy, 2009; Volume III. [Google Scholar]
- Sykora, S. Mathematical Means and Averages: Generalized Heronian Means; Stan’s Library: Castano Primo, Italy, 2009; Volume III. [Google Scholar]
- Høibakk, R.; Lukkassen, D. Power means with integer values. Elem. Math. 2009, 64, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Høibakk, R.; Jorstad, T.; Lukkassen, D.; Lystad, L.-P. Integer crossed ladders; parametric representation and minimal integer values. Normat 2008, 56, 68–79. [Google Scholar]
- Lukkassen, D.; Høibakk, R.; Meidell, A. Nonlinear laminates where the effective conductivity is integer valued. Appl. Math. Lett. 2012, 25, 937–940. [Google Scholar] [CrossRef]
- Meidell, A.; Høibakk, R.; Lukkassen, D.; Beeri, G. Two-component composites whose effective conductivities are power means of the local conductivities. Eur. J. Appl. Math. 2008, 19, 507–517. [Google Scholar] [CrossRef]
- Pahikkala, J. On Contraharmonic mean and Pythagorean triples. Elem. Math. 2010, 65, 62–67. [Google Scholar] [CrossRef] [PubMed]
- Ercolaneo, J. Geometric interpretations of some classical inequalities. Math. Mag. 1972, 45, 226. [Google Scholar] [CrossRef]
- Eves, H. Means appearing in geometric figures. Math. Mag. 2003, 76, 292–294. [Google Scholar] [CrossRef]
- Mathematics Stack Exchange. Available online: https://math.stackexchange.com/users/137524/semiclassical). Which Means Are Constructible? (n.d.), URL (version: 2014-08-21). Available online: https://math.stackexchange.com/q/898349 (accessed on 1 February 2018).
- Porubsky, S. Pythagorean Means, Interactive Portal for Algorithmic Mathematics; Research Report; Institute of Computer Science of the Czech Academy of Sciences: Prague, Czech Republic, 2006. [Google Scholar]
- Tooth, S.M.; Dobelman, J.A. A new look at generalized means. Appl. Math. 2016, 7, 468–472. [Google Scholar] [CrossRef]
- Tuckey, C.O. The construction for mean proportional. Math. Gaz. 1929, 14, 542–544. [Google Scholar] [CrossRef]
- Umberger, S. Some “Mean” Trapezoid; Research Report; Department of Mathematics Education, The University of Georgia: Athens, GA, USA, 2000. [Google Scholar]
- Wisdom, N. An Exploration of the Pythagorean Means; Research Report; Department of Mathematics Education, The University of Georgia: Athens, GA, USA, 2006. [Google Scholar]
- Triangle Median (n.d). Wikipedia. Available online: https://en.wikipedia.org/wiki/Median_(geometry) (accessed on 1 October 2017).
- Høibakk, R.; Lukkassen, D.; Meidell, A.; Persson, L. On some power means and their geometric constructions. Math. Aeterna 2018, 8, 139–158. [Google Scholar]
- Høibakk, R.; Lukkassen, D. Crossed ladders and power means. Elem. Math. 2008, 63, 137–140. [Google Scholar] [CrossRef] [PubMed]
- Høibakk, R.; Meidell, D.L.A.; Persson, L.-E. On geometric construction of some power means. Math. Eng. Sci. Aeros. 2018. under press. [Google Scholar]
- Lehmer, D.H. On the compounding of certain mean. J. Math. Appl. 1971, 36, 183–200. [Google Scholar] [CrossRef]

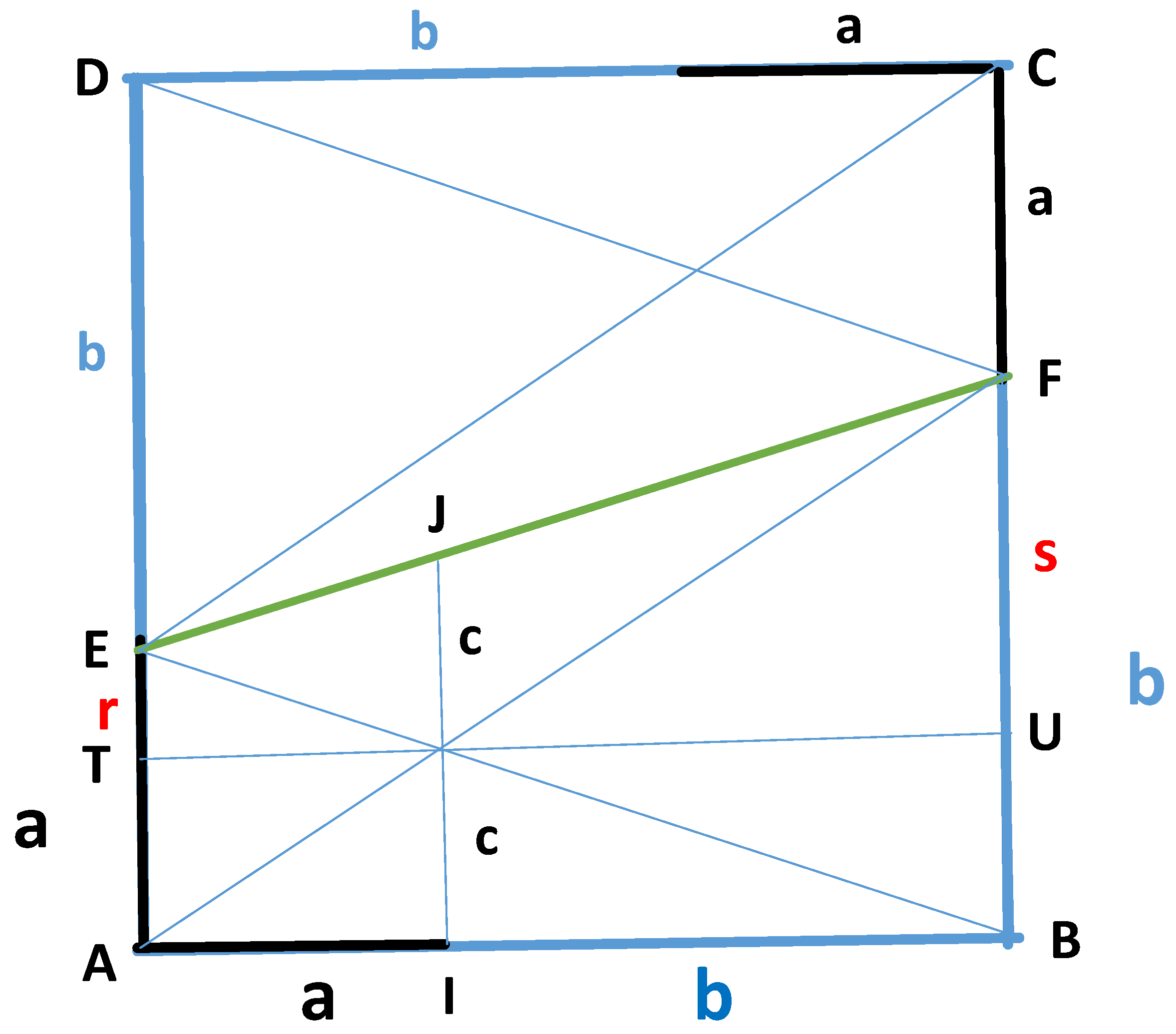
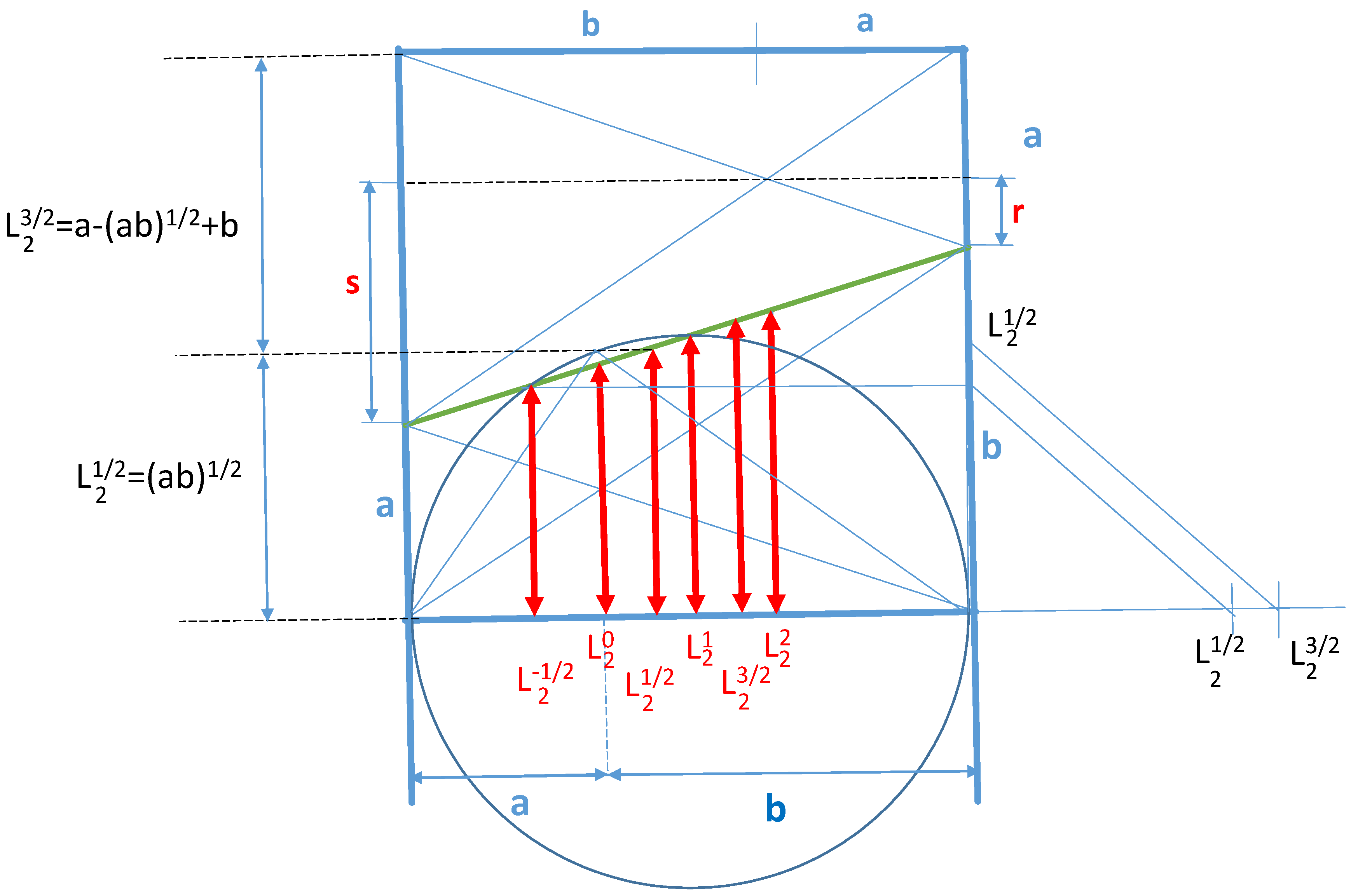





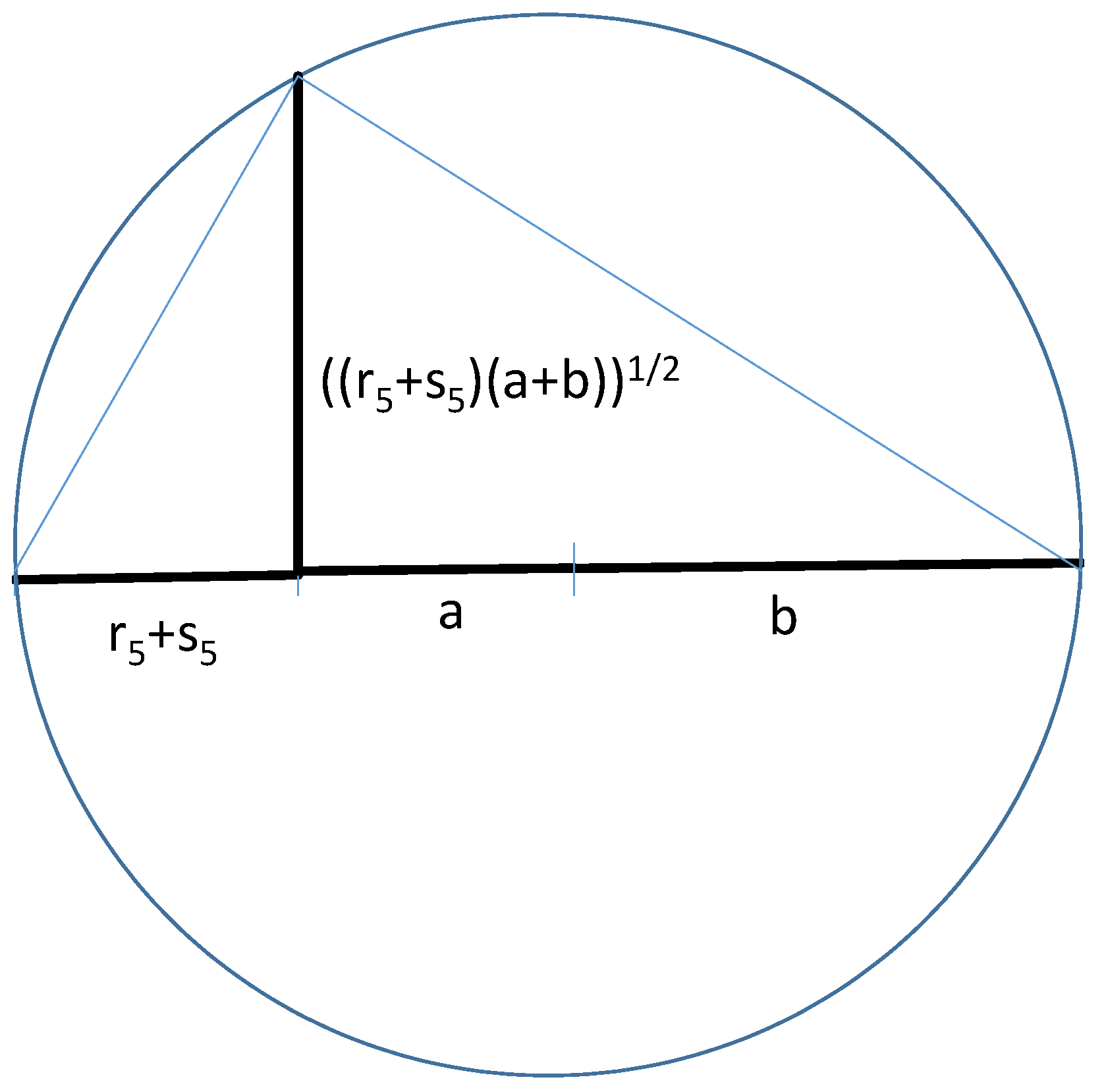





| Mean | Proportions | Modern Definition | M1 | M2 | M3 | M4 | M5 |
|---|---|---|---|---|---|---|---|
| 1. Arithmetic | Y | Y | Y | Y | Y | ||
| 2. Geometric | Y | Y | Y | Y | Y | ||
| 3. Harmonic | Y | Y | Y | Y | Y | ||
| 4. Contraharmonic | Y | Y | Y | Y | Y | ||
| 5. Quadratic | Y | Y | Y | Y | Y | ||
| 6. | Y | N | Y | N | Y | ||
| 7. | Y | N | Y | N | Y | ||
| 8. | Y | N | Y | Y | Y | ||
| 9. | Y | N | Y | N | Y | ||
| 10. | Y | N | Y | Y | Y | ||
| 11. | Y | N | Y | N | Y | ||
| 12. | Y | N | Y | Y | Y |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Høibakk, R.; Lukkassen, D.; Meidell, A.; Persson, L.-E. Geometric Construction of Some Lehmer Means. Mathematics 2018, 6, 251. https://doi.org/10.3390/math6110251
Høibakk R, Lukkassen D, Meidell A, Persson L-E. Geometric Construction of Some Lehmer Means. Mathematics. 2018; 6(11):251. https://doi.org/10.3390/math6110251
Chicago/Turabian StyleHøibakk, Ralph, Dag Lukkassen, Annette Meidell, and Lars-Erik Persson. 2018. "Geometric Construction of Some Lehmer Means" Mathematics 6, no. 11: 251. https://doi.org/10.3390/math6110251
APA StyleHøibakk, R., Lukkassen, D., Meidell, A., & Persson, L.-E. (2018). Geometric Construction of Some Lehmer Means. Mathematics, 6(11), 251. https://doi.org/10.3390/math6110251




