Some Identities Involving Hermite Kampé de Fériet Polynomials Arising from Differential Equations and Location of Their Zeros
Abstract
:1. Introduction
2. Differential Equations Associated with Hermite Kamp de Friet Polynomials
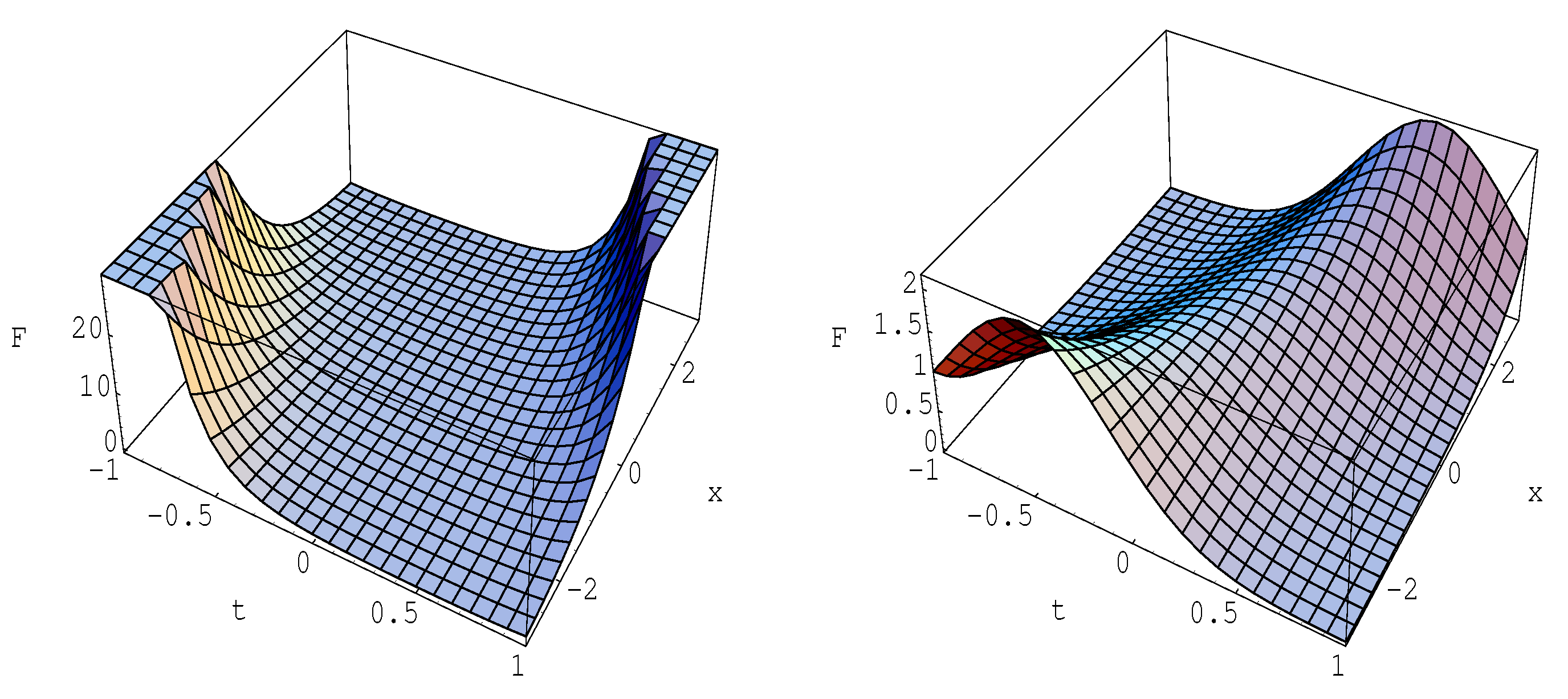
3. Zeros of the Hermite Kamp de Friet Polynomials
4. Conclusions and Future Developments
Funding
Acknowledgments
Conflicts of Interest
References
- Andrews, L.C. Special Functions for Engineers and Mathematicians; Macmillan. Co.: New York, NY, USA, 1985. [Google Scholar]
- Appell, P.; de Fériet, J.K. Fonctions Hypergéométriques et Hypersphériques: Polynomes d Hermite; Gauthier-Villars: Paris, France, 1926. [Google Scholar]
- Erdelyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions; Krieger: New York, NY, USA, 1981; Volume 3. [Google Scholar]
- Gala, S.; Ragusa, M.A.; Sawano, Y.; Tanaka, H. Uniqueness criterion of weak solutions for the dissipative quasi-geostrophic equations in Orlicz-Morrey spaces. Appl. Anal. 2014, 93, 356–368. [Google Scholar] [CrossRef]
- Guariglia, E. On Dieudonns boundedness theorem. J. Math. Anal. Appl. 1990, 145, 447–454. [Google Scholar] [CrossRef]
- Kang, J.Y.; Lee, H.Y.; Jung, N.S. Some relations of the twisted q-Genocchi numbers and polynomials with weight α and weak Weight β. Abstr. Appl. Anal. 2012, 2012, 860921. [Google Scholar] [CrossRef]
- Kim, M.S.; Hu, S. On p-adic Hurwitz-type Euler Zeta functions. J. Number Theory 2012, 132, 2977–3015. [Google Scholar] [CrossRef]
- Kim, T.; Kim, D.S.; Kwon, H.I.; Ryoo, C.S. Differential equations associated with Mahler and Sheffer-Mahler polynomials. To appear in Nonlinear Functional Analysis and Application.
- Kim, T.; Kim, D.S. Identities involving degenerate Euler numbers and polynomials arising from non-linear differential equations. J. Nonlinear Sci. Appl. 2016, 9, 2086–2098. [Google Scholar] [CrossRef] [Green Version]
- Ozden, H.; Simsek, Y. A new extension of q-Euler numbers and polynomials related to their interpolation functions. Appl. Math. Lett. 2008, 21, 934–938. [Google Scholar] [CrossRef]
- Robert, A.M. A Course in p-adic Analysis. In Graduate Text in Mathematics; Springer: Berlin/Heidelberg, Germany, 2000; Volume 198. [Google Scholar]
- Roman, S. The Umbral Calculus, Pure and Applied Mathematics; Academic, Press Inc.: New York, NY, USA; Harcourt Brace Jovanovich Publishes: San Diego, CA, USA, 1984; Volume 111. [Google Scholar]
- Simsek, Y. Complete Sum of Products of (h,q)-Extension of Euler Polynomials and Numbers. J. Differ. Equ. Appl. 2010, 16, 1331–1348. [Google Scholar] [CrossRef]
- Ryoo, C.S. Differential equations associated with generalized Bell polynomials and their zeros. Open Math. 2016, 14, 807–815. [Google Scholar] [CrossRef]
- Ryoo, C.S. Differential equations associated with the generalized Euler polynomials of the second kind. J. Comput. Appl. Math. 2018, 24, 711–716. [Google Scholar]
- Ryoo, C.S.; Agarwal, R.P.; Kang, J.Y. Differential equations associated with Bell-Carlitz polynomials and their zeros. Neural Parallel Sci. Comput. 2016, 24, 453–462. [Google Scholar]

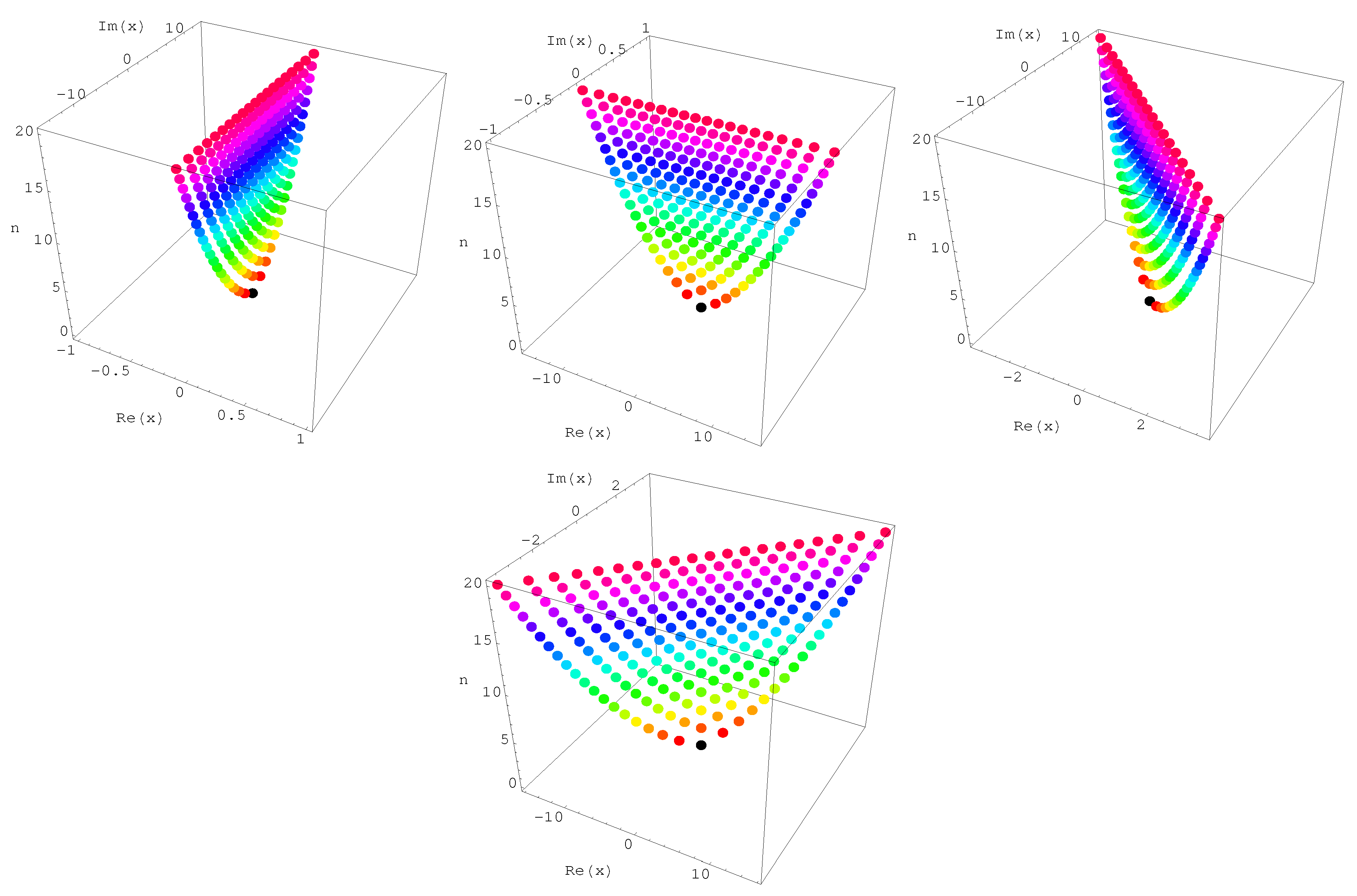
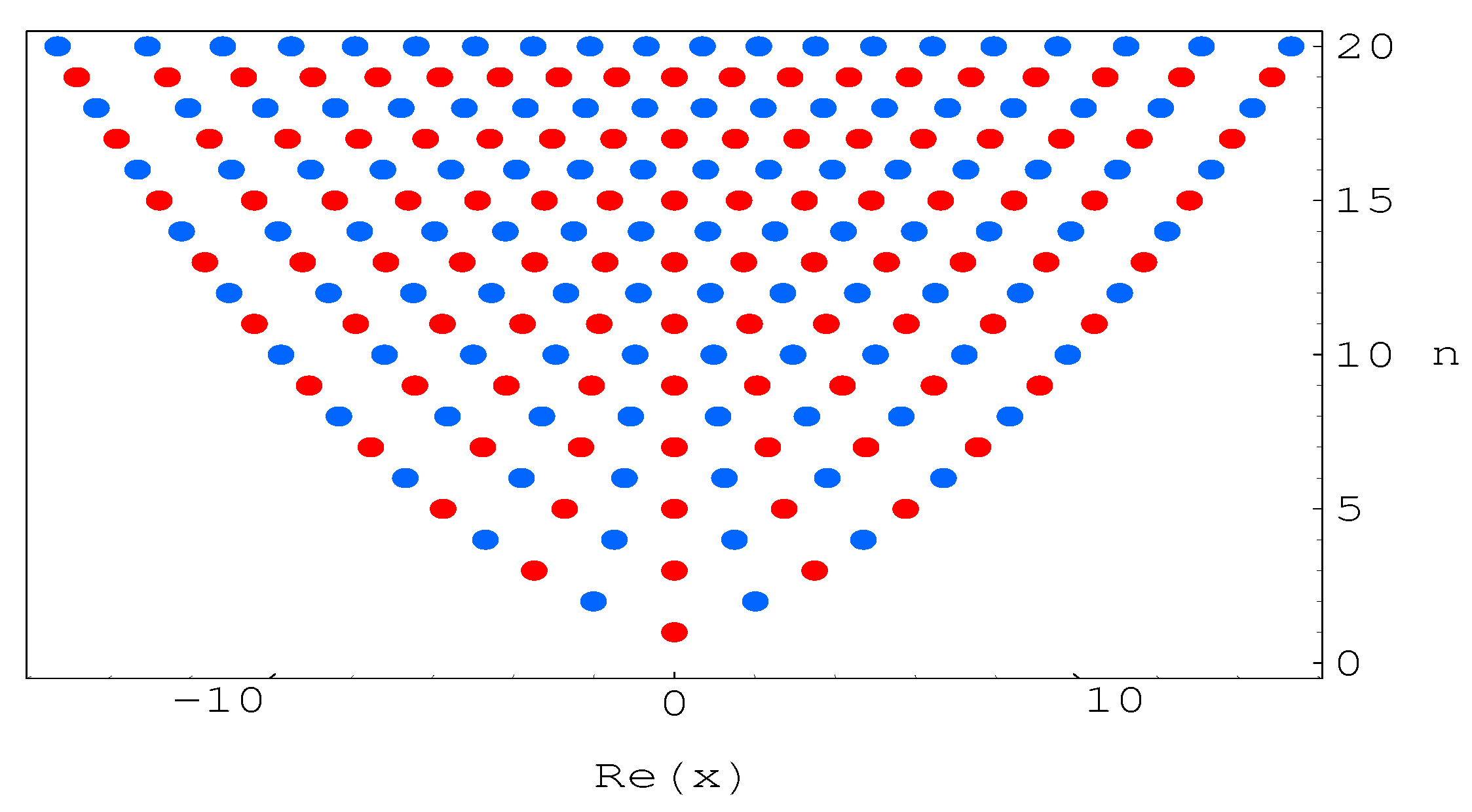
| Degree n | Real Zeros | Complex Zeros |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 2 | 0 |
| 3 | 3 | 0 |
| 4 | 4 | 0 |
| 5 | 5 | 0 |
| 6 | 6 | 0 |
| 7 | 7 | 0 |
| 8 | 8 | 0 |
| 9 | 9 | 0 |
| 10 | 10 | 0 |
| 11 | 11 | 0 |
| 12 | 12 | 0 |
| 13 | 13 | 0 |
| 14 | 14 | 0 |
| ⋮ | ⋮ | ⋮ |
| 29 | 29 | 0 |
| 30 | 30 | 0 |
| Degree n | Real Zeros | Complex Zeros |
|---|---|---|
| 1 | 0 | 1 |
| 2 | 0 | 2 |
| 3 | 0 | 3 |
| 4 | 0 | 4 |
| 5 | 0 | 5 |
| 6 | 0 | 6 |
| 7 | 0 | 7 |
| 8 | 0 | 8 |
| 9 | 0 | 9 |
| 10 | 0 | 10 |
| 11 | 0 | 11 |
| 12 | 0 | 12 |
| 13 | 0 | 13 |
| 14 | 0 | 14 |
| ⋮ | ⋮ | ⋮ |
| 29 | 0 | 29 |
| 30 | 0 | 30 |
| Degree n | x |
|---|---|
| 1 | 0 |
| 2 | −2.0000, 2.0000 |
| 3 | −3.4641, 0, 3.4641 |
| 4 | −4.669, −1.4839, 1.4839, 4.669 |
| 5 | −5.714, −2.711, 0, 2.711, 5.714 |
| 6 | −6.65, −3.778, −1.233, 1.233, 3.778, 6.65 |
| 7 | −7.50, −4.73, −2.309, 0, 2.309, 4.73, 7.50 |
| 8 | −8.3, −5.6, −3.27, −1.078, 1.078, 3.27, 5.6, 8.3 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryoo, C.S. Some Identities Involving Hermite Kampé de Fériet Polynomials Arising from Differential Equations and Location of Their Zeros. Mathematics 2019, 7, 23. https://doi.org/10.3390/math7010023
Ryoo CS. Some Identities Involving Hermite Kampé de Fériet Polynomials Arising from Differential Equations and Location of Their Zeros. Mathematics. 2019; 7(1):23. https://doi.org/10.3390/math7010023
Chicago/Turabian StyleRyoo, Cheon Seoung. 2019. "Some Identities Involving Hermite Kampé de Fériet Polynomials Arising from Differential Equations and Location of Their Zeros" Mathematics 7, no. 1: 23. https://doi.org/10.3390/math7010023
APA StyleRyoo, C. S. (2019). Some Identities Involving Hermite Kampé de Fériet Polynomials Arising from Differential Equations and Location of Their Zeros. Mathematics, 7(1), 23. https://doi.org/10.3390/math7010023




