Constructions of Helicoidal Surfaces in a 3-Dimensional Complete Manifold with Density
Abstract
1. Introduction
2. Preliminaries
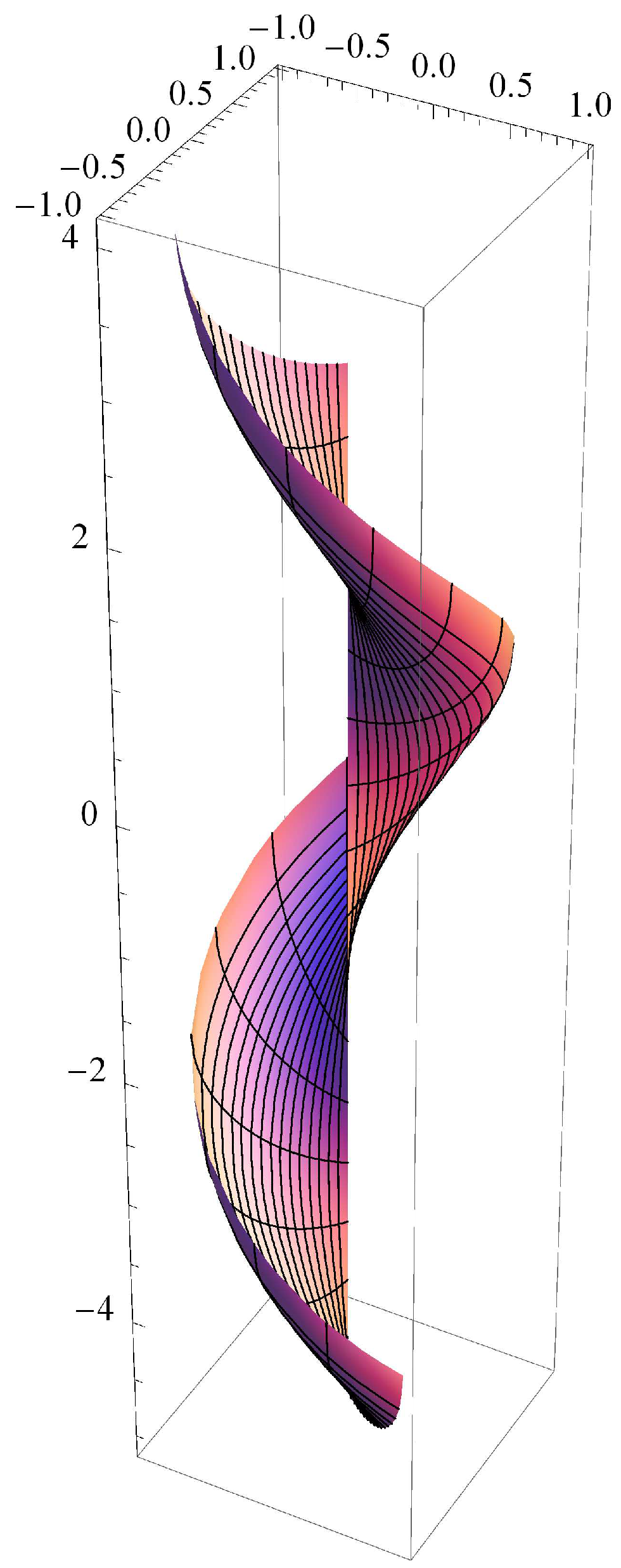
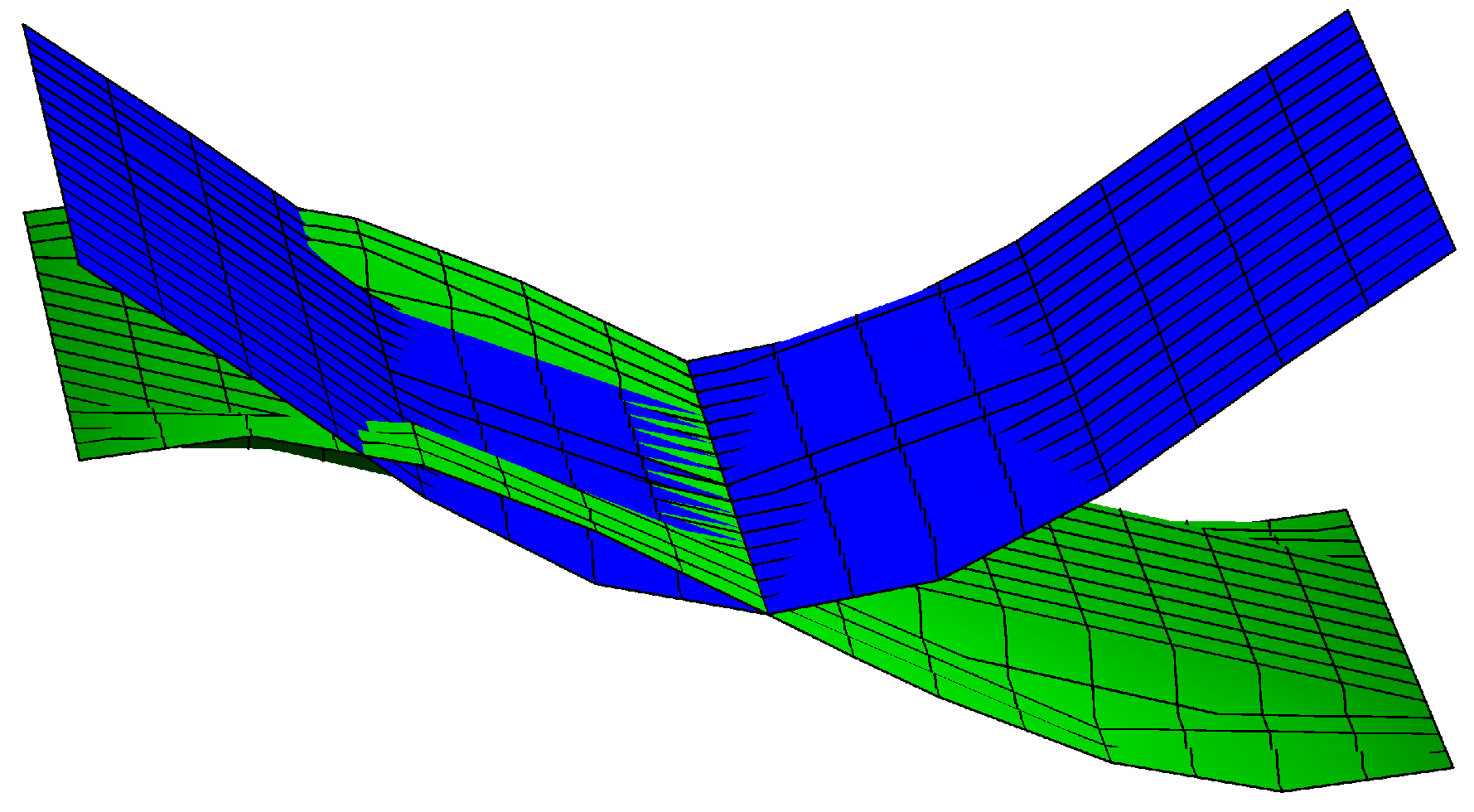
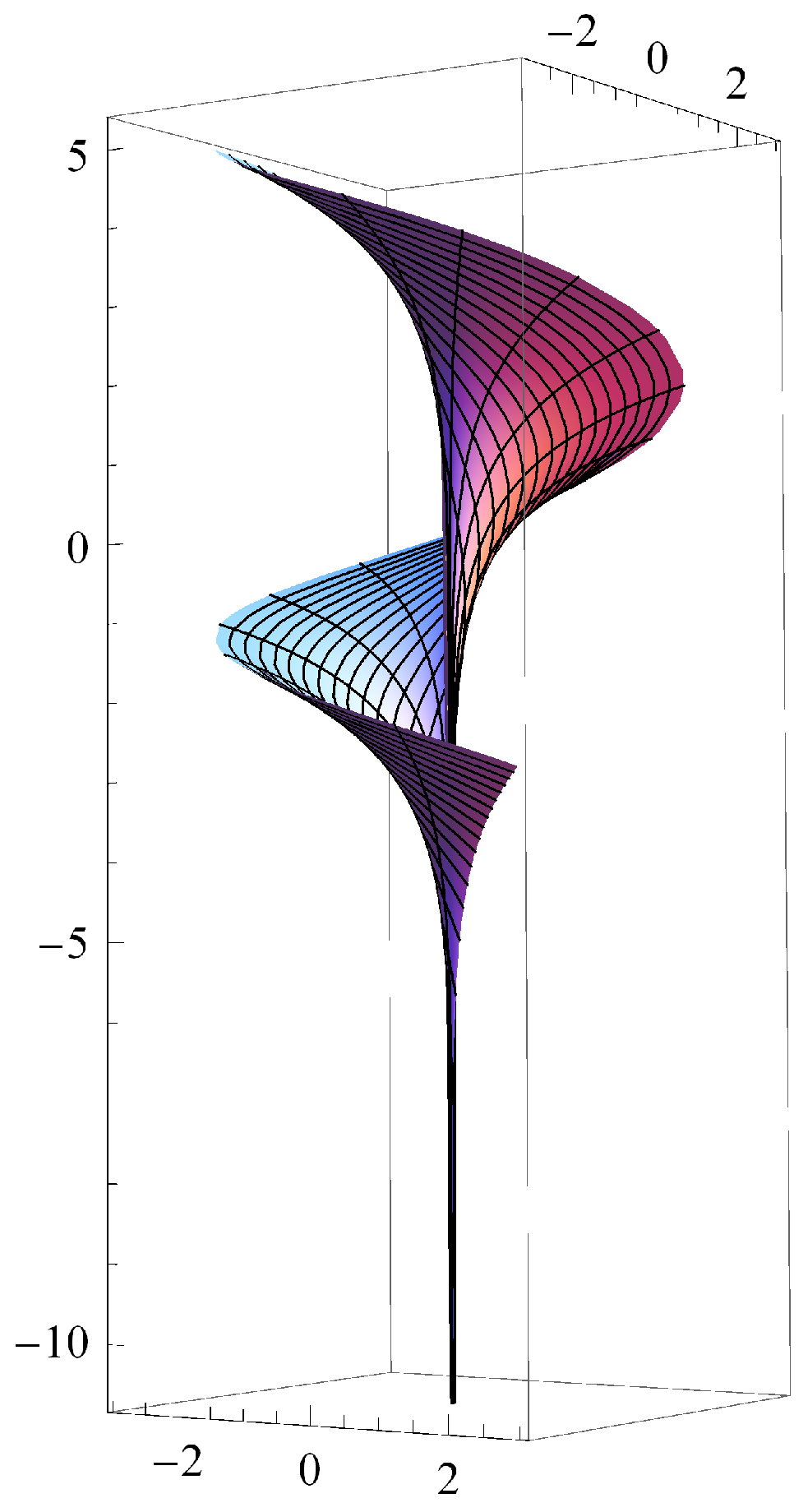
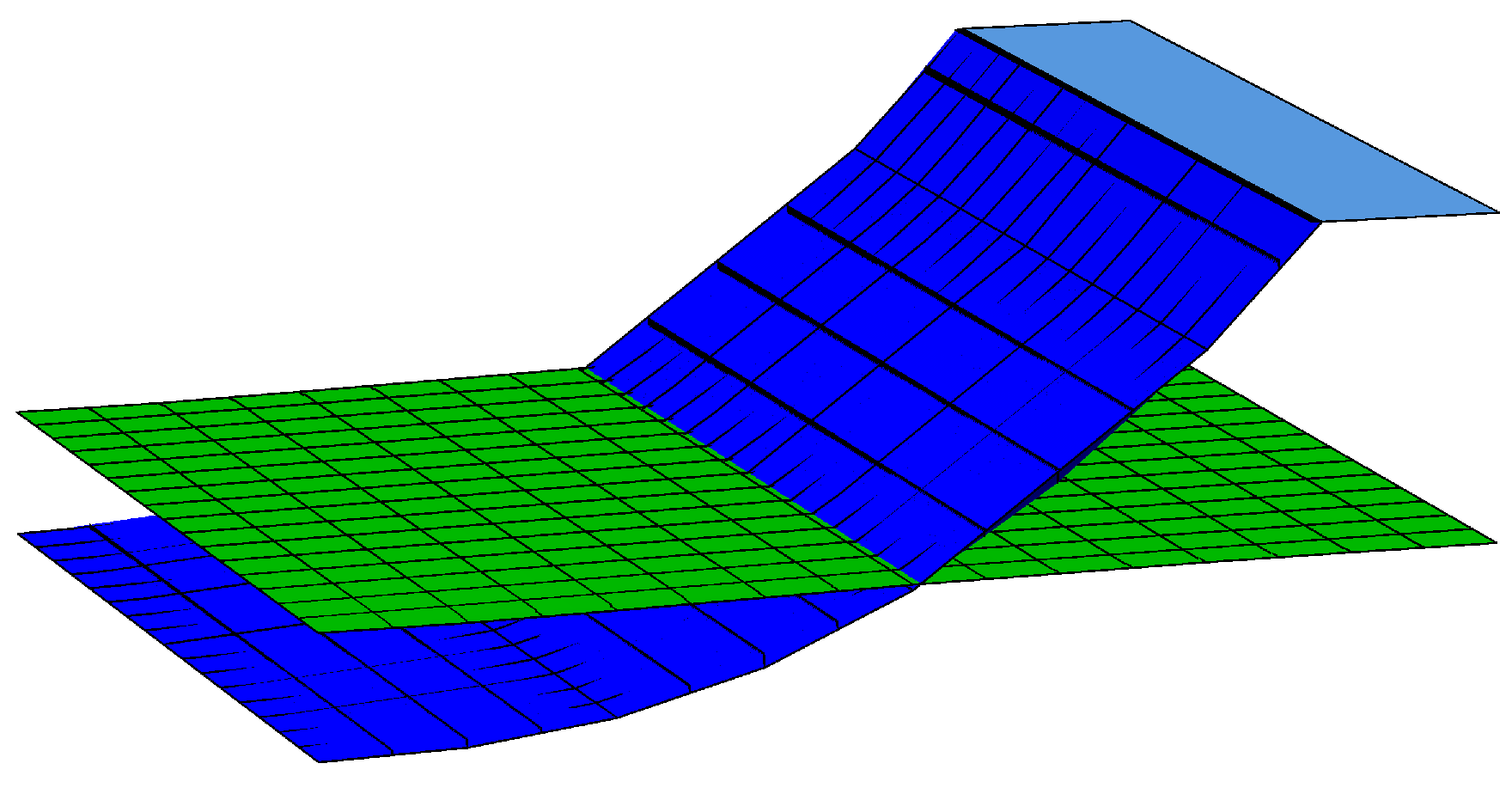
3. Helicoidal Surfaces with Prescribed Weighted Mean or Weighted Extrinsic Curvature
4. Conclusions and Future Work
Funding
Conflicts of Interest
References
- Araujo, K.O.; Cui, N.; Pina, R.D.S. Helicoidal minimal surfaces in a conformally flat 3-space. Bull. Korean Math. Soc. 2016, 53, 531–540. [Google Scholar] [CrossRef]
- Baba-Hamed, C.; Bekkar, M. Helicoidal surfaces in the three-dimensional Lorentz-Minkowski space satisfying ΔIIri = λiri. J. Geom. 2011, 100, 1. [Google Scholar] [CrossRef]
- Choi, M.K.; Kim, Y.H.; Liu, H.; Yoon, D.W. Helicoidal surfaces and their Gauss map in Minkowski 3-space. Bull. Korean Math. Soc. 2010, 47, 859–881. [Google Scholar] [CrossRef]
- Delaunay, C.H. Sur la surface de révolution dont la courbure moyenne est constante. J. Math. Appl. 1841, 6, 309–314. [Google Scholar]
- Do Carmo, M.P.; Dajczer, M. Helicoidal surfaces with constant mean curvature. Tohoku Math. J. 1982, 34, 425–435. [Google Scholar]
- Güler, E.; Turgut Vanli, A. On the mean, gauss, the second gaussıan and the second mean curvature of the Helicoidal surfaces with light-like axis in . Tsukuba J. Math. 2008, 32, 49–65. [Google Scholar] [CrossRef]
- Güler, E. A new kind helicoidal surface of value m. Int. Electron. J. Geom. 2014, 7, 154–162. [Google Scholar]
- Güler, E. Isometric deformation of (m,n)-type helicoidal surface in the three dimensional Euclidean Space. Mathematics 2018, 6, 226. [Google Scholar] [CrossRef]
- Ji, F.; Hou, Z.H. Helicoidal surfaces under the cubic screw motion in Minkowski 3-space. J. Math. Anal. Appl. 2006, 318, 634–647. [Google Scholar] [CrossRef]
- Lee, C.W.; Lee, J.W.; Yoon, D.W. On Helicoidal Surfaces in a Conformally Flat 3-Space. Mediterr. J. Math. 2017, 14, 164. [Google Scholar] [CrossRef]
- Rafael, L.; Demir, E. Helicoidal surfaces in Minkowski space with constant mean curvature and constant Gauss curvature. Open Math. 2014, 12, 1349–1361. [Google Scholar]
- Roussos, I.M. The helicoidal surfaces as Bonnet surfaces. Tohoku Math. J. Second Ser. 1988, 40, 485–490. [Google Scholar] [CrossRef]
- Baikoussis, C.; Koufogiorgos, T. Helicoidal surfaces with prescribed mean or Gaussian curvature. J. Geom. 1998, 63, 25–29. [Google Scholar] [CrossRef]
- Beneki, C.C.; Kaimakamis, G.; Papantoniou, B.J. Helicoidal surfaces in three-dimensional Minkowski space. J. Math. Anal. Appl. 2002, 275, 586–614. [Google Scholar] [CrossRef]
- Ji, F.; Hou, Z.H. A kind of helicoidal surfaces in 3-dimensional Minkowski space. J. Math. Anal. Appl. 2005, 304, 632–643. [Google Scholar] [CrossRef]
- Yoon, D.W.; Kim, D.S.; Kim, Y.H.; Lee, J.W. Constructions of Helicoidal Surfaces in Euclidean Space with Density. Symmetry 2017, 9, 173. [Google Scholar] [CrossRef]
- Yıldız, Ö.G.; Hızal, S.; Akyiğit, M. Type I+ Helicoidal Surfaces with Prescribed Weighted Mean or Gaussian Curvature in Minkowski Space with Density. Anal. Univ. “Ovidius” Constanta-Ser. Mat. 2018, 26, 1–11. [Google Scholar]
- Hıeu, D.T.; Hoang, N.M. Ruled minimal surfaces in with density ez. Pac. J. Math. 2009, 243, 277–285. [Google Scholar]
- Morgan, F. Geometric Measure Theory: A Beginner’s Guide; Academic Press: New York, NY, USA, 2016. [Google Scholar]
- Morgan, F. Manifolds with density. Not. AMS 2005, 52, 853–858. [Google Scholar]
- Morgan, F. Myers’ theorem with density. Kodai Math. J. 2006, 29, 455–461. [Google Scholar] [CrossRef]
- Morgan, F. Manifolds with Density and Perelman’s Proof of the Poincaré Conjecture. Am. Math. Mon. 2009, 116, 134–142. [Google Scholar] [CrossRef]
- Rayón, P.; Gromov, M. Isoperimetry of waists and concentration of maps. Geom. Funct. Anal. 2003, 13, 178–215. [Google Scholar] [CrossRef]
- Rosales, C.; Cañete, A.; Bayle, V.; Morgan, M. On the isoperimetric problem in Euclidean space with density. Calcul. Var. Partial Differ. Equ. 2008, 31, 27–46. [Google Scholar] [CrossRef]
- Yoon, D.W. Weighted minimal translation surfaces in Minkowski 3-space with density. Int. J. Geom. Methods Mod. Phys. 2017, 14, 1750178. [Google Scholar] [CrossRef]
- Pina, A.V.R.; Souza, M. Surfaces of rotation with constant extrinsic curvature in a conformally flat 3-space. Results Math. 2011, 60, 225. [Google Scholar]
- Corwin, I.; Hoffman, N.; Hurder, S.; Šešum, V.; Xu, Y. Differential geometry of manifolds with density. Rose-Hulman Undergrad. Math. J. 2006, 7, 1–15. [Google Scholar]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yıldız, Ö.G. Constructions of Helicoidal Surfaces in a 3-Dimensional Complete Manifold with Density. Mathematics 2019, 7, 27. https://doi.org/10.3390/math7010027
Yıldız ÖG. Constructions of Helicoidal Surfaces in a 3-Dimensional Complete Manifold with Density. Mathematics. 2019; 7(1):27. https://doi.org/10.3390/math7010027
Chicago/Turabian StyleYıldız, Önder Gökmen. 2019. "Constructions of Helicoidal Surfaces in a 3-Dimensional Complete Manifold with Density" Mathematics 7, no. 1: 27. https://doi.org/10.3390/math7010027
APA StyleYıldız, Ö. G. (2019). Constructions of Helicoidal Surfaces in a 3-Dimensional Complete Manifold with Density. Mathematics, 7(1), 27. https://doi.org/10.3390/math7010027




