Time-Space Fractional Coupled Generalized Zakharov-Kuznetsov Equations Set for Rossby Solitary Waves in Two-Layer Fluids
Abstract
:1. Introduction
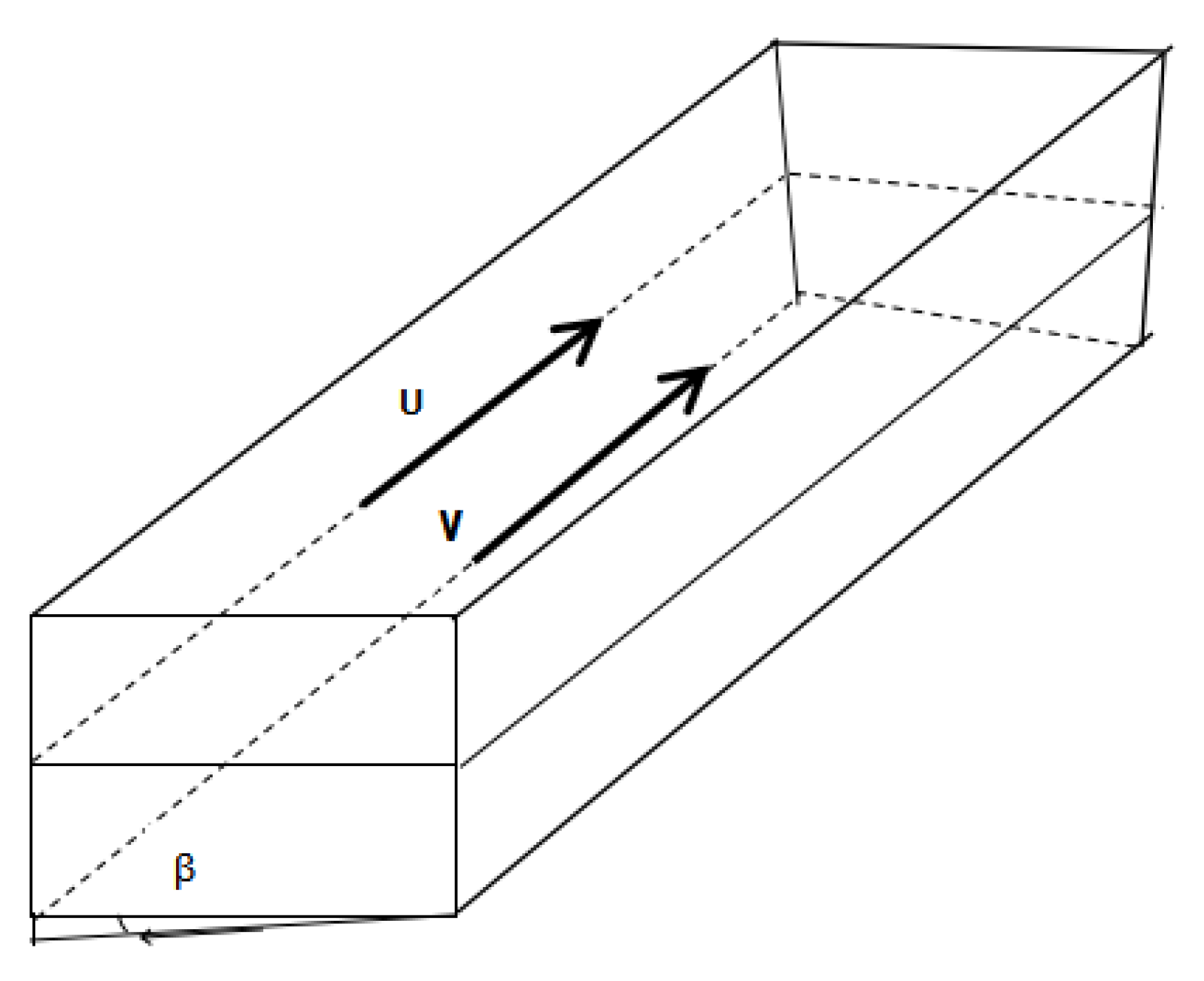
2. Derivation of Coupled gZK Equations Set
3. The Time-Space Fractional Coupled gZK Equations set
4. Solutions of Time-Space Fractional Coupled gZK Equations Set
- (i)
- When , the hyperbolic solutions as:
- (ii)
- When , the trigonometric solutions as:
- (iii)
- When , the solutions as:where are arbitrary constants, .
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pedlosky, J. Geophysical Fluid Dynamics; Springer-Verlag: New York, NY, USA, 1987. [Google Scholar]
- Yang, H.W.; Zhao, Q.F.; Yin, B.S.; Dong, H.H. A new integro-differential equation for Rossby solitary waves with topography effect in deep rotational fluids. Abstr. Appl. Anal. 2013, 2013, 597807. [Google Scholar] [CrossRef]
- Guo, M.; Dong, H.Y.; Liu, J.X.; Yang, H.W. The time-fractional mZK equation for gravity solitarywaves and solutions using sech-tanh and radial basic function method. Nonlinear Anal. Model. Control 2018, 24, 1–19. [Google Scholar] [CrossRef]
- Caillol, P.; Grimshaw, R.H. Rossby solitary waves in the presence of a critical layer. Stud. Appl. Math. 2007, 118, 313–364. [Google Scholar] [CrossRef]
- Yuan, C.; Grimshaw, R.; Johnson, E.; Chen, X. The propagation of internal solitary waves over variable topography in a horizontally two-dimensional framework. J. Phys. Oceanogr. 2018, 48, 283–300. [Google Scholar] [CrossRef]
- Yuan, C.; Grimshaw, R.; Johnson, E.; Wang, Z. Topographic effect on oblique internal wave-wave interactions. J. Fluid Mech. 2018, 856, 36–60. [Google Scholar] [CrossRef]
- Preusse, M.; Freistühler, H.; Peeters, F. Seasonal variation of solitary wave properties in Lake Constance. J. Geophys. Res. 2012, 117, C04026. [Google Scholar] [CrossRef]
- Ulloa, H.N.; de la Fuente, A.; Niño, Y. An experimental study of the free evolution of rotating, nonlinear internal gravity waves in a two-layer stratified fluid. J. Fluid Mech. 2014, 742, 308–339. [Google Scholar] [CrossRef]
- Ulloa, H.N.; de la Fuente, A.; Niño, Y. Degeneration of internal Kelvin waves in a continuous two-layer stratification. J. Fluid Mech. 2015, 777, 68–96. [Google Scholar] [CrossRef]
- Hukuda, H. Solitary Rossby waves in a two-layer system. Tellus 1979, 31, 161–169. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.J.; Wang, R.Y.; Sun, W.J.; Yang, H.W. Combined ZK-mZK equation for Rossby solitary waves with complete coriolis force and its conservation laws as well as exact solutions. Adv. Differ. Equ. 2018, 2018, 42. [Google Scholar] [CrossRef]
- Yang, H.W.; Chen, X.; Guo, M.; Chen, Y.D. A new ZK-BO equation for three-dimensional algebraic Rossby solitary waves and its solution as well as fission property. Nonlinear Dyn. 2017, 91, 2019–2032. [Google Scholar] [CrossRef]
- Tang, X.Y.; Liang, Z.F.; Hao, X.Z. Nonlinear waves of a nonlocal modified KdV equation in the atmospheric and oceanic dynamical system. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 62–71. [Google Scholar] [CrossRef]
- Yin, J.L.; Ding, S.Y.; Tian, L.X.; Fan, X.H.; Deng, X.Y. Existence of exotic waves for the nonlinear dispersive mKdV equation. Appl. Math. Comput. 2014, 229, 499–504. [Google Scholar] [CrossRef]
- Lu, C.N.; Fu, C.; Yang, H.W. Time-fractional generalized Boussinesq Equation for Rossby solitary waves with dissipation effect in stratified fluid and conservation laws as well as exact solutions. Appl. Math. Comput. 2018, 327, 104–116. [Google Scholar] [CrossRef]
- Yin, X.J.; Yang, L.G.; Liu, Q.S.; Wu, G.R. (2+1)-dimensional ZK-Burgers equation with the generalized beta effect and its exact solitary solution. Comput. Math. Appl. 2019, 77, 302–310. [Google Scholar] [CrossRef]
- Yang, H.W.; Guo, M.; He, H.L. Conservation laws of space-time fractional mZK equation for Rossby solitary waves with complete coriolis force. Int. J. Nonlinear Sci. Numer. Simul. 2018. [Google Scholar] [CrossRef]
- Zou, L.; Yu, Z.B.; Wang, X.B. Dynamics of the breather waves, rogue waves and solitary waves in an extend Kadomtsev-Petviashvili equation. Appl. Math. Lett. 2018, 83, 73–79. [Google Scholar] [CrossRef]
- Bracco, A.; Pedlosky, J. Votex generation by topopraphy in locally unstable baroclinic flows. J. Phys. Oceanogr. 2003, 33, 207–219. [Google Scholar] [CrossRef]
- Atangana, A.; Secer, A. The time-fractional coupled-Korteweg-de-Vries equations. Abstr. Appl. Anal. 2013, 2013, 947986. [Google Scholar] [CrossRef]
- Eslami, M. Exact traveling wave solutions to the fractional coupled nonlinear Schrodiger equations. Appl. Math. Comput. 2016, 285, 141–148. [Google Scholar]
- Lou, S.Y.; Tong, B.; Hu, H.C.; Tang, X.Y. Coupled KdV equations derived from two-layer fluids. J. Phys. Math. Gen. 2005, 38, 1–15. [Google Scholar] [CrossRef]
- Farwig, R.; Qian, C. Asymptotic behavior for the quasi-geostrophic equations with fractional dissipation in R2. J. Differ. Equ. 2018. [Google Scholar] [CrossRef]
- Fu, C.; Lu, C.N.; Yang, H.W. Time-space fractional (2 + 1)-dimensional nonlinear Schrodinger equation for envelope gravity waves in baroclinic atmosphere and conservation laws as well as exact solutions. Adv. Differ. Equ. 2018, 2018, 56. [Google Scholar] [CrossRef]
- Yang, H.W.; Yin, B.S.; Shi, Y.L.; Wang, Q.B. Forced ILW-Burgers equation as a model for Rossby solitary waves generated by topography in finite depth fluids. J. Appl. Math. 2012, 2012, 491343. [Google Scholar] [CrossRef]
- Yang, H.W.; Xu, Z.H.; Yang, D.Z.; Feng, X.R.; Yin, B.S.; Dong, H.H. ZK-Burgers equation for three-dimensional Rossby solitary waves and its solutions as well as chirp effect. Adv. Differ. Equ. 2016, 2016, 167. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.A.T.; Baleanu, D. Exact traveling-wave solution for local fractional boussinesq equation in fractal domain. Fractals 2017, 25, 1740006. [Google Scholar] [CrossRef]
- Guo, M.; Fu, C.; Zhang, Y.; Liu, J.X.; Yang, H.W. Study of Ion-Acoustic solitary waves in a magnetized plasma using the three-dimensional time-space fractional Schamel-KdV equation. Complexity 2018, 2018, 6852548. [Google Scholar] [CrossRef]
- Zhang, L.F.; He, Z.H.; Conti, C.; Wang, Z.T.; Hu, Y.H.; Lei, D.J.; Li, Y.; Fan, D.Y. Modulational instability in fractional nonlinear Schrodinger equation. Commum. Nonlinear Sci. Numer Simul. 2017, 48, 531–540. [Google Scholar] [CrossRef]
- Yang, H.W.; Sun, J.C.; Fu, C. Time-fractional Benjamin-Ono equation for algebraic gravity solitary waves in baroclinic atmosphere and exact multi-soliton solution as well as interaction. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 187–201. [Google Scholar] [CrossRef]
- I-Wakil, S.A.E.; Abulwafa, E.M.; I-Shewy, E.K.E.; Mahmoud, A.A. Ion-acoustic waves in unmagnetized collisionless weakly relativistic plasma of warm-ion and isothermal-electron using time-fractional KdV equation. Sci. Verse Sci. Direct. 2012, 49, 1721–1727. [Google Scholar]
- Ma, W.X.; Yong, X.L.; Zhang, H.Q. Diversity of interaction solutions to the (2+1)-dimensional Ito equation. Comput. Math. Appl. 2018, 75, 289–295. [Google Scholar] [CrossRef]
- Wang, X.H.; Wang, Z.; Huang, X.; Li, Y.X. Dynamic analysis of a fractional-order delayed SIR model with saturated incidence and treatment functions. Int. J. Bifurc. Chaos 2018, 28, 1850180. [Google Scholar]
- Yang, X.J.; Gao, F.; Srivastava, M.H. A new computational approach for solving nonlinear local fractional PDEs. J. Comput. Appl. Math. 2018, 339, 285–296. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhou, Y. Lump solutions to nonlinear partial differential equations via hirota bilinear forms. J. Differ. Equ. 2018, 264, 2639–2659. [Google Scholar] [CrossRef]
- Zhao, H.Q.; Ma, W.X. Mixed lump-kink solutions to the KP equation. Comput. Math. Appl. 2017, 74, 1399–1405. [Google Scholar] [CrossRef]
- Guner, O.; Aksoy, E.; Bekir, A.; Cevikel, A.C. Different methods for (3+1)-dimensional space-time fractional modified KdV-Zakharov-Kuznetsov equation. Comput. Math. Appl. 2016, 71, 1259–1269. [Google Scholar] [CrossRef]
- Guo, M.; Zhang, Y.; Wang, M.; Chen, Y.D.; Yang, H.W. A new ZK-ILW equation for algebraic gravity solitary waves in finite depth stratified atmosphere and the research of squall lines formation mechanism. Comput. Math. Appl. 2018, 75, 3589–3603. [Google Scholar] [CrossRef]
- Tao, M.S.; Dong, H.H. Algebro-Geometric solutions for a discrete integrable equation. Discret. Dyn. Nat. Soc. 2017, 2017, 5258375. [Google Scholar] [CrossRef]
- Zou, Y.M.; Cui, Y.J. Existence results for a functional boundary value problem of fractional differential equations. Adv. Differ. Equ. 2013, 1, 233. [Google Scholar] [CrossRef]
- Bai, Z.B.; Sun, W.C. Existence and multiplicity of positive solutions for singular fractional boundary value problems. Comput. Math. Appl. 2012, 63, 1369–1381. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, S.; Ray, S.S. Solitary wave solutions for time fractional third order modified KdV equation using two raliable techniques (G′/G)-expansion method and improved (G′/G)-expansion method. Phys. A 2016, 448, 265–282. [Google Scholar] [CrossRef]
- Islam, M.N.; Akbar, M.A. New exact wave solutions to the space-time fractional coupled Burgers equationa and the space-time fractional foam drainage equation. Cog. Phys. 2018, 5, 1422957. [Google Scholar]
- Sahoo, S.; Ray, S.S. Improved fractional sun-equation method for (3+1)-dimensional generalized fractional KdV-Zakharov-Kuznetsov equations. Comput. Math. Appl. 2015, 70, 158–166. [Google Scholar] [CrossRef]
- He, J.H.; Wu, G.C.; Austin, F. The variational iteration method which should be followed. Nonlinear Sci. Lett. A Math. Phys. Mech. 2010, 1, 1–30. [Google Scholar]
- Shallal, M.A.; Jabbar, H.N.; Ali, K.K. Analytic solution for the space-time fractional Klein-Gordon and coupled conformable Boussinesq equations. Results Phys. 2018, 8, 372–378. [Google Scholar] [CrossRef]
- Khater, M.A.; Seadawy, A.R.; Lu, D. Elliptic and solitary wave solutions for Bogoyavlenskii equations system, coupled Boiti-Leon-Pempinelli equations system and time-fractional Cahn-Allen equation. Results Phys. 2017, 7, 2325–2333. [Google Scholar] [CrossRef]
- Zeidan, D. Assessment of mixture two-phase flow equations for volcanic flows using Godunov-type methods. Appl. Math. Comput. 2016, 272, 707–719. [Google Scholar] [CrossRef]
- Tao, M.S.; Zhang, N.; Gao, D.Z.; Yang, H.W. Symmetry analysis for three-dimensional dissipation Rossby waves. Adv. Differ. Equ. 2018, 2018, 300. [Google Scholar] [CrossRef]
- Ma, W.X. Conservation laws by symmetries and adjoint symmetries. Discret. Conti. Dyn. Syst. Ser. S 2018, 11, 707–721. [Google Scholar] [CrossRef]
- Shi, Y.L.; Yin, B.S.; Yang, H.W.; Yang, D.Z.; Xu, Z.H. Dissipative nonlinear Schrodinger equation ror envelope solitary Rossby waves with dissipation effect in stratified fluids and its solution. Abstr. Appl. Anal. 2014, 2014, 643652. [Google Scholar] [CrossRef]
- I-Wakil, S.A.E.; Abulwafa, E.M. Formulation and solution of space-time fractional Boussinesq equation. Nonlinear Dyn. 2015, 80, 167–175. [Google Scholar] [CrossRef]
- Agrawal, O.P. Formulation of Euler-Lagrange equation for fractional variational problems. J. Math. Anal. Appl. 2002, 272, 368–379. [Google Scholar] [CrossRef]
- I-Wakil, S.A.E.; Abulwafa, E.M.; Zahran, M.A.; Mahmoud, A.A. Time-fractional KdV equational: formulation and solution using variational methods. Nonlinear Dyn. 2011, 65, 55–63. [Google Scholar] [CrossRef]
- He, J.H. A tutorial and heuristic review on Lagrange multiplier for optimal problems. Nonlinear Sci. Lett. A 2017, 8, 121–148. [Google Scholar]
- He, J.H. Fractal calculus and its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- Baleanu, D.; Muslih, S.I. Lagrangian formulationof classical fields within Riemann-Liouville fractional derivatives. Phys. Scr. 2005, 72, 119–123. [Google Scholar] [CrossRef]
- Agrawal, O.P. A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 2004, 38, 323–337. [Google Scholar] [CrossRef]
- Agrawal, O.P. Fractional variational calculus and thetransversality conditions. J. Phys. A Math. Gen. 2006, 39, 10375. [Google Scholar] [CrossRef]
- Agrawal, O.P. Fractional variational calculus in terms of Riesz fractional derivatives. J. Phys. A Math. Theor. 2007, 40, 6287–6303. [Google Scholar] [CrossRef]
- Zeidan, D.; Sekhar, T.R. On the wave interactions in the drift-flux equations of two-phase flows. Appl. Math. Comput. 2018, 327, 117–131. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Chen, Y.; Yang, H. Time-Space Fractional Coupled Generalized Zakharov-Kuznetsov Equations Set for Rossby Solitary Waves in Two-Layer Fluids. Mathematics 2019, 7, 41. https://doi.org/10.3390/math7010041
Fu L, Chen Y, Yang H. Time-Space Fractional Coupled Generalized Zakharov-Kuznetsov Equations Set for Rossby Solitary Waves in Two-Layer Fluids. Mathematics. 2019; 7(1):41. https://doi.org/10.3390/math7010041
Chicago/Turabian StyleFu, Lei, Yaodeng Chen, and Hongwei Yang. 2019. "Time-Space Fractional Coupled Generalized Zakharov-Kuznetsov Equations Set for Rossby Solitary Waves in Two-Layer Fluids" Mathematics 7, no. 1: 41. https://doi.org/10.3390/math7010041
APA StyleFu, L., Chen, Y., & Yang, H. (2019). Time-Space Fractional Coupled Generalized Zakharov-Kuznetsov Equations Set for Rossby Solitary Waves in Two-Layer Fluids. Mathematics, 7(1), 41. https://doi.org/10.3390/math7010041





