Explicit Solutions and Bifurcations for a System of Rational Difference Equations
Abstract
:1. Introduction and Preliminaries
2. The General Solution
3. Bifurcation Analysis
- (i)
- The fixed point is stable for and unstable for .
- (ii)
- The fixed point is stable for and unstable for .
- (iii)
- The fixed point is stable for and unstable for .
- (i)
- The fixed points and lose stability via a 1:4 resonance Neimark–Sacker bifurcation point (NS) when for which , .
- (ii)
- The fixed points and lose stability via a branching point (BP) when for which . The BP corresponds to the appearance where the curves of the fixed points and are intersect. This indicates the existence of other cycles with higher periods.
- (iii)
- The fixed points and lose stability via a fold-flip period-doubling bifurcation point (PD) when for which and .
- (iv)
- We can always find a neutral-saddle point (nS) points for which along the curves of the fixed points
- (a)
- when .
- (b)
- when .
Author Contributions
Funding
Conflicts of Interest
References
- Kelley, W.; Peterson, A. Difference Equations: An Introduction with Applications, 2nd ed.; Academic Press: New York, NY, USA, 2001. [Google Scholar]
- Mickens, R.E. Difference Equations: Theory, Applications and Advanced Topics, 3rd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- Kocic, V.L.; Ladas, G. Global Behavior of Nonlinear Difference Equations of Higher Order with Applications; Kluwer Academic: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Kulenovic, M.R.S.; Ladas, G. Dynamics of Second Order Rational Difference Equations: With Open Problems and Conjectures; Chapman and Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Kulenovic, M.R.S.; Merino, O. Discrete Dynamical Systems and Difference Equations with Mathematica; Chapman & Hall/CRC: London, UK, 2002. [Google Scholar]
- Amleh, A.M.; Grove, E.A.; Ladas, G.; Georgiou, D.A. On the Recursive Sequence xn+1 = α + xn−1/xn. J. Math. Anal. Appl. 1999, 2332, 790–798. [Google Scholar] [CrossRef]
- Cinar, C. On the positive solutions of the difference equation system xn+1 = 1/yn, yn+1 = yn/(xn−1yn−1). Appl. Math. Comput. 2004, 158, 303–305. [Google Scholar]
- Clark, C.A.; Kulenovic, M.R.S.; Selgrade, J.F. On a system of rational difference equations. J. Differ. Equ. Appl. 2005, 11, 565–580. [Google Scholar] [CrossRef]
- Kurbanli, A.S.; Cinar, C.; Yalcinkaya, I. On the behavior of positive solutions of the system of rational difference equations xn+1 = xn−1/(ynxn−1 + 1), yn+1 = yn−1/(xnyn−1 + 1). Math. Comput. Model. 2011, 53, 1261–1267. [Google Scholar] [CrossRef]
- Yalcinkaya, I.; Cinar, C.; Atalay, M. On the solutions of systems of difference equations. Adv. Differ. Equ. 2008, 2008, 143943. [Google Scholar] [CrossRef]
- Khyat, T. Bifurcations of Some Planar Discrete Dynamical Systems with Applications. Ph.D. Thesis, University of Rhode Island, Kingston, RI, USA, 2017. [Google Scholar]
- Kurbanli, A.S. On the behavior of solutions of the system of rational difference equations xn+1 = xn−1/(ynxn−1 − 1), yn+1 = yn−1/(xnyn−1 − 1), zn+1 = 1/(ynzn). Adv. Differ. Equ. 2011, 2011, 40. [Google Scholar] [CrossRef]
- Elsayed, E.M.; El-Metwally, H. On the solutions of some nonlinear systems of difference equations. Adv. Differ. Equ. 2013, 2013, 161. [Google Scholar] [CrossRef] [Green Version]
- El-Dessoky, M.M. On a solvable for some systems of rational difference equations. J. Nonlinear Sci. Appl. 2016, 9, 3744–3759. [Google Scholar] [CrossRef] [Green Version]
- Elaydi, S. Discrete Chaos; Chapman & Hall/CRC: London, UK, 2000. [Google Scholar]
- Arnold, V.I. Geometrical Methods in the Theory of Ordinary Differential Equations; Springer: New York, NY, USA; Heidelberg/Berlin, Germany, 1983. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory, 3rd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Khoshsiar Ghaziani, R. Bifurcations of Maps: Numerical Algorithms and Applications. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2008. [Google Scholar]
- Govaerts, W.; Kuznetsov, Y.A.; Khoshsiar Ghaziani, R.; Meijer, H.G.E. CL_MATCONTM: A Toolbox for Continuation and Bifurcation of Cycles of Maps; Report; Ghent University: Ghent, Belgium; Utrecht University: Utrecht, The Netherlands, 2008. [Google Scholar]
- Neirynck, N.; Al-Hdaibat, B.; Govaerts, W.; Kuznetsov, Y.A.; Meijer, H.G.E. Using MatContM in the study of a nonlinear map in economics. J. Phys. Conf. Ser. 2016, 692, 012013. [Google Scholar] [CrossRef] [Green Version]
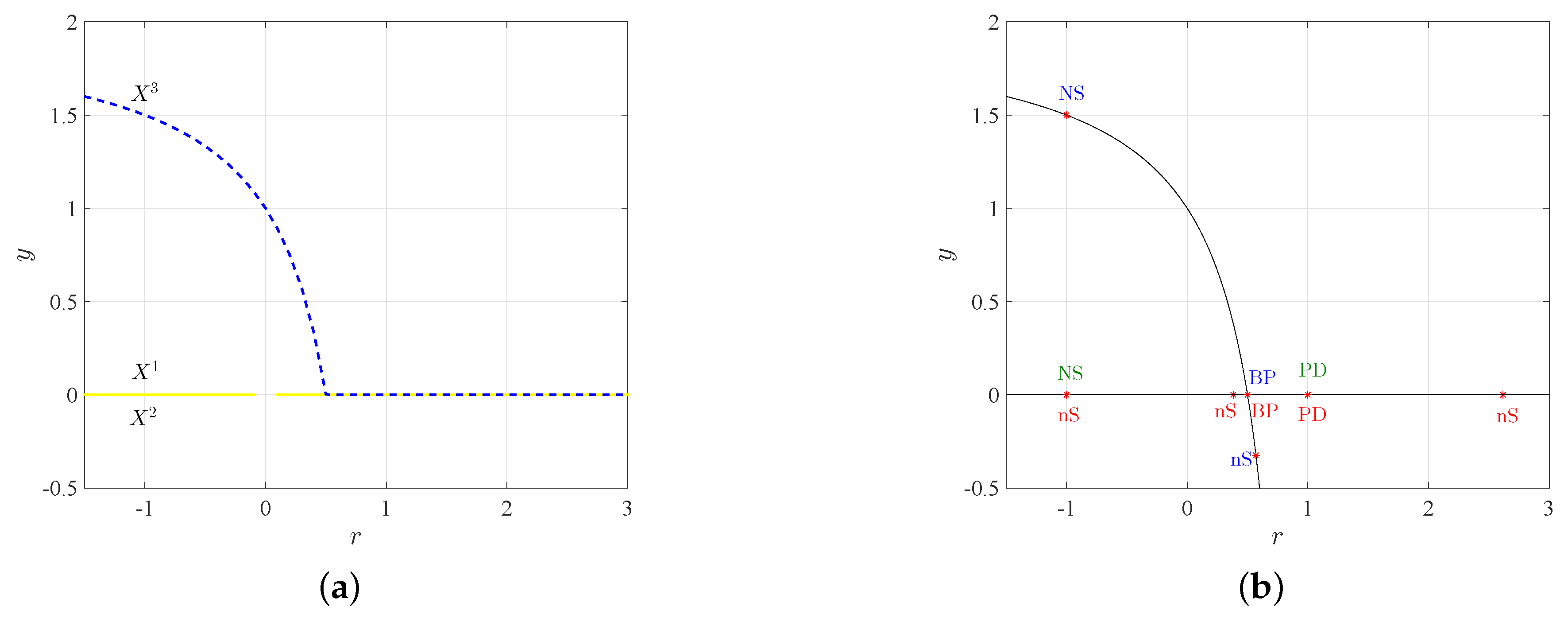

| Fixed Point | |||
|---|---|---|---|
| 0 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Hdaibat, B.; Al-Ashhab, S.; Sabra, R. Explicit Solutions and Bifurcations for a System of Rational Difference Equations. Mathematics 2019, 7, 69. https://doi.org/10.3390/math7010069
Al-Hdaibat B, Al-Ashhab S, Sabra R. Explicit Solutions and Bifurcations for a System of Rational Difference Equations. Mathematics. 2019; 7(1):69. https://doi.org/10.3390/math7010069
Chicago/Turabian StyleAl-Hdaibat, Bashir, Saleem Al-Ashhab, and Ramadan Sabra. 2019. "Explicit Solutions and Bifurcations for a System of Rational Difference Equations" Mathematics 7, no. 1: 69. https://doi.org/10.3390/math7010069




