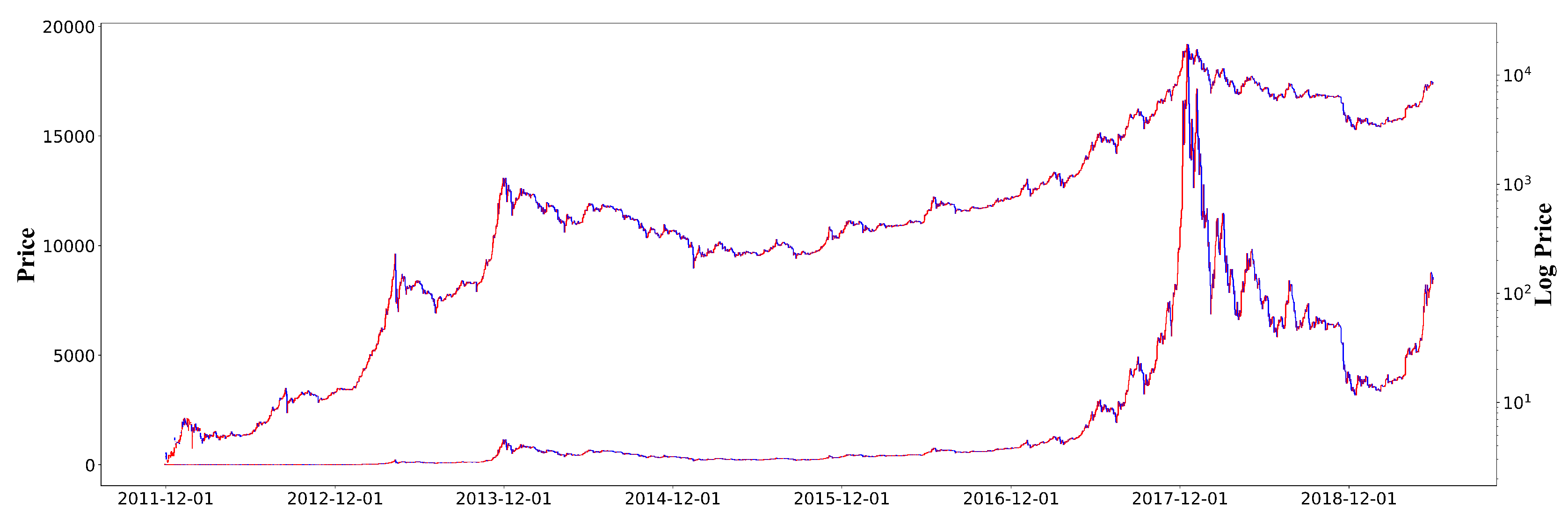
Figure 1.
Bitcoin daily prices on Bitstamp (USD) from 29 November 2011 to 31 December 2018. The upper line shows log prices, whereas the lower line shows plain prices. Some recurring patterns seem to exist when considering the log value of the Bitcoin price.
Figure 1.
Bitcoin daily prices on Bitstamp (USD) from 29 November 2011 to 31 December 2018. The upper line shows log prices, whereas the lower line shows plain prices. Some recurring patterns seem to exist when considering the log value of the Bitcoin price.
Figure 2.
Spearman rank correlation coefficient matrix between Bitcoin blockchain features.
Figure 2.
Spearman rank correlation coefficient matrix between Bitcoin blockchain features.
Figure 3.
Changes in the values of selected features.
Figure 3.
Changes in the values of selected features.
Figure 4.
Data preprocessing. A total of sequence data are generated from the whole dataset of 2590 days if m consecutive days are analyzed to predict the next Bitcoin price.
Figure 4.
Data preprocessing. A total of sequence data are generated from the whole dataset of 2590 days if m consecutive days are analyzed to predict the next Bitcoin price.
Figure 5.
An example of fully-connected deep neural network (DNN) model.
Figure 5.
An example of fully-connected deep neural network (DNN) model.
Figure 6.
Recurrent neural network (RNN) model (left) and long short-term memory (LSTM) model (right).
Figure 6.
Recurrent neural network (RNN) model (left) and long short-term memory (LSTM) model (right).
Figure 7.
Our CNN model. It consists of a single 2D convolution layer where 36 filters of size are used for convolution. An input matrix is translated into an matrix by the Conv2D layer.
Figure 7.
Our CNN model. It consists of a single 2D convolution layer where 36 filters of size are used for convolution. An input matrix is translated into an matrix by the Conv2D layer.
Figure 8.
Our ResNet model. It uses four residual blocks which implement shortcut connections between two convolution layers.
Figure 8.
Our ResNet model. It uses four residual blocks which implement shortcut connections between two convolution layers.
Figure 9.
Our CRNN model (a combination of CNNs and RNNs) that combines the results of CNN and LSTM models using a concatenation operator. The Conv2D block represents the 2D convolution layer in
Figure 7 and the LSTM block represents the LSTM model discussed in Secion
Section 3.2.2.
Figure 9.
Our CRNN model (a combination of CNNs and RNNs) that combines the results of CNN and LSTM models using a concatenation operator. The Conv2D block represents the 2D convolution layer in
Figure 7 and the LSTM block represents the LSTM model discussed in Secion
Section 3.2.2.
Figure 10.
Stacking ensemble model: DNN, LSTM, and CNN are used as base learners at the first level and another DNN as a meta learner at the second level.
Figure 10.
Stacking ensemble model: DNN, LSTM, and CNN are used as base learners at the first level and another DNN as a meta learner at the second level.
Figure 11.
Prediction results of the DNN model with . The log values of the major features, the sequential partitioning, and the first value-based normalization were used.
Figure 11.
Prediction results of the DNN model with . The log values of the major features, the sequential partitioning, and the first value-based normalization were used.
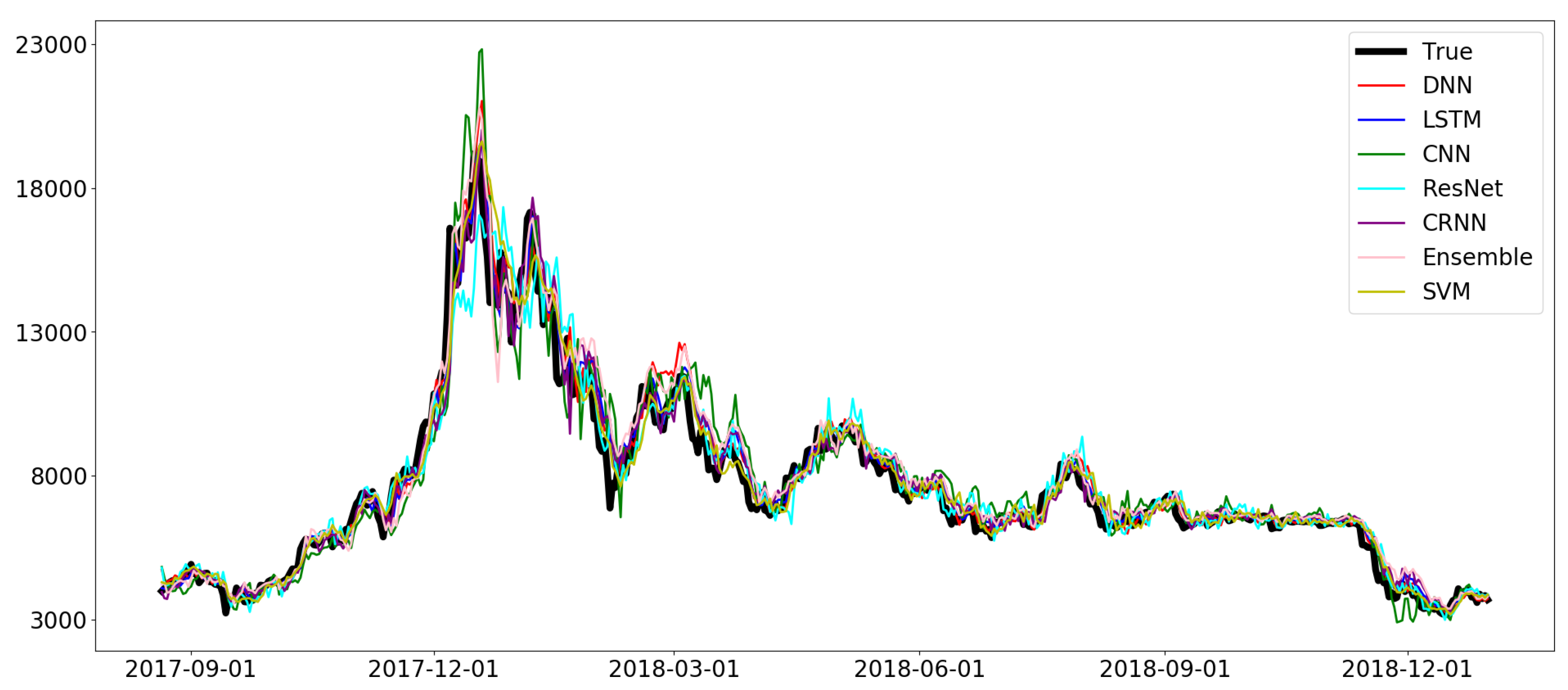
Figure 12.
Prediction results of the proposed models with . The log values of the major features, the sequential partitioning, and the first value-based normalization were used.
Figure 12.
Prediction results of the proposed models with . The log values of the major features, the sequential partitioning, and the first value-based normalization were used.
Figure 13.
Prediction results of DNN with
(
left) and prediction results of DNN and LSTM with
(
right) from 1 December 2017 to 1 April 2018, excerpted from
Figure 11 and
Figure 12.
Figure 13.
Prediction results of DNN with
(
left) and prediction results of DNN and LSTM with
(
right) from 1 December 2017 to 1 April 2018, excerpted from
Figure 11 and
Figure 12.
Figure 14.
Prediction results of the DNN model with different normalization methods. The sequence size . The log values of the major features and the sequential partitioning were used.
Figure 14.
Prediction results of the DNN model with different normalization methods. The sequence size . The log values of the major features and the sequential partitioning were used.
Table 1.
Bitcoin blockchain features.
Table 1.
Bitcoin blockchain features.
| Feature | Description |
|---|
| avg-block-size | The 24 h average block size in MB. |
| blockchain-size | The total size of all block headers and transactions. |
| cost-per-trans | Miners revenue divided by the number of transactions. |
| cost-per-trans-pct | Miners revenue as percentage of the transaction volume. |
| difficulty | A relative measure of difficulty in finding a new block. |
| est-trans-vol | The estimated value of transactions on the Bitcoin blockchain in BTC. |
| est-trans-vol-usd | The estimated USD value of transactions. |
| hash-rate | The estimated number of tera hashes per second the Bitcoin network is performing. |
| market-cap | The total USD value of Bitcoin supply in circulation. |
| market-price | The average USD market price across major Bitcoin exchanges. |
| med-cfm-time | The median time for a transaction to be accepted into a mined block. |
| mempool-count | The number of transactions waiting to be confirmed. |
| mempool-growth | The rate of the memory pool (mempool) growth per second. |
| mempool-size | The aggregate size of transactions waiting to be confirmed. |
| miners-revenue | The total value of Coinbase block rewards and transaction fees paid to miners. |
| my-wallets | The total number of blockchain wallets created. |
| n-trans | The number of daily confirmed Bitcoin transactions. |
| n-trans-excl-100 | The total number of transactions per day excluding the chains longer than 100. |
| n-trans-excl-popular | The total number of transactions, excluding those involving any of the network’s |
| | 100 most popular addresses. |
| n-trans-per-block | The average number of transactions per block. |
| n-trans-total | The total number of transactions. |
| n-unique-addr | The total number of unique addresses used on the Bitcoin blockchain. |
| output-val | The total value of all transaction outputs per day. |
| total-bitcoins | The total number of Bitcoins that have already been mined. |
| trade-vol | The total USD value of trading volume on major Bitcoin exchanges. |
| trans-fees | The total BTC value of all transaction fees paid to miners. |
| trans-fees-usd | The total USD value of all transaction fees paid to miners. |
| trans-per-sec | The number of Bitcoin transactions added to the mempool per second. |
| utxo-count | The number of unspent Bitcoin transactions outputs. |
Table 2.
Spearman correlation coefficients between the Bitcoin price and various features.
Table 2.
Spearman correlation coefficients between the Bitcoin price and various features.
| Bitcoin Feature | Coefficient | Bitcoin Feature | Coefficient |
|---|
| avg-block-size | 0.8496 | n-trans | 0.8162 |
| blockchain-size | 0.9030 | n-trans-excl-100 | 0.8469 |
| cost-per-trans | 0.7542 | n-trans-excl-popular | 0.8233 |
| cost-per-trans-pct | −0.4874 | n-trans-per-block | 0.8070 |
| difficulty | 0.9033 | n-trans-total | 0.9030 |
| est-trans-vol | −0.0595 | n-unique-addr | 0.8655 |
| est-trans-vol-usd | 0.9436 | output-vol | 0.1537 |
| hash-rate | 0.9033 | total-bitcoins | 0.9030 |
| market-cap | 0.9975 | trade-vol | 0.8977 |
| market-price | 0.9997 | trans-fees | 0.4227 |
| med-cfm-time | 0.0895 | trans-fees-usd | 0.9390 |
| miners-revenue | 0.9692 | utxo-count | 0.9067 |
| my-wallets | 0.9030 | | |
Table 3.
List of notations.
Table 3.
List of notations.
| Notation | Definition |
|---|
| S | A raw dataset |
| The sequence from to |
| X | A data window of size m, |
| The i-th data point in X |
| The value of the j-th dimension of the i-th data point in X |
Table 4.
Effect of the sequence size m on regression (MAPE, %). The log values of the major features, the sequential partitioning, and the first value-based normalization were used.
Table 4.
Effect of the sequence size m on regression (MAPE, %). The log values of the major features, the sequential partitioning, and the first value-based normalization were used.
| Size | DNN | LSTM | CNN | ResNet | CRNN | Ensemble | SVM |
|---|
| 5 | 3.61 | 3.79 | 4.27 | 4.95 | 4.12 | 4.02 | 4.75 |
| 10 | 4.00 | 3.96 | 4.88 | 7.12 | 4.26 | 4.80 | 4.88 |
| 20 | 4.81 | 4.46 | 7.93 | 8.96 | 5.90 | 6.19 | 5.19 |
| 50 | 10.88 | 6.68 | 20.00 | 16.91 | 10.11 | 11.45 | 6.34 |
| 100 | 21.44 | 27.75 | 115.22 | 52.10 | 39.13 | 48.87 | 12.77 |
Table 5.
Effect of the sequence size m on classification (accuracy). The log values of the major features, the sequential partitioning, and the first value-based normalization were used.
Table 5.
Effect of the sequence size m on classification (accuracy). The log values of the major features, the sequential partitioning, and the first value-based normalization were used.
| Size | DNN | LSTM | CNN | ResNet | CRNN | Ensemble | SVM | Base | Random |
|---|
| 5 | 49.16% | 50.43% | 50.14% | 50.88% | 50.02% | 49.14% | 50.88% | 50.88% | 51.38% |
| 10 | 48.19% | 50.22% | 48.74% | 50.51% | 48.37% | 49.43% | 50.79% | 50.79% | 50.62% |
| 20 | 50.64% | 49.70% | 50.78% | 49.84% | 48.86% | 51.02% | 50.80% | 50.80% | 49.68% |
| 50 | 53.06% | 50.94% | 52.48% | 49.83% | 51.52% | 52.02% | 50.85% | 50.85% | 50.98% |
| 100 | 48.16% | 48.89% | 48.49% | 50.00% | 48.59% | 49.40% | 50.00% | 50.00% | 48.61% |
Table 6.
Model evaluation under various measures when . The log values of the major features, the sequential partitioning, and the first value-based normalization were used.
Table 6.
Model evaluation under various measures when . The log values of the major features, the sequential partitioning, and the first value-based normalization were used.
| Measure | DNN | LSTM | CNN | ResNet | CRNN | Ensemble | SVM | Base | Random |
|---|
| Accuracy | 53.06% | 50.94% | 52.48% | 49.83% | 51.52% | 52.02% | 50.85% | 50.85% | 50.98% |
| Precision | 52.90% | 51.40% | 52.70% | 20.40% | 52.00% | 51.89% | 51.00% | 51.00% | 51.80% |
| Recall | 69.70% | 66.70% | 66.80% | 40.00% | 63.50% | 75.22% | 100.00% | 100.00% | 51.20% |
| Specificity | 53.70% | 50.00% | 52.30% | 29.40% | 50.80% | 52.33% | 0.00% | 0.00% | 50.20% |
| F1 score | 60.00% | 57.90% | 58.50% | 26.80% | 56.90% | 61.33% | 67.00% | 67.00% | 51.50% |
Table 7.
Effect of using log values on regression (MAPE, %). The sequence size . The sequential partitioning and the first value-based normalization were used.
Table 7.
Effect of using log values on regression (MAPE, %). The sequence size . The sequential partitioning and the first value-based normalization were used.
| | DNN | LSTM | CNN | ResNet | CRNN | Ensemble | SVM |
|---|
| Log values | 4.81 | 4.46 | 7.93 | 8.96 | 5.90 | 6.19 | 5.19 |
| Plain values | 5.48 | 5.21 | 10.13 | 8.94 | 7.50 | 6.40 | 7.02 |
Table 8.
Effect of using log values on classification (accuracy). The sequence size is . The sequential partitioning and the first value-based normalization were used.
Table 8.
Effect of using log values on classification (accuracy). The sequence size is . The sequential partitioning and the first value-based normalization were used.
| | DNN | LSTM | CNN | ResNet | CRNN | Ensemble | SVM | Base | Random |
|---|
| Log values | 53.06% | 50.94% | 52.48% | 49.83% | 51.52% | 52.02% | 50.85% | 50.85% | 50.98% |
| Plain values | 50.85% | 50.53% | 49.83% | 50.81% | 52.22% | 49.74% | 50.85% | 50.85% | 49.76% |
Table 9.
Effect of data split methods on regression (MAPE, %). The sequence size . The log values of the major features and the first value-based normalization were used.
Table 9.
Effect of data split methods on regression (MAPE, %). The sequence size . The log values of the major features and the first value-based normalization were used.
| | DNN | LSTM | CNN | ResNet | CRNN | Ensemble | SVM |
|---|
| sequential | 4.81 | 4.46 | 7.93 | 8.96 | 5.90 | 6.19 | 5.19 |
| random | 3.65 | 3.52 | 4.93 | 5.26 | 5.20 | 4.16 | 4.23 |
| 5-fold CV | 4.83 | 4.09 | 6.80 | 9.75 | 7.12 | 5.18 | 5.04 |
Table 10.
Effect of data split methods on classification (accuracy). The sequence size . The log values of the major features and the first value-based normalization were used.
Table 10.
Effect of data split methods on classification (accuracy). The sequence size . The log values of the major features and the first value-based normalization were used.
| | DNN | LSTM | CNN | ResNet | CRNN | Ensemble | SVM | Base | Random |
|---|
| sequential | 53.06% | 50.94% | 52.48% | 49.83% | 51.52% | 52.02% | 50.85% | 50.85% | 50.98% |
| random | 52.46% | 52.24% | 52.17% | 49.76% | 52.40% | 52.09% | 50.97% | 51.18% | 50.63% |
| 5-fold CV | 53.60% | 51.82% | 51.07% | 51.92% | 51.06% | 51.14% | 53.76% | 54.00% | 50.68% |
Table 11.
Effect of normalization methods on regression (MAPE, %). The sequence size . The log values of the major features and the sequential partitioning were used.
Table 11.
Effect of normalization methods on regression (MAPE, %). The sequence size . The log values of the major features and the sequential partitioning were used.
| | DNN | LSTM | CNN | ResNet | CRNN | Ensemble | SVM |
|---|
| first value | 4.81 | 4.46 | 7.93 | 8.96 | 5.90 | 6.19 | 5.19 |
| minmax | 14.23 | 14.18 | 157.00 | 92.68 | 35.73 | 22.34 | 34.44 |
Table 12.
Effect of normalization methods on classification (accuracy). The sequence size . The log values of the major features and the sequential partitioning were used.
Table 12.
Effect of normalization methods on classification (accuracy). The sequence size . The log values of the major features and the sequential partitioning were used.
| | DNN | LSTM | CNN | ResNet | CRNN | Ensemble | SVM | Base | Random |
|---|
| first value | 53.06% | 50.94% | 52.48% | 49.83% | 51.52% | 52.02% | 50.85% | 50.85% | 50.98% |
| minmax | 51.71% | 51.28% | 49.83% | 50.85% | 49.36% | 49.44% | 50.85% | 50.85% | 49.82% |
Table 13.
Results of a profitability analysis. was used for regression models and for classification models. The log values of the major features, the sequential partitioning, and the first value-based normalization were used. For every model, the initial budget was 10,000 USD and the final value of investment is shown in the table.
Table 13.
Results of a profitability analysis. was used for regression models and for classification models. The log values of the major features, the sequential partitioning, and the first value-based normalization were used. For every model, the initial budget was 10,000 USD and the final value of investment is shown in the table.
| | DNN | LSTM | CNN | ResNet | CRNN | Ensemble | SVM | Base | Random |
|---|
| regression | 6755.55 | 8806.72 | 6616.87 | 7608.35 | 8102.71 | 5772.99 | 9842.95 | − | − |
| classification | 10877.07 | 10359.42 | 10422.19 | 10619.98 | 10315.18 | 10432.44 | 9532.43 | 9532.43 | 9918.70 |