Figure 1.
Important ways to present graphs illustrated by the example of . The top row is a surface and contour plot of . The surface is plotted out to in order to give a good view of the surface structure as it approached the natural boundary. For larger values of the singularities of the natural boundary dominate the graph and obstruct the view. The bottom row representations are particularly useful for this work. The contour plot is truncated at the unity level set and shown on the left and only the main contour of the unity level set is shown on the right. For the contour plots, blue shading represents low values and orange shading represents high values.
Figure 1.
Important ways to present graphs illustrated by the example of . The top row is a surface and contour plot of . The surface is plotted out to in order to give a good view of the surface structure as it approached the natural boundary. For larger values of the singularities of the natural boundary dominate the graph and obstruct the view. The bottom row representations are particularly useful for this work. The contour plot is truncated at the unity level set and shown on the left and only the main contour of the unity level set is shown on the right. For the contour plots, blue shading represents low values and orange shading represents high values.
Figure 2.
Contour plot of for to and . The 30 contours (level sets) in each graph are plotted from 0 to 1. Blue shading represent low values and orange shading represents high values. The rotational symmetry (equal to k) of the graphs are visually apparent. Further, the contours are not rough (referred to here as “polished”). Both of these features are special to centered polygonal lacunary sequences.
Figure 2.
Contour plot of for to and . The 30 contours (level sets) in each graph are plotted from 0 to 1. Blue shading represent low values and orange shading represents high values. The rotational symmetry (equal to k) of the graphs are visually apparent. Further, the contours are not rough (referred to here as “polished”). Both of these features are special to centered polygonal lacunary sequences.
Figure 3.
Contour plot of
for a variety of
and
. The 30 contours (level sets) are plotted from 0 to 1. Blue shading represent low values and orange shading represents high values. The top row is
for
. The second row is
for
. The third row is
,
,
, where
is the
Fibonacci number and
. The strict rotational symmetry is broken but a quasi-rotational symmetry persists for all but the last three cases. In contrast to the plots of
Figure 2, the contours are rough in all cases. This is typically the case for general lacunary functions.
Figure 3.
Contour plot of
for a variety of
and
. The 30 contours (level sets) are plotted from 0 to 1. Blue shading represent low values and orange shading represents high values. The top row is
for
. The second row is
for
. The third row is
,
,
, where
is the
Fibonacci number and
. The strict rotational symmetry is broken but a quasi-rotational symmetry persists for all but the last three cases. In contrast to the plots of
Figure 2, the contours are rough in all cases. This is typically the case for general lacunary functions.
Figure 4.
Inverse stereographic projection of the piecewise function for and for . Here, the natural boundary gets mapped to the equator. The northern hemisphere is the image of the interior of the unit disk, while the southern hemisphere is the image of the exterior of the unit disk.
Figure 4.
Inverse stereographic projection of the piecewise function for and for . Here, the natural boundary gets mapped to the equator. The northern hemisphere is the image of the interior of the unit disk, while the southern hemisphere is the image of the exterior of the unit disk.
Figure 5.
Various viewpoints of the whole sphere mapping of for the case of . The natural boundary is mapped to the south pole and is seen most clearly in the bottom left panel.
Figure 5.
Various viewpoints of the whole sphere mapping of for the case of . The natural boundary is mapped to the south pole and is seen most clearly in the bottom left panel.
Figure 6.
The case of
. The top row consists of plots of the real part (
left) and imaginary part (
right) of
. The bottom left graph is of
exactly as in
Figure 2. The bottom right shows
superimposed with the zero curves of the real (blue) and imaginary (red) parts of
. Of note is that the real and imaginary parts do not carry the symmetry nor polishness of the modulus.
Figure 6.
The case of
. The top row consists of plots of the real part (
left) and imaginary part (
right) of
. The bottom left graph is of
exactly as in
Figure 2. The bottom right shows
superimposed with the zero curves of the real (blue) and imaginary (red) parts of
. Of note is that the real and imaginary parts do not carry the symmetry nor polishness of the modulus.
Figure 7.
Top set, first symmetry angle: Limit value of (real part, blue; imaginary part, red) at as a function of N. Bottom set, second symmetry angle: Limit value of (real part, blue; imaginary part, red) at the same values of as above.
Figure 7.
Top set, first symmetry angle: Limit value of (real part, blue; imaginary part, red) at as a function of N. Bottom set, second symmetry angle: Limit value of (real part, blue; imaginary part, red) at the same values of as above.
Figure 8.
Sections for the example of for (top left), (top right), and (bottom). The base space is shown as a blue line and as blue points on that line. The fibers are shown as orange and the sections are the black dots. The black lines are simply to help the eye when comparing sections.
Figure 8.
Sections for the example of for (top left), (top right), and (bottom). The base space is shown as a blue line and as blue points on that line. The fibers are shown as orange and the sections are the black dots. The black lines are simply to help the eye when comparing sections.
Figure 9.
Some of the infinite number of similar sections to that of the fourth section in the set for
of
(bottom set in
Figure 8). This forms the equivalence class
.
Figure 9.
Some of the infinite number of similar sections to that of the fourth section in the set for
of
(bottom set in
Figure 8). This forms the equivalence class
.
Figure 10.
The section for the case. For this degenerate case, two pairs of the six members of coalesce, leaving four distinct points in the base space (blue dots). This results in those points having multiplier values that are twice that of the non-coalesced points.
Figure 10.
The section for the case. For this degenerate case, two pairs of the six members of coalesce, leaving four distinct points in the base space (blue dots). This results in those points having multiplier values that are twice that of the non-coalesced points.
Figure 11.
A comparison of the section for the case of and and . One notes that the general shape is the same although the numerical values of the change. All sets of sections exhibit this type of similarity across values of k. Increasing k shifts the fiber positions to the left.
Figure 11.
A comparison of the section for the case of and and . One notes that the general shape is the same although the numerical values of the change. All sets of sections exhibit this type of similarity across values of k. Increasing k shifts the fiber positions to the left.
Figure 12.
Examples of fiber position diagrams for the cases (left-to-right) of
, 5, 12, 32. The blue dots are the positions of the fibers on the base space and the grey dots represent equal divisions of the circle in units of
. For example the bottom panel of
Figure 8 corresponds to the first diagram. The unit cell size is (left-to-right) 1/8, 1/2, 1/8, 1/64. The saturation value is (left-to-right) 1, 3/5, 2/3, 1.
Figure 12.
Examples of fiber position diagrams for the cases (left-to-right) of
, 5, 12, 32. The blue dots are the positions of the fibers on the base space and the grey dots represent equal divisions of the circle in units of
. For example the bottom panel of
Figure 8 corresponds to the first diagram. The unit cell size is (left-to-right) 1/8, 1/2, 1/8, 1/64. The saturation value is (left-to-right) 1, 3/5, 2/3, 1.
Figure 13.
Several plots of data sets exposing some of the structure of the limit values of the centered polygonal lacunary sequences. These data are independent of k and thus hold for all centered polygonal lacunary functions at once. In all cases, the data are plotted as a function of p from to 128 (the horizontal axis). The top left panel shows the unit cell size as a function of p from to 128. The top right panel shows the saturation value versus p from to 128. The bottom left panel shows the saturation as a function of unit cell size. The bottom right panel shows the number of fiber positions on the base space.
Figure 13.
Several plots of data sets exposing some of the structure of the limit values of the centered polygonal lacunary sequences. These data are independent of k and thus hold for all centered polygonal lacunary functions at once. In all cases, the data are plotted as a function of p from to 128 (the horizontal axis). The top left panel shows the unit cell size as a function of p from to 128. The top right panel shows the saturation value versus p from to 128. The bottom left panel shows the saturation as a function of unit cell size. The bottom right panel shows the number of fiber positions on the base space.
Figure 14.
Fiber position diagrams and their corresponding autocorrelations for (top left), (top right) which is non-Pythagorean, (bottom left), and (bottom right), which is Pythagorean. It is difficult for the eye to discern subtle details in the structure of the fiber position diagrams, especially for large p values. The autocorrelations, however, are quite distinct for these four similar cases.
Figure 14.
Fiber position diagrams and their corresponding autocorrelations for (top left), (top right) which is non-Pythagorean, (bottom left), and (bottom right), which is Pythagorean. It is difficult for the eye to discern subtle details in the structure of the fiber position diagrams, especially for large p values. The autocorrelations, however, are quite distinct for these four similar cases.
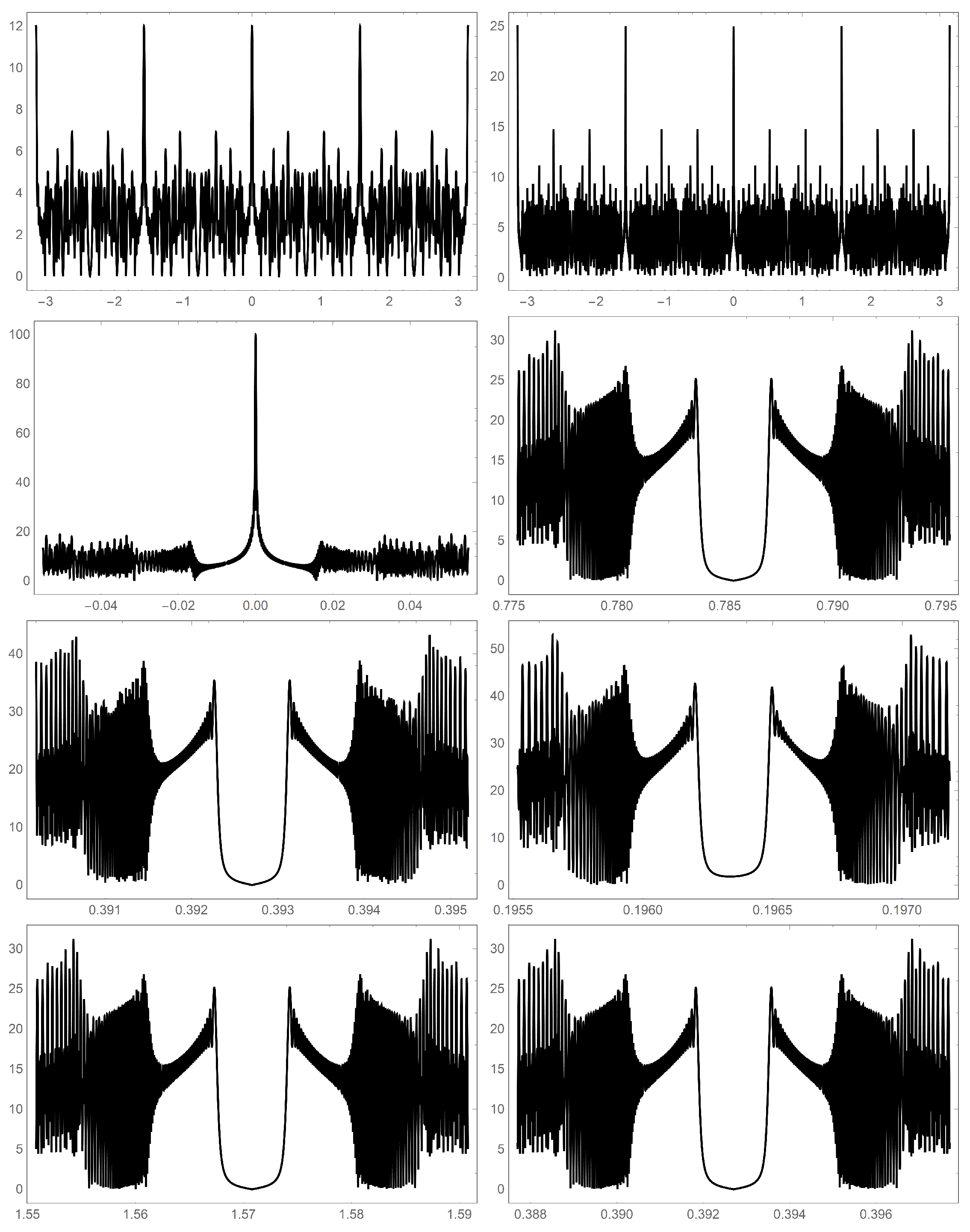
Figure 15.
The lacunary trigonometric system obtained from by setting . The top row compares the full range for the case of (left panel) and (right panel). The left panel in the second row shows a blow-up around and . The right panel in the second row and the two panels in the third row expose the scaling property of the system. Note the similarity of the graphs. The right panel in the second row is at the first symmetry angle, , with and a plot range of 0.02. The left panel in the third row is centered at the second symmetry angle, , now with and a full plot domain of a fourth of that of the second row right panel. The right panel in the third row is centered at the third symmetry angle, . Here, and a full plot domain is one-twelfth that of the second row right panel. The bottom row shows scaling similarity across different values of k. The first symmetry angle is shown. The bottom left panel shows the case of and the right panel shows the case of . In both cases . For the case, the range is twice that for the case, while for the case, the range is half that of .
Figure 15.
The lacunary trigonometric system obtained from by setting . The top row compares the full range for the case of (left panel) and (right panel). The left panel in the second row shows a blow-up around and . The right panel in the second row and the two panels in the third row expose the scaling property of the system. Note the similarity of the graphs. The right panel in the second row is at the first symmetry angle, , with and a plot range of 0.02. The left panel in the third row is centered at the second symmetry angle, , now with and a full plot domain of a fourth of that of the second row right panel. The right panel in the third row is centered at the third symmetry angle, . Here, and a full plot domain is one-twelfth that of the second row right panel. The bottom row shows scaling similarity across different values of k. The first symmetry angle is shown. The bottom left panel shows the case of and the right panel shows the case of . In both cases . For the case, the range is twice that for the case, while for the case, the range is half that of .
![Mathematics 07 00943 g015 Mathematics 07 00943 g015]()
Figure 16.
The scaling behavior with N of lacunary trigonometric system obtained from by setting . The four panels show the region around the first symmetry zero (). Quasi-self-similarity is seen as N changes: top left, ; top right, ; bottom left, , bottom right, . The domain size scales as .
Figure 16.
The scaling behavior with N of lacunary trigonometric system obtained from by setting . The four panels show the region around the first symmetry zero (). Quasi-self-similarity is seen as N changes: top left, ; top right, ; bottom left, , bottom right, . The domain size scales as .
Figure 17.
Radial plots of for various values of p. The right panel shows the first 10 symmetry angles. The top curve, which is also most skewed to the right, corresponds to whereas the bottom curve corresponds to . It is true, in general, that along the symmetry angles exhibits an increasing maximum value with increasing p and that the position of the maximum migrates towards the unit circle. The right panel displays as “heat map” (blue—low value, red—high value) superimposed on the contour plot of .
Figure 17.
Radial plots of for various values of p. The right panel shows the first 10 symmetry angles. The top curve, which is also most skewed to the right, corresponds to whereas the bottom curve corresponds to . It is true, in general, that along the symmetry angles exhibits an increasing maximum value with increasing p and that the position of the maximum migrates towards the unit circle. The right panel displays as “heat map” (blue—low value, red—high value) superimposed on the contour plot of .
Figure 18.
Maximum of the radial function along the symmetry angles. The maximum values (black dots) closely follow (orange curve). The inset shows that for low values of p there is deviation from .
Figure 18.
Maximum of the radial function along the symmetry angles. The maximum values (black dots) closely follow (orange curve). The inset shows that for low values of p there is deviation from .
Figure 19.
Illustration of the first convergence approximates to the radial function. The top row shows the case of for (left) and (right) and the bottom row shows the case of for (left) and (right). The approximation is exceptional up to the peak maximum in all cases. Beyond the peak maximum, the approximation improves both when k increases and when p increases. The black curve is the “exact” case, and the orange is the first convergence approximate. The green is the residual.
Figure 19.
Illustration of the first convergence approximates to the radial function. The top row shows the case of for (left) and (right) and the bottom row shows the case of for (left) and (right). The approximation is exceptional up to the peak maximum in all cases. Beyond the peak maximum, the approximation improves both when k increases and when p increases. The black curve is the “exact” case, and the orange is the first convergence approximate. The green is the residual.
Figure 20.
The first, second, and third separatrixes for the case of and are shown in orange and are superimposed on the contour plot. The value of the level sets occur at approximately and , respectively.
Figure 20.
The first, second, and third separatrixes for the case of and are shown in orange and are superimposed on the contour plot. The value of the level sets occur at approximately and , respectively.
Figure 21.
Plots of data for
(
left) and
(
right) versus
k from
Table 1. Each data set is fit to a Langmuir isotherm
. Fit values: (
;
,
,
) and (
;
,
,
).
Figure 21.
Plots of data for
(
left) and
(
right) versus
k from
Table 1. Each data set is fit to a Langmuir isotherm
. Fit values: (
;
,
,
) and (
;
,
,
).
Figure 22.
Analysis related to scaling of to (in this case ). The top row of panels pertain to the main unity contour for . The top left shows the main unity contour. This translated to a versus plot in the middle panel. The top right panel shows the Fourier decomposition of the curve in the middle panel (the constant coefficient is 0.84 but has been cut off at 0.2 in order to show the other coefficients more clearly). The bottom left and middle panels are the analog of the top left and middle panels but for . The bottom right panel shows (black), (purple), and quadratically scaled (green), ( and ). Finally, the residual is shown as well.
Figure 22.
Analysis related to scaling of to (in this case ). The top row of panels pertain to the main unity contour for . The top left shows the main unity contour. This translated to a versus plot in the middle panel. The top right panel shows the Fourier decomposition of the curve in the middle panel (the constant coefficient is 0.84 but has been cut off at 0.2 in order to show the other coefficients more clearly). The bottom left and middle panels are the analog of the top left and middle panels but for . The bottom right panel shows (black), (purple), and quadratically scaled (green), ( and ). Finally, the residual is shown as well.
Figure 23.
Plots of the real (blue), imaginary (red) and modulus (black) of for the first six symmetry angles and for . In all cases, the graphs skew toward unity and increase in maximum value as the symmetry angle increases (The top curve in each case corresponds to whereas the bottom curve corresponds to ). The bottom right panel shows the value of the integral of the real (blue), imaginary (red) and modulus (black) of as a function of symmetry angle, p.
Figure 23.
Plots of the real (blue), imaginary (red) and modulus (black) of for the first six symmetry angles and for . In all cases, the graphs skew toward unity and increase in maximum value as the symmetry angle increases (The top curve in each case corresponds to whereas the bottom curve corresponds to ). The bottom right panel shows the value of the integral of the real (blue), imaginary (red) and modulus (black) of as a function of symmetry angle, p.
Table 1.
“Exact” values of and corresponding the separatrix level set value, for the first and second separatrix. The “exact” values were calculated using the member of each lacunary sequence.
Table 1.
“Exact” values of and corresponding the separatrix level set value, for the first and second separatrix. The “exact” values were calculated using the member of each lacunary sequence.
| | | | |
| 1 | 0.392403 | 0.216179 | 0.688551 | 0.647672 |
| 2 | 0.531789 | 0.369646 | 0.794944 | 0.795392 |
| 3 | 0.606321 | 0.464533 | 0.843906 | 0.861992 |
| 4 | 0.654943 | 0.530380 | 0.872941 | 0.900589 |
| 5 | 0.690101 | 0.579452 | 0.892416 | 0.925975 |
| 6 | 0.717165 | 0.617789 | 0.906488 | 0.944015 |
| 7 | 0.738884 | 0.648762 | 0.917177 | 0.957529 |
| 8 | 0.756839 | 0.674420 | 0.925596 | 0.968047 |
| 9 | 0.772015 | 0.696095 | 0.932413 | 0.976475 |
| 10 | 0.785063 | 0.714696 | 0.938053 | 0.983384 |
| 11 | 0.796438 | 0.730866 | 0.942802 | 0.989155 |
| 12 | 0.806467 | 0.745076 | 0.946858 | 0.994050 |
Table 2.
Quadratic (left set) and cubic (right set) estimated values of
and corresponding separatrix level set value, for the first separatrix. The percent error is given relative to the “exact” values from
Table 1.
Table 2.
Quadratic (left set) and cubic (right set) estimated values of
and corresponding separatrix level set value, for the first separatrix. The percent error is given relative to the “exact” values from
Table 1.
| | %error | | %error | | %error | | %error |
| 1 | 0.500000 | 27.4 | 0.250000 | 15.6 | 0.344334 | −12.3 | 0.203199 | −6.00 |
| 2 | 0.577350 | 8.57 | 0.384900 | 4.13 | 0.515208 | −3.12 | 0.365099 | −1.23 |
| 3 | 0.629961 | 3.90 | 0.472470 | 1.71 | 0.599184 | −1.18 | 0.462625 | −0.41 |
| 4 | 0.668740 | 2.11 | 0.534992 | 0.87 | 0.651413 | −0.54 | 0.529459 | −0.17 |
| 5 | 0.698827 | 1.26 | 0.582356 | 0.50 | 0.688176 | −0.28 | 0.578958 | −0.09 |
| 6 | 0.723020 | 0.82 | 0.619731 | 0.31 | 0.716035 | −0.16 | 0.617503 | −0.05 |
| 7 | 0.742997 | 0.56 | 0.650123 | 0.21 | 0.738181 | −0.10 | 0.648585 | −0.03 |
| 8 | 0.759836 | 0.40 | 0.675409 | 0.15 | 0.756380 | −0.06 | 0.674305 | −0.02 |
| 9 | 0.774264 | 0.29 | 0.696837 | 0.11 | 0.771703 | −0.04 | 0.696018 | −0.01 |
| 10 | 0.786793 | 0.22 | 0.715267 | 0.08 | 0.784845 | −0.03 | 0.714642 | −0.01 |
| 11 | 0.797797 | 0.17 | 0.731314 | 0.06 | 0.796281 | −0.02 | 0.730827 | −0.01 |
| 12 | 0.807554 | 0.13 | 0.745434 | 0.05 | 0.806351 | −0.01 | 0.745047 | 0.00 |