Fractional Derivatives: The Perspective of System Theory
Abstract
:1. Introduction
- What do we mean by “derivative”?
- What is the relation between derivative and integral?
- Frequently different notions of “integral” are mixed. Should not we use different notations or distinct names?
- When can we say that an operator is fractional?
- Should we consider a framework where integer and non integer orders co-exist and are mixed?
- What do we mean by fractional calculus? Should it be the calculus involving, at least, one “non integer order” derivative?
- Can we consider as “fractional operator” any expression involving a convolution of a function and a given kernel?
- Is it reasonable to choose a classic operator, to change its form by introducing a parameter and to call it FD?
- How can we call “fractional derivative” to an operator that is itself solution of a linear differential equation?
- The existence of a non integer parameter is reason for the use of the word “fractional”?
2. Glossary and Assumptions
- Anti-causalAn anti-causal system is causal under reverse time flow. A system is anti-causal if the output at any instant depends only on values of the input at the present and future time.
- Anti-derivativeThe operator that is simultaneously the left and right inverse of the derivative will be called anti-derivative. It will be used to compute the definite integral through the Barrow formula [20]. This should be not confused with the negative order derivative, that needs not to be inverse of a derivative.
- BackwardReverse time flow—from future to past.
- Causal operator or systemA system is causal if the output at any instant depends only on values of the input at the present and past time [21].
- DerivativeDerivative (first order) of a function, is the limit of the ratio of the change in such function to the corresponding change in its independent variable as the latter change approaches zero. It will be represented by or .
- ForwardNormal time flow—from past to future.
- FractionalFractional will have the meaning of non integer real number.
- IntegralIn strict mathematical therms, there are several definitions of integral. However, the simplest is the Riemann integral that we can state as the numerical measure of the area under the graph of a given positive function, above the horizontal axis, and bounded on the sides by ordinates drawn at the endpoints of a specified interval. This is usually called definite integral and it is distinct from the indefinite integral, also called primitive.
- PrimitiveThe operator that is only the right inverse of the derivative will be called primitive.
- We work on . Nonetheless, this is not a limitation. If the function at hand is defined on any sub-interval in , we can extend the definition of the function to the whole real line with null values.
- We do not address the proof of existence of the operators.
- We use the two-sided Laplace transform (LT):where is any function defined on and is its transform, provided that it has a non empty region of convergence
- The Fourier transform (FT), , is obtained from the LT through the substitution with and
- The functions and distributions have Laplace and/or Fourier transforms
- Current properties of the Dirac delta distribution, , and its derivatives, will be used
- The standard convolution operation will be adopted
- The order of any fractional derivative, , is any real number. We will not consider the complex order, since it gives non Hermitian derivatives.
- The multi-valued expressions and will be used. To obtain functions from them we will fix for branch-cut lines the negative real half axis for the first and the positive real half axis for the second; for both the first Riemann surface is chosen.
- The Heaviside unit step will be represented by and the signum function by . These functions are related by
- We define the “floor” of a real number as the integer verifying
3. The Classic Derivatives and Their Inverses
3.1. Elemental Derivatives
- Forward or causal
- Backward or anti-causal
- Forward or causal
- Backward or anti-causal
- Two-sided or acausal
3.2. First Unification
3.3. Second Unification
3.4. Third Unification
- We can combine two derivatives of any orders, and to obtain a third derivative
- The corresponding frequency responses are given byThis result is important, since it expresses very clearly the unification of the derivatives and motivates a further development as discussed in the next subsection.
3.5. Fourth Unification
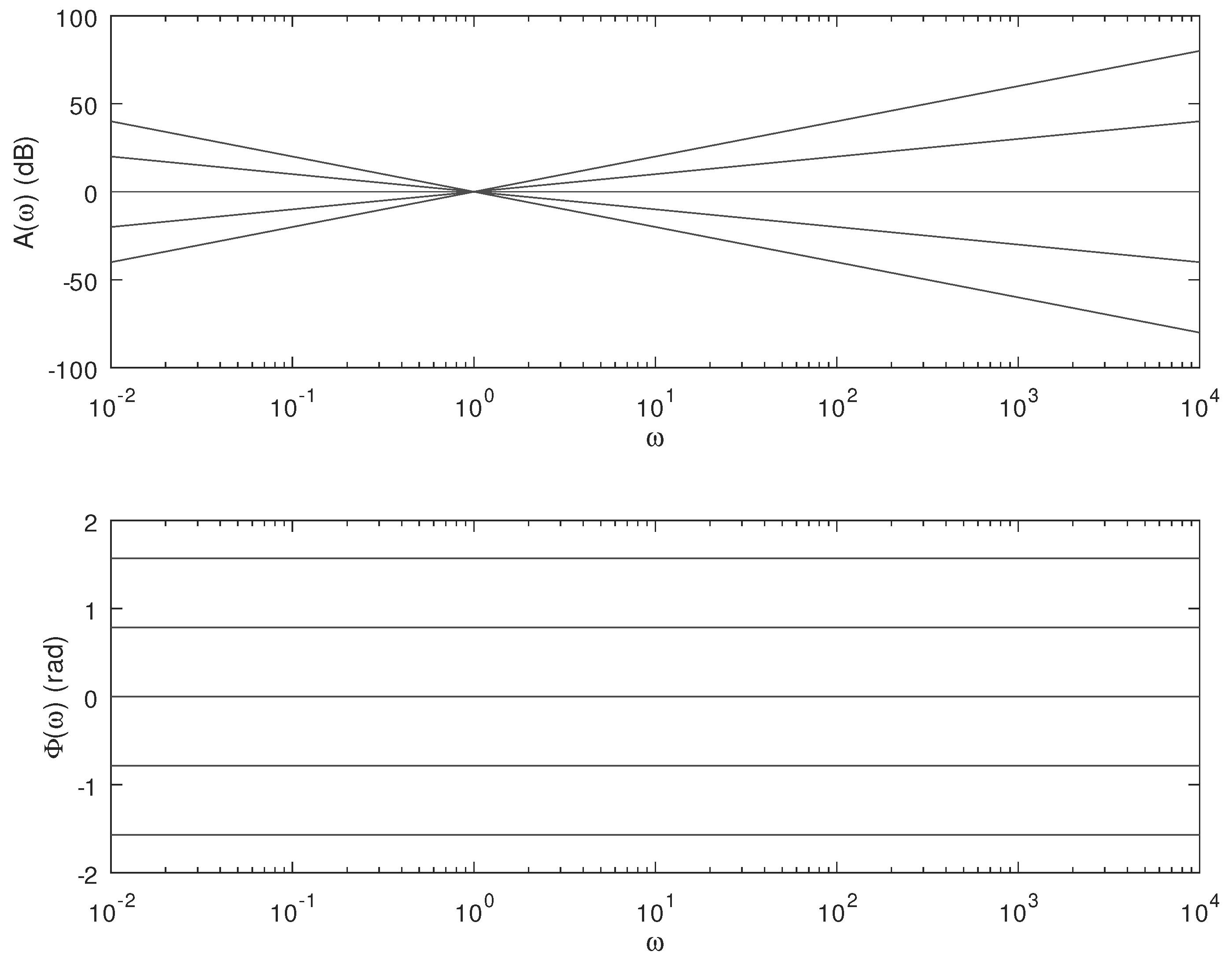
3.6. Bode Diagrams
4. Derivative Definition Through Integral Formulations
4.1. Definition
4.2. A General Kernel
4.3. Some Particular Kernels
- In this case, and It yieldsstating a well known property of the impulse distribution.
- In this case, and We obtaincorresponding to the causal Liouville anti-derivative (line 2 in Table 1).
- andIn this case, and Then, it resultsthat corresponds to line 6 in Table 1.
- Let This is essentially the previous case 2 that leads to (43). However, the inverse FT produces a kernel that originates a singular integral. To avoid this problem we can use the properties of the pseudo-functions [27] that allow us to regularize (43) and use it for the derivative case. Let . We can write (43) as [28]that we will call regularized Liouville derivative. Similar regularised integrals can be obtained for (44).Remark 7.If and , then we getthat coincides with the Marchaud derivative [1]. Nonetheless, for , the Marchaud operator is no longer a derivative.
- andIn this case, we have two possibilities:
- (a)
- (b)
The corresponding right derivatives are easily obtained. - and
- and
4.4. Classic Riemann-Liouville, Caputo, and Hadamard derivatives
5. On the Discrete-Time Derivatives
- The frequency response is obtained from the TF given by when s assumes values on the Hilger circle: , where h is the sampling interval. Therefore, the domain is defined by ;
- The eigenvalue of the nabla derivative corresponding to the eigenvector is . If h is very small, then Therefore, only for small values of h the derivative is represented by straight lines in log plots;
- There are no studies for the two-sided derivatives recovering to the one described in Section 3.5. The one proposed in [34] has a different formulation and properties.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FD | Fractional derivative |
| FI | Fractional integral |
| RL | Riemann-Liouville |
| L | Liouville |
| C | Caputo |
| GL | Grünwald-Letnikov |
| H | Hadamard |
References
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Dugowson, S. Les Différentielles Métaphysiques. Ph.D. Thesis, Université Paris Nord, Villetaneuse, France, 1994. [Google Scholar]
- Kiryakova, V. A long standing conjecture failed? In Transform Methods and Special Functions; Institute of Mathematics and Informatics, Bulgarian Academy of Sciences: Sofia, Bulgaria, 1998; pp. 579–588. [Google Scholar]
- Kiryakova, V. A brief story about the operators of the generalized Fractional Calculus. Fract. Calc. Appl. Anal. 2008, 11, 203–220. [Google Scholar]
- Magin, R. Fractional Calculus in Bioengineering; Begell House Inc.: Redding, CT, USA, 2006. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Nonlinear Physical Science; Springer: Beijing, China, 2010. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers: Background and Theory; Nonlinear Physical Science; Springer: Beijing, China, 2013. [Google Scholar]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers, 2nd ed.; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific Publishing Co.: Singapore, 2011. [Google Scholar]
- Ortigueira, M.D.; Machado, J.A.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Ortigueira, M.; Machado, J.T. Which Derivative? Fract. Fract. 2017, 1, 3. [Google Scholar] [CrossRef]
- Tarasov, V.E. No violation of the Leibniz rule. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2945–2948. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. A critical analysis of the Caputo–Fabrizio operator. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 608–611. [Google Scholar] [CrossRef]
- Giusti, A. A comment on some new definitions of fractional derivative. Nonlinear Dyn. 2018, 93, 1757–1763. [Google Scholar] [CrossRef]
- Tarasov, V.E. No nonlocality: No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 157–163. [Google Scholar] [CrossRef]
- Abdelhakim, A.; Machado, J.A.T. A critical analysis of the conformable derivative. Nonlinear Dyn. 2019, 1–11. [Google Scholar] [CrossRef]
- Machado, J.T.; Mainardi, F.; Kiryakova, V. Fractional Calculus: Quo Vadimus? (Where are we Going?). Fract. Calc. Appl. Anal. 2015, 18, 495–526. [Google Scholar] [CrossRef]
- Machado, J.T.; Mainardi, F.; Kiryakova, V.; Atanackovic, T. Fractional Calculus: D’où Venons-Nous? Que Sommes-Nous? Où Allons-Nous? (Contributions to Round Table Discussion held at ICFDA 2016). Fract. Calc. Appl. Anal. 2016, 19, 1074–1104. [Google Scholar] [CrossRef]
- Ortigueira, M.; Machado, J.T. Fractional Definite Integral. Fract. Fract. 2017, 1, 2. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Willsky, A.S.; Hamid, S. Signals and Systems, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Ortigueira, M.D. The fractional quantum derivative and its integral representations. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 956–962. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Riesz potential operators and inverses via fractional centred derivatives. Int. J. Math. Math. Sci. 2006, 2006, 6. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Fractional central differences and derivatives. J. Vib. Control 2008, 14, 1255–1266. [Google Scholar] [CrossRef]
- Roberts, M. Signals and Systems: Analysis Using Transform Methods And Matlab, 2nd ed.; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Liouville, J. Memóire sur le calcul des différentielles à indices quelconques. J. l’École Polytech. Paris 1832, 13, 71–162. [Google Scholar]
- Gel’fand, I.M.; Shilov, G.E. Generalized Functions. Volume I: Properties and Operations; Academic Press: New York, NY, USA; London, UK, 1964. [Google Scholar]
- Ortigueira, M.D.; Magin, R.L.; Trujillo, J.J.; Velasco, M.P. A real regularised fractional derivative. Signal Image Video Process. 2012, 6, 351–358. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Y.; Cheng, S.; Wang, Y. A note on short memory principle of fractional calculus. Fract. Calc. Appl. Anal. 2017, 20, 1382–1404. [Google Scholar] [CrossRef]
- Bastos, N.R.O. Fractional Calculus on Time Scales. Ph.D. Thesis, Aveiro University, Aveiro, Portugal, 2012. [Google Scholar]
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Ortigueira, M.D.; Coito, F.J.; Trujillo, J.J. Discrete-time differential systems. Signal Process. 2015, 107, 198–217. [Google Scholar] [CrossRef]
- Tarasov, V.E. Exact Discrete Analogs of Derivatives of Integer Orders: Differences as Infinite Series. J. Math. 2015, 2015, 134842. [Google Scholar] [CrossRef]
- Tarasov, V.E. Exact discretization by Fourier transforms. Commun. Nonlinear Sci. Numer. Simul. 2016, 37, 31–61. [Google Scholar] [CrossRef]
| Freq. Response | Name | |||
|---|---|---|---|---|
| 1 | causal derivative/Grünwald-Letnikov | |||
| 2 | causal anti-derivative/Grünwald-Letnikov/Liouville | |||
| 3 | causal/Liouville | |||
| 4 | causal/Liouville-Caputo | |||
| 5 | right derivative/Grünwald-Letnikov | |||
| 6 | right anti-derivative/Grünwald-Letnikov/Liouville | |||
| 7 | anti-causal/Liouville | |||
| 8 | right/Liouville-Caputo | |||
| 9 | 0 | symmetric two-sided | ||
| 10 | 0 | Riesz potential | ||
| 11 | anti-symmetric two-sided | |||
| 12 | 0 | Feller potential |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duarte Ortigueira, M.; Tenreiro Machado, J. Fractional Derivatives: The Perspective of System Theory. Mathematics 2019, 7, 150. https://doi.org/10.3390/math7020150
Duarte Ortigueira M, Tenreiro Machado J. Fractional Derivatives: The Perspective of System Theory. Mathematics. 2019; 7(2):150. https://doi.org/10.3390/math7020150
Chicago/Turabian StyleDuarte Ortigueira, Manuel, and José Tenreiro Machado. 2019. "Fractional Derivatives: The Perspective of System Theory" Mathematics 7, no. 2: 150. https://doi.org/10.3390/math7020150






