Role of Media and Effects of Infodemics and Escapes in the Spatial Spread of Epidemics: A Stochastic Multi-Region Model with Optimal Control Approach
Abstract
:1. Introduction
2. Model Description and Definitions
Presentation of the Stochastic Model without Control
3. The Model with Vaccination
3.1. Presentation of the Control Model
3.2. A Stochastic Optimal Control Approach
3.2.1. Optimal Control Characterization and Necessary Conditions
- -
- If, then; therefore:
- -
- If , then ;, therefore, , implying that.Due to and we obtain
- -
- If , then ; thus, implying that.In view of and we get .
3.2.2. Existence of Solutions and Sufficient Conditions
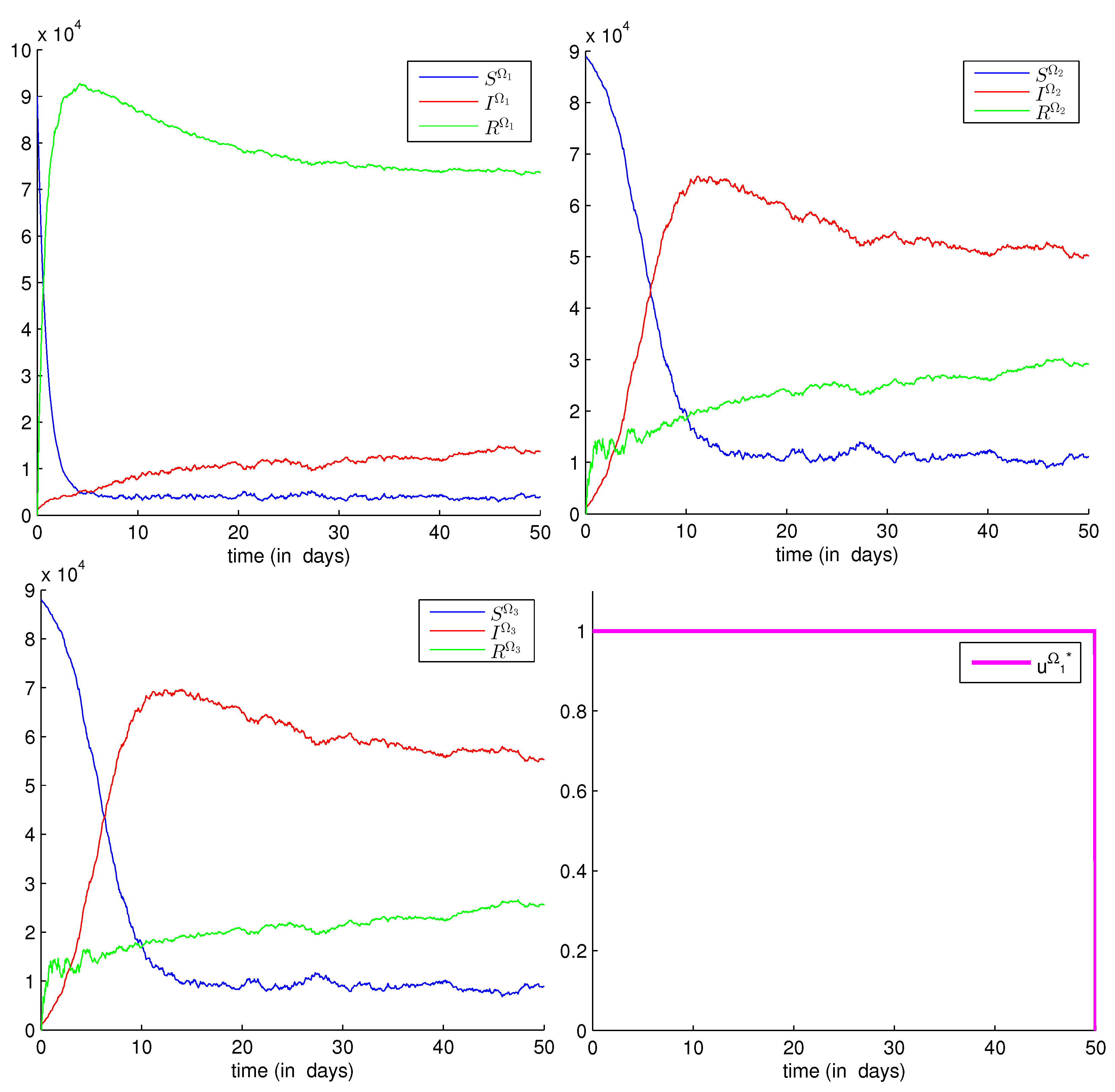
3.2.3. Numerical Results
- -
- We study three regions, denoted by , , and and that are all assumed to be infected.
- -
- are replaced by just to avoid more complications in the program code. In other words, we assume that the probability to be infected does not depend on the source location of susceptibility, but on the source location of infectivity only, namely . More explicitly, ; they are represented by , ; they are represented by and, finally, ; and they are represented by .
- -
- The unit of the parameters and is ∀ fixed j and mobile k.
- -
- with h the time step.
- -
- The coefficients in diffusions , , and are assumed to be all equal to 0.125. Larger values can be considered; however, they only increase the level of stochasticity, and this is not very interesting here.
4. The Model with Vaccination Plus Movement Restriction
4.1. Presentation of the Control Model
4.2. A Stochastic Optimal Control Approach
4.2.1. Optimal Control Characterization and Necessary Conditions
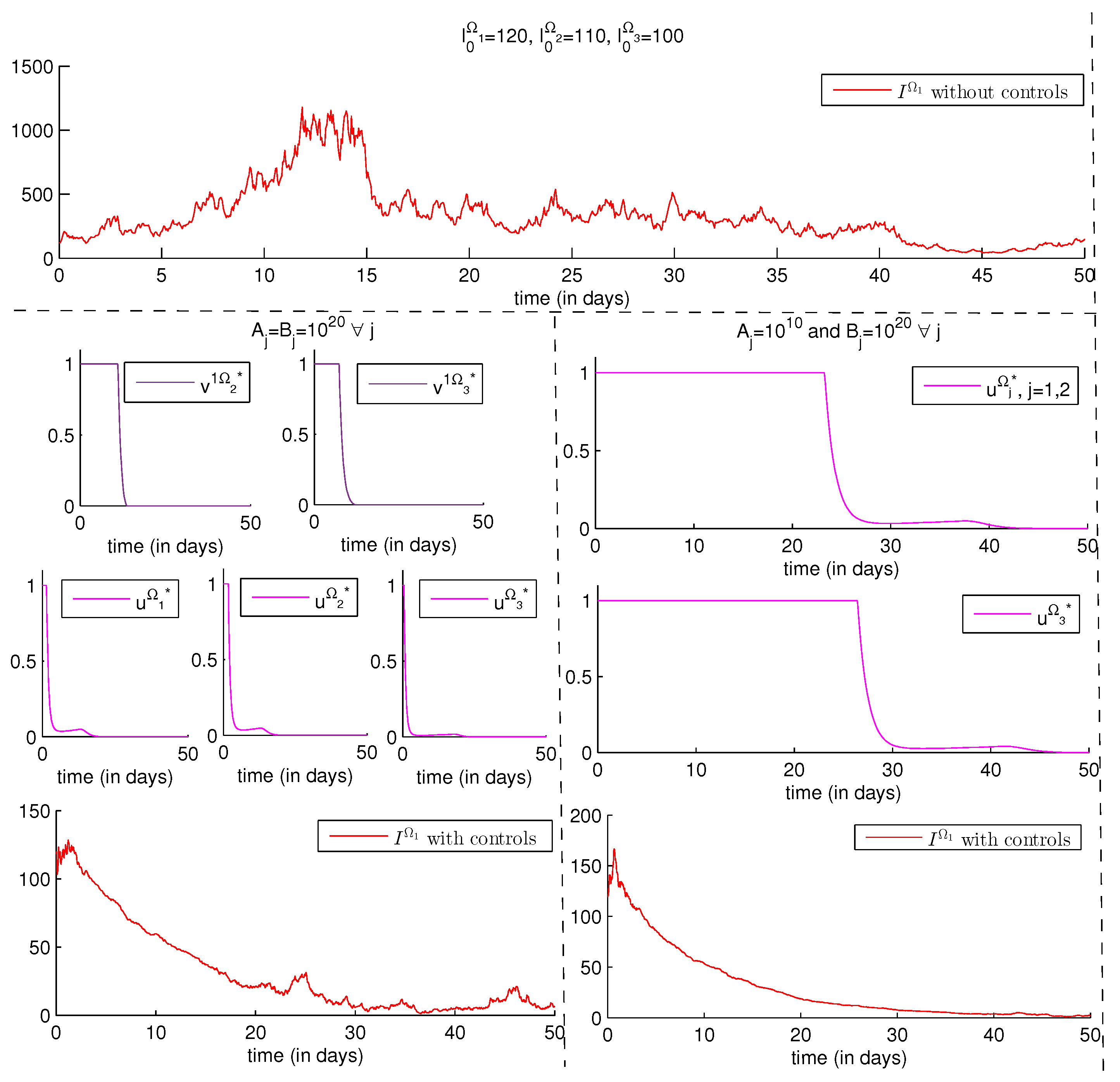
4.2.2. Numerical Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| t | time |
| T | time horizon |
| a large domain or region | |
| random state vector associated with | |
| random control vector associated with | |
| probability space | |
| vector-valued Wiener process associated with all over | |
| f | vector-valued nonlinear function |
| g | matrix-valued nonlinear diffusion |
| a region, an area, or subdomain of | |
| number of susceptibles in | |
| number of infectives in | |
| number of removed in | |
| stochastic proportion of adequate contacts in between a susceptible from and an infective from | |
| deterministic proportion of adequate contacts in between a susceptible from and an infective from | |
| intensities of fluctuations caused by media | |
| birth and death rate | |
| recovery rate | |
| population size corresponding to | |
| vaccination control introduced in | |
| perturbation of control function associated with | |
| minimal bound of | |
| maximal bound of | |
| J | objective function |
| current gain function | |
| weight parameter associated with the number of infectives in | |
| weight parameter associated with the number of removed in | |
| vaccination control severity weight in | |
| movement restriction control severity weight in | |
| vaccination control set | |
| adjoint state variable associated with | |
| adjoint matrix diffusion associated with g | |
| set of indices of regions at a high-risk of infection | |
| movement restriction control set | |
| movement restriction control introduced in to prevent infection from | |
| perturbation of control function associated to | |
| intensities of fluctuations caused by escapes | |
| minimal bound of | |
| maximal bound of |
References
- Liu, R.; Wu, J.; Zhu, H. Media/psychological impact on multiple outbreaks of emerging infectious diseases. Comput. Math. Methods Med. 2007, 8, 153–164. [Google Scholar] [CrossRef]
- Sahu, G.P.; Dhar, J. Dynamics of an SEQIHRS epidemic model with media coverage, quarantine and isolation in a community with pre-existing immunity. J. Math. Anal. Appl. 2015, 421, 1651–1672. [Google Scholar] [CrossRef]
- Wang, A.; Xiao, Y. A Filippov system describing media effects on the spread of infectious diseases. Nonlinear Anal. Hybrid Syst. 2014, 11, 84–97. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, J.A. The impact of media coverage on the dynamics of infectious disease. Int. J. Biomath. 2008, 1, 65–74. [Google Scholar] [CrossRef]
- Samanta, S.; Rana, S.; Sharma, A.; Misra, A.K.; Chattopadhyay, J. Effect of awareness programs by media on the epidemic outbreaks: A mathematical model. Appl. Math. Comput. 2013, 219, 6965–6977. [Google Scholar] [CrossRef]
- Misra, A.K.; Sharma, A.; Shukla, J.B. Stability analysis and optimal control of an epidemic model with awareness programs by media. Biosystems 2015, 138, 53–62. [Google Scholar] [CrossRef]
- Yuan, X.; Xue, Y.; Liu, M. Analysis of an epidemic model with awareness programs by media on complex networks. Chaos Solitons Fractals 2013, 48, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, J.; Jin, Z.; Zhang, H.; Sun, G.Q. Impact of media coverage on epidemic spreading in complex networks. Phys. A Stat. Mech. Its Appl. 2013, 392, 5824–5835. [Google Scholar] [CrossRef]
- World Health Organization. Managing Epidemics: Key Facts About Major Deadly Diseases; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Zakary, O.; Larrache, A.; Rachik, M.; Elmouki, I. Effect of awareness programs and travel-blocking operations in the control of HIV/AIDS outbreaks: A multi-domains SIR model. Adv. Differ. Equ. 2016, 2016, 169. [Google Scholar] [CrossRef]
- Zakary, O.; Rachik, M.; Elmouki, I. A multi-regional epidemic model for controlling the spread of Ebola: Awareness, treatment, and travel-blocking optimal control approaches. Math. Methods Appl. Sci. 2017, 40, 1265–1279. [Google Scholar] [CrossRef]
- Zakary, O.; Rachik, M.; Elmouki, I. On the analysis of a multi-regions discrete SIR epidemic model: An optimal control approach. Int. J. Dyn. Control 2017, 5, 917–930. [Google Scholar] [CrossRef]
- Zakary, O.; Rachik, M.; Elmouki, I. A new analysis of infection dynamics: Multi-regions discrete epidemic model with an extended optimal control approach. Int. J. Dyn. Control 2017, 5, 1010–1019. [Google Scholar] [CrossRef]
- Abouelkheir, I.; El Kihal, F.; Rachik, M.; Zakary, O.; Elmouki, I. A multi-regions SIRS discrete epidemic model with a travel-blocking vicinity optimal control approach on cells. Br. J. Math. Comput. Sci. 2017, 20, 1–16. [Google Scholar] [CrossRef] [PubMed]
- El Kihal, F.; Rachik, M.; Zakary, O.; Elmouki, I. A multi-regions SEIRS discrete epidemic model with a travel-blocking vicinity optimal control approach on cells. Int. J. Adv. Appl. Math. Mech. 2017, 4, 60–71. [Google Scholar]
- Abouelkheir, I.; Rachik, M.; Zakary, O.; Elmouki, I. A multi-regions SIS discrete influenza pandemic model with a travel-blocking vicinity optimal control approach on cells. Am. J. Comput. Appl. Math. 2017, 7, 37–45. [Google Scholar]
- Zakary, O.; Rachik, M.; Elmouki, I.; Lazaiz, S. A multi-regions discrete-time epidemic model with a travel-blocking vicinity optimal control approach on patches. Adv. Differ. Equ. 2017, 2017, 120. [Google Scholar] [CrossRef]
- Chouayakh, K.; Rachik, M.; Zakary, O.; Elmouki, I. A multi-regions SEIS discrete epidemic model with a travel-blocking vicinity optimal control approach on cells. J. Math. Comput. Sci. 2017, 7, 468–484. [Google Scholar]
- Zakary, O.; Rachik, M.; Elmouki, I. A new epidemic modeling approach: Multi-regions discrete-time model with travel-blocking vicinity optimal control strategy. Infect. Dis. Model. 2017, 2, 304–322. [Google Scholar] [CrossRef] [PubMed]
- Bidah, S.; Rachik, M.; Zakary, O.; Boutayeb, H.; Elmouki, I. Travel-blocking Optimal Control Policy on Borders of a Chain of Regions Subject to SIRS Discrete Epidemic Model. Asian J. Res. Infect. Dis. 2018, 1, 1–12. [Google Scholar]
- Zakary, O.; Bidah, S.; Rachik, M.; Elmouki, I. Cell and patch vicinity travel restrictions in a multi-regions SI discrete epidemic control model. Int. J. Adv. Appl. Math. Mech. 2019, 6, 30–41. [Google Scholar]
- Zhang, X.B.; Huo, H.F.; Xiang, H.; Meng, X.Y. Dynamics of the deterministic and stochastic SIQS epidemic model with non-linear incidence. Appl. Math. Comput. 2014, 243, 546–558. [Google Scholar] [CrossRef]
- Ji, C.; Jiang, D. Threshold behaviour of a stochastic SIR model. Appl. Math. Model. 2014, 38, 5067–5079. [Google Scholar] [CrossRef]
- Ji, C.; Jiang, D.; Shi, N. The behavior of an SIR epidemic model with stochastic perturbation. Stoch. Anal. Appl. 2012, 30, 755–773. [Google Scholar] [CrossRef]
- Jiang, D.; Ji, C.; Shi, N.; Yu, J. The long time behavior of DI SIR epidemic model with stochastic perturbation. J. Math. Anal. Appl. 2010, 372, 162–180. [Google Scholar] [CrossRef] [Green Version]
- Liu, W. A SIRS epidemic model incorporating media coverage with random perturbation. In Abstract and Applied Analysis; Hindawi: Cairo, Egypt, 2013; Volume 2013. [Google Scholar]
- Cai, Y.; Wang, X.; Wang, W.; Zhao, M. Stochastic dynamics of an SIRS epidemic model with ratio-dependent incidence rate. In Abstract and Applied Analysis; Hindawi: Cairo, Egypt, 2013; Volume 2013. [Google Scholar]
- Cai, Y.; Kang, Y.; Wang, W. A stochastic SIRS epidemic model with nonlinear incidence rate. Appl. Math. Comput. 2017, 305, 221–240. [Google Scholar] [CrossRef]
- Cai, Y.; Kang, Y.; Banerjee, M.; Wang, W. A stochastic SIRS epidemic model with infectious force under intervention strategies. J. Differ. Equ. 2015, 259, 7463–7502. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, D. The threshold of a stochastic SIRS epidemic model with saturated incidence. Appl. Math. Lett. 2014, 34, 90–93. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, D. Dynamics of stochastically perturbed SIS epidemic model with vaccination. In Abstract and Applied Analysis; Hindawi: Cairo, Egypt, 2013; Volume 2013. [Google Scholar]
- Zhao, Y.; Jiang, D.; O’Regan, D. The extinction and persistence of the stochastic SIS epidemic model with vaccination. Phys. A Stat. Mech. Its Appl. 2013, 392, 4916–4927. [Google Scholar] [CrossRef]
- Lin, Y.; Jiang, D.; Wang, S. Stationary distribution of a stochastic SIS epidemic model with vaccination. Phys. A Stat. Mech. Its Appl. 2014, 394, 187–197. [Google Scholar] [CrossRef]
- Witbooi, P.J. Stability of an SEIR epidemic model with independent stochastic perturbations. Phys. A Stat. Mech. Its Appl. 2013, 392, 4928–4936. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Zhang, W.; Yuan, S. Survival and stationary distribution of a SIR epidemic model with stochastic perturbations. Appl. Math. Comput. 2014, 244, 118–131. [Google Scholar] [CrossRef]
- Gray, A.; Greenhalgh, D.; Hu, L.; Mao, X.; Pan, J. A stochastic differential equation SIS epidemic model. SIAM J. Appl. Math. 2011, 71, 876–902. [Google Scholar] [CrossRef]
- Meng, X.; Zhao, S.; Feng, T.; Zhang, T. Dynamics of a novel nonlinear stochastic SIS epidemic model with double epidemic hypothesis. J. Math. Anal. Appl. 2016, 433, 227–242. [Google Scholar] [CrossRef]
- Hethcote, H.W.; Waltman, P. Optimal vaccination schedules in a deterministic epidemic model. Math. Biosci. 1973, 18, 365–381. [Google Scholar] [CrossRef]
- Yong, J.; Zhou, X.Y. Stochastic Controls Hamiltonian Systems and HJB equations. In Application of Mathematics; Springer: New York, NY, USA, 1999. [Google Scholar]
- Bahlali, K.; Mezerdi, B.; Ouknine, Y. The maximum principle for optimal control of diffusions with non-smooth coeffcients. Stoch. Stoch. Rep. 1996, 57, 303–316. [Google Scholar] [CrossRef]
- Peng, S. A general stochastic maximum principle for optimal control problems. SIAM J. Control Optim. 1990, 28, 966–979. [Google Scholar] [CrossRef]
- Ma, J.; Protter, P.; Yong, J. Solving Forward-Backward Stochastic Differential Equations Explicitly—A Four Step Scheme. J. Probab. Theory. Relat. Fields 1994, 98, 339–3359. [Google Scholar] [CrossRef]
- Ladyz̆henskaia, O.A.; Solonnikov, V.A.; Ural’ceva, N.N. Linear and Quasi-Linear Equations of Parabolic Type; American Mathematical Soc.: Washington, DC, USA, 1968; Volume 23. [Google Scholar]
- Düring, B.; Jüngel, A. Existence and uniqueness of solutions to a quasilinear parabolic equation with quadratic gradients in financial markets. Nonlinear Anal. Theory Methods Appl. 2005, 62, 519–544. [Google Scholar] [CrossRef]
- Aboulaich, R.; Darouichi, A.; Elmouki, I.; Jraifi, A. A Stochastic Optimal Control Model for BCG Immunotherapy in Superficial Bladder Cancer. Math. Model. Nat. Phenom. 2017, 12, 99–119. [Google Scholar] [CrossRef]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Kihal, F.; Abouelkheir, I.; Rachik, M.; Elmouki, I. Role of Media and Effects of Infodemics and Escapes in the Spatial Spread of Epidemics: A Stochastic Multi-Region Model with Optimal Control Approach. Mathematics 2019, 7, 304. https://doi.org/10.3390/math7030304
El Kihal F, Abouelkheir I, Rachik M, Elmouki I. Role of Media and Effects of Infodemics and Escapes in the Spatial Spread of Epidemics: A Stochastic Multi-Region Model with Optimal Control Approach. Mathematics. 2019; 7(3):304. https://doi.org/10.3390/math7030304
Chicago/Turabian StyleEl Kihal, Fadwa, Imane Abouelkheir, Mostafa Rachik, and Ilias Elmouki. 2019. "Role of Media and Effects of Infodemics and Escapes in the Spatial Spread of Epidemics: A Stochastic Multi-Region Model with Optimal Control Approach" Mathematics 7, no. 3: 304. https://doi.org/10.3390/math7030304




