Generalized Viscosity Implicit Iterative Process for Asymptotically Non-Expansive Mappings in Banach Spaces
Abstract
1. Introduction
2. Preliminaries
- (i)
- and and
- (ii)
- either or
3. Main Results
4. Applications
4.1. Application to Zero-Point Problems
4.2. Application to Equilibrium Problems
- (H1)
- for all ;
- (H2)
- , for all ;
- (H3)
- for each ,; and
- (H4)
- for all , is convex and weakly lower semi-continuous.
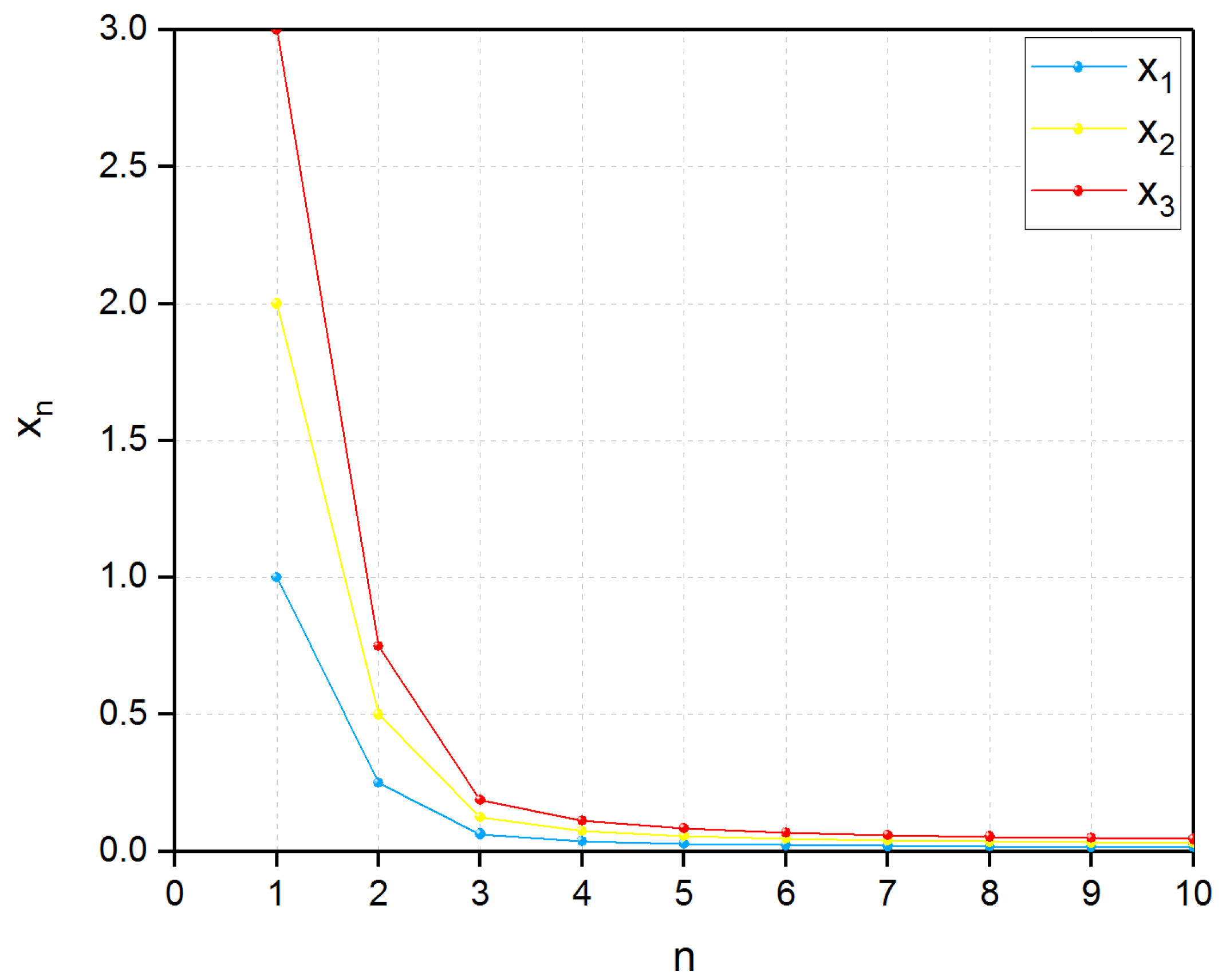
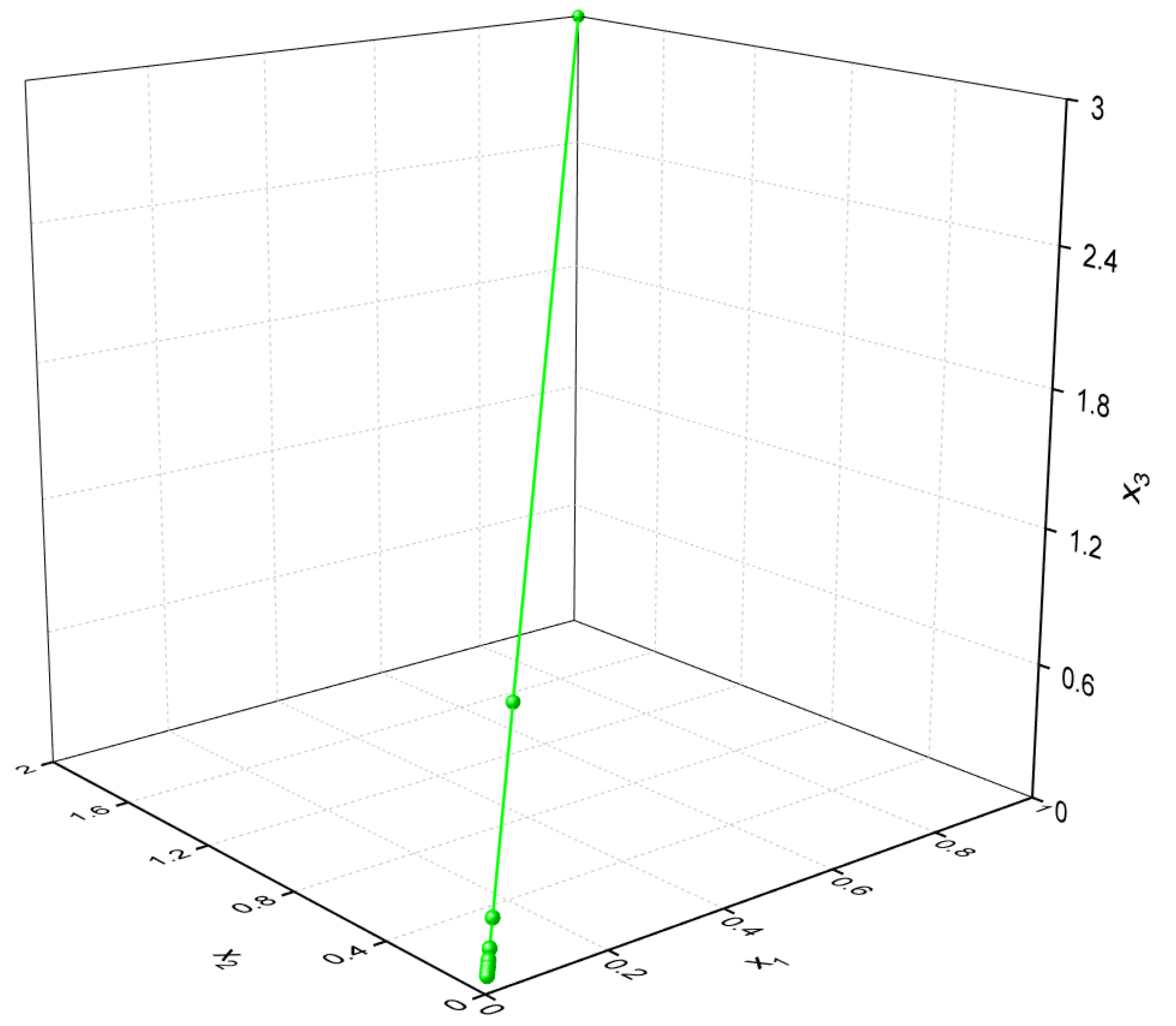
5. Numerical Examples
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Iiduka, H.; Takahashi, W.; Toyoda, M.; Toyoda, M. Approximation of solutions of variational inequalities for monotone mappings. Pan. Math. J. 2004, 14, 49–61. [Google Scholar]
- La Sen, M.D. Stability and convergence results based on fixed point theory for a generalized viscosity iterative scheme. Fixed Point Theory Appl. 2009, 19, 314581. [Google Scholar] [CrossRef][Green Version]
- Yao, Y.; Leng, L.; Postolache, M.; Zheng, X. Mann type iteration method for solving the split common fixed point problem. J. Nonlinear Convex Anal. 2017, 18, 875–882. [Google Scholar]
- Song, Y.; Chen, R.; Zho, H. Viscosity approximation methods for nonexpansive mapping sequences in Banach spaces. Nonlinear Anal. 2007, 66, 1016–1024. [Google Scholar] [CrossRef]
- Yao, Y.; Maruster, S. Strong convergence of an iterative algorithm for variational inequalities in Banach spaces. Math. Comput. Model. 2011, 54, 325–329. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, L. Viscosity Approximation Methods for Multivalued Nonexpansive Mappings. Mediterr. J. Math. 2016, 13, 2645–2657. [Google Scholar] [CrossRef]
- Yao, Y.; Yao, J.C.; Liou, Y.C.; Postolache, M. Iterative algorithms for split common fixed points of demicontractive operators without priori knowledge of operator norms. Carpathian J. Math. 2018, 34, 459–466. [Google Scholar]
- Sunthrayuth, P.; Kumam, P. Viscosity approximation methods base on generalized contraction mappings for a countable family of strict pseudo-contractions, a general system of variational inequalities and a generalized mixed equilibrium problem in Banach spaces. Math. Comput. Model. 2013, 58, 1814–1828. [Google Scholar] [CrossRef]
- Yao, Y.; Postolache, M.; Yao, J.C. An iterative algorithm for solving the generalized variational inequalities and fixed points problems. Mathematics 2019, 7, 61. [Google Scholar] [CrossRef]
- Bader, G.; Deuflhard, P. A semi-implicit mid-point rule for stiff systems of ordinary differential equations. Numer. Math. 1983, 41, 373–398. [Google Scholar] [CrossRef]
- Somalia, S. Implicit midpoint rule to the nonlinear degenerate boundary value problems. Int. J. Comput. Math. 2002, 79, 327–332. [Google Scholar] [CrossRef]
- Zhang, H.C.; Qu, Y.H.; Su, Y.F. Strong convergence theorems for fixed point problems for nonexpansive mappings and zero point problems for accretive operators using viscosity implicit midpoint rules in Banach Spaces. Mathematics 2018, 6, 257. [Google Scholar] [CrossRef]
- Cai, G.; Shehu, Y.; Iyiola, O.S. Modified viscosity implicit rules for nonexpansive mappings in hilbert spaces. Fixed Point Theory Appl. 2017. [Google Scholar] [CrossRef]
- Luo, P.; Cai, G.; Shehu, Y. The viscosity iterative algorithms for the implicit midpoint rule of nonexpansive mappings in uniformly smooth banach spaces. J. Inequal. Appl. 2017, 2017, 154. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.H.; Shahzad, N.; Liou, Y.C. Modified semi-implicit midpoint rule for nonexpansive mappings. Fixed Point Theory Appl. 2015, 2015, 166. [Google Scholar] [CrossRef]
- Xu, H.K.; Alghamdi, M.; Shahzad, N. The implicit midpoint rule of nonexpansive mappings in Banach spaces. Fixed Point Theory 2016, 17, 509–518. [Google Scholar]
- Xu, H.K.; Alghamdi, M.; Shahzad, N. The viscosity technique for the implicit midpoint rule of nonexpansive mappings in hilbert spaces. Fixed Point Theory Appl. 2015, 2015, 41. [Google Scholar] [CrossRef]
- Ke, Y.F.; Ma, C.F. The generalized viscosity implicit rules of nonexpansive mappings in Hilbert spaces. Fixed Point Theory Appl. 2015, 2015, 190. [Google Scholar] [CrossRef]
- He, S.J.; Mao, Y.D.; Zhou, Z.; Zhang, J.Q. The generalized viscosity implicit rules of asymptotically nonexpansive mappings in Hilbert spaces. Appl. Math. Sci. 2017, 12, 549–560. [Google Scholar] [CrossRef]
- Liu, L.S. Iterative processes with errors for nonlinear strongly accretive mappings in Banach spaces. J. Math. Anal. Appl. 1995, 194, 114–125. [Google Scholar] [CrossRef]
- Lim, T.C.; Xu, H.K. Fixed point theorems for asymptotically nonexpansive mappings. Nonlinear Anal. 1994, 22, 1345–1355. [Google Scholar] [CrossRef]
- Xu, H.K. Viscosity approximation methods for nonexpansive mappings. J. Math. Anal. Appl. 2004, 298, 279–291. [Google Scholar] [CrossRef]
- Chancelier, J.P. Iterative schemes for computing fixed points of nonexpansive mappings in Banach spaces. J. Math. Anal. Appl. 2009, 353, 141–153. [Google Scholar] [CrossRef]
- Yan, Q.; Cai, G. Convergence analysis of modified viscosity implicit rules of asymptotically nonexpansive mappings in Hilbert spaces. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A Matemáticas 2018, 112, 1125–1140. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.; Wang, Y. Generalized Viscosity Implicit Iterative Process for Asymptotically Non-Expansive Mappings in Banach Spaces. Mathematics 2019, 7, 379. https://doi.org/10.3390/math7050379
Pan C, Wang Y. Generalized Viscosity Implicit Iterative Process for Asymptotically Non-Expansive Mappings in Banach Spaces. Mathematics. 2019; 7(5):379. https://doi.org/10.3390/math7050379
Chicago/Turabian StylePan, Chanjuan, and Yuanheng Wang. 2019. "Generalized Viscosity Implicit Iterative Process for Asymptotically Non-Expansive Mappings in Banach Spaces" Mathematics 7, no. 5: 379. https://doi.org/10.3390/math7050379
APA StylePan, C., & Wang, Y. (2019). Generalized Viscosity Implicit Iterative Process for Asymptotically Non-Expansive Mappings in Banach Spaces. Mathematics, 7(5), 379. https://doi.org/10.3390/math7050379




