Abstract
Complex fuzzy set (CFS) is a recent development in the field of fuzzy set (FS) theory. The significance of CFS lies in the fact that CFS assigned membership grades from a unit circle in the complex plane, i.e., in the form of a complex number whose amplitude term belongs to a interval. The interval-valued complex fuzzy set (IVCFS) is one of the extensions of the CFS in which the amplitude term is extended from the real numbers to the interval-valued numbers. The novelty of IVCFS lies in its larger range comparative to CFS. We often use fuzzy distance measures to solve some problems in our daily life. Hence, this paper develops some series of distance measures between IVCFSs by using Hamming and Euclidean metrics. The boundaries of these distance measures for IVCFSs are obtained. Finally, we study two geometric properties include rotational invariance and reflectional invariance of these distance measures.
1. Introduction
Complex fuzzy set [] and some extensions of complex fuzzy set such as complex intuitionistic fuzzy sets [], complex neutrosophic set [], interval complex neutrosophic set [], complex multi-fuzzy soft set [], complex interval-valued intuitionistic fuzzy sets [], complex vague soft sets [] and interval-valued complex fuzzy sets [,] have been introduced and used in a variety of fields such as signal processing [,,], decision-making [,,,,], time series prediction [,,,] and image restoration [].
The concept of distance measure can be defined as a numerical description of the difference between two objects. There are many distance measures introduced by numerous scholars to solve some problems in many fields to solve some problems and discover several applications. Among these distances, Euclidean distance and Hamming distance are widely used in several fields. It is well known that distance measure is also an important issue on fuzzy set and its extensions [,,,,,,,]. As defined in [], each complex membership grade includes an amplitude term and a phase term. Hence, many researchers defined distances of CFSs by combining the difference between the phase terms and the difference between the amplitude terms. In this way, Zhang et al. [] defined a distance measure of CFSs. Hu et al. [] and Alkouri et al. [] also introduced some distances for CFSs. These distance measures in [,] are defined by using Hamming and Euclidean metrics. Recently, several concepts including the parallelity [,] and entropy measures [] of complex fuzzy sets and distances of complex intuitionistic fuzzy sets [], complex vague soft sets [,,] and complex multi-fuzzy soft set [] have been developed. Since Greenfield et al. [,] introduced the concept of an interval-valued complex fuzzy sets (IVCFSs), which is a generalization of the complex fuzzy set introduced by Ramot et al. [], some progress has been made in various subjects related to the IVCFS. How to measure the difference between IVCFSs is an interesting subject that may be used as a useful tool for decision-making, predictions and pattern recognition in the form of IVCFSs. This paper considers the distance measures between interval-valued complex fuzzy sets.
In [], Dick proposed the concept of rotational invariance for complex fuzzy operations, which is an intuitive and desirable feature. Then, this feature is examined for interval-valued complex fuzzy operations in [], complex fuzzy aggregation operators in [] and entropy measures of CFSs in []. Moreover, Bi et al. [] proposed a novel feature called reflectional invariance for complex fuzzy aggregation operators. These two feature criteria serve as two criteria for choices of complex fuzzy operations and complex fuzzy aggregation operators in some real applications. After giving the distance measures for IVCFSs, we then examine the rotational invariance and reflectional invariance for distance measures of IVCFSs. In addition, the results proposed in this paper might serve as criteria for choices of distance measures of CFSs and IVCFSs.
The rest of the chapter is organized in the following way: In Section 2, we review the basic concepts relates to interval-valued complex fuzzy sets. In Section 3, we develop some distance measures of interval-valued complex fuzzy sets based on the Hamming distance and Euclidean distance. In Section 4, we study rotational invariance and reflectional invariance of these distance measures. In Section 5, we apply these distance measures to solve a decision-making problem with interval-valued complex fuzzy information. Conclusions are given in Section 6.
2. Preliminaries
Firstly, let us review the basic concepts relates to interval-valued complex fuzzy sets [,].
Let D be the set of values on complex unit disk, i.e., . Suppose is a fixed universe. A mapping is called a complex fuzzy set on U.
Let be the set of all closed subintervals of and be the boundary set of D i.e., . Suppose are two classical sets, and their dot product set is denoted as:
A mapping is called an interval-valued complex fuzzy set [,] on U. For any , the membership function is
where , is the interval-valued amplitude part and is the phase part. We use the notation to denote the set of all IVCFSs of U.
3. Distance Measures between IVCFSs
In this section, we introduce several distances in interval-valued complex fuzzy sets case. First, we give the definition of distance between interval-valued complex fuzzy sets as follows:
Definition 1.
A distance of interval-valued complex fuzzy sets is a function which satisfies the following conditions: for any :
- (i)
- and if and only if ,
- (ii)
- ,
- (iii)
- .
Now, we define the Hamming, Euclidean, Normalized Hamming, and Normalized Euclidean distances in interval-valued complex fuzzy sets case as follows: for any ,
- The Hamming distance:
- The Euclidean distance:
- The normalized Hamming distance:
- The normalized Euclidean distance:
Clearly, it is easy to notice that the above Equations (3)–(6) have the following results:
Theorem 1.
All functions defined in Equations (3)–(6) are distance measures of IVCFSs.
Proof.
It is easy to see that all the distance Equations (3)–(6) satisfy conditions (i) and (ii). Thus, we just go to prove the condition number (iii), i.e., the triangular inequality for .
Let ; for the Hamming distance, we have
For the Euclidean distance, we have
analogously, for the proof of the normalized Hamming and the normalized Euclidean distances. ☐
Example 1.
Let A and B be two IVCFSs on , which are given as follows:
Using Equations (3)–(6), we have the following results:
and
However, in practice, the different sets may have taken different weights i.e., , , and , for each element . Thus, we introduce the normalized weighted Hamming and Euclidean distance measures for IVCFSs.
- The normalized weighted Hamming distance:
- The normalized weighted Euclidean distance:
Theorem 2.
All functions defined in Equations (7) and (8) are distance measures of IVCFSs.
Proof.
The proof is similar to that of Theorem 1. ☐
Obviously, when for all , then Equations (7) and (8) reduce to Equations (5) and (6), respectively. In addition, the above distance Equations (7) and (8) have the following results:
Example 2.
Let A and B be two IVCFSs defined in Example 1 and the weight of is .
Using Equations (7) and (8), we have the following results:
By the relations among IVCFS, CFS, interval-valued fuzzy sets (IVFS) and FS, we established the comparison of the proposed distance measures of IVCFSs with CFS, IVFS and FS. It is proposed that these distance measures reduce the environments of CFS, IVFS and FS. The comparison is demonstrated in Remarks 1–3.
Remark 1.
The distance measures proposed in Equations (3)–(6) for IVCFSs reduce to the environment of CFSs as defined in [].
Remark 2.
The distance measures proposed in Equations (3)–(6) for IVCFSs reduce to the environment of IVFSs if we considered the phase term as zero as defined in [].
Remark 3.
The distance measures proposed in Equations (7) and (8) for IVCFSs reduce to the environment of CFSs as defined in Equations (9) and (10):
Here, we demonstrate the advantages of the proposed distance measures of IVCFSs. Firstly, the distance measures of CFSs, IVFSs, and FS could not handle the information provided in the form of IVCFSs. On the other hand, from Remarks 1 and 2, the proposed distance measures in Equations (3)–(6) can solve some problem that lies in the region of CFSs, IVFSs, and FS. Moreover, the distance measures proposed in Remark 3 for CFSs are two new distance Equations for CFSs.
4. Rotational Invariance and Reflectional Invariance
Let A be a IVCFS on U with membership function , and then we define the following two set operations for IVCFSs:
The rotation of an IVCFS A by radians, denoted is defined as
The reflection of an IVCFS A, denoted is defined as
Moreover, we define the following:
Definition 2.
A distance d on IVCFS is rotationally invariant if
for any θ and .
Definition 3.
A distance d on IVCFS is reflectionally invariant if
for any .
Definitions 2 and 3 give two intuitive properties of distance measures of IVCFSs, named rotational invariance and reflectional invariance, respectively. They mean that the distance measure is invariant under a rotation or a reflection. More specifically, if two IVCFSs are rotated by a fixed value, rotational invariance states that the distance between two new IVCFSs will not change. If two IVCFSs are reflected, reflectional invariance states that the distance between two new IVCFSs will not change as well, which are respectively shown in Figure 1, is equal to after reflecting or rotating.
Theorem 3.
All functions defined in Equations (3)–(8) are reflectionally invariant.
Proof.
It is easy from that for any . ☐
Theorem 4.
All functions defined in Equations (3)–(8) are not rotationally invariant.
Proof.
Since the domain of the phase term is , so the above rotation operation is addition modulo . Consider two IVCFSs on the set ; let and for any . Then, and . By using Equations (3)–(8), we have
Thus, the distance functions defined in Equations (3)–(8) are not rotationally invariant. ☐
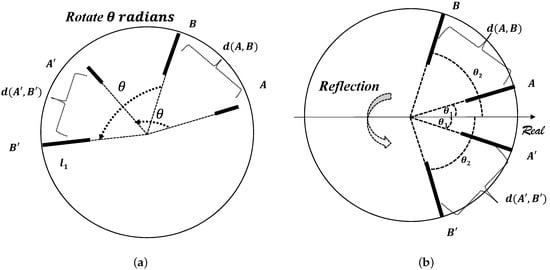
Figure 1.
(a) reflectional invariance and (b) rotational invariance.
Obviously, the concepts of rotational invariance and reflectional invariance can be examined for distance measures of CFSs when IVCFSs are reduced to CFSs. Then, we can study the rotational invariance and reflectional invariance of distance measures of CFSs.
Remark 4.
The concepts of rotational invariance and reflectional invariance proposed respectively in Definitions 2 and 3 for distance measures of IVCFSs reduce to the environment of CFSs.
With the combination of Remark 1, we have the following results for the distance measures of CFSs.
Corollary 1.
Distance measures of CFSs defined in [] are reflectionally invariant.
Corollary 2.
Distance measures of CFSs defined in [] are not rotationally invariant.
With the combination of Remark 3, we have the following results for the distance measures of CFSs.
Corollary 3.
Distance functions of CFSs defined in Equations (9) and (10) are reflectionally invariant.
Corollary 4.
Distance functions of CFSs defined in Equations (9) and (10) are not rotationally invariant.
5. Numerical Example for Decision-Making
In this section, we consider a decision-making problem under an interval-valued complex fuzzy environment.
Assume that a customer decides to purchase a new computer for his own private use. There are four alternatives () with different production dates. The customer considers five attributes, namely : Performance, : Appearance, : Service, : Experience and : Price with the weight vectors for selecting computer. The corresponding rating values of attributes of alternatives are interval-valued complex fuzzy values as shown in Table 1. For instance, the rating value of the alternative under attribute is the interval-valued complex fuzzy value , which means that the performance of the computer at is marked by an interval value , and the customer satisfied 80% with the suitability of production date of the computer at ; this explanation of the phase part is referred to Garg et al.’s works on complex intuitionistic fuzzy aggregation operators [,]. The customer wants to select a computer among the four alternatives above. Here, we use the principle of minimum degree of difference between IVCFSs to solve the given problem.

Table 1.
Feature values of the facial expressions.
Now, we calculate the distance between the ideal choice (each rating value is ) and () with the weighting vector w. We consider the distances as defined in Equations (3)–(8) and obtain the results as shown in Table 2.

Table 2.
Distance results.
From Table 2, we get an ordering of the choices for each case as shown in Table 3. Clearly, the best alternative is , which is the one with the lowest distance to the ideal choice.

Table 3.
Ordering of the alternatives.
6. Conclusions
In this paper, we have presented several distance measures in the case of the interval-valued complex fuzzy sets, which are very useful to deal with the decision information represented in interval-valued complex fuzzy values under uncertain situations. These distance measures include a family of Hamming and Euclidean distances such as the Hamming distance, the normalized Hamming distance, the normalized weighted Hamming distance, the Euclidean distance, the normalized Euclidean distance and the normalized weighted Euclidean distance. Furthermore, these distance measures are reflectionally invariant but not rotationally invariant. Finally, based on these measures, we presented an illustrative example for decision-making under interval-valued complex fuzzy information.
As future work, we can consider distance measures for interval-valued complex fuzzy sets that are both reflectionally invariant and rotationally invariant.
Author Contributions
Conceptualization, S.D.; Funding acquisition, L.B. and B.H.; Writing—original draft, S.D.; Writing—review and editing, L.B. and B.H.
Funding
This research was funded by the Opening Foundation of Guangxi Colleges and Universities Key Laboratory of Complex System Optimization and Big Data Processing OF FUNDER Grant No. 2017CSOBDP0103.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ramot, D.; Milo, R.; Friedman, M.; Kandel, A. Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 2002, 10, 171–186. [Google Scholar] [CrossRef]
- Alkouri, A.M.J.S.; Salleh, A.R. Complex intuitionistic fuzzy sets. In Proceedings of the International Conference on Fundamental and Applied Sciences (ICFAS 2012), Kuala Lumpur, Malaysia, 12–14 June 2012; pp. 464–470. [Google Scholar]
- Ali, M.; Smarandache, F. Complex neutrosophic set. Neural Comput. Appl. 2017, 28, 1–18. [Google Scholar] [CrossRef]
- Ali, M.; Dat, L.Q.; Smarandache, F. Interval complex neutrosophic set: Formulation and applications in decision-making. Int. J. Fuzzy Syst. 2018, 20, 986–999. [Google Scholar] [CrossRef]
- Al-Qudah, Y.; Hassan, N. Complex multi-fuzzy soft set: Its entropy and similarity measure. IEEE Access 2018, 6, 65002–65017. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Complex interval-valued intuitionistic fuzzy sets and their aggregation operators. Fundam. Inform. 2019, 164, 61–101. [Google Scholar] [CrossRef]
- Selvachandran, G.; Maji, P.K.; Abed, I.E.; Salleh, A.R. Complex vague soft sets and its distance measures. J. Intell. Fuzzy Syst. 2016, 31, 55–68. [Google Scholar] [CrossRef]
- Greenfield, S.; Chiclana, F.; Dick, S. Interval-valued complex fuzzy logic. In Proceedings of the 2016 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Vancouver, BC, Canada, 24–29 July 2016; pp. 2014–2019. [Google Scholar]
- Greenfield, S.; Chiclana, F.; Dick, S. Join and meet operations for interval-valued complex fuzzy logic. In Proceedings of the 2016 Annual Conference of the North American Fuzzy Information Processing Society (NAFIPS), El Paso, TX, USA, 31 October–4 November 2016; pp. 1–5. [Google Scholar]
- Ramot, D.; Friedman, M.; Langholz, G.; Kandel, A. Complex fuzzy logic. IEEE Trans. Fuzzy Syst. 2003, 11, 450–461. [Google Scholar] [CrossRef]
- Zhang, G.; Dillon, T.S.; Cai, K.-Y.; Ma, J.; Lu, J. Operation properties and delta-equalities of complex fuzzy sets. Int. J. Approx. Reason. 2009, 50, 1227–1249. [Google Scholar] [CrossRef]
- Hu, B.; Bi, L.; Dai, S. The Orthogonality between Complex Fuzzy Sets and Its Application to Signal Detection. Symmetry 2017, 9, 175. [Google Scholar] [CrossRef]
- Rani, D.; Garg, H. Complex intuitionistic fuzzy power aggregation operators and their applications in multicriteria decision-making. Expert Syst. 2018, e12325. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Some Generalized Complex Intuitionistic Fuzzy Aggregation Operators and Their Application to Multicriteria Decision-Making Process. Arab. J. Sci. Eng. 2019, 44, 2679–2698. [Google Scholar] [CrossRef]
- Bi, L.; Dai, S.; Hu, B. Complex fuzzy geometric aggregation operators. Symmetry 2018, 10, 251. [Google Scholar] [CrossRef]
- Bi, L.; Dai, S.; Hu, B.; Li, S. Complex fuzzy arithmetic aggregation operators. J. Intell. Fuzzy Syst. 2019, 26, 2765–2771. [Google Scholar] [CrossRef]
- Chen, Z.; Aghakhani, S.; Man, J.; Dick, S. ANCFIS: A Neuro-Fuzzy Architecture Employing Complex Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2011, 19, 305–322. [Google Scholar] [CrossRef]
- Li, C. Complex Neuro-Fuzzy ARIMA Forecasting. A New Approach Using Complex Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2013, 21, 567–584. [Google Scholar] [CrossRef]
- Li, C.; Chiang, T.-W.; Yeh, L.-C. A novel self-organizing complex neuro-fuzzy approach to the problem of time series forecasting. Neurocomputing 2013, 99, 467–476. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, G.; Lu, J. A method for multiple periodic factor prediction problems using complex fuzzy sets. IEEE Trans. Fuzzy Syst. 2012, 20, 32–45. [Google Scholar]
- Li, C.; Wu, T.; Chan, F.-T. Self-learning complex neuro-fuzzy system with complex fuzzy sets and its application to adaptive image noise canceling. Neurocomputing 2012, 94, 121–139. [Google Scholar] [CrossRef]
- Liu, X. Entropy, distance measure and similarity measure of fuzzy sets and their relations. Fuzzy Sets Syst. 1992, 52, 305–318. [Google Scholar]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, L. New distance measures between intuitionistic fuzzy sets and interval-valued fuzzy sets. Inf. Sci. 2013, 245, 181–196. [Google Scholar] [CrossRef]
- Wang, W.Q.; Xin, X.L. Distance measure between intuitionistic fuzzy sets. Pattern Recognit. Lett. 2005, 26, 2063–2069. [Google Scholar] [CrossRef]
- Grzegorzewski, P. Distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff metric. Fuzzy Sets Syst. 2004, 148, 319–328. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, J. An overview of distance and similarity measures of intuitionistic fuzzy sets. Int. J. Uncertain. Fuzz. Knowl.-Based Syst. 2008, 16, 529–555. [Google Scholar] [CrossRef]
- Zeng, W.Y.; Guo, P. Normalized distance, similarity measure, inclusion measure and entropy of interval-valued fuzzy sets and their relationship. Inf. Sci. 2008, 178, 1334–1342. [Google Scholar] [CrossRef]
- Hu, B.; Bi, L.; Dai, S.; Li, S. Distances of Complex Fuzzy Sets and Continuity of Complex Fuzzy Operations. J. Intell. Fuzzy Syst. 2018, 35, 2247–2255. [Google Scholar] [CrossRef]
- Alkouri, A.U.M.; Salleh, A.R. Linguistic variables, hedges and several distances on complex fuzzy sets. J. Intell. Fuzzy Syst. 2014, 26, 2527–2535. [Google Scholar]
- Bi, L.; Hu, B.; Li, S.; Dai, S. The Parallelity of Complex Fuzzy sets and Parallelity Preserving Operators. J. Intell. Fuzzy Syst. 2018, 34, 4173–4180. [Google Scholar] [CrossRef]
- Hu, B.; Bi, L.; Dai, S.; Li, S. The approximate parallelity of complex fuzzy sets. J. Intell. Fuzzy Syst. 2018, 35, 6343–6351. [Google Scholar] [CrossRef]
- Bi, L.; Zeng, Z.; Hu, B.; Dai, S. Two Classes of Entropy Measures for Complex Fuzzy Sets. Mathematics 2019, 7, 96. [Google Scholar] [CrossRef]
- Rani, D.; Garg, H. Distance measures between the complex intuitionistic fuzzy sets and its applications to the decision-making process. Int. J. Uncertain. Quantif. 2017, 7, 423–439. [Google Scholar] [CrossRef]
- Selvachandran, G.; Garg, H.; Alaroud, M.H.; Salleh, A.R. Similarity measure of complex vague soft sets and its application to pattern recognition. Int. J. Fuzzy Syst. 2018, 20, 1901–1914. [Google Scholar] [CrossRef]
- Selvachandran, G.; Garg, H.; Quek, S. Vague entropy measure for complex vague soft sets. Entropy 2018, 20, 403. [Google Scholar] [CrossRef]
- Dick, S. Towards Complex Fuzzy Logic. IEEE Trans. Fuzzy Syst. 2005, 13, 405–414. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).