The Mittag-Leffler Fitting of the Phillips Curve
Abstract
1. Introduction
2. Preliminaries: Mittag-Leffler Function and Its Generalisations
3. Modelling the Phillips Curve
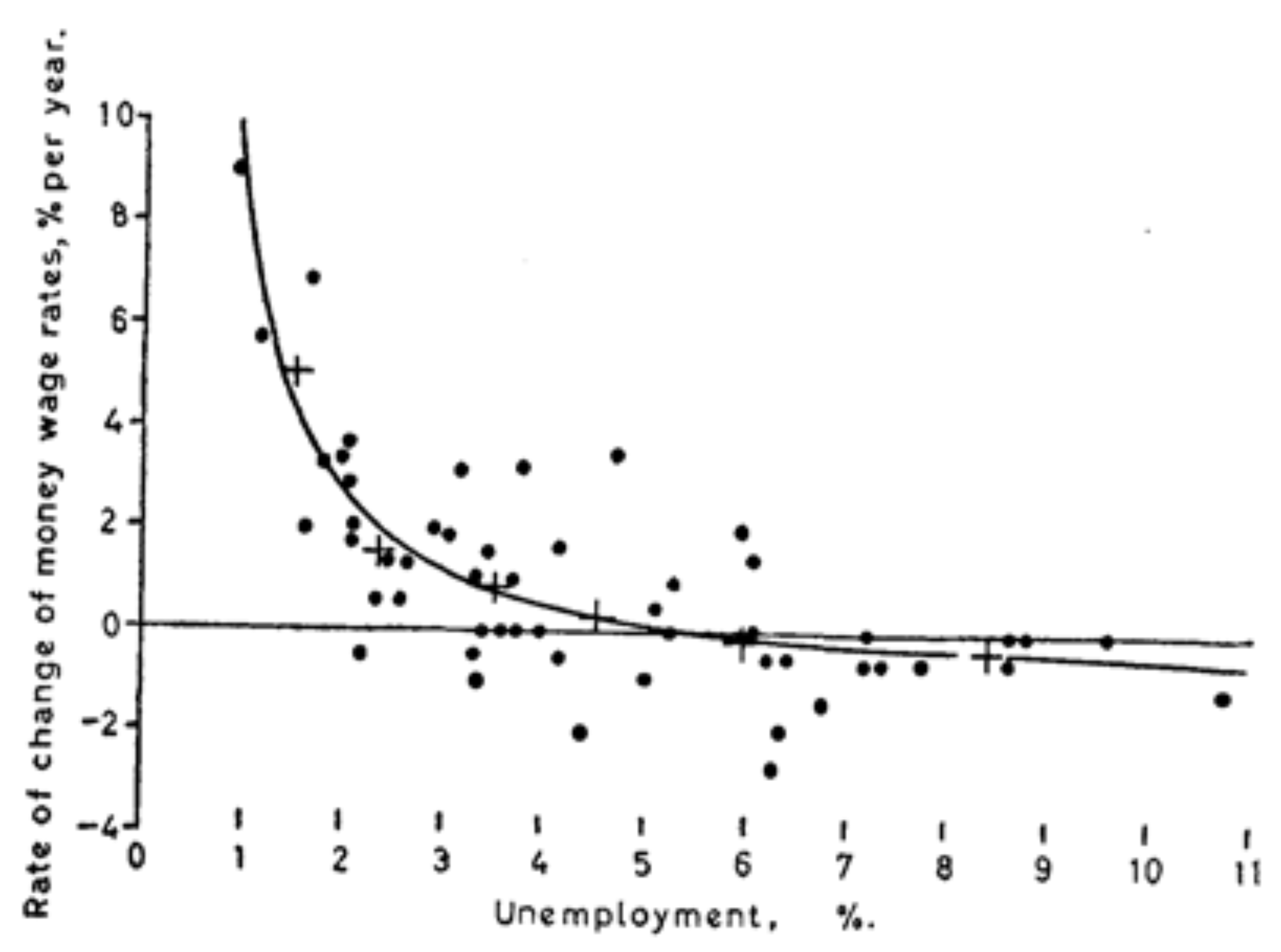
3.1. The “Original” Phillips Curve
3.2. The Mittag-Leffler Model for Fitting the Phillips Curve
- the usual shape of the PC, used in the literature, which reminds on the exponential-type function:
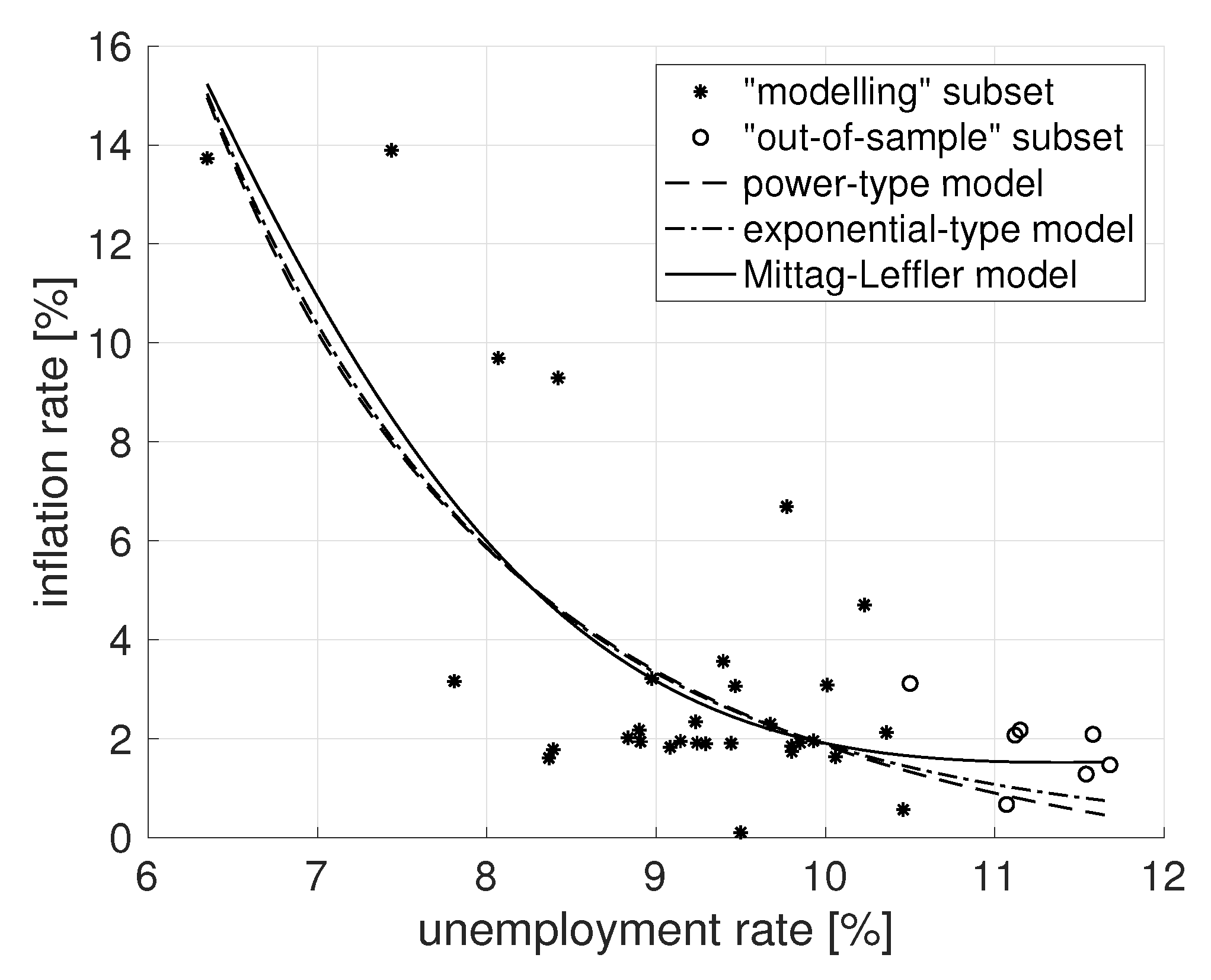
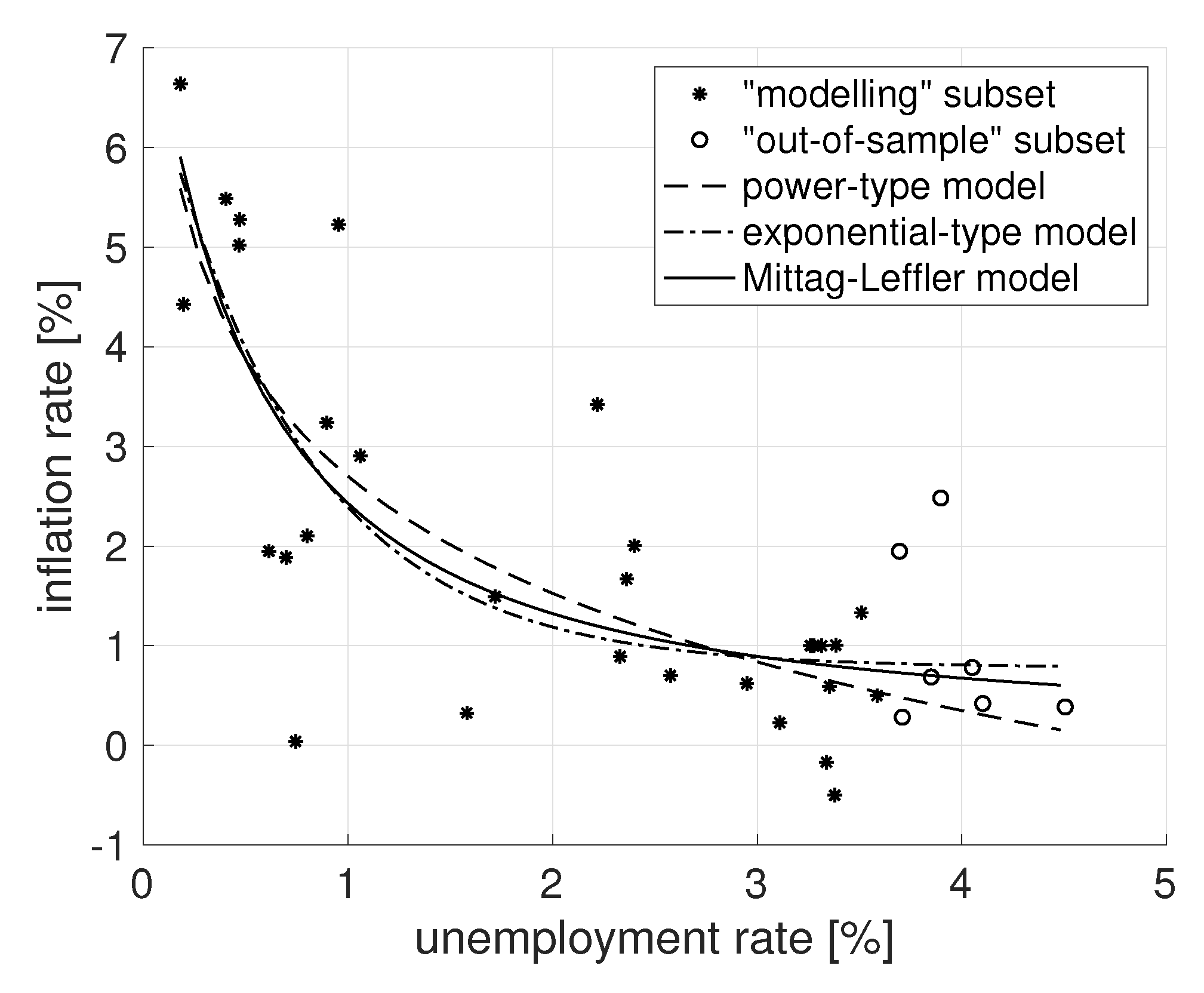
4. Numerical Results and Discussion
4.1. Goodness-of-Fit Statistics and Data Preprocessing
4.2. Experiments
5. Conclusions
Funding
Conflicts of Interest
Appendix A. The Econometric Dataset
| Year | France | Switzerland | ||
|---|---|---|---|---|
| Unemployment Rate [%] | Inflation Rate [%] | Unemployment Rate [%] | Inflation Rate [%] | |
| 1980 | 6.3490 | 13.7300 | 0.1970 | 4.4260 |
| 1981 | 7.4380 | 13.8900 | 0.1810 | 6.6370 |
| 1982 | 8.0690 | 9.6910 | 0.4040 | 5.4850 |
| 1983 | 8.4210 | 9.2920 | 0.8010 | 2.1000 |
| 1984 | 9.7710 | 6.6900 | 1.0590 | 2.9040 |
| 1985 | 10.2300 | 4.7030 | 0.8970 | 3.2380 |
| 1986 | 10.3600 | 2.1210 | 0.7440 | 0.0400 |
| 1987 | 10.5000 | 3.1150 | 0.6970 | 1.8870 |
| 1988 | 10.0100 | 3.0810 | 0.6130 | 1.9490 |
| 1989 | 9.3960 | 3.5630 | 0.4690 | 5.0220 |
| 1990 | 8.9750 | 3.2120 | 0.4720 | 5.2760 |
| 1991 | 9.4670 | 3.0630 | 0.9550 | 5.2270 |
| 1992 | 9.8500 | 1.9180 | 2.2190 | 3.4210 |
| 1993 | 11.1200 | 2.0700 | 3.8970 | 2.4820 |
| 1994 | 11.6800 | 1.4690 | 4.1020 | 0.4200 |
| 1995 | 11.1500 | 2.1720 | 3.6950 | 1.9480 |
| 1996 | 11.5800 | 2.0860 | 4.0510 | 0.7810 |
| 1997 | 11.5400 | 1.2820 | 4.5050 | 0.3860 |
| 1998 | 11.0700 | 0.6680 | 3.3380 | −0.1680 |
| 1999 | 10.4600 | 0.5620 | 2.3620 | 1.6680 |
| 2000 | 9.0830 | 1.8270 | 1.7190 | 1.4930 |
| 2001 | 8.3920 | 1.7810 | 1.5810 | 0.3250 |
| 2002 | 8.9080 | 1.9380 | 2.3300 | 0.8910 |
| 2003 | 8.9000 | 2.1690 | 3.3530 | 0.5940 |
| 2004 | 9.2330 | 2.3420 | 3.5090 | 1.3320 |
| 2005 | 9.2920 | 1.9000 | 3.3840 | 1.0060 |
| 2006 | 9.2420 | 1.9120 | 2.9490 | 0.6210 |
| 2007 | 8.3670 | 1.6070 | 2.4000 | 2.0040 |
| 2008 | 7.8080 | 3.1590 | 2.5760 | 0.7010 |
| 2009 | 9.5000 | 0.1030 | 3.7090 | 0.2830 |
| 2010 | 9.8020 | 1.7360 | 3.8500 | 0.6860 |
| 2011 | 9.6750 | 2.2930 | 3.1100 | 0.2280 |
| 2012 | 9.9290 | 1.9520 | 3.3790 | −0.5000 |
| 2013 | 10.0600 | 1.6300 | 3.5850 | 0.5000 |
| 2014 | 9.8010 | 1.8480 | 3.3150 | 1.0000 |
| 2015 | 9.4430 | 1.9040 | 3.2780 | 1.0000 |
| 2016 | 9.1440 | 1.9490 | 3.2590 | 1.0000 |
| 2017 | 8.8350 | 2.0150 | 3.2620 | 1.0000 |
References
- Samuelson, P.A.; Solow, R.M. Analytical aspects of anti-inflation policy. Am. Econ. Rev. 1960, 50, 177–194. [Google Scholar]
- Fisher, I. A Statistical Relation between Unemployment and Price Changes. Int. Labour Rev. 1926, 13, 785–792. [Google Scholar]
- Phillips, A.W. The relation between unemployment and the rate of change of money wage rates in the United Kingdom, 1861–1957. Economica 1958, 25, 283–299. [Google Scholar] [CrossRef]
- Brown, A.J. Great Inflation 1939–1951; Oxford University Press: London, UK, 1955. [Google Scholar]
- Lipsey, R.G. The relation between unemployment and the rate of change of money wage rates in the United Kingdom, 1862–1957: A further analysis. Economica 1960, 27, 1–31. [Google Scholar] [CrossRef]
- Bowen, W.G. Wage Behavior in the Postwar Period: An Empirical Analysis; Princeton University: Princeton, NJ, USA, 1960. [Google Scholar]
- Bodkin, R.G. The Wage-Price-Productivity Nexus; University of Pennsylvania Press: Philadelphia, PA, USA, 1966. [Google Scholar]
- Taylor, J.B. Aggregate dynamics and staggered contracts. J. Polit. Econ. 1980, 88, 1–23. [Google Scholar] [CrossRef]
- Calvo, G.A. Staggered Prices In A Utility-maximizing Framework. J. Monetary Econ. 1983, 12, 383–398. [Google Scholar] [CrossRef]
- Rotemberg, J.J.; Woodford, M. An Optimization-Based Econometric Framework for the Evaluation of Monetary Policy. In NBER Macroeconomics Annual; MIT Press: Cambridge, MA, USA, 1997; pp. 297–346. [Google Scholar]
- Friedman, M. The role of monetary policy. Am. Econ. Rev. 1968, 58, 1–17. [Google Scholar]
- Phelps, E.S. Money-Wage Dynamics and Labor Market Equilibrium. J. Polit. Econ. 1968, 76, 678–711. [Google Scholar] [CrossRef]
- Clarida, R.; Galí, J.; Gertler, M. The science of monetary policy: A new Keynesian perspective. J. Econ. Lit. 1999, 37, 1661–1707. [Google Scholar] [CrossRef]
- Galí, J.; Gertler, M.; López-Salido, J.D. Robustness of the Estimates of the Hybrid New Keynesian Phillips Curve. J. Monetary Econ. 2005, 52, 1107–1118. [Google Scholar] [CrossRef]
- Mittag-Leffler, M.G. Une generalisation de l’integrale de Laplace-Abel. Comptes Rendus de l’Académie des Sciences 1903, 137, 537–539. [Google Scholar]
- Mittag-Leffler, M.G. Sur la nouvelle fonction Eα(x). Comptes Rendus de l’Académie des Sciences 1903, 137, 554–558. [Google Scholar]
- Dzhrbashyan, M.M. Integral Transforms and Representations of Functions in Complex Plane; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Caputo, M.; Mainardi, F. Linear models of dissipation in anelastic solids. La Rivista del Nuovo Cimento 1971, 1, 161–198. [Google Scholar] [CrossRef]
- Blair, G.W.S. Psychorheology: links between the past and the present. J. Texture Stud. 1974, 5, 3–12. [Google Scholar] [CrossRef]
- Torvik, P.J.; Bagley, R.L. On the appearance of the fractional derivative in the behaviour of real materials. J. Appl. Mech. 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer Monographs in Mathematics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integral Transform. Spec. Funct. 2004, 15, 31–49. [Google Scholar] [CrossRef]
- Mainardi, F.; Gorenflo, R. On Mittag-Leffler-type functions in fractional evolution processes. J. Comput. Appl. Math. 2000, 118, 283–299. [Google Scholar] [CrossRef]
- West, B.; Mauro Bologna, M.; Grigolini, P. Physics of Fractal Operators; Springer: New York, NY, USA, 2003. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler functions and their applications. J. Appl. Math. 2011, 2011, 51. [Google Scholar] [CrossRef]
- Chen, Y. Generalized Generalized Mittag-Leffler function. MathWorks, Inc. Matlab Central File Exchange. 2008. Available online: http://www.mathworks.com/matlabcentral/fileexchange/21454 (accessed on 21 May 2019).
- Podlubny, I. Mittag-Leffler Function. MathWorks, Inc. Matlab Central File Exchange. 2005. Available online: http://www.mathworks.com/matlabcentral/fileexchange/8738 (accessed on 21 May 2019).
- Garrappa, R. The Mittag-Leffler function. MathWorks, Inc. Matlab Central File Exchange. 2015. Available online: http://www.mathworks.com/matlabcentral/fileexchange/48154 (accessed on 21 May 2019).
- Capelas de Oliveira, E.; Mainardi, F.; Vaz, J., Jr. Models based on Mittag-Leffler functions for anomalous relaxation in dielectrics. Eur. Phys. J. Spec. Top. 2011, 193, 161–171. [Google Scholar] [CrossRef]
- Petras, I.; Sierociuk, D.; Podlubny, I. Identification of Parameters of a Half-Order System. IEEE Trans. Signal Process. 2012, 60, 5561–5566. [Google Scholar] [CrossRef]
- Maindardi, F. Fractional Calculus and Waves in Linear Vescoelasticity: An Introduction to Mathematical Models (Second Revised Edition); Imperial College Press: London, UK, 2018. [Google Scholar]
- Samuel, S.; Ricon, J.; Podlubny, I. Modelling combustion in internal combustion engines using the Mittag-Leffler function. In Proceedings of the ICFDA 16: International Conference on Fractional Differentiation and its Applications, Novi Sad, Serbia, 18–20 July 2016; pp. 551–552. [Google Scholar]
- Zeng, C.; Chen, Y.; Podlubny, I. Is our universe accelerating dynamics fractional order? In Proceedings of the 2015 ASME/IEEE International Conference on Mechatronic and Embedded Systems and Applications, Boston, MA, USA, 2–5 August 2015. Paper No. DETC2015-46216. [Google Scholar]
- Atangana, A.; Baleanu, D. New Fractional Derivatives With Non-Local And Non-Singular Kernel: Theory and Application to Heat Transfer Model. Therm. Sci. 2016, 20-2, 763–769. [Google Scholar] [CrossRef]
- Scalas, E.; Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance. Phys. A Stat. Mech. Its Appl. 2000, 284, 376–384. [Google Scholar] [CrossRef]
- Cartea, A.; del Castillo-Negrete, D. Fractional diffusion models of option prices in markets with jumps. Phys. A Stat. Mech. Its Appl. 2007, 374, 749–763. [Google Scholar] [CrossRef]
- Garibaldi, U.; Scalas, E. Finitary Probabilistic Methods in Econophysics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Skovranek, T.; Podlubny, I.; Petras, I. Modeling of the national economies in state-space: A fractional calculus approach. Econ. Model. 2012, 29, 1322–1327. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Tarasova, V.V. Macroeconomic models with long dynamic memory: Fractional calculus approach. Appl. Math. Comput. 2018, 338, 466–486. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Tarasova, V.V. Phillips model with exponentially distributed lag and power-law memory. Comput. Appl. Math. 2019, 38, 13. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Tarasova, V.V. Dynamic Keynesian Model of Economic Growth with Memory and Lag. Mathematics 2019, 7, 178. [Google Scholar] [CrossRef]
- Econstats.com. EconStats: World Economic Outlook (WEO) data, IMF. 2019. Available online: http://www.econstats.com (accessed on 21 May 2019).
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1955; Volume 3. [Google Scholar]
- Mittag-Leffler, M.G. Sopra la funzione Eα(x). Comptes Rendus de l’Académie des Sciences 1904, 13, 3–5. [Google Scholar]
- Wiman, A. Über den Fundamentalsatz in der Teorie der Funktionen Eα(x). Acta Math. 1905, 29, 191–201. [Google Scholar] [CrossRef]
- Pollard, H. The completely monotonic character of the Mittag-Leffler function Ea(−x). Bull. Am. Math. Soc. 1948, 54, 1115–1116. [Google Scholar] [CrossRef]
- Humbert, P.; Agarwal, R.P. Sur la fonction de Mittag-Leffler et quelques-unes de ses généralisations. Bulletin des Sciences Mathématiques 1953, 77, 180–185. [Google Scholar]
- Cover, J.P. Asymmetric effects of positive and negative money-supply shocks. Q. J. Econ. 1992, 107, 1261–1282. [Google Scholar] [CrossRef]
- Karras, G. Are the output effects of monetary policy asymmetric? Evidence from a sample of European countries. Oxf. Bull. Econ. Stat. 1996, 58, 267–278. [Google Scholar] [CrossRef]
- Nobay, A.R.; Peel, D.A. Optimal monetary policy with a nonlinear Phillips curve. Econ. Lett. 2000, 67, 159–164. [Google Scholar] [CrossRef]
- Schaling, E. The nonlinear Phillips curve and inflation forecast targeting: Symmetric versus asymmetric monetary policy rules. J. Money Credit Bank. 2004, 36, 361–386. [Google Scholar] [CrossRef][Green Version]
- Stiglitz, J. Reflections on the natural rate hypothesis. J. Econ. Perspect. 1997, 11, 3–10. [Google Scholar] [CrossRef]
- Filardo, A. New evidence on the output cost of fighting inflation. Fed. Reserve Bank Kansas City Econ. Rev. 1998, 83, 33–61. [Google Scholar]
- Brown, P.; Hopkins, S. The Course of Wage-Rates in Five Countries, 1860–1939. Oxf. Econ. Pap. 1950, 2, 226–296. [Google Scholar] [CrossRef]
- Beveridge, H.W. Full Employment in a Free Society; W. W. Norton & Co., Inc.: New York, NY, USA, 1945. [Google Scholar]
- Podlubny, I. Fitting Data Using the Mittag-Leffler Function. MathWorks, Inc. Matlab Central File Exchange. 2011. Available online: http://www.mathworks.com/matlabcentral/fileexchange/32170 (accessed on 21 May 2019).
- MathWorks, Inc. Evaluating Goodness of Fit. 2019. Available online: https://www.mathworks.com/help/curvefit/evaluating-goodness-of-fit.html (accessed on 21 May 2019).
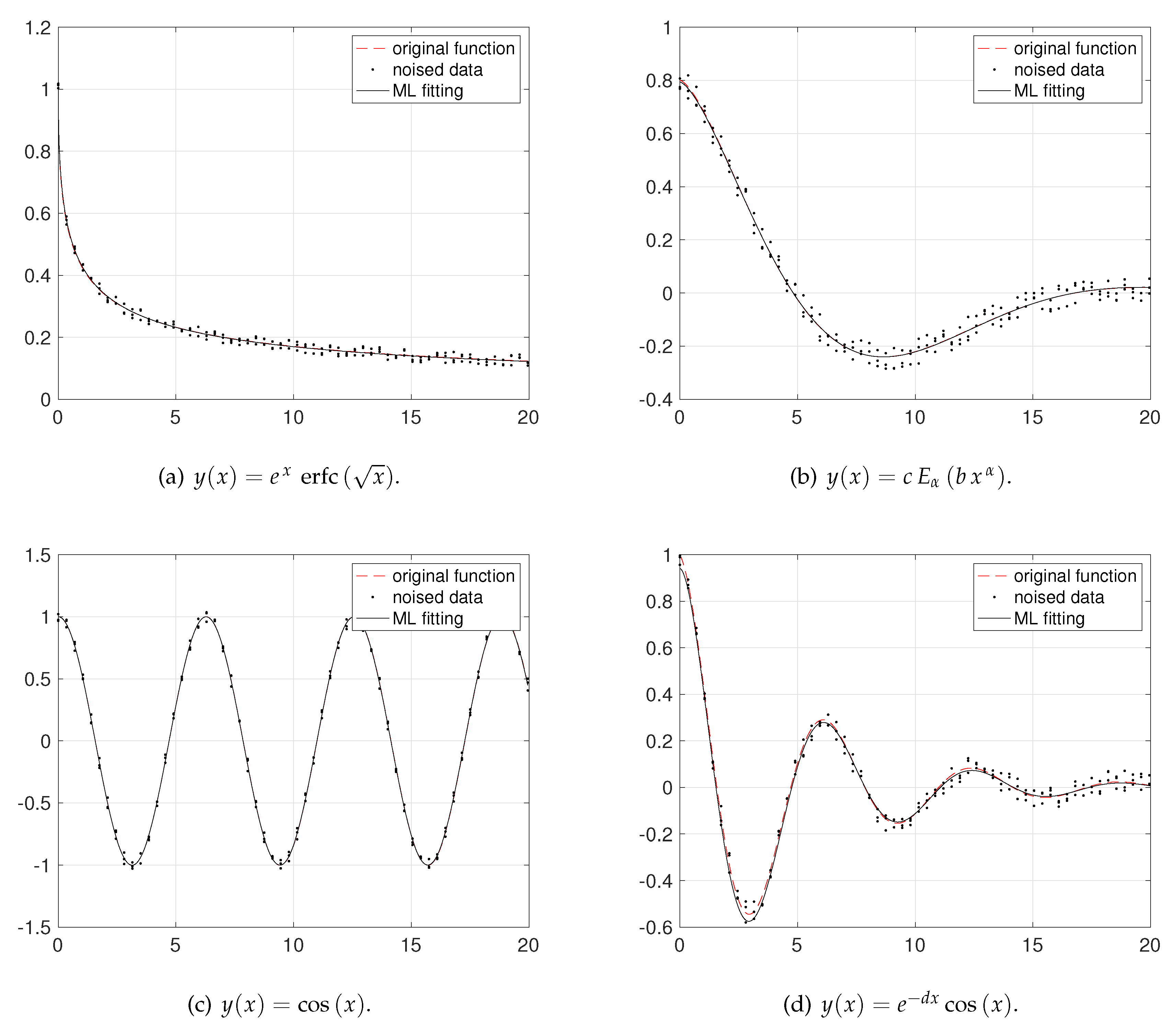
| c | - | 0.8 | - | - | |
| generating | - | 1.5 | - | - | |
| parameters | b | - | −0.2 | - | - |
| d | - | - | - | 0.2 | |
| c | 0.9982 | 0.7869 | 1.0045 | 0.9722 | |
| identified | 0.5008 | 1.4999 | 2.0000 | 1.7538 | |
| parameters | b | −0.9974 | −0.1988 | −0.9999 | −1.0327 |
| Power-Type Model | Exponential-Type Model | ML Model | |
|---|---|---|---|
| SSE to “modelling’’ subset | 157.8422 | 155.8276 | 149.6035 |
| SSE to “out-of-sample’’ subset | 10.9024 | 8.0347 | 3.9904 |
| SSE to complete dataset | 168.7446 | 163.8623 | 153.5939 |
| R-square | 0.5634 | 0.5690 | 0.5862 |
| adjusted R-square | 0.5322 | 0.5382 | 0.5567 |
| RMSE | 2.3740 | 2.3590 | 2.3110 |
| Model | |||
| definition | |||
| Identified | |||
| parameters |
| Power-Type Model | Exponential-Type Model | ML Model | |
|---|---|---|---|
| SSE to “modelling’’ subset | 39.6506 | 40.0588 | 39.2992 |
| SSE to “out-of-sample’’ subset | 6.8961 | 4.6826 | 5.0041 |
| SSE to complete dataset | 46.5466 | 44.7414 | 44.3033 |
| R-square | 0.6389 | 0.6351 | 0.6420 |
| adjusted R-square | 0.6131 | 0.6091 | 0.6165 |
| RMSE | 1.1900 | 1.1960 | 1.1850 |
| Model | |||
| definition | |||
| Identified | |||
| parameters |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skovranek, T. The Mittag-Leffler Fitting of the Phillips Curve. Mathematics 2019, 7, 589. https://doi.org/10.3390/math7070589
Skovranek T. The Mittag-Leffler Fitting of the Phillips Curve. Mathematics. 2019; 7(7):589. https://doi.org/10.3390/math7070589
Chicago/Turabian StyleSkovranek, Tomas. 2019. "The Mittag-Leffler Fitting of the Phillips Curve" Mathematics 7, no. 7: 589. https://doi.org/10.3390/math7070589
APA StyleSkovranek, T. (2019). The Mittag-Leffler Fitting of the Phillips Curve. Mathematics, 7(7), 589. https://doi.org/10.3390/math7070589





