On the Solution of an Imprecisely Defined Nonlinear Time-Fractional Dynamical Model of Marriage
Abstract
:1. Introduction
2. Preliminaries
- (a)
- There exists exactly onewith(is called the mean value of), whereis called the membership function of the fuzzy set.
- (b)
- is piecewise continuous.
- (i)
- is a left-bounded nondecreasing continuous function over.
- (ii)
- is a right-bounded nonincreasing continuous function over.
- (iii)
- , where
- (i)
- if and only ifand.
- (ii)
- .
- (iii)
- .
- (iv)
3. Fractional Reduced Differential Transform Method
- (i)
- If, then, whereandare constants.
- (ii)
- If, then.
- (iii)
- If, thenwhere.
- (iv)
- If, then.
- (v)
- If, then.
- (vi)
- If, then.
- (i)
- If,then.
- (ii)
- If, then.
4. Double-Parametric-Based Solution of an Uncertain FDMM Using FRDTM
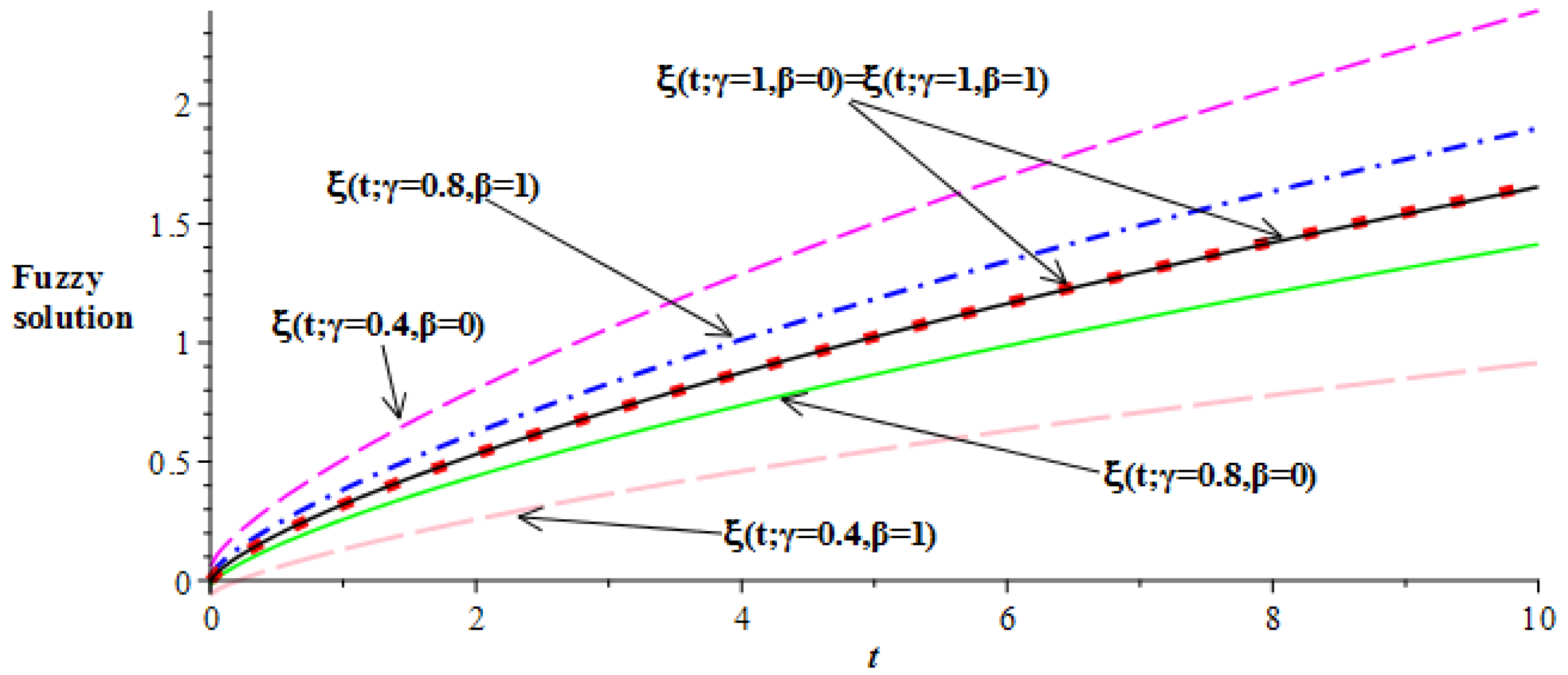
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jena, R.M.; Chakraverty, S.; Jena, S.K. Dynamic Response Analysis of Fractionally Damped Beams Subjected to External Loads using Homotopy Analysis Method. J. Appl. Comput. Mech. 2019, 5, 355–366. [Google Scholar]
- Jena, R.M.; Chakraverty, S. Solving time-fractional Navier–Stokes equations using homotopy perturbation Elzaki transform. SN Appl. Sci. 2019, 1, 16. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S. Residual Power Series Method for Solving Time-fractional Model of Vibration Equation of Large Membranes. J. Appl. Comput. Mech. 2019, 5, 603–615. [Google Scholar]
- Jena, R.M.; Chakraverty, S. A new iterative method based solution for fractional Black–Scholes option pricing equations (BSOPE). SN Appl. Sci. 2019, 1, 95–105. [Google Scholar] [CrossRef]
- Edeki, S.O.; Motsepa, T.; Khalique, C.M.; Akinlabi, G.O. The Greek parameters of a continuous arithmetic Asian option pricing model via Laplace Adomian decomposition method. Open Phys. 2018, 16, 780–785. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematical Studies; Elsevier Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2006; Volume 204. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Boston, MA, USA: 2012. [Google Scholar]
- Baleanu, D.; Machado, J.A.T.; Luo, A.C. Fractional Dynamics and Control; Springer: Berlin, Germany, 2012. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; A Wiley-Interscience Publication; John Wiley and Sons: New York, NY, USA; Chichester, UK; Brisbane, Australian; Toronto, ON, Canada; Singapore, 1993. [Google Scholar]
- Barley, K.; Cherif, A. Stochastic nonlinear dynamics of interpersonal and romantic relationships. Appl. Math. Comput. 2011, 217, 6273–6281. [Google Scholar] [CrossRef]
- Rinaldi, S. Love dynamics: The case of linear couples. Appl. Math. Comput. 1998, 95, 181–192. [Google Scholar] [CrossRef]
- Ozalp, N.; Koca, I. A fractional order nonlinear dynamical model of interpersonal relationships. Adv. Differ. Equ. 2012, 189, 1–7. [Google Scholar] [CrossRef]
- Khader, M.M.; Alqahtani, R. Approximate solution for system of fractional non-linear dynamical marriage model using Bernstein polynomials. J. Nonlinear Sci. Appl. 2017, 10, 865–873. [Google Scholar] [CrossRef] [Green Version]
- Khader, M.M.; Shloof, A.; Ali, H. On the numerical simulation and convergence study for system of non-linear fractional dynamical model of marriage. NTMSCI 2017, 5, 130–141. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Qurashi, M.A.; Baleanu, D. A Novel Numerical Approach for a Nonlinear Fractional Dynamical Model of Interpersonal and Romantic Relationships. Entropy 2017, 19, 375. [Google Scholar] [CrossRef]
- Goyal, M.; Prakash, A.; Gupta, S. Numerical simulation for time-fractional nonlinear coupled dynamical model of romantic and interpersonal relationships. Pramana J. Phys. 2019, 92, 82. [Google Scholar] [CrossRef]
- Martin, M.T.C.; Bumpass, B.L. Recent trends in marital disruption. Demography 1989, 26, 37–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering; Reading, M.A., Ed.; Addison-Wesley: Boston, MA, USA, 1994. [Google Scholar]
- Gottman, J.M.; Murray, J.D.; Swanson, C.C.; Tyson, R.; Swanson, K.R. The Mathematics of Marriage; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Chang, S.L.; Zadeh, L.A. On fuzzy mapping and control. IEEE Trans. Syst. Man Cybern. 1972, 2, 30–34. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Towards fuzzy differential calculus part 3: Differentiation. Fuzzy Sets Syst. 1982, 8, 225–233. [Google Scholar] [CrossRef]
- Kaleva, O. The Cauchy problem for fuzzy differential equations. Fuzzy Sets Syst. 1990, 35, 389–396. [Google Scholar] [CrossRef]
- Seikkala, S. On the fuzzy initial value problem. Fuzzy Sets Syst. 1987, 24, 319–330. [Google Scholar] [CrossRef]
- Chakraverty, S.; Tapaswini, S.; Behera, D. Fuzzy Arbitrary Order System: Fuzzy Fractional Differential Equations and Applications; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Chakraverty, S.; Tapaswini, S.; Behera, D. Fuzzy Differential Equations and Applications for Engineers and Scientists; Taylor and Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar]
- Chakraverty, S.; Sahoo, D.M.; Mahato, N.R. Concepts of Soft Computing: Fuzzy and ANN with Programming; Springer: Singapore, 2019. [Google Scholar]
- Momani, S.; Odibat, Z. A generalized differential transform method for linear partial differential equations of fractional order. Appl. Math. Lett. 2008, 21, 194–199. [Google Scholar] [Green Version]
- Singh, B.K.; Kumar, P. FRDTM for numerical simulation of multi-dimensional, time-fractional model of Navier–Stokes equation. Ain Shams Eng. J. 2018, 9, 827–834. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Swroop, R.; Kumar, S. An efficient computational approach for time-fractional Rosenau–Hyman equation. Neural Comput. Appl. 2018, 30, 3063–3070. [Google Scholar] [CrossRef]
- Rawashdeh, M.S. An Efficient Approach for Time–Fractional Damped Burger and Time—Sharma—Tasso—Olver Equations Using the FRDTM. Appl. Math. Inf. Sci. 2015, 9, 1239–1246. [Google Scholar]
- Keskin, Y.; Oturan, G. Reduced Differential Transform Method for Partial Differential Equations. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 741–749. [Google Scholar] [CrossRef]

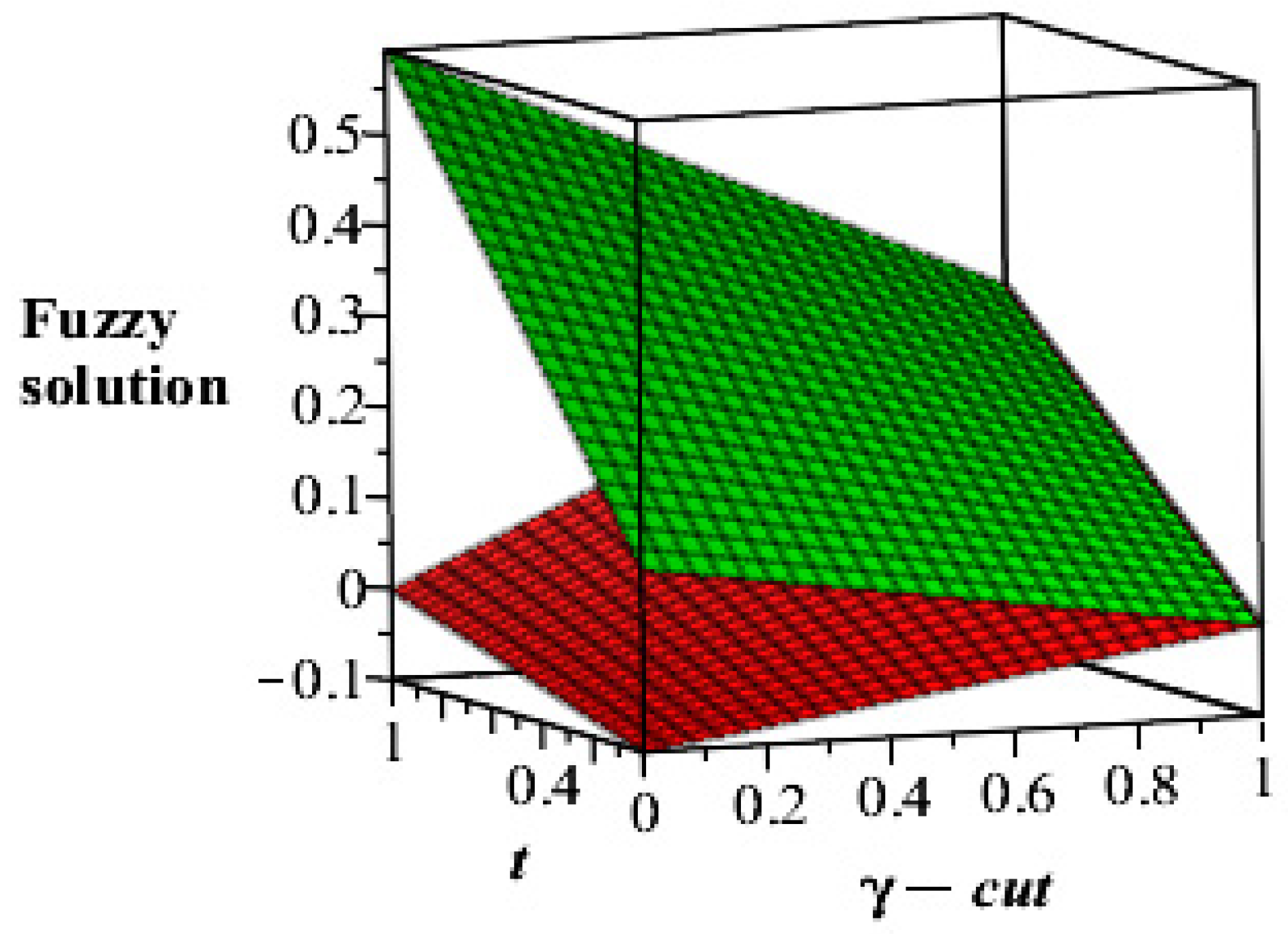
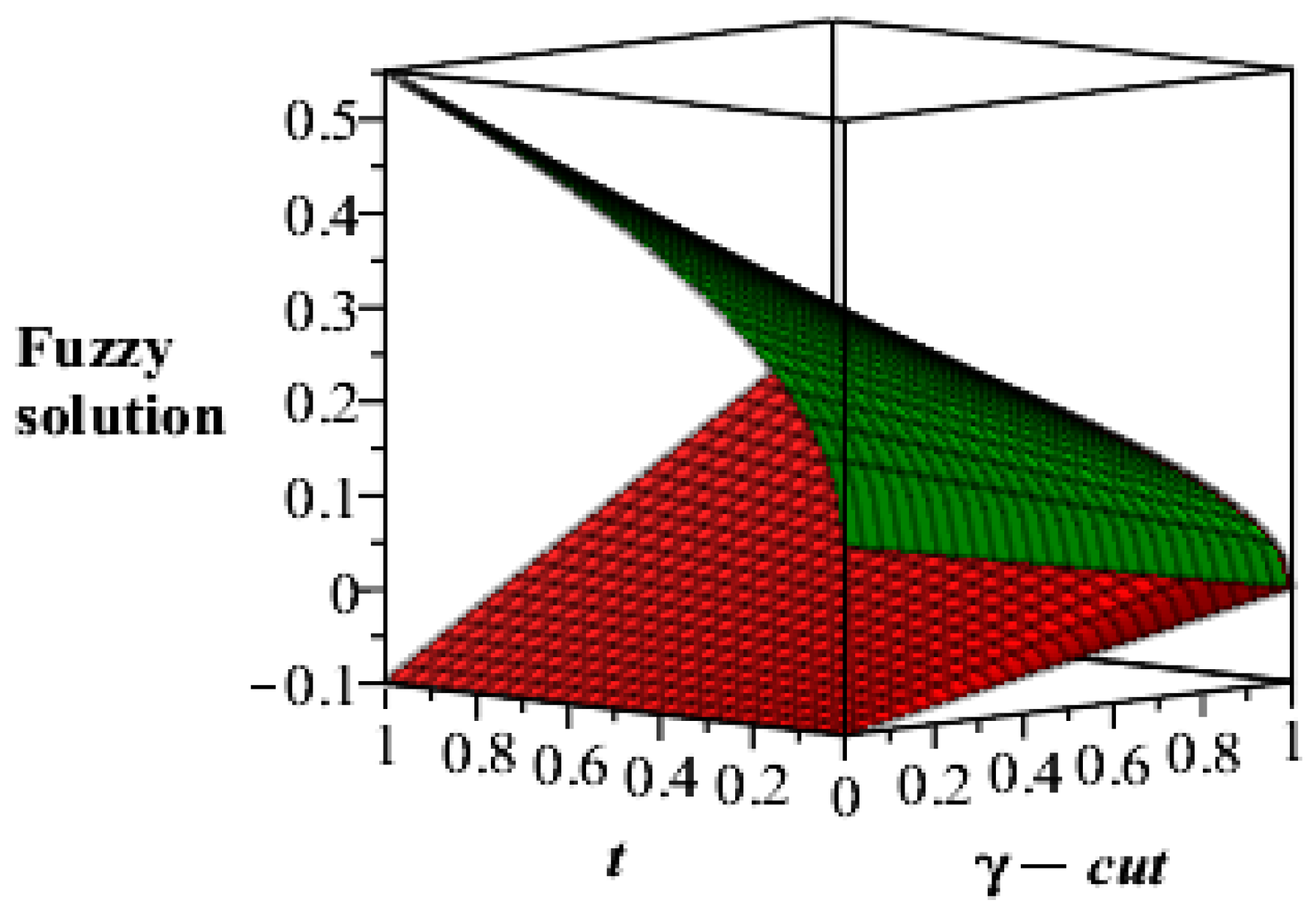
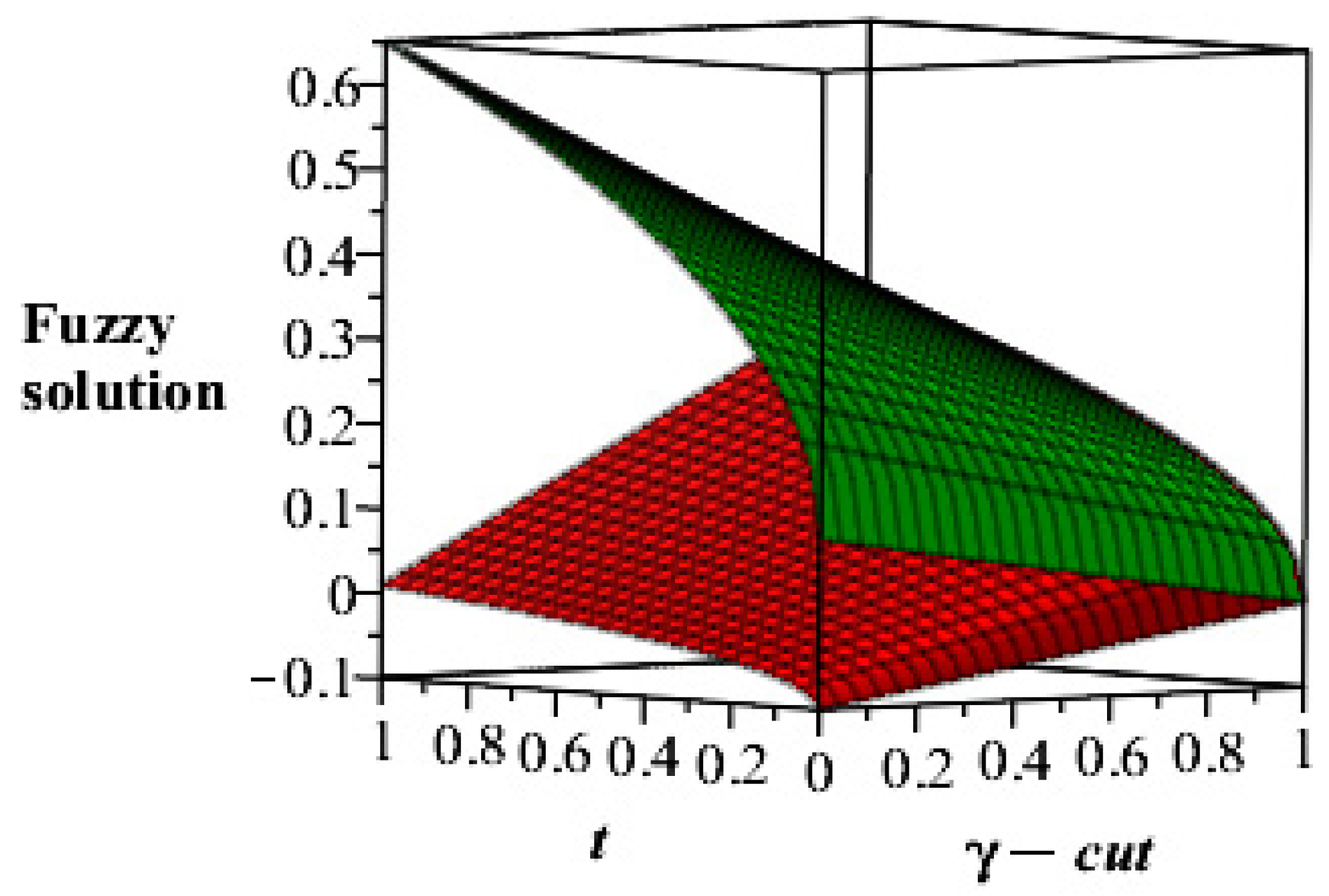
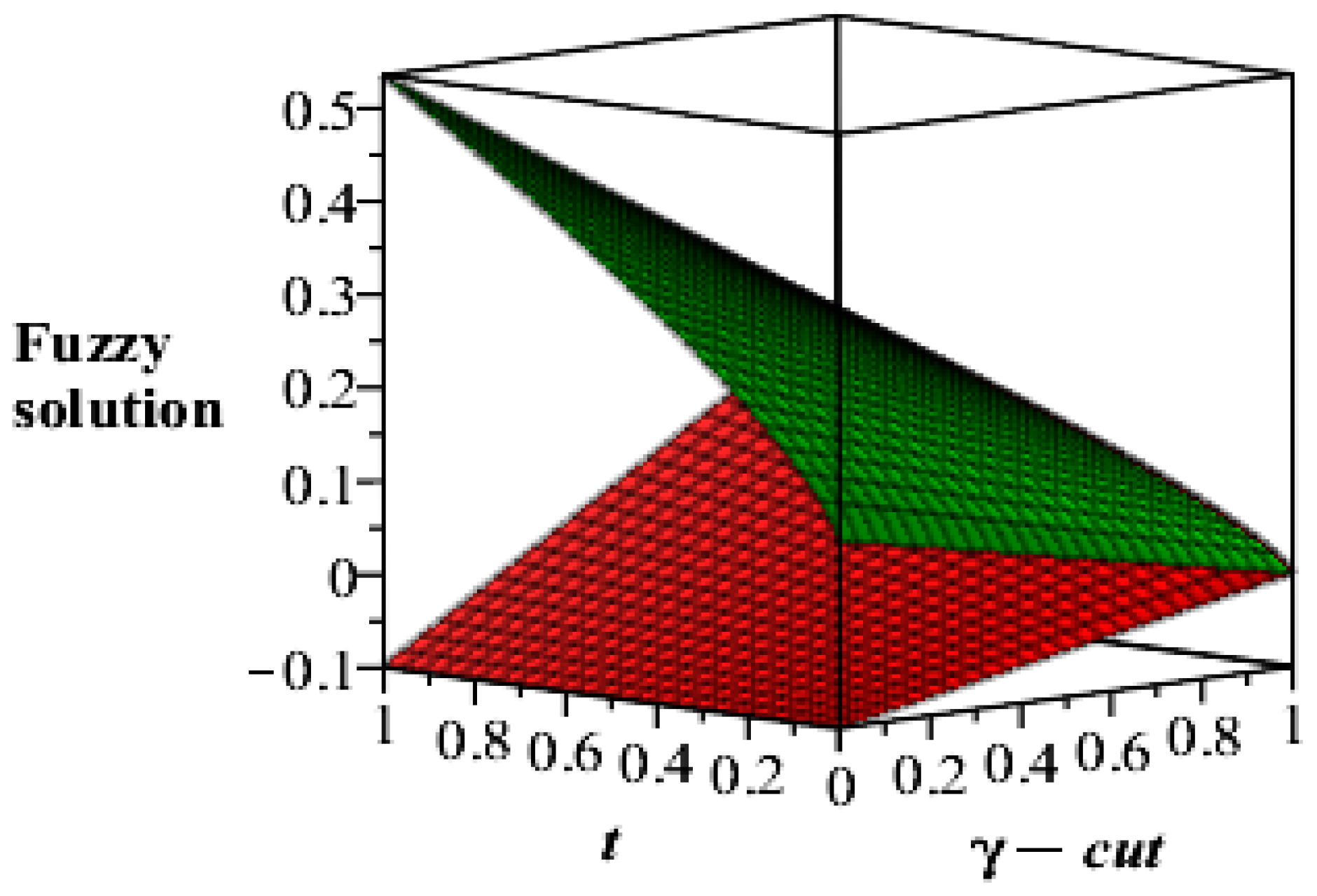
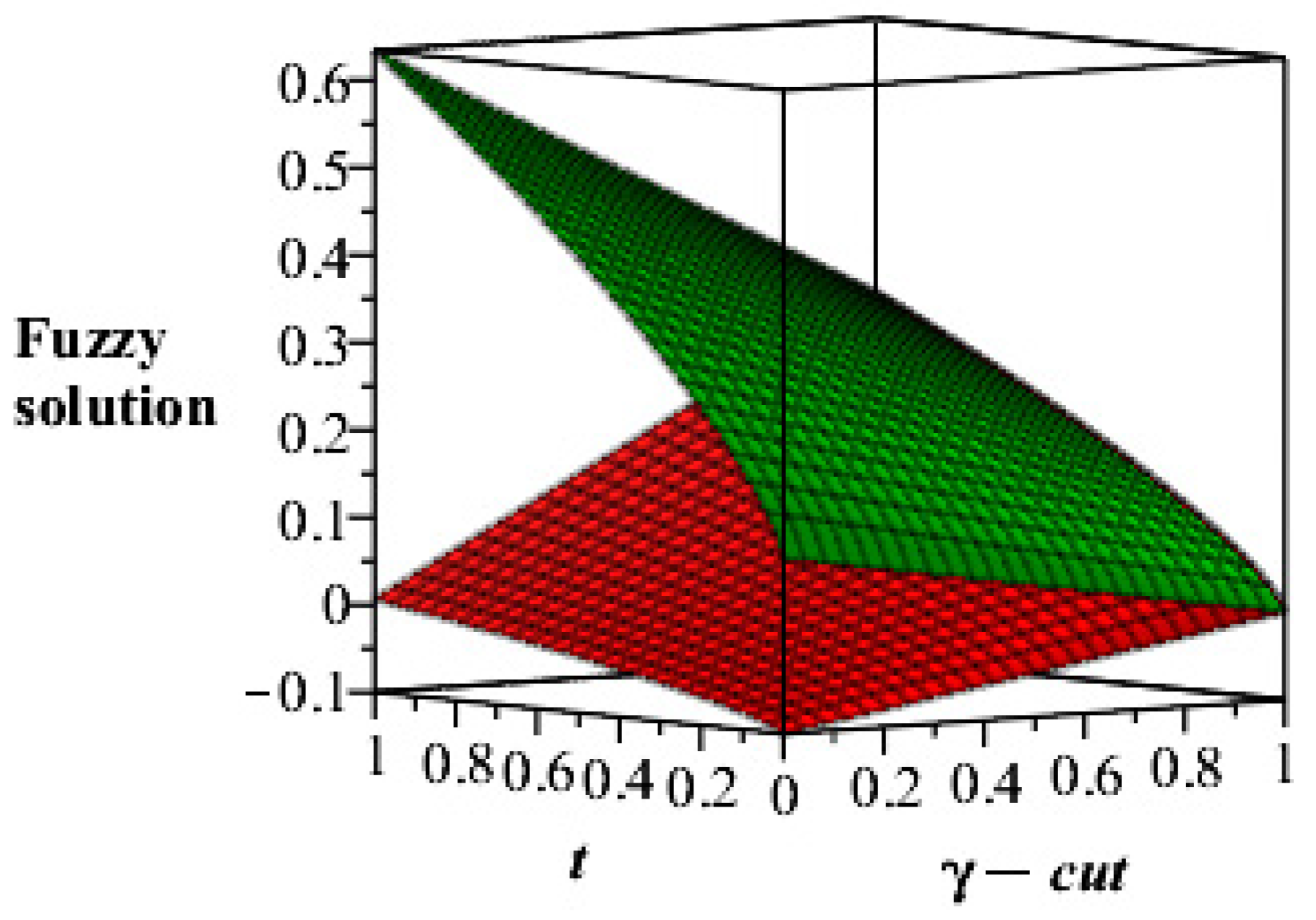
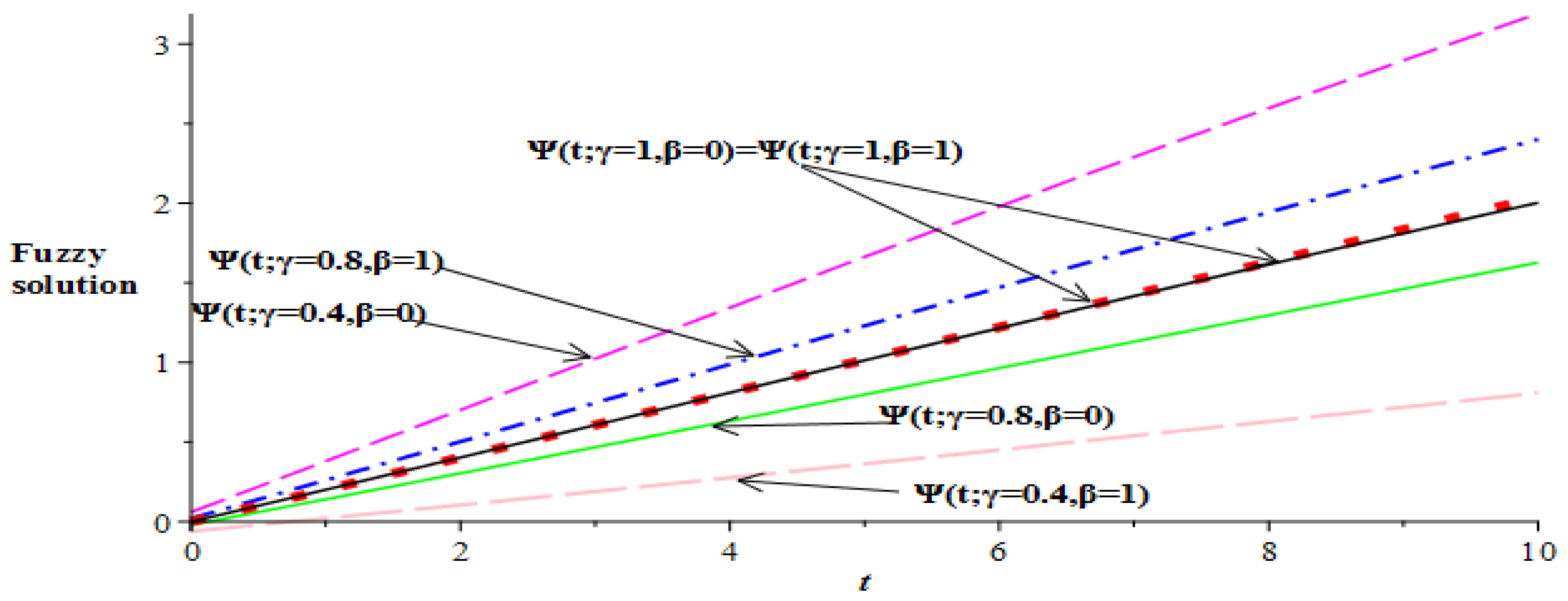
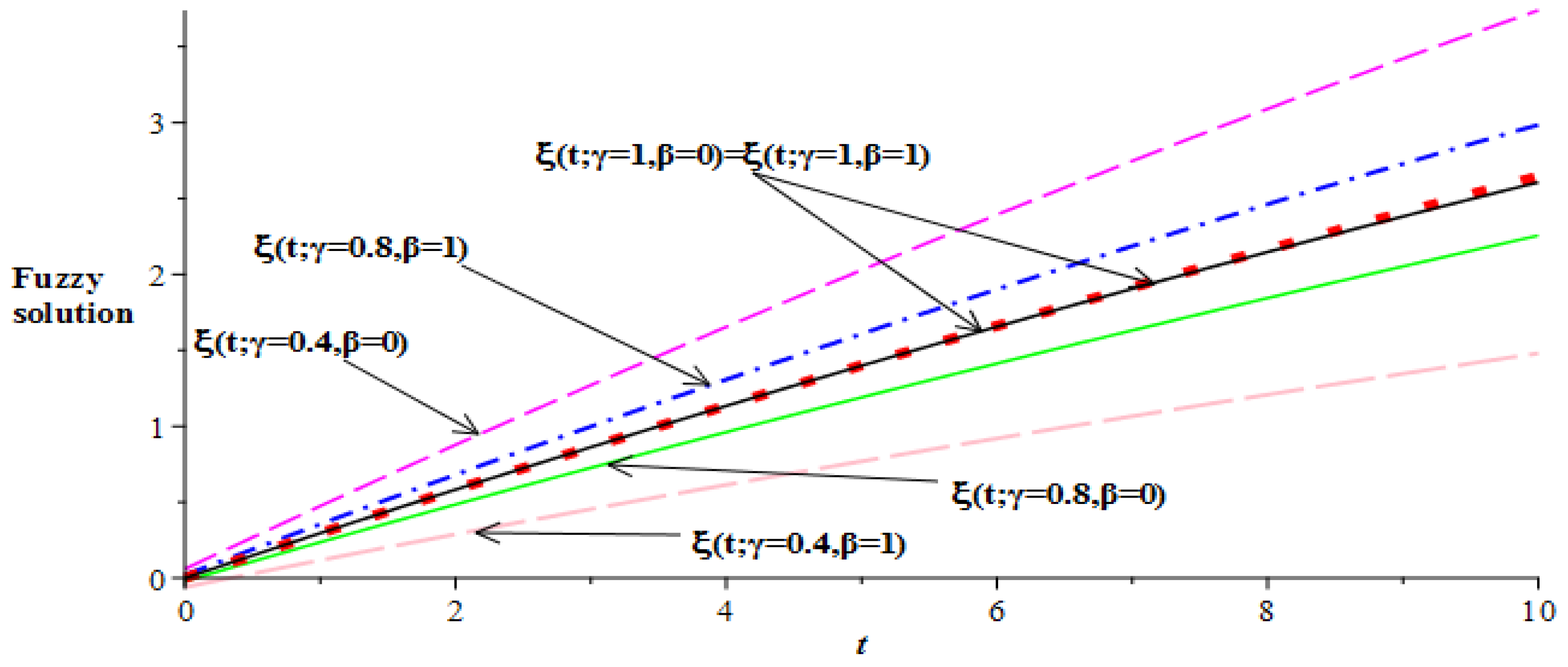

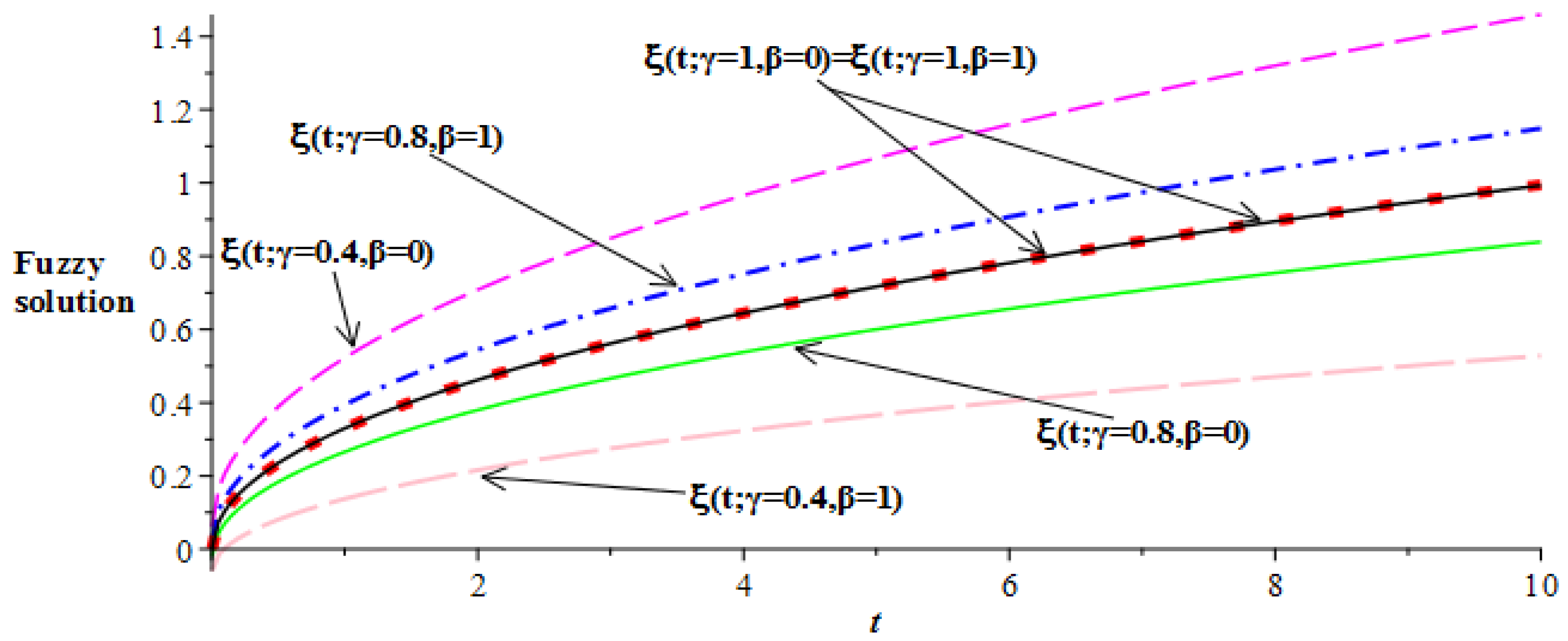

 No of Approximation  | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
|---|---|---|---|---|---|---|
| [0,0] | [0.04,0.03999] | [0.08,0.07999] | [0.12,0.119999] | [0.16,0.159999] | [0.20,0.199999] | |
| [0,0] | [0.04,0.04003] | [0.0801,0.0802] | [0.1203,0.120359] | [0.1606,0.16064] | [0.2009,0.20099] | |
| [0,0] | [0.04,0.04003] | [0.0801,0.08015] | [0.1203,0.120342] | [0.1606,160599] | [0.2009,0.20092] | |
| [0,0] | [0.04,0.04004] | [0.0801,0.08015] | [0.1203,0.120342] | [0.1606,160597] | [0.2009,0.20092] | |
| [0,0] | [0.04,0.04004] | [0.0801,0.08015] | [0.1203,0.120342] | [ 0.1606,160597] | [0.2009,0.20092] | |
| Refs. [16,17] Crisp value at | 0 | 0.04 | 0.0801 | 0.1203 | 0.1606 | 0.2009 |
 No of Approximation  | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
|---|---|---|---|---|---|---|
| [0,0] | [0.06,0.059999] | [0.12,0.1199] | [0.18,0.179999] | [0.24,0.239999] | [0.30,0.29999] | |
| [0,0] | [0.0598,0.0598] | [0.1192,0.1197] | [0.1783,0.178389] | [0.2371,0.237189] | [0.2954,0.29549] | |
| [0,0] | [0.0598,0.0598] | [0.1192,0.1192] | [0.1784,0.178406] | [0.2371,0.237182] | [0.2956,0.29562] | |
| [0,0] | [0.0598,0.0598] | [0.1192,0.1192] | [0.1784,0.178405] | [0.2371,0.237179] | [0.2956,0.29561] | |
| [0,0] | [0.0598,0.0598] | [0.1192,0.1192] | [0.1784,0.178405] | [0.2371,0.237179] | [0.2956,0.29561] | |
| Refs. [16,17] Crisp value at | 0 | 0.0598 | 0.1192 | 0.1784 | 0.2371 | 0.2956 |
  | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
|---|---|---|---|---|---|---|
| [−0.1,0.1] | [−0.991,0.3016] | [−0.0985,0.3853] | [−0.0980,0.4496] | [−0.0975,0.5038] | [−0.0970,0.5515] | |
| [−0.08,0.08] | [−0.059,0.2616] | [−0.0501,0.3370] | [−0.0432,0.3949] | [−0.0373,0.4437] | [−0.0321,0.4867] | |
| [−0.06,0.06] | [−0.0189,0.2215] | [−0.0017,0.2886] | [0.0115,0.3401] | [0.0228,0.3836] | [0.0328,0.4219] | |
| [−0.04,0.04] | [0.0211,0.1814] | [0.0467,0.2402] | [0.0663,0.2854] | [0.0829, 0.3234] | [0.0976,0.3570] | |
| [−0.02,0.02] | [0.0613,0.1414] | [0.0950,0.1918] | [0.1211,0.2306] | [0.1431,0.2633] | [0.1625, 0.2922] | |
| [0,0] | [0.1013,0.1013] | [0.1434, 0.1434] | [0.1759, 0.1758] | [0.2032, 0.2032] | [0.2273, 0.2273] | |
| Refs. [16,17] Crisp value at | 0 | 0.1013 | 0.1434 | 0.1759 | 0.2032 | 0.2273 |
  | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
|---|---|---|---|---|---|---|
| [−0.1,0.1] | [−0.0500,0.3493] | [−0.0299,0.4511] | [−0.0146,0.5288] | [−0.0019,0.5938] | [0.0092,0.6509] | |
| [−0.08,0.08] | [−0.0101,0.3094] | [0.0182,0.4030] | [0.0397,0.4744] | [0.0577, 0.5343] | [0.0734,0.5867] | |
| [−0.06,0.06] | [0.0298,0.2694] | [0.0663,0.3549] | [0.0940,0.4200] | [0.1172,0.4747] | [0.1375,0.5226] | |
| [−0.04,0.04] | [0.0698,0.2295] | [0.1144,0.3068] | [0.1484,0.3657] | [0.1768,0.4151] | [0.2017, 0.4584] | |
| [−0.02,0.02] | [0.1097,0.1896] | [0.1625,0.2587] | [0.2027,0.3114] | [0.2364,0.355] | [0.2659, 0.3942] | |
| [0,0] | [0.1496,0.1496] | [0.2106,0.2106] | [0.2570,0.2570] | [0.2960,0.2960] | [0.3300,0.3300] | |
| Refs. [16,17] Crisp value at | 0 | 0.1496 | 0.2106 | 0.2570 | 0.2960 | 0.3300 |
  | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
|---|---|---|---|---|---|---|
| [−0.1,0.1] | [−0.0995,0.2210] | [−0.0991,0.3187] | [−0.0986,0.3965] | [−0.0980,0.4681] | [−0.0974,0.5353] | |
| [−0.08,0.08] | [−0.0666,0.1970] | [−0.0573,0.2769] | [−0.0491,0.3470] | [−0.0414,0.4115] | [−0.0342,0.4720] | |
| [−0.06,0.06] | [−0.0336,0.1640] | [−0.0155,0.2351] | [0.0005,0.2975] | [0.0152,0.3549] | [0.0291,0.4087] | |
| [−0.04,0.04] | [−0.0007,0.1311] | [0.0263,0.1933] | [0.0410,0.2480] | [0.0718,0.2983] | [0.0924,0.3455] | |
| [−0.02,0.02] | [0.0323,0.0982] | [0.0680,0.1516] | [0.0995,0.1985] | [0.12843,0.2417] | [0.1557,0.2822] | |
| [0,0] | [0.0652,0.0652] | [0.1098,0.1098] | [0.1490,0.1490] | [0.1850,0.1850] | [0.2189,0.2189] | |
| Refs. [16,17] Crisp value at | 0 | 0.0652 | 0.1098 | 0.1490 | 0.1850 | 0.2189 |
  | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
|---|---|---|---|---|---|---|
| [−0.1,0.1] | [−0.0675,0.2615] | [−0.0457,0.3707] | [−0.0268,0.4658] | [−0.0097,0.5526] | [0.0063,0.6336] | |
| [−0.08,0.08] | [−0.0346,0.2286] | [−0.0040,0.3290] | [0.0225,0.4165] | [0.0466,0.4963] | [0.0690,0.5709] | |
| [−0.06,0.06] | [−0.0017,0.1957] | [0.0376,0.2874] | [0.0717,0.3672] | [0.1028,0.4401] | [0.1317,0.5081] | |
| [−0.04,0.04] | [0.0312,0.1628] | [0.0792,0.2457] | [0.1210,0.3179] | [0.1590,0.3839] | [0.1945,0.4454] | |
| [−0.02,0.02] | [0.0641,0.1299] | [0.1209,0.2041] | [0.1702,0.2687] | [0.2152,0.3276] | [0.2572,0.3827] | |
| [0,0] | [0.0970,0.0970] | [0.1625,0.1625] | [0.2195, 0.2195] | [0.2714,0.2714] | [0.3199,0.3199] | |
| Refs. [16,17] Crisp value at | 0 | 0.097 | 0.1625 | 0.2195 | 0.2714 | 0.3199 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jena, R.M.; Chakraverty, S.; Baleanu, D. On the Solution of an Imprecisely Defined Nonlinear Time-Fractional Dynamical Model of Marriage. Mathematics 2019, 7, 689. https://doi.org/10.3390/math7080689
Jena RM, Chakraverty S, Baleanu D. On the Solution of an Imprecisely Defined Nonlinear Time-Fractional Dynamical Model of Marriage. Mathematics. 2019; 7(8):689. https://doi.org/10.3390/math7080689
Chicago/Turabian StyleJena, Rajarama Mohan, Snehashish Chakraverty, and Dumitru Baleanu. 2019. "On the Solution of an Imprecisely Defined Nonlinear Time-Fractional Dynamical Model of Marriage" Mathematics 7, no. 8: 689. https://doi.org/10.3390/math7080689





