Development of Public Key Cryptographic Algorithm Using Matrix Pattern for Tele-Ultrasound Applications
Abstract
:1. Introduction
2. Preliminary
2.1. RSA Algorithm
2.1.1. Key Generation Step
- (A)
- Randomly choose two prime number integers p and q,where (p, q) is the greatest common divisor of p and q.(p, q) = 1,
- (B)
- Compute n = p × q, where n is used as modulo for both the public and private key.
- (C)
- Compute Euler’s function Φ(n) using the two prime numbers p and q.Φ(n) = Φ (p ∙ q) = Φ(p) ∙ Φ(q) = (p − 1) ∙ (q − 1).
- (D)
- Choose an integer e such thatwhere 1 < e < Φ(n).(Φ(n), e) = 1,
- (E)
- Since (Φ(n), (e)=1 by Equation (3), there exist integers d and t such that ed + Φ(n)t = 1. Thus, we can compute d by using Euclid’s theorem so that the product of e and d is as follows:e ∙ d ≡ 1 (mod Φ(n)).
- (F)
- Select the integers n and e as the public key, then, select the integers p, q, and d as the private key.
2.1.2. Encoding Step
- (A)
- M is a separated memory block which is stored into the M1, M2, …, Mn such that it represents a value in the range of 1 to n.M= (M1, M2, …, Mn).
- (B)
- Encode to cipher block using the public key n and e to obtain Mi:where i = 1, 2, ….
2.1.3. Decoding Step
- (A)
- The cipher block Ci is decrypted into Mi.
- (B)
- Decode to plain block using the key p, q, and d.
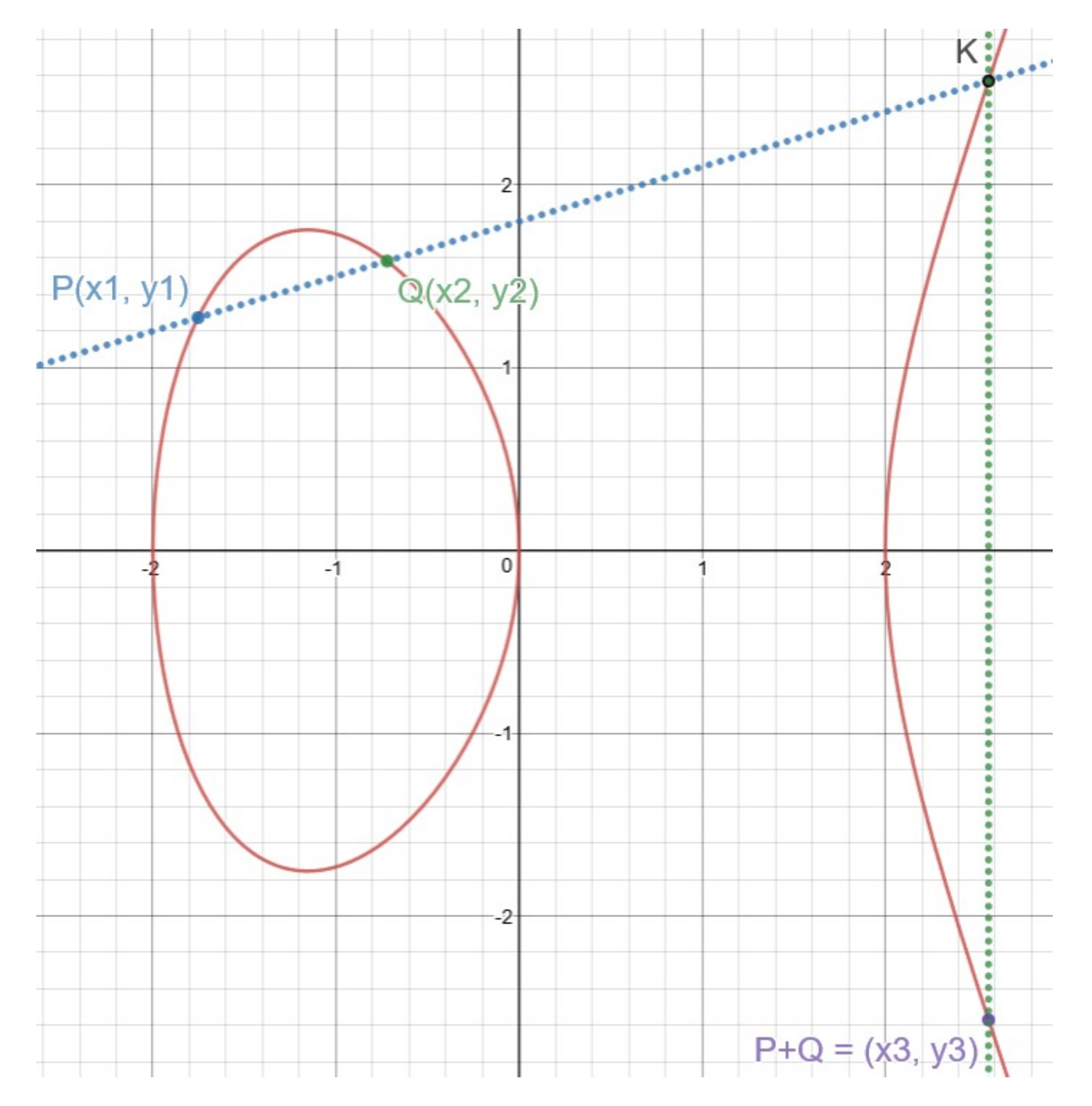
2.2. Elliptic Curve Cryptographic Algorithm
2.2.1. Key Generation Step
- (A)
- Select an elliptic curve group E(F) of a finite field F and select a maximum characteristic element P of E(F).
- (B)
- Select any integer and calculate the element Q.Q = αP.
- (C)
- Select (F, E(F)), elements P and Q as a public key, then select an integer α as a private key.
2.2.2. Encoding Step
- (A)
- Prepare a plain memory block for the encoding of E(F).
- (B)
- Select any integer k ∈ Z and encode the plain memory block M to cipher like a (C1, C2).C1 = kP, C2 = M + KQ.
2.2.3. Decoding Step
- (A)
- Decode the cipher block.C2 − αC1 = (M + KQ) − α(kP) = (M + kQ) − k Q = M.
3. Proposed Algorithm
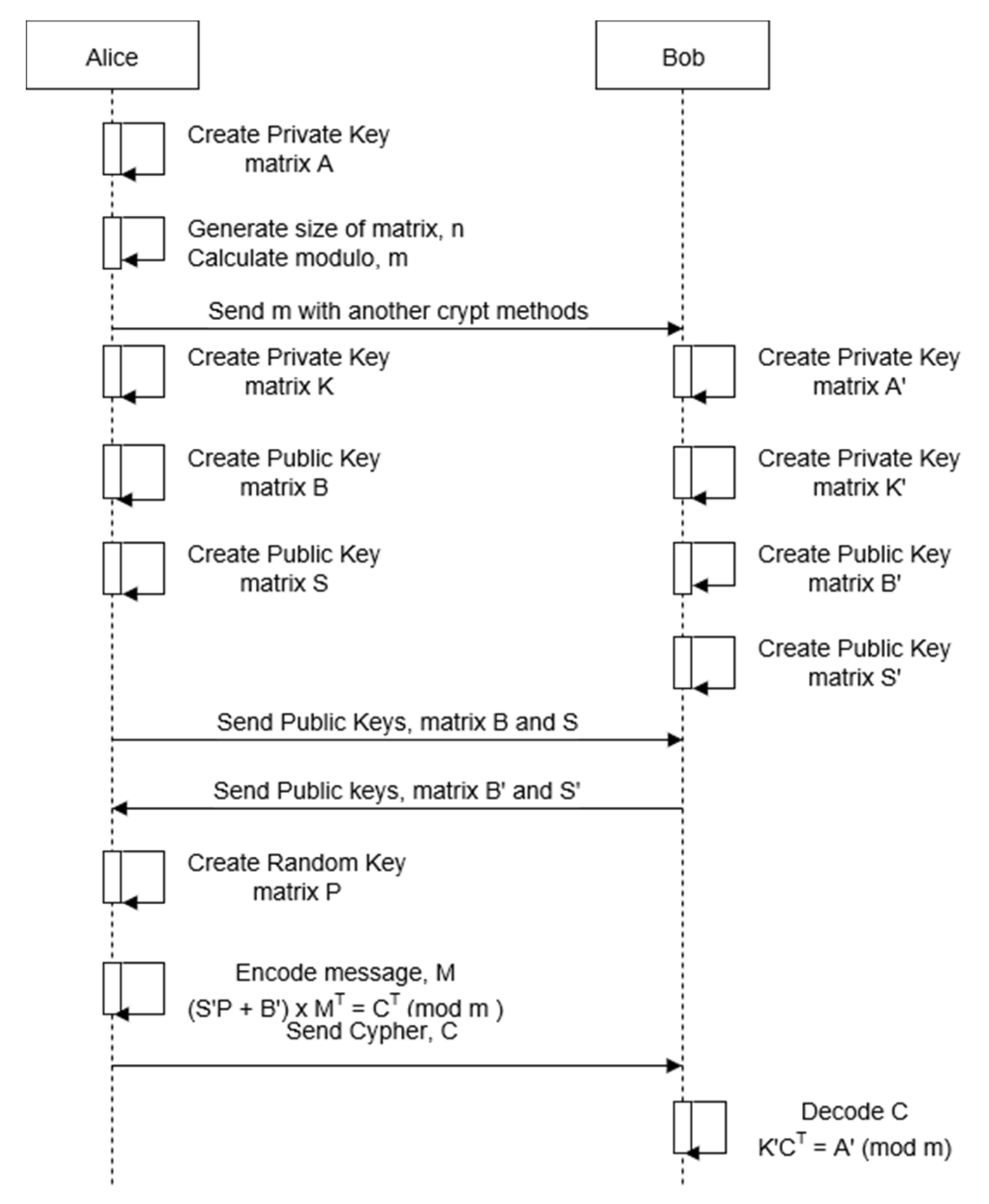
3.1. Key Generation Algorithm
- (A)
- (B)
- Select a positive integer m such thatwhere m is used as a modulus of congruence.(a1 + a2 + …, an) < m,
- (C)
- Select a 1 × n matrix K in Zm to use as a second private key.where is the least complete residue class modulo m.K = (k1, k2, …, kn),
- (D)
- Select Si (1 ≤ i ≤ n) in Zm such thatwhere ki (1 ≤ I ≤ n) are the integers selected in (C).(k1S1 + k2S2 + … + knSn) ≡ O (mod m),
- (E)
- S is described as an n × n matrix to use as a first public key.where Si (1 ≤ i ≤ n) are the integers selected in (D).
- (F)
- Select an n × n matrix B in Zm to use as a second public key such thatwhere ai and Si (1 ≤ i ≤ n) are the integers selected in (A) and (C), respectively.KB ≡ (a1, a2, …, an) (mod m),
- (G)
- Use as public keys n, m, S, and B.
3.2. Encoding Algorithm
- (A)
- Select an n × n random matrix P to use the element pij as a salt:where pij ∈ Zm, 1≤ i, j ≤ n.P = (Pij),
- (B)
- The plain memory block M to binary memory block:where , j = 1,2, …, n.M = (m1, m2, …, mn),
- (C)
- Encoding the plain memory block M:where C is a cipher block, S is a matrix using Equation (27), B is a matrix using Equation (28), P is a matrix using Equation (29), and MT and CT are matrix transforms.(SP + B) × MT ≡ CT (mod m),
3.3. Decoding Algorithm
- (A)
- Find a positive integer α such thatwhere α ≡ (k1m1 + k2m2 + … + knmn) (mod m). Notice that α ≡ (α 1m1 + α 2m2 + … + α nmn) (mod m).KCT ≡ α (mod m),
- (B)
- Find a plain memory block.
- Key Generation StepLet n = 4, the super-increasing sequence and let m = 30. SelectThen, KS ≡ O (mod 30) and KB ≡ A (mod 30).
- Public Keys: n, m, S, B and Private Keys: A, K
- Encoding StepLet the plain text.M ≡ [m1 m2 m3 m4] = [1 0 1 1].Choose any 4 × 4 matrixThe plain text M is encrypted by computing.The cipher text is C = [7 5 13 18].
- Decoding StepComputeThis yields m1 + 3m2 + 5m3 + 15m4 = 21. Therefore, the cipher text C is decrypted as
3.4. Proof of the Algorithm
- (A)
- We already know private key K when using Equation (25), cipher CT, and Equation (31).α ≡ KCT (mod m).
- (B)
- We can transfer CT to Equation (37) when using Equation (31).
- (C)
- We can calculate Equation (36).
- (D)
- (KS) equals to the matrix O when using Equation (26). Therefore, we obtain the following equation:
- (E)
- (KB) represents Equation (38) when using Equation (28).
- (F)
- In Equation (39), we re-write Equation (32) to Equation (38).
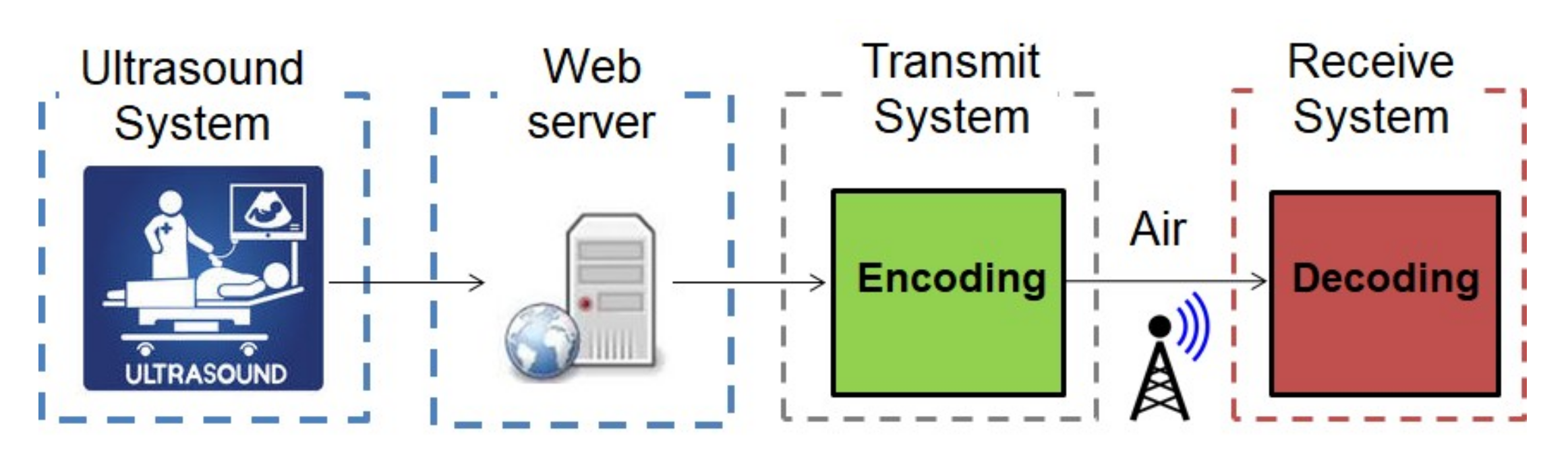
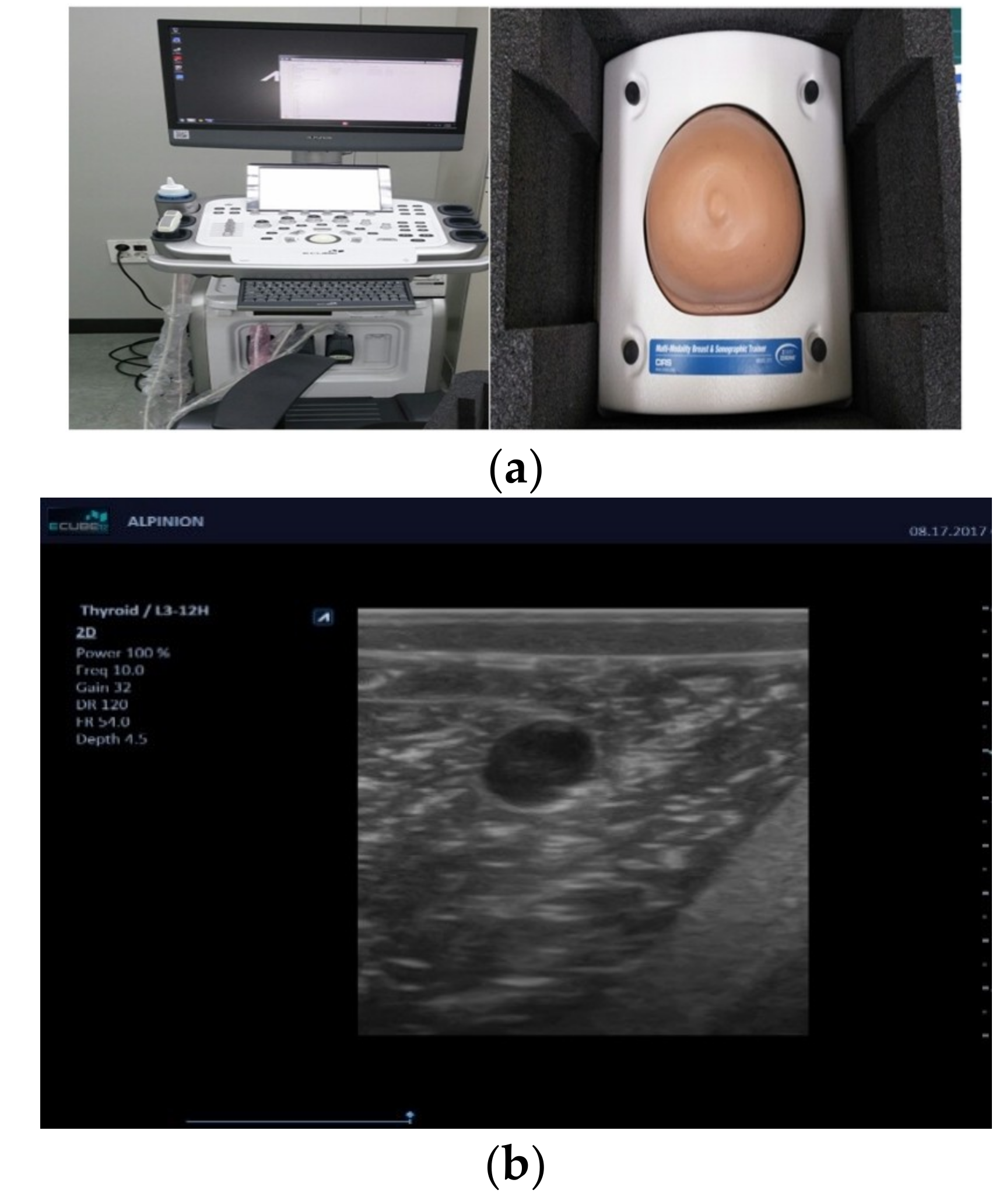
4. Results and Discussion
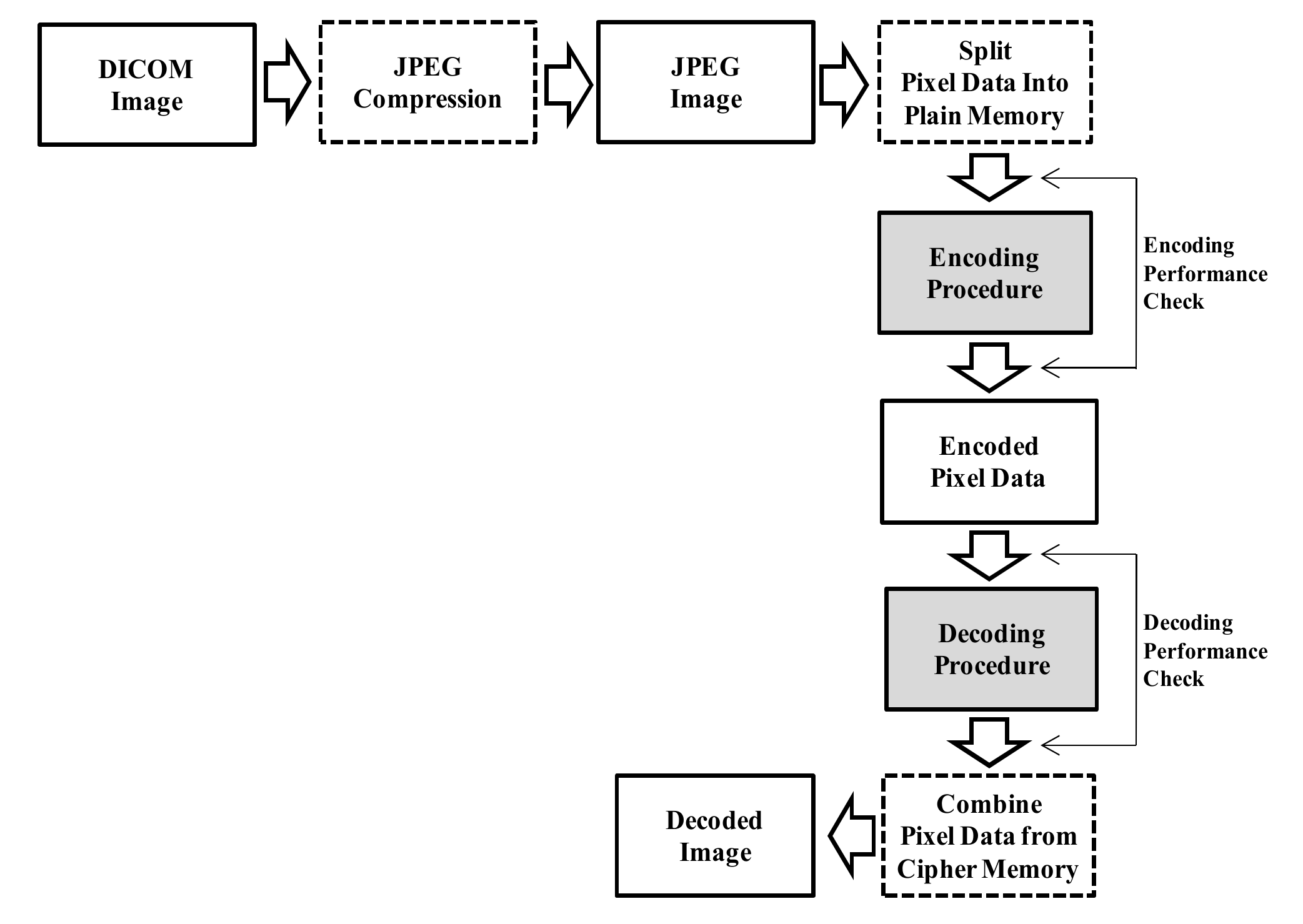
- The DICOM image is converted to a JPEG image that is then reduced in size.
- The JPEG image splits pixel data into plain memory by the encoder.
- The encoding procedure performs the encoding process from the pixel data to the encoded data.
- The decoding procedure performs the decoding process from the encoded data to the decoded data.
- A JPEG image is produced by the decoder.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Postema, M. Fundamentals of Medical Ultrasound; Taylor and Francis: New York, NJ, USA, 2011. [Google Scholar]
- Choi, H.; Yeom, J.-Y.; Ryu, J.-M. Development of a Multiwavelength Visible-Range-Supported Opto–Ultrasound Instrument Using a Light-Emitting Diode and Ultrasound Transducer. Sensors 2018, 18, 3324. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.; Ryu, J.; Kim, J. A Novel Fisheye-Lens-Based Photoacoustic System. Sensors 2016, 16, 2185. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.; Ryu, J.-M.; Yeom, J.-Y. Development of a Double-Gauss Lens Based Setup for Optoacoustic Applications. Sensors 2017, 17, 496. [Google Scholar] [CrossRef] [PubMed]
- Choe, S.-W.; Choi, H. Suppression Technique of HeLa Cell Proliferation Using Ultrasonic Power Amplifiers Integrated with a Series-Diode Linearizer. Sensors 2018, 18, 4248. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.; Woo, P.C.; Yeom, J.-Y.; Yoon, C. Power MOSFET Linearizer of a High-Voltage Power Amplifier for High-Frequency Pulse-Echo Instrumentation. Sensors 2017, 17, 764. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.J.; Choi, H. An impedance measurement system for piezoelectric array element transducers. Measurement 2017, 97, 138–144. [Google Scholar] [CrossRef]
- Choi, H. Prelinearized Class-B Power Amplifier for Piezoelectric Transducers and Portable Ultrasound Systems. Sensors 2019, 19, 287. [Google Scholar] [CrossRef]
- Choi, H.; Choe, S.-W. Acoustic Stimulation by Shunt-Diode Pre-Linearizer Using Very High Frequency Piezoelectric Transducer for Cancer Therapeutics. Sensors 2019, 19, 357. [Google Scholar] [CrossRef]
- Choi, H.; Park, C.; Kim, J.; Jung, H. Bias-Voltage Stabilizer for HVHF Amplifiers in VHF Pulse-Echo Measurement Systems. Sensors 2017, 17, 2425. [Google Scholar] [CrossRef]
- Grüll, H.; Langereis, S. Hyperthermia-triggered drug delivery from temperature-sensitive liposomes using MRI-guided high intensity focused ultrasound. J. Control. Release 2012, 161, 317–327. [Google Scholar] [CrossRef]
- Jolesz, F.A. MRI-guided focused ultrasound surgery. Annu. Rev. Med. 2009, 60, 417–430. [Google Scholar] [CrossRef] [PubMed]
- Szabo, T.L. Diagnostic Ultrasound Imaging: Inside Out; Elsevier Academic Press: London, UK, 2013. [Google Scholar]
- Choi, H.; Choe, S.-W. Therapeutic Effect Enhancement by Dual-Bias High-Voltage Circuit of Transmit Amplifier for Immersion Ultrasound Transducer Applications. Sensors 2018, 18, 4210. [Google Scholar] [CrossRef] [PubMed]
- Hoskins, P.R.; Martin, K.; Thrush, A. Diagnostic Ultrasound: Physics and Equipment; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Daniels, J.M.; Hoppmann, R.A. Practical Point-of-Care Medical Ultrasound; Springer: New York, NJ, USA, 2016. [Google Scholar]
- Su, M.-J.; Ma, H.-M.; Ko, C.-I.; Chiang, W.-C.; Yang, C.-W.; Chen, S.-J.; Chen, R.; Chen, H.-S. Application of tele-ultrasound in emergency medical services. Telemed. E Health 2008, 14, 816–824. [Google Scholar] [CrossRef] [PubMed]
- Moore, C.L.; Copel, J.A. Point-of-care Ultrasonography. N. Engl. J. Med. 2011, 364, 749–757. [Google Scholar] [CrossRef] [PubMed]
- David Cone, J.H.B.; Theodore, R.; Delbridge, J.; Brent, M. Emergency Medical Services: Clinical Practice and Systems Oversight; Wiley Online Library: Hoboken, NJ, USA, 2015. [Google Scholar]
- Lee, T.H. The Design of CMOS Radio-Frequency Integrated Circuits; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Choi, H. Class-C Linearized Amplifier for Portable Ultrasound Instruments. Sensors 2019, 19, 898. [Google Scholar] [CrossRef]
- Choi, H.; Yoon, C.; Yeom, J.-Y. A Wideband High-Voltage Power Amplifier Post-Linearizer for Medical Ultrasound Transducers. Appl. Sci. 2017, 7, 354. [Google Scholar] [CrossRef]
- Zennaro, F.; Neri, E.; Nappi, F.; Grosso, D.; Triunfo, R.; Cabras, F.; Frexia, F.; Norbedo, S.; Guastalla, P.; Gregori, M. Real-Time Tele-Mentored Low Cost “Point-of-Care US” in the Hands of Paediatricians in the Emergency Department: Diagnostic Accuracy Compared to Expert Radiologists. PLoS ONE 2016, 11, e0164539. [Google Scholar] [CrossRef]
- Levine, A.R.; McCurdy, M.T.; Zubrow, M.T.; Papali, A.; Mallemat, H.A.; Verceles, A.C. Tele-intensivists can instruct non-physicians to acquire high-quality ultrasound images. J. Crit. Care 2015, 30, 871–875. [Google Scholar] [CrossRef]
- Brooks, A.; Price, V.; Simms, M. FAST on operational military deployment. Emerg. Med. J. 2005, 22, 263–265. [Google Scholar] [CrossRef]
- Wagner, M.S.; Garcia, K.; Martin, D.S. Point-of-care Ultrasound in Aerospace Medicine: Known and Potential Applications. Aviat. Space Environ. Med. 2014, 85, 730–739. [Google Scholar] [CrossRef]
- Emery, M.; Flannigan, M. How useful are clinical findings in patients with blunt abdominal trauma? Ann. Emerg. Med. 2014, 63, 463–464. [Google Scholar] [CrossRef]
- Kim, C.; Cha, H.; Kang, B.S.; Choi, H.J.; Lim, T.H.; Oh, J. A feasibility study of smartphone-based telesonography for evaluating cardiac dynamic function and diagnosing acute appendicitis with control of the image quality of the transmitted videos. J. Digit. Imaging 2016, 29, 347–356. [Google Scholar] [CrossRef]
- Eren, H.; Webster, J.G. Telemedicine and Electronic Medicine; CRC Press: Boca Ration, FL, USA, 2015. [Google Scholar]
- Kobayashi, L.O.M.; Furuie, S.S.; Barreto, P.S.L.M. Providing integrity and authenticity in DICOM images: A novel approach. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 582–589. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.; Cardoza-Avendaño, L.; López-Gutiérrez, R.; Cruz-Hernández, C. A Double Chaotic Layer Encryption Algorithm for Clinical Signals in Telemedicine. J. Med. Syst. 2017, 41, 59. [Google Scholar] [CrossRef]
- Mehta, G.; Dutta, M.K.; Kim, P.S. An Efficient and Lossless Cryptosystem for Security in Tele-Ophthalmology Applications Using Chaotic Theory. Ophthalmology: Breakthroughs in Research and Practice: Breakthroughs in Research and Practice; Information Resources Management Association: Hershey, PA, USA, 2018; Volume 189. [Google Scholar]
- Kishore, P.; Venkatram, N.; Sarvya, C.; Reddy, L. Medical Image Watermarking Using RSA Encryption in Wavelet Domain. In Proceedings of the 2014 First International Conference on Networks & Soft Computing (ICNSC2014), Guntur, India, 19–20 August 2014; pp. 258–262. [Google Scholar]
- Kanakis, A. Implementations of Wireless and Wired Intelligent Systems for Healthcare with Focus on Diabetes and Ultrasound Applications. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2013. [Google Scholar]
- Huang, H. PACS and Imaging Informatics: Basic Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Slone, R.M.; Muka, E.; Pilgram, T.K. Irreversible JPEG compression of digital chest radiographs for primary interpretation: Assessment of visually lossless threshold. Radiology 2003, 228, 425–429. [Google Scholar] [CrossRef] [PubMed]
- Paar, C.; Pelzl, J. Understanding Cryptography: A Textbook for Students and Practitioners; Springer Science & Business Media: New York, NJ, USA, 2009. [Google Scholar]
- Strang, G. Differential Equations and Linear Algebra; Wellesley-Cambridge Press: Welleslely, MA, USA, 2014. [Google Scholar]
- Lehmer, D. On Euler’s totient function. Bull. Am. Math. Soc. 1932, 38, 745–751. [Google Scholar] [CrossRef]
- Hendy, M. Euclid and the fundamental theorem of arithmetic. Hist. Math. 1975, 2, 189–191. [Google Scholar] [CrossRef] [Green Version]
- Menezes, A.J.; Katz, J.; Van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Stallings, W. Cryptography and Network Security: Principles and Practice; Pearson Education: London, UK, 2003. [Google Scholar]
- Bach, E.; Shallit, J.O. Algorithmic Number Theory: Efficient Algorithms; MIT Press: Cambridge, MA, USA, 1996; Volume 1. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer Science & Business Media: New York, NJ, USA, 2006. [Google Scholar]
- Stallings, W. Network Security Essentials: Applications and Standards; Pearson Education: London, UK, 2000. [Google Scholar]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Lenstra, H. Integer programming and cryptography. Math. Intell. 1984, 6, 14–21. [Google Scholar] [CrossRef] [Green Version]
- Chor, B.; Rivest, R.L. A knapsack-type public key cryptosystem based on arithmetic in finite fields. IEEE Trans. Inf. Theory 1988, 34, 901–909. [Google Scholar] [CrossRef]
- Shang, Y. Deffuant model with general opinion distributions: First impression and critical confidence bound. Complexity 2013, 19, 38–49. [Google Scholar] [CrossRef]
- Shang, Y. Deffuant model of opinion formation in one-dimensional multiplex networks. J. Phys. A Math. Theor. 2015, 48, 395101. [Google Scholar] [CrossRef]
- Forouzan, B.A.; Mukhopadhyay, D. Cryptography and Network Security (Sie); McGraw-Hill Education: New York, NJ, USA, 2011. [Google Scholar]
- Boniface, K.S.; Shokoohi, H.; Smith, E.R.; Scantlebury, K. Tele-ultrasound and paramedics: real-time remote physician guidance of the Focused Assessment with Sonography for Trauma examination. Am. J. Emerg. Med. 2011, 29, 477–481. [Google Scholar] [CrossRef]
- Al-Haj, A.; Abandah, G.; Hussein, N. Crypto-based algorithms for secured medical image transmission. IET Inf. Secur. 2015, 9, 365–373. [Google Scholar] [CrossRef]
- Bernstein, D.J. Introduction to Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- OpenSSL Cryptography and SSL/TLS Tookit. Available online: https://www.openssl.org/ (accessed on 16 April 2018).
- Shang, Y. Resilient multiscale coordination control against adversarial nodes. Energies 2018, 11, 1844. [Google Scholar] [CrossRef]
- Shang, Y. Resilient consensus of switched multi-agent systems. Syst. Control Lett. 2018, 122, 12–18. [Google Scholar] [CrossRef]
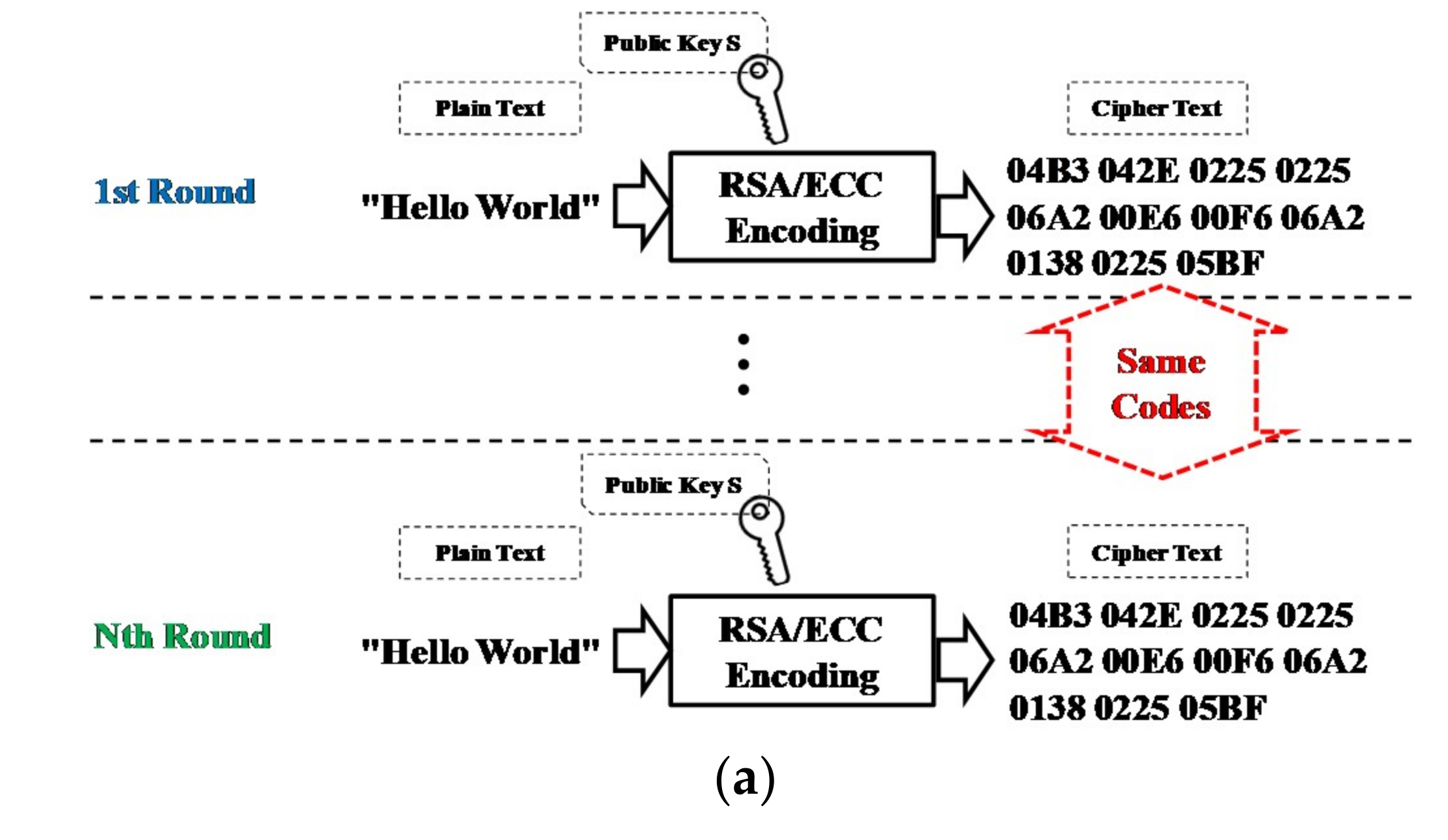
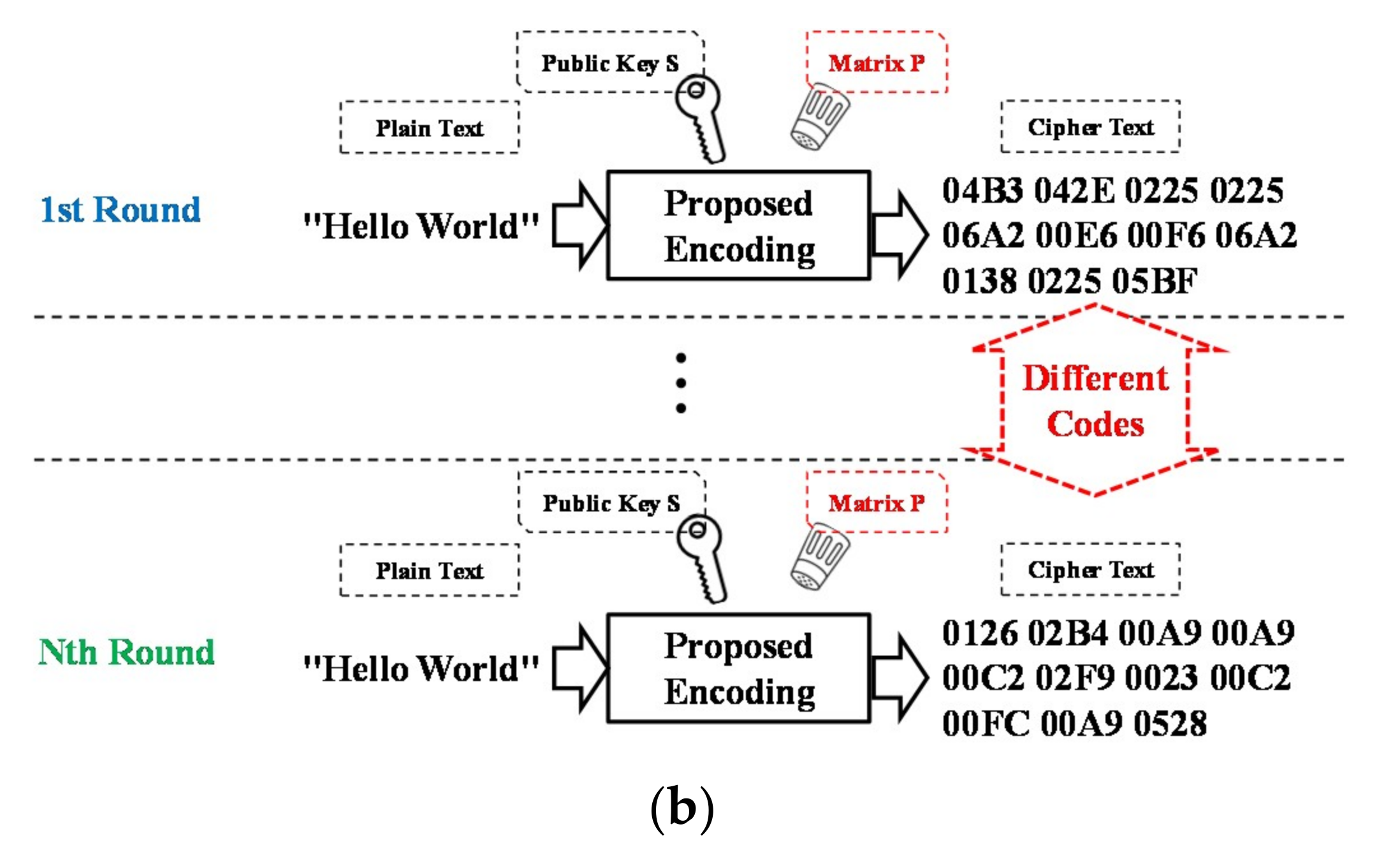
| Algorithm. Find a plain memory |
| INPUT: matrix A, OUTPUT: matrix R alpha = procedure Decoding() WHILE row > 0 DO WHILE column > 0 DO Set sumA to sum from A(1,1) to A(row, column) IF alpha >= sumK THEN Compute alpha as alpha - sumK Set R(row,column) to 1 ELSE Set R(row,column) to 0 ENDIF Compute column as column - 1 ENDWHILE Compute row as row - 1 ENDWHILE RETURN with error code |
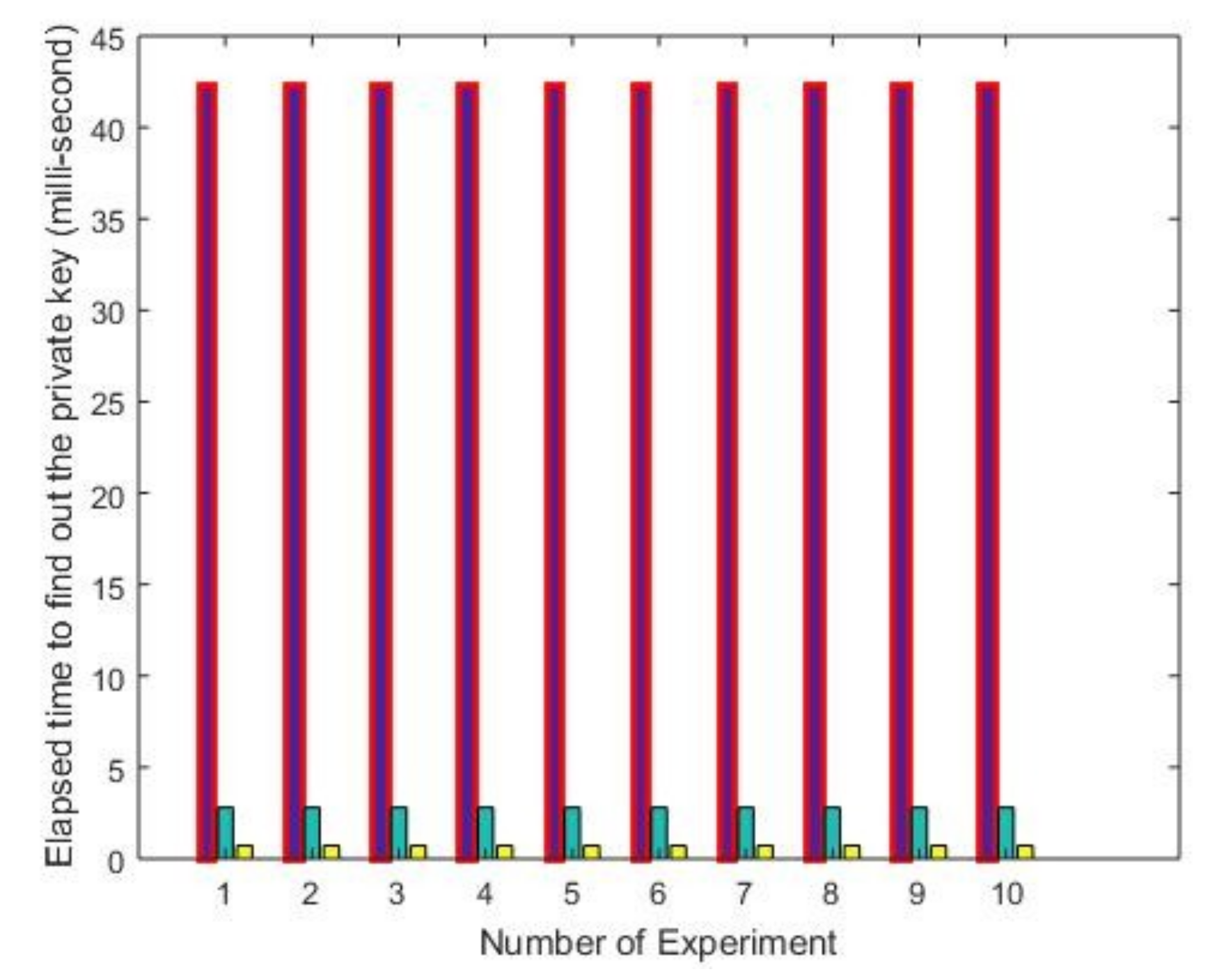
| Number of Experiments | RSA | ECC | Proposed |
|---|---|---|---|
| 1 | 2.8101 | 0.7209 | 42.4272 |
| 2 | 2.8092 | 0.7211 | 42.4146 |
| 3 | 2.8101 | 0.7214 | 42.4151 |
| 4 | 2.8078 | 0.7219 | 42.4147 |
| 5 | 2.8106 | 0.7166 | 42.4159 |
| 6 | 2.8089 | 0.7218 | 42.4216 |
| 7 | 2.8036 | 0.7212 | 42.4183 |
| 8 | 2.8092 | 0.7222 | 42.4131 |
| 9 | 2.8095 | 0.7218 | 42.4194 |
| 10 | 2.8098 | 0.7217 | 42.4154 |
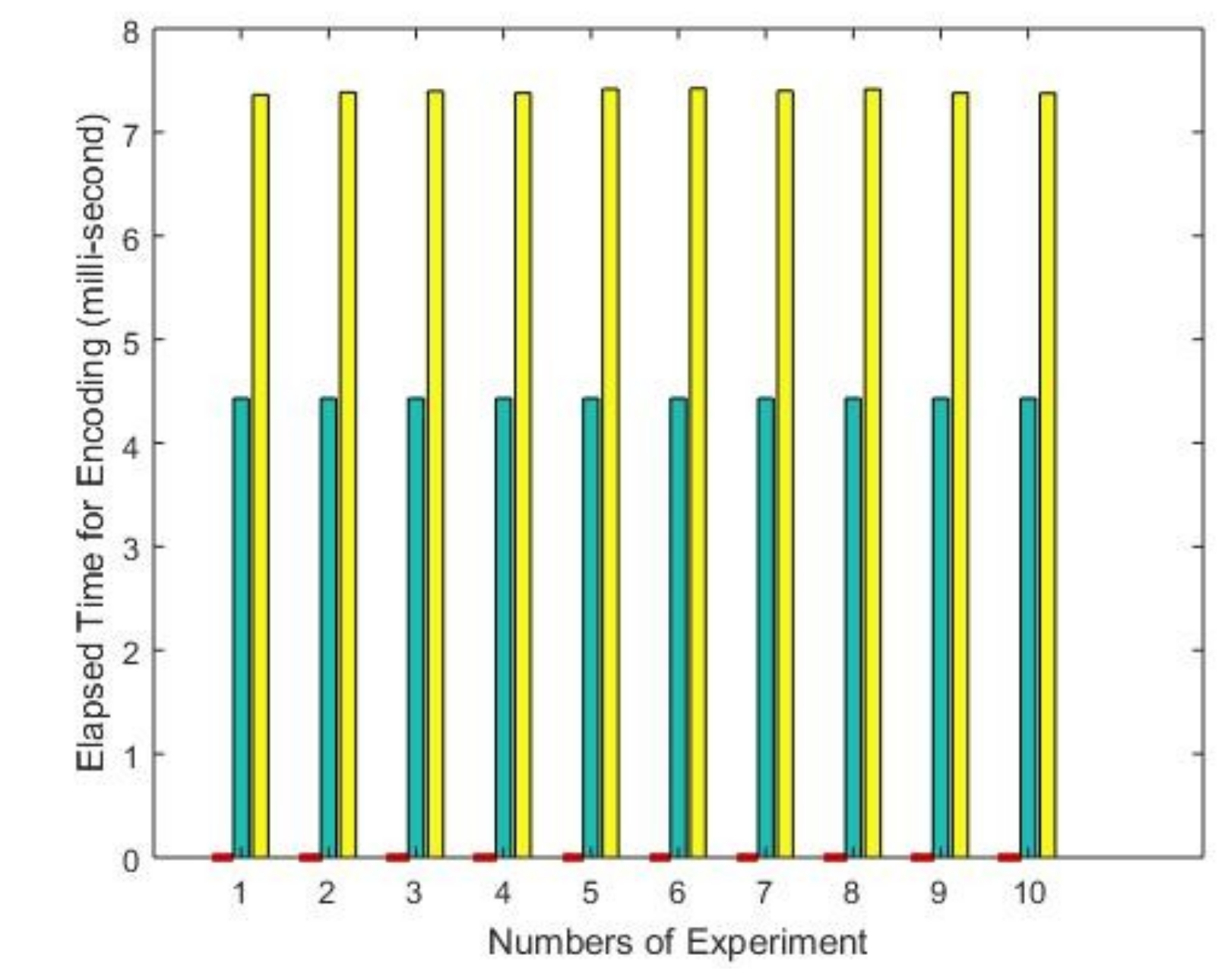
| Number of Experiments | RSA | ECC | Proposed |
|---|---|---|---|
| 1 | 4.4304 | 7.3606 | 0.0185 |
| 2 | 4.4315 | 7.3862 | 0.0184 |
| 3 | 4.4320 | 7.3959 | 0.0185 |
| 4 | 4.4315 | 7.3779 | 0.0185 |
| 5 | 4.4314 | 7.4165 | 0.0185 |
| 6 | 4.4317 | 7.4220 | 0.0184 |
| 7 | 4.4316 | 7.4005 | 0.0184 |
| 8 | 4.4306 | 7.4154 | 0.0299 |
| 9 | 4.4301 | 7.3790 | 0.0183 |
| 10 | 4.4309 | 7.3773 | 0.0183 |
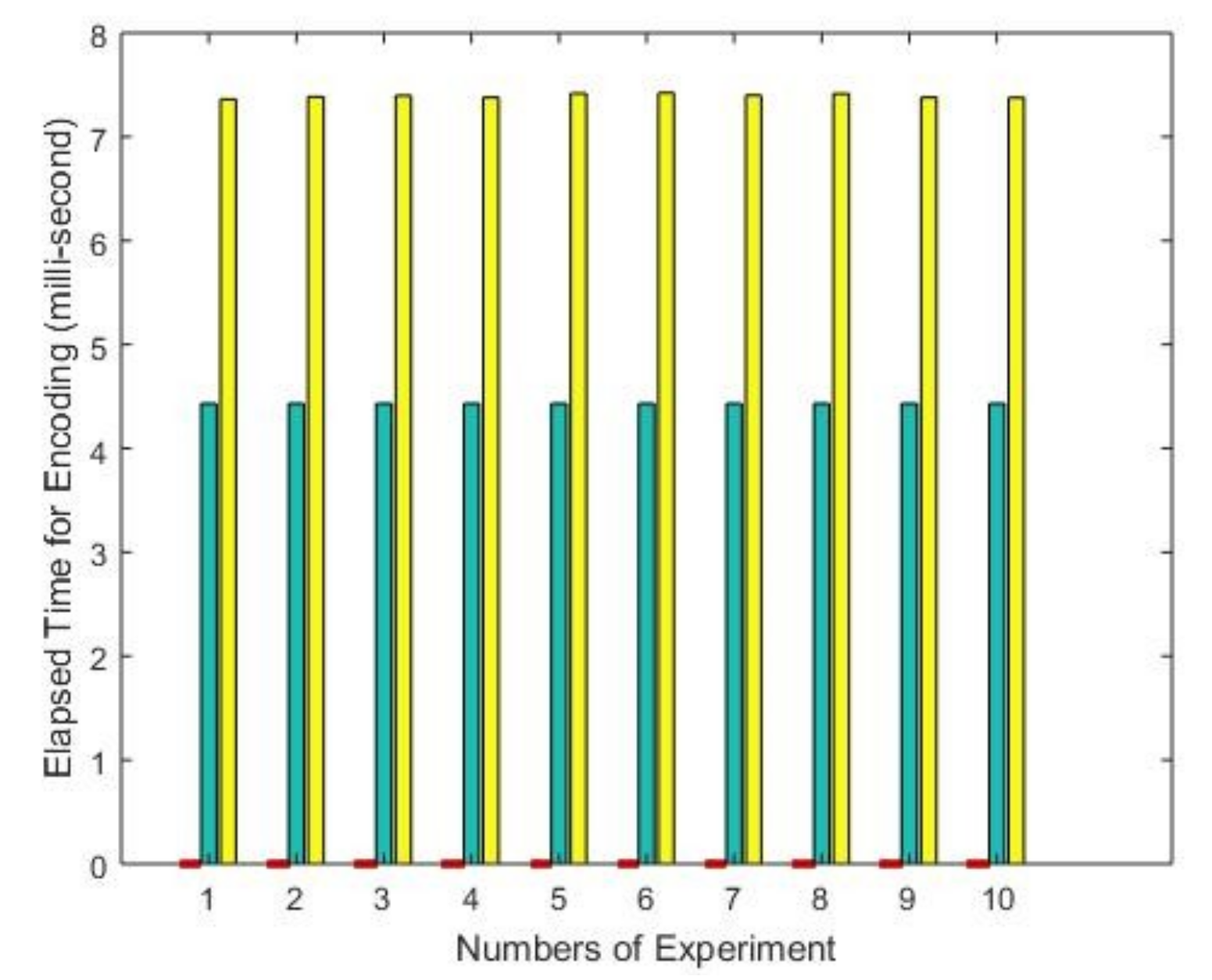
| Number of Experiments | RSA | ECC | Proposed |
|---|---|---|---|
| 1 | 4.4316 | 7.3736 | 0.0185 |
| 2 | 4.4320 | 7.3836 | 0.0185 |
| 3 | 4.4309 | 7.3850 | 0.0184 |
| 4 | 4.4312 | 7.3900 | 0.0184 |
| 5 | 4.4329 | 7.4220 | 0.0185 |
| 6 | 4.4315 | 7.3790 | 0.0185 |
| 7 | 4.4318 | 7.3886 | 0.0184 |
| 8 | 4.4320 | 7.3830 | 0.0183 |
| 9 | 4.4318 | 7.4070 | 0.0187 |
| 10 | 4.4312 | 7.3798 | 0.0184 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, S.-H.; Yoo, W.-S.; Choi, H. Development of Public Key Cryptographic Algorithm Using Matrix Pattern for Tele-Ultrasound Applications. Mathematics 2019, 7, 752. https://doi.org/10.3390/math7080752
Shin S-H, Yoo W-S, Choi H. Development of Public Key Cryptographic Algorithm Using Matrix Pattern for Tele-Ultrasound Applications. Mathematics. 2019; 7(8):752. https://doi.org/10.3390/math7080752
Chicago/Turabian StyleShin, Seung-Hyeok, Won-Sok Yoo, and Hojong Choi. 2019. "Development of Public Key Cryptographic Algorithm Using Matrix Pattern for Tele-Ultrasound Applications" Mathematics 7, no. 8: 752. https://doi.org/10.3390/math7080752
APA StyleShin, S. -H., Yoo, W. -S., & Choi, H. (2019). Development of Public Key Cryptographic Algorithm Using Matrix Pattern for Tele-Ultrasound Applications. Mathematics, 7(8), 752. https://doi.org/10.3390/math7080752




