Complete Ensemble Empirical Mode Decomposition on FPGA for Condition Monitoring of Broken Bars in Induction Motors
Abstract
:1. Introduction
2. Theoretical Background
2.1. EMD
- Detect all the extrema of the target signal x(t).
- Join the minima and maxima points by employing a cubic spline to get the lower envelope emin(t) and the upper envelope emax(t), respectively.
- Estimate the mean mj(t) with j = 1 as the average of upper and lower envelopes.
- Determinate the local oscillation mode c1(t).
- Evaluate if c1(t) satisfies the two criteria to be an IMF; if it does not satisfy the criteria, steps (1–4) by setting x(t) = c1(t) must be repeated; on the contrary, if c1(t) is an IMF save it as IMFk, where k = 1, …, K represents the modes.
- Calculate the residue r(t) = x(t) − ck(t) and
- Evaluate if r(t) is a monotonic function; if it is not, repeat the overall process by setting x(t) = r(t) and increase j by one. On the contrary, if r(t) is a monotonic function the signal analysis or decomposition is complete.
2.2. EEMD
- Generate xj(t) = x(t) + wj(t), where wj(t), for j = 1, …, N, are different white noise series.
- Decompose each time signal xj(t) by using the EMD method for estimating its frequency bands or , where k = 1, …, K indicates the modes.
- Define the “true” IMFs, , for the k-th mode of x(t) as the average of their corresponding
2.3. CEEMD
- Decompose N realizations of , i = 1,…, N using EMD, where and represent the noise standard deviation and the white noise, respectively; then, ensemble all of the first modes to obtain a true as:
- Calculate a unique first residue at the first stage (k = 1) as:
- Decompose N realizations of , i = 1, …, N. is an operator that for a given signal produces the j-th mode obtained by EMD. Next use EMD to obtain the second mode:
- For the next stages (k = 2, …, K), keep computing the k-th residue and obtain the next IMFs by:Steps 3 to 4 continues until the residue does not have at least two extrema.
- The final residue can be calculated with K equal to the total number of modes as:Hence, the original signal can be expressed as:
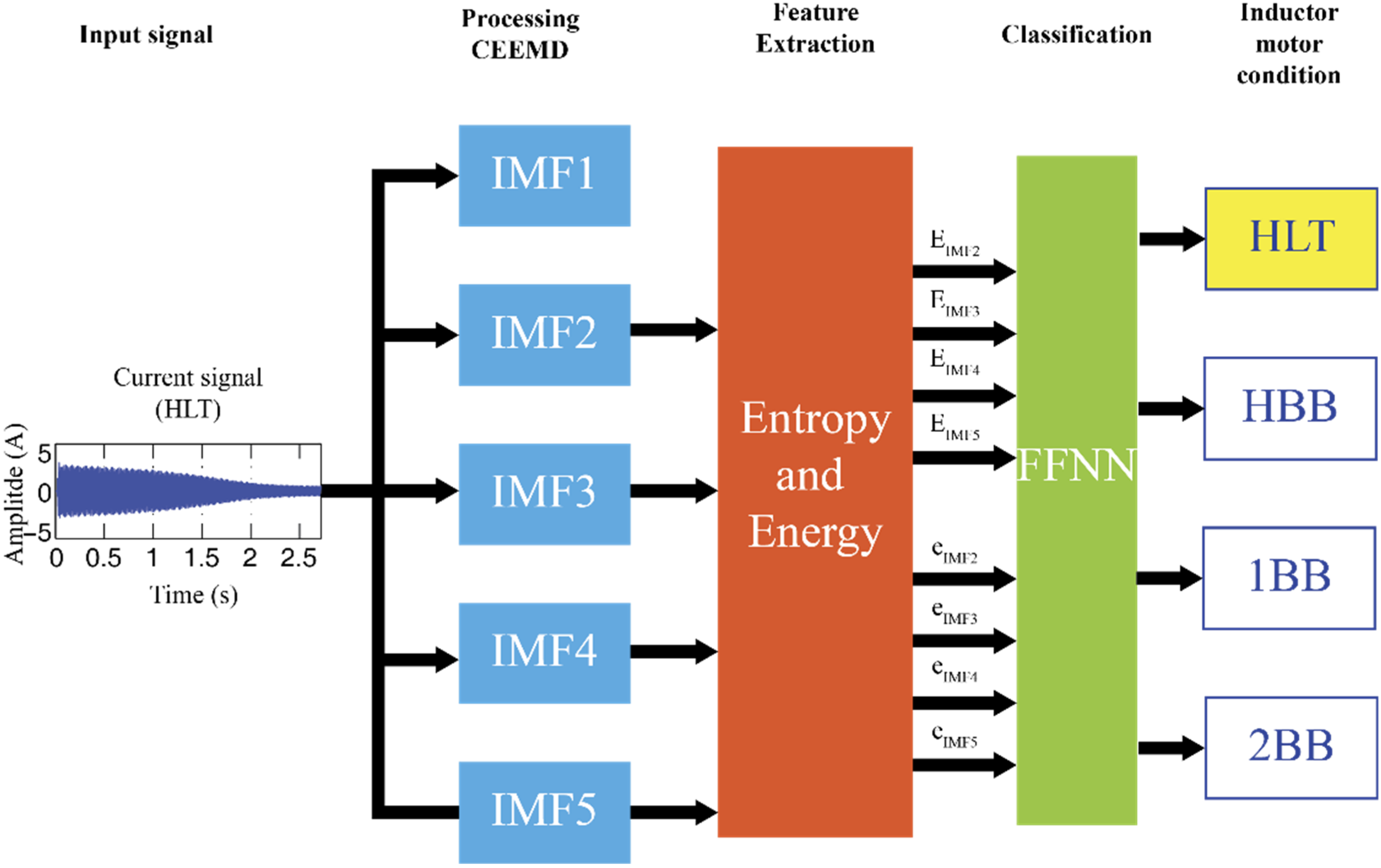
3. Proposed Methodology and Its FPGA Implementation
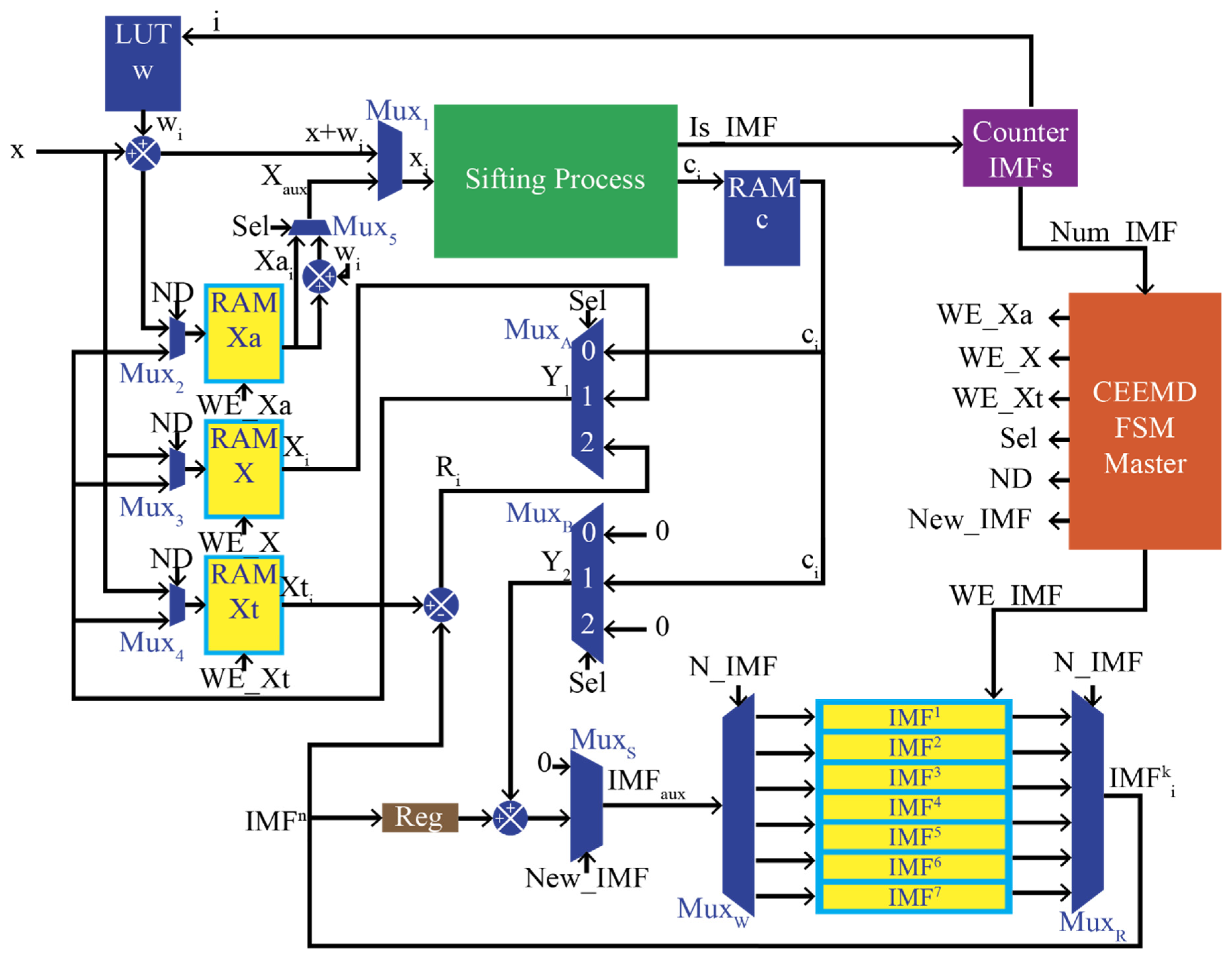
4. FPGA Processor
4.1. CEEMD Module
4.2. Sifting Module
4.3. Feature Extraction Module
4.3.1. Entropy
4.3.2. Energy
4.4. FFNN Module
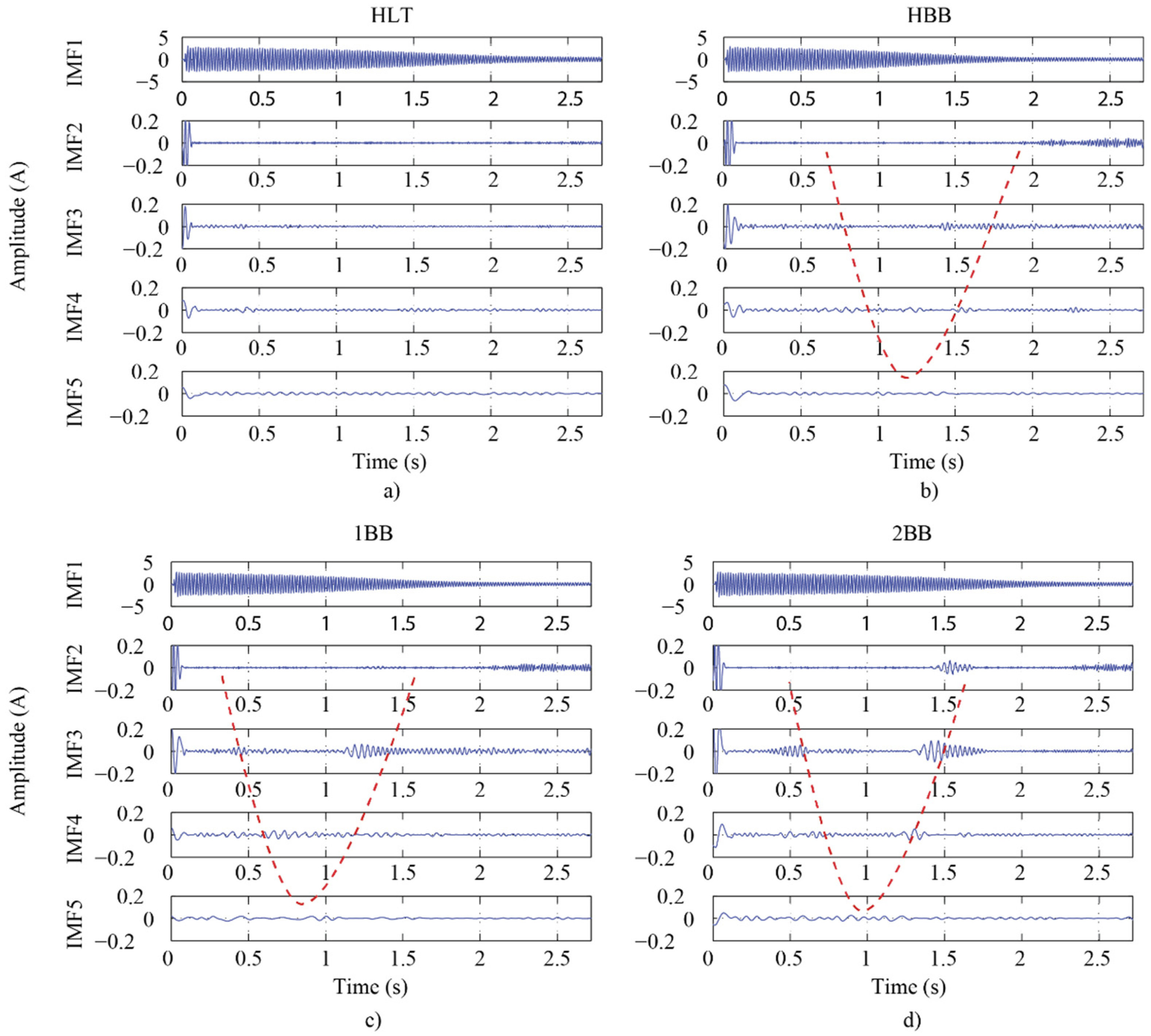
5. Results
5.1. FPGA Results
5.2. Fault Diagnosis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rangel-Magdaleno, J.D.J.; Romero-Troncoso, R.D.J.; Osornio-Rios, R.A.; Cabal-Yepez, E.; Contreras-Medina, L.M. Novel methodology for online half-broken-bar detection on induction motors. IEEE Trans. Instrum. Meas. 2009, 58, 1690–1698. [Google Scholar] [CrossRef]
- Garcia-Perez, A.; Romero-Troncoso, R.J.; Cabal-Yepez, E.; Osornio-Rios, R.A.; Rangel-Magdaleno, J.D.J.; Miranda, H. Startup current analysis of incipient broken rotor bar in induction motors using high-resolution spectral analysis. In Proceedings of the SDEMPED 2011 8th IEEE Symposium Diagnostics Electrical Machines Power Electronics and Drives, Bologna, Italy, 5–8 September 2011; pp. 657–663. [Google Scholar]
- Kurek, J.; Osowski, S. Support vector machine for fault diagnosis of the broken rotor bars of squirrel-cage induction motor. Neural Comput. Appl. 2010, 19, 557–564. [Google Scholar] [CrossRef]
- da Silva, A.M.; Povinelli, R.J.; Demerdash, N.A.O. Rotor bar fault monitoring method based on analysis of air-gap torques of induction motors. IEEE Trans. Ind. Inform. 2013, 9, 2274–2283. [Google Scholar] [CrossRef]
- Nemec, M.; Ambrožič, V.; Fišer, R.; Nedeljković, D.; Drobnič, K. Induction Motor Broken Rotor Bar Detection Based on Rotor Flux Angle Monitoring. Energies 2019, 12, 794. [Google Scholar] [CrossRef]
- Faiz, J.; Ghorbanian, V.; Ebrahimi, B.M. A survey on condition monitoring and fault diagnosis in line-start and inverter-fed broken bar induction motors. In Proceedings of the PEDES 2012 IEEE International Conference Power Electronics Drives Energy Systems, Bengaluru, India, 16–19 December 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Antonino-Daviu, J.; Riera-Guasp, M.; Pons-Llinares, J.; Park, J.; Lee, S.B.; Yoo, J.; Kral, C. Detection of broken outer cage bars for double cage induction motors under the startup transient. In Proceedings of the SDEMPED 2011 8th IEEE Symposium Diagnostics Electrical Machines Power Electron. Drives, Bologna, Italy, 5–8 September 2011; pp. 1–8. [Google Scholar]
- Wei, Y.; Shi, B.; Cui, G.; Yin, J. Broken rotor bar detection in induction motors via wavelet ridge. In Proceedings of the 2009 International Conference Measuring Technology Mechatronics Automatronics ICMTMA, Hunan, China, 11–12 April 2009; Volume 2, pp. 625–628. [Google Scholar] [CrossRef]
- Pineda-Sanchez, M.; Riera-Guasp, M.; Perez-Cruz, J.; Puche-Panadero, R. Transient motor current signature analysis via modulus of the continuous complex wavelet: A pattern approach. Energy Convers. Manag. 2013, 73, 26–36. [Google Scholar] [CrossRef]
- Riera-Guasp, M.; Antonino-Daviu, J.A.; Pineda-Sanchez, M.; Puche-Panadero, R.; Perez-Cruz, J. A general approach for the transient detection of slip-dependent fault components based on the discrete wavelet transform. IEEE Trans. Ind. Electron. 2008, 55, 4167–4180. [Google Scholar] [CrossRef]
- Kechida, R.; Menacer, A. DWT wavelet transform for the rotor bars faults detection in induction motor. In Proceedings of the 2011 2nd International Conference Electrical Power Energy Conversion System EPECS, Sharjah, UAE, 15–17 November 2011. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef] [Green Version]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Rolling element bearing fault diagnosis using wavelet transform. Neurocomputing 2011, 74, 1638–1645. [Google Scholar] [CrossRef]
- Manjula, M.; Sarma, A.V.R.S. Comparison of Empirical Mode Decomposition and Wavelet Based Classification of Power Quality Events. Energy Procedia 2012, 14, 1156–1162. [Google Scholar] [CrossRef] [Green Version]
- Antonino-Daviu, J.A.; Riera-Guasp, M.; Pineda-Sanchez, M.; Perez, R.B. A critical comparison between DWT and Hilbert-Huang-based methods for the diagnosis of rotor bar failures in induction machines. IEEE Trans. Ind. Appl. 2009, 45, 1794–1803. [Google Scholar] [CrossRef]
- Antonino-Daviu, J.; Aviyente, S.; Strangas, E.G.; Riera-Guasp, M.; Roger-Folch, J. An EMD-based invariant feature extraction algorithm for rotor bar condition monitoring. In Proceedings of the SDEMPED 2011 8th IEEE Symposium Diagnostics Electrical Machines Power Electronics Drives, Bologna, Italy, 5–8 September 2011; pp. 669–675. [Google Scholar]
- Valles-Novo, R.; Rangel-Magdaleno, J.D.J.; Ramirez-Cortes, J.M.; Peregrina-Barreto, H.; Morales-Caporal, R. Empirical Mode Decomposition Analysis for Broken-Bar Detection on Squirrel Cage Induction Motors. IEEE Trans. Instrum. Meas. 2015, 64, 1118–1128. [Google Scholar] [CrossRef]
- Hong, X.Z.; Yong, H.S. Method of EMD and ZOOM-FFT to Detect the Broken Bars Fault in Induction Motor. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Korea, 10–13 October 2010. [Google Scholar]
- Camarena-Martinez, D.; Osornio-Rios, R.A.; Romero-troncoso, R.D.J.; Garcia-Perez, A. Fused Empirical Mode Decomposition and MUSIC algorithms for detecting multiple combined faults in induction motors. J. Appl. Res. Technol. 2015, 13, 160–167. [Google Scholar] [CrossRef]
- Wang, L.; Vai, M.I.; Mak, P.U.; Ieong, C.I. Hardware-Accelerated Implementation of EMD Hardware and Software Co-design Evalution for HHT; University of Macau: Macau, China, 2010; pp. 912–915. [Google Scholar]
- Lee, S.; Member, M.; Shyu, K.; Lee, P. Hardware Implementation of EMD Using DSP and FPGA for Online Signal Processing. IEEE Trans. Ind. Electr. 2011, 58, 2473–2481. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Bao, Y.Q. FPGA Implementation for Real-Time Empirical Mode Decomposition. IEEE Trans. Instrum. Meas. 2012, 61, 1–10. [Google Scholar] [CrossRef]
- Camarena-Martinez, D.; Valtierra-Rodriguez, M.; Garcia-Perez, A.; Osornio-Rios, R.A.; Romero-Troncoso, R.D.J. Empirical Mode Decomposition and Neural Networks on FPGA for Fault Diagnosis in Induction Motors. Sci. World J. 2014, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.Y.; Lai, Y.C.; Zheng, J.Y. Hardware Design and Implementation for Empirical Mode Decomposition. IEEE Trans. Ind. Electron. 2016, 63, 3686–3694. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. Partly ensemble empirical mode decomposition: An improved noise-assisted method for eliminating mode mixing. Signal Process. 2014, 96, 362–374. [Google Scholar] [CrossRef]
- Flandrin, P.; Torres, E.; Colominas, M.A. A Complete Ensemble Empirical Mode Decomposition Laboratorio de Se˜ nales y Din’ amicas no Lineales, Universidad Nacional de Entre R´ Laboratoire de Physique (UMR CNRS 5672); Ecole Normale Sup erieure de Lyon: Lyon, France, 2011; pp. 4144–4147. [Google Scholar]
- Satija, U.; Ramkumar, B.; Manikandan, M.S. Automated ECG noise detection and classification system for unsupervised healthcare monitoring. IEEE J. Biomed. Health Inform. 2018, 22, 722–732. [Google Scholar] [CrossRef]
- Hassan, A.R.; Bhuiyan, M.I.H. Computer-aided sleep staging using Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and bootstrap aggregating. Biomed. Signal Process. Control 2016, 24, 1–10. [Google Scholar] [CrossRef]
- Das, A.B.; Bhuiyan, M.I.H. Discrimination of focal and non-focal EEG signals using entropy-based features in EEMD and CEEMDAN domains. In Proceedings of the 2016 9th International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 20–22 December 2017; pp. 435–438. [Google Scholar] [CrossRef]
- Guarascio, M.; Puthusserypady, S. Automatic minimization of ocular artifacts from electroencephalogram: A novel approach by combining Complete EEMD with Adaptive Noise and Renyi’s Entropy. Biomed. Signal Process. Control 2017, 36, 63–75. [Google Scholar] [CrossRef]
- Bian, J.; Wang, P.; Mei, Q.; Lei, M. Fault Detection of Rolling Bearings through Vibration Analysis via the hybrid CEEMD-EMD Approach. In Proceedings of the 2014 Prognostics and System Health Management Conference (PHM-2014 Hunan), Zhangjiajie, China, 24–27 August 2014; pp. 245–250. [Google Scholar]
- Abdelkader, R.; Kaddour, A.; Derouiche, Z.; Bendiabdellah, A. Rolling Bearing Fault Diagnosis based on an Improved Denoising Method Using the Complete Ensemble Empirical Mode Decomposition and the Optimized Thresholding Operation. IEEE Sens. J. 2018, 18, 7166–7172. [Google Scholar] [CrossRef]
- Lee, C.; Huang, K.; Hsieh, Y.; Chen, P. Optimal Intrinsic Mode Function Based Detection of Motor Bearing Damages. Appl. Sci. 2019, 9, 2587. [Google Scholar] [CrossRef]
- Camarena-Martinez, D.; Valtierra-Rodriguez, M.; Perez-Ramirez, C.A.; Amezquita-Sanchez, J.P.; Romero-Troncoso, R.d.; Garcia-Perez, A. Novel Downsampling Empirical Mode Decomposition Approach for Power Quality Analysis. IEEE Trans. Ind. Electron. 2016, 63, 2369–2378. [Google Scholar] [CrossRef]
- Rangel-Magdaleno, J.D.J.; Peregrina-Barreto, H.; Ramirez-Cortes, J.M.; Member, S.; Gomez-Gil, P.; Morales-Caporal, R. FPGA-Based Broken Bars Detection on Induction Motors Under Different Load Using Motor Current Signature Analysis and Mathematical Morphology. IEEE Trans. Instrum. Meas. 2014, 63, 1032–1040. [Google Scholar] [CrossRef]
- Huang, N.E.; Zheng, S.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Panagiotou, P.A.; Arvanitakis, I.; Lophitis, N.; Antonino-Daviu, J.A.; Gyftakis, K.N. FEM approach for diagnosis of induction machines’ non-adjacent broken rotor bars by short-time Fourier transform spectrogram. J. Eng. 2019, 2019, 4566–4570. [Google Scholar] [CrossRef]
- Cabal-Yepez, E.; Valtierra-Rodriguez, M.; Romero-Troncoso, R.J.; Garcia-Perez, A.; Osornio-Rios, R.A.; Miranda-Vidales, H.; Alvarez-Salas, R. FPGA-based entropy neural processor for online detection of multiple combined faults on induction motors. Mech. Syst. Signal Process. 2012, 30, 123–130. [Google Scholar] [CrossRef]
- Mejia-Barron, A.; Valtierra-Rodriguez, M.; Granados-Lieberman, D.; Olivares-Galvan, J.C.; Escarela-Perez, R. The application of EMD-based methods for diagnosis of winding faults in a transformer using transient and steady state currents. Measurement 2018, 117, 371–379. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Liu, Y.; Bazzi, A.M. A review and comparison of fault detection and diagnosis methods for squirrel-cage induction motors: State of the art. ISA Trans. 2017, 70, 400–409. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, A.; Goyal, D.; Shimi, S.L.; Akula, A. Condition Monitoring and Fault Diagnosis of Induction Motors: A Review. Arch. Comput. Methods Eng. 2018, 1–18. [Google Scholar] [CrossRef]
- Cabal-Yepez, E.; Saucedo-Gallaga, R.; Garcia-Ramirez, A.G.; Fernandez-Jaramillo, A.A.; Pena-Anaya, M.; Valtierra-Rodriguez, M. FPGA-based online detection of multiple-combined faults through information entropy and neural networks. In Proceedings of the 2010 International Conference on Reconfigurable Computing and FPGAs, Quintana Roo, Mexico, 13–15 December 2010; pp. 244–249. [Google Scholar]









| Relative Error (%) | |||
|---|---|---|---|
| Mean | Standard Deviation | Peak Error | |
| HLT | 0.3191 | 0.0613 | 0.4476 |
| HBB | 0.3825 | 0.0603 | 0.4506 |
| 1BB | 0.4546 | 0.0960 | 0.7902 |
| 2BB | 0.2380 | 0.0422 | 0.3083 |
| Resource Utilization | Logic Elements | Memory Bits | Registers | Multipliers | Clock Cycles |
|---|---|---|---|---|---|
| CEEMD | 7089 | 372,736 | 4061 | 122 | 5,391,330,480 |
| Feature extraction | 432 | 4340 | 210 | 2 | 84,340 |
| FFNN | 1410 | 3815 | 326 | 2 | 237 |
| Total | 8931 | 378,891 | 4597 | 126 | 5,391,415,057 |
| Available resources into the FPGA | 114,480 | 3,983,312 | 114,480 | 532 | |
| Usage (%) | 7.80 | 9.51 | 4.01 | 23.68 |
| Entropy (µ, σ) | ||||
|---|---|---|---|---|
| IMF2 | IMF3 | IMF4 | IMF5 | |
| HLT | 4.2517, 0.0267 | 4.4336, 0.0684 | 4.9468, 0.0565 | 5.0074, 0.0778 |
| HBB | 5.0001, 0.0323 | 5.3585, 0.0580 | 5.1019, 0.0450 | 5.0424, 0.0829 |
| 1BB | 4.9307, 0.0313 | 5.9221, 0.0457 | 5.2000, 0.0633 | 4.7444, 0.0875 |
| 2BB | 4.9466, 0.0435 | 5.7725, 0.0452 | 5.3938, 0.0472 | 4.9526, 0.0737 |
| Energy (µ, σ) | ||||
|---|---|---|---|---|
| IMF2 | IMF3 | IMF4 | IMF5 | |
| HLT | 0.1899, 0.0389 | 0.1022, 0.0253 | 0.1208, 0.0211 | 0.1267, 0.0248 |
| HBB | 0.5026, 0.0302 | 0.2248, 0.0418 | 0.2050, 0.0459 | 0.1684, 0.0251 |
| 1BB | 0.4179, 0.0397 | 0.3772, 0.0294 | 0.1431, 0.0266 | 0.1164, 0.0324 |
| 2BB | 0.3767, 0.0282 | 0.4663, 0.0439 | 0.2222, 0.0303 | 0.1291, 0.0289 |
| HLT | HBB | 1BB | 2BB | Effectiveness (%) | |
|---|---|---|---|---|---|
| HLT | 20 | 0 | 0 | 0 | 100 |
| HBB | 0 | 18 | 2 | 0 | 90 |
| 1BB | 0 | 1 | 19 | 0 | 95 |
| 2BB | 0 | 0 | 0 | 20 | 100 |
| Average | 96.25 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valtierra-Rodriguez, M.; Amezquita-Sanchez, J.P.; Garcia-Perez, A.; Camarena-Martinez, D. Complete Ensemble Empirical Mode Decomposition on FPGA for Condition Monitoring of Broken Bars in Induction Motors. Mathematics 2019, 7, 783. https://doi.org/10.3390/math7090783
Valtierra-Rodriguez M, Amezquita-Sanchez JP, Garcia-Perez A, Camarena-Martinez D. Complete Ensemble Empirical Mode Decomposition on FPGA for Condition Monitoring of Broken Bars in Induction Motors. Mathematics. 2019; 7(9):783. https://doi.org/10.3390/math7090783
Chicago/Turabian StyleValtierra-Rodriguez, Martin, Juan Pablo Amezquita-Sanchez, Arturo Garcia-Perez, and David Camarena-Martinez. 2019. "Complete Ensemble Empirical Mode Decomposition on FPGA for Condition Monitoring of Broken Bars in Induction Motors" Mathematics 7, no. 9: 783. https://doi.org/10.3390/math7090783
APA StyleValtierra-Rodriguez, M., Amezquita-Sanchez, J. P., Garcia-Perez, A., & Camarena-Martinez, D. (2019). Complete Ensemble Empirical Mode Decomposition on FPGA for Condition Monitoring of Broken Bars in Induction Motors. Mathematics, 7(9), 783. https://doi.org/10.3390/math7090783







