On Fixed-Point Results in Controlled Partial Metric Type Spaces with a Graph

Abstract

Recently, Mlaiki et al. introduced the notion of a controlled metric type space which is a generalization of the b-metric space. In this work, we define the controlled partial metric type space and give some fixed-point theorems for extensions of Kannan contraction in this space with suitable conditions. Moreover, as an application, we derive a fixed-point theorem for graphic contraction on the considered metric space endowed with a graph.

1. Introduction

During last decade the fixed-point theory has had a lot of interest due to its various applications in several fields of mathematics, such as differential equations, nonlinear analysis, graph theory, etc. [1,2,3]. Many researchers focused on developing new metric spaces and several contractions [4,5,6,7,8,9,10]. There is a large body of work that contributes to the development of this theory. One well known generalization of metric spaces is the b-metric spaces introduced in 1989 by Bakhtin [11] and formally defined later by Czerwik [12] by presenting a new fixed-point theorem in this space.

We recall the definition of b-metric spaces.

Definition 1

([11]). Let X be a nonempty set and $s\ge 1$ be a real number. The function $d:X\times X\to [0,\infty )$ is a b-metric on X if

• $d(x_1,x_2)=0$ ⟺ $x_1=x_2$,
• $d(x_1,x_2)=d(x_2,x_1)$,
• $d(x_1,x_2)\le s[d(x_1,x_3)+d(x_3,x_2)]$,

for all $x_1,x_2,x_3\in X$. The pair $(X,d)$ is said to be a b-metric space.

The concept of the b-metric space has inspired many researchers to investigate fixed-point theorems under different hypotheses [13,14,15,16]. Also, several generalizations of this metric space have been developed [17,18,19,20,21,22]. In 2017, Kamran et al. [23] generalized the concept of the b-metric space by replacing on the triangle inequality the constant s by a function $s(x_1,x_2)$, then they obtained an extended b-metric space defined as follows.

Definition 2

([23]). Let X be a nonempty set and $s:X\times X\to [1,\infty )$. An extended b-metric is a function $d:X\times X\to [0,\infty )$ such that for all $x_1,x_2,x_3\in X$,

1. 

$d(x_1,x_2)=0$ ⟺ $x_1=x_2$,

2. 

$d(x_1,x_2)=d(x_2,x_1)$,

3. 

$d(x_1,x_2)\le s(x_1,x_2)[d(x_1,x_3)+d(x_3,x_2)]$.

In 2018, Mlaiki et al. [24] presented a new metric space which is said to be a controlled metric space that is a generalization of extended b-metric spaces. The introduced metric is distinguished by the triangular inequality that has the form

$$d(x_1,x_2)\le \alpha (x_1,x_3)d(x_1,x_3)+\alpha (x_3,x_2)d(x_3,x_2),$$

for all $x_1,x_2,x_3\in X$. Notice that every extended b-metric space is a controlled metric space but the converse is not true; see [24].

In this paper, we discuss the controlled partial metric type space, which is an extension of the controlled metric type space. We investigate the existence and uniqueness of the fixed-point for extensions of Kannan contractions. Furthermore, we establish a new fixed-point result in this space endowed with a graph. We study the existence and uniqueness of fixed-points for graphic $G_{\varphi }$-contraction.

First, we remind the reader of the definition of a controlled metric space.

Definition 3

([24]). Let X be a nonempty set and $\alpha :X\times X\to [1,\infty )$ be a mapping. The function $\xi :X\times X\to [0,\infty )$ is called a controlled metric type if

(d1) 

$\xi (x_1,x_2)=0$ ⟺ $x_1=x_2$,

(d2) 

$\xi (x_1,x_2)=\xi (x_2,x_1)$,

(d3) 

$\xi (x_1,x_2)\le \alpha (x_1,x_3)\xi (x_1,x_3)+\alpha (x_3,x_2)\xi (x_3,x_2)$,

for all $x_1,x_2,x_3\in X$. The pair $(X,\xi )$ is said to be a controlled metric space.

Now, we introduce the definition of the controlled partial metric type space.

Definition 4.

Let X be a nonempty set and $\alpha :X\times X\to [1,\infty )$ be a mapping. The function $\xi :X\times X\to [0,\infty )$ is called a controlled partial metric type if

(p1) 

$x_1=x_2$ if and only if $\xi (x_1,x_2)=\xi (x_1,x_1)=\xi (x_2,x_2)$,

(p2) 

$\xi (x_1,x_2)=\xi (x_2,x_1)$,

(p3) 

$\xi (x_1,x_1)\le \xi (x_1,x_2)$,

(p4) 

$\xi (x_1,x_2)\le \alpha (x_1,x_3)\xi (x_1,x_3)+\alpha (x_3,x_2)\xi (x_3,x_2)$,

for all $x_1,x_2,x_3\in X$. The pair $(X,\xi )$ is called a controlled partial metric type space.

Note that the controlled partial metric space is more extensive than the controlled metric space since a controlled partial metric space is not necessarily a controlled metric space. The following example illustrates this case.

Example 1.

Let $X=\{1,2,\cdots \}$. Take $\xi :X\times X\to [0,\infty )$ as

$$\xi (a,a)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{a^2}},\hfill & \mathit{if} a \mathit{is} \mathit{even},\hfill \\ 0,\hfill & \mathit{if} a \mathit{is} \mathit{odd}.\hfill \end{array}\right.$$

$$andif a\ne b,\xi (a,b)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{a}},\hfill & \mathit{if} a \mathit{is} \mathit{even} \mathit{and} b\mathit{is} \mathit{odd},\hfill \\ {\displaystyle \frac{1}{b}},\hfill & \mathit{if} a \mathit{is} \mathit{odd} \mathit{and} b \mathit{is} \mathit{even},\hfill \\ 1,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Consider $\alpha :X\times X\to [1,\infty )$ as

$$\alpha (a,b)=\left\{\begin{array}{cc}a,\hfill & \mathit{if} a \mathit{is} \mathit{even} \mathit{and} b \mathit{is} \mathit{odd},\hfill \\ b,\hfill & \mathit{if} a \mathit{is} \mathit{odd} \mathit{and} b \mathit{is} \mathit{even},\hfill \\ 1,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

It is easy to verify that ($p_1$) and ($p_2$) are true. Let’s prove ($p_3$) that is $\xi (a,a)\le \xi (a,b)$ for all $a\ne b$.

Let $a,b\in X$, $a\ne b$.

Case 1:

If a is even then $\xi (a,a)={\displaystyle \frac{1}{a^2}}$, $\xi (a,b)={\displaystyle \frac{1}{a}}$ or 1 and in both cases we have $\xi (a,a)\le \xi (a,b)$.

Case 2:

If a is odd then $\xi (a,a)=0$, it is clear that $\xi (a,a)\le \xi (a,b)$ for all $b\in X$.

We will prove the property $\left(p_4\right)$.

Case 1:

If $c=a$ or $c=b$, ($p_4$) is satisfied.

Case 1:

If $c\ne a$ and $c\ne b$, ($p_4$) holds when $a=b$. In the following, suppose that $a\ne b$. Then, we have $a\ne b\ne c$. It is easy to verify that ($p_4$) holds in all following possible subcases:

Subcase 1:

$a,b,c$ are odd.

Subcase 2:

$a,b$ are odd and c is even;

Subcase 3:

$a,b,c$ are even;

Subcase 4:

$a,c$ are even and b is odd;

Subcase 5:

$a,c$ are odd and b is even;

Subcase 6:

$a,b$ are even and c is odd;

Subcase 7:

a is even and $b,c$ are odd;

Subcase 8:

$a,c$ are even and b is odd;

Therefore, ξ is a controlled partial metric type but ξ is not a controlled metric type since $\xi (a,a)$ is not equal to zero all the time.

We define Cauchy and convergent sequences in controlled partial metric type spaces as follows:

Definition 5.

Let $(X,\xi )$ be a controlled partial metric type space and ${\left\{x_n\right\}}_{n\ge 0}$ be a sequence in X.

1. 

We say that the sequence $\left\{x_n\right\}$ converges to some x in $X,$ if ${\displaystyle \underset{n\to \infty }{lim}\xi (x_n,x)=\xi (x,x)}$. In this case, we write ${\displaystyle \underset{n\to \infty }{lim}{x}_n=x.}$

2. 

We say that the sequence $\left\{x_n\right\}$ is Cauchy, if ${\displaystyle \underset{n,m\to \infty }{lim}\xi (x_n,x_m)}$ exists and is finite.

3. 

The controlled partial metric type space $(X,\xi )$ is called complete if every Cauchy sequence $\left\{x_n\right\}$ in X converges to a point $x\in X$ that is ${\displaystyle \xi (x,x)=\underset{n,m\to \infty }{lim}\xi (x_n,x_m)}$.

Definition 6.

Let $(X,\xi )$ be a controlled partial metric type space. Let $x\in X$ and $\epsilon >0$.

(i) 

The open ball $B_p(x,\epsilon )$ is

$$B_p(x,\epsilon )=\{y\in X,\xi (x,y)<\xi (x,x)+\epsilon \}.$$

(ii) 

The mapping $T:X\to X$ is said to be continuous at $x\in X$ if for all $\epsilon >0$, there exists $\delta >0$ such that $T\left(B_p(x,\delta )\right)\subseteq B_p(Tx,\epsilon )$.

Obviously, if T is continuous at x in the controlled partial metric type space $(X,\xi )$, then $x_n\to x$ implies that $T{x}_n\to Tx$ as $n\to \infty$.

2. Fixed-Point Results in Controlled Partial Metric Spaces

Theorem 1.

Let $(X,\xi )$ be a complete controlled partial metric type space. Let $f:X\to X$ be a continuous mapping such that

$$\xi (fx,fy)\le a\left[\xi \right(x,fx)+\xi (y,fy\left)\right],$$

(1)

for all $x,y\in X$, where $a\in (0,\frac{1}{2})$. For $x_0\in X$, take $x_n=f^n{x}_0$. Suppose that

$$\underset{m\ge 1}{sup}\underset{i\to \infty }{lim}\alpha (x_i,x_{i+1})\alpha (x_i,x_m)<\frac{1-a}{a}.$$

(2)

Furthermore, assume that for every $x\in X$,

$$\underset{n\to \infty }{lim}\alpha (x_n,x)\mathit{and}\underset{n\to \infty }{lim}\alpha (x,x_n)\mathit{exist}\mathit{and}\mathit{are}\mathit{finite}.$$

(3)

Then the sequence $\left\{x_n\right\}$ converges to some $u\in X$.

Moreover if α satisfies the following assumption,

$$\underset{n\to \infty }{lim}{\displaystyle \frac{\alpha (u,x_{n+1})}{1-a\alpha (x_{n+1},fu)}}\le 0,$$

(4)

then, f has a unique fixed-point.

Proof. 

Consider $\{x_n=f^n{x}_0\}$. Let $x_1\in X$ be arbitrary, and let $x_2=f{x}_1$ and $x_3=f{x}_2$ be chosen. By using (1), we get

$$\begin{array}{cc}\xi (x_2,x_3)\hfill & =\xi (f{x}_1,f{x}_2)\hfill \\ \hfill & \le a[\xi (x_1,f{x}_1)+\xi (x_2,f{x}_2)]\hfill \\ \hfill & =a[\xi (x_1,x_2)+\xi (x_2,x_3)].\hfill \end{array}$$

Then

$$\xi (x_2,x_3)\le {\displaystyle \frac{a}{1-a}}\xi (x_1,x_2) \mathrm{where} {\displaystyle \frac{a}{1-a}}=A\in [0,1).$$

(5)

By repeating the procedure of (5), we have

$$\xi (x_n,x_{n+1})\le A^{n-1}\xi (x_1,x_2).$$

(6)

We prove that $\left\{x_n\right\}$ is a Cauchy sequence. For all natural numbers with $n<m$, we have

$$\begin{array}{cc}\xi (x_n,x_m)\hfill & \le \alpha (x_n,x_{n+1})\xi (x_n,x_{n+1})+\alpha (x_{n+1},x_m)\xi (x_{n+1},x_m)\hfill \\ \hfill & \le \alpha (x_n,x_{n+1})\xi (x_n,x_{n+1})+\alpha (x_{n+1},x_m)\alpha (x_{n+1},x_{n+2})\xi (x_{n+1},x_{n+2})\hfill \\ \hfill & +\alpha (x_{n+1},x_m)\alpha (x_{n+2},x_m)\xi (x_{n+2},x_m)\hfill \\ \hfill & \le \alpha (x_n,x_{n+1})\xi (x_n,x_{n+1})+\alpha (x_{n+1},x_m)\alpha (x_{n+1},x_{n+2})\xi (x_{n+1},x_{n+2})\hfill \\ \hfill & +\alpha (x_{n+1},x_m)\alpha (x_{n+2},x_m)\alpha (x_{n+2},x_{n+3})\xi (x_{n+2},x_{n+3})\hfill \\ \hfill & +\alpha (x_{n+1},x_m)\alpha (x_{n+2},x_m)\alpha (x_{n+3},x_m)\xi (x_{n+3},x_m)\hfill \\ \hfill & \le \cdots \hfill \\ \hfill & \le \alpha (x_n,x_{n+1})\xi (x_n,x_{n+1})+\sum _{i=n+1}^{m-2}\left(\prod _{j=n+1}^i\alpha (x_j,x_m)\right)\alpha (x_i,x_{i+1})\xi (x_i,x_{i+1})\hfill \\ \hfill & +\prod _{k=n+1}^{m-1}\alpha (x_k,x_m)\xi (x_{m-1},x_m)\hfill \\ \hfill & \le \alpha (x_n,x_{n+1})A^n\xi (x_0,x_1)+\sum _{i=n+1}^{m-2}\left(\prod _{j=n+1}^i\alpha (x_j,x_m)\right)\alpha (x_i,x_{i+1})A^i\xi (x_0,x_1)\hfill \\ \hfill & +\prod _{i=n+1}^{m-1}\alpha (x_i,x_m)A^{m-1}\xi (x_0,x_1)\hfill \\ \hfill & \le \alpha (x_n,x_{n+1})A^n\xi (x_0,x_1)+\sum _{i=n+1}^{m-2}\left(\prod _{j=n+1}^i\alpha (x_j,x_m)\right)\alpha (x_i,x_{i+1})A^i\xi (x_0,x_1)\hfill \\ \hfill & +\left(\prod _{i=n+1}^{m-1}\alpha (x_i,x_m)\right)A^{m-1}\alpha (x_{m-1},x_m)\xi (x_0,x_1)\hfill \\ \hfill & =\alpha (x_n,x_{n+1})A^n\xi (x_0,x_1)+\sum _{i=n+1}^{m-1}\left(\prod _{j=n+1}^i\alpha (x_j,x_m)\right)\alpha (x_i,x_{i+1})A^i\xi (x_0,x_1)\hfill \\ \hfill & \le \alpha (x_n,x_{n+1})A^n\xi (x_0,x_1)+\sum _{i=n+1}^{m-1}\left(\prod _{j=0}^i\alpha (x_j,x_m)\right)\alpha (x_i,x_{i+1})A^i\xi (x_0,x_1).\hfill \end{array}$$

Above, we make use of that $\alpha (x,y)\ge 1$. Let

$$S_p=\sum _{i=0}^p\left(\prod _{j=0}^i\alpha (x_j,x_m)\right)\alpha (x_i,x_{i+1})A^i.$$

Then, we obtain

$$\xi (x_n,x_m)\le \xi (x_0,x_1)\left[A^n\alpha (x_n,x_{n+1})+(S_{m-1}-S_n)\right].$$

(7)

From condition (2), we can assert that ${lim}_{n\to \infty }{S}_n$ exists and that the sequence $\left\{S_n\right\}$ is Cauchy. Therefore, if we take the limit in the inequality (7) as $n,m\to \infty ,$ we conclude that

$$\underset{n,m\to \infty }{lim}\xi (x_n,x_m)=0,$$

(8)

which implies that $\left\{x_n\right\}$ is a Cauchy sequence in the complete controlled partial metric type space $(X,\xi )$, so $\left\{x_n\right\}$ converges to some $u\in X.$ Next, we prove that u is a fixed-point of T. We need to verify that $\xi (u,fu)=\xi (u,u)=\xi (fu,fu)$.

From $\left(p3\right)$ we have

$$\begin{array}{ccc}\xi (u,u)\hfill & \le & \xi (u,fu)\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\xi (fu,fu)\hfill & \le & \xi (u,fu),\hfill \end{array}$$

(10)

So it is sufficient to prove that $\xi (u,u)\ge \xi (u,fu)$ and $\xi (fu,fu)\ge \xi (u,fu)$ to get $fu=u$. The triangular inequality yields that

$$\begin{array}{ccc}\xi (u,fu)\hfill & \le & \alpha (u,x_{n+1})\xi (u,x_{n+1})+\alpha (x_{n+1},fu)\xi (x_{n+1},fu)\hfill \\ & \le & \alpha (u,x_{n+1})\xi (u,x_{n+1})+\alpha (x_{n+1},fu)\xi (f{x}_n,fu)\hfill \\ & \le & \alpha (u,x_{n+1})\xi (u,x_{n+1})+\alpha (x_{n+1},fu)a\xi (x_n,f{x}_n)+\alpha (x_{n+1},fu)a\xi (u,fu).\hfill \end{array}$$

(11)

By taking the limit as $n⟶\infty$ in (11) we obtain

$$\xi (u,fu)\le \underset{n\to \infty }{lim}{\displaystyle \frac{\alpha (u,x_{n+1})}{1-a\alpha (x_{n+1},fu)}}\xi (u,u),$$

then by using the condition (4) we get

$$\xi (u,fu)\le \xi (u,u).$$

(12)

On the other hand,

$$\begin{array}{ccc}\xi (u,fu)\hfill & \le & \alpha (u,fu)\xi (u,fu)+\alpha (fu,fu)\xi (fu,fu)\hfill \\ & \le & {\displaystyle \frac{\alpha (fu,fu)}{1-\alpha (u,fu)}}\xi (fu,fu)\hfill \\ & \le & \xi (fu,fu).\hfill \end{array}$$

(13)

Finally, from (9), (10), (12) and (13) we obtain $fu=u$ as desired.

Assume that T has two fixed-points, say u and $v.$ Then,

$$\xi (u,v)=\xi (fu,fv)\le a\left[\xi \right(u,fu)+\xi (v,fv\left)\right]=a\left[\xi \right(u,u)+\xi (v,v\left)\right].$$

Furthermore, we have $\xi (u,u)=\xi (fu,fu)\le 2a\xi (u,fu)=2a\xi (u,u)$. Note that $a>1$, then $\xi (u,u)=0$. Similarly, $\xi (v,v)=\xi (fv,fv)\le 2a\xi (v,fv)=2a\xi (v,v)$ then $\xi (v,v)=0$. Since $\xi (u,u)=\xi (v,v)=0$ then $\xi (u,v)=0$. Therefore, $\xi (u,u)=\xi (v,v)=\xi (u,v)$ which gives $u=v.$ Hence, T has a unique fixed-point. □

Definition 7.

Let $(X,\xi )$ be a complete controlled partial metric type space. We say that a mapping $f:X\to X$ is sequentially convergent if the following assertion is satisfied: For every sequence $\left\{x_n\right\}$, if $\left\{f{x}_n\right\}$ is convergent then $\left\{x_n\right\}$ also converges.

f is said to be subsequentially convergent if the following assertion is correct: For every sequence $\left\{x_n\right\}$, if $\left\{f{x}_n\right\}$ is convergent then $\left\{x_n\right\}$ has a convergent subsequence.

Theorem 2.

Let $(X,\xi )$ be a complete controlled partial metric type space. Let $f,g:X\to X$ be mappings such that f is continuous, one-to-one, subsequentially convergent and

$$\xi (fgx,fgy)\le a\left[\xi \right(fx,fgx)+\xi (fy,fgy\left)\right]\forall x,y\in X,$$

(14)

where $a\in (0,\frac{1}{2})$. For $x_0\in X$, take $x_n=g^n{x}_0$. Suppose that

$$\underset{m\ge 1}{sup}\underset{i\to \infty }{lim}\alpha (f{x}_i,f{x}_{i+1})\alpha (f{x}_i,f{x}_m)<\frac{1-a}{a}.$$

(15)

Moreover, assume that, for every $x\in X$,

$$\underset{n\to \infty }{lim}\alpha (x_n,x)\mathit{and}\underset{n\to \infty }{lim}\alpha (x,x_n)\mathit{exist}\mathit{and}\mathit{are}\mathit{finite}.$$

(16)

Then, g has a unique fixed-point.

Proof. 

Let $x_0$ be an arbitrary point in X and consider the sequence $\left\{x_n\right\}$ as defined in the hypothesis of the theorem. From (14) we obtain

$$\begin{array}{ccc}\xi (f{x}_n,f{x}_{n+1})\hfill & =& \xi (fg{x}_{n-1},fg{x}_n)\hfill \\ & \le & a[\xi (f{x}_{n-1},fg{x}_{n-1})+\xi (f{x}_n,fg{x}_n)]\hfill \\ & =& a[\xi (f{x}_{n-1},fg{x}_{n-1})+\xi (f{x}_n,f{x}_{n+1})]\hfill \\ & \le & {\displaystyle \frac{a}{1-a}}\xi (f{x}_{n-1},fg{x}_{n-1}).\hfill \end{array}$$

By induction, we get

$$\xi (f{x}_n,f{x}_{n+1})\le {\left({\displaystyle \frac{a}{1-a}}\right)}^n\xi (f{x}_0,fg{x}_0)=C^n\xi (f{x}_0,f{x}_1),$$

(17)

where $C={\displaystyle \frac{a}{1-a}}$.

We prove that the sequence $\left\{f{x}_n\right\}$ is Cauchy. Similarly to Theorem 1, for every $m,n\in \mathbb{N}$ such that $m>n$ we have from the triangular inequality and (17)

$$\begin{array}{ccc}\xi (f{x}_n,f{x}_m)\hfill & \le & \alpha (f{x}_n,f{x}_{n+1})\xi (f{x}_n,f{x}_{n+1})+\alpha (f{x}_{n+1},f{x}_m)\xi (f{x}_{n+1},f{x}_m)\hfill \\ & \le & \alpha (f{x}_n,f{x}_{n+1})\xi (f{x}_n,f{x}_{n+1})+\alpha (f{x}_{n+1},f{x}_m)\alpha (f{x}_{n+1},f{x}_{n+2})\xi (f{x}_{n+1},f{x}_{n+2})\hfill \\ & +& \alpha (f{x}_{n+1},f{x}_m)\alpha (f{x}_{n+2},f{x}_m)\xi (f{x}_{n+2},f{x}_m).\hfill \end{array}$$

$$\begin{array}{ccc}\xi (f{x}_n,f{x}_m)\hfill & \le & \alpha (f{x}_n,f{x}_{n+1})\xi (f{x}_n,f{x}_{n+1})+\sum _{i=n+1}^{m-2}\left(\prod _{j=n+1}^i\alpha (f{x}_j,f{x}_m)\right)\alpha (f{x}_i,f{x}_{i+1})\hfill \\ & \times & \xi (f{x}_i,f{x}_{i+1})+\prod _{k=n+1}^{m-1}\alpha (f{x}_k,f{x}_m)\xi (f{x}_{m-1},f{x}_m)\hfill \\ & \le & \alpha (f{x}_n,f{x}_{n+1})C^n\xi (f{x}_0,f{x}_1)+\sum _{i=n+1}^{m-2}\left(\prod _{j=n+1}^i\alpha (f{x}_j,f{x}_m)\right)\alpha (f{x}_i,f{x}_{i+1})\hfill \\ & \times & C^i\xi (f{x}_0,f{x}_1)+\prod _{k=n+1}^{m-1}\alpha (f{x}_k,f{x}_m)C^{m-1}\xi (f{x}_0,f{x}_1)\hfill \\ & \le & \alpha (f{x}_n,f{x}_{n+1})C^n\xi (f{x}_0,f{x}_1)+\sum _{i=n+1}^{m-2}\left(\prod _{j=n+1}^i\alpha (f{x}_j,f{x}_m)\right)\alpha (f{x}_i,f{x}_{i+1})C^i\hfill \\ & \times & \xi (f{x}_0,f{x}_1)+\prod _{i=n+1}^{m-1}\alpha (f{x}_i,f{x}_m)C^{m-1}\alpha (f{x}_{m-1},f{x}_m)C^{m-1}\xi (f{x}_0,f{x}_1)\hfill \\ & =& \alpha (f{x}_n,f{x}_{n+1})C^n\xi (f{x}_0,f{x}_1)+\sum _{i=n+1}^{m-1}\left(\prod _{j=n+1}^i\alpha (f{x}_j,f{x}_m)\right)\alpha (f{x}_i,f{x}_{i+1})\times \hfill \\ & \times & C^i\xi (f{x}_0,f{x}_1)\hfill \\ & \le & \alpha (f{x}_n,f{x}_{n+1})C^n\xi (f{x}_0,f{x}_1)+\sum _{i=n+1}^{m-1}\left(\prod _{j=0}^i\alpha (f{x}_j,f{x}_m)\right)\alpha (f{x}_i,f{x}_{i+1})\hfill \\ & \times & C^i\xi (f{x}_0,f{x}_1).\hfill \end{array}$$

Then,

$$\xi (f{x}_n,f{x}_m)\le \xi (f{x}_0,f{x}_1)[C^n\alpha (f{x}_n,f{x}_{n+1})+S_{m-1}-S_n],$$

(18)

where ${\displaystyle S_p=\sum _{i=0}^p\left(\prod _{j=0}^i\alpha (f{x}_j,f{x}_m)\right)\alpha (f{x}_i,f{x}_{i+1})C^i}$.

Then from condition (15) we obtain that the sequence $\left\{S_n\right\}$ has a finite limit. Subsequently the sequence $\left\{S_n\right\}$ is Cauchy. Thereafter, by taking the limit in the inequality (18) as $n,m⟶\infty$, we deduce that

$${\displaystyle \underset{n,m\to \infty }{lim}\xi (f{x}_n,f{x}_m)=0.}$$

(19)

Finally, $\left\{f{x}_n\right\}$ is a Cauchy sequence and from the completeness of the space X, there exists $v\in X$ such that

$${\displaystyle \underset{n\to \infty }{lim}f{x}_n=v.}$$

(20)

Since f is a subsequentially convergent, the sequence $\left\{x_n\right\}$ has a convergent subsequence denoted by ${\left\{x_{n_k}\right\}}_{k=1}^{\infty }$ such that

$${\displaystyle \underset{k\to \infty }{lim}{x}_{n_k}=u,}$$

(21)

which, using the continuity of f, gives

$${\displaystyle \underset{k\to \infty }{lim}f{x}_{n_k}=fu.}$$

(22)

From (20) and (22) we conclude that $fu=v$. Then by using the triangular inequality we get

$$\begin{array}{ccc}\xi (fgu,fu)\hfill & \le & \alpha (fgu,f{g}^{n_k}{x}_0)\xi (fgu,f{g}^{n_k}{x}_0)+\alpha (f{g}^{n_k}{x}_0,fu)\xi (f{g}^{n_k}{x}_0,fu)\hfill \\ & \le & \alpha (fgu,f{g}^{n_k}{x}_0)a[\xi (fu,fgu)+\xi (f{g}^{n_k-1}{x}_0,f{g}^{n_k}{x}_0)]+\alpha (f{g}^{n_k}{x}_0,fu)\hfill \\ & \times & \xi (f{g}^{n_k}{x}_0,fu)\hfill \\ & \le & a\alpha (fgu,f{g}^{n_k}{x}_0)\xi (fu,fgu)+a\alpha (fgu,f{g}^{n_k}{x}_0)\xi (f{g}^{n_k-1}{x}_0,f{g}^{n_k}{x}_0)\hfill \\ & +& \alpha (f{g}^{n_k}{x}_0,fu)\xi (f{g}^{n_k}{x}_0,fu)\hfill \\ & \le & {\displaystyle \frac{a}{1-a\alpha (fgu,f{g}^{n_k}{x}_0)}}\alpha (fgu,f{g}^{n_k}{x}_0)\xi (f{g}^{n_k-1}{x}_0,f{g}^{n_k}{x}_0)\hfill \\ & +& {\displaystyle \frac{1}{1-a\alpha (fgu,f{g}^{n_k}{x}_0)}}\alpha (f{g}^{n_k}{x}_0,fu)\xi (f{g}^{n_k}{x}_0,fu)\hfill \\ & \le & {\displaystyle \frac{a}{1-a\alpha (fgu,f{x}_{n_k})}}\alpha (fgu,f{x}_{n_k})\xi (f{x}_{n_{k-1}},f{x}_{n_k})\hfill \\ & +& {\displaystyle \frac{1}{1-a\alpha (fgu,f{x}_{n_k})}}\alpha (f{x}_{n_k},fu)\xi (f{x}_{n_k},fu)\hfill \\ & \le & {\displaystyle \frac{a}{1-a\alpha (fgu,f{x}_{n_k})}}\alpha (fgu,f{x}_{n_k}){\left({\displaystyle \frac{a}{1-a}}\right)}^{n_k-1}\xi (f{x}_0,f{x}_1)\hfill \\ & +& {\displaystyle \frac{\alpha (f{x}_{n_k},fu)}{1-a\alpha (fgu,f{x}_{n_k})}}\xi (f{x}_{n_k},fu).\hfill \end{array}$$

(23)

If $k⟶\infty$, then we obtain

$$\xi (fgu,fu)\le constant\times \xi (fu,fu).$$

(24)

We prove that $\xi (fu,fu)=0$.

From the triangular inequality we have $\xi (fu,fu)\le \alpha (fu,u)\xi (fu,u)+\alpha (u,fu)\xi (u,fu)$. We suppose that w.l.o.g $\alpha (fu,u)\le \alpha (u,fu)$. Then

$$\xi (fu,fu)\le 2\alpha (u,fu)\xi (u,fu).$$

(25)

On the other hand,

$$\begin{array}{ccc}\xi (u,fu)\hfill & \le & \alpha (u,u)\xi (u,u)+\alpha (u,fu)\xi (u,fu)\hfill \\ & \le & {\displaystyle \frac{\alpha (u,u)}{1-\alpha (u,fu)}}\xi (u,u).\hfill \end{array}$$

Note that if $\alpha :X\times X\to [1,\infty )$, then $1-\alpha (u,fu)\le 0$ and we get $\xi (u,fu)=0$. Thus from (25) we obtain

$$\xi (fu,fu)=0.$$

(26)

From (24) and (26) we deduce that $\xi (fgu,fu)=0$. Since $\xi$ is a controlled partial metric, to prove that $fgu=fu$ we need to check the property $\left(p_1\right)$ that is $\xi (fgu,fu)=\xi (fu,fu)=\xi (fgu,fgu)$. From (26) we have $\xi (fgu,fu)=\xi (fu,fu)=0$. It is easy to see that $\xi (fgu,fgu)=0$. Indeed, $\xi (fgu,fgu)\le a\left[\xi \right(fu,fgu)+\xi (fu,fgu\left)\right]=2a\xi (fu,fgu)=0$. Therefore $fgu=gu$. Since f is one-to-one, $gu=u$. Therefore u is a fixed-point of g.

Let $u,v$ two fixed-points of g then $gu=u$ and $gv=v.$ From $\left(p3\right)$ of Definition 4 we have

$$\begin{array}{ccc}\xi (fv,fv)\hfill & \le & \xi (fu,fv),\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\xi (fu,fu)\hfill & \le & \xi (fu,fv).\hfill \end{array}$$

(28)

On the other hand, using the triangular inequality we get

$$\begin{array}{ccc}\xi (fu,fv)=\xi (u,v)\hfill & \le & \alpha (u,u)\xi (u,u)+\alpha (u,v)\xi (u,v)\hfill \\ & \le & {\displaystyle \frac{\alpha (u,u)}{1-\alpha (u,v)}}\xi (u,u).\hfill \end{array}$$

Since $\alpha \ge 1$, $\xi (fu,fv)=0$. Therefore, from (27) and (28) we obtain that $\xi (fu,fv)=\xi (fu,fu)=\xi (fv,fv)=0$. Using the property $\left(p_1\right)$ of the controlled partial metric we obtain $fu=fv$. By noting that f is one-to-one, we conclude that $u=v$.

Finally, by replacing $\left\{n_k\right\}$ with $\left\{n\right\}$ we conclude that $\left\{x_n\right\}$ converges to u as $n⟶\infty$ and thus the sequence $\left\{x_n\right\}$ converges to the unique fixed-point of g. □

3. Fixed-Point Results for Graphic Contractions in Controlled Partial Metric Spaces

In this section we establish some iterative scheme results for graphic $G_{\varphi }$-contractive maps on the graph. The idea was inspired from the work of Jachymski [25] who provided strong results on combining fixed-point theory and graph theory. Afterwards, many researchers have developed this approach for different metric spaces with several contractions [26,27,28,29,30]. For the reader’s convenience, we present some basic concepts and terminology of graph theory.

Let $(X,\xi )$ be a complete controlled partial metric type space. We denote by $\Delta$ the diagonal of the Cartesian product $X\times X$. A graph G is defined by the pair $(V,E)$ where V is a set of vertices coinciding with X and E is the set of its edges such that $\Delta \subset E$. Moreover, throughout this paper, we assume that the graph G has no parallel edges, that is, we do not allow it to get two or more edges that are incident to the same two vertices.

Definition 8

([25]). Let a and b be two vertices in a graph G. A path in G from a to b of length k ($k\in \mathbb{N}\cup \left\{0\right\}$) is a sequence ${\left(t_i\right)}_{i=0}^k$ of $k+1$ distinct vertices such that $t_0=a$, $t_n=b$ and $(t_i,t_{i+1})\in E\left(G\right)$ for $i=1,2,\dots ,k$.

Let $(X,\xi )$ be a complete controlled partial metric type space. The graph G may be converted to a weighted graph by assigning to each edge the distance given by the controlled partial metric between its vertices.

Notation 1.

We denote by $X^f=\{x\in X/(x,fx)\in E\left(G\right) or (fx,x)\in E\left(G\right)\}$.

We define the notion of graphic $G_{\varphi }$-contraction.

Definition 9.

Let $(X,\xi )$ be a complete controlled partial metric type space endowed with a graph G. The mapping $f:X\to X$ is called as a $G_{\varphi }$-contraction if the following conditions are satisfied:

• $$for all x,y\in X,(x,y)\in E\left(G\right)⟹(fx,fy)\in E\left(G\right),$$

  (29)
• there exists a function $\varphi :{\mathbb{R}}^{+}⟶{\mathbb{R}}^{+}$ such that

  $$\xi (fx,f^{2}x)\le \varphi \left(\xi (x,fx)\right)\forall x\in X^f,$$

  (30)

  where ϕ is a nondecreasing function and ${\left\{{\varphi }^n\left(t\right)\right\}}_{n\in \mathbb{N}}$ converges to 0 for all $t>0$.

Definition 10.

Let $f:X⟶X$ be a mapping. f is said to be orbitally G-continuous if for all $a,b\in X$ and any positive sequence ${\left\{s_n\right\}}_{n\in \mathbb{N}}$,

$$f^{s_n}a⟶b,(f^{s_n}a,f^{s_{n+1}}a)\in E\left(G\right)⟹f\left(f^{s_n}a\right)⟶fb as n\to \infty .$$

Lemma 1.

Let $(X,\xi )$ be a complete controlled partial metric type space endowed with a graph G. Let $f:X\to X$ be a $G_{\varphi }$-contraction. If $x\in X^f$ then there exists $r\left(x\right)\ge 0$ such that

$$\xi (f^{n}x,f^{n+1}x)\le {\varphi }^n\left(r\left(x\right)\right)\forall n\in \mathbb{N},$$

(31)

where $r\left(x\right)=\xi (x,fx)$.

Proof. 

Let $x\in X^f$ then $(x,fx)\in E\left(G\right)$ or $(fx,x)\in E\left(G\right)$. Let us suppose that w.l.o.g $(x,fx)\in E\left(G\right)$. Then by induction we get

$$(f^n,f^{n+1}x)\in E\left(G\right)\forall n\in \mathbb{N}.$$

(32)

Therefore, we have

$$\begin{array}{ccc}\xi (f^{n}x,f^{n+1}x)\hfill & \le & \varphi \left(\xi (f^{n-1}x,f^{n}x)\right)\hfill \\ & \le & {\varphi }^2\left(\xi (f^{n-2}x,f^{n-1}x)\right)\hfill \\ & \le & ⋮\hfill \\ & \le & {\varphi }^n\left(\xi (x,fx)\right)={\varphi }^n\left(r\left(x\right)\right).\hfill \end{array}$$

□

Theorem 3.

Let $(X,\xi ,G)$ be a complete controlled partial metric type space with a graph G. Let $f:X\to X$ be a $G_{\varphi }$-contraction which is oribitally G-continuous. We assume the following property $\left(P\right)$: for any ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in X, if $x_n⟶x$ and $(x_n,x_{n+1})\in E\left(G\right)$ then there is a subsequence ${\left\{x_{k_n}\right\}}_{n\in \mathbb{N}}$ with $(x_{k_n},x)\in E\left(G\right)$.

Moreover, assume that, for every $x\in X$, we have

$$\underset{n\to \infty }{lim}\alpha (f^{i}x,f^{n}x)(\forall i\ge 1)\mathit{and}\underset{n\to \infty }{lim}\alpha (f^{n}x,f^{n+1}x)\mathit{exist}\mathit{and}\mathit{are}\mathit{finite}.$$

(33)

Then the restriction of $f_{{|\left[x\right]}_{\tilde{G}}}$ to ${\left[x\right]}_{\tilde{G}}$ has a unique fixed-point.

Proof. 

Let $x\in X^f$. Then from Lemma 1 there exists $r\left(x\right)\ge 0$ such that

$$\xi (f^{n}x,f^{n+1}x)\le {\varphi }^n\left(r\left(x\right)\right).$$

We claim that the sequence ${\left(f^{n}x\right)}_{n\in \mathbb{N}}$ converges to some $u\in X$. We have to prove that ${\left\{f^{n}x\right\}}_{n\in \mathbb{N}}$ is a Cauchy sequence. Let $n,m\in \mathbb{N}$, using the triangular inequality and Lemma 1 we obtain

$$\begin{array}{ccc}\xi (f^{n}x,f^{n+m}x)\hfill & \le & \alpha (f^{n}x,f^{n+1}x)\xi (f^{n}x,f^{n+1}x)+\alpha (f^{n+1}x,f^{n+m}x)\xi (f^{n+1}x,f^{n+m}x)\hfill \\ & \le & \alpha (f^{n}x,f^{n+1}x)\xi (f^{n}x,f^{n+1}x)+\alpha (f^{n+1}x,f^{n+m}x)\alpha (f^{n+1}x,f^{n+2}x)\hfill \\ & \times & \xi (f^{n+1}x,f^{n+2}x)\hfill \\ & +& \alpha (f^{n+1}x,f^{n+m}x)\alpha (f^{n+2}x,f^{n+m}x)\xi (f^{n+2}x,f^{n+m}x)\hfill \\ & \le & ⋮\hfill \\ & \le & {\displaystyle \alpha (f^{n}x,f^{n+1}x)\xi (f^{n}x,f^{n+1}x)+\sum _{i=n+1}^{n+m-2}\left(\prod _{j=n+1}^i\alpha (f^{j}x,f^{n+m}x)\right)\alpha (f^{i}x,f^{i+1}x)}\hfill \\ & \times & {\displaystyle \xi (f^{i}x,f^{i+1}x)+\prod _{k=n+1}^{n+m-1}\alpha (f^{k}x,f^{n+m}x)\xi (f^{n+m-1}x,f^{n+m}x)}\hfill \\ & \le & {\displaystyle \alpha (f^{n}x,f^{n+1}x){\varphi }^n\left(r\left(x\right)\right)+\sum _{i=n+1}^{n+m-2}\left(\prod _{j=n+1}^i\alpha (f^{j}x,f^{n+m}x)\right)\alpha (f^{i}x,f^{i+1}x){\varphi }^i\left(r\left(x\right)\right)}\hfill \\ & +& {\displaystyle \prod _{k=n+1}^{n+m-1}\alpha (f^{k}x,f^{n+m}x){\varphi }^{n+m-1}\left(r\left(x\right)\right)\alpha (f^{n+m-1}x,f^{n+m}x)}\hfill \\ & \le & {\displaystyle \alpha (f^{n}x,f^{n+1}x){\varphi }^n\left(r\left(x\right)\right)+\sum _{i=n+1}^{n+m-1}\left(\prod _{j=0}^i\alpha (f^{j}x,f^{n+m}x)\right)\alpha (f^{i}x,f^{i+1}x){\varphi }^i\left(r\left(x\right)\right)}\hfill \\ & \le & {\displaystyle \prod _{j=0}^n\alpha (f^{j}x,f^{n+m}x))\alpha (f^{n}x,f^{n+1}x){\varphi }^n\left(r\left(x\right)\right)}\hfill \\ & +& {\displaystyle \sum _{i=n+1}^{n+m-1}\left(\prod _{j=0}^i\alpha (f^{j}x,f^{n+m}x)\right)\alpha (f^{i}x,f^{i+1}x){\varphi }^i\left(r\left(x\right)\right)}\hfill \\ & =& {\displaystyle \sum _{i=n}^{n+m-1}\left(\prod _{j=0}^i\alpha (f^{j}x,f^{n+m}x)\right)\alpha (f^{i}x,f^{i+1}x){\varphi }^i\left(r\left(x\right)\right)}\hfill \\ & =& {\displaystyle \sum _{i=n}^{n+m-1}{\beta }_i{\varphi }^i\left(r\left(x\right)\right),where{\beta }_i=\left(\prod _{j=0}^i\alpha (f^{j}x,f^{n+m}x)\right)\alpha (f^{i}x,f^{i+1}x)}\hfill \\ & =& {\displaystyle \sum _{i=1}^m{\beta }_i^{n+i-1}{\varphi }^{n+i-1}\left(r\left(x\right)\right).}\hfill \end{array}$$

Using the property of $\varphi$ and (33) we conclude that ${\displaystyle \sum _{i=1}^m{\beta }_i^{n+i-1}{\varphi }^{n+i-1}\left(r\left(x\right)\right)}$ converges to 0 as $n,m⟶\infty$. Therefore the sequence ${\left\{f^{n}x\right\}}_n$ is a Cauchy sequence. From the completeness of the space X, there exists $u\in X$ such that

$$f^{n}x⟶u \mathrm{as} n⟶\infty ,$$

(34)

which proves the claim.

Since $x\in X^f$, $f^{n}x\in X^f$ for every $n\in \mathbb{N}$. As we can assume that $(x,fx)\in E\left(G\right)$, from property $\left(P\right)$ there exists a subsequence ${\left\{f^{k_n}x\right\}}_{n\in \mathbb{N}}$ of ${\left\{f^{n}x\right\}}_{n\in \mathbb{N}}$ such that $(f^{k_n}x,u)\in E\left(G\right)$ for all $n\in \mathbb{N}$. A path in G can be formed by using the points $x,fx,...,f^{k_1},u$ and then $u\in {\left[x\right]}_{\tilde{G}}$. Since f is oribitally G-continuous then

$$f\left(f^{k_n}x\right)⟶fu \mathrm{as} n⟶\infty .$$

(35)

It follows from (34) and (35) that u is a fixed-point of ${f|}_{{\left[x\right]}_{\tilde{G}}}$.

To prove the uniqueness of the fixed-point, we assume that if there exists two fixed-points u and v then $fu=u$ and $fv=v$. From the property ($p3$) of Definition 4 we have

$$\begin{array}{ccc}\xi (u,u)\hfill & \le & \xi (u,v),\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\xi (v,v)\hfill & \le & \xi (u,v).\hfill \end{array}$$

(37)

On the other hand,

$$\begin{array}{ccc}\xi (u,v)\hfill & \le & \alpha (u,u)\xi (u,u)+\alpha (u,v)\xi (u,v)\hfill \\ & \le & {\displaystyle \frac{\alpha (u,u)}{1-\alpha (u,v)}\xi (u,u).}\hfill \end{array}$$

Since $\alpha \ge 1$, then $\xi (u,v)=0$, and from (36) and (37) we get $\xi (u,v)=\xi (u,u)=\xi (v,v)=0$. This completes the proof. □

4. Conclusions and Perspectives

In this work we introduced the concept of controlled partial metric spaces, which is an extension of b-metric spaces. We presented two fixed-point theorems using the generalized Kannan contraction. The obtained results generalize recent fixed-point results in b-metric spaces and controlled metric spaces [24].

In the third section, we have introduced the notion of a graph which represents a very interesting theoretical framework for future work. The proved result is an extension of the work presented in [31]. However, several real problems can be modeled due to the fact that controlled partial metric type spaces generalize most of the knowing metric spaces. For example, in the area of telecommunications, we can build a graph whose nodes represent public or private telephone exchange, terminals or communication centers. 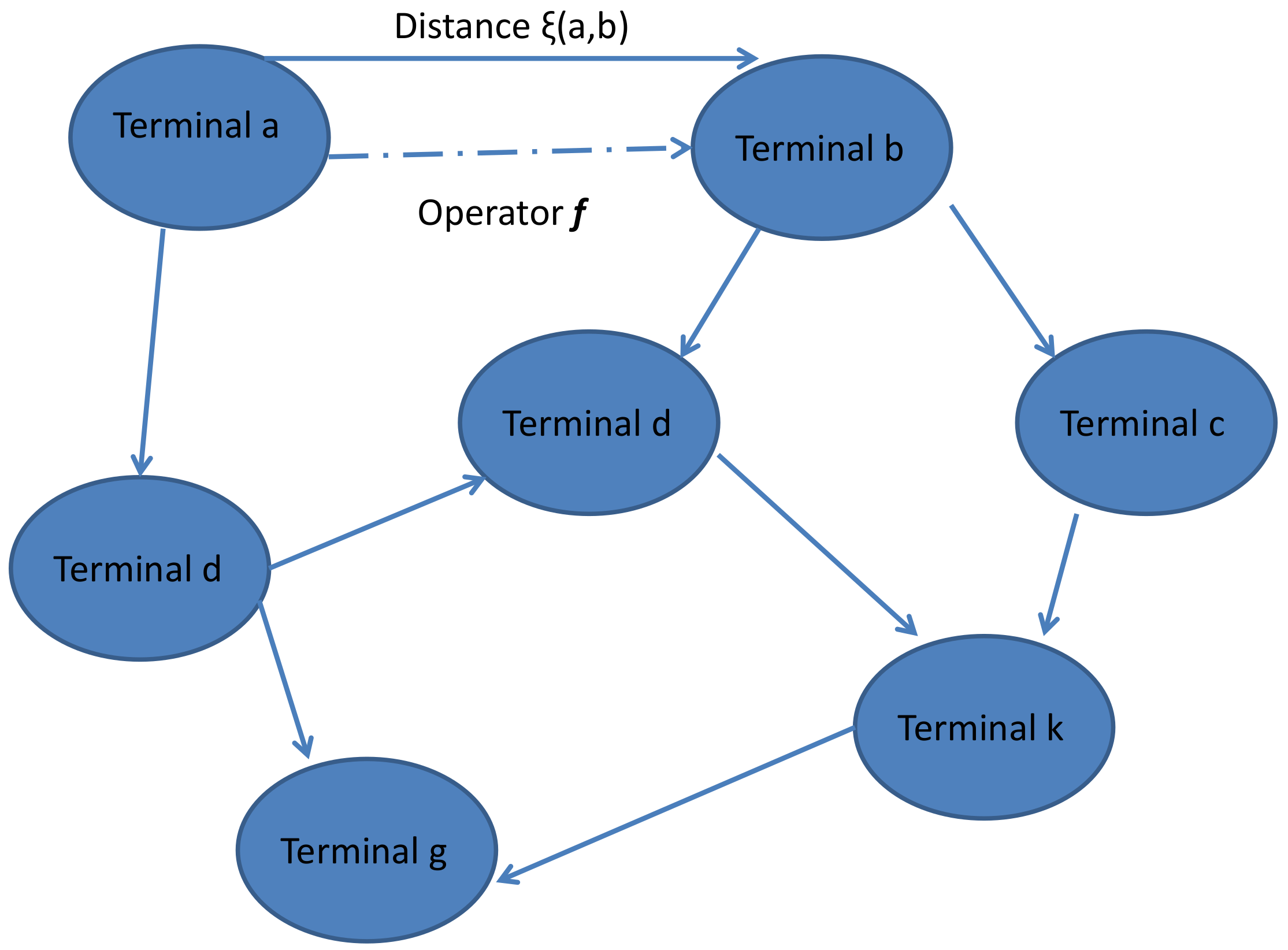In the obtained graph the contraction f can be considered as an operator used by several aspects as the flow rate. The distance between nodes is given by the controlled partial metric. Moreover, the notion of fixed-point is very important, since in a graph it is through it that we can switch the signal to reach the correct destination terminal. Figure 1 describes this application. The blue spheres represent the networks nodes (terminals) and $\xi (a,b)$ represents the distance between node a and node $b.$ Using the mapping operator (the dotted line) f, the source node tries to select a neighbour node.

Subsequently, since the theoretical foundation is ready, future works attempting to adapt this theorem to real problems is highly recommended.