Evaluation of Elite Athletes Training Management Efficiency Based on Multiple Criteria Measure of Conditioning Using Fewer Data

Abstract

Innovative solutions and techniques in the sports industry are commonly used and tested in real conditions. Elite athletes have to achieve their peak performance before the main competition of the year, which is the World Championship, and every fourth year before the Olympic Games, when the main competition of athletes takes place. The present study aims to analyze and evaluate the ability of elite kayakers to achieve the best form at the right times, with the Olympic Games taking the greatest importance. Target values for multiple measures of conditioning are compared to target values set by experts. A weighted least squares metric with weights varied by time period is developed as a measure of fulfillment of the athletes’ conditioning plans. The novelty of the paper is the idea of using linear combination of polynomials and trigonometric functions for approximating the target functions and application of the proposed methodology for the optimization and evaluation of athletic training.

1. Introduction

Sports are a phenomenon of global importance. The investment in professional athletes is a particularly important process. Sporting events promote the development of powerful worldwide industries. A key factor in sports is the ability to develop training schedules to optimize the athletes’ training conditions. The optimization and evaluation of athletic training is the most important problem for sports scientists, coaches, and athletes. Elite athletes are willing to perform more voluminous and high-quality training routines, and this process requires effective management. Elite athletes attain a world-class status in endurance sports after four to seven years of specialized training [1]. Over this period, they usually have 3000–7000 h of effective training and cover distances of 3000–4000 km/yr [2]. Winning medals in international competitions requires not only outstanding abilities and the long-term training of athletes, it is also crucial that they achieve peak performance at the right time.

The Olympic Games is the main competition for the Olympic sports athletes. There are four years of the Olympic training cycle, with its organizational structure and training methodology directed at making the successful start of athletes in the Olympic Games [3]. The elite athletes’ training must be carefully planned for several years in the future and based on individual indicators (training load specification and the athlete’s body adaptation to a particular training load). The process of the elite athletes’ training is complex and difficult to predict because of a number of unknown factors (i.e., accidents, acclimatization, illnesses, psychological changes, the pace of recovery, etc.) [4].

The Olympic training cycle consists of four one-year macro cycles, with the main competition, the World Championship, taking place in each of these cycles. The athletes make strenuous efforts to be in their best form before the World Championship. In the last year of the Olympic cycle, some of the athletes get a chance to participate in the Olympic Games during the World Championship. It means that athletes have to achieve their peak performance twice a year. In this case, the management of training is very complicated, because the athletes need to achieve their peak performance in a short time [5,6].

Monitoring the training load and athletes’ physiological adaptation is essential for optimizing training and minimizing the risk of overtraining, injuries, illnesses, etc. Usually, sports managers and scientists are restricted in publishing the data on the athletes’ condition before competitions. In elite sports, monitoring is extensive, but most of the data remain confidential [7].

Scientists are searching for novel approaches to visualize and analyze the data obtained in the training sessions. One of the most relevant research topics is visualization for motion analysis, which is important for training optimization, technical and tactical improvements, as well as the prevention of injuries [8]. However, not only motion optimization is required for achieving good results. The growing need causes the necessity for making a training process much more technologically advanced, and this is an important field of interest for athletes, coaches, and scientists. Massive amounts of data are generated and used in sports medicine, including preventative care and rehabilitation. Most major professional teams today make data-driven decisions and employ the analytical staff to help prepare training plans, predict athlete risks, and prescribe personalized recovery strategies. Most of the athletes use trackers to measure, accompany, and control the data (e.g., power, velocity, duration, altitude, and heart rate) obtained in training and later perform an individual analysis and online planning [9]. The present study focuses on the visualization of the training process based on the physiological condition of athletes.

The optimization of the athletic training process is an appropriate application of operational research (OR). Prediction management and decision making in athletic training should be based on objective data analysis and parameter estimation [10].

Reviewing the literature related to the application of mathematical models and methods used for solving similar problems has shown that the authors use various approaches. For example, Armstrong, Weidner, and Walker [11] have elaborated on the analysis of variance (ANOVA) and t-test of independent samples for clinical proficiency evaluation in athletic training. A qualitative analysis of the respondents’ comments has also been performed.

Li, Zhu, Chen, and Xue [12] have elaborated on the balanced approach of data envelopment analysis (DEA) to cross-efficiency evaluation. An iterative algorithm for obtaining the final optimal and balanced cross-efficiency score has been developed by the authors.

Four imbalance indicators for measuring the difference between standard distribution and the ideally balanced distribution have been proposed by Karsu and Morton [13]. The interesting phenomenon is the total componentwise proportional deviation because it is an individual-oriented measure, which is the weighted sum of fractional misallocations for each party.

The Delphi method has been used by Reefke and Sundaram [14] to identify a set of key sustainable supply chain management (SSCM) problems and the associated research opportunities. The data components have been synthesized, and the parameters have been estimated according to their relative importance based on the experts’ judgments. New insights into the potential dependencies between the factors and their influence on the success of SSCM have been provided in this work. The development of the schedule for the sporting activities of the Ecuadorian football federation under a set of constraints with the use of integer programming has been proposed by Recalde, Torres, and Vaca [15]. A heuristic three-phase approach has also been adjusted to solve the considered problem. The developed methodology provides more benefits than the empirical method.

Algorithms based on multiple criteria decision making are often used in solving various problems in sports management. Dadelo, Turskis, Zavadskas, and Dadelienė [16] have described a novel framework for practical assessment and the ranking of basketball players based on the adjusted well-known Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method. The graphical visualization of similarities provides further insights [17,18]. Visualization solutions of processes are better understood, allowing one to intuitively select a more appropriate optimization method. The visualization of processes is particularly useful for the cases with a variety of large and small factors, which should be controlled [19]. This is particularly important for inexperienced (non-professional) users.

The present study aims to analyze the ability of elite kayakers to achieve peak performance at the right times, with the Olympic Games taking the greatest importance. Real data is collected from two Olympic kayakers, and regression analysis is used (a combination of polynomial and trigonometric functions) to model how well their conditioning fits the ideal. A weighted least squares metric with weights varied by time period is developed as a measure of fulfillment of the athletes’ conditioning plans.

In our knowledge, the proposed methodology for the first time was applied for sports management process optimization. However, the scope of the methodology is not limited to the field of athletic training analysis and optimization. Another challenge in this study is the limited amount of data available. The data of two athletes’ Olympic training cycles are available. In addition, the data are not independent, as both athletes compete in a pair. This complicates the application of other methods, such as statistical methods, to address this problem. Therefore, in this application, the visualization approach should be defined for monitoring the condition of top kayakers during the three-year macro cycles before the Olympic Games.

Except for the Introduction, the article is organized as follows. In Section 2, the description of the experiment and the measured and expected target values of the indicators set by experts are provided. Section 3 is focused on justifying the selection of the approximation function. In Section 4, the research methodology, based on the approximation of functions by using a linear combination of polynomials and trigonometric functions, is described, and the calculated unknown coefficients are given. Section 5 describes visualization of the approximation of the target and the measured functions, and presents a measure of the difference between the target and the measurement functions, which defines the athlete’s condition. Section 6 provides the discussion of the investigated problem and conclusions.

2. The Investigation Object and the Initial Data

2.1. The athletes’ Participation in the Study

The research was performed in the second, third, and the fourth year of the Olympic four-year cycle, at the time of athletic training for Rio de Janeiro Olympic Games in 2016. Two (1, 2) elite flat-water kayak paddlers (a racing team), performing at the international competitive level at the distance of 1000 m (whose ages were 27 and 26 years, and body mass were 88.5 and 84.5 kg, respectively), volunteered to take part in the investigation. These two athletes gained fifth place in a 1000 m event (K-2) in the 2016 Olympic Games in Rio de Janeiro.

2.2. The Description of the Experiment

A council, consisting of 22 Lithuanian kayaking elite experts (trainers and sports researchers), with no less than 10 years of experience in execution and organization in kayaking, have rated the competences and created the dynamics of the ideal curves of indicators based on correlations between indicators and sports outcomes [20].

The training volume and intensity were carefully controlled and quantified by using the Garmin Connect Forerunner 910 XT during each training session throughout the cycle. The data obtained from the devices were sent to three delegates from the sports science experts’ council, who are the creators of the athletes’ training programs. During the study, the athletes were encouraged to undertake their standard training sessions but not to train on the day before each test. The athletes were acquainted with the experimental procedures prior to testing and gave a written consent to participate in the study. All experimental procedures were approved by the Lithuanian Ethics Committee.

The testing lasted for three seasons (macro cycles): in each season, the training period lasted for 8 months, the competition period lasted for 3 months, and the transition period lasted for 1 month. Physiological testing of the athletes’ condition was performed at the Lithuanian University of Education Science. For each athlete, all tests were conducted at the same time of the day, between 09:00 and 11:00, and 24 h after the last training session. During the testing session, the tests were performed in the same order. Prior to beginning the study, the sports doctor examined the kayakers to exclude any medical disorders that could limit their participation in the investigation.

During the macro cycles (I, II, III), the athletes were tested in six periods of time: in (T1), in the first week of the introductory training period, in (T2), at the beginning of the general training period, in (T3), at the beginning of the specific training period, in (T4), at the beginning of the competitive training period, in (T5), at the beginning of the main competition period, and in (T6), at the time after the main competition period.

Standard methodologies were applied to determine the athletes’ physical parameters, i.e., their height (cm) and body mass (kg) [21].

The resting heart rate (b/min) was determined for each athlete in the supine position and in the period after the application of the standard physical load (30 squats within 45 s) by using the Garmin Connect Forerunner 910 XT.

Hemoglobin concentration (g/L) was determined by using a Hemocue analyzer. A trace amount of blood samples was taken from the fingertips of the athletes in the resting position.

The ergometer test was performed, using Oxycon Mobile 781023-052, version 5.2 (Cardinal Health Germany 234 GmbH, Höchberg, Germany). Gas analyzers were calibrated before and verified after each test. Each athlete performed the incremental submaximal ergometer test, using a calibrated kayak ergometer (Dansprint PRO, KE001 ergo, Hvidovre, Denmark) for determining the maximum oxygen uptake (VO₂max) [22]. Five minutes before performing the submaximal ergometer test, the athletes completed a 15-min warm up. The incremental test began with the application of the initial workload of 100 W, and increments of 20 W were applied at the intervals of 30 s to bring the athlete to the limit of tolerance in 8–12 min. During the last minute, the athlete was encouraged to do as much work as he could. Then, the values were averaged over the intervals of 30 s. Pulmonary ventilation (PV) (1/min), oxygen uptake (VO₂) (1/min, mL/min/kg), work capacity (W), and speed (km/h) were recorded at the point of the critical intensity limit (CIL).

For reaching the aim of the present study, all tests were arranged in hierarchical order by the experts’ board (from the most informative to the least informative indicator), which influenced the outcome of a sporting event, measured in percent (

Table 1. Test indicators presented in the hierarchical order set by the experts from the most to the least important indicator.

Hierarchic Value	Test Indicator	Importance in Percent
1	Speed (km/h) at the point of the CIL	30
2	Work capacity (W), at the point of the CIL	20
3	Oxygen uptake (1/min, mL/min/kg) at the point of the CIL	15
4	Pulmonary ventilation (1/min) at the point of the CIL	10
5	Resting heart rate (b/min)	10
6	Heart rate (b/min) after the standard physical load	10
7	Haemoglobin concentration (g/L)	5

). In addition, all the testing sessions were also arranged in the hierarchical order. Their importance is shown in

Table 2. Importance of the testing sessions presented in the chronological order from the least (1) to the most (10) important session and their hierarchical order set by the experts.

No	Date	Testing Sessions	Hierarchical Order	Athletic Training Phase
1	2013 09 13	IT1	1	Transitional period after the season
2	2013 12 18	IT2	3	The first half of the training period (without water)
3	2014 03 28	IT3	4	The second half of the training period (with water)
4	2014 05 15	IT4	5	The period of non-core competitions
5	2014 07 15	IT5	6	European Championship
6	2014 08 12	IT6	7	World Championship
7	2014 09 12	IIT1	2	Transitional period after the season
8	2014 12 18	IIT2	4	The first half of the training period (without water)
9	2015 03 28	IIT3	5	The second half of the training period (with water)
10	2015 05 13	IIT4	6	The period of non-core competitions
11	2015 07 15	IIT5	7	European Championship
12	2015 08 12	IIT6	8	World Championship
13	2015 09 29	IIIT1	4	Transitional period after the season
14	2015 12 22	IIIT2	6	The first half of the training period (without water)
15	2016 03 04	IIIT3	7	The second half of the training period (with water)
16	2016 04 04	IIIT4	8	The period of non-core competitions
17	2016 07 07	IIIT5	9	European Championship/ Olympic selection
18	2016 08 01	IIIT6	10	Olympic Games

.

In

Table 3. Measurements of seven indicators for two athletes $R_i^{\left(l,j\right)}$ (the first row) and the expected target values$S_i^{\left(l,j\right)}$ (the second row).

$\mathit{i}$	$\mathit{j}=1$		$\mathit{j}=2$		$\mathit{j}=3$		$\mathit{j}=4$		$\mathit{j}=5$		$\mathit{j}=6$		$\mathit{j}=7$
1	260	260	180	185	60.9	48	186	146	48	56	106	126	158	180
	310		180		53		170	140	56		131		140
2	280	280	195	185	60.7	48	189	149	48	48	109	132	164	179
	315		188		55		175	147	53.5		128		145
3	290	290	200	200	61.8	44	198	167	44	52	106	130	167	163
	323		197		58		180	155	51		124		152
4	300	300	205	200	64	56	187	167	56	56	111	105	146	170
	328		203		60		183	160	49		122		157
5	320	320	213	205	62	48	189	171	48	52	109	129	165	173
	336		211		63		187	166	47		118		164
6	320	320	215	215	57.2	48	186	170	48	48	119	118	134	162
	340		215		65		190	170	46		115		168
7	300	300	190	212	62.1	48	159	159	48	60	111	114	156	169
	320		190		58		180	155	54		128		154
8	310	310	195	195	59	48	195	156	48	52	114	120	159	177
	326		197		60.5		183	160	51.5		123		158
9	320	320	210	211	55	56	188	163	56	56	119	128	161	175
	334		205		63.5		188	165	48.5		119		163
10	340	340	216	216	63.7	44	193	160	44	52	113	116	166	174
	338		210		65		190	168	47		116		167
11	320	320	220	220	62.6	48	193	155	48	44	113	125	156	172
	346		217		67		193	173	45		112		171
12	340	340	220	221	63.9	48	191	162	48	52	110	121	163	182
	350		220		68		195	175	44		109		174
13	300	300	200	195	60.2	52	193	161	52	48	122	117	174	178
	330		195		60		185	160	52		123		160
14	320	320	210	205	54.1	44	192	167	44	56	103	120	166	176
	338		203		62.5		188.5	165	49.5		118		165
15	340	340	217	216	50	48	185	164	48	52	108	108	159	164
	345		210		65		192	170	47		113		169
16	350	350	220	221	59.4	48	190	172	48	48	111	112	167	162
	348		213		66		194	172	46		110		171
17	340	340	224	224	58.2	52	192	157	52	44	113	106	164	180
	357		223		69		198.5	178	43		103		178
18	340	340	217	217	57.8	52	181	154	52	48	121	102	160	167
	360		225		70		200	180	42		100		180

, the results of measurements of seven indicators for both athletes $R_i^{\left(l,j\right)}$ and the expected target values $S_i^{\left(l,j\right)}$ determined by the experts are presented. Here, $l$ denotes the athletes$\left(l=1,2\right)$, $j$ is the number of the indicator$\left(j=1,2,\dots ,7\right)$, and $i$ is the number of the measurement$\left(i=1,2,\dots ,18\right)$. For example, $R_4^{\left(2,6\right)}=105, R_2^{\left(1,3\right)}=60.7, S_6^{\left(1,7\right)}= S_6^{\left(2,7\right)}=168$. The expected target values $S_i^{\left(l,j\right)}$ differ for athletes 1 and 2 only in the case of$j=4$ because of the different lung volumes of the athletes.

3. The Selection of the Approximating Functions

The shape of the approximating functions was determined only for the target curves, which were created according to experts’ judgments. The available data were compared with the ideal (target) curves. The following factors were taken into account for the selection of the suitable functions for the curves:

• The approximation curve should not only describe the upward or downward trend, but also show the characteristic phase of the fall and the subsequent growth phase of the considered processes.
• The shape of the functions should be the same for all the curves and be simple enough. Its parameter values were determined by the least squares method.

Let us show how the ideal curve was constructed for the case of RN2. The values of the normalized data $\left(t_j,s_j\right), j=1,2,\dots ,18$ were as follows:

(0.0,1.0), (0.091,1.044), (0.186,1.094), (0.232,1.172), (0.290,1.150), (0.316,1.194), (0.346,1.056),

(0.438,1.094), (0.533,1.139), (0.576,1.167), (0.636,1.206), (0.663,1.222), (0.708,1.083), (0.788,1.128),

(0.857,1.167), (0.887,1.183), (0.976,1.239), (1.0,1.250).

The shape of the selected curve with the coefficients determined by the least squares method was as follows:

$$w\left(t\right)=1.019 + 0.245t-0.010t^2+ 0.044 \sin \left(2\pi t\right)-0.013\cos \left(2\pi t\right)$$

The curve $w\left(t\right)$ and the linear interpolation $I$ of the points $\left(t_j,s_j\right)$are depicted in Figure 1. Note that the graphical accuracy is sufficient for the purpose of the study, because the curve $w\left(t\right)$ satisfies requirements 1 and 2. On the other hand, describing all the fluctuations of the linear interpolation $I$ does not make sense, because the similarity of these real data points can be hardly realized in practice. It should also be noted that the authors did not intend to construct the best curves, and therefore constructed the curves of sufficient approximation. However, other combinations of algebraic and trigonometric polynomials, which were acceptable, were also tested. The final decision about the choice of the formula was taken according to requirement 2 (the formula is appropriate for all the cases considered).

Figure 2 shows the functions

$$y\left(t\right)=1.133 + 0.020\mathrm{t}, z\left(t\right)=1.046 + 0.24183t - 0.081t^2$$

with the coefficients determined by the least squares method based on the same data. We can see that the curves $y\left(t\right)$ and $z\left(t\right)$ do not satisfy requirement 1. The values of the error function were calculated as follows:

$$S_f=\sqrt{{\displaystyle \sum }_{i=1}^{18}{\left(s_j-f\left(t_j\right)\right)}^2},$$

where $f$ is equal to $y\left(t\right),z\left(t\right),w\left(t\right)$. The following error function values were obtained: $S_y=0.0642,$ $S_z=0.0487,$ $S_w=0.0430$. One can see that the best result was achieved by incorporating trigonometric components into the approximation function.

4. Research Methodology

In the first step, all the initial data points (Table 3) were normalized to eliminate the influence of the measurement units on the final results. The values $R_i^{\left(l,j\right)}$ and $S_i^{\left(l,j\right)}$ were normalized by the equations:

$${\tilde{r}}_i^{\left(l,j\right)}=\frac{R_i^{\left(l,j\right)}}{S_1^{\left(l,j\right)}}, {\tilde{s}}_i^{\left(l,j\right)}=\frac{S_i^{\left(l,j\right)}}{S_1^{\left(l,j\right)}}$$

This method of data normalization, when each measurement $R_i^{\left(l,j\right)}$ and target value $S_i^{\left(l,j\right)}$were divided by the first target value of the respective measurement, was chosen for the convenience of data representation. In this case, the graphs of all the target values of the indicators have the same initial point of 1.

The measurement time was normalized as follows:

$$t_i=\frac{T_i}{T_{18}}$$

where $T_i$ is the number of days passed since the first measurement, $T_1=0$. The respective values are shown in

Table 4. Normalized time values$t_i$.

$T_i$	0	96	196	244	305	333	364	461	561
$t_i=T_i/T_{18}$	0	0.0912	0.1861	0.2317	0.2896	0.3162	0.3457	0.4378	0.5328
$T_i$	607	670	698	746	830	903	934	1028	1053
$t_i=T_i/T_{18}$	0.5764	0.6363	0.6629	0.7085	0.7882	0.8576	0.8870	0.9763	1.000

.

The goal was to find the functions most suitable for approximating the athlete’s indicators. The target values for a multiple measure of conditioning were compared to the targets set by the experts. The regression analysis was used to model how well their conditioning could fit the target. The weighted least square metric is a measure of the fulfillment of the athletes’ conditioning plans. The expression with five undefined coefficients, $a,b,c,A,B$, was chosen for approximating the functions${\tilde{r}}^{\left(l,j\right)}\left(t\right), {\tilde{s}}^{\left(l,j\right)}\left(t\right)$ as follows:

$$f\left(t\right)=a+bt+c{t}^2+A\sin 2\pi t+B\cos 2\pi t$$

(1)

where $t\in \left[0;1\right]$ is the normalized time. The unknown coefficients were determined by a standard method of the least squares [23]:

$${\displaystyle \sum }_{i=1}^{18}{\left(f\left(t_i\right)-f_i\right)}^2\to min.$$

(2)

The system of linear equations was obtained from Equations (1) and (2) as follows:

$$\left(\begin{array}{ccccc}{a}_{11}& a_{12}& a_{13}& a_{14}& a_{15}\\ a_{21}& a_{22}& a_{23}& a_{24}& a_{25}\\ a_{31}& a_{32}& a_{33}& a_{34}& a_{35}\\ a_{41}& a_{42}& a_{43}& a_{44}& a_{45}\\ a_{51}& a_{52}& a_{53}& a_{54}& a_{55}\end{array}\right)\cdot \left(\begin{array}{c}a\\ b\\ c\\ A\\ B\end{array}\right)=\left(\begin{array}{c}{b}_1\\ b_2\\ b_3\\ b_4\\ b_5\end{array}\right)$$

where

$a_{11}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}1=18,$	$a_{12}=a_{21}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{t}_i,$	$a_{13}=a_{31}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{t}_i^2,$	$a_{14}=a_{41}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}\sin 2\pi t_i,$	$a_{15}=a_{51}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}\cos 2\pi t_i,$
$a_{22}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{t}_i^2,$	$a_{23}=a_{32}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{t}_i^3,$	$a_{24}=a_{42}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{t}_i\sin 2\pi t_i,$	$a_{25}=a_{52}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{t}_i\cos 2\pi t_i,$	$a_{33}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{t}_i^4,$
$a_{34}=a_{43}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{t}_i^2\sin 2\pi t_i,$	$a_{35}=a_{53}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{t}_i^2\cos 2\pi t_i,$	$a_{44}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{\sin }^{2}2\pi t_i,$	$a_{45}=a_{54}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}\sin 2\pi t_i\times \cos 2\pi t_i,$	$a_{55}={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{\cos }^{2}2\pi t_i.$

The coefficients $b_1,b_2,\dots ,b_5$ were calculated by the equations:

$b_1={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{f}_i,$

$b_2={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{f}_i{t}_i,$

$b_3={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{f}_i{t}_i^2,$

$b_4={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{f}_i\sin 2\pi t_i,$

$b_5={\displaystyle {\displaystyle \sum }_{i=1}^{18}}{f}_i\cos 2\pi t_i,$

where the functions $f_i$ obtained the values ${\tilde{r}}^{\left(l,j\right)}\left(t\right)$ and ${\tilde{s}}^{\left(l,j\right)}\left(t\right)$, i.e., the coefficients $a,b,c,A,B$ were calculated separately for each athlete $l=1,2$ and each indicator $j=1,2,\dots ,7$ for the functions $\tilde{r}$ and $\tilde{s}$.

The matrix $A={\left(a_{ij}\right)}_{5\times 5}$, depending only on the values $t_i$, was calculated only once:

$$\mathrm{A}=\left(\begin{array}{ccccc}18& 9.5242& 6.6505& -0.2485& 0.5155\\ 9.5242& 6.6505& 5.1966& -2.7916& 0.7607\\ 6.6505& 5.1966& 4.3262& -2.7751& 1.6716\\ -0.2485& -2.7916& -2.7751& 9.2166& -0.0602\\ 0.5155& 0.7607& 1.6716& -0.0602& 8.7834\end{array}\right)$$

For calculating the coefficients $a,b,c,A,B,$ the inverse matrix method is convenient to use (see, for example, [24]):

$$\left(\begin{array}{c}a\\ b\\ c\\ A\\ B\end{array}\right)=A^{-1}\cdot \left(\begin{array}{c}{b}_1\\ b_2\\ b_3\\ b_4\\ b_5\end{array}\right)$$

(3)

$$A^{-1}=\left(\begin{array}{ccccc}2.7001& -14.5727& 13.8234& -0.1888& -1.5284\\ -14.5727& 85.2846& -83.4043& 0.3864& 9.3445\\ 13.8234& -83.4043& 82.7523& -0.0333& -9.3368\\ -0.1888& 0.3864& -0.0333& 0.2103& -0.0146\\ -1.5284& 9.3445& -9.3368& -0.0146& 1.7111\end{array}\right)$$

In

Table 5. Calculated values of the coefficients$a,b,c,A,B$.

			$\mathit{a}$	$\mathit{b}$	$\mathit{c}$	$\mathit{A}$	$\mathit{B}$
$j=1$	$l=1$	$\tilde{r}$	0.835	0.529	−0.257	0.030	0.002
		$\tilde{s}$	1.011	0.094	0.062	0.018	−0.010
	$l=2$	$\tilde{r}$	0.915	0.169	0.019	0.028	−0.007
		$\tilde{s}$	1.011	0.094	0.062	0.018	−0.010
$j=2$	$l=1$	$\tilde{r}$	0.976	0.651	−0.446	0.022	0.036
		$\tilde{s}$	1.019	0.245	−0.010	0.044	−0.013
	$l=2$	$\tilde{r}$	1.038	0.237	−0.018	0.032	−0.023
		$\tilde{s}$	1.019	0.245	−0.010	0.044	−0.013
$j=3$	$l=1$	$\tilde{r}$	1.207	−0.323	0.240	0.007	−0.049
		$\tilde{s}$	1.062	0.045	0.267	0.041	−0.058
	$l=2$	$\tilde{r}$	1.024	0.795	−0.836	0.033	0.052
		$\tilde{s}$	1.062	0.045	0.267	0.041	−0.058
$j=4$	$l=1$	$\tilde{r}$	1.079	0.244	−0.279	−0.030	0.033
		$\tilde{s}$	1.017	0.140	0.031	0.021	−0.014
	$l=2$	$\tilde{r}$	0.876	1.467	−1.368	0.033	0.133
		$\tilde{s}$	1.023	0.312	−0.035	0.041	−0.021
$j=5$	$l=1$	$\tilde{r}$	0.930	−0.501	0.569	0.029	−0.067
		$\tilde{s}$	0.969	−0.145	−0.080	−0.037	0.018
	$l=2$	$\tilde{r}$	0.952	0.029	−0.136	−0.005	−0.005
		$\tilde{s}$	0.969	−0.145	−0.080	−0.037	0.018
$j=6$	$l=1$	$\tilde{r}$	0.907	−0.484	0.561	0.021	−0.085
		$\tilde{s}$	0.962	0.089	−0.310	−0.030	0.031
	$l=2$	$\tilde{r}$	0.990	−0.058	−0.154	−0.047	0.001
		$\tilde{s}$	0.962	0.089	−0.310	−0.030	0.031
$j=7$	$l=1$	$\tilde{r}$	1.125	0.151	−0.167	−0.047	0.032
		$\tilde{s}$	1.029	0.214	0.066	0.036	−0.029
	$l=2$	$\tilde{r}$	1.389	−0.779	0.692	−0.042	−0.081
		$\tilde{s}$	1.029	0.214	0.066	0.036	−0.029

, the values of the coefficients $a,b,c,A,B,$ which were calculated by Equation (3), are presented for $j=1,2,\dots ,7, l=1,2$ for the functions $\tilde{r}$ and$\tilde{s}$.

5. Visualization of the Results and Measurement of the Athlete’s Condition

The graphs of approximations of the functions $\tilde{r}\left(t\right)$ and $\tilde{s}\left(t\right)$, with the coefficient values$a,b,c,A,B,$ which are given in Table 5, are presented in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. The graphs of the approximations of the function $\tilde{r}\left(t\right)$ are depicted in black, while the approximations of the function $\tilde{s}\left(t\right)$ are shown in green.

Visualization of the results provides information about the quality of the athletes’ training management and gives an understanding of the time periods when the maximum discrepancy between the ideal and the real curves can be observed. This allows the coaches to quickly change the athletes’ workouts. To assess the numerical value of this mismatch, the measurement of the difference between the respective functions is required.

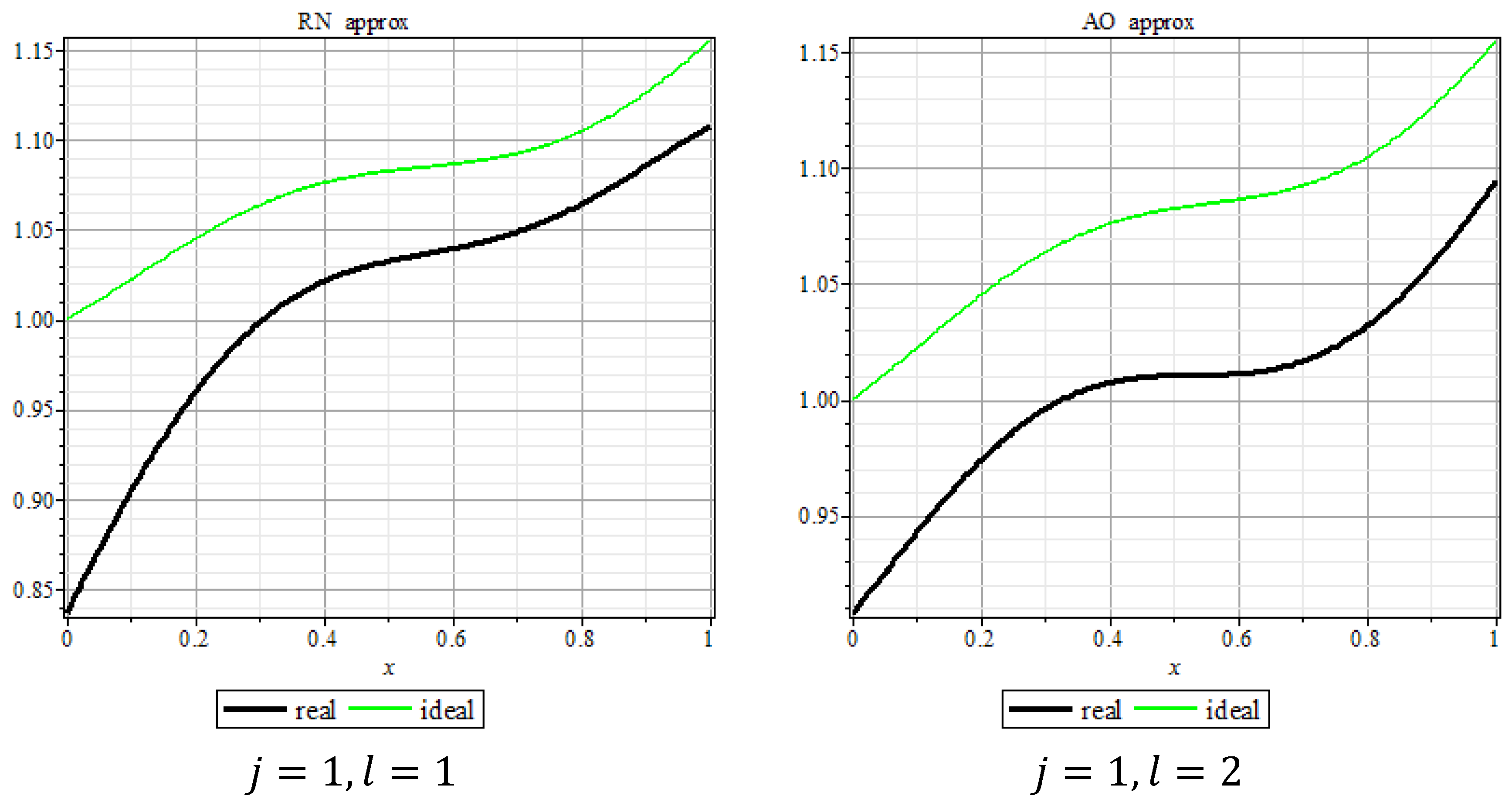
It is worth noting that five indicators have a direct relationship with the target, while two indicators, i.e., resting heart rate (5) and heart rate after the standard physical load (6), have the inverse relation with it. By analyzing speed at the point of the CIL (Figure 3), it could be observed that the athlete RN could consistently approach the target (ideal) indicators, although the AO progress was much slower. The tested athletes could not maximally synchronize their efforts (with respect to the above indicator). This can be accounted for by the specific character of their adaptation.

The evaluation of the athletes’ work capacity at the point of the CIL (Figure 4) allows the authors to state that the dynamics of this indicator for the tested athletes was close to the target values, and they achieved their planned peak performance before the beginning of the Olympic Games.

Evaluation of the dynamics of the criteria describing oxygen uptake at the point of the CIL (Figure 5) showed the decreasing trend of VO₂max during the testing period and its considerable difference from the target value. This can be accounted for by the specific character of the athletes’ training aimed at increasing the load in the muscles’ area where glycolytic energy is generated. This phenomenon requires further investigation.

When evaluating the variation in the criteria values of pulmonary ventilation at the point of the CIL (Figure 6), a similar trend could be observed as that characteristic of the criteria describing oxygen uptake at the point of the CIL. It can be assumed that the athletes’ aerobic capacity had a tendency to decrease. This can be associated with the striving of athletes to increase their capacity of energy generation in the training period.

Evaluation of the variation of criteria describing the resting heart rate (Figure 7) in a resting position and the heart rate after the application of a standard physical load (Figure 8) showed that the adaptation of the athletes’ circulatory system to training was different. Thus, it was unstable for RN, while AO consistently approached the ideal values of indicators.

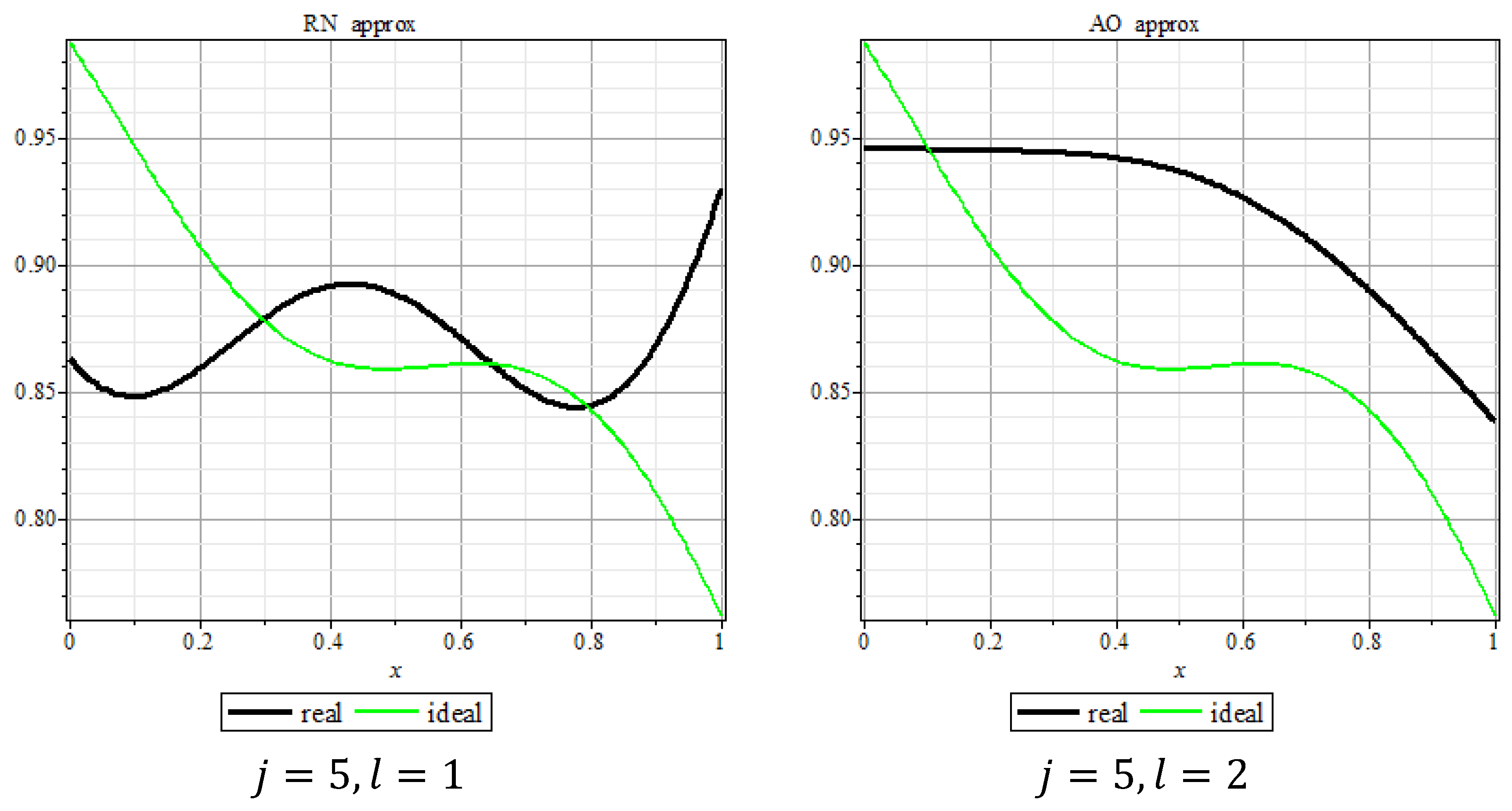
The analysis of the variation in hemoglobin concentration of the athletes (Figure 9) has shown that this indicator was difficult to control. In the training process, hemoglobin concentration varied considerably. As a result, the target values could not be achieved before the main competitions.

In the ideal case, when the athlete’s training plan is fully realized, the curves $\tilde{r}\left(t\right)$and $\tilde{s}\left(t\right)$coincide. In practice, this objective can only be achieved partially; therefore, it is necessary to quantify the difference between the real and the ideal curves.

This difference is a measure of the athletes’ condition. The fact that the differences $\left|\tilde{r}\left(t\right)-\tilde{s}\left(t\right) \right|$ observed in various time intervals are of various importance is taken into account. The relative importance of the time intervals was determined in the following way. The relative importance of the period prior to measuring was equal to 1, while the importance of other periods was higher, ranging from 2 to 10. The definitions of the time intervals, their relative importance, and the dates and lengths of the intervals (in percent) are given in

Table 6. Relative importance of the time intervals.

Date	Definition of the Time Interval	Relative Importance of the Interval	Interval	The Interval’s Length, in Percent
2013 09 13	The transitional period after the season	1	Till $T_1$	-
2013 12 18	The first half of the training period (without water)	3	$[T_1,T_2]$	9.1
2014 03 28	The second half of the training period (with water)	4	$[T_2,T_3]$	9.5
2014 05 15	The period of non-core competitions	5	$[T_3,T_4]$	4.6
2014 07 15	European Championship	6	$[T_4,T_5]$	5.8
2014 08 12	World Championship	7	$[T_5,T_6]$	2.7
2014 09 12	The transitional period after the season	2	$[T_6,T_7]$	2.9
2014 12 18	The first half of the training period (without water)	4	$[T_7,T_8]$	9.2
2015 03 28	The second half of the training period (with water)	5	$[T_8,T_9]$	9.5
2015 05 13	The period of non-core competitions	6	$[T_9,T_{10}]$	4.4
2015 07 15	European Championship	7	$[T_{10},T_{11}]$	6.0
2015 08 12	World Championship	8	$[T_{11},T_{12}]$	2.7
2015 09 29	The transitional period after the season	4	$[T_{12},T_{13}]$	4.6
2015 12 22	The first half of the training period (without water)	6	$[T_{13},T_{14}]$	7.9
2016 03 04	The second half of the training period (with water)	7	$[T_{14},T_{15}]$	6.9
2016 04 04	The period of non-core competitions	8	$[T_{15},T_{16}]$	2.9
2016 07 07	European Championship/Olympic selection	9	$[T_{16},T_{17}]$	8.9
2016 08 01	Olympic Games	10	$[T_{17},T_{18}]$	2.4

.

Depending on the relative importance of the time intervals and their relative length, the weights $w_k$ were assigned to the normalized time intervals$[t_{k-1},t_k]$. In this case, $t_0=0, t_k=\frac{k}{100} \mathrm{and} k=1,2,\dots ,100$. The weights of the time intervals are given in

Table 7. The weights of the time intervals.

$w_1$	$w_2$	$w_3=\dots =w_9$	$w_{10}=\dots =w_{18}$	$w_{19}=\dots =w_{23}$	$w_{24}=\dots =w_{29}$	$w_{30}=\dots =w_{32}$	$w_{33}$
0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.06
$w_{34}$	$w_{35}$	$w_{36}$	$w_{37}$	$w_{38}$	$w_{39}=\dots =w_{44}$	$w_{45}=\dots =w_{53}$	$w_{54}=\dots =w_{57}$
0.05	0.04	0.03	0.02	0.03	0.04	0.05	0.06
$w_{58}=\dots =w_{63}$	$w_{64}=\dots =w_{66}$	$w_{67}$	$w_{68}$	$w_{69}$	$w_{70}=\dots =w_{71}$	$w_{72}$	$w_{73}=\dots =w_{79}$
0.07	0.08	0.07	0.06	0.05	0.04	0.05	0.06
$w_{80}=\dots =w_{86}$	$w_{87}=\dots =w_{89}$	$w_{90}=\dots =w_{98}$	$w_{99}=\dots =w_{100}$
0.07	0.08	0.09	0.10

.

It should be emphasized that the fluctuations of the relative importance values in Table 6 were smoothed out. For example, $w_{66}=0.08$ and the intermediate values $w_{67}=0.07, w_{68}=0.06, w_{69}=0.05$appeared before $w_{70}=0.04$, since it was difficult to detect the exact moment of their sudden decrease.

Thus, the difference between the functions $\tilde{r}\left(t\right)$ and $\tilde{s}\left(t\right)$ was measured as the weighted sum as follows:

$$||\tilde{r}\left(t\right)-\tilde{s}\left(t\right)||=\frac{{{\displaystyle \sum }}_{k=1}^{100}{w}_k\left|\tilde{r}\left(t_k\right)-\tilde{s}\left(t_k\right)\right|}{{{\displaystyle \sum }}_{k=1}^{100}{w}_k\tilde{s}\left(t_k\right)}.$$

The values $\left|\right|\tilde{r}\left(t\right)-\tilde{s}\left(t\right)\left|\right|$ calculated for each indicator and both athletes are given in

Table 8. The values $\left|\right|\tilde{r}\left(t\right)-\tilde{s}\left(t\right)\left|\right|$ for seven indicators and two athletes.

$\mathit{j}$	$\mathit{l}=1$	$\mathit{l}=2$
1	0.066	0.053
2	0.011	0.015
3	0.085	0.084
4	0.046	0.024
5	0.067	0.049
6	0.019	0.062
7	0.058	0.039

.

The results provided in Table 8 are summarized as the weighted sums $S^{\left(l\right)}, l=1,2$, with the respective criteria $j=1,2,\dots ,7$ weights: ${\tilde{w}}_1=0.3, {\tilde{w}}_2=0.2, {\tilde{w}}_3=0.15, {\tilde{w}}_4={\tilde{w}}_5={\tilde{w}}_6=0.1,{\tilde{w}}_7=0.05$ (see the data in Table 1). The weighted sums were as follows:

$$S^{\left(l\right)}={\displaystyle \sum }_{j=1}^7{\tilde{w}}_j||{\tilde{r}}^{\left(l,j\right)}\left(t\right)-{\tilde{s}}^{\left(l,j\right)}\left(t\right)||.$$

(4)

Therefore, $S^{\left(1\right)}=0.051, S^{\left(2\right)}=0.047$. The values $S^{\left(l\right)}$ have an inverse relationship with the athletic training. The higher these values, the lower the achievement of the goals by the athlete. Then, the values of $K^{\left(l\right)}=1-S^{\left(l\right)}$, describing the results of the athletic training, were calculated as follows:

$$K^{\left(1\right)}=0.949, K^{\left(2\right)}=0.953.$$

The higher the value of the indicator K, the higher the level of the fulfillment of the athlete’s training plan. It can be concluded that the results of the second athlete are better than the results obtained by the first athlete. The indicator K is important for the implementation and improvement (optimization) of the athlete’s training plan development.

6. Discussion and Conclusions

The optimization and evaluation of athletic training has become an increasingly important problem for sports scientists, coaches, and athletes [25]. The character of the identification factors of the elite athlete’s condition and their integration into the processes of strategic planning, management, and parameter estimation have not been thoroughly investigated, but they are obviously important. To govern the process of elite athletes’ training, it is required to consider this process both as a whole and in detail. Not all the aspects of the executed cycle can be in compliance. Therefore, the research should not be performed in terms of the standardized compliance management. The OR methods allow us to define the criteria and the limits of their permissible pursuit [14].

The papers considered do not offer a unique view of past research, and the integration they provide is likely to be only fractional. Therefore, real research data are needed. Usually, the research data seem to be more significant than dimensions. They present (1) the constructs and their relational properties and (2) consistency in the measurement of phenomena. The combinations of these dimensions can yield the following results: (1) theoretical plurality and empirical convergence, (2) the dominant paradigm, (3) fragmentation, and (4) the convergent theory and empirical plurality. The integration will require fostering both taxonomic and methodological commensurability among the different sub-fields and contributing disciplines [26]. The method of parameter estimation of the dynamics of the factors presents a viable research approach in this context [27]. It is particularly useful for the investigation of the process cycle, e.g., its long-term effects and results [28]. Interactive data visualization is an evolving approach, providing wide opportunities for managing and decision making in the case of multidimensional decision problems and planning processes.

The proposed methodology of the athletic training visualization makes it easier to identify the advantages and disadvantages of training and shows when (at what stages of training) physical loads (or training methods and techniques) do not match the adaptive capacities of the tested athletes. It also provides new opportunities for streamlining and optimizing the key factors influencing the process by modifying its components. The authors believe that data visualization allows for achieving a better way of informing athletes and coaches about the mistakes and the right choices in the considered training period. According to Xu and Ding [29], visualization allows for identifying the deviations of the indicator values. The automated alarm system, warning about critical deviations of the process components, could help to optimize the process management and prevent hazardous incidents [30].

To the author’s best knowledge, no cases of applying the methodology based on the goal function’s approximation by a linear combination of polynomials and trigonometric functions can be found in the scientific literature on sports management. Meanwhile, this methodology, in conjunction with the least squares method, yields fairly accurate approximation results.

The described methodology (algorithm) has a number of advantages over other similar approaches. The visualization of measurement and target approximation functions enables sports scientists and coaches to perform the following functions:

• to supervise the athletes’ training process,
• to identify undesirable tendencies,
• to correct them immediately (if necessary).

The proposed Formula (4) for measuring the differences between the indicators and the current and target functions enables the researchers to identify the athlete’s condition, as well as showing his/her potential and providing more accurate predictions of sports results.

New opportunities are provided by the proposed method, which:

• Facilitate the understanding and achievement of the goal;
• Make processes clearer to the general public;
• Allow for effective management of the processes.

The provided high-quality, effective alternative solutions to the problem of achieving the final goals of the considered management process give a deeper insight into the effectiveness of a solution, which can support a decision-making process. The principles of the model of the parameter estimation provide visualization capabilities, allowing for evaluating the possibilities to reach the goal, which is the effective management process. This method also allows for predicting the future achievements of athletes.

The proposed model for evaluating the planning of athletic training is used in other sports and can be applied not only to sports practice, but also to the implementation of many various strategies. Moreover, based on the proposed visualization method, an application could be created that would make this method a more widely used technique.