Comprehensive Review of Deep Reinforcement Learning Methods and Applications in Economics

Abstract

The popularity of deep reinforcement learning (DRL) applications in economics has increased exponentially. DRL, through a wide range of capabilities from reinforcement learning (RL) to deep learning (DL), offers vast opportunities for handling sophisticated dynamic economics systems. DRL is characterized by scalability with the potential to be applied to high-dimensional problems in conjunction with noisy and nonlinear patterns of economic data. In this paper, we initially consider a brief review of DL, RL, and deep RL methods in diverse applications in economics, providing an in-depth insight into the state-of-the-art. Furthermore, the architecture of DRL applied to economic applications is investigated in order to highlight the complexity, robustness, accuracy, performance, computational tasks, risk constraints, and profitability. The survey results indicate that DRL can provide better performance and higher efficiency as compared to the traditional algorithms while facing real economic problems in the presence of risk parameters and the ever-increasing uncertainties.

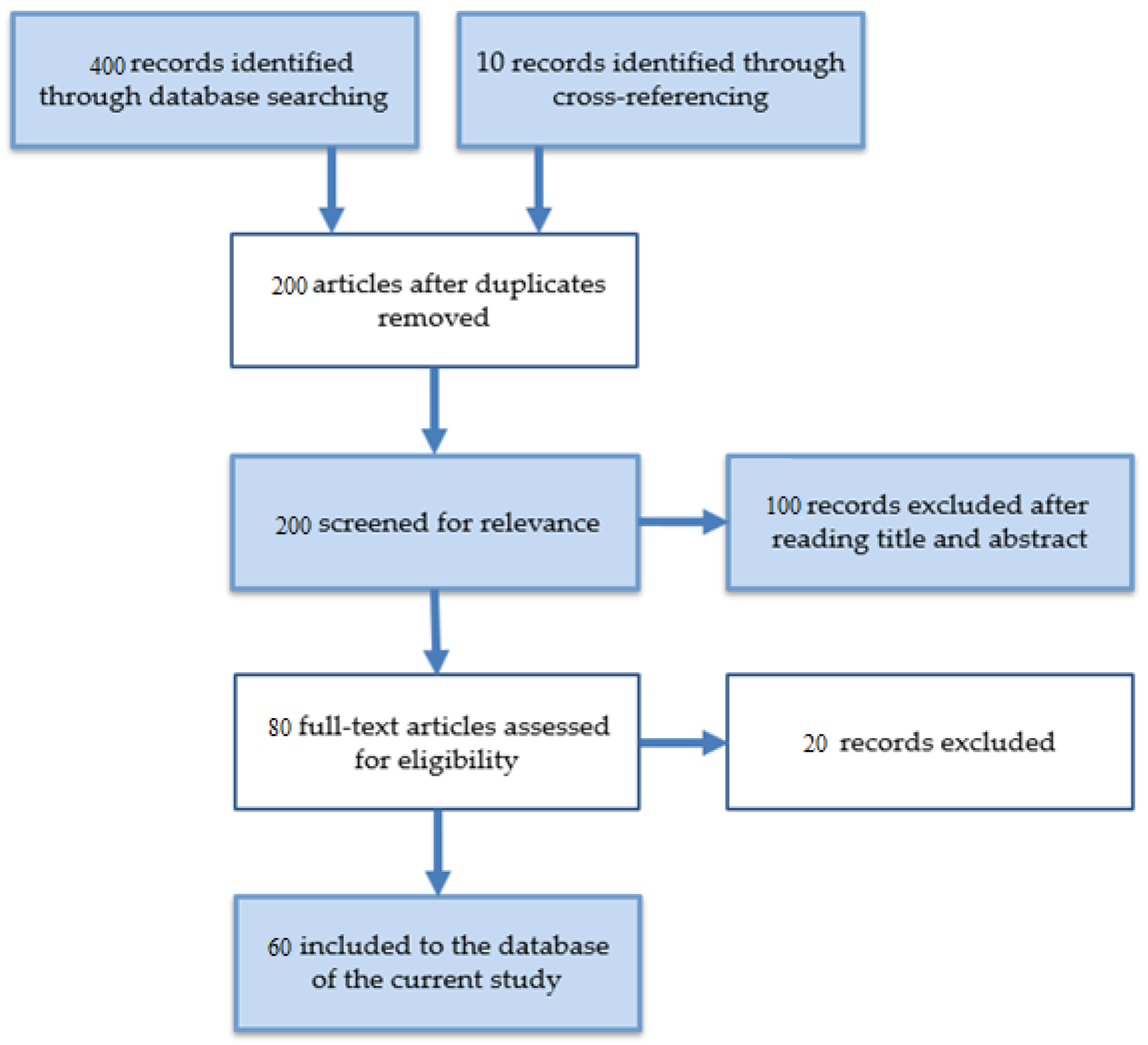
1. Introduction

Deep learning (DL) techniques are based on the use of multi-neurons that rely on the multi-layer architectures to accomplish a learning task. In DL, the neurons are linked to the input data in conjunction with a loss function for the purpose of updating their weights and maximizing the fitting to the inbound data [1,2]. In the structure of a multi-layer, every node takes the outputs of all the prior layers in order to represent outputs set by diminishing the approximation of the primary input data, while multi-neurons learn various weights for the same data at the same time. There is a great demand for the appropriate mechanisms to improve productivity and product quality in the current market development. DL enables predicting and investigating complicated market trends compared to the traditional algorithms in ML. DL presents great potential to provide powerful tools to learn from stochastic data arising from multiple sources that can efficiently extract complicated relationships and features from the given data. DL is reported as an efficient predictive tool to analyze the market [3,4]. Additionally, compared to the traditional algorithms, DL is able to prevent the over-fitting problem, to provide more efficient sample fitting associated with complicated interactions, and to outstretch input data to cover all the essential features of the relevant problem [5].

Reinforcement learning (RL) [6] is a powerful mathematical framework for experience-driven autonomous learning [7]. In RL, the agents interact directly with the environment by taking actions to enhance its efficiency by trial-and-error to optimize the cumulative reward without requiring labeled data. Policy search and value function approximation are critical tools of autonomous learning. The search policy of RL is to detect an optimal (stochastic) policy applying gradient-based or gradient-free approaches dealing with both continuous and discrete state-action settings [8]. The value function strategy is to estimate the expected return in order to find the optimal policy dealing with all possible actions based on the given state. While considering an economic problem, despite traditional approaches [9], reinforcement learning methods prevent suboptimal performance, namely, by imposing significant market constraints that lead to finding an optimal strategy in terms of market analysis and forecast [10]. Despite RL successes in recent years [11,12,13], these results suffer the lack of scalability and cannot manage high dimensional problems. The DRL technique, by combining both RL and DL methods, where DL is equipped with the vigorous function approximation, representation learning properties of deep neural networks (DNN), and handling complex and nonlinear patterns of economic data, can efficiently overcome these problems [14,15]. Ultimately, the purpose of this paper is to comprehensively provide an overview of the state-of-the-art in the application of both DL and DRL approaches in economics. However, in this paper, we focus on the state-of-the-art papers that employ DL, RL, and DRL methods in economics issues. The main contributions of this paper can be summarized as follows:

• Classification of the existing DL, RL, and DRL approaches in economics.
• Providing extensive insights into the accuracy and applicability of DL-, RL-, and DRL-based economic models.
• Discussing the core technologies and architecture of DRL in economic technologies.
• Proposing a general architecture of DRL in economics.
• Presenting open issues and challenges in current deep reinforcement learning models in economics.

The survey is organized as follows. We briefly review the common DL and DRL techniques in Section 2. Section 3 proposes the core architecture and applicability of DL and DRL approaches in economics. Finally, we follow the discussion and present real-world challenges in the DRL model in economics in Section 4 with a conclusion to work in Section 5.

2. Methodology and Taxonomy of the Survey

The survey adopts the Prisma standard to identify and review the DL and DRL methods used in economics. As stated in [16], a systematic review based on the Prisma method includes four steps: (1) identification, (2) screening, (3) eligibility, (4) inclusion. In the identification stage, the documents are identified through an initial search among the mentioned databases. Through Thomson Reuters Web-of-Science (WoS) and Elsevier Scopus, 400 of the most relevant articles are identified. The screening step includes two stages in which, first, duplicate articles are eliminated. As a result, 200 unique articles moved to the next stage, where the relevance of the articles is examined on the basis of their title and abstract. The result of this step was 80 articles for further consideration. The next step of the Prisma model is eligibility, in which the full text of articles was read by the authors, and 57 of them considered eligible for final review in this study. The last step of the Prisma model is the creation of the database of the study, which is used for qualitative and quantitative analyses. The database of the current research comprises 57 articles, and all the analyses in this study took place based on these articles. Figure 1 illustrates the steps of creating the database of the current research based on the Prisma method.

Taxonomy of the survey is given in Figure 2, where the notable methods DRL are presented.

2.1. Deep Learning Methods

In this section, we review the most commonly used DL algorithms, which have been applied in various fields [16,17,18,19,20]. These deep networks comprise stacked auto-encoders (SAEs), deep belief networks (DBNs), convolutional neural networks (CNNs), and recurrent neural networks (RNNs). A fundamental structure of a neural network is presented in Figure 3.

2.2. Stacked Auto-Encoders (SAEs)

The basic building block of the stacked AE is called an AE, which includes one visible input layer and one hidden layer [17]. It has two steps in the training process. In mathematics, they can be explained as Equations (1) and (2):

$$h=f\left(w_{h}x+b_h\right)$$

(1)

$$\mathcal{Y}=f\left(w_{y}x+b_y\right)$$

(2)

The hidden layer $h$ can be transformed to provide the output value $\mathcal{Y}$. Here, $x\in {ℝ}^d$ represents the input values, and $h\in {ℝ}^L$ denotes the hidden layer, i.e., the encoder. $w_h$ and $w_y$ represent the input-to-hidden and hidden-to-input weights, respectively. $b_h$ and $b_y$ refer to the bias of the hidden and output terms, respectively, and $f(.)$ indicates an activation function. One can estimate the error term utilizing the Euclidean distance for approximating input data $x$ while minimizing ${\Vert x-y\Vert }_2^2$. Figure 4 presents the architecture of an AE.

2.3. Deep Belief Networks (DBNs)

The basic building block of deep belief networks is known as a restricted Boltzmann machine (RBM) which is a layer-wise training model [18]. It contains a two-layer network with visible and hidden units. One can express the joint configuration energy of the units as Equation (3):

$$E\left(v,h;\theta \right)=-{\sum }_{i=1}^d{b}_i{v}_i-{\sum }_{j=1}^L{a}_j{h}_j-{\sum }_{i=1}^d{\sum }_{j=1}^L{w}_{ij}{v}_i{h}_j=-b^{T}v-a^{T}h-v^{T}wh$$

(3)

where $b_i$ and $a_j$ are the bias term of the visible and hidden units, respectively. Here, $w_{ij}$ denotes the weight between the visible unit $i$ and hidden unit $j$. In RBM, the hidden units can capture an unbiased sample from the given data vector, as they are conditionally independent from knowing the visible states. One can improve the feature representation of a single RBM by cumulating diverse RBMs one after another, which constructs a DBN for detecting a deep hierarchical representation of the training data. Figure 5 presents a simple architecture of an RBM.

2.4. Convolutional Neural Networks (CNNs)

CNNs are composed of a stack of periodic convolution layers and pooling layers with multiple fully connected layers. In the convolutional layer, CNNs employ a set of kernels to convolve the input data and intermediate features to yield various feature maps. In general, the pooling layer follows a convolutional layer, which is utilized to diminish the dimensions of feature maps and the network parameters. Finally, by utilizing the fully connected layers, these obtained maps can be transformed into feature vectors. We present the formula of the vital parts of the CNNs, which are the convolution layers. Assume that $X$ is the input cube with the size of $m\times n\times d$ where $m\times n$ refers to the spatial level of $X$, and $d$ counts the channels. The $j$-th filter is specified with weight $w_j$ and bias $b_j$. Then, one can express the $j$-th output associated with the convolution layer as Equation (4):

$$y_j={\sum }_{i=1}^{d}f\left(x_i\ast w_j+b_j\right),j=1,2,\dots ,k$$

(4)

Here, the activation function $f(.)$ is used to enhance the network’s nonlinearity. Currently, ReLU [19] is the most popular activation function that leads to notably rapid convergence and robustness in terms of gradient vanishing [20]. Figure 6 presents the convolution procedure.

2.5. Recurrent Neural Networks (RNNs)

RNNs extended the conventional neural network with loops in connections and were developed in [21]; RNNs can identify patterns in sequential data and dynamic temporal specification by utilizing recurrent hidden states compared to the feedforward neural network. Suppose that $x$ is the input vector. The recurrent hidden state $h^{\langle t\rangle }$ of the RNN can be updated by Equation (5):

$$h^{\langle t\rangle }=\{\begin{array}{c}o\\ f_1(h^{\langle t-1\rangle },x^{\langle t\rangle })\end{array}\begin{array}{c}ift=o\\ otherwise\end{array},$$

(5)

where $f_1$ denotes a nonlinear function, such as a hyperbolic agent function. The update rule of the recurrent hidden state can be expressed as Equation (6):

$$h^{\langle t\rangle }=f_1(u{h}^{\langle t-1\rangle }+w{x}^{\langle t\rangle }+b_h),$$

(6)

where $w$ and $u$ indicate the coefficient matrices for the input in the current state and the activation of recurrent hidden units at the prior step, respectively. $b_h$ is the bias vector. Therefore, the output ${\mathcal{Y}}^{\langle t\rangle }$ at time $t$ is presented as Equation (7):

$${\mathcal{Y}}^{\langle t\rangle }=f_2(p{h}^{\langle t\rangle }+b_y).$$

(7)

Here, $f$ is the nonlinear function, and $p$ is the coefficient matrix for the activation of recurrent hidden units in the current step, and $b_h$ represents the bias vector. Due to the vanishing gradient of traditional RNNs, long-short-term memory (LSTM) [22] and gated recurrent units [23] were introduced to handle huge sequential data. The convolution procedure is presented in [24]. Figure 7 illustrates a schematic for an RNN.

2.6. Deep Reinforcement Learning Methods

In this section, we mainly focus on the most commonly used deep RL algorithms, such as value-based methods, policy gradient methods, and model-based methods.

We first describe how to formulate the RL problem for the agent dealing with an environment while the goal is to maximize cumulative rewards. The two important characteristics of RL are as follows: first, the agent has the capability of learning good behavior incrementally and second, the RL agent enjoys the trial-and-error experience by only dealing with the environment and gathers information (see Figure 6). It is worth mentioning that RL methods are able to practically provide the most appropriate method in terms of computational efficiency as compared to some traditional approaches. One can model the RL problem with a Markov Decision Process (MDP) with a 5-tuple ($\mathcal{S}$, $\mathcal{A}$, T, $\mathcal{R}$, $\lambda$) where $\mathcal{S}$ (state-space), $\mathcal{A}$ (action space), T $\in$ [0,1] (transition function), $\mathcal{R}$ (reward function), and $\gamma$ $\in$ [0,1) (discount factor). The RL agent aims to search for the optimal expected return base on the value function $V^{\pi }\left(s\right)$ by Equation (8).

$$V^{\pi }\left(s\right)=\mathbb{E}\left({\sum }_{k=0}^{\infty }{\gamma }^k{r}_{k+t}|s_t=s.\pi \right)\mathrm{where}{V}^{*}=\underset{\pi \in \Pi }{\max }{V}^{\pi }\left(s\right)$$

(8)

where:

$$r_t=\underset{a~\pi \left(s_t,.\right)}{\mathbb{E}}\mathcal{R}\left(s_t,a,s_{t+1}\right),$$

(9)

$$\mathbb{P}\left(s_{t+1}|s_t,a_t\right)=\mathrm{T}(s_t.a_t.s_{t+1})\mathrm{with}{a}_t~\pi \left(s_t\right)$$

(10)

Analogously, the Q value function can be expressed as Equation (11):

$$Q^{\pi }\left(s.a\right)=\mathbb{E}\left({\sum }_{k=0}^{\infty }{\gamma }^k{r}_{k+t}|s_t=s.a_t=a.\pi \right)\mathrm{where}{Q}^{*}=\underset{\pi \in \Pi }{\max }{Q}^{\pi }\left(s.a\right)$$

(11)

One can see the general architecture of the DRL algorithms in Figure 8 adapted from [25].

2.6.1. Value-Based Methods

The value-based algorithms allow us to construct a value function for defining a policy. We discuss the Q-learning algorithm [26] and the deep q-network (DQN) algorithm [6] with great success when playing ATARI games. We then give a brief review of the improved DQN algorithm.

2.6.2. Q-Learning

The basic value-based algorithm is called the Q-learning algorithm. Assume Q is the value function; then, the optimal value of the Q-learning algorithm using the Bellman equation [27] can be expressed as Equation (12):

$$Q^{*}\left(s.a\right)=(\mathcal{B}{Q}^{*})(s.a)$$

(12)

where the Bellman operator ($\mathcal{B}$) can be described as Equation (13):

$$\left(\mathcal{B}K\right)\left(s,a\right)={\sum }_{\acute{s}\in S}\mathrm{T}\left(s,a,\acute{s}\right)(\mathcal{R}\left(s,a,\acute{s}\right)+\gamma \underset{\acute{a}\in \mathcal{A}}{\max }\mathrm{K}\left(\acute{s},\acute{a}\right))$$

(13)

Here, the unique optimal solution of the Q value function is $Q^{*}$ (s, a). One can check out the theoretical analysis of the optimal Q function in discrete space with sufficient exploration guarantee in [26]. In practice, a parameterized value function is able to overcome the high dimensional problems (possibly continuous space).

2.6.3. Deep Q-Networks (DQN)

The DQN algorithm is presented by Mnih et al. [6] that can obtain good results for ATARI games in an online framework. In deep Q-learning, we make use of a neural net to estimate a complex, nonlinear Q-value function. Imagine the target function as Equation (14):

$$Y_k^Q=r+\gamma \underset{\acute{a}\in \mathcal{A}}{\max }Q(\acute{s},\acute{a};{\overline{\theta }}_k)$$

(14)

The ${\overline{\theta }}_k$ parameter, which defines the values of the Q function at the $k^{th}$ iteration, will be updated only every $A$ $\in \mathbb{N}$ iteration to keep the stability and diminish the risk of divergence. In order to bound the instabilities, DQN uses two heuristics, i.e., the target Q-network and the replay memory [28]. Additionally, DQN takes the advantage of other heuristics such as clipping the rewards for maintaining reasonable target values and for ensuring proper learning. An interesting aspect of DQN is that a variety of deep learning techniques are used to practically improve its performance such as the preprocessing step of the inputs, convolutional layers, and the optimization (stochastic gradient descent) [29]. We show the general scheme of the DQN algorithm [25] in Figure 9.

2.6.4. Double DQN

In Q-learning, the DQN-value function utilizes a similar amount as Q-value in order to identify and evaluate an action which may cause overestimated values and upward bias in the algorithm. Thus, the double estimator method can be used for each variable to efficiently remove the positive bias in the action estimation process [30]. The Double DQN is independent of any source of error, namely, stochastic environmental error. The target value function in the double DQN (DDQN) can be described as Equation (15):

$$Y_k^{DDQN}=r+\gamma Q(\acute{s},\arg \underset{a\in \mathcal{A}}{\max }Q\left(\acute{s},a;{\theta }_k\right);{\overline{\theta }}_k)$$

(15)

Compared to the Q-network, DDQN is usually able to improve stability and to obtain a more accurate Q-value function as well.

2.6.5. Distributional DQN

The idea of approaches explained in the previous subsections was to estimate the expected cumulative return. Another interesting method is to represent a value distribution which allows us to better detect the inherent stochastic rewards and agent transitions in conjunction with the environment. One can define the random distribution return function associated with policy $\pi$ as follows in Equation (16):

$${\mathrm{Z}}^{\pi }(s,a)=\mathcal{R}(s,a,\acute{S})+\gamma {\mathrm{Z}}^{\pi }(\acute{S},\acute{A})$$

(16)

Equation (16) includes random state-action pairs ($\acute{S}$, $\acute{A}$) and $\acute{A}~\pi (.|\acute{S})$. Thus, the Q value function can be expressed as Equation (17):

$$Q^{\pi }(s,a)=\mathbb{E}[{\mathrm{Z}}^{\pi }(s,a)]$$

(17)

In practice, the distributional Bellman equation, which interacts with deep learning, can play the role of the approximation function [31,32,33]. The main benefit of this approach is the implementation of risk-aware behavior [34], and improved learning provides a richer set of training signals [35].

2.7. Policy Gradient Methods

This section discusses policy gradient (PG) methods that are frequently used algorithms in reinforcement learning [36] which follows a class of policy-based methods. The method is to find a neural network parameterized policy in order to maximize the expected cumulative reward [37].

2.7.1. Stochastic Policy Gradient (SPG)

The easiest approach to obtain the policy gradient estimator could be to utilize algorithm [38]. The general approach to derive the estimated gradient is shown in Equation (18):

$${\nabla }_{\omega }{\pi }_{\omega }(s,a)={\pi }_{\omega }(s,a){\nabla }_{\omega }\log ({\pi }_{\omega }\left(s,a\right))$$

(18)

while

$${\nabla }_{\omega }{V}^{{\pi }_{\omega }}\left(s_0\right)={\mathbb{E}}_{s~{\rho }^{\pi }\omega ,a~{\pi }_{\omega }}[{\nabla }_{\omega }(\log {\pi }_{\omega }\left(s,a\right))Q^{{\pi }_{\omega }}\left(s,a\right)]$$

(19)

Note that, in these methods, the policy evaluation estimates the Q-function, and the policy improvement optimizes the policy by taking a gradient step, utilizing the value function approximation. The easy way of estimating the Q-function is to exchange it with a cumulative return from entire trajectories. A value-based method such as the actor-critic method can be used to estimate the return efficiently. In general, an entropy function can be used for the policy randomness and efficient exploration purpose. Additionally, it is common to employ an advantage value function where conducts a measurement of comparison to the expected return for each action. In practice, this replacement improves the numerical efficiency.

2.7.2. Deterministic Policy Gradient (DPG)

The DPG approach is the expected gradient of the action–value function. The deterministic policy gradient can be approximated without using an integral term over the action space. It can be demonstrated that the DPG algorithms can perform better than SPG algorithms in high-dimensional action spaces [39]. NFQ and DQN algorithms can resolve the problematic discrete actions using the Deep Deterministic Policy Gradient (DDPG) [39] and the Neural Fitted Q Iteration with Continuous Actions (NFQCA) [40] algorithms, with the direct representation of a policy. An approach proposed by [41] was developed to overcome the global optimization problem while updating greedy policy at each step. They defined a differentiable deterministic policy that can be moved to the gradient direction of the value function for deriving the DDPG algorithm, Equation (20):

$${\nabla }_{\omega }{V}^{{\pi }_{\omega }}\left(s_0\right)={\mathbb{E}}_{s~{\rho }^{\pi }\omega }[{\nabla }_{\omega }({\pi }_{\omega }){\nabla }_a\left(Q^{{\pi }_{\omega }}\left(s,a\right)\right)|a={\pi }_{\omega }\left(s\right)]$$

(20)

which shows that Equation (20) is based on ${\nabla }_a(Q^{{\pi }_{\omega }}\left(s,a\right))$.

2.7.3. Actor–Critic Methods

An actor–critic architecture is a common approach where the actor updates the policy distribution with policy gradients, and the critic estimates the value function for the current policy [42], Equation (21).

$${\nabla }_{\omega }{V}^{{\pi }_{\omega }}\left(s_0\right)={\mathbb{E}}_{s~{\rho }^{{\pi }_{\beta }},a~{\pi }_{\beta }}[{\nabla }_{\theta }(\log {\pi }_{\omega }\left(s,a\right)Q^{{\pi }_{\omega }}\left(s,a\right))].$$

(21)

where $\beta$ is behavior policy that makes the gradient biased, and the critic with parameter $\theta$ estimates the value function, $Q\left(s,a;\theta \right)$, with the current policy $\pi$.

In deep reinforcement learning, the actor–critic functions can be parameterized with nonlinear neural networks [36]. The approach proposed by Sutton [7] was quite simple but not computationally efficient. The ideal is to design an architecture to profit from the reasonably fast reward propagation, the stability, and the capability using replay memory. However, the new approach utilized in the actor–critic framework presented by Wang et al. [43] and Gruslys et al. [44] has sample efficiency and is computationally efficient as well.

2.7.4. Combined Policy Gradient and Q-Learning

In order to improve the policy strategy in RL, an efficient technique needs to be engaged, such as a policy gradient, applying a sample-efficient approach and value function approximation associated with the policy. These algorithms enable us to work with continuous action spaces, to construct the policies for explicit exploration, and to apply the policies to multiagent setting where the problem deals with the stochastic optimal policy. However, the idea of combining policy gradient methods with optimal policy Q-learning was proposed by O Donoghue et al. [45] while summing the equations with an entropy function, Equation (22):

$${\nabla }_{\omega }{V}^{{\pi }_{\omega }}(s_0)={\mathbb{E}}_{s,a}[{\nabla }_{\omega }(\log {\pi }_{\omega }\left(s,a\right))Q^{{\pi }_{\omega }}\left(s,a\right)]+\alpha {\mathbb{E}}_s\left[{\nabla }_{\omega }{\mathrm{H}}^{{\pi }_{\omega }}\right(s\left)\right]$$

(22)

where

$${\mathrm{H}}^{\pi }\left(s\right)={\sum }_a\pi \left(s,a\right)\log \pi \left(s,a\right)$$

(23)

It showed that in some specific settings, both value-based and policy-based approaches have a fairly similar structure [46,47,48].

2.8. Model-Based Methods

We have discussed so far, the value-based or the policy-based methods which belong to the model-free approach. In this section, we focus on the model-based approach where the model deals with the dynamics of the environment and the reward function.

2.8.1. Pure Model-Based Methods

When the explicit model is not known, it can be learned from experience by the function approximators [49,50,51]. The model plays the actual environment role to recommend an action. The common approach in the case of discrete actions is look ahead search, and trajectory optimization can be utilized in a continuous case. A lookahead search is to generate potential trajectories with the difficulty of exploration and exploitation trade-off in sampling trajectories. The popular approaches for lookahead search are Monte Carlo tree search (MCTS) methods such that the MCTS algorithm recommends an action (see Figure 9). Recently, instead of using explicit tree search techniques, learning an end-to-end model was developed [52] with improved sample efficiency and performance as well. Lookahead search techniques are useless in a continuous environment. Another approach is PILCO, i.e., apply Gaussian processes in order to produce a probabilistic model with reasonable sample efficiency [53]. However, the gaussian processes are reliable only in low-dimensional problems. One can take the benefit of the generalization capabilities of DL approaches to build the model of the environment in higher dimensions. For example, a DNN can be utilized in a latent state space [54]. Another approach aims at leveraging the trajectory optimization such as guided policy search [55] by taking a few sequences of actions and then learns the policy from these sequences. The illustration of the MCTS process is presented in Figure 10 and was adopted from [25].

2.8.2. Integrating Model-Free and Model-Based Methods (IMF&MBM)

The choice of model-free versus model-based approaches mainly depends on the model architecture such as policy and value function. As an example to clearly explain the key point, assume that an agent needs to pass the street randomly while the best choice is to take the step unless something unusual happens in front of the agent. In this situation, using the model-based approach may be problematic due to the randomness of the model, while a model-free approach to find the optimal policy is highly recommended. There is a possibility of integrating planning and learning to produce a practical algorithm which is computationally efficient. In the absence of a model where the limited number of trajectories is known, one approach is to build an algorithm to generalize or to construct a model to generate more samples for model-free problems [56]. Another choice could be utilizing a model-based approach to accomplish primary tasks and apply model-free fine-tuning to achieve the goal successfully [57]. The tree employs a model to search techniques directly [58]. The notion of a neural network is able to combine these two approaches. The model proposed by Heess et al. [59] engaged a backpropagation algorithm to estimate a value function. Another example is the work presented by Schema Networks [60] that uses prolific structured architecture where it leads to robust generalization.

3. Review Section

This section discusses an overview of various interesting uses of both DL and deep RL approaches in economics.

3.1. Deep Learning Application in Economics

The recent attractive application of deep learning in a variety of economics domains is discussed in this section.

3.1.1. Deep Learning in Stock Pricing

From an economic point of view, the stock market value and its development are essential to business growth. In the current economic situation, there are many investors around the world that are interested in the stock market in order to receive quick and better return compared to other sectors. The presence of uncertainty and risk in the forecasting of stock pricing bring challenges to the researcher to design a market model for prediction. Despite all advances to develop mathematical models for forecasting, they are still not that successful [61]. The deep learning topic attracts scientists and practitioners as it is useful for high revenue while enhancing the prediction accuracy with DL methods.

Table 1. Application of deep learning in stock price prediction.

References	Methods	Application
[62]	Two-Streamed gated recurrent unit network	Deep learning framework for stock value prediction
[63]	Filtering methods	Novel filtering approach
[64]	Pattern techniques	Pattern matching algorithm for forecasting the stock value
[65]	Multilayer deep Approach	Advanced DL framework for the stock value price

presents recent research.

According to Table 1, Minh et al. [62] presented a more realistic framework for forecasting stock price movement concerning financial news and sentiment dictionary, as previous studies mostly relied on an inefficient sentiment dataset, which are crucial in stock trends, which led to poor performance. They proposed the Two-stream Gated Recurrent Unit (TGRU) using deep learning techniques that perform better than the LSTM model. Where it takes the advantage of applying two states that enable the model to provide much better information. They presented a sentiment Stock2Vec embedding with the proof of the model robustness in terms of market risk while using Harvard IV-4. Additionally, they provided a simulation system for investors in order to calculate their actual return. Results were evaluated using accuracy, precision, and recall values to compare TGRU and LSTM techniques with GRU. Figure 11 presents the relative percentage of performance factors for TGRU and LSTM in comparison with that for GRU.

As is clear from Figure 11, TGRU presents higher improvement in relative values for performance factors in comparison with LSTM. Also, TGRU provides higher improvement in recall values.

Song et al. [63] presented work to apply spotlighted deep learning techniques for forecasting stock trends. The research developed a deep learning model with a novel input-feature mainly focused on filtering techniques in terms of delivering better training accuracy. Results were evaluated by accuracy values in a training step. Comparing profit values for the developed approaches indicated that the novel filtering technology and stock price model by employing 715 features provided the highest return value by more than 130$. Figure 12 presents a visualized comparison for accuracy values. The comparative analysis for the methods developed by Song et al. [63] is presented in Figure 12.

Based on Figure 12, the highest accuracy is related to a simple feature model without filtering, and the lowest accuracy is related to a novel feature model with plunge filtering. By considering the trend, it can be concluded that the absence of the filtering process has a considerable effect on increasing the accuracy.

In another study, Go and Hong [64] employed the DL technique to forecast stock value streams while analysing the pattern in stock price. The study designed a DNN deep learning algorithm to find the pattern utilizing the time series technique which had a high accuracy performance. Results were evaluated by the percentage of test sets of 20 companies. The accuracy value for DNN was calculated to be 86%. However, DNN had some disadvantages such as over fitting and complexity. Therefore, it was proposed to employ CNN and RNN.

In the study by Das and Mishra [65], a new multilayer deep learning approach was used by employing the time series concept for data representation to forecast the close price of current stock. Results were evaluated by prediction error and accuracy values compared to the results obtained from the related studies. Based on the results, the prediction error was very low based on the outcome graph, and the predicted price was fairly close to the reliable price in a time series data. Figure 13 provides a comparison of the proposed method with the similar method reported by different studies in terms of accuracy. Figure 13 reports the comparative analysis from Das and Mishra [65].

Based on Figure 13, the proposed method by employing the related dataset could considerably improve the accuracy value by about 34, 13, and 1.5% compared with Huynh et al. [66], Mingyue et al. [67], and Weng et al. [68], respectively.

The used approach in [62] has the strong advantage of utilizing forward and backward learning states at the same time to present more useful information. Part of the mathematical forward pass formula for the update gate is given in Equation (24):

$$\overrightarrow{z_t}=\sigma (\overrightarrow{W_z}{x}_t+\overrightarrow{U_z}\overrightarrow{h_{t-1}}+\overrightarrow{b_z})$$

(24)

and the backward pass formula is shown in Equation (25):

$$\overleftarrow{z_t}=\sigma (\overleftarrow{W_z}{x}_t+\overleftarrow{U_z}\overleftarrow{h_{t-1}}+\overleftarrow{b_z})$$

(25)

where $x_t$ is the input vector, and b is the bias. $\sigma$ denotes the logistic function. $h_t$ is the activation function and W, U are the weights. In the construction of TGRU, both forward and backward passes linked into a single context for the stock forecasting, which led to dramatically enhanced accuracy of the prediction by applying more efficient financial indicators regarding financial analysis. In Figure 13 one can see the whole architecture of the proposed model. The TGRU structure is presented in Figure 14, adopted from [62].

3.1.2. Deep Learning in Insurance

Another application of DL methods is the insurance sector. One of the challenges of insurance companies is to efficiently manage fraud detection (see

Table 2. Application of deep learning in the Insurance industry.

Reference	Methods	Application
[69]	Cycling algorithms	Fraud detection in car insurance
[70]	LDA-based appraoch	Insurance fraud
[71]	Autoencoder technique	Evaluation of risk in car insurance

). In recent years, ML techniques have been widely used to develop practical algorithms in this field due to the high market demand for new approaches compared with traditional methods to practically measure all types of risks (Brockett et al. 2002; Pathak et al. 2005, Derrig, 2002). For instance, there are many demands for car insurance that forces companies to find novel strategies in order to meliorate and upgrade their system. Table 2 summarizes the most notable studies for the application of DL techniques in insurance.

Bodaghi and Teimourpour [69] proposed a new method to detect professional fraud in car insurance for big data by using social network analysis. Their approach employed cycling, which plays crucial roles in network systems, to construct an indirect collisions network and to then identify doubtful cycles in order to make more profit concerning more realistic market assumption. Fraud detection may affect pricing strategies and long-term profit while dealing with the insurance industry. Evaluation of the methods for suspicious components was performed by the probability of being fraudulent in the actual data. Fraud probability was calculated for different numbers of nodes in various community IDs and cycle IDs. Based on results, the highest Fraud probability for a community was obtained at node number 10, by 3.759, and the lowest Fraud probability for a community was obtained at node number 25, by 0.638. Also, the highest Fraud probability for a cycle was obtained at node number 10, by 7.898, which was about 110% higher than that for the community, and the lowest Fraud probability for the cycle was obtained at node number 12, by 1.638, which was about 156% higher than that for the community.

Recently, a new deep learning model was presented to investigate fraud in car insurance by Wang and Xu [70]. The proposed model outperforms the traditional method where the combination of latent Dirichlet allocation (LDA) [60] and the DNN technique is utilized to extract the text features of the accidents comprising traditional features and text features. Another important topic that brings interest to the insurance industry is telematics devices that deal with detecting hidden information inside the data efficiently. Results were evaluated by accuracy and precision performance factors in two scenarios, “with LDA” and “without LDA”, to consider the effect of LDA on the prediction process. Figure 14 presents the visualized results. A comparative analysis of SVM, RF, and DNN by Wang and Xu [70] is illustrated in Figure 15.

According to Figure 15, LDA has a positive effect on the accuracy of DNN and RF that could successfully increase the accuracy of DNN and RF by about 7% and 1%, respectively, but reduce the accuracy of SVM by about 1.2%. On the other hand, LDA could successfully increase the precision of SVM, RF, and DNN by about 10, 1.2 and 4%, respectively.

Recent work proposed an algorithm combining an auto-encoder technique with telematics data to forecast the risk associated with insurance customers [71]. To efficiently deal with a large dataset, one requires powerful updated tools for detecting valuable information such as telematics devices [71]. The work utilized a conceptual model in conjunction with telematics technology to forecast the risk (see Figure 16). While the risk score (RS) calculated by Equation (26):

$${\left(RS\right)}_j={\sum }_i{W}_{c_i}*O_{ij}\mathrm{where}{W}_{c_i}=\frac{{\sum }_i{\sum }_j{O}_{ij}}{{\sum }_j{O}_{ij}}$$

(26)

where $W$ and $O$ represent the risk weight and driving style, respectively. Their experimental results showed the superiority of their proposed approach (see figure adopted for the model [71]).

3.1.3. Deep Learning in Auction Mechanisms

Auction design has a major importance in practice that allows the organizations to present better services to their customers. A great challenge to learn a trustable auction is that its bidders require optimal strategy for maximizing profit. In this direction, Myerson designed an optimal auction with only a single item [72]. There are many works with results for single bidders but most often with partial optimality [73,74,75].

Table 3. Application of deep learning in auction design.

Reference	Methods	Application
[76]	Augmented Lagrangian Technique	Optimal auction design
[77]	Extended RegretNet method	Maximized return in auction
[78]	Data-Driven Method	Mechanism design in auction
[79]	Multi-layer neural Network method	Auction in mobile networks

presents the notable studies developed by DL techniques in Auction Mechanisms.

Dütting et al. [80] designed a compatible auction with multi-bidders that maximizes the profit by applying multi-layer neural networks for encoding its mechanisms. The proposed method was able to solve much more complex tasks while using the augmented Lagrangian technique than LP-based approach. Results were evaluated by comparing the total revenue. Despite all previous results, the proposed approach had great capability to be applied to the large setting with high profit and low regret. Figure 17 presents the revenue outcomes for the study by Dütting et al. [80].

According to Figure 17, RegretNet as the proposed technique increased the revenue by about 2.32 and 2% compared with VVCA and AMAbsym, respectively.

Another study used the deep learning approach to extend the result in [76] in terms of both budget constraints and Bayesian compatibility [77]. The method demonstrated that neural networks are able to efficiently design novel optimal-revenue auctions by focusing on multiple setting problems with different valuation distributions. Additionally, a new method proposed by [78] improved the result in [80] by constructing different mechanisms to apply DL techniques. The approach makes use of strategy under the assumption that multiple bids can be applied to each bidder. Another attractive approach applied to mobile blockchain networks constructed an effective auction using a multi-layer neural network technique [79]. Neural networks trained by formulating parameters maximize the profit of the problem, which considerably outperformed the baseline approach. The main recent work mentioned in Table 3 indicates that this field is growing fast.

The proposed approach in [77] modified the regret definition in order to handle budget constraints while designing an auction with multiple item settings (see Figure 18). The main expected regret is shown in Equation (27):

$$rg{t}_i={\mathbb{E}}_{t_i~F_i}\left[\underset{\acute{t_i}\in {\mathcal{T}}_i}{\max }\chi (p_{i(\acute{t_i})}\le b_i)({\mathcal{U}}_i(t_i,\acute{t_i})-{\mathcal{U}}_i(t_i,t_i))\right],$$

(27)

where $\chi$ is the indicator function, $\mathcal{U}$ is the interim utility, and $p$ is the interim payment. The method improved the state-of-the-art utilized DL concepts to optimally design an auction applied to the multiple items with high-profit. Figure 18 represents an adaptation of RegretNet [77].

3.1.4. Deep Learning in Banking and Online Markets

In current technology improvement, fraud detection is a challenging application of deep learning, namely, in online shopping and credit cards. There is a high market demand to construct an efficient system for fraud detection in order to keep the involved system safe (see

Table 4. Application of deep learning in the banking system and online market.

Reference	Methods	Application
[81]	AE	Fraud detection in unbalanced datasets
[82]	Network topology	credit card transactions
[83]	Natural language Processing	Anti-money laundering detection
[84]	AE and RBM architecture	Fraud detection in credit cards

).

Unsupervised learning could be used to investigate online transactions due to variable patterns of fraud and change in customer’s behavior. An interesting work relied on employing deep learning methods such as AE and RBM to mimic irregularity from regular patterns by rebuilding regular transactions in real-time [84]. The applied fundamental experiments to confirm that AE and RBM approaches are able to accurately detect credit cards using a huge dataset. Although deep learning approaches enable us to fairly detect the fraud problem in credit cards, model building makes use of diverse parameters that affect its outcomes. The work of Abhimanyu [82] evaluated commonly used methods in deep learning to efficiently check out previous fraud detection problems in terms of class inconsistency and scalability. A plenary advice was provided by the authors regarding analysis of model parameter sensitivity and its tuning while applying neural network architecture to the fraud detection problems in credit cards. Another study by [81] designed an autoencoder algorithm in order to model the fraudulent activities, as efficient automated tools need to accurately handle huge daily transactions around the world. The model enables investigators to give a report regarding unbalanced datasets where there is no need to use data balanced approaches such as the Under-Sampling approach. One of the world’s largest industries is money laundering, which is the unlawful process of hiding the original source of received money unlawfully by transmitting it through a complicated banking transaction. A recent work, considering anti-money laundering detection, designed a new framework using natural language processing (NLP) technology [83]. Here, the main reason for constructing a deep learning framework is decreasing the cost of human capital and time consumption. The distributed and scalable method (e.g., NLP) performs complex mechanisms associated with various data sources such as news and tweets in order to make the decision simpler while providing more records.

It is a great challenge to design a practical algorithm to prevent fraudulent transactions in financial sectors while dealing with a credit card. The work in [81] presented an efficient algorithm that has the superiority of controlling unbalanced data compared to traditional algorithms. Where anomaly detection can be handled by the reconstruction loss function, we depicted their proposed AE algorithm in Algorithm 1 [81].

Algorithm 1. AE pseudo algorithm
Steps	Processes
Step 1:Prepare the input data	Input Matrix X II input dataset Parameter of the matrix//parameter (w,bx,bh) where: w: Weight between layers, bx Encoder’s parameters, bh Decoder’s Parameters
Step 2: initial Variables	h←null // vector for the hidden layer X←null // Reconstructed x L←null II vector for Loss Function 1←batch number i←0
Step 3: loop statement	While i < 1 do II Encoder function maps an input X to hidden representation h: h = f (p[i ].w + p[i] bx) /* Decoder function maps hidden representation h back to a Reconstruction X:*/ X = g(p[i ].l/ + p[i] bx) /*For nonlinear reconstruction, the reconstruction loss is generally from cross-entropy :*/ L = −sum(x *log(X) + (1 − x) *log(l − X)) /* For linear reconstruction, the reconstruction loss is generally from the squared error:*/ L = sum(x − X)2 Min θ[i] = p L(x − X) End while Return θ
Step 4: output	θ←<null matrix>//objective function /*Training an auto-encoder involves finding parameters = (W,hx,bb) that minimize the reconstruction loss in the given dataset X and the objective function*/

3.1.5. Deep Learning in Macroeconomics

Macroeconomic prediction approaches have gained much interest in recent years, which are helpful for investigating economics growth and business changes [85]. There are many proposed methods that can forecast macroeconomic indicators, but these approaches require huge amounts of data and suffer from model dependency.

Table 5. Application of deep learning in macroeconomics.

Reference	Methods	Application
[86]	Encoder-decoder	Indicator prediction
[87]	Backpropagation Approach	Forecasting inflation
[88]	Feed-Forward neural Network	Asset allocation

shows the recent results which are more acceptable than the previous ones.

Application of deep learning in macroeconomics has been exponentially growing during the past few years [89,90,91]. Smalter and Cook [92] presented a new robust model called an encoder–decoder that makes use of deep neural architecture to increase the accuracy of prediction with a low data demand concerning unemployment problems. The mean absolute error (MAE) was employed for evaluating the results. Figure 19 visualizes the average values of MAE obtained by Smalter and Cook [88]. This visualization compares average MAE values for CNN, LSTM, AE, DARM, and the Survey of Professional Forecasters (SPF).

According to Figure 19, the lowest average MAE is related to AE followed by SPF with additional advantages such as supplying nice single-series efficiency, higher accuracy of predicting, and better model specification.

Haider and Hanif [87] employed an ANN method applied to forecast macroeconomic indicators for inflation. Results were evaluated by RMSE values for comparing the performance of ANN, AR, and ARIMA techniques. Figure 20 presents the average RMSE values for comparison.

According to Figure 20, the study with model simulation based on a backpropagation approach outperformed previous models such as the autoregressive integrated moving average (ARIMA) model. Another useful application of DL architecture is to deal with investment decisions in conjunction with macroeconomic data. Chakravorty et al. [88] used a feed-forward neural network to perform tactical asset allocation while applying macroeconomic indicators and price-volume trends. They proposed two different methods in order to build a portfolio; the first one estimated expected returns and uncertainty, and the second approach obtained allocation directly using neural network architecture and the optimized portfolio Sharpe. Their methods with the adopted trading strategy demonstrated a comparable achievement with previous results.

A new technique was used in [86] to enhance the indicator prediction accuracy; the model requires few data. Experimental results indicate that the encoder–decoder outperformed the highly cited SPF prediction. The results in

Table 6. Inflection point prediction for Unemployment around 2007.

Time Horizon	SPF	Encoder–Decoder
3-month horizon model	Q3 2007	Q1 2007
6-month horizon model	Q3 2007	Q2 2007
9-month horizon model	Q2 2007	Q3 2007
12-month horizon model	Q3 2008	Q1 2008

showed that the encoder–decoder is more responsive than the SPF prediction or is more adaptable to data changes [86].

3.1.6. Deep Learning in Financial Markets (Service & Risk Management)

In financial markets, it is crucial to efficiently handle the risk arising from credits. Due to recent advance in big data technology, DL models can design a reliable financial model in order to forecast credit risk in banking systems (see

Table 7. Application of deep learning in financial markets (services and risk management).

Reference	Methods	Application
[89]	Binary Classification Technique	Loan pricing
[90]	Feature selection	Credit risk analysis
[91]	AE	Portfolio management
[92]	Likelihood Esrtimation	Mortgage risk

).

Addo et al. [89] employed a binary classification technique to identify essential features of selected ML and DL models in order to evaluate the stability of the classifiers based on their performance. The study used the models separately to forecast loan default probability, by considering the selected features and the selected algorithm, which are the crucial keys in loan pricing processes. In credit risk management, it is important to distinguish the good and the bad customers which oblige us to construct very efficient classification models by using deep learning tools. Figure 21 presents the results visualized for the study by Addo et al. [89] to compare the performance of LR, RF, Gboosting, and DNN in terms of RMSE and area under the curve values (see Figure 21).

In general, credit data include useless and unneeded features that need to be filtered by the feature selection strategy to provide the classifier with high accuracy.

Ha and Nguyen [90] studied a novel feature selection method that helps financial institution sto perform credit assessment with less workload while focusing on important variables and to improve the classification accuracy in terms of credit scoring and customer rating. The accuracy value was employed for comparing the performance of Linear SVM, CART, k-NN, Naïve Bayes, MLP, and RF techniques. Figure 22 presents the comparison results related to the study by Ha and Nguyen [90] (see Figure 22).

Figure 22 contains the base type of methods and their integration with GA, PSO, LR, LDA, and t-tests as different scenarios except RF which is in its baseline type. In all the cases except linear SVM, integrating with optimizers and filters such as GA, PSO, and LR improved the accuracy compared with their baseline type. However, in SVM, the baseline model provided higher accuracy compared with other scenarios.

A study applied hierarchical models to present high performance regarding big data [91]. They constructed a deep portfolio with the four processes of auto-encoding, calibrating, validating, and verifying the application of a portfolio including put and call options with underlying stocks. Their methods are able to find the optimal strategy in the theory of deep portfolios by ameliorating the deep feature. Another work developed a deep learning model in mortgage risk applied to huge data sets that discovered the nonlinearity relationship between the variables and debtor behavior which can be affected by the local economic situation [92]. Their research demonstrated that the unemployment variable is substantial in the risk of mortgage which brings the importance of implications to the relevant practitioners.

3.1.7. Deep Learning in Investment

Financial problems generally need to be analyzed in terms of datasets from multiple sources. Thus, it is substantial to construct a reliable model for handling unusual interactions and features from the data for efficient forecasting.

Table 8. Application of deep learning in stock price prediction.

Reference	Methods	Application
[93]	LSTM and AE	Market investment
[94]	Hyper-parameter	Option pricing in finance
[95]	LSTM and SVR	Quantitative strategy in investment
[96]	R-NN and genetic method	Smart financial investment

comprises the recent results of using deep learning approaches in financial investment.

Aggarwal and Aggarwal [93] designed a deep learning model applied to an economic investment problem with the capability of extracting nonlinear data patterns. They presented a decision model using neural network architecture such as LSTM, auto-encoding, and smart indexing to better estimate the risk of portfolio selection with securities for the investment problem. Culkin and Das [94] investigated the option pricing problem using DNN architecture to reconstruct the well-known Black and Scholes formula with considerable accuracy. The study tried to revisit the previous result [97] and made the model more accurate with the diverse selection of hyper-parameters. The experimental result showed that the model can price the options with minor error. Fang et al. [95] investigated the option pricing problem in conjunction with transaction complexity where the research goal is to explore efficient investment strategy in a high-frequency trading manner. The work used the delta hedging concept to handle the risk in addition to the several key components of the pricing such as implied volatility and historical volatility, etc. LSTM-SVR models were applied to forecast the final transaction price with experimental results. Results were evaluated by the deviation value and were compared with single RF and single LSTM methods. Figure 23 presents the visualized results to compare results more clearly for the study by Culkin and Das [94].

Based on the results, the single DL approach outperforms the traditional RF approach with higher return in adopted investment strategy, but its deviation is considerably higher than that for the hybrid DL (LSTM-SVR) method. A novel learning Genetic Algorithm is proposed by Serrano [96] concerning Smart Investment that uses the R-NN model to emulate human behavior. The model makes use of complicated deep learning architecture where reinforcement learning occurs for fast decision-making purposes, deep learning for constructing stock identity, clusters for the overall decision-making purpose, and genetics for the transfer purpose. The created algorithm improved the return regarding the market risk with minor error performance.

The authors in [96] constructed a complex model while the genetic algorithm using network weights was used to imitate the human brain where applying the following formula for the encoding–decoding organism, Equation (28):

$$\mathit{min}\Vert X-\zeta \left(W_2\zeta \left(X{W}_1\right)\right)\Vert \hspace{1em}\mathrm{s}.\mathrm{t}.W_1\ge 0$$

(28)

and

$$W_2=\mathrm{pinv}\left(\zeta \left(X{W}_1\right)\right)X\hspace{1em},\hspace{1em}\mathrm{pinv}\left(x\right)=(x^{T}x)x^T$$

(29)

where $x$ is the input vector, $W$ is the weight matrix. $Q_1$ = $\zeta \left(X{W}_1\right)$ represents the neuron vector, and $Q_2=\zeta \left(W_2{Q}_1\right)$ represents the cell vector. We illustrate the whole structure of the model in Figure 24 adopted from [96].

3.1.8. Deep Learning in Retail

New applications of DL as well as novel DRL in retail industry are emerging in a fast pace [98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117]. Augmented reality (AR) enables customers to improve their experience while buying/finding a product from real stores. This algorithm is frequently used by researchers in the field.

Table 9. Application of deep learning in retail markets.

Reference	Methods	Application
[98]	Augmented reality and image classification	Improving shopping in retail markets
[99]	DNN methods	Sale prediction
[100]	CNN	Investigation in retail stores
[101]	Adaptable CNN	Validation in the food industry

presents the notable studies.

Cruz et al. [98] combined the DL technique and augmented reality approaches in order to provide information for clients. They presented a mobile application that is able to locate clients by means of the image classification technique in deep learning. Then, employed AR approaches to efficiently advise finding the selected product with all helpful information regarding that product in large stores. Another interesting application of deep learning methods is in fashion retail with large supply and demand where precise sales prediction is tied to the company’s profit. Nogueira et al. [99] designed a novel DNN to accurately forecast future sales where the model uses a huge and completely different set of variables such as physical specifications of the product and the idea of subject-matter expert. Their experimental work indicated that DNN model performance is comparable with other shallow approaches such as RF and SVR. An important issue for retail is to analyze client behavior in order to maximize revenue that can be performed by computer vision techniques in the study by De Sousa Ribeiro et al. [100]. The proposed CNN regression model deals with counting problems where assessing the number of available persons in the stores and detecting crucial spots. The work also designed a foreground/background approach for detecting the behavior of people in retail markets. The results of the proposed method were compared with a common CNN technique in terms of accuracy. Figure 25 presents the visualized result for the study by De Sousa Ribeiro et al. [100].

According to Figure 25, the proposed model is robust enough and performs better than common CNN methods in both datasets. In the current situation of the food retail industry, it is crucial to distribute the products to the market with proper information and remove the possibility of mislabeling in terms of public health.

A new adaptable convolutional neural network approach for Optical Character Verification was presented with the aim to automatically identify the use by the dates in a large dataset [101]. The model applies both a k-means algorithm and k-nearest neighbor to incorporate calculated centroids to the CNN for efficient separation and adaptation. Developed models allow us to better manage the precision and the readability of important use related to dates and to better control the tractability information in food producing processes. The most notable research is collected in Table 9 with the application of DL in retail market. The adaptation method in [117] interconnects C and Z cluster centroids illustrated in Figure 11. This is to construct a new augmented cluster including information from both networks in CNN1 and CNN2 using k-NN classification [101] (see Figure 26). The methodologies lead to considerably improved food safety and correct labelling.

3.1.9. Deep Learning in Business (Intelligence)

Nowadays, big data solutions play the key role in business services and productivities to efficiently reinforce the market. To solve the complex business intelligence (BI) problems dealing with market data, DL techniques are useful (see

Table 10. Application of deep learning in business intelligence.

Reference	Methods	Application
[102]	MLP	BI with client data
[103]	MLS and SAE	Feature selection in market data
[104]	RNN	Information detection in business data
[105]	RNN	Predicting procedure in business

). Table 10 presents the notable studies for the application of deep learning in business intelligence.

Fombellida et al. [102] engaged the concept of meta plasticity, which has the capability of improving the flexibility of learning mechanisms to detect more useful information and learning from data. The study focused on MLP where the output is in the application of BI while utilizing the client data. The developed work approved that the model reinforces learning over the classical MLPs and other systems in terms of learning evolution and ultimate accomplishment regarding precision and stability. The results of the proposed method were compared with MOE developed by West [106] and MCQP developed by Peng et al. [107] and Fombellida et al. [102] in terms of accuracy and sensitivity. Results are presented in Figure 27.

As is clear from Figure 27, the proposed method provided higher sensitivity compared with other methods and a lower accuracy value.

Business intelligence Net, which is a recurrent neural network for exploiting irregularity in business procedures, was designed to mainly manage the data aspect of business procedures. Where, this Net does not depend on any given information about the procedure and clean dataset by Nolle et al. [104]. The study presented a heuristic setting that decreased the handy workload. The proposed approach can be applied to model the time dimension in sequential phenomenon which is useful for anomalies. It is proven by the experimental results that BI Net is a trustable approach with high capability of anomaly detection in business phenomenon logs. An alternative strategy to the ML algorithm needs to manage huge amounts of data generated by enlargement and broader use of digital technology. DL enables us to dramatically handle large datasets with heterogeneous properties. Singh and Verma [103] designed a new multi-layer feature selection interacting with a stacked auto-encoder (SAE) to detect crucial representations of data. The novel presented method performed better than commonly used ML algorithms applied to the Farm Ads dataset. Results were evaluated by employing accuracy and area under the curve factors. Figure 28 presents the visualized results according to Singh and Verma [103].

According to Figure 28, RBF-based SVM provided higher accuracy and AUC, and the lowest accuracy and AUC were related to the RF method. The kernel type is the most important factor for the performance of SVM, and the RBF kernel provides higher performance compared with that for the linear kernel.

A new approach [105] used recurrent neural network architecture for forecasting the business procedure manner. Their approach was equipped with an explicit process characteristic, with no need for a model, where the RNN inputs build by means of an embedded space with demonstrated results regarding the validation accuracy and the feasibility of this method.

The work in [103] utilized novel multi-layer SAE architecture to handle Farm Ads data setting where the traditional ML algorithm did not perform well regarding high dimensionality and the huge sample size characteristics of Farm Ads data. Their feature selection approach has high capability of dimensionality reduction and enhancing the classifier performance. We depict the complete process of the algorithm in Figure 29.

Although DL utilizes the representation learning property of DNN and handles complex problems involving nonlinear patterns of economic data, DL methods generally cannot align the learning problem with the goal of the trader and the significant market constraint to detect the optimal strategy associated with economics problems. RL approaches enable us to fill the gap with their powerful mathematical structure.

3.2. Deep Reinforcement Learning Application in Economics

Despite the traditional approaches, DRL has the important capability of capturing substantial market conditions to provide the best strategy in economics, which also provides the potential of scalability and efficient handling of high-dimensional problems. Thus, we are motivated to consider the recent advance of deep RL applications in economics and the financial market.

3.3. Deep Reinforcement Learning in Stock Trading

Financial companies need to detect the optimal strategy while dealing with stock trading in the dynamic and complicated environment in order to maximize their revenue. Traditional methods applied to stock market trading are quite difficult for experimentation when the practitioner wants to consider transaction costs. RL approaches are not efficient enough to find the best strategy due to the lack of scalability of the models to handle high-dimensional problems [108].

Table 11. Application of deep RLs in the stock market.

Reference	Methods	Application
[109]	DDPG	Dynamic stock market
[110]	Adaptive DDPG	Stock portfolio strategy
[111]	DQN methods	Efficient market strategy
[112]	RCNN	Automated trading

presents the most notable studies developed by deep RLs in the stock market.

Xiong et al. [109] used the deep deterministic policy gradient (DDPG) algorithm as an alternative to explore the optimal strategy in dynamic stock markets. The algorithm components handle large action-state space, taking care of the stability, removing sample correlation, and enhancing data utilization. Results demonstrated that the applied model is robust in terms of equilibrating risk and performs better as compared to traditional approaches with the guarantee of higher return. Xinyi et al. [110] designed a new Adaptive Deep Deterministic Reinforcement Learning framework (Adaptive DDPG) dealing with detecting optimal strategy in dynamic and complicated stock markets. The model combined an optimistic and pessimistic deep RL that relies on both negative and positive forecasting errors. Under complicated market situations, the model has the capability to gain better portfolio profit based on the Dow Jones stocks.

Li et al. [111] did survey studies on deep RL for analyzing the multiple algorithms for stock decision-making mechanism. Their experimental results, based on three classical models, DQN, Double DQN and Dueling DQN, showed that among them, DQN models enable us to attain a better investment strategy in order to optimize the return in stock trading where applying empirical data to validate the model. Azhikodan et al. [112] focused on automating oscillation in securities trading using deep RL where they employed a recurrent convolutional neural network (RCNN) approach for forecasting stock value from the economic news. The original goal of the work was to demonstrate that deep RL techniques are able to efficiently detect the stock trading tricks. The recent deep RL results in the application of stock markets can be viewed in

Table 12. Application of deep reinforcement learning in portfolio management.

References	Methods	Application
[109,113]	DDPG	Algorithmic trading
[114]	Model-less CNN	Financial portfolio algorithm
[15]	Model-free	Advanced strategy in portfolio trading
[115]	Model-based	Dynamic portfolio optimization

. An adaptive DDPG [110] comprising both an actor network $\mu \left(s|{\theta }^{\mu }\right)$ and a critic network $Q\left(s,a|{\theta }^Q\right)$ utilized for the stock portfolio with a different update structure than the DDPG approach is given by Equation (30):

$$\begin{gathered} {\theta }^{\acute{Q}}\leftarrow \tau {\theta }^Q+(1-\tau ){\theta }^{\acute{Q}} \\ {\theta }^{\acute{\mu }}\leftarrow \tau {\theta }^{\mu }+(1-\tau ){\theta }^{\acute{\mu }} \end{gathered}$$

(30)

where the new target function is Equation (31):

$${\mathcal{Y}}_i=r_i+\gamma \acute{Q}(s_{i+1},\acute{\mu }(s_{i+1}|{\theta }^{\acute{\mu }},{\theta }^{\acute{Q}}))$$

(31)

Experimental results indicated that the model outperformed the DDPG with high portfolio return as compared to the previous methods. One can check the structure of the model in Figure 30 adopted from [110].

3.3.1. Deep Reinforcement Learning in Portfolio Management

Algorithmic trading area is currently using deep RL techniques for portfolio management with fixed allocation of capital into various financial products (see Table 12). Table 12 presents the notable studies in the application of deep reinforcement learning in portfolio management.

Liang et al. [113] engaged different RL methods, such as DDPG, Proximal Policy Optimization (PPO), and PG methods, to obtain the strategy associated with financial portfolio in continuous action-space. They compared the performance of the models in various settings in conjunction with the China asset market and indicated that PG is more favorable in stock trading than the two others. The study also presented a novel Adversarial Training approach for ameliorate the training efficiency and the mean-return, where the new training approach ameliorated the performance of PG as compared to uniform constant rebalanced portfolios (UCRP). Recent work by Jiang et al. [114] employed a deterministic deep reinforcement learning approach based on cryptocurrency to obtain the optimal strategy in financial problem settings. Cryptocurrencies, such as Bitcoin, can be used in place of governmental money. The study designed a model-less convolutional neural network (RNN) where the inputs are historical asset prices from a cryptocurrency exchange with the aim to produce the set of portfolio weights. The proposed models try to optimize the return using the network reward function in the reinforcement learning manner. The performance of their presented CNN approach obtained good results as compared to other benchmark algorithms in portfolio management. Another trading algorithm was proposed as the model-free Reinforcement Learning framework [15] where the reward function was engaged by applying a fully exploiting DPG approach so as to optimize the accumulated return. The model includes Ensemble of Identical independent evaluators (EIIE) topology to incorporate large sets of neural-net in terms of weight-sharing and a portfolio-vector memory (PVM) in order to prevent the gradient destruction problem. There is an online stochastic batch learning (OSBL) scheme to consecutively analyze steady inbound market information, in conjunction with CNN, LSTM, and RNN models. The results indicated that the models, while interacting with benchmark models, performed better than previous portfolio management algorithms based on a cryptocurrency market database. A novel model-based deep RL scheme was designed by Yu et al. [115] in the sense of automated trading to take action and make the decisions sequentially associated with global goals. The model architecture includes an infused prediction module (IPM), a generative adversarial data augmentation module (DAM), and a behavior cloning module (BCM), dealing with designed back-testing. empirical results, using historical market data, proved that the model is stable and gains more return as compared to baseline approaches and other recent model-free methods. Portfolio optimization is a challenging task while trading stock in the market. Authors in [115] utilized a novel efficient RL architecture associated with a risk-sensitive portfolio combining IPM to forecast the stock trend with historical asset prices for improving the performance of the RL agent, DAM to control the over-fitting problem, and BCM to handle unexpected movement in portfolio weights and to retain the portfolio with low volatility (see Figure 31). The results demonstrate the complex model is more robust and profitable as compared to the prior approaches [115].

3.3.2. Deep Reinforcement Learning in Online Services

In current development of online services, the users face the challenge of detecting their interested items efficiently where recommendation techniques enable us to give the right solutions to this problem. Various recommendation methods are presented such as content-based collaborative filtering, factorization machines, multi-armed bandits, to name a few. These proposed approaches are mostly limited to where the users and recommender systems interact statically and focus on short-term rewards.

Table 13. Application of deep reinforcement learning in online services.

Reference	Methods	Application
[116]	Actor–critic method	Recommendation architecture
[117]	SS-RTB method	Bidding optimization in advertising
[118]	DDPG and DQN	Pricing algorithm for online market
[119]	DQN scheme	Online news recommendation

presents the notable studies in the application of deep reinforcement learning in online services.

Feng et al. [116] applied a new recommendation using an actor–critic model in RL that can explicitly have a dynamic interaction and long-term rewards in consecutive decision-making processes. The experimental work utilizing practical datasets proved that the presented approach outperforms the prior methods. A key task in online advertising is to optimize advertisers’ gain in the framework of bidding optimization.

Zhao et al. [117] focused on real-time bidding (RTB) applied to sponsored search (SS) auction in a complicated stochastic environment associated with user action and bidding policies (see Algorithm 2). Their model, the so-called SS-RTB, engaged reinforcement learning concepts to adjust a robust Markov Decision Process (MDP) model in a changing environment, is based on a suitable aggregation level of datasets from auction market. Empirical results of both online and offline evaluation based on the Alibaba auction platform indicated the usefulness of the proposed method. In the rapid growing of business, online retailers face more complicated operations that heavily require detection of updated pricing methodology in order to optimize their profit. Liu et al. [118] proposed a pricing algorithm that models the problem in the framework of MDP based on E-commerce platform. They used deep reinforcement learning approaches to effectively deal with the dynamic market environment and market changes and to set efficient reward functions associated with the complex environment. Online testing for such models is impossible as legally the same prices have to be presented to the various customers simultaneously. The model engages deep RL techniques to maximize the long-term return while applying both discrete and continuous setting for pricing problems. Empirical experiments showed that the obtained policies from DDPG and DQN methods were much better than other pricing strategies based on various business database.s Based on reports of Kompan and Bieliková [120], news aggregator services are the favorite online services able to supply massive volume of content for the users. Therefore, it is important to design news recommendation approaches for boosting the user experience. Results were evaluated by precision and recall values into two scenarios: SME.SK and manually annotated. Figure 32 presents the visualized results for the study by Kompan and Bieliková [120].

Algorithm 2 [117]: DQN Leaming

1:  for epsode = 1 to n do

2:  Initialize replay memory D to capacity N

3:  Initialize action value functions (Qtrain.Qep. Qtarget)

with weights Otrain.Oep.Otarget

4:  for t = 1 to m do

5:    With probability E select a random action at

6:    otherwise select at = arg max 0 Qep(St, a;θep )

7:    Execute action at to auction simulator and observe

state St+I and reward rt

8:    if budget of St+ 1 < 0, then continue

9:    Store transition (s1,at,r1, s1+1 ) in D

10:    Sample random rmru batch of transitions

(sj,aj,rj, Sj+1 ) from D

11:   if j = m then

12:     Set Yi = ri

13:  else

14:     Set Yi = ri + y arg maxa, Qiarget (si+1• a.,θtarget)

15:    end if

16:    Perform a gradient descent step on the loss function

(Yi − Qirain(si.ai;θ1rain)) 2

17:  end for

18:  Update θep with θ

19:  Every C steps, update θ1arget with θ

20: end for

As is clear from Figure 32, in both scenarios, the proposed method provided the lowest recall and precision compared with TFIDF. A recent research by Zheng et al. [119] designed a new framework using the DQN scheme for online news recommendation with the capability of taking both current and future rewards. The study considered user activeness and also the Dueling Bandit Gradient Descent approach to meliorate the recommendation accuracy. Wide empirical results, based on online and offline tests, indicated the superiority of their novel approach.

To deal with the bidding optimization problem is the real-world challenge in online advertising. Despite the prior methods, recent work [117] used an approach called SS-RTB to handle sophisticated changing environments associated with bidding policies (see Table 13). More importantly, the model was extended to the multi-agent problem using robust MDP and then evaluated by the performance metric PUR_AMT/COST that showed the model considerably outperform the PUR_AMT/COST. The PUR_AMT/COST is a metric of optimizing the buying amount with high correlation of minimizing the cost.

4. Discussion

A comparative result of DL and DRL models was applied to the multiple economic domains discussed in

Table 14. Comparative study of DL and DRL models in economics.

Methods	Dataset Type	Complexity	Detection Efficiency	Accuracy & Processing Rate	Profit & Risk	Application
TGRU	Historical	High	Reasonable	High-Reasonable	Reasonable profit	Stock pricing
DNN	Historical	Reasonably high	Reasonable	High-Reasonable	Reasonable profit	Stock pricing
AE	Historical	High	High	High-Reasonably high	Reasonably low risk	Insurance
RgretNet	Historical	High	Reasonable	High-Reasonable	High profit	Auction design
AE & RBM	Historical	Reasonably high	Reasonable	High-Reasonable	Low risk	Credit card fraud
ENDE	Historical	Reasonable	Reasonable	High-Reasonable	---	Macroeconomic
AE	Historical	High	High	High-Reasonable	High-Low	Risk management
LSTM-SVR	Historical	High	Reasonable	Reasonably-high-High	High-Low	Investment
CNNR	Historical	Reasonable	High	Reasonably high-High	Reasonably high	profit Retail market
RNN	Historical	Reasonable	High	Reasonable-Reasonable	---	Business intelligence
DDPG	Historical	High	High	Reasonably high-High	High-Low	Stock trading
IMF&MBM	Historical	High	High	Reasonabley high-High	High profit	portfolio managing
DQN	Historical	High	High	High-High	High-Low	Online services

and Figure 33. Different aspects of proposed models were summarized such as model complexity, accuracy and speed, source of dataset, internal detection property of the models, and profitability of the model regarding to revenue and managing the risk. Our work indicated that both DL and DRL algorithms are useful for prediction purposes with almost the same quality of prediction in terms of statistical error. Deep learning models such as AE methods in risk management [91] and LSTM-SVR approaches [95] in investment problems showed that they enable agents to considerably maximize their revenue while taking care of risk constraints with reasonably high performance as it is quite important to the economic markets. In addition, reinforcement learning is able to simulate more efficient models with more realistic market constraints, while deep RL goes further to solve the scalability problem of RL algorithms, which is crucial for fast users and market growth, and that efficiently work with high-dimensional settings as it is highly desired in the financial market. DRL can give notable help to design more efficient algorithms for forecasting and analyzing the market with real-word parameters. The deep deterministic policy gradient (DDPG) method used by [109] in stock trading demonstrated how the model is able to handle large settings concerning stability, improving data use, and equilibrating risk while optimizing the return with a high performance guarantee. Another example in the deep RL framework made use of the DQN scheme [119] to ameliorate the news recommendation accuracy dealing with huge users at the same time with a considerably high-performance guarantee of the method. Our review demonstrated that there is great potential in improving deep learning methods applied to the RL problems to better analyze the relevant problem for finding the best strategy in a wide range of economic domains. Furthermore, RL is widely growing research in DL. However, most of the well-known results in RL have been in single-agent environments, while the cumulative reward just involves single state-action spaces. It would be interesting to consider multi-agent scenarios in RL that comprise more than one agent where the cumulative reward can be affected by the actions of other agents. There is some recent research that applied multi-agent reinforcement learning (MARL) scenarios to a small set of agents but not to a large set of agents [121]. For instance, in the financial markets where there are a huge number of agents at the same time, the acts of particular agents, concerning the optimization problem, might be affected by the decisions of the other agents. The MARL can provide an imprecise model and then inexact prediction while considering infinite agents. On the other hand, mathematicians use the theory of mean-field games (MFGs) to model a huge variety of non-cooperative agents in a complicated multi-agent dynamic environment, but in theory, MFG modeling might often lead to derive unsolvable partial differential equations (PDE) while dealing with large numbers of agents. Therefore, the big challenge in the application of the MARL is to efficiently model a huge number of agents and then solve the real-world problem using MFGs, dealing with economics and financial markets. Now, the big challenges might be applying MFGs to MARL systems while involving infinite agents. Note that MGFs are able to efficiently model the problem but give unsolvable equations [122,123]. Recent advanced research demonstrated that using MFGs can diminish the complexity of the MARL system dealing with infinite agents. Thus, the question is how to effectively present the combination of MGFs (mathematically), and MARL that can help out to solve unsolvable equations applied to economic and financial problems. For example, the goal of all the high-frequency traders is to dramatically optimize the profit where MARL scenarios can be modeled by MFGs, assuming that all the agents have the same cumulative reward.

Figure 34 illustrates a comprehensive evaluation of models’ performance in the surveyed manuscript. LSTM, CNN, DNN, RNN, and GRU generally produced higher RMSE. The identified DRL methods with higher performance can be further used in emerging applications, e.g., pandemic modeling, financial markets, and 5G communication.

5. Conclusions

In the current fast economics and market growth, there is a high demand for the appropriate mechanisms in order to considerably enhance the productivity and quality of the product. Thus, DL can contribute to effectively forecast and detect complex market trends, as compared to the traditional ML algorithms, with the major advantage of a high-level feature extraction property and proficiency of the problem solver methods. Furthermore, reinforcement learning enables us to construct more efficient frameworks regarding the integration of the prediction problem with the portfolio structure task, considering crucial market constraints and better performance, while using deep reinforcement learning architecture and the combination of both DL and RL approaches, for RL to resolve the problem of scalability and to be applied to the high-dimensional problems as desired in real-world market settings. Several DL and deep RL approaches, such as DNN, Autoencoder, RBM, LSTM-SVR, CNN, RNN, DDPG, DQN, and a few others, were reviewed in the various application of economic and market domains, where the advanced models improved prediction to extract better information and to find the optimal strategy mostly in complicated and dynamic market conditions. This brief work represents the basic issue that all proposed approaches are mainly to fairly deal with the model complexity, robustness, accuracy, performance, computational tasks, risk constraints, and profitability. Practitioners can employ a variety of both DL and deep RL techniques, with the relevant strengths and weaknesses, that serve in economic problems to enable the machine to detect the optimal strategy associated with the market. Recent works showed that the novel techniques in DNN, and recent interaction with reinforcement learning, so-called deep RL, have the potential to considerably enhance the model performance and accuracy while handling real-world economic problems. We mention that our work indicates the recent approaches in both DL and deep RL perform better than the classical ML approaches. Significant progress can be obtained by designing more efficient novel algorithms using deep neural architectures in conjunction with reinforcement learning concepts to detect the optimal strategy, namely, optimize the profit and minimize the loss while considering the risk parameters in a highly competitive market. For future research, a survey of machine learning and deep learning in 5G, cloud computing, cellular network, and COVID-19 outbreak is suggested.