Finite-Time H∞ Static Output Feedback Control for Itô Stochastic Markovian Jump Systems
Abstract
:1. Introduction
2. Problem Statement and Preliminaries
3. Main Results
3.1. MJS with CKTR
- ,
- ,
- ,
- ,
- .
- ,
- ,
- .
- ,
- ,
- ,
- , Beyond that,
3.2. MJS with PKTR
- ,
- ,
- .
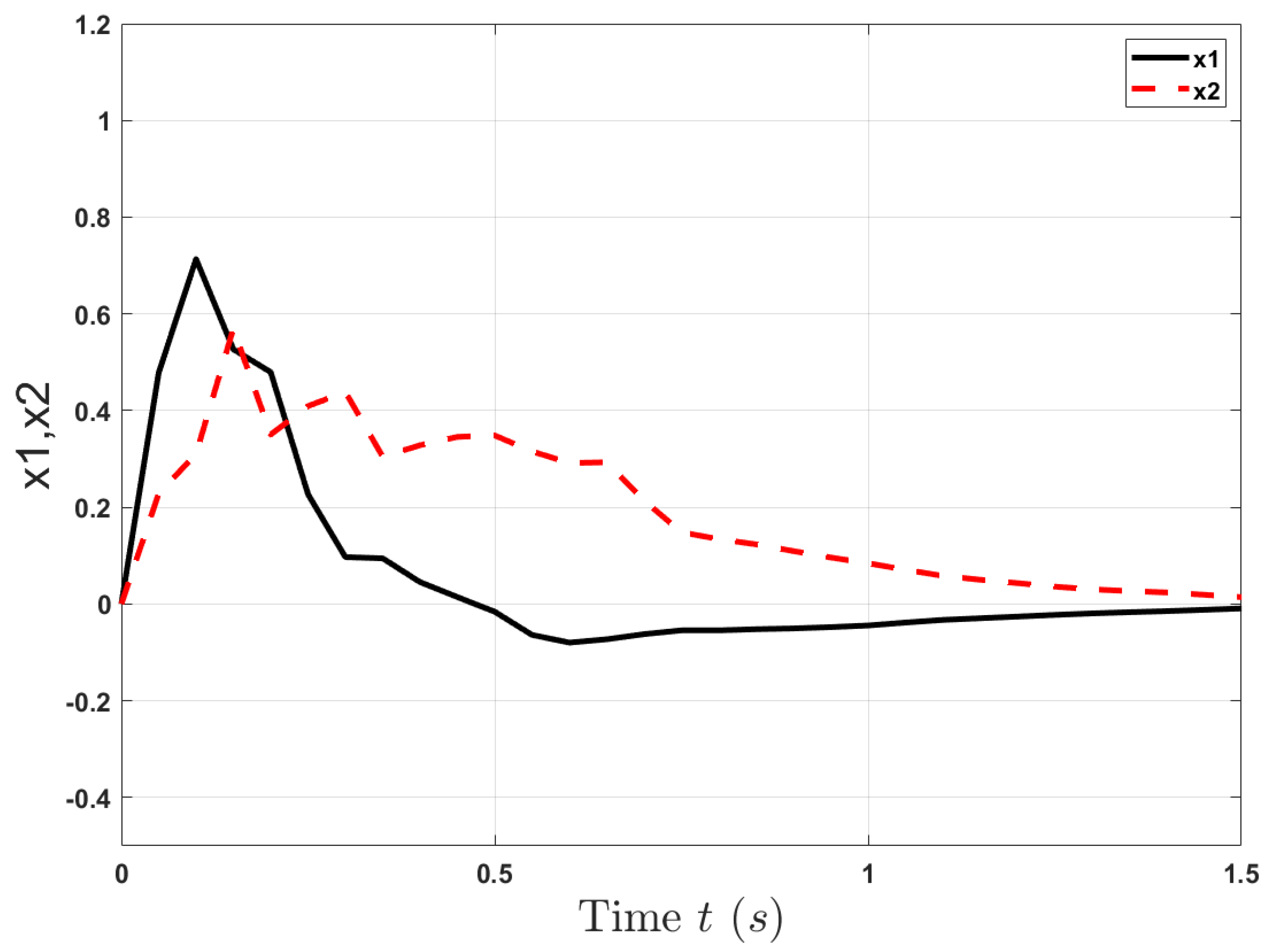
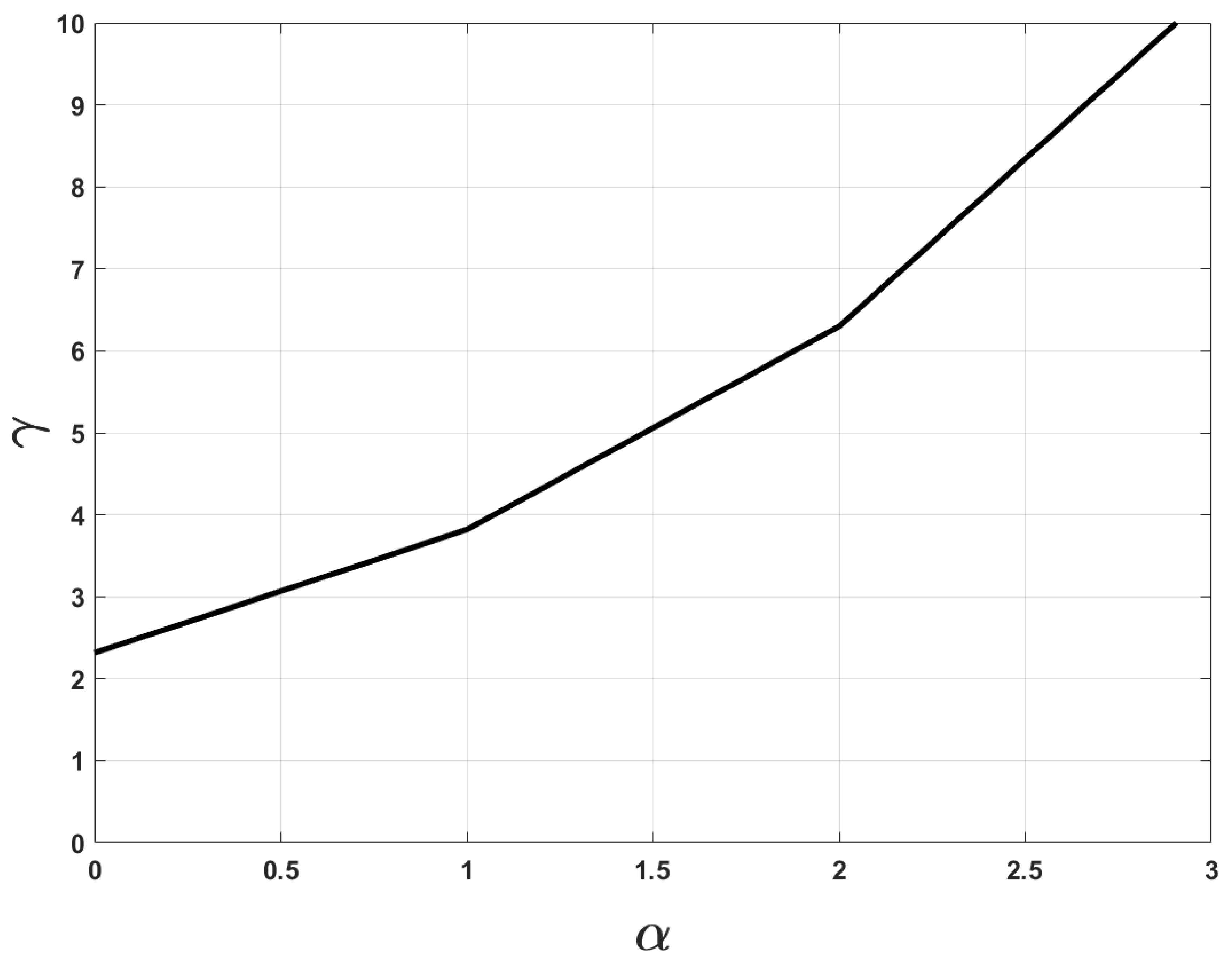
4. Numerical Examples
- .
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Costa, O.L.V.; Fragoso, M.D.; Todorov, M.G. Continuous-Time Markov Jump Linear Systems; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zhang, L.; Lam, J. Necessary and sufficient conditions for analysis and synthesis of Markov jump linear systems with incomplete transition descriptions. IEEE Trans. Autom. Control. 2010, 55, 1695–1701. [Google Scholar] [CrossRef] [Green Version]
- Hua, M.; Zhang, L.; Yao, F. Robust H∞ filtering for continuous-time nonhomogeneous Markov jump nonlinear systems with randomly occurring uncertainties. Signal Process. 2018, 148, 250–259. [Google Scholar] [CrossRef]
- Li, H.; Shi, P.; Wu, L. Observer-based adaptive sliding mode control for nonlinear Markovian jump systems. Automatica 2016, 64, 133–142. [Google Scholar] [CrossRef]
- Stadtmann, F.; Costa, O.L.V. H2 control of continuous-time hidden Markov jump linear systems. IEEE Trans. Autom. Control. 2017, 62, 4031–4037. [Google Scholar] [CrossRef]
- Hukaidani, H.; Xu, H.; Shima, T.; Dragan, V. A stochastic multiple-leader-follower incentive Stackelberg strategy for Markov jump linear systems. IEEE Control Syst. Lett. 2017, 1, 250–255. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, W.; Li, Y. H−index for continuous-time stochastic systems with Markov jump and multiplicative noise. Automatica 2019, 105, 167–178. [Google Scholar] [CrossRef]
- Du, B.; Lam, J.; Zou, Y.; Zhan, S. Stability and stabilization for Markovian jump time-delay systems with partially unknown transition rates. IEEE Trans. Circ. Syst. 2013, 62, 341–351. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Lam, J.; Gao, H.; Xiong, J. H∞ and H2 filtering for linear systems with uncertain Markov transition. Automatica 2016, 67, 252–266. [Google Scholar] [CrossRef]
- Caron, F.; Davy, M.; Duflos, E. Particle filtering for multisensor data fusion with switching observation models: Application to land vehicle positioning. IEEE Trans. Signal Process. 2007, 55, 2703–2719. [Google Scholar] [CrossRef]
- Martino, L.; Read, J.; Elvira, V.; Louzada, F. Cooperative parallel particle filters for on-line model selection and Applications to urban mobility. Digit. Signal Process. 2017, 60, 172–185. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Black, M.J.; Mumford, D.; Gao, Y.; Bienenstock, E.; Donoghue, J.P. Modeling and decoding motor cortical activity using a switching Kalman filter. IEEE Trans. Biomed. Eng. 2004, 51, 933–942. [Google Scholar] [CrossRef] [Green Version]
- Dorato, P. Short time stability in linear time-varying systems. In Proceedings of the IRE International Convention Record Part 4, New York, NY, USA, 26 October 1961; pp. 83–87. [Google Scholar]
- Amato, F.; Ariola, M.; Cosentino, C. Finite-time stability of linear time-varying systems: Analysis and controller design. IEEE Trans. Autom. Control 2010, 55, 1003–1008. [Google Scholar] [CrossRef]
- Amato, F.; Darouach, M.; Tommasi, G. Finite-time stabilization, detectability, and dynamic output feedback finite-time stabilization of linear systems. IEEE Trans. Autom. Control 2017, 62, 6521–6528. [Google Scholar] [CrossRef]
- Amato, F.; Cosentino, C.; Merola, A. Sufficient conditions for finite-time stability and stabilization of nonlinear quadratic systems. IEEE Trans. Autom. Control 2010, 55, 430–434. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, Y.; Shi, P. Resilient and robust finite-time H∞ control for uncertain discrete-time jump nonlinear systems. Appl. Math. Model. 2017, 49, 612–629. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, W.; Zhang, G. Finite-time stability and stabilization of Itô stochastic systems with Markovian switching: Mode-dependent parameter approach. IEEE Trans. Autom. Control 2015, 60, 2428–2433. [Google Scholar] [CrossRef]
- Yan, Z.; Park, J.; Zhang, W. Finite-time guaranteed cost control for Itô stochastic Markovian jump systems with incomplete transition rates. Int. J. Robust Nonlinear Control 2017, 27, 66–83. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Q.; Li, Y. Finite-time guaranteed cost control for uncertain mean-field stochastic systems. J. Frankl. Inst. 2020, 57, 2813–2829. [Google Scholar] [CrossRef]
- Hinrichsen, D.; Pritchard, A. Stochastic H∞. Siam J. Control Optim. 1998, 36, 1504–1538. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Mu, X. Robust finite-time H∞ control of singular stochastic systems via static output feedback. Appl. Math. Comput. 2012, 218, 5629–5640. [Google Scholar] [CrossRef]
- Oliveira, A.; Costa, O.; Daafouz, J. Suboptimal H2 and H∞ static output feedback control of hidden Markov jump linear systems. Eur. J. Control 2020, 51, 10–18. [Google Scholar] [CrossRef]
- Wang, J.; Ma, S.; Zhang, C. Finite-time H∞ control for T-S fuzzy descriptor semi-Markov jump systems via static output feedback. Fuzzy Sets Syst. 2019, 365, 60–80. [Google Scholar] [CrossRef]
- Shen, M.; Yan, S.; Zhang, G.; Park, J. Finite-time H∞ static output control of Markov jump systems with an auxiliary approach. Math. Comput. 2016, 273, 553–561. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xikui, L.; Yapeng, T.; Yan, L. Finite-Time H∞ Static Output Feedback Control for Itô Stochastic Markovian Jump Systems. Mathematics 2020, 8, 1709. https://doi.org/10.3390/math8101709
Xikui L, Yapeng T, Yan L. Finite-Time H∞ Static Output Feedback Control for Itô Stochastic Markovian Jump Systems. Mathematics. 2020; 8(10):1709. https://doi.org/10.3390/math8101709
Chicago/Turabian StyleXikui, Liu, Teng Yapeng, and Li Yan. 2020. "Finite-Time H∞ Static Output Feedback Control for Itô Stochastic Markovian Jump Systems" Mathematics 8, no. 10: 1709. https://doi.org/10.3390/math8101709
APA StyleXikui, L., Yapeng, T., & Yan, L. (2020). Finite-Time H∞ Static Output Feedback Control for Itô Stochastic Markovian Jump Systems. Mathematics, 8(10), 1709. https://doi.org/10.3390/math8101709




