CBRR Model for Predicting the Dynamics of the COVID-19 Epidemic in Real Time
Abstract
:1. Introduction
2. Materials and Methods
2.1. Related Works
2.2. Preliminary Insight on Recurrent Relations
2.3. Case-Based Rate Reasoning Method
3. Results
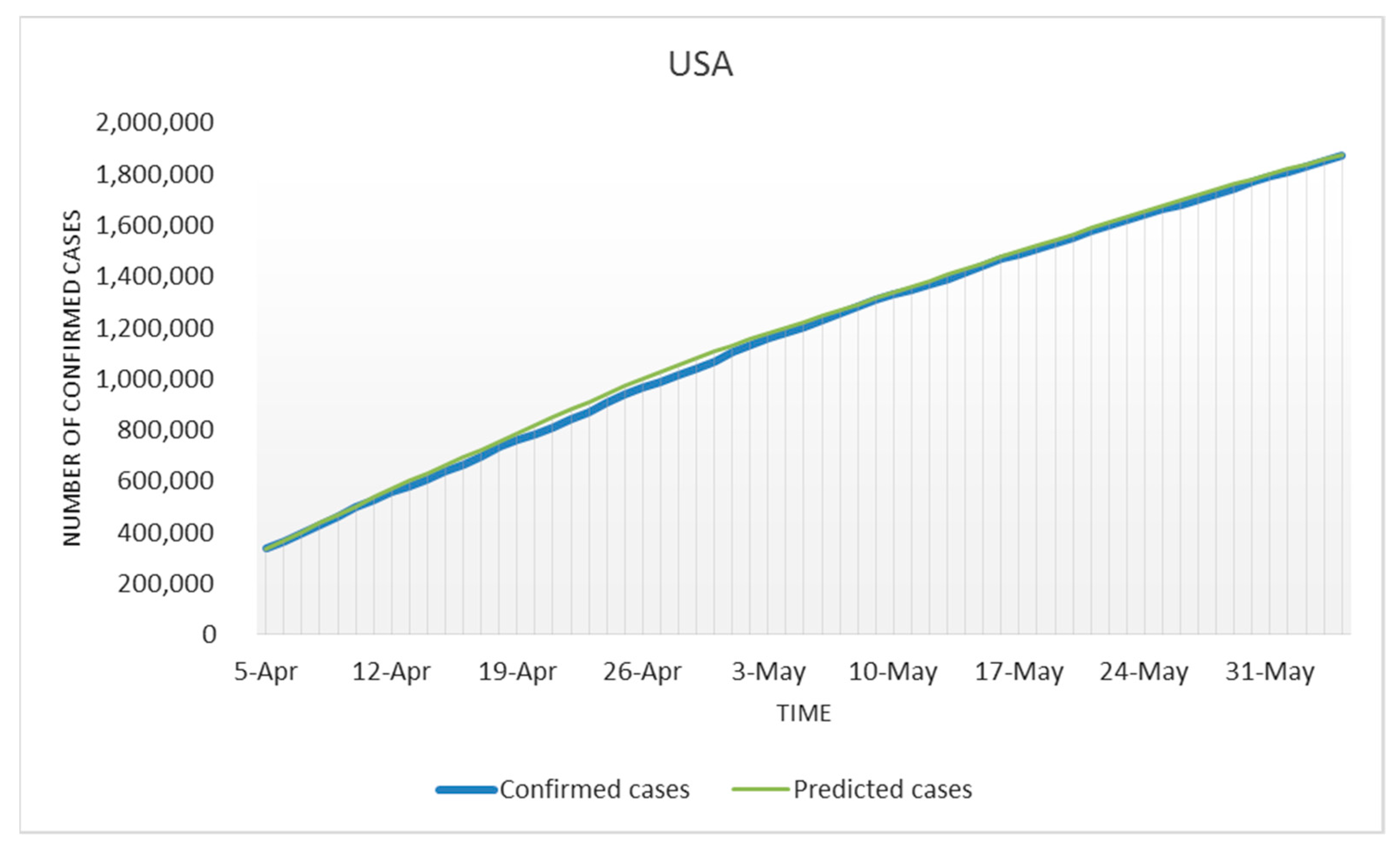
3.1. Modeling for the USA
3.2. Modeling for Russia
Simulation Results for Russia
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Layne, S.P.; Hyman, J.M.; Morens, D.M.; Taubenberger, J.K. New coronavirus outbreak: Framing questions for pandemic prevention. Sci. Transl. Med. 2020, 12, eabb1469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- The Novel Coronavirus Pneumonia Emergency Response Epidemiology Team. Vital surveillances: The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases (COVID-19)-China 2020. China CDC Wkly. 2020, 2, 113–122. [Google Scholar] [CrossRef]
- Wu, J.T.; Leung, K.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 2020, 395, 689–697. [Google Scholar] [CrossRef] [Green Version]
- MIDAS Coordination Center. Models of Infectious Disease Agent Study (University of Pittsburgh, 2020). Available online: https://midasnetwork.us/ (accessed on 23 June 2020).
- Kondratyev, M.A. Forecasting methods and models of disease spread. Comput. Res. Model. 2013, 5, 863–882. [Google Scholar] [CrossRef]
- Mandal, M.; Jana, S.; Nandi, S.; Khatua, A.; Adak, S.; Kar, T.K. A model based study on the dynamics of COVID-19: Prediction and control. Chaos Solitons Fractals 2020, 136, 109889. [Google Scholar] [CrossRef] [PubMed]
- Bekirosab, S.; Kouloumpou, D. SBDiEM: A new mathematical model of infectious disease dynamics. Chaos Solitons Fractals 2020, 136, 109828. [Google Scholar] [CrossRef]
- Barmparis, G.D.; Tsironis, G.P. Estimating the infection horizon of COVID-19 in eight countries with a data-driven approach. Chaos Solitons Fractals 2020, 135, 109842. [Google Scholar] [CrossRef]
- Kissler, S.M.; Tedijanto, C.; Goldstein, E.; Grad, Y.H.; Lipsitch, M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science 2020, 368, 860–868. [Google Scholar] [CrossRef]
- Fanelli, D.; Piazza, F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals 2020, 134, 109761. [Google Scholar] [CrossRef]
- López, L.; Rodó, X. The end of social confinement and COVID-19 re-emergence risk. Nat. Hum. Behav. 2020, 4, 746–755. [Google Scholar] [CrossRef]
- Otunuga, O.M.; Ogunsolu, M.O. Qualitative analysis of a stochastic SEITR epidemic model with multiple stages of infection and treatment. Infect. Dis. Model. 2020, 5, 61–90. [Google Scholar] [CrossRef] [PubMed]
- Cooper, I.; Mondal, A.; Antonopoulos, C.G. A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fractals 2020, 139, 110057. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.K.; Rani, M.; Bhagavathula, A.S.; Sah, R.; Rodriguez-Morales, A.J.; Kalita, H.; Nanda, C.; Sharma, S.; Sharma, Y.D.; Rabaan, A.A.; et al. Prediction of the COVID-19 pandemic for the top 15 affected countries: Advanced autoregressive integrated moving average (ARIMA) model. JMIR Public Health Surveill. 2020, 6, e19115. [Google Scholar] [CrossRef]
- Sharma, V.K.; Nigam, U. Modeling and forecasting of Covid-19 growth curve in India. MedRxiv 2020. [Google Scholar] [CrossRef]
- Zhang, T.; Ma, Y.; Xiao, X.; Lin, Y.; Zhang, X.; Yin, F.; Li, X. Dynamic bayesian network in infectious diseases surveillance: A simulation study. Sci. Rep. 2019, 9, 10376. [Google Scholar] [CrossRef]
- Akhtar, M.; Kraemer, M.U.G.; Gardner, L.M. A dynamic neural network model for predicting risk of Zika in real time. BMC Med. 2019, 17, 171. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, R.; Waligora, T. Influenza forecast: Case-based reasoning or statistics? In Lecture Notes in Computer Science, Proceedings of the 11th International Conference on Knowledge-Based Intelligent Information and Engineering Systems, Vietri sul Mare, Italy, 12–14 September 2007; Apolloni, B., Howlett, R.J., Jain, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4692, pp. 287–294. [Google Scholar] [CrossRef]
- Viboud, C.; Boelle, P.Y.; Carrat, F.; Valleron, A.J.; Flahault, A. Prediction of the spread of influenza epidemics by the method of analogues. Am. J. Epidemiol. 2003, 158, 996–1006. [Google Scholar] [CrossRef] [Green Version]
- Relich, M.; Pawlewski, P. A case-based reasoning approach to cost estimation of new product development. Neurocomputing 2018, 272, 40–45. [Google Scholar] [CrossRef]
- Kaedi, M.; Ghasem-Aghaee, N. Improving case-based reasoning in solving optimization problems using Bayesian optimization algorithm. Intell. Data Anal. 2012, 16, 199–210. [Google Scholar] [CrossRef]
- Teles, P. Predicting the evolution of SARS-Covid-2 in portugal using an adapted SIR model previously used in south Korea for the MERS outbreak. MedRxiv 2020. [Google Scholar] [CrossRef]
- COVID-19 Dashboard by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University. Available online: https://coronavirus.jhu.edu/map.html (accessed on 4 August 2020).
- Popkov, Y.; Popkov, A.; Dubnov, Y.; Solomatine, D. Entropy-randomized forecasting of stochastic dynamic regression models. Mathematics 2020, 8, 1119. [Google Scholar] [CrossRef]
- Zakharov, V.; Balykina, Y. Predicting the dynamics of the coronavirus (COVID-19) epidemic based on the case-based reasoning approach. Appl. Math. Comput. Sci. Control Process. 2020, 3, 249–259. [Google Scholar]
- Coronavirus Epidemic in Russia. Dynamics Modeling and Forecasting. Available online: http://hdl.handle.net/11701/18124 (accessed on 7 September 2020).
- The Coronavirus Epidemic in Russia. Intelligent Logistics Center Analytical Notes. Available online: http://www.apmath.spbu.ru/cil/ (accessed on 20 September 2020).




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakharov, V.; Balykina, Y.; Petrosian, O.; Gao, H. CBRR Model for Predicting the Dynamics of the COVID-19 Epidemic in Real Time. Mathematics 2020, 8, 1727. https://doi.org/10.3390/math8101727
Zakharov V, Balykina Y, Petrosian O, Gao H. CBRR Model for Predicting the Dynamics of the COVID-19 Epidemic in Real Time. Mathematics. 2020; 8(10):1727. https://doi.org/10.3390/math8101727
Chicago/Turabian StyleZakharov, Victor, Yulia Balykina, Ovanes Petrosian, and Hongwei Gao. 2020. "CBRR Model for Predicting the Dynamics of the COVID-19 Epidemic in Real Time" Mathematics 8, no. 10: 1727. https://doi.org/10.3390/math8101727
APA StyleZakharov, V., Balykina, Y., Petrosian, O., & Gao, H. (2020). CBRR Model for Predicting the Dynamics of the COVID-19 Epidemic in Real Time. Mathematics, 8(10), 1727. https://doi.org/10.3390/math8101727





