The Effect of O2O Retail Service Quality in Supply Chain Management

Abstract

The present study focuses on a single-vendor, single-buyer supply chain model for a single type of product with upgraded service provided to the buyer by the vendor. Vendors often increase their profit by providing a lower quality of a particular product. In this study, an advanced supply chain model is developed to increase service in the presence of an unreliable vendor and an online-to-offline (O2O) channeling system. The vendor provides lower quality items to the customer, even though they had committed to providing a certain quality product, in order to increase their profit. For more realistic results, demand is considered to be price-, quality-, and service-dependent. To advertise and sell the products, the manufacturer uses an online system, which the buyer also uses to choose and order the product, where the particular product is delivered to the customer by a third (offline) party; that is, the concept of an O2O retail channel is adopted to improve the service level of the supply chain management (SCM). To control the out-of-control state and improve the production quality, investment is used. Contrary to the literature, service is considered to be constrained, which makes the model more realistic. A classical optimization technique is used to solve the model analytically and a two-echelon supply chain model is obtained under the advanced O2O retail channel, along with optimized profit, shipment volume, selling price, ordering cost, service, back-ordered price discount, lead time, and safety factor values. Some numerical examples and a sensitivity analysis of the key parameters are provided, along with graphical representation, in order to validate the model.

1. Introduction

A single-vendor, single-buyer supply chain management (SCM) system considering a single type of item is developed in this study. At present, consumers are concerned about the price and quality of products, as well as the services provided by companies. They want higher quality and service levels while paying a lower price. To provide a product with a lower price, the quality of the product is sometimes reduced by the manufacturer, which may not be known to the retailer before purchasing. A supply chain system is needed to run a business smoothly in any industry. A company can earn more profits when they have their own production house. Thus, to run a business properly with greater profits, a supply chain system is more effective in the modern business environment. At present, many people are much too busy in their daily life, and so they do not have much time to spend in shopping malls or shops to purchase their required products. However, almost everyone is now connected to the internet or an online networking system. Thus, modern companies also make use of the benefits of online systems. A large variety of products are available in the online system and customers have many choices and options to pick from, while particular companies send these products to the customers. Many businesses now use this online-to-offline (O2O) strategy to optimize their profits.

At present, consumers are concerned about the services provided by a company. For example, when a customer goes to a mobile shop to purchase a smart phone, before purchasing, they are worried about customer care. This means that they are indirectly worried about the service related to that particular product. Keeping this in mind, companies have become much more conscious about the services that they provide to their customer, which indirectly increases demand and their brand image. Customers are very satisfied if they get more service for a particular product from a particular company; such customer satisfaction increases the sale of a particular product, which directly increases the profit of the company. Keeping in mind the competitive business market situation, demand is considered to be price-, quality-, and service-dependent, which directly increases the product demand as well as profit of the company. However, due to long-term production, processes can produce some imperfect items in an “out-of-control” state, which a follows certain distribution. Many strategies have been developed by several researchers to increase the profit of the companies; however, in this research, a pioneering attempt is made to improve the service of a company in an O2O channeling system. The main aim of this research is to improve the service provided by companies to the customers from the time of ordering to the end of the product’s life, introducing three strategies to reduce ordering and setup cost and to improve the reliability of the production process. This study develops a supply chain model where demand is dependent on price, quality, and service, along with the above-mentioned three strategies to increase the total system’s profit. Contradictory to the literature, when increasing the profit, buyers may feel cheated when they are provided with a lower quality product, as they thought they were buying a product of a certain quality, as well as when their experience is hampered by a long delivery time.

Gaps in the Literature

At present, O2O systems in supply chain management are very effective. Every person wants their necessities delivered to their doorstep. In the modern competitive market, every company wishes to optimize their profit, and therefore considers different types of strategies; O2O is one such strategy. In the O2O strategy, the buyer orders products online and a vendor delivers the products to their doorstep. Using this model, we aim to develop the service of the SCM through the O2O environment. In this model, one can easily find that when the service of the system is upgraded and when the service is treated as a constraint, the profit can be increased. Previous studies have developed integrated or supply chain models under the consideration of O2O channeling or price-dependent demand under different considerations. However, there is still a large gap in the research regarding O2O channels with upgraded product quality where demand is dependent on the price and quality of the product and the service of the company. Furthermore, we introduce three novel strategies for reducing ordering and setup costs, and improving the processing quality for an unreliable vendor. In reality, service cannot be infinite; thus, to make the model more realistic, service is considered as a constraint—a pioneering strategy for any integrated system with upgraded quality in an unreliable O2O supply chain. Generally, unreliability is always harmful in any supply chain system. In this study, the vendor is considered unreliable in providing the exact quality of the product, which directly increases the system’s profit. This is also a new approach, compared to the existing literature.

The contributions of previous studies are elaborated in the literature review presented in the following Section. The problem definition, along with the associated notation and assumptions, are described in Section 3. In Section 4, the solution procedure of the model is discussed, followed by the mathematical model in Section 5. Section 6 consists of some numerical examples to elaborate the model, while a sensitivity analysis is provided in Section 7. Some managerial insights are described in Section 8. Finally, some concluding remarks and future research directions are discussed in the conclusion section.

2. Literature Review

2.1. O2O Retail Supply Chain System

Adaptation of O2O retail channels in supply chain management is one of most relevant and new policies. The concept of offline or home delivery of products was introduced by Visser et al. [1], as a review model of the importance of home delivery and urban freight delivery. The use of O2O in e-commerce markets considering a hidden semi-Markov model has been investigated by Xiao and Dong [2]. Different pricing strategies and location evolution for competitive O2O markets have been proposed by He et al. [3]. In this model, they maximized the total system profit based on understanding of customer behaviors. Furthermore, they adopted the policy of customer reviews, such that any company could develop their strategies and policies in order to satisfy their customers and increase their total gross profit. In the following year, Li et al. [4] developed a supply chain model where different advertisement strategies were used in an O2O supply chain. Based on advertisement strategies, Li et al. [4] developed three models and proved that the Bilateral co-op advertising model was more beneficial, compared to the other models. In 2017, Choi et al. [5] improved a supply chain model in an O2O environment using the concept of choice of postponement and contracts. These strategies attract more customers, as they have the choice to postpone their order any time before delivery and also have the choice to change products before delivery. This model was developed by Yan and Pei [6] by considering return policies. Customers can return a product within a certain time period after the delivery of the products. Thus, the system is like any offline market. If the product is faulty or if the customer wishes to change products, they can do so very easily within a certain time period. As a result, the customer moves towards e-commerce marketing. To attract more customers, companies now give some reward points or gifts that customers can use for their next purchase (Yan et al. [7]), which increases the brand image of the company and maximizes the total system profit. The concept of ratings and recommendations is another most important issue in O2O supply chain management (Yachen et al. [8]). Good recommendations and ratings increase the demand for products, thus increasing the total system profit. A closed-loop supply chain in an O2O environment was developed by Zand et al. [9]. This model was developed by considering recycling management. When companies give some discount or cash-back to customers who return used products, they can reuse the good parts of those products or can re-manufacture the faulty parts to make brand new products, whereas the customer gets some benefits from those used products. Different supply chain models in O2O environments have been developed by different researchers, but a supply chain model in which the demand depends on the quality and price of the product, as well as the service, along with upgraded quality and reduced ordering and setup cost in an O2O environment, has still not considered by any researcher. This is a big research gap in the O2O-based supply-chain-model literature, which is fulfilled by this research.

Table 1. Research gaps and contributions of previous author(s).

Author(s)	Quality Upgradation	Ordering Cost Reduction	Variable Safety Factor	Service	Setup Cost Reduction
Ben-Daya and Raouf [28]			√
Chang and Lo [31]
Dey et al. [38]			√		√
Dhargalkar et al. [11]	√
Huang et al. [33]			√		√
Majumder et al. [37]			√		√
Ouyang et al. [30]					√
Sarkar and Moon [35]				√
Vareda [10]	√				√
Dey et al. [15]	√		√
This model	√	√	√	√	√

provides the research gaps and previous research in this research direction.

2.2. Quality- and Price-Dependent Demand

Quality is a major factor to attract buyers for a particular product. It is also apparent that buyers are concerned with the quality of a product, no matter what its cost is. If the quality of a particular product is higher than that of others, its cost is not an issue for the consumer. Keeping this in mind, every production house tries to produce higher quality items with lower cost. To increase profits, companies are always trying to upgrade the quality of their products. Investment helps to upgrade the quality of products and reduce the total cost of the system, as stated by Vareda [10]. A model for product development and upgrading of the quality of products has been presented by Dhargalkar et al. [11]. A model for multiple life cycle products has been critically reviewed by Aziz et al. [12], in which they optimized the upgradability in the design of the multiple life cycle product. Reviewing the environmental issue, Sarkar et al. [13] developed an imperfect production model where they upgraded the quality of returned/re-manufactured products. The concept of quality upgradation in a close-loop supply chain was discussed by Sarkar et al. [14]. Recently, a price- and quality-dependent smart production system has been developed by Dey et al. [15], where the authors proved that the profit is optimized when the defect rate follows a Chi-square distribution. All of these studies have considered quality and/or price but, along with quality and price, service also has an important impact in supply chains, which has still not been considered by any researcher. Thus, a pioneering attempt is taken in this research, in which an O2O supply chain is developed under the consideration of a selling price-, quality-, and service-dependent demand pattern.

2.3. Unreliable Supply Chain

Consumers want higher quality products with less cost. In the current business environment, the loyalty of vendors often comes into question. All companies claim that their product is the best, but which one is truly the best is an open question. Companies may cheat their customers in a casual manner by providing lower quality items, even though they promised to deliver a high-quality product. The brand image of a particular product depends on the reliability or loyalty of the vendor, according to Chiou et al. [16]. Sometimes, unreliability in the supply system makes a vendor unreliable; as a result, a negative impact is experienced by that vendor [17]. Due to system unreliability, a vendor may face many problems [18]. A vendor may sell a product in two cycles: first, selling good quality products at the original price. When the vendor has an imperfect product, they then sell the product in a second cycle at a lower cost [19]. When there are many suppliers/vendors of a particular product in the market, the consumer must make a decision about which supplier/vendor is better than the others, with regard to replenishment, production, or quality inspection. All of these consequences have been considered by Hlioui et al. [20]. They also considered an unreliable vendor that operates in a dynamic stochastic context. All researchers in the literature have considered the quality of products or unreliable vendors; however, the situation where the profit can be maximized by providing a lower quality item, although the vendor had promised to the buyer that the quality of the product would be upgraded, has not been considered by any researcher. Thus, we provide a novel attempt to maximize profit in an integrated model where service is upgraded by the use of an O2O channeling system.

Many researchers have recently considered the joint profits of buyers and vendors, rather than a single one, as in Sarkar [21]. Thus, an integrated inventory model is quite interesting to study, with respect to the modern business environment. A pioneering attempt regarding an integrated model was made by Goyal [22], who developed a model considering a single buyer and single vendor. Goyal’s [22] model has been extended by Banerjee [23] assuming a lot-for-lot policy, and extended by Goyal [24] by considering an SSMD policy. A single vendor and single multiplier integrated model with lot splitting has been developed by Ha and Kim [25]. In 2014, Cárdenas-Barrón and Sana [26] introduced a vendor–buyer supply chain model, in which demand is based on sales teams’ capabilities. Most researchers have developed different types of integrated or supply chain models with different types of demand patterns; however, none have considered lead time along with service. In the current research, a supply chain is presented along with upgraded service through an O2O channeling system, which make this model more advanced. Different researchers have developed different models considering the reliability of the vendor or buyer; however, a supply chain model under a smart O2O retail channel with price-, quality-, and service-dependent demand and an unreliable vendor (where the vendor is unreliable in providing the exact quality of product) has still not been considered by any researcher. Thus, this is a big research gap, which is fulfilled by the current study.

2.4. Lead Time Reduction

At present, buyer satisfaction is a key factor for any business. Satisfying the lead time reduction for buyers is one of the most vital issues for any vendor. The lead time is a unique decision variable first considered by Liao and Shyu [27]. Ben-Daya and Rauf [28] extended Liao and Shyu’s [27] model, where lead time is a decision variable with continuous lead time and no shortages. By considering discrete lead time and shortages, Ben-Daya and Rauf’s [28] model has been extended by Ouyang et al. [29]. Reduction in setup cost and lead time for an imperfect production model was introduced by Ouyang et al. [30]. This model discussed the improvement in the quality of products. Chang and Lo [31] discussed two types of lead time—continuous and discrete—along with back-orders and lost sales in an inventory model. A controllable lead time with lost sales reduction model has been proposed by Annadurai and Uthayakumar [32].

An integrated model with discreetly reduced manufacturing cost has been proposed by Huang et al. [33]. In this model, during the lead time, the total number of consumers follows a compound Poisson process. In 2013, Sarkar and Majumder [34] developed an integrated distribution-free model, in which two types of investment were used to improve the quality of the production process and reduce setup costs. Sarkar and Moon [35] expanded an imperfect production model with variable back-order costs, reduced setup cost, and improved the quality of the process. The quality of the production process can be improved by additional investments in an integrated model, as discussed by Sarkar et al. [13]. Recently, Majumder et al. [36] presented an integrated model with a single manufacturer and multiple vendors with consideration of variable production rates. Several researchers have developed many integrated models with reduced setup costs and improved quality in the production process, such as Majumder et al. [37] and Dey et al. [38]. To obtain more realistic results, Dey et al. [38] considered selling price-dependent demand and considered that the consumer follows a Poisson distribution during lead time. However, a reduction in lead time with upgraded service in the presence of an O2O channeling system has still not been considered by any researcher. This big research gap is fulfilled by the present study.

2.5. Service Level Improvement

Customer satisfaction always leads to better profits in any industry, and better service always attracts customers, which is beneficial for any industry. In the presented model, the service is developed by considering an O2O channeling system in SCM. Chen and Krass [39] investigated an inventory model where the stockout cost is replaced by a minimal service level constraint. In 2002, Hwang [40] designed a logistic supply chain system under the consideration of service level. An imperfect production model with rework and optimized production lot size has been studied by Chiu et al. [41]. In this model, the authors used a service level constraint and optimized the scrap rate. Service level has been considered as a decision variable by Jodlbauer and Reitner [42], who also optimized the total cost for a stochastic multi-item make-to-order production system. A min–max distribution-free model with continuous review has been presented by Moon et al. [43]. In this model, they considered variable lead time and service level as a constraint.

At present, one of the biggest problems worldwide is pollution. The environment is generally polluted by various industries; thus, it is a challenge for everyone to reduce pollution. Generally, carbon is the main subject of each type of environmental pollution. Thus, every industry has been targeted to reduce their carbon emissions. The effect of carbon emissions in a three-echelon supply chain model has been calculated by Sarkar et al. [44]. A different game strategy was used by Sarkar et al. [45] to solve an integrated model, in which they calculated the carbon-emission cost along with a reduced setup cost. In this line, two multi-stage cleaner production models have been developed by Tayyab and Sarkar [46] and Kim and Sarkar [47]. Omair et al. [48] proposed a sustainable model for minimum lubrication and carbon footprints. Recently, two sustainable supply chain models have been designed by Sarkar et al. [49] and Ahmed and Sarkar [50], in which the effects of carbon emissions were calculated along with a single-setup, multiple-delivery policy.

A two-echelon supply chain model under an O2O environment is developed in this current study, where the vendor is unreliable in providing the exact quality of the product, although the vendor had previously committed to providing a certain quality product. The O2O environment upgrades the service level of the vendor. To construct a real and applicable model, the demand is considered dependent on the selling price, quality, and service level of the vendor. Moreover, two continuous and one discrete investment are introduced, in order to improve the service level and optimize the total system profit. In the current study, it is also proven that a service constraint is beneficial. To transport the product, an SSMD transportation strategy is utilized, which makes the model more realistic. Finally, the total system profit is optimized when the defect rate follows a Beta distribution, along with optimized values of the decision variables.

3. Problem Definition, Notation, and Assumptions

In this section, the problem under consideration is discussed, along with the notation and assumptions for the model.

3.1. Problem Definition

We consider a two-echelon supply chain model, in which an O2O channeling strategy is used to develop the service. Customer satisfaction is one of the key parameters for optimizing the profit of any industry; keeping this in mind, the online-to-offline concept is adopted in this model to increase the service level. To attract more customers, demand is considered to be dependent on price, quality, and service. Different investments are incorporated to improve the service of companies and to optimize the total system profit. Furthermore, the vendors are considered to be unreliable in providing quality products. Although the vendor commits to providing a certain quality of the product, at the time of transport, they provide a lower quality item to maximize total system profit. To reduce the ordering cost, the buyer uses an investment; while, to reduce setup cost and improve the production quality, the vendor uses discrete and continuous investments. These reductions help to improve the quality of the service. For a more realistic result, the demand is considered as selling price-, quality-, and service-dependent, along with a service constraint (as service cannot be infinite). Vendors use a single-setup multi-delivery (SSMD) policy to increase their profit in the presence of full back-orders. Finally, the total system profit is maximized, along with the optimum values of the decision variables.

3.2. Notation

To formulate the model, the following notation and assumptions are used:

Index
x	minimum duration lead time component $(x=1,2,\dots ,n)$
y	normal duration lead time component $(y=1,2,\dots ,n)$
Decision Variables
$S_v$	volume of each shipment (unit)
$s_f$	safety factor ($/week)
$L_t$	lead time (weeks)
$S_p$	product selling-price ($/unit)
$B_{pd}$	back-order price discount per item offered by vendor ($/unit)
$q_v$	quality upgradation variable
$P_{\theta }$	probability to go to the out-of-control state
$O_c$	ordering cost for the buyer ($/unit)
s	service level
Parameters
m	number of product shipments per lot (a positive integer)
$Q_s$	lot size (units)
$W_i$	$i^{\mathrm{th}}$ demand quantity, $i=1,2,\dots ,m$ (units)
$D_r$	demand rate of buyer, $D_r=A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi }$ (units)
$P_v$	production rate of vendor, $P_v>D_r$ (units/time)
$C_T$	cycle time, $C_T=Q_s/D_r=m{S}_v/D_r$ (time)
$I_h$	inventory holding cost per unit per unit time ($/unit/unit time)
$P_{cv}$	vendor’s unit production cost per unit ($/unit)
$P_{cb}$	buyer’s unit purchase cost per unit ($/unit purchased)
$u_c$	unit shortage cost per unit ($/unit shortage)
$C_q$	quality improvement cost ($/unit)
$S_A$	setup cost ($S_c$) reduction investment ($)
$S_{C_0}$	initial setup cost per production run ($/setup)
$S_c$	setup cost, which is necessarily a decreasing function of $S_A$,
	with $S_c(S_A)=S_{c_0}{e}^{-r{S}_A}$, where r is a parameter ($/unit)
$q_{p_v}$	minimum quality for the acceptance of the finished product
$q_p$	product quality of the perfect product
q	quality ordered by buyer $q>q_{p_v}$
$C_{q_v}$	cost to make a product with quality q ($/unit)
$\psi$	standard normal probability density function
$A_f$	annual fractional cost for the capital investment ($/investment)
$\zeta$	service level constant
$\gamma$	price elasticity parameter
${\beta }_r$	back-order ratio, $0<{\beta }_r<1$
${\beta }_0$	upper bound of the back-order ratio
$\eta$	deterioration rate, which follows a certain distribution
$\mathsf{\Phi }$	standard normal cumulative distribution function
M	maximum available service (unit)
$\varphi$	constant related to service level
$\delta$	parameter for improving the quality of the product
$\tau$	collection rate of imperfect products in per cycle
$I(L)$	total number of consumers under lead time L
$R(L)$	total amount purchased by time L
$G(L)$	total crashing cost is related to the lead time ($/week)
$a_x$	$i^{\mathrm{th}}$ component of lead time, with $a_x$ as minimum duration (days)
$b_x$	$i^{\mathrm{th}}$ component of lead time, with $b_x$ as normal duration (days)
$F_{ccb}$	fixed carbon emission cost of consumer ($/shipment)
$V_{ccb}$	variable carbon emission cost of consumer ($/unit)
$F_{ccv}$	fixed carbon emission cost of vendor ($/shipment)
$V_{ccv}$	variable carbon emission cost of vendor ($/unit)
$T_F$	fixed transportation cost ($/shipment)
$T_V$	variable transportation cost ($/unit)
$T{C}_B$	total cost component of buyer ($/cycle)
$T{C}_V$	total cost component of vendor ($/cycle)

3.3. Assumptions

To develop the model, we considered the following assumptions:

• This paper deals with a single-buyer single-vendor supply chain model in the presence of an O2O environment with a single type of item, where service is upgraded through O2O channeling.
• The total number of consumers, $I(L)$, follows a Poisson distribution during the lead time with mean $\lambda L_t$. The $W_i$ are independent and normally distributed with mean $\mu$ and standard deviation $\sigma$, while $\{R(L)={\sum }_{(i=1)}^{I(L)}{W}_i,L_t\ge 0\}$ is a compound Poisson process (Huang et al. [33]).
• Most researchers consider a constant setup cost to formulate their production or supply chain models; however, using a continuous investment in setup can reduced the total setup cost, which can also improve the service that is provided by the companies to their customers (see, e.g., Sarkar and Moon [35]). It is not necessary to invest continuously to reduce the total setup cost for each step, though, which is why discrete investment is sometimes more beneficial to reduce the setup cost and improve the quality of service provided to customers. Thus, a discrete function is utilized to reduce the setup cost and improve the service of the total supply chain (see, e.g., Huang et al. [33]); specifically, $S_c(S_{A_i})=S_{c_0}{e}^{-r{S}_A},$ where $i=0,1,\dots ,m$ and $S_{A_0}=0.$
• Reduction of lead time is another component leading to service improvements. Different crashing costs associated with reducing the lead time for different mutually independent components are considered in this model. Let $b_x$ be the normal duration of the $x^{\mathrm{th}}$ component and $a_x$ be the minimum duration, where the crashing costs per unit time $u_x$ satisfy $u_1\le u_2\le \dots \le u_m.$ Suppose that $L_{t_x}$ is the length of the lead time for which components $1,2,3,\dots ,x$ crash to their minimum duration and let $L_{t_0}={\sum }_{y=1}^m{b}_y$. Then, $L_{t_x}=L_{t_0}-{\sum }_{y=1}^x(b_y-a_y)$ and the crashing cost $G(L)$ can be written as $G(L)=u_x(L_{t_x}-L_t)+{\sum }_{y=1}^x(b_y-a_y)$ for $x=1,2,\dots ,m$ [38].
• The backorder ratio ${\beta }_r$ is considered as a variable which is proportional to the back-order price discount $B_{pd}$ offered by the supplier. As ${\beta }_r$ is the back-order rate and a price discount is considered on the back-order, it is assumed that ${\beta }_r=\frac{{\beta }_0{B}_{pd}}{{\pi }_0}$, $0\le {\beta }_0<1$, and $0\le B_{pd}\le {\pi }_0$, where $B_{pd}$ is the price discount during the maximum of back-order ${\beta }_0$ and ${\pi }_0$ is the marginal profit per unit. The supplier makes decisions in order to obtain profits. Therefore, if the back-order price discount $B_{pd}$ is greater than the marginal profit ${\pi }_0$, the vendor may decide against offering the price discount (see, e.g., Pan et al. [51] and Lin [52]).
• The buyer’s demand for a particular product is $D_r$, with minimum quality q, and the vendor has committed to deliver all demanded products with quality q, which the vendor has charged the buyer for; however, the vendor produces an item with quality $q_{min}$, where $q_{min}<q$. At the time of delivery of the product, the vendor delivers a lesser quality product but the charge was the same as that which was charged for the product of quality q.
• A single-setup multi-delivery (SSMD) policy is adopted for transportation in this model. The vendor produces the products in a single lot and transports them in a multi-delivery process. The main reason for adopting the SSMD policy is that this policy makes the supply chain model more in line with an O2O environment. As multiple delivery was used, this increases the number of deliveries as well as the transportation cost. Thus, there is a trade-off between the buyer’s holding cost and the increased transportation cost. For transportation, variable and fixed transportation costs, as well as carbon emission costs, are considered, in order to make the model more sustainable.
• The safety stock and the sum of the expected demand during the lead time measures the re-order point (i.e., $Pp=D_r{L}_t+s_f\sigma \sqrt{L_t}$). To make the model more sustainable, demand is considered to be dependent on quality as well as the selling price of products and service of the vendor; more specifically, $D_r=A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi }$.
• To order something, the buyer incurs a cost which is known as the ordering cost. Continuous investment can reduce the ordering cost and increase the total profit of the system. When a production system goes through a long-run process, due to different issues, it may move from an “in-control” to “out-of-control” state and may produce defective items. Thus, an improvement in process quality is required, which is incorporated into the model along with reduced ordering cost, which improves the service provided to the customers.
• Fully back-ordered shortages are permitted.

4. Mathematical Model

In the proposed model, a single-vendor single-buyer SCM model is developed for a single type of product. Furthermore, it is a supply chain model in an O2O environment. The service of the total SCM is upgraded through the O2O channeling system, which also helps to optimize the total system profit. Vendors maximize their total system profit by providing lower quality items. Besides this, to make the model more realistic, demand is considered as price-, quality-, and service-dependent. As service cannot be infinite for any vendor, the service level is constrained.

4.1. Buyer’s Profit

The cost component for buyer is discussed here The re-order point is $Pp=\lambda a{L}_t+s_f\mathsf{\Sigma }\sqrt{\lambda L_t}$, where ${\mathsf{\Sigma }}^2=a^2+{\sigma }^2.$ Based on the model of Ouyang et al. [30], replenishment cycle shortages are represented by $C(r)=\mathsf{\Sigma }\sqrt{\lambda L_t}\mathsf{\Psi }(k)$, where $\mathsf{\Psi }(k)=\psi (k)-k[1-\mathsf{\Phi }(k)]$.

The average inventory for the buyer (Figure 1) is $\left(\frac{Q_s}{2m}\right)+s_f\mathsf{\Sigma }\sqrt{\lambda L_t}$.

Ordering cost

In an O2O supply chain model, ordering of the products is done through an online system and some cost is incurred by the online order, which is called the ordering cost. The online ordering cost for the customer/buyer in this O2O supply chain model is given by

$$\begin{array}{c}\hfill \frac{O_c(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{S_v}.\end{array}$$

Investment to improve the service by reducing ordering cost

As the buyer orders the product from the vendor, an investment can be used to reduce the ordering cost. For example, internet facilities are required for an O2O SCM and different service providers have different tariff charges for internet facilities in India. With an initial investment, the buyer can reduce the ordering cost in the O2O SCM. To reduce the ordering cost of the buyer, an investment is added as an ordering cost reduction investment. The reduction of ordering cost improves the service that is provided to the buyer by the vendor. This investment is defined as follows:

$$\begin{array}{ccc}\hfill O_i& =& gln\frac{O_{c_0}}{O_c}.\hfill \end{array}$$

Holding cost

Some places needed to hold the products that are ordered by the consumer/buyer online. These ordered products may be kept, for example, in a warehouse, which may be owned or rented. For the warehouse, the buyer incurs some cost, which is known as the holding cost. In this O2O supply chain model, the average inventory for the consumer/buyer is given by

$$\begin{array}{c}\hfill \left[\frac{S_v}{2}+s_f\mathsf{\Sigma }\sqrt{\lambda L_t}+(1-(\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}))E{(R-r)}^{+}\right].\end{array}$$

Thus, the estimated holding cost for the customer is

$$\begin{array}{c}\hfill I_h{P}_{cb}\left[\frac{S_v}{2}+s_f\mathsf{\Sigma }\sqrt{\lambda L_t}+(1-(\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}))E{(R-r)}^{+}\right].\end{array}$$

Shortage cost

Basically, shortages arise due to a lack of products, which means that over-demand of a particular product may lead to shortages of that product. Shortages of any product affect the brand images of companies and serve to reduce the profit in an O2O supply chain system. Thus, in the proposed model, the shortages per replenish cycle is defined as $C(r)=\mathsf{\Sigma }\sqrt{\lambda L_t}\mathsf{\Psi }(s_f)$, where $\mathsf{\Psi }(s_f)=\psi (s_f)-s_f[1-\mathsf{\Phi }(s_f)]$. Thus, the shortage cost for the O2O supply chain is given by

$$\begin{array}{c}\hfill \frac{u_c(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{S_v}C(r).\end{array}$$

Lead time crashing cost

The time gap between placing an order and receiving the product in hand is known as the lead time. In an O2O supply chain model, the lead time cannot be negligible, whereas most researchers have considered the lead time to be negligible. In a competitive business environment, consumers want their ordered products as early as possible and, so, the vendors also wish to reduce the lead time. A crashing cost is needed to diminish the lead time. Reduction of lead time is generally treated as a good service by customers. Thus, the cost for lead time crashing is given by

$$\begin{array}{c}\hfill \frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{m{S}_v}G(L).\end{array}$$

Therefore, the buyer’s total cost is given by

$$\begin{array}{ccc}& & T{C}_B(S_v,s_f,L_t,s_p,O_c,q_v,s)\hfill \\ & =& I_h{P}_{cb}\left[\frac{S_v}{2}+k\mathsf{\Sigma }\sqrt{\lambda L_t}+(1-(\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}))\psi (s_f)\right]\hfill \\ & +& \frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{m{S}_v}G(L)+\frac{O_c(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{S_v}\hfill \\ & +& \frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{m{S}_v}\left(B_{pd}(\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0})+{\pi }_0(1-(\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}))\right)\psi (s_f)\hfill \\ & +& gln\frac{O_{c_0}}{O_c}.\hfill \end{array}$$

(1)

The revenue for the buyer is $(P_{cv}-P_{cb})(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })$. Thus, the profit function for the buyer under O2O channeling along with better service is given by

$$\begin{array}{ccc}& & {\mathrm{Profit}}_B(S_v,s_f,L_t,s_p,O_c,q_v,s)\hfill \\ & =& (P_{cv}-P_{cb})(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })-T{C}_B(S_v,s_f,L_t,s_p,O_c,q_v)\hfill \\ & =& (P_{cv}-P_{cb})(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })-[I_h{P}_{cb}(\frac{S_v}{2}+s_f\mathsf{\Sigma }\sqrt{\lambda L_t}\hfill \\ & +& \left(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}\right)\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f))+\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{m{S}_v}G(L)\hfill \\ & +& \frac{O_c(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{S_v}+gln\frac{O_{c_0}}{O_c}\hfill \\ & +& \frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{m{S}_v}\left(\frac{{\beta }_0{B}_{pd}^2{q}_v}{{\pi }_0}+{\pi }_0(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0})\right)\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f)].\hfill \end{array}$$

(2)

4.2. Vendor’s Profit

The cost components for the vendor are as follows:

The stockpiling and attenuation process of the vendor is shown in Figure 2.

Carbon emissions cost for the supply chain model $(C{E}_v)$

Carbon emissions are an important issue in current environmental industrial concerns. Due to the SSMD transportation policy, the effects of carbon on the environment are considered. Fixed and variable carbon emissions costs for the vendor are considered in the model, where the fixed carbon emissions cost for the vendor is $V_{ccv}m$ and the variable cost (with respect to the number of received shipments) is ($F_{ccv}n$). Thus, the total carbon emissions cost is $C{E}_v=F_{ccv}m+V_{ccv}m{S}_v=F_{ccv}m+V_{ccv}m{S}_v$.

Quality upgrade cost for products

$QU{C}_v$ is the quality upgrade cost for manufacture and re-manufacture, where

$$\begin{array}{ccc}\hfill QU{C}_v& =& C_q{q}_p^2(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })(1-\tau )+\tau (A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })C_q(q_p^2-q_{p_v}^2).\hfill \end{array}$$

Profit due to lower quality of the product

In the considered scenario, the vendor does not deliver the required quality of the product to the buyer, even though they promised to do so. Due to the lower quality, a profit was gained by vendor, defined as follows:

$$\begin{array}{ccc}\hfill P_u& =& (q-q_{p_v})(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })(C_{q_v}-P_{cv}),\hfill \end{array}$$

where $P_u$ is the profit due to unreliability in quality

Setup cost for supply chain model

To build up any production process, an initial setup is required and, for that, some costs are incurred, which are called the setup costs. Generally, a fixed setup cost is required for any basic production system. However, in this O2O supply chain system, a discrete investment is implied to diminish the initial setup cost. Reduction in the setup cost serves to provide better service to the customers. Thus, the vendor’s combined investment and setup cost is obtained as follows

$$\begin{array}{c}\hfill S_{C_0}{e}^{-r{S}_A}+S_A.\end{array}$$

Transportation costs for supply chain model

Without transportation, a supply chain cannot run. Thus, transportation is necessary to deliver the product from the production house to the customer’s warehouse. In this model, an offline transportation model is utilized to deliver the products to the customers and provide the best service to the customers. Thus, the SSMD transportation policy is adopted by the companies. Due to this SSMD policy, the amount of transport is increased and, thus, both fixed and variable carbon emissions are contemplated for quality improvement.

Thus, the cost for transportation is $m{T}_F+m{T}_V{S}_v$.

Investment

The amount of defective items is $\frac{S_c(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })Q_s{P}_{\theta }}{2}$, while the quality improvement is given by

$$\begin{array}{c}\hfill bln\left(\frac{P_{{\theta }_0}}{P_{\theta }}\right).\end{array}$$

Holding cost for product of the vendor

In an O2O supply chain system, the produced products need to be stored in a warehouse (owned or rented), in order to provide the best service to the customers. For that purpose, the vendor incurs a holding cost. From Figure 2, one can calculate the average inventory for the vendor, as follows:

$$\begin{array}{ccc}& & \frac{[\mathrm{shaded}-\mathrm{area}]}{Q_s/(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}\hfill \\ & =& \left[\frac{S_v}{2}+\frac{(m-2)S_v}{2}\left(1-\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{(1-\eta )P_v}\right)\right].\hfill \end{array}$$

Therefore, vendor’s total holding cost for the green product is given by

$$\begin{array}{c}\hfill =\left[\frac{S_v}{2}+\frac{(m-2)S_v}{2}\left(1-\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{(1-\eta )P_v}\right)\right]P_{cv}{I}_h.\end{array}$$

Thus, the vendor’s annual total cost for the product is given by

$$\begin{array}{ccc}& & T{C}_V(S_v,s_f,s_p,P_{\theta },B_{pd},q_v,s)\hfill \\ & =& \frac{S_{C_0}{e}^{-r{S}_A}}{m{S}_v}+\frac{S_v}{2}\left[1+(m-2)\left(1-\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{(1-\eta )P_v}\right)\right]P_{cv}{I}_h\hfill \\ & +& \frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })S_A}{m{S}_v}+\frac{mS(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })S_v{P}_{\theta }}{2}+bln\frac{P_{{\theta }_0}}{P_{\theta }}\hfill \\ & +& \frac{T_F(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{S_v}+T_V(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })\hfill \\ & +& \frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })F_{ccv}}{S_v}+V_{ccv}(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })+QU{C}_v.\hfill \end{array}$$

(3)

The vendor’s revenue is given by $(s_p-P_{cv})(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })+P_u$.

Thus, the profit function of the vendor is given by

$$\begin{array}{ccc}& & {\mathrm{Profit}}_V(S_v,k,p,\theta ,{\pi }_x,q_v,s)\hfill \\ & =& (s_p-P_{cv})(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })-T{C}_V(S_v,s_f,s_p,P_{\theta },q_v,s)\hfill \\ & =& (s_p-P_{cv})(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })-[\frac{S_{C_0}{e}^{-r{S}_A}}{m{S}_v}\hfill \\ & +& \frac{S_v}{2}\left[1+(m-2)\left(1-\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{(1-\eta )P_v}\right)\right]P_{cv}{I}_h+\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })S_A}{m{S}_v}\hfill \end{array}$$

$$\begin{array}{ccc}& +& \frac{m{S}_v{S}_c(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })P_{\theta }}{2}+bln\frac{P_{{\theta }_0}}{P_{\theta }}+\frac{T_F(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{S_v}\hfill \\ & +& T_V(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })+\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })F_{ccv}}{S_v}+V_{ccv}(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })\hfill \\ & +& QU{C}_v]+P_u.\hfill \end{array}$$

(4)

Therefore, the total profits of the buyer and vendor are given by Equations (2) and (4), respectively, and the joint total expected annual profit of the supply chain is given by:

$$\begin{array}{ccc}& & \mathrm{Total}\mathrm{profit}(S_v,L_t,s_f,s_p,P_{\theta },B_{pd},O_c,q_v,s)\hfill \\ & =& (s_p-P_{cb})(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })-TC(S_v,s_f,s_p,P_{\theta },O_c,B_{pd},q_v,s)\hfill \\ & =& (s_p-P_{cb})(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })-\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{S_v}\left[\frac{S_{C_0}{e}^{-r{S}_A}}{m}+\frac{S_A}{m}+O_c\right]\hfill \\ & -& gln\left(\frac{O_{c_0}}{O_c}\right)-\frac{S_v}{2}{I}_h\left\{1+(m-2)\left(1-\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{(1-\eta )P_v}\right)\right\}{P}_{cv}\hfill \\ & -& \frac{S_v{I}_h}{2}{P}_{cb}-I_h{P}_{cb}\mathsf{\Sigma }\sqrt{\lambda L_t}\left(s_f+(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0})\psi (s_f)\right)-\frac{m{S}_v{S}_c(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })\theta }{2}\hfill \\ & -& bln\left(\frac{P_{{\theta }_0}}{P_{\theta }}\right)-\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{m{S}_v}G(L)-\frac{T_F(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}{S_v}\hfill \\ & -& T_V(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })-\frac{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })F_{ccv}}{S_v}-V_{ccv}(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })\hfill \\ & -& \frac{m{S}_v}{(A_f{s_p}^{-\gamma }+\rho q_v^{\delta }+\zeta s^{\varphi })}\left[B_{pd}\left(\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}\right)+{\pi }_0\left(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}\right)\right]\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f)\hfill \\ & -& QU{C}_v+P_u.\hfill \end{array}$$

(5)

As service cannot be infinite, the maximum service is considered as M. The resulting service constraint is as follows

$$\begin{array}{ccc}\hfill \sum _{i=1}^{n}Q{S}_{i}s& \le & M\hfill \\ \hfill (\mathrm{i}.\mathrm{e}.,m{S}_{v}s& \le & M).\hfill \end{array}$$

(6)

In this model, the defect rate is $\eta =E[f(x)]$, where $f(x)$ follows a (1) Uniform distribution, (2) Triangular distribution, or (3) Beta distribution and a different algebraic procedure is used to find the optimal solution. We then compare the profit determined by the different models.

5. Solution Methodology

A classical optimization technique is utilized to solve the current model. The framework is provided in Figure 3, in order to clarify the optimization technique.

To satisfy the necessary conditions of the optimization technique, taking the first-order derivatives of Equation (5) with respect to the decision variables $S_v$, $L_t$, $s_f$, $s_p$, $P_{\theta }$, $B_{pd}$, $O_c$, $q_v$, and s, one can obtain:

$$\begin{array}{ccc}\hfill \frac{\partial TP}{\partial s_f}& =& -I_h{P}_{cb}\mathsf{\Sigma }\sqrt{\lambda L_t}-I_h{P}_{cb}\mathsf{\Sigma }\sqrt{\lambda L_t}\left(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}\right)\left(\psi (s_f)-1\right)\hfill \\ & -& \frac{m{S}_v}{D_r}\left[B_{pd}\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}+{\pi }_0\left(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}\right)\right]\mathsf{\Sigma }\sqrt{\lambda L}\left(\mathsf{\Phi }(s_f)-1\right),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill \frac{\partial TP}{\partial S_v}& =& \frac{D}{S_v^2}\left[\frac{1}{m}\left(S_{c_0}{e}^{-r{S}_A}+S_A+G(L)\right)+O_c+T_F+F_{ccv}\right]\hfill \\ & -& \frac{I_h}{2}\left[\left\{1+(m-2)\left(1-\frac{D_r}{(1-\eta )P_v}\right)\right\}{P}_{cv}+P_{cb}\right]-\frac{m{S}_c{D}_r{P}_{\theta }}{2}\hfill \\ & -& \frac{m}{D_r}\left[B_{pd}(\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0})+{\pi }_0(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0})\right]\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \frac{\partial TP}{\partial P_{\theta }}& =& -\frac{m{S}_v{S}_c{D}_r}{2}+\frac{b}{P_{\theta }},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \frac{\partial TP}{\partial O_c}& =& -\frac{D_r}{S_v}+\frac{g}{O_c},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill \frac{\partial TP}{\partial s_p}& =& -A_f{s_p}^{-1-\gamma }\gamma {\beta }_1+\alpha p^{-\gamma },\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill \mathrm{where}{\beta }_1& =& [\left[s_p-P_{cb}-T_V-V_{ccv}+(C_{q_v}-P_{cv})(q-q_{p_v})-q_p^2(1-\tau )C_q-(q_p^2-q_{p_v}^2)\tau C_q\right]\hfill \\ & +& S_v\left[\frac{I_h(m-2)P_{cv}}{2P_v(1-\eta )}-\frac{m{S}_c{P}_{\theta }}{2}+\frac{m\left(\frac{B_{pd}{q}_v{\beta }_0}{{\pi }_0}(B_{pd}-{\pi }_0)+{\pi }_0\right)\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f)}{{\left(A_s{s_p}^{-\gamma }+\zeta s^{\varphi }+\rho q_v^{\delta }\right)}^2}\right]\hfill \\ & -& \frac{\left[\frac{S_A}{m}+\frac{S_{C_0}{e}^{-r{S}_A}}{m}+\frac{G(L)}{m}+O_c+T_F+F_{ccv}\right]}{S_v}-\left(\zeta s^{\varphi }+\rho q_v^{\delta }\right)],\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill \frac{\partial TP}{\partial q_v}& =& \rho \delta q_v^{-1+\delta }{\beta }_5+S_v\rho \delta q_v^{-1+\delta }{\beta }_6-\frac{\rho \delta q_v^{-1+\delta }}{S_v}{\beta }_7-{\beta }_8,\hfill \\ \hfill \mathrm{where}{\beta }_5& =& \left[s_p-P_{cb}-T_V-V_{ccv}+(C_{q_v}-P_{cv})(q-q_{p_v})-q_p^2(1-\tau )C_q-(q_p^2-q_{p_v}^2)\tau C_q\right],\hfill \\ \hfill {\beta }_6& =& \left[\frac{I_h(m-2)P_{cv}}{2P_v(1-\eta )}+\frac{m\left(\frac{B_{pd}{q}_v{\beta }_0}{{\pi }_0}(B_{pd}-{\pi }_0)+{\pi }_0\right)\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f)}{{\left(A_f{s_p}^{-\gamma }+\zeta s^{\varphi }+\rho q_v^{\delta }\right)}^2}-\frac{m{S}_c{P}_{\theta }}{2}\right],\hfill \\ \hfill {\beta }_7& =& \left[\frac{S_A}{m}+\frac{S_{C_0}{e}^{-r{S}_A}}{m}+\frac{G(L)}{m}+O_c+F+F_{ccv},\right]\hfill \\ \hfill {\beta }_8& =& \frac{S_{v}m\left(\frac{{B_{pd}}_x^2{\beta }_0}{{\pi }_0}-B_{pd}{\beta }_0\right)\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f)}{\left(A_f{s_p}^{-\gamma }+\zeta s^{\varphi }+\rho q_v^{\delta }\right)}-\frac{I_h{P}_{cb}{B}_{pd}{\beta }_0\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f)}{{\pi }_0},\hfill \\ \hfill \frac{\partial TP}{\partial B_{pd}}& =& -\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f)\left[-\frac{I_h{P}_{cb}{\beta }_0{q}_v}{{\pi }_0}+\frac{m{S}_v}{D_r}\left(\frac{2{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}-{\beta }_0{q}_v\right)\right],\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill \frac{\partial TP}{\partial s}& =& S_v\zeta \varphi s^{-1+\varphi }\left[\frac{I_h(m-2)P_{cv}}{2P_v(1-\eta )}-\frac{m{S}_c{P}_{\theta }}{2}+\frac{m\left(\frac{B_{pd}{q}_v{\beta }_0}{{\pi }_0}(B_{pd}-{\pi }_0)+{\pi }_0\right)\mathsf{\Sigma }\sqrt{\lambda L}\psi (s_f)}{{\left(A_f{s_p}^{-\gamma }+\zeta s^{\varphi }+\rho q_v^{\delta }\right)}^2}\right]\hfill \\ & +& \zeta \varphi s^{-1+\varphi }{\beta }_2+\frac{\zeta \varphi s^{-1+\varphi }}{S_v}{\beta }_3,\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill \mathrm{where}{\beta }_2& =& \left[s_p-P_{cb}-T_V-V_{ccv}+(C_{q_v}-P_{cv})(q-q_{p_v})-q_p^2(1-\tau )C_q-(q_p^2-q_{p_v}^2)\tau C_q\right],\hfill \\ \hfill {\beta }_3& =& \left[\frac{S_A}{m}+\frac{S_{c_0}{e}^{-r{S}_A}}{m}+\frac{G(L)}{m}+O_c+T_F+F_{ccv}\right],\hfill \end{array}$$

(15)

$$\begin{array}{c}\\ \hfill \frac{\partial TP}{\partial L_t}& =& -\frac{I_h{C}_B}{2}\mathsf{\Sigma }\sqrt{\frac{\lambda }{L_t}}\left(s_f+(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0})\psi (s_f)\right)\hfill \\ & -& \frac{m{S}_v}{2D_r}\mathsf{\Sigma }\sqrt{\frac{\lambda }{L_t}}\psi (s_f)\left[B_{pd}\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}+{\pi }_0\left(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}\right)\right]-\frac{D_r}{m{S}_v}{m}_i.\hfill \end{array}$$

(16)

For fixed values of $S_v$, $s_f$, $s_p$, $P_{\theta }$, $B_{pd}$, $O_c$, $q_v$, and s, $L_t$ is always convex, as

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}TP}{\partial L_t^2}& =& \frac{I_h{P}_{cb}}{4}\mathsf{\Sigma }\sqrt{\frac{\lambda }{L_t^3}}\left(s_f+(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0})\psi (s_f)\right)\hfill \\ & +& \frac{m{S}_v}{4D_r}\mathsf{\Sigma }\sqrt{\frac{\lambda }{L_t^3}}\psi (s_f)\left[B_{pd}\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}+{\pi }_0\left(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}\right)\right]>0.\hfill \end{array}$$

(17)

Now, by equating all first-order partial derivatives to zero, one can obtain the optimum values of the decision variables $S_v$, $s_f$, $s_p$, $P_{\theta }$, $B_{pd}$, $O_c$, $q_v$, and s (i.e., $S_v^{*}$, $s_f^{*}$, $s_p^{*}$, $P_{\theta }^{*}$, $B_{pd}^{*}$, $O_c^{*}$, $q_v^{*}$, and $s^{*}$) as follows

$$\begin{array}{ccc}\hfill S_v^{*}& =& \sqrt{\frac{2D_r^2\left[\frac{1}{m}\left(S_{c_0}{e}^{-r{S}_A}+S_A+G(L)\right)+O_c+T_F+F_{ccv}\right]}{I_h{D}_{r}J+m{S}_c{D}_r^2{P}_{\theta }-2m\left[\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}(B_{pd}-{\pi }_0)+{\pi }_0\right]\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f)}},\hfill \\ \hfill \mathrm{where}J& =& \left[\left\{1+(m-2)\left(1-\frac{D_r}{(1-\eta )P_v}\right)\right\}{P}_{cv}+P_{cb}\right],\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill \mathsf{\Phi }(s_f^{*})& =& 1-\frac{I_h{P}_{cb}}{I_h{P}_{cb}\left(1-\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}\right)+\frac{m{S}_v}{D_r}\left[\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}(B_{pd}-{\pi }_0)+{\pi }_0\right],}\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill s_p^{*}& =& \gamma {\beta }_1,\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill P_{\theta }^{*}& =& \frac{2b}{S_c{D}_r{S}_{v}m},\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill O_c^{*}& =& \frac{g{S}_v}{D_r},\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill B_{pd}^{*}& =& \frac{I_h{P}_{cb}{D}_r+m{S}_v{\pi }_0}{2m{S}_v},\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill q_v^{*}& =& {\left[\frac{S_v{\beta }_8}{\rho \delta [S_v^2{\beta }_6+S_v{\beta }_5-{\beta }_7]}\right]}^{\frac{1}{\delta -1}},\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill s^{*}& =& {\left[\frac{\sqrt{{\beta }_4}-(A_f{s_p}^{-\gamma }+\rho q_v^{\delta })}{\zeta }\right]}^{\frac{1}{\varphi }},\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill \mathrm{where}{\beta }_4& =& {(A_f{s_p}^{-\gamma }+\rho q_v^{\delta })}^2-[(A_f^2{s_p}^{-2\gamma }+{\rho }^2{q}_v^{2\delta }+2\alpha \rho p^{-\gamma }{q}_v^{\delta })\hfill \\ & -& \frac{m\left[\frac{{\beta }_0{B}_{pd}{q}_v}{{\pi }_0}(B_{pd}-{\pi }_0)+{\pi }_0\right]\mathsf{\Sigma }\sqrt{\lambda L_t}\psi (s_f)}{\left[\frac{{\beta }_3}{S_v^2}-\frac{{\beta }_2}{S_v}+\frac{mS{P}_{\theta }}{2}-\frac{I_h(m-2)C_v}{2P_v(1-\eta )}\right]}]\hfill \end{array}$$

and the service constraint, ${\lambda }_1$, is given by

$$\begin{array}{ccc}\hfill {\lambda }_1& =& \frac{M}{m{S}_v^{*}{s}^{*}}:\hfill \end{array}$$

(26)

The sufficient condition for the concavity is proven in Lemma 1 below.

Lemma 1.

For the given optimum values of $S_v$, $s_f$, $P_{\theta }$, $s_p$, $O_c$, $B_{pd}$, $q_v$, and s (i.e., for $S_v^{*}$, $s_f^{*}$, $P_{\theta }^{*}$, $s_p^{*}$, $O_c^{*}$, $B_{pd}^{*}$, $q_v^{*}$, and $s^{*}$), $TP(S_v,s_f,\theta ,p,O_c,B_{pd},q_v,s)$ attains its global maximum at $S_v^{*}$, $k^{*}$, $P_{\theta }^{*}$, $s_p^{*}$, $O_c^{*}$, $B_{pd}^{*}$, $q_v^{*}$, and $s^{*}$, where $L_t\in [L_{t_i},L_{t_{i-1}}]$.

Proof. 

See Appendix A for the proof of Lemma 1. □

6. Numerical Experiment

To validate the proposed method, some numerical examples are provided in this section, along with a comparison with other methods in the existing literature. As this is not a survey paper, no interview was undertaken with any industry and the data for the numerical examples were simply taken from the existing literature. The values of the parameters were obtained from the works of Dey et al. [38] and Dey et al. [15], for their best fit.

Example 1.

For the first numerical experiment, data of the parameters were taken from Dey et al. [38] and Dey et al. [15], as follows: $P_{cb}=\$20/unit$, $P_{cv}=\$10/unit$, ${\beta }_0=1.2$, ${\pi }_0=1.5$, $S_c=\$2000/batch$, $b=2000$, ${\theta }_0=0.0002$, $A_f=5$, $\rho =8$, $\gamma =7$, $\delta =5$, $\zeta =5$, $S_{C_0}=\$1000/setup$, $r=0.01$, $m=5$, $\mathsf{\Sigma }=2$, $\lambda =4$, $g=300$, $O_{C_0}=\$50/order$, $I_h=\$0.2/unit$, $P_v=3200unit$, $G(L)=22.4$, $T_V=0.4$, $F_{ccv}=\$0.2/unit$, $V_{ccv}=\$0.1/unit$, $C_q=\$6/unit$, $\tau =0.42$, $q=0.8$, $C_{q_v}=\$15/unit$, $q_p=0.6$, $\varphi =1.3$, and $q_{p_v}=0.5$. The values of the scaling parameters for the Uniform, Triangular, and Beta distributions were $(0.03,0.07)$, $(0.03,0.07,0.04)$, and $(0.03,0.07)$, respectively. The setup cost reduction due to discrete investment is provided in

Table 2. Setup cost investment data.

Investment $(\mathbf{\$})$	Setup Cost $(\mathbf{\$})$
0	1000
50	606
100	368
200	135

. It was found that the profit was maximum when the setup cost investment was $S_A=\$200/setup$.

The profit was then maximised for the optimum value of the decision variables, which is shown in

Table 3. Optimum Values without Service Constraint.

	Uniform Distribution	Triangular Distribution	Beta Distribution
$S_v^{*}$ (units)	$10.052$	$10.052$	$10.053$
$s_p^{*}$ ($/unit)	$28.406$	$28.406$	$28.407$
$q_v^{*}$	$0.466$	$0.466$	$0.466$
$s^{*}$	$0.332$	$0.332$	$0.333$
$B_{pd}^{*}$	$0.799$	$0.800$	$0.799$
$P_{\theta }^{*}$	$0.0005$	$0.0005$	$0.0005$
$L_t^{*}$ (weeks)	4	4	4
$s_f^{*}$	$3.2$	$3.2$	$3.2$
$O_c^{*}$	$159.996$	$159.996$	$159.996$
$TP$ ($)	$7984.8263$	$7984.8260$	${7984.8300}^{*}$

. The values of the service constraint were $(0.36,0.36,0.36)$.

The profit was maximum when defect rate followed the Beta distribution. From Table 3, it is clear that the profit was $\$7984.83$ when there was no constraint and, when service was treated as constrained, the joint profit of the system was $\$8312.86$. From the two Tables below, one can easily see that use of a service constraint was beneficial.

With maximum service of 1000 units, the optimal values under the service constraint are given in

Table 4. Optimum Values with Service Constraint.

	Uniform Distribution	Triangular Distribution	Beta Distribution
$S_v^{*}$ (units)	$10.057$	$10.057$	$10.057$
$s_p^{*}$ ($/unit)	$30.995$	$30.996$	$30.996$
$q_v^{*}$	$0.463$	$0.463$	$0.463$
$s^{*}$	$0.327$	$0.327$	$0.326$
$B_{pd}^{*}$	$0.799$	$0.800$	$0.799$
$P_{\theta }^{*}$	$0.0006$	$0.0006$	$0.0006$
$L_t^{*}$ (weeks)	4	4	4
$s_f^{*}$	$3.2$	$3.2$	$3.2$
$O_c^{*}$	$159.996$	$159.996$	$159.996$
$TP$ ($)	$8312.8432$	$8312.8431$	$8312.{8600}^{*}$

.

Example 2.

For the second numerical experiment, data of the parameters were taken from Dey et al. [38] and Dey et al. [15], as follows: $P_{cb}=\$28/unit$, $P_{cv}=\$10/unit$, ${\beta }_0=1.2$, ${\pi }_0=1.5$, $S_c=\$2500/batch$, $b=2000$, ${\theta }_0=0.0001$, $A_f=5$, $\rho =8$, $\gamma =7$, $\delta =5$, $\zeta =5$, $S_0=\$1000/setup$, $r=0.01$, $A=200/setup$, $n=5$, $\mathsf{\Sigma }=2$, $\lambda =4$, $g=300$, $O_{C_0}=\$50/order$, $I_h=\$0.2/unit$, $P_v=3200unit$, $G(L)=22.4$, $T_V=0.4$, $F_{ccv}=\$0.2/unit$, $V_{ccv}=\$0.1/unit$, $C_q=\$6/unit$, $\tau =0.42$, $q=0.8$, $C_{q_v}=\$15/unit$, $q_p=0.6$, $\varphi =1.3$, and $q_{p_v}=0.5$. The values of the scaling parameters for the Uniform, Triangular, and Beta distributions were $(0.04,0.08)$, $(0.04,0.07,0.08)$, and $(0.04,0.09)$, respectively. The setup cost investment data is provided in Table 2. The profit was maximized for the optimum value of the decision variables, as shown in

Table 5. Optimum values without service constraint.

	Uniform Distribution	Triangular Distribution	Beta Distribution
$S_v^{*}$ (units)	$10.062$	$10.013$	$10.046$
$s_p^{*}$ ($/unit)	$22.816$	$4.65$	$17.980$
$q_v^{*}$	$0.466$	$0.486$	$0.474$
$s^{*}$	$0.522$	$0.570$	$0.350$
$B_{pd}^{*}$	$0.670$	$0.670$	$0.599$
$P_{\theta }^{*}$	$0.0002$	$0.0002$	$0.0003$
$L^{*}$ (weeks)	4	4	4
$s_f^{*}$	$4.2$	$4.2$	$4.2$
$O_c^{*}$	$287.998$	$368.996$	$267.998$
$TP$ ($)	$8322.87$	$8202.0300$	$9297.{9800}^{*}$

. The values of the service constraint were $(0.34,0.17,0.32)$. The optimum result, along with optimum values of the decision variables, are provided in Table 5. The profit was maximal when the defect rate followed the Beta distribution.

With maximum service of 2000 units, then optimal values obtained when using the service constraint are given in

Table 6. Optimum values with service constraint.

	Uniform Distribution	Triangular Distribution	Beta Distribution
$S_v^{*}$ (units)	$10.054$	$10.017$	$10.045$
$s_p^{*}$ ($/unit)	$19.891$	$5.962$	$17.73$
$q_v^{*}$	$0.475$	$0.485$	$0.480$
$s^{*}$	$0.544$	$0.565$	$0.357$
$B_{pd}^{*}$	$0.699$	$0.699$	$0.799$
$P_{\theta }^{*}$	$0.0002$	$0.0002$	$0.0004$
$L_t^{*}$ (weeks)	4	4	4
$s_f^{*}$	$4.2$	$4.2$	$3.2$
$O_c^{*}$	$287.998$	$367.999$	$267.998$
$TP$ ($)	$8770.3900$	$8494.7400$	$9779.{9800}^{*}$

.

One can easily see, from both of the above examples, that profit was maximum when the defect rate followed a Beta distribution under the service constraint. The optimal profit was $\$9779.98$ per cycle.

From

Table 7. Comparison of total profit with previous methods.

	Dey et al. [38]	Dey et al. [15]	This Model
Total Profit ($/cycle)	1802	6860	9780

, one can easily see that the proposed model was more beneficial, compared to those of Dey et al. [38] and Dey et al. [15]. In Dey et al. [38], the total profit was $\$1802$, the defect rate and lead time data followed a Poisson distribution, and the demand depended on only selling price. Similarly, when the defect rate followed the Chi-square distribution and demand depended on selling price and quality in the study of Dey et al. [15], the total profit of the production system was $\$6860$. In contrast, using the proposed model, the profit was maximized, where the defect rate followed a Beta distribution and the demand depended on the selling price, quality of the product, and service level of the company. In the current study, the profit was about five times better than that of Dey et al. [38] and more than $\$2500$ better that that of Dey et al. [15].

Considering the results above, it is clear that O2O and service have a great impact in any supply chain system; in particular, they should be considered when optimizing the total system profit.

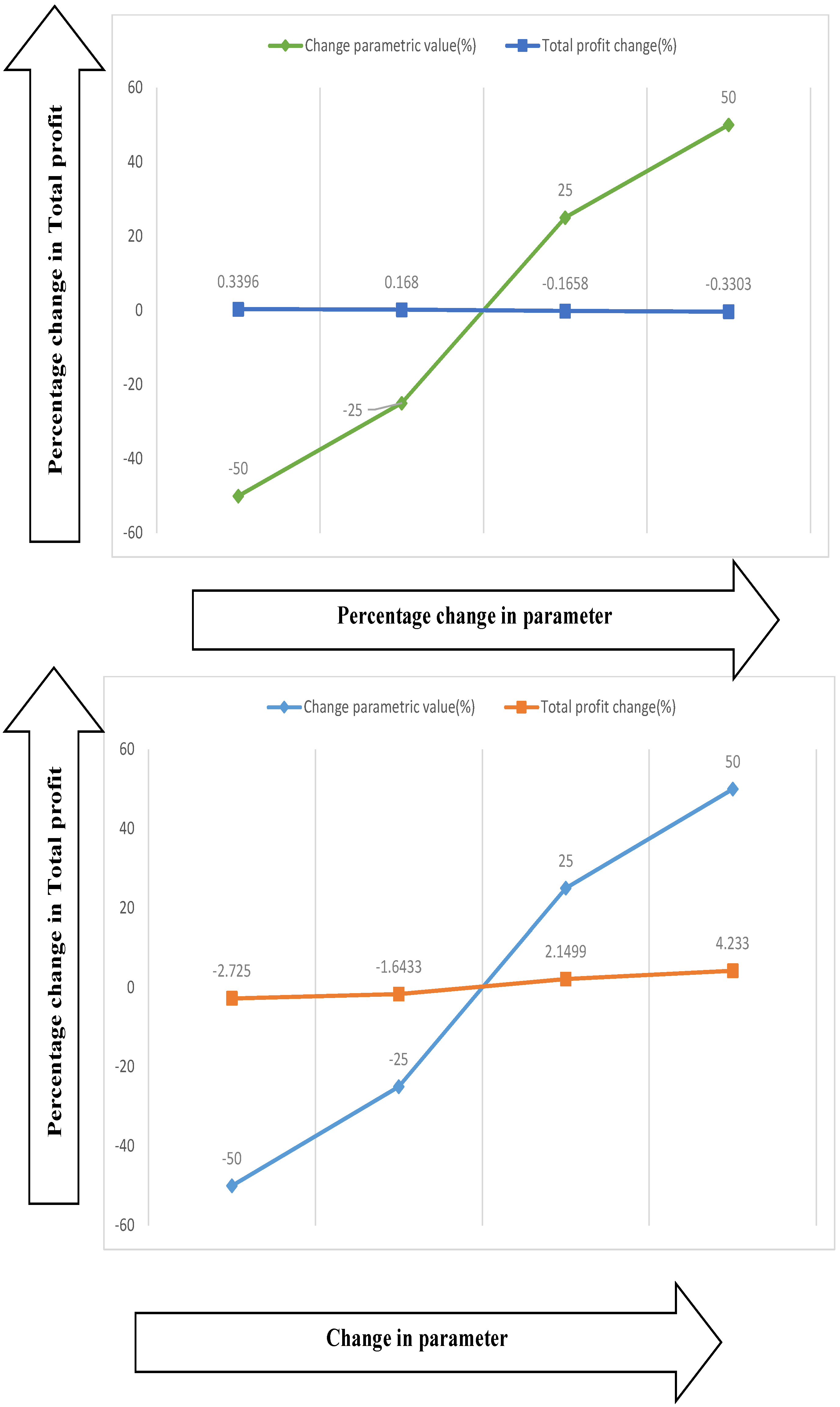
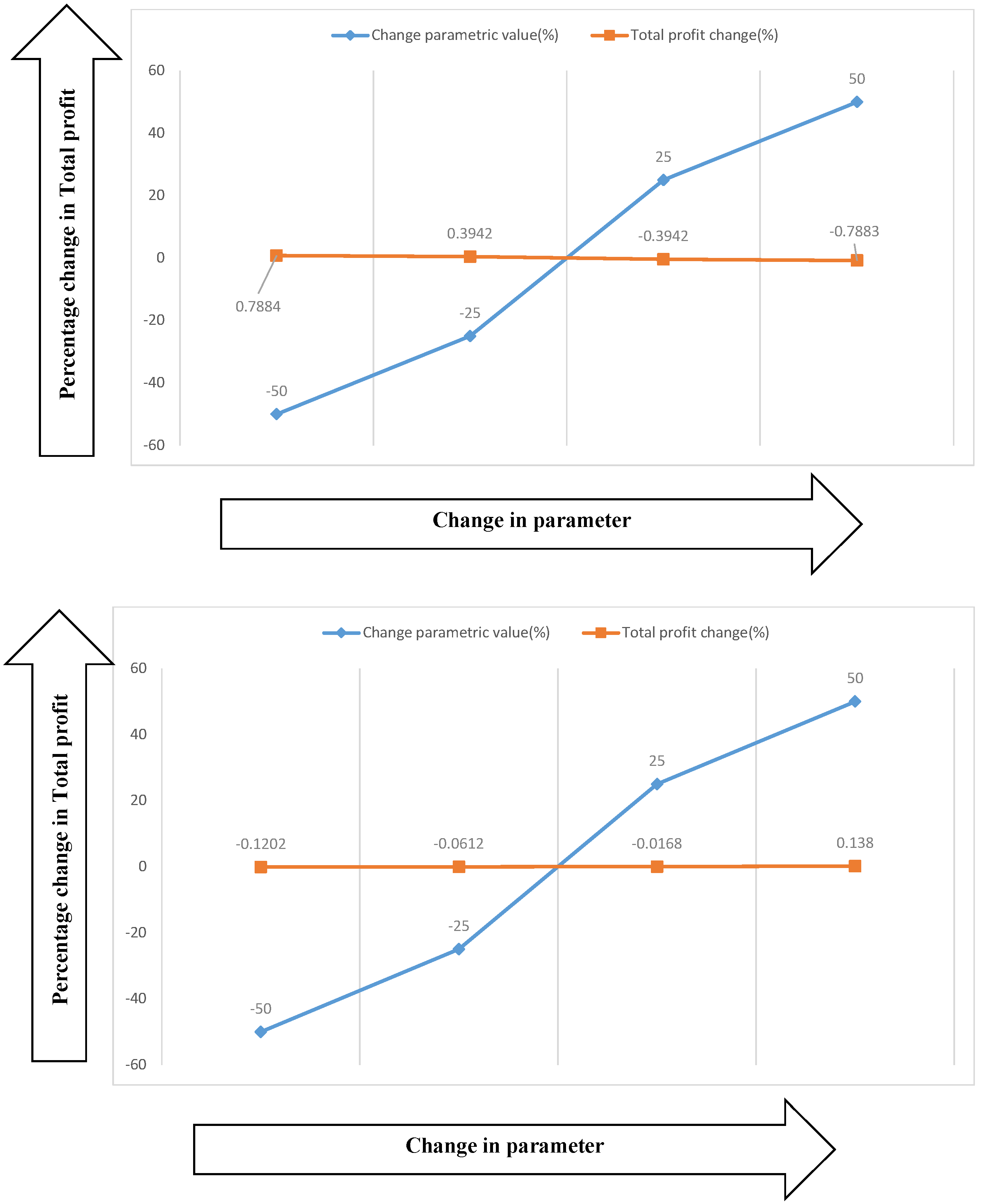
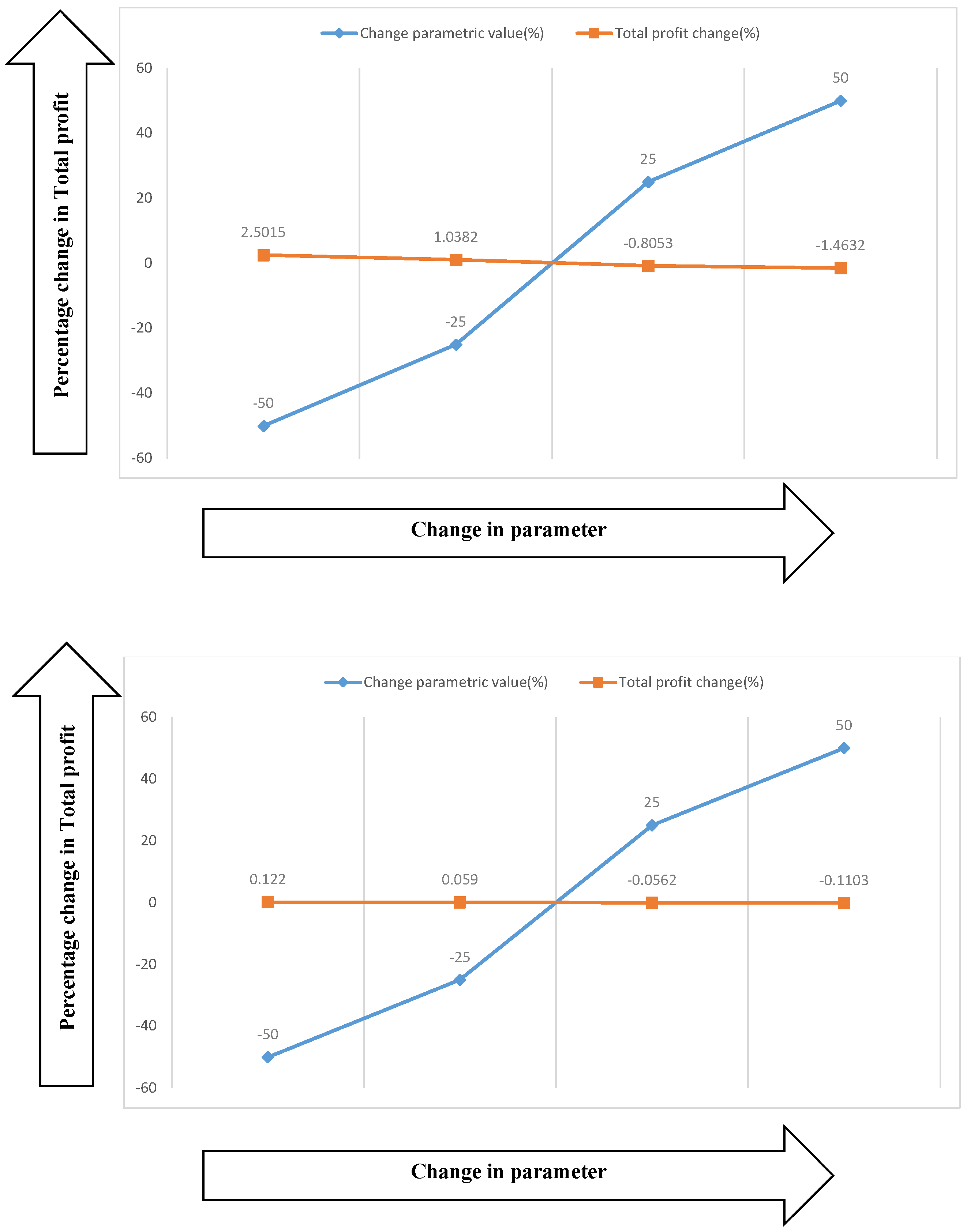
7. Sensitivity Analysis

In this section, the effects of change in different key parameters by ($-50\%$, $-25\%$, $+25\%$, $+50\%$) on the total profit are calculated. Graphical representations are shown in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, in order to demonstrate the effects of the key parameters on the total profit. From the sensitivity results presented in

Table 8. Sensitivity analysis table.

Parameters	Changes (in%)	${TP}^{*}$ (in%)	Parameters	Changes (in%)	${TP}^{*}$ (in%)
$P_{cv}$	$-50$	$+0.3396$	$C_{fcv}$	$-50$	$+0.0008$
	$-25$	$+0.1680$		$-25$	$+0.0004$
	$+25$	$-0.1658$		$+25$	$-0.0004$
	$+50$	$-0.3303$		$+50$	$-0.0008$
${\beta }_0$	$-50$	$+0.0059$	$C_{vcv}$	−50	$+0.0031$
	$-25$	$+0.0030$		$-25$	$+0.0016$
	$+25$	$-0.0030$		$+25$	$-0.0016$
	$+50$	$-0.0059$		$+50$	$-0.0031$
${\pi }_0$	$-50$	$-0.0377$	$C_q$	$-50$	$+0.0494$
	$-25$	$-0.0228$		$-25$	$+0.0243$
	$+25$	$+0.0260$		$+25$	$-0.0237$
	$+50$	$+0.0536$		$+50$	$-0.0470$
$O_{C_0}$	$-50$	$+2.5015$	$\tau$	$-50$	$-0.0196$
	$-25$	$+1.0382$		$-25$	$-0.0098$
	$+25$	$-0.8053$		$+25$	$+0.0099$
	$+50$	$-1.4632$		$+50$	$+0.0199$
$S_A$	$-50$	$-0.1176$	$q_{p_v}$	$-50$	$+0.0502$
	$-25$	$-0.06261$		$-25$	$+0.0221$
	$+25$	$+0.0055$		$+25$	$-0.0168$
	$+50$	$-0.0243$		$+50$	$-0.0286$
$S_{c_0}$	$-50$	$+0.1220$	q	$-50$	$-0.1202$
	$-25$	$+0.0590$		$-25$	$-0.0612$
	$+25$	$-0.0562$		$+25$	$-0.0168$
	$+50$	$-0.1103$		$+50$	$+0.1380$
$I_h$	$-50$	$+0.7884$	M	$-50$	$-2.7250$
	$-25$	$+0.3942$		$-25$	$-1.6433$
	$+25$	$-0.3942$		$+25$	$+2.1499$
	$+50$	$-0.7883$		$+50$	$+4.2330$
$P_v$	$-50$	$+0.0005$	V	$-50$	$+0.0126$
	$-25$	$+0.0002$		$-25$	$+0.0063$
	$+25$	$-0.0001$		$+25$	$-0.0063$
	$+50$	$-0.0002$		$+50$	$-0.0123$

, one can conclude that:

(i)

The initial ordering cost and service are more sensitive in this supply chain model (i.e., in the presence of an O2O environment). It is quite natural that the best service always provides more profit, which can be seen in the sensitivity table.

(ii)

When providing good service, holding and production costs are less sensitive in this supply chain model.

(iii)

Considering the environmental issue, fixed and variable carbon emissions costs also have an effect on the total profit.

(iv)

The quality ordered by the buyer also has an effect on the total profit.

(v)

The effect of the vendor production rate $P_v$ is almost negligible.

(vi)

All other parameters only have a small effect on the total system profit.

8. Managerial Insights

(i)

We consider SCM in the presence of an unreliable vendor and O2O environment, where joint total profit of the supply chain is optimized along with the optimized values of service, quality of the products, shipment size, lead time period, backorder price discount, safety factor, selling price, ordering cost for the buyer, and probability to transfer the production process from an “in-control” to “out-of-control” state.

(ii)

We developed this supply chain model in the presence of an unreliable vendor, where unreliability occurs in quality of the product. Furthermore, the online-to-offline concept is adopted and the best service is provided to the customers.

(iii)

This is a integrated supply chain model, in which the effect of carbon emissions is also considered. Thus, the proposed model is much more effective for the modern, earth-conscious business environment; further, customers obtain upgraded service from the vendor.

(iv)

The ordering and setup costs of the supply chain system can be reduced through continuous investment, which improves the service of the total SCM and also makes this model more sustainable. The process quality is also improved by investment, which has a great impact on the total joint expected profit of the supply chain, as well as on the service provided by the vendor.

(v)

The quality of any product plays a major role in increasing demand for the product. To maintain the brand image of the company and optimize the total profit, quality upgrading is considered in this study. Better service is provided to the customers along with a better quality product. This concept should be gladly accepted by any industry, in order to optimize their profit.

(vi)

Service for any particular item cannot be infinite. Any company has a maximum capability to provide services to their customers. The result of this model were more appropriate, due to consideration of a service constraint, which should be considered a very effective concept in any industry.

(vii)

Lead time and shortages create a bad image for any company, as well as affecting the service provided by the company to its customers. In the proposed model, the lead time period and safety factor are optimized along with various other decision variables, thus providing better service and making the model more sustainable. Moreover, the lead time was shown to be reduced, which is beneficial for any industry.

9. Conclusions

In this paper, we developed a single-vendor single-buyer supply chain model in which different real-world issues are considered. To date, it has been found that the selling price of any product plays a vital role in adjusting the demand for the product. However, at the same time, the quality of the product also plays a vital role in increasing its demand (Dey et al. [15]). Besides selling price and quality, the service of a company is another key parameter for increasing profits, which was made clear in this study. To model a modern situation, an advanced O2O retail channel system was considered, in order to upgrade the quality of service. The use of an online–offline system is considered to be profitable for any supply chain system, along with the better service that provided by the associated companies to their customers. A continuous investment was incorporated to reduce the ordering cost, another novel aspect of this study. Generally, ordering cost is treated as fixed for any supply chain; however, continuous investment can reduce the ordering cost, as well as increase the system profit. Moreover, a discrete investment was considered to reduce the setup costs of the vendor. To optimize the total system profit, the vendor cheats the buyer by providing lower quality product, where some cost was also involved for upgrading the quality of the product. Due to the lower quality, the vendor optimize their profit and the total system profit was optimized. Considering the SSMD policy for transportation, variable and fixed carbon emissions costs and a transportation cost were utilized in the development of the proposed model, in order to provide upgraded services to buyers. The model considered continuous investment to improve the process quality, which is a limitation of the model. The total system profit was optimized along with the optimized values of shipment volume, safety factor, lead time, selling price, quality, service, ordering cost, setup cost, and probability of transferring to an “out-of-control” state. We demonstrated that a service constraint can provide a better result, compared to optimization without the service constraint. We also found that the result was optimal when the defect rate followed a Beta distribution; in contrast, in the literature, it has been shown to be optimal when the defect rate followed a Chi-square distribution.

The proposed model upgrades the quality of the product along with a fixed service. This model may be extended by considering outsourcing for quantity and an advanced Radio Frequency Identifer Device (RFID) technology (see, e.g., Ullah and Sarkar [53]) can be implemented to prevent unreliability in the quantity provided by vendors. We consider imperfect production, which is why shortages arise and processes may produce defective items; thus, the proposed model can be extended by considering an inspection policy. Such a production process can utilize an advanced smart production process, if one considers automated inspection (see, e.g., Sarkar et al. [54]), which is an interesting research gap. Instead of a single product, this model can also be extended by considering a multi-item production process or an assembled production process. The use of a fixed production rate is another limitation of this model; thus, one could consider the use of a variable production rate (Dey et al. [15]), which is another very interesting research direction. This model can also be developed by considering deteriorating items under the tread-credit policy (see, e.g., Sarkar et al. [55]). Instead of a two-echelon supply chain, the model could extended by considering a multi-echelon supply chain (Sarkar et al. [56]). It could also be developed by considering product greenness (Liu et al. [57]). Interesting findings may be obtained by considering different types of warehouses for holding the items. Finally, this model may also developed by considering different types of pricing strategies for offline and online sales.