Sage Revised Reiterative Even Zernike Polynomials Neural Network Control with Modified Fish School Search Applied in SSCCRIM Impelled System
Abstract
1. Introduction
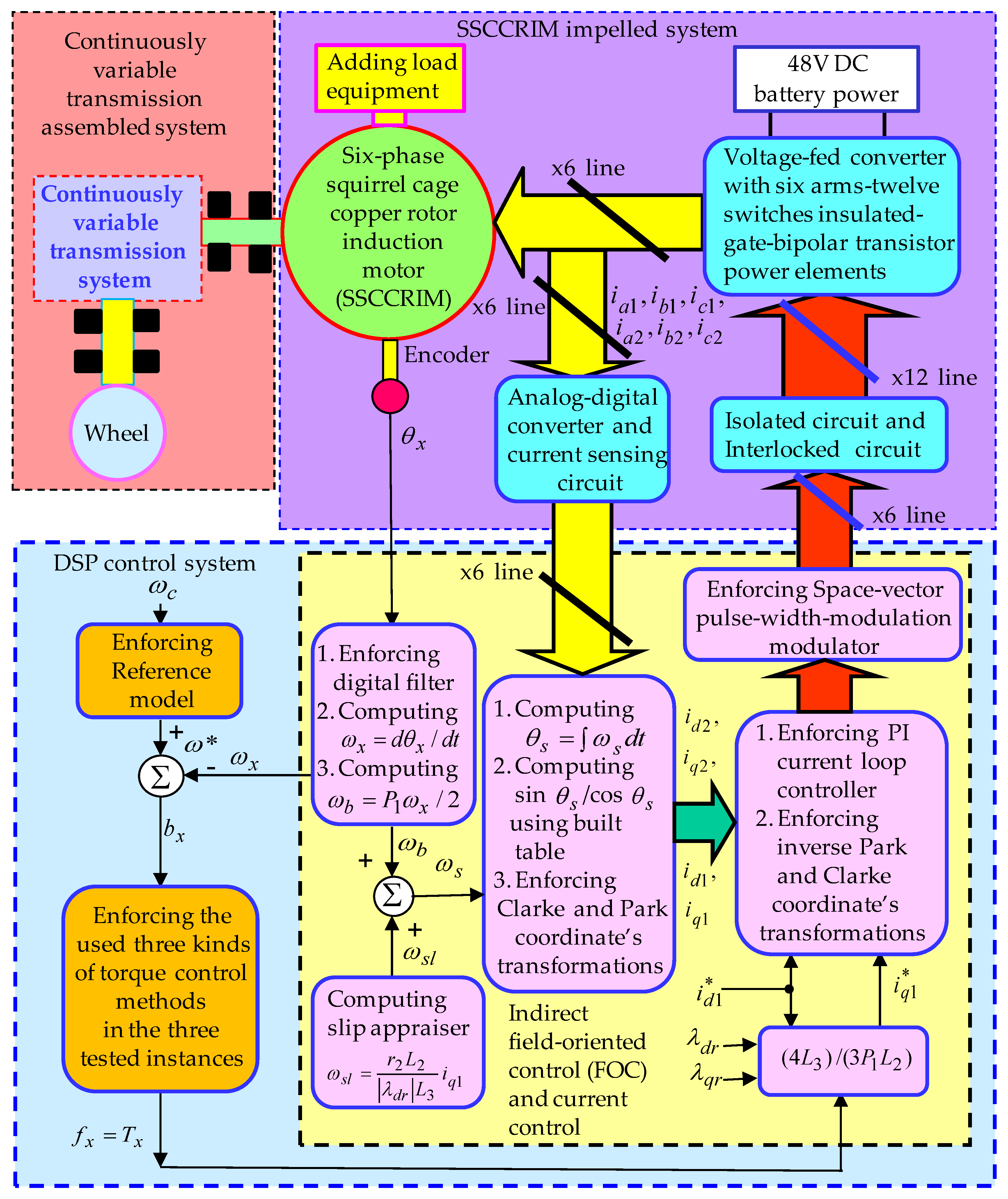
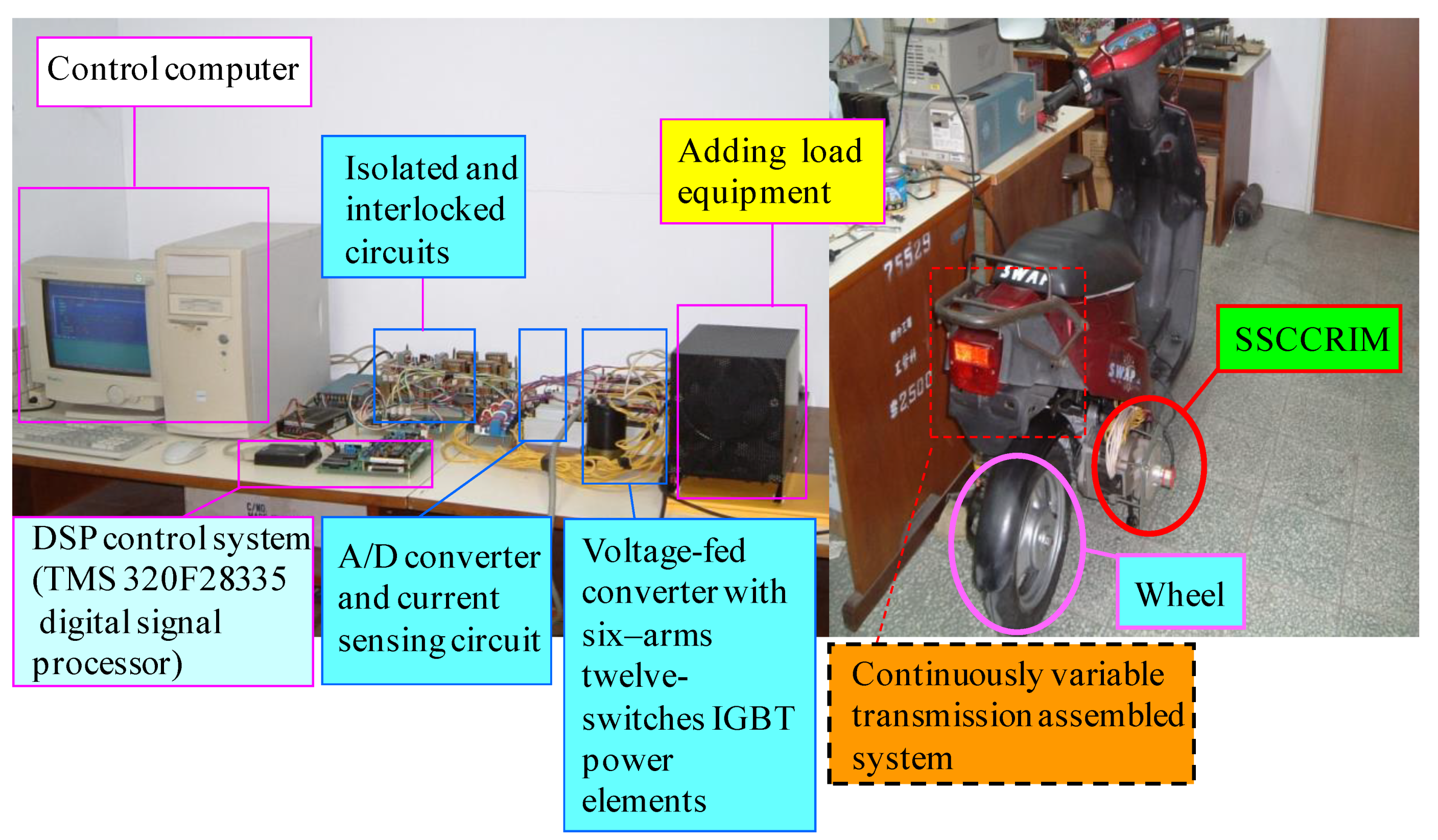
2. Descriptions of Entire System
2.1. Continuously Variable Transmission Assembled System
2.2. SSCCRIM Modeling System
2.3. SSCCRIM Impelled System
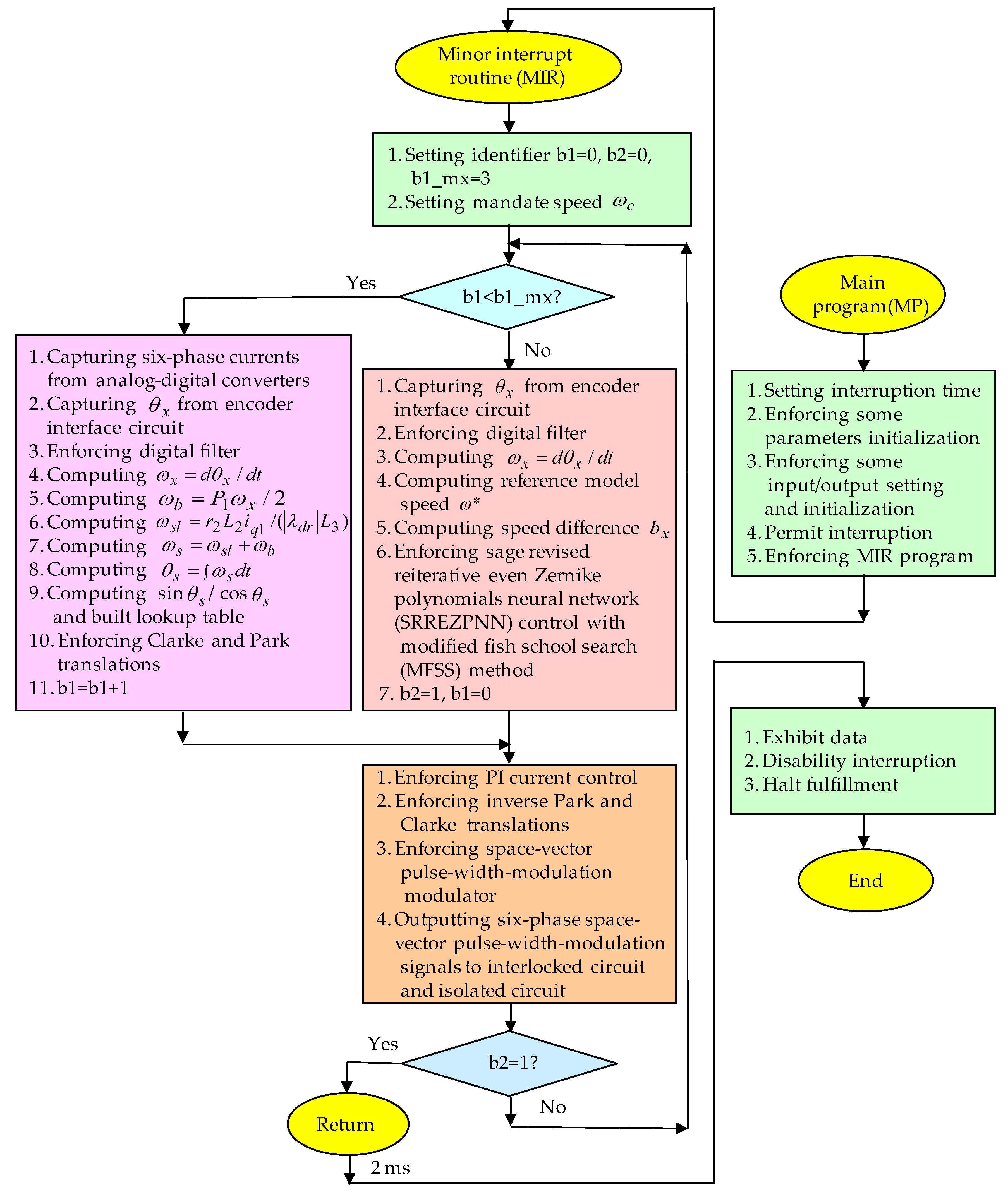
3. Explanations of Applied Methods
3.1. SRREZPNN Control Method
3.2. MFSS Method
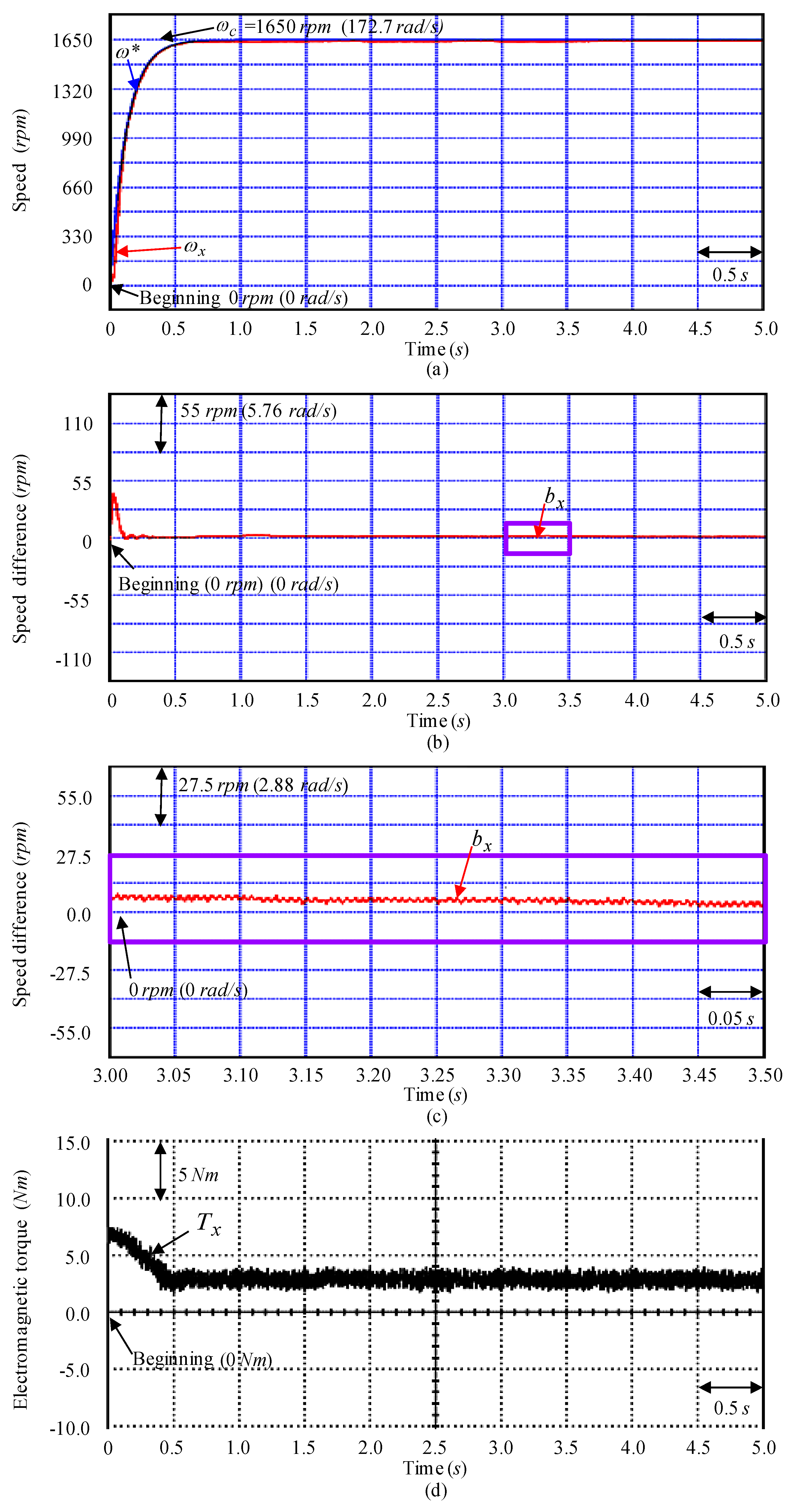
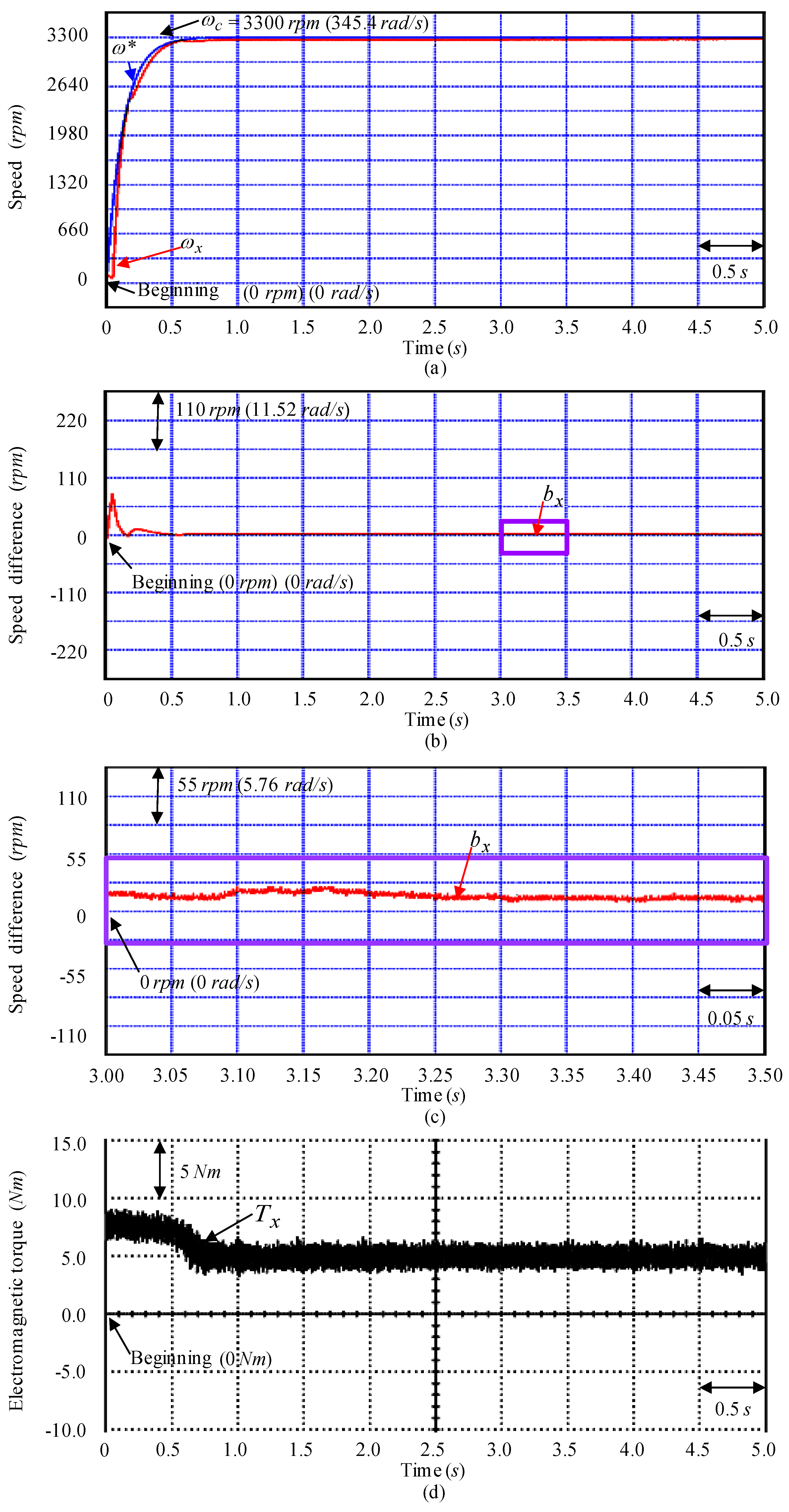
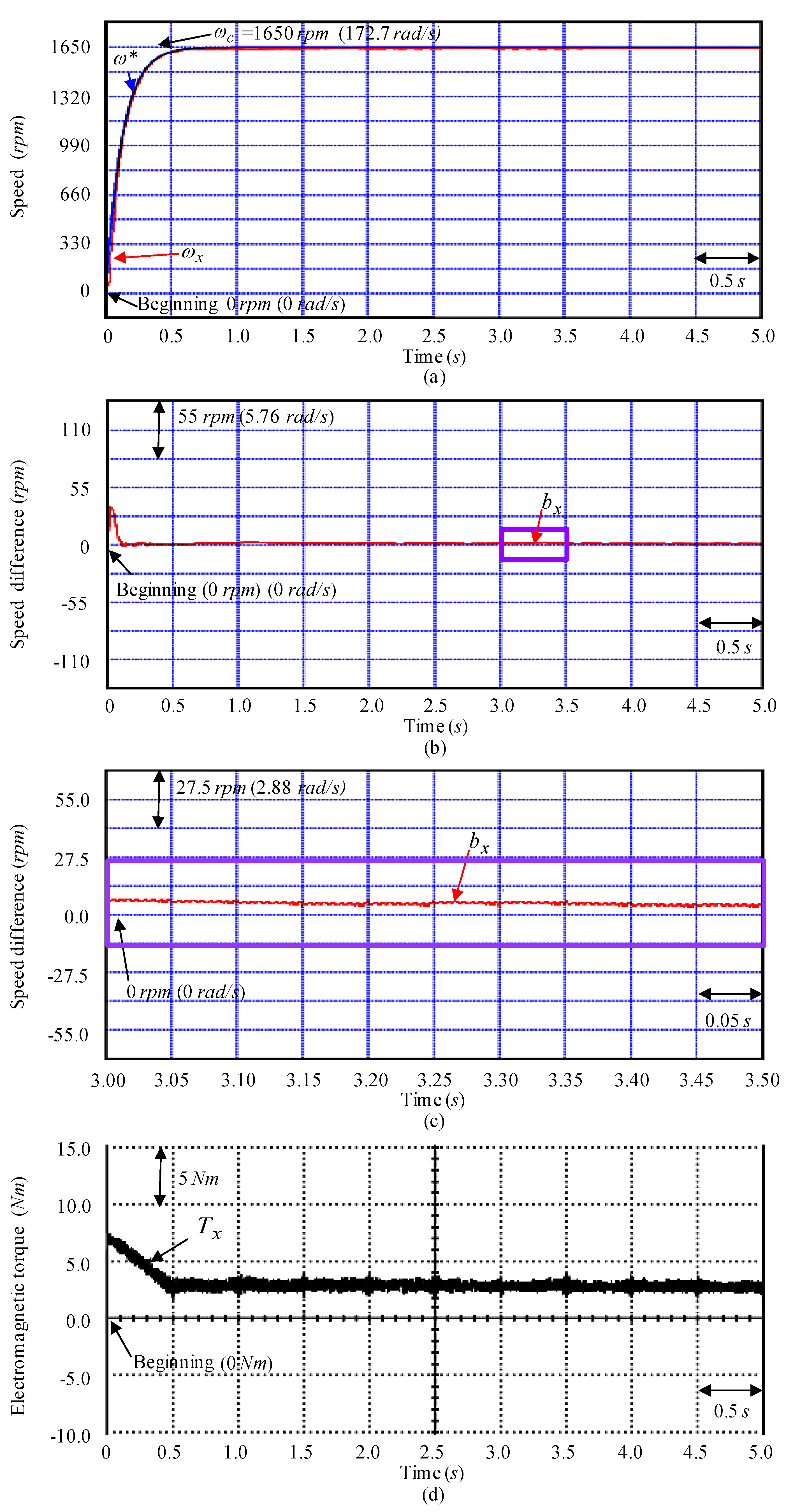
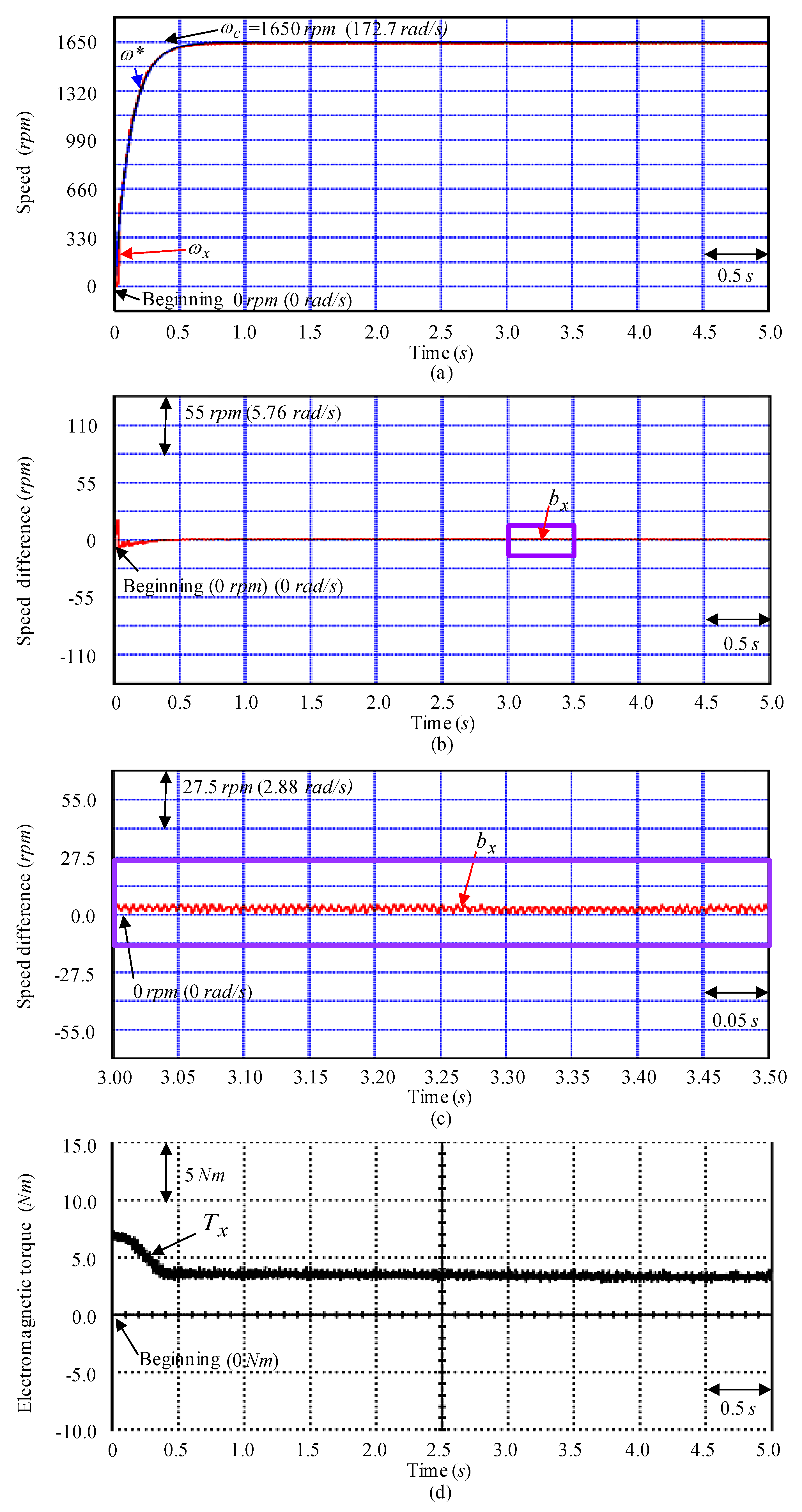
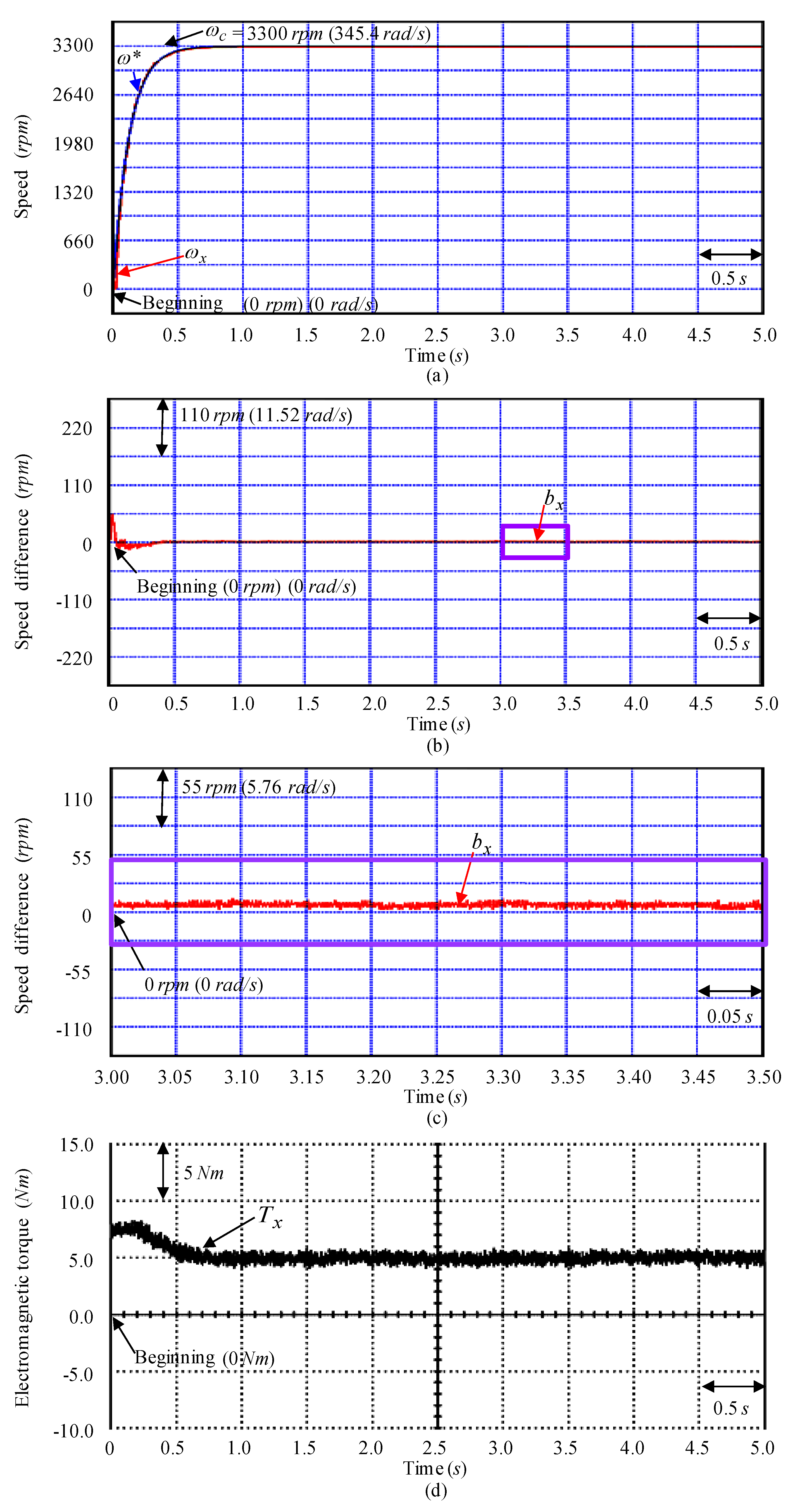
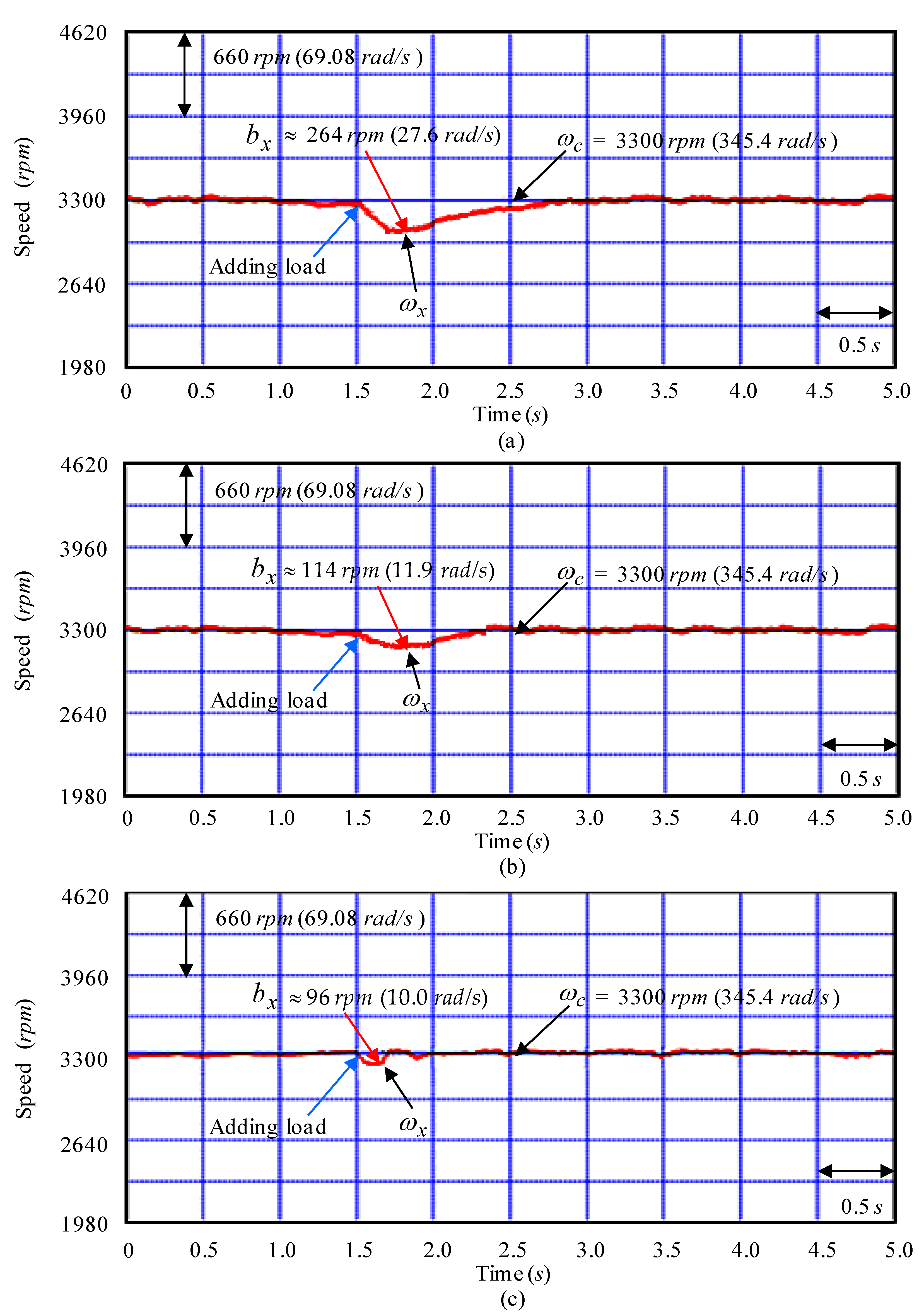
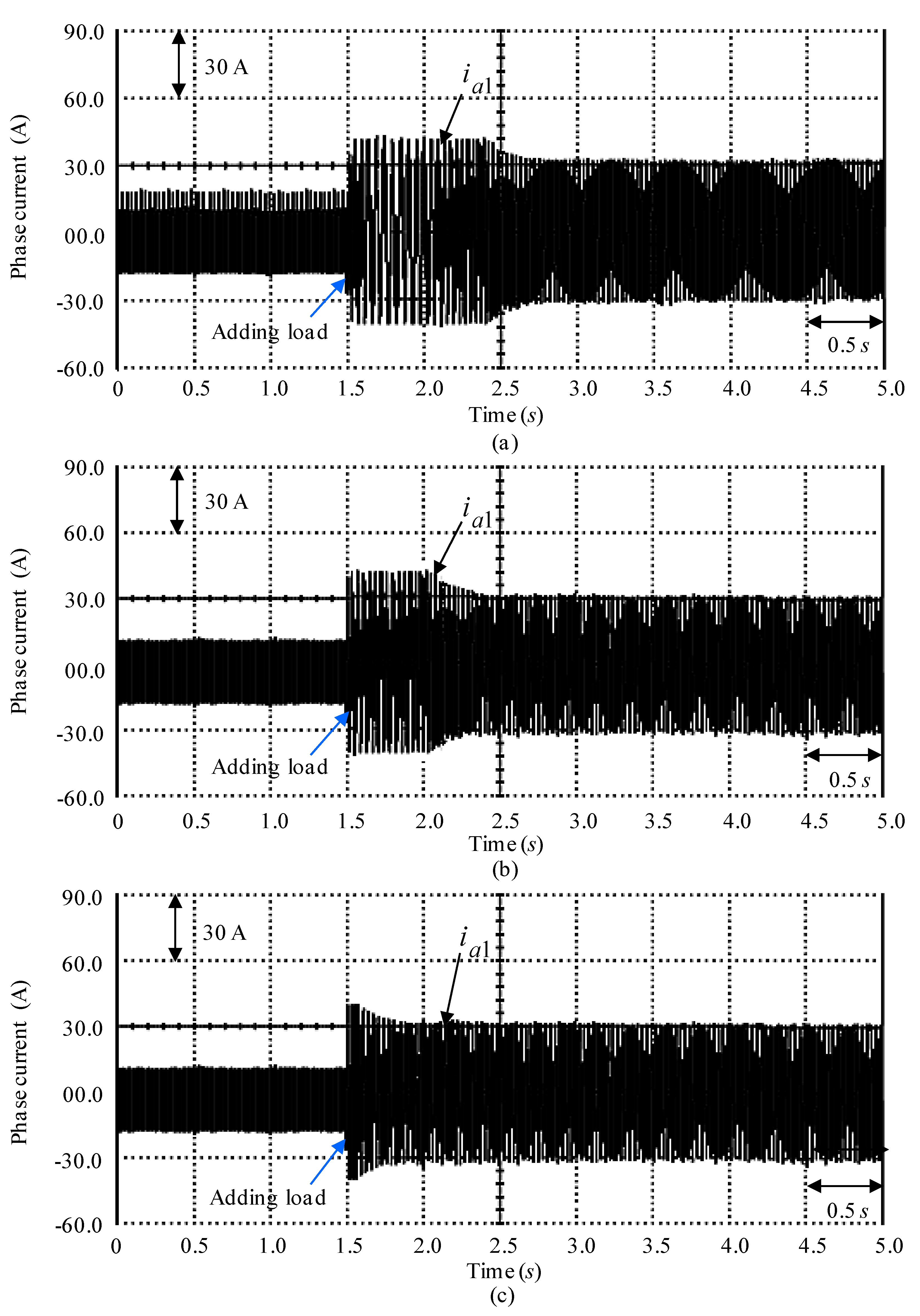
4. Tests and Experimental Results
5. Discussions and Analyses
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Shih, P.C.; Chiu, C.Y.; Chou, C.H. Using dynamic adjusting NGHS-ANN for predicting the recidivism rate of commuted prisoners. Mathematics 2019, 7, 1187. [Google Scholar] [CrossRef]
- Behzad, M.; Mahyar, G.; Mohammad, H.A.; Heydar, M.; Shahabddin, S. Moisture estimation in cabinet dryers with thin-layer relationships using a genetic algorithm and neural network. Mathematics 2019, 7, 1042. [Google Scholar]
- Shao, Y.E.; Lin, S.C. Using a time delay neural network approach to diagnose the out-of-control signals for a multivariate normal process with variance shifts. Mathematics 2019, 7, 959. [Google Scholar] [CrossRef]
- Heydar, M.; Milad, S.; Mohammad, H.A.; Ravinder, K.; Shahaboddin, S. Modeling and efficiency optimization of steam boilers by employing neural networks and response-surface method (RSM). Mathematics 2019, 7, 629. [Google Scholar]
- Chak, C.H.; Feng, G.; Cheng, C.H. Orthogonal polynomials neural network for function approximation and system modeling. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; p. 5255864. [Google Scholar]
- Purwar, S.; Kar, I.N.; Jha, A.N. On-line system identification of complex systems using Chebyshev neural networks. Appl. Soft Comput. 2007, 7, 364–372. [Google Scholar] [CrossRef]
- Wang, L.; Duan, M.; Duan, S. Memristive Chebyshev neural network and its applications in function approximation. Math. Probl. Eng. 2013, 2013, 429402. [Google Scholar] [CrossRef]
- Lin, C.H. Comparative dynamic control for continuously variable transmission with nonlinear uncertainty using blend amend recurrent Gegenbauer-functional-expansions neural network. Nonlinear Dyn. 2017, 87, 1467–1493. [Google Scholar] [CrossRef]
- Iskander, D.R.; Collins, M.J.; Davis, B. Optimal modeling of corneal surfaces with Zernike polynomials. IEEE Trans. Biomed. Eng. 2001, 48, 87–95. [Google Scholar] [CrossRef]
- Wong, W.C.; Chee, E.; Li, J.; Wang, X. Recurrent neural network-based model predictive control for continuous pharmaceutical manufacturing. Mathematics 2018, 6, 242. [Google Scholar] [CrossRef]
- Rubio, J.J.; Yu, W. Nonlinear system identification with recurrent neural networks and dead-zone Kalman filter algorithm. Neurocomputing 2007, 70, 2460–2466. [Google Scholar] [CrossRef]
- Abbasvandi, Z.; Nasrabadi, A.M. A self-organized recurrent neural network for estimating the effective connectivity and its application to EEG data. Comput. Biol. Med. 2019, 110, 93–107. [Google Scholar] [CrossRef]
- Chen, D.F.; Shih, Y.C.; Li, S.C.; Chen, C.T.; Ting, J.C. Mixed modified recurring Rogers-Szego polynomials neural network control with mended grey wolf optimization applied in SIM expelling system. Mathematics 2020, 8, 754. [Google Scholar] [CrossRef]
- Carmelo, J.A.B.F.; Fernando, B.L.N.; Anthony, J.C.C.L.; Antonio, I.S.N.; Marilia, P.L. A novel search algorithm based on fish school behavior. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Singapore, 12–15 October 2008; pp. 2646–2651. [Google Scholar]
- Salomao, S.M.; Fernando, B.L.N.; Carmelo, J.A.B.F.; Elliackin, M.N.F. Density as the segregation mechanism in fish school search for multimodal optimization problems. In Proceedings of the International Conference in Swarm Intelligence (ICSI 2011): Advances in Swarm Intelligence, Chongqing, China, 12–15 June 2011; pp. 563–572. [Google Scholar]
- Fernando, B.L.N.; Marcelo, G.P.L. Weight based fish school search. In Proceedings of the IEEE International Conference on Systems Man, and Cybernetics (SMC), San Diego, CA, USA, 5–8 October 2014; p. 14790101. [Google Scholar]
- Munoz, A.R.; Lipo, T.A. Dual stator winding induction machine drive. IEEE Trans. Ind. Appl. 2000, 36, 1369–1379. [Google Scholar] [CrossRef]
- Ojo, O.; Davidson, I.E. PWM-VSI inverter assisted stand-alone dual stator winding induction generator. IEEE Trans. Ind. Appl. 2000, 36, 1604–1611. [Google Scholar]
- Singh, G.K.; Nam, K.; Lim, S.K. A simple indirect field-oriented control scheme for multiphase induction machine. IEEE Trans. Ind. Electron. 2005, 52, 1177–1184. [Google Scholar] [CrossRef]
- Lin, C.H.; Hwang, C.C. Multiobjective optimization design for a six-phase copper rotor induction motor mounted with a scroll compressor. IEEE Trans. Magn. 2016, 52, 9401604. [Google Scholar] [CrossRef]
- Lin, C.H. Altered grey wolf optimization and Taguchi method with FEA for six-phase copper squirrel cage rotor induction motor design. Energies 2020, 13, 2282. [Google Scholar] [CrossRef]
- Srivastava, N.; Haque, I. Transient dynamics of metal V-belt CVT: Effects of bandpack slip and friction characteristic. Mech. Mach. Theory 2008, 43, 457–479. [Google Scholar] [CrossRef]
- Srivastava, N.; Haque, I. A review on belt and chain continuously variable transmissions (CVT): Dynamics and control. Mech. Mach. Theory 2009, 44, 19–41. [Google Scholar] [CrossRef]
- Lin, C.H. Modelling and control of six-phase induction motor servo-driven continuously variable transmission system using blend modified recurrent Gegenbauer orthogonal polynomial neural network control system and amended artificial bee colony optimization. Int. J. Numer. Model. Electron. Netw. Devices Fields 2016, 29, 915–942. [Google Scholar] [CrossRef]
- Lin, C.H. Blend modified recurrent Gegenbauer orthogonal polynomial neural network control for six-phase copper rotor induction motor servo-driven continuously variable transmission system using amended artificial bee colony optimization. Trans. Inst. Meas. Control 2017, 39, 921–950. [Google Scholar] [CrossRef]
- Astrom, K.J.; Hagglund, T. PID Controller: Theory, Design, and Tuning; Instrument Society of America: Research Triangle Park, NC, USA, 1995. [Google Scholar]
- Hagglund, T.; Astrom, K.J. Revisiting the Ziegler-Nichols tuning rules for PI control. Asian J. Control 2002, 4, 364–380. [Google Scholar] [CrossRef]
- Hagglund, T.; Astrom, K.J. Revisiting the Ziegler-Nichols tuning rules for PI control-part II: The frequency response method. Asian J. Control 2004, 6, 469–482. [Google Scholar] [CrossRef]
- Rdzanek, W.P. Sound radiation of a vibrating elastically supported circular plate embedded into a flat screen revisited using the Zernike circle polynomials. J. Sound Vib. 2018, 434, 91–125. [Google Scholar] [CrossRef]
- Astrom, K.J.; Wittenmark, B. Adaptive Control; Addison-Wesley: New York, NY, USA, 1995. [Google Scholar]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]





© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-H. Sage Revised Reiterative Even Zernike Polynomials Neural Network Control with Modified Fish School Search Applied in SSCCRIM Impelled System. Mathematics 2020, 8, 1760. https://doi.org/10.3390/math8101760
Lin C-H. Sage Revised Reiterative Even Zernike Polynomials Neural Network Control with Modified Fish School Search Applied in SSCCRIM Impelled System. Mathematics. 2020; 8(10):1760. https://doi.org/10.3390/math8101760
Chicago/Turabian StyleLin, Chih-Hong. 2020. "Sage Revised Reiterative Even Zernike Polynomials Neural Network Control with Modified Fish School Search Applied in SSCCRIM Impelled System" Mathematics 8, no. 10: 1760. https://doi.org/10.3390/math8101760
APA StyleLin, C.-H. (2020). Sage Revised Reiterative Even Zernike Polynomials Neural Network Control with Modified Fish School Search Applied in SSCCRIM Impelled System. Mathematics, 8(10), 1760. https://doi.org/10.3390/math8101760




