Efficient Implementation of ARX-Based Block Ciphers on 8-Bit AVR Microcontrollers

Abstract

As the development of Internet of Things (IoT), the data exchanged through the network has significantly increased. To secure the sensitive data with user’s personal information, it is necessary to encrypt the transmitted data. Since resource-constrained wireless devices are typically used for IoT services, it is required to optimize the performance of cryptographic algorithms which are computation-intensive tasks. In this paper, we present efficient implementations of ARX-based Korean Block Ciphers (HIGHT and LEA) with CounTeR (CTR) mode of operation, and CTR_DRBG, one of the most widely used DRBGs (Deterministic Random Bit Generators), on 8-bit AVR Microcontrollers (MCUs). Since 8-bit AVR MCUs are widely used for various types of IoT devices, we select it as the target platform in this paper. We present an efficient implementation of HIGHT and LEA by making full use of the property of CTR mode, where the nonce value is fixed, and only the counter value changes during the encryption. On our implementation, the cost of additional function calls occurred by the generation of look-up table can be reduced. With respect to CTR_DRBG, we identified several parts that do not need to be computed. Thus, precomputing those parts in offline and using them online can result in performance improvements for CTR_DRBG. Furthermore, we applied several optimization techniques by making full use of target devices’ characteristics with AVR assembly codes on 8-bit AVR MCUs. Our proposed table generation way can reduce the cost for building a precomputation table by around 6.7% and 9.1% in the case of LEA and HIGHT, respectively. Proposed implementations of LEA and HIGHT with CTR mode on 8-bit AVR MCUs provide 6.3% and 3.8% of improved performance, compared with the previous best results, respectively. Our implementations are the fastest compared to previous LEA and HIGHT implementations on 8-bit AVR MCUs. In addition, the proposed CTR_DRBG implementations on AVR provide better performance by 37.2% and 8.7% when the underlying block cipher is LEA and HIGHT, respectively.

1. Introduction

With the advent of Internet of Things (IoT), new types of services have become available. In these IoT services, a number of small and wireless devices around users collect the user data or surrounding information. Since the collected data are transmitted through wireless communication, the data can be easily revealed to attackers. For this reason, the sensitive data should be properly encrypted by a secure cryptographic algorithm before the transmission. Since it is required to transmit the data in an encrypted form rather than the original form, applying cryptographic algorithms is a fundamental building block for providing robust and secure communication in these IoT services. However, the implementing cryptographic algorithm on low-end IoT devices is not an easy task because typical client devices for these IoT services equip only limited resources, in terms of CPU, RAM, and ROM. For example, 8-bit AVR-based sensor nodes use in wireless sensor networks (WSNs), which is one of the representative IoT services, have only 4 KB of RAM, 128 KB of ROM, and 7.3728 MHz of computing frequency.

Recently, several lightweight block ciphers have been developed for efficient performance on IoT devices. Lightweight block ciphers ensure low-cost and simple computations. The computational structure is based on ARX (Addition, Rotation, and XOR) architecture. In South Korea, two ARX-based lightweight block ciphers, HIGHT [1] and LEA [2], have been developed and have been widely used. When data are larger than basic processing blocks (64-bit in HIGHT and 128-bit in LEA), the mode of operation needs to be applied. There are several modes of operations and CTR mode is the most popular among them. Until now, these ARX-based lightweight block ciphers have been optimized on resource-constrained 8-bit AVR Microcontrollers [1,3,4,5], which are widely used as sensor nodes in wireless sensor networks that are representative IoT services.

In addition to applying block ciphers to data to be transmitted, it is also important to securely generate secret keys used in block ciphers. If a weak key is used in a block cipher, the ciphertext can be revealed to attackers even if the underlying block cipher is secure. DRBGs (Deterministic Random Bit Generators) are widely used to generate secret information including keys. Among standardized DRBGs [6], CTR_DRBG provides strong resistance against backward security and forward security. Since CTR_DRBG makes use of CBC-MAC and CTR mode of operation in its derivation function and output generation function, it takes a larger execution time than executing block cipher algorithms. Thus, optimizing the performance of CTR_DRBG on the resource-constrained AVR-based devices is important for constructing secure and robust communications in IoT services [7].

In this paper, using a look-up table, we present optimized implementation of ARX-based lightweight block ciphers (HIGHT and LEA) on CTR mode and optimized CTR_DRBG implementation in an 8-bit AVR Microcontroller.

The contribution of this paper is as follows:

• Fast implementation for CTR mode of operation for LEA and HIGHT on 8-bit AVR MCUs
  As nonce is repeatedly used in CTR mode, the result has an identical value when the nonce part is encrypted. Therefore, look-up tables can be generated using the results of encryption data of nonce. In this paper, we present efficient methods that generate look-up tables. Using the optimal implementation, we proposed, in a fixed key scenario, the performance of encryption can be improved by skipping the calculation procedure while loading only the calculation result from the look-up table. For better performance, optimizations of rotation operation and memory access are utilized. Finally, the implementation of LEA-CTR and HIGHT-CTR outperforms previous works by 6.3% and 3.8% than previous works, respectively. Our implementations of LEA and HIGHT are the fastest implementation compared to the previous implementation on 8-bit AVR MCUs. Furthermore, unlike the typical look-up table generation using a separated way, our implementation generates the look-up table, simultaneously, while executing the encryption process. Therefore, in our implementation, the cost of additional function calls that occurred from the generation of look-up table can be reduced. By using this, we obtained performance improvement of 6.7% and 9.1% compared to the previous separated encryption process which generates the look-up table, respectively.
• Optimized CTR_DRBG implementations on 8-bit AVR MCUs for fast random bit generation
  The implementation of CTR_DRBG is optimized with the look-up table. In CBC-MAC of the Derivation Function, the look-up table is created for the encryption result of data depending on the initial block bit. The optimization of the Update Function is achieved with the look-up table by taking advantage of the condition that the initial Operational Status is zero. In addition, the look-up table does not require an update, but also requires a low cost of 96 bytes, making it effectively applicable to 8-bit AVR Microcontrollers. Moreover, we presented methods to optimize Korean block cipher in the Extract Function on 8-bit AVR Microcontrollers. The Extract Function is optimized by utilizing the table for the CTR mode that uses fixed keys to reduce the execution timing. Our works of Derivation Function and Update Function outperform previous works by 13.3% and 72.4%, respectively. By applying CTR optimization methods, implementations of Extract Function using LEA and HIGHT outperform the standard implementation of Extract Function by 36.4% and 3.5%, respectively. By combining the proposed Derivation Function, Update Function, and Extract Function, overall, our CTR_DRBG implementation provides 37.2% and 8.7% of performance improvement compared with the native CTR_DRBG implementation using the works from [3,4,5] as an underlying block cipher of Extract Function.
• Proposing optimization methods that can be applied to various platforms
  In this paper, we propose general optimization methods for ARX-based block ciphers using the CTR mode. These methods have the advantage to be extended to other Addition-Rotation-XOR (ARX) based ciphers such as CHAM, Simon, and Speck [8,9]. While the significance of DBRG is increasing with the advent of the IoT era, there have been a few academic papers on optimization for CTR_DRBG that are popular to use. In this paper, we present CTR_DRBG optimization methods on 8-bit AVR Microcontrollers, the most limited IoT device. Our work is meaningful as it is the first attempt to optimize CTR_DRBG. Furthermore, our proposed Korean block cipher optimization methods and CTR_DRBG optimization methods are not only applicable to 8-bit AVR Microcontroller, but also to other low-end-processors and high-end-processors such as 16-bit MSP430, 32-bit ARM, and the CPU environment.

The rest of this paper is organized as follows. In Section 2, target platform, target ARX ciphers (LEA and HIGHT), target mode of operation, CTR_DRBG, and previous implementations are given. In Section 3, related work of Korean block ciphers (LEA and HIGHT) and CTR_DRBG is presented. In Section 4, optimized implementation of counter mode of operation is presented. In Section 5, optimized implementation of CTR_DRBG is presented. In Section 6, the performance is evaluated. Finally, Section 7 concludes the paper.

2. Background

2.1. 8-Bit AVR Microcontroller

AVR Microcontroller is based on Harvard architecture. All AVR commands require less than four clock cycles to execute.

Table 1. 8-bit AVR Assembly Instruction, $cc$ means clock cycle [10,12].

Asm	Operands	Description	Operation	cc
ADD	Rd, Rr	Add without Carry	Rd ← Rd+Rr	1
ADC	Rd, Rr	Add with Carry	Rd ← Rd+Rr+C	1
EOR	Rd, Rr	Exclusive OR	Rd ← Rd⊕Rr	1
LSL	Rd	Logical Shift Left	C∣Rd ← Rd<<1	1
LSR	Rd	Logical Shift Right	Rd∣C ← 1>>Rd	1
ROL	Rd	Rotate Left Through Carry	C∣Rd ← Rd<<1$\mid \mid$C	1
ROR	Rd	Rotate Right Through Carry	Rd∣C ← C$\mid \mid$1>>Rd	1
BST	Rd, b	Bit store from Bit in Reg to T Flag	T ← Rd(b)	1
BLD	Rd, b	Bit load from T Flag to a Bit in Reg	Rd(b) ← T	1
MOV	Rd, Rr	Copy Register	Rd ← Rr	1
MOVW	Rd, Rr	Copy Register Word	Rd+1:Rd ← Rr+1:Rr	1
LDI	Rd, K	Load Immediate	Rd ← K	1
LD	Rd, X	Load Indirect from	Rd ← (X)	2
LPM	Rd, Z	Load Program Memory	Rd ← (Z)	3
ST	Z, Rr	Store Indirect	(Z) ← Rr	2

shows operand and clock cycles of commands used in this paper. Currently, there are various types of AVR Microcontrollers, and they have various peripherals and memory sizes. This structure ensures that instructions always can be executed in a single cycle. There are 32 general-purpose registers with a single clock cycle. Of the 32 registers, six registers used for 16-bit indirect address register pointer for addressing, which these registers called X, Y, and Z registers [10]. These address pointers can also be used as a pointer for Flash Program memory. Our target device, in this paper, is ATmega128, which is used worldwide in the IoT era [11]. ATmega128 has a 128 KB of programmable flash memory, 4 KB SRAM, and 4 KB EEPROM.

2.2. Target Block Ciphers

2.2.1. LEA Block Cipher

In WISA’13, lightweight block cipher LEA was presented [2]. With the development of IoT, it was developed to provide confidentiality in various embedded devices, cloud service, mobile environments, and so on. LEA is an algorithm that encrypts 128-bit data blocks. It can use 128, 192, and 256-bit secret keys, and its uses are classified according to required safety standards. LEA-128/128, LEA-128/192, and LEA-128/256 require 24, 28, and 32 rounds, respectively. While ensuring safety, it is possible to implement lightweight by eliminating the use of S-box. More information on parameters are shown in

Table 2. Parameters of LEA block cipher, where n, k, $rk$, and r represent block size (bit), key size (bit), round key size (bit), and the number of rounds, respectively [2].

Cipher	n	k	rk	r
LEA-128/128	128	128	192	24
LEA-128/192	128	192	192	28
LEA-128/256	128	256	192	32

.

LEA block cipher performs encryption for 3 32-bit words in one round that represented in Figure 1. In the figure, the $X_i\left[0\right]$ word of round i directly becomes the input value to $X_{i+1}\left[3\right]$ word of round $i+1$. All words are moved to the left every end of rounds.

2.2.2. HIGHT Block Cipher

HIGHT is a transformed Feistel ARX structure that encrypts 64-bit plaintext with a 128-bit secret key. The encryption process comprises of initial conversion, round functions, and final conversion. The key scheduling generates a round key of 136 bytes to be used for encryption with a 128-bit secret key. HIGHT performs encryption using 8-bit wise addition, rotate–shift, and XOR operation. Both encryption and decryption consist of 32 rounds. The structure of Round function in HIGHT block cipher is shown in Figure 2. During every single round, eight 8-bit words are encrypted. In each round in HIGHT, the four words are through by the F${}_0$ or F${}_1$ function. F${}_0$ and F${}_1$ functions perform left shift operation that is expressed in the following equations:

F₀(X) = X⋘1 ⊕ X⋘2 ⊕ X⋘7

F₁(X) = X⋘3 ⊕ X⋘4 ⊕ X⋘6

In each round, HIGHT uses a 64-bit round key. Since the number of round of HIGHT is 32, 2048-bit memory space is needed for storing roundkeys of each round. HIGHT parameters are represented in

Table 3. Parameters of HIGHT block cipher, where n, k, $rk$, and r represent block size (bit), key size (bit), round key size (bit), and the number of rounds, respectively [1].

Cipher	n	k	rk	r
HIGHT-64/128	64	128	64	32

.

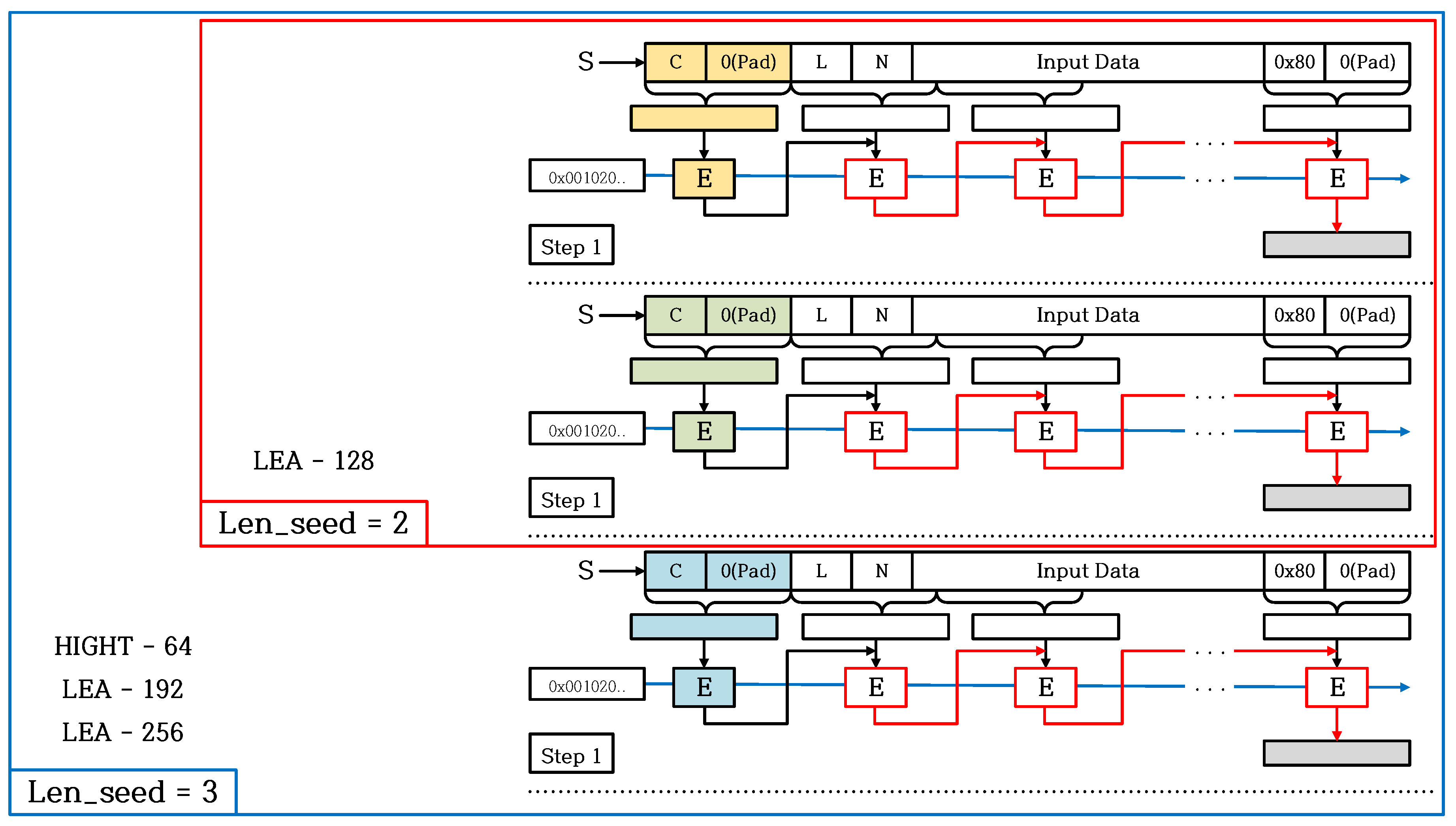
2.3. CTR_DRBG

With the development of IoT, it is important to securely generate security keys when communicating with each other in WSNs (Wireless Sensor Network). For generating a security key safely, a true random bit generator should be used; however, in reality, the creation of a true random bit is almost impossible. Therefore, in the field, we use pseudo-random bits that are difficult to distinguish from true random bits. As pseudo-random bit generators, DRBGs (Deterministic Random Bit Generators) are used to securely generate random bit information, including secret keys, initial vectors, nonces, and so on [6,7]. There are CTR_DRBG based on a block cipher algorithm, HASH_DRBG using HASH Function, and HMAC_DRBG using HMAC among various types of pseudo-random number generators. HASH Function used in HASH_DRBG and HMAC_DRBG is mainly the SHA-2 Family. However, it is difficult to maintain the internal status of SHA-2 Family in the general-purpose register on 8-bit AVR MCUs. Note that internal states of SHA-256 and SHA-512 are 512-bit and 1024-bit, respectively [13,14]. However, with respect to the lightweight cryptography, blocks of LEA and HIGHT are 128-bit and 64-bit, respectively. Therefore, these blocks (states of LEA and HIGHT) can be stored in a general-purpose register.

Table 4. Notations for CTR_DRBG [6,7].

Notation	Descriptions
Personalization String	Information for differentiating the instances being created, non-confidential input (optional).
Nonce	Input information used to generate a seed during instance Function.
Internal State	Information used during CTR_DRBG. It consists of Operational Status and Control Information.
Operational Status	Information directly used for random number output. Consisting of C and V, C is the key used for block cipher, and V is the plain text used for block cipher.
Control Information	Information consists of security strength, Prediction Resistance flag and Derivation Function flag.
Prediction Resistance	Characteristics of the exposure of internal status information of CTR_DRBG without affecting future output.
Instantiate Function	Function to create and initialize CTR_DRBG instances as needed.
Derivation Function	Function called from an Instantiate Function to generate a seed using entropy input, Nonce and Personalization String.
Update Function	Function to update Internal State, using the CTR mode encryption
Reseed Function	Function to update Internal State using entropy and additional input. This function is affected by Reseed Counter.
Generate Function	Function to generate an output(random number) using Internal State and update Internal State.
Extract Function	Function to generate random number sequence, using the CTR mode encryption.

defines notations used in this paper and

Table 5. Constant parameters of CTR_DRBG depending on block cipher [6,7].

Parameters	HIGHT-64/128	LEA-128/128	LEA-128/192	LEA-128/256
Key Bit	128	128	192	256
Block Bit	64	128	128	128
Seed Bit	192	256	320	384
N	0 × 18	0 × 20	0 × 30	0 × 40
Len_seed	3	2	3	3

shows parameters based on the block ciphers used in CTR_DRBG. Seed Bit is the addition of Key bit and Block Bit, and N is the representation of Seed Bit in bytes. Len_seed is the value of Seed Bit divided by Block Bit.

Figure 3 shows the detailed operational process of CTR_DRBG. Instantiate Function generates seed with Derivation Function. In addition, Instantiate Function updates Internal State, using the seed and Update Function. Reseed Function consists of Derivation Function and Update Function, and Generate Function consists of Reseed Function, Extract Function, and Update Function. Note that Update Function is called Instantiate Function, Generate Function, and Reseed Function. Generate Function outputs the random bits based on the internal state by using Extract Function. Before Extract Function is executed, if it supports Prediction Resistance or if Reseed Counter is greater than Reseed Interval, Generate Function calls Reseed Function to update Operational Status. In the opposite case, Generate Function calls an Extract Function to generate a random number, and calls the Update Function to update the Operational Status. When additional requests occur for random bit generations, a series of functions except for Instantiate Function are repeated.

Figure 4 shows the structure of Derivation Function of CTR_DRBG. Derivation Function makes use of CBC-MAC in order to produce an output of seed length by inputting variable data S. Derivation Function is called in Instantiate Function and Reseed Function. Step 1 is a CBC-MAC encryption process by using counter value C. Step 2 is the process of CBC mode which encrypts V with Key generated from Step 1. First, it formats input S for CBC-MAC using Input Data consisting of Entropy, Nonce, and Personalization String. C, L, and N are 32-bit data. The initial C is zero, and padded to zero after C by the length of Block Bit minus 32-bit. L and N are byte lengths of Input Data and seed. Derivation Function makes S using C, L, N and Input Data. At this sequence of generating S, the length of S is padded to 0 so that it is a multiple of Block Bit. Then, Derivation Function increases C of S by 1 and repeats CBC-MAC as many times as Len_seed. Using the results of CBC-MAC as key and V, Derivation Function performs CBC mode encryption as many times as Len_seed to generate seed.

Figure 5 shows the structure of the Update Function in CTR_DRBG. Update Function updates C and V of Operational Status using CTR mode and Input data. Update Function performs with CTR mode encryption as many times as Len_seed. Update Function executes XOR operation on Input data and results generated in CTR mode encryption. Note that Update Function is called by Instantiate Function, Generate Function, and Reseed Function.

Generate Function consists of Reseed Function, Extract Function, and Update Function. As shown in Figure 3, Generate Function generates a random number using Extract Function. Figure 6 shows the structure of Extract Function called in Generate Function. Extract Function is a function that uses the same CTR mode as Update Function. Therefore, using Operational Status C as the key and V as the counter, Extract Function generates a random number by using CTR mode.

3. Related Works

3.1. Block Cipher Implementations on AVR

Various studies have been conducted to improve performance for block ciphers in 8-bit AVR Microcontrollers. In 8-bit AVR MCUs, which are low-end-processors, the study of optimization has been mainly done using minimize memory access and pre-computation tables.

There are two main categories of block ciphers: Addition, Rotation, and eXclusive-or (ARX) based block ciphers and Substitution Permutation Network (SPN) based block ciphers.

Efficient implementations of ARX-based ciphers have been studied in various ways in an 8-bit AVR MCUs environment [1,2,3,4,5,8,15,16,17,18,19,20,21].

In WISA’13, the Institute of Electronics and Telecommunications Research Institute (ETRI) presented a light-weight LEA block cipher. In 8-bit AVR MCUs, the first LEA’s implementation needed 3040 clock cycles for encryption [2].

In [19], the hardware design and implementation of LEA was proposed. Based on the key size, Ref. [19] introduced suitable hardware designs. For the area-optimized version, resource-shared structure for LEA was proposed.

In WISA’15, an efficient LEA implementation technique of dividing a 32-bit word operation using 4-byte units was proposed [3]. The method proposed in [3] minimizes memory access. A technique for efficiently operating rotate–shift used in 8-bit AVR MCUs was proposed. The proposed technique implicitly performs a byte-wise rotate–shift [3]. In addition, the source code was reduced by maximizing the use of the instruction set, and internal states of LEA were efficiently placed in general-purpose registers [3].

In [4], efficient implementation of LEA and method of rotate–shift-right were proposed, fully utilizing the AVR assembly instruction set and general-purpose registers in 8-bit AVR MCUs. For the optimized LEA implementation, Ref. [4] presented a compact ARX task on a target 8-bit AVR Microcontroller. Using both BST and BLD instructions in the AVR instruction, Ref. [4] improved the right rotation by 1 bit. By using the BST instruction in a 1-bit shift-right, the first bit of the register is reflected in the status flag. After that, rotate–shift–right is performed, using LSR and ROR instruction. Finally, Ref. [4] applied the status flag to the 8th bit in the register by using BLD instruction. By using this, when implementing LEA in 8-bit AVR MCUs, less than seven clock cycles are incurred for all rotate–shift operations. In addition, Ref. [4] efficiently places the LEA’s internal state in a general-purpose register. Using MOVW instruction, clock cycles of execution time were reduced.

In [15], efficient LEA implementation was proposed in ARM Cortex-M3 processors. The general purpose registers are fully utilized to retain the required variables for the key scheduling and encryption operations and the rotation operation is optimized away by using the barrel-shifter technique. Since the on-the-fly method does not store the round keys, the RAM requirements are minimized.

In [5], efficient techniques using general-purpose registers were presented. The general-purpose registers in 8-bit AVR MCUs are compactly used for storing results during the key scheduling of LEA.

The HIGHT’s implementation was first presented in [16]. Execution time of HIGHT for encryption and decryption in 8-bit AVR MCUs is 2438 and 2520 clock cycles, respectively [16].

In [21], efficient implementation using parallel architecture to enhance throughput was proposed. It shares key scheduling block for encryption and decryption to reduce hardware complexity.

In [20], hardware implementation for a significant reduction in the number of memory resources was proposed. Its implementation is useful for wireless applications such as a radio frequency identification system (RFID).

In [4], efficient rotation operations were introduced, and they achieved high performance. Like the LEA implementation proposed in [4], an efficient rotate–shift was used. Its implementation won the second round of Fair Evaluation of Lightweight Cryptographic Systems (FELCS).

In [17], fast HIGHT implementation was proposed. For optimizing delta update, F0 function, and F1 function, Ref. [17] uses the Look-Up Table (LUT). In addition, [17] proposed the memory-efficient way for F0 and F1 function, using bit-wise operations.

In 2015, SIMON and SPECK were presented by The US National Security Agency (NSA) [18]. Both SIMON and SPECK have advantages for efficient implementation in hardware and software environments. These two block ciphers support various block sizes and various key sizes. Therefore, in various IoT devices, SIMON and SPECK can be widely used. For 8-bit AVR MCUs, efficient implementation was presented in [8] using RAM-minimizing.

In an 8-bit AVR MCUs environment, block ciphers based on SPN also have also been actively studied. Since Advanced Encryption Standard (AES) is an international standard, AES implementations have widely studied.

In 2010, Ref. [22] presented efficient techniques for AES implementation, using a Z address pointer to perform SubBytes operation. In [22], MixColumns were implemented by a branch instruction set. Previous AES implementation in 8-bit AVR MCUs mainly focused on ECB Mode; however, in the field, AES-CTR Mode is more widely used (e.g., TLS/SSL) [23].

In ICISC’19, Fast AES-CTR Mode Encryption LIGHT (FACE-LIGHT) was presented by [24]. FACE-LIGHT is a variant of FACE implementation suggested by [25] in 8-bit AVR MCUs. FACE-LIGHT uses LUT for caching repeated data in IV. By using LUT, some operations can be omitted in 0,1, and 2 Round.

In WISA’20, efficient AES implementation was presented by [11]. The column-wise implementation was proposed. Proposed techniques have advantages for constant-time implementation and low cost for generating LUT. In addition, using 0 round optimization, Ref. [11] presented the optimized AES-CTR mode encryption for Wireless Sensor Network (WSN).

3.2. DRBG Implementations on AVR

To the best of our knowledge, the implementation of DRBG has not been presented in academic papers. The commercial product provides the AES-DRBG, but the performance is much slower than our work (http://cryptovia.com/cryptographic-libraries-for-avr-cpu/). Furthermore, the detailed information is not available. For this reason, our work is the-state-of-art work.

4. Optimized Implementations of LEA-CTR and HIGHT-CTR

The optimized implementation of a counter mode of operation for block cipher utilizes unique features of fixed nonce and variable counter values. The counter value indicates the block number, while the nonce is a fixed random value. Every block has the same nonce value. The calculation based on the nonce block is always a constant value. For this reason, the part can be pre-computed. The CTR implementation is categorized into two different scenarios, including fixed-key and variable-key. In this paper, we optimize both cases for various applications.

In the fixed-key scenario, the key value is fixed. For this reason, the precomputation result is always same and the precomputation table does not require update. In the implementation, the LDI instruction was used instead of the LD instruction to load the precomputation value from table. The LDI instruction operates at one cycle faster than the LD instruction.

On the other hand, the LDI instruction cannot be used for the variable-key scenario because the LDI instruction can only load the fixed value. Furthermore, the pre-computed table should be updated efficiently whenever the key is updated. This implementation shows the lower performance than that of fixed-key implementation. However, the variable-key implementation is able to perform the encryption with updated keys, which is more suitable for practical usages than fixed-key.

4.1. Optimized Implementation of LEA-CTR

The LEA algorithm was suggested [2]. However, we use [4] implementation. [4] has optimized key scheduling; in particular, LEA-128/128 can reuse some round keys.

-

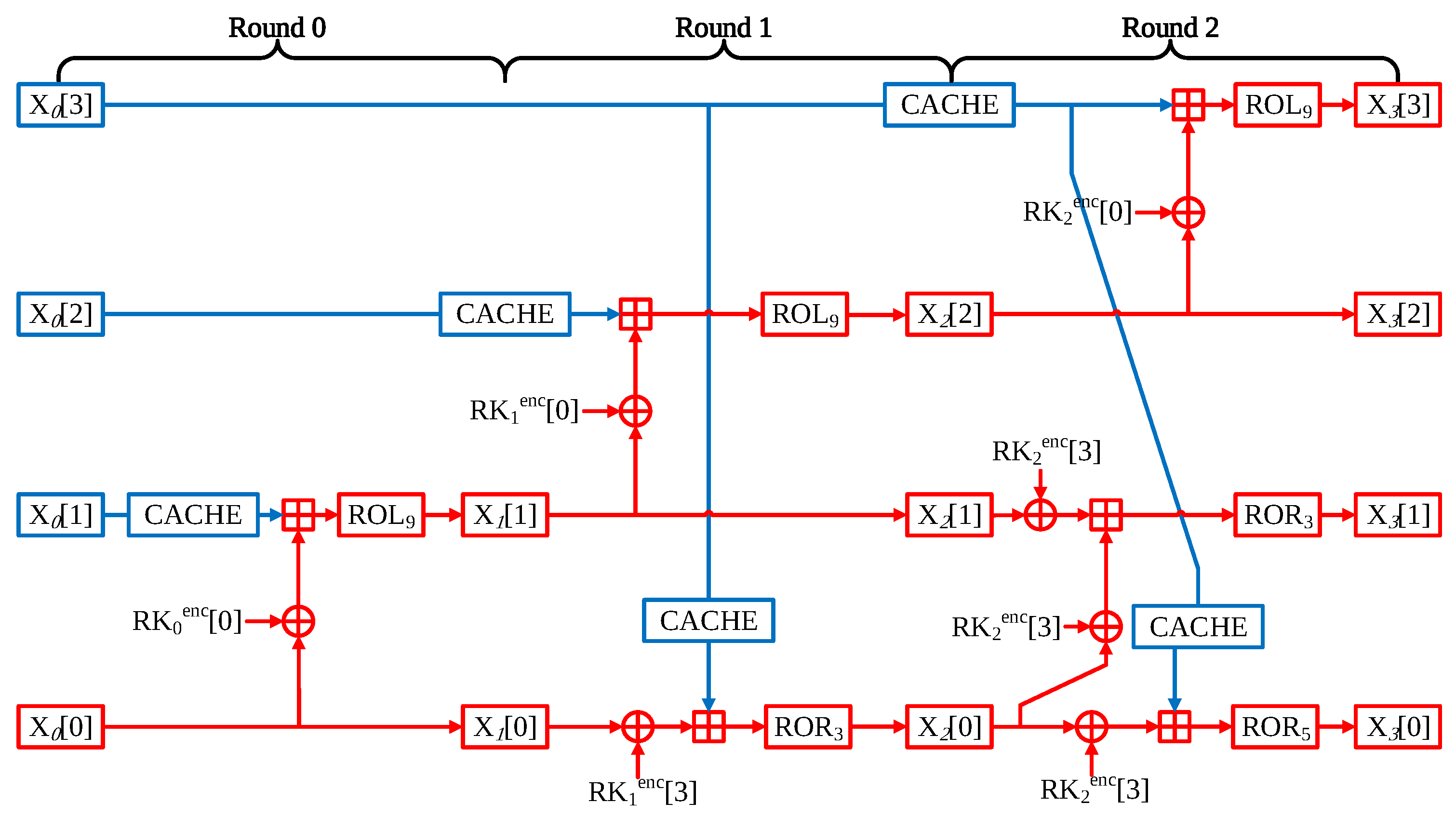
Round 0 In one round of LEA, the operations are performed in three parts. In Round 0, only X${}_0$[0] word has a counterpart of IV. Consequently, two words can be implemented through the precomputation method.

-

Round 1 However, due to the Round 0, the X${}_1$[1] word is also beginning to be affected by the counter value. For this reason, it might be thought that the precomputation part is only available at X${}_1$[2] word. The part where X${}_1$[3] word is used as the input value of X${}_1$[0] in Round 1 can be expressed by the following equation:

$${\mathrm{ROL}}_3\left(\right({\mathrm{X}}_1\left[3\right]\oplus {\mathrm{RK}}_1^{enc}\left[2\right])⊞({\mathrm{X}}_1\left[0\right]\oplus {\mathrm{RK}}_1^{enc}\left[3\right]\left)\right)$$

At this equation, it can be seen that the blue parts X${}_1$[3] word and round key are fixed values. Consequently, XOR instruction between X${}_1$[3] word and round key part can be skipped.

-

Round 2 In Round 2, only the X${}_2$[3] word is not affected by counter value. Therefore, precomputation is not applicable as a whole. However, like the previous round, in order to use X${}_2$[3] word as an input value for X${}_3$[0] word, the operation part that performs XOR instruction with a round key can be a precomputation implement. The optimized LEA-128/128 CTR mode of operation is described in Figure 7.

-

Generation of look-up table When generating a look-up table, it has the advantage that the table can be generated during the encryption process. CACHE can be saved in the look-up table through the result of the operation in executing each round. When creating the look-up table, only the address translation cost based on ST instruction is incurred.

Optimization for LEA-128/192 and LEA-128/256

Our optimization strategy for LEA-128/128 can be directly applied to both LEA-128/192 and LEA-128/256 because their computational structures are identical except for the number of rounds. In addition, we combine each four rounds into one for better performance in our LEA implementations.

4.2. Optimized Implementation of HIGHT-CTR

The HIGHT-64/128 split input value into eight 8-bit words. The CTR mode of operation using 32-bit counter, so four words are affected by counter of IV in the initial round. Figure 8 shows this.

-

Round 0 The HIGHT performs four operations in a single round. In Round 0, the operation is performed using the following word pairs; X${}_0$[0] with X${}_0$[1], X${}_0$[2] with X${}_0$[3], X${}_0$[4] with X${}_0$[5], and X${}_0$[6] with X${}_0$[7]. First of all, words of X${}_0$[0], X${}_0$[1], X${}_0$[2], X${}_0$[3] have counter values, which is variable. Thus, two of the four operations must be implemented. However, the other operations part uses only fixed values, which are nonce, and round keys, so precomputation is available for these parts.

-

Round 1 Unlike the previous round, the pair of words participating in the operation is slightly different. In this time, the X${}_1$[4] word is affected by the counter value; then, precomputation is not possible. X${}_1$[5] and X${}_1$[6] words still have nonce value, so this part is precomputation implementation available. In addition, lastly, X${}_1$[0] word operates with a X${}_1$[7] word that has nonce value. The whole operations cannot be skipped, but the result of X${}_1$[7] operation through the F1 function is can be omitted because X${}_1$[7] has nonce value, and the F1 function only conducts left shift operation.

-

Round 2 Round 2 has a similar structure to Round 0. However, in this time, X${}_2$[4] words are affected by counter value, so the precomputation part is reduced by one place and then the Round 0.

-

Round 3 Likewise this time, the Round 3 scheme is like Round 1. The difference is that the X${}_4$[6] word is affected by the counter value. For this reason, precomputation implementation is possible in only one part.

-

Generation of look-up table In the same method as the proposed look-up table of LEA, the proposed method for HIGHT implementation has the advantage of generating a look-up table during the encryption process. CACHE data are saved during the CTR mode encryption. When creating the look-up table, only the address translation cost based on ST instruction is incurred.

4.3. Optimized Implementation of Rotation Operation

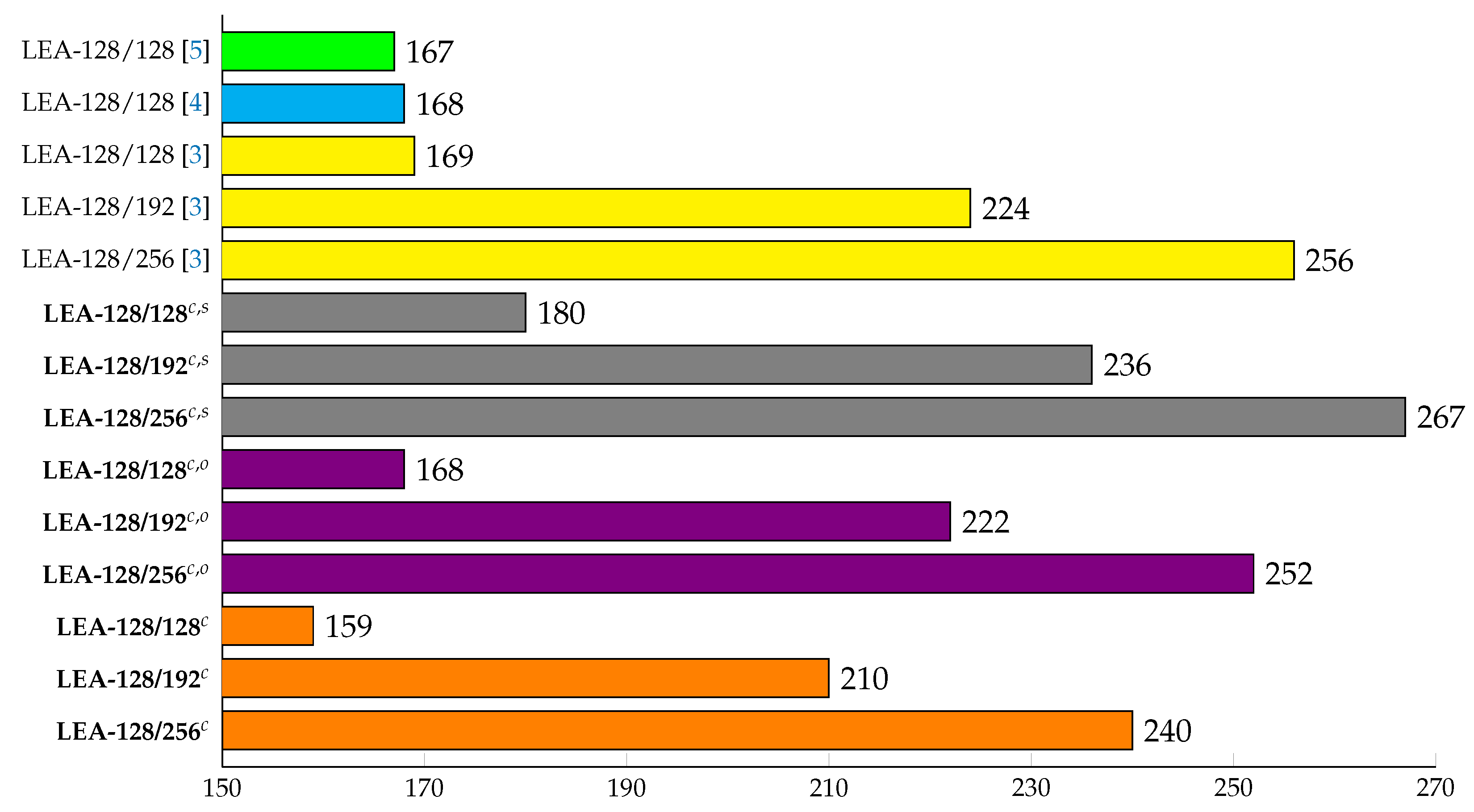
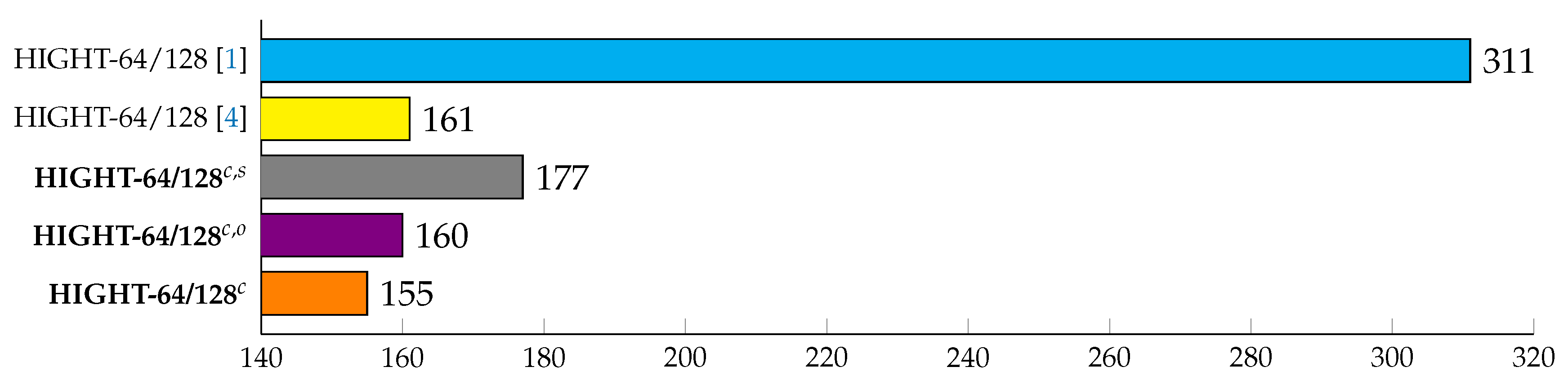
The 8-bit AVR microcontroller supports rotation instructions of 8-bit operands by one bit to left (ROL) and right (ROR). Since one general-purpose register in an 8-bit AVR microcontroller is 8-bit in size, additional computation is required to apply the rotate operation to data above 8-bit. If the offset of rotation operation is a multiple of 8-bit, the rotation operation can be optimized away by indexing the register directly. The optimized 16/32-bit word rotation operations are given in

Table 6. Optimized 16/32-bit word rotation operations on 8-bit AVR Microcontroller.

16-bit ROL1	16-bit ROL8	32-bit ROL1	32-bit ROL8
LSL LOW  ROL HIGH  ADC LOW, ZERO	MOV TEMP, LOW  MOV LOW, HIGH  MOV HIGH, TEMP	LSL R0  ROL R1  ROL R2  ROL R3  ADC R0, ZERO	MOV TEMP, R3  MOV R3, R2  MOV R2, R1  MOV R1, R0  MOV R0, TEMP
3 cycles	3 cycles	5 cycles	5 cycles

.

5. Optimization for CTR_DRBG on 8-Bit AVR Microcontroller

In this section, we present optimization methods for an Instantiate Function of CTR_DRBG. The proposed method optimizes the constant data in Derivation Function and Update Functions called from Instantiate Function. This can be applied to any block ciphers used in CTR_DRBG. The proposed optimization approach with the constant data for Derivation Function and Update Function used in Instantiate Function is to generate a look-up table for the constant data.

In short, our strategy to speed-up an Instantiate Function is to generate the look-up table for the result of encryption for size of block from msb of S, which is used in CBC-MAC of Derivation Function. In addition, we optimize Instantiate Function by generating the look-up table for the result of Update Function called from an Instantiate Function by using the fact that both C and V values of the initial Operational Status are zero.

Figure 9 shows our optimization method for Derivation Function in an Instantiate Function. As mentioned in Section 2.3, Step 1 of Derivation Function uses CBC-MAC. When CBC-MAC is called in Derivation Function, the data from msb to Block Bit of S is zero. CBC-MAC executes encryption with increasing C by the number of times Len_seed. Since, at this time, the key used in CBC-MAC is fixed (0x00010203..), the result for encryption of Block Bit including C can be stored in a look-up table. For LEA-128/128, as shown in the yellow and green parts in Figure 9, the Derivation Function can reduce two encryptions during CBC-MAC computation. For other cases (HIGHT-64/128, LEA-128/192, and LEA-128/256), as shown in the yellow, green, and blue parts, Derivation Function can reduce three encryptions in the CBC-MAC computation process. The optimized method of Derivation Function we propose is applicable regardless of the length of Input Data entered in S. In addition, for CTR_DRBG that supports Prediction Resistance, Reseed Function is called from the Generate Function; even at this time, our main idea for Derivation Function is applicable. The constant data on the look-up table is the fixed data and requires the cost of Block Byte ∗ Len_seed. Based on the target block ciphers used in this paper, the look-up table requires up to 48 bytes. Since the look-up table is used as being semi-permanent when it is created (look-up table is constant data), the generation time of look-up table is not considered. Therefore, the look-up table can be used in environments where CTR_DRBG is repeatedly called.

Figure 10 shows the proposed optimization method for the Update Function of Instantiate Function. When the Instantiate Function is called, the Derivation Function generates the seed. After generating the seed, Instantiate Function calls the Update Function to execute an initial updating process for Operational Status. The initial Operational Status has a value of zero (C = 0, V = 0). Since Operational Status is zero when Instantiate Function generates the seed and updates Internal State, we can store the results of Update Function in the look-up table. The orange part in Figure 10 is the omitted encryption part. That is, the Instantiate Function can perform XOR operation immediately using Seed (red part) and look-up table without executing the Update Function. The proposed method that can be applied regardless of the block cipher algorithm, such as the optimization method applied to the Derivation Function. In addition, the look-up table for Update Function is a constant data table that can be used regardless of the number of calls made to CTR_DRBG, just like the look-up table generated by Derivation Function. The look-up table for Update Function requires up-to 48 bytes, the same as the look-up table generated for the Derivation Function.

The propose method for the Instantiate Function are to omit the encryption process as much as possible by using the look-up table. The cost of the look-up table requires up to 96 bytes. We can replace up-to six encryption operations using just 96 bytes. In the case of ATmega128, the most popular MCU in an 8-bit AVR MCUs environment, as mentioned in Section 2, has 4 KB of SRAM. Therefore, a maximum 96 bytes of the look-up table for the Instantiate Function can be stored in SRAM of ATmega128 sufficiently. In addition, the optimization methods we propose for Instantiate Function have the advantage of being applicable to various platforms such as low-end platforms and high-end platforms without relying on specific platforms.

The Extract Function called in the Generate Function is a function of extracting random numbers using the CTR mode. Figure 11 shows the proposed optimization method for the Extract Function of the Generate Function. The Extract Function uses C and V in Operational Status as a key and a counter to perform CTR mode to extract random numbers. Using the optimized CTR mode proposed in Section 4, we apply the optimized CTR mode of Extract Function. In order to apply the optimized CTR mode using the look-up table proposed in Section 4 to the Extract Function, the look-up table must be generated first. When Counter is V+1, we apply the optimized CTR mode with precomputation; through this process, we generate a look-up table. Note that the optimized CTR mode with precomputation only applies when the counter is V+1. If the counter is V+2 or higher, the optimized CTR mode using a look-up table is applied for the encryption of all CTR modes during Extraction Function.

6. Implementation Results

Proposed implementations of CTR mode and CTR_DRBG were evaluated on 8-bit AVR MCUs. The performance was measured in Clock cycles Per Byte (CPB). The measurement environment is Atmel Studio 7 and all code was compiled using an -O2 option.

The comparison criteria are as follows. For comparison, we define three versions of our implementations: the separation version (denoted as $(c,s)$), online version (denoted as $(c,o)$), and optimized encryption version (denoted as $\left(c\right)$ in Figure 12). Both the separation version and the online version build the precomputation table by taking advantage of the property of CTR mode for fast encryption. Actually, they include the process for precomputation table generation and encryption. The difference between the separation version and the online version is that online version builds the precomputation table while executing encryption (Separation version builds the precomputation table separately from the encryption). Our optimized encryption version makes use of the precomputation table generated from either the separation version or the online version for fast encryption. Our three versions of LEA and HIGHT implementations will be compared with the previous best works from [3,4,5] and from  [1,4], respectively.

6.1. LEA-CTR on 8-bit AVR Microcontrollers

The LEA implementation result is shown in Figure 12. Three LEA implementations exist on AVR environments [3,4,5]. The latest research is [5], but it contains only LEA-128 implementation. Therefore, in the case of LEA-128/192 and LEA-128/256, we compare our implementations to [3].

The separation version (denoted as $(c,s)$ in the figure) of LEA-128 has worse performance by about 7.3% compared to [5]. In addition, LEA-128/192 and LEA-128/256 have slightly lower speeds than [3].

However, the precomputation in online version (denoted as $(c,o)$ in the figure) of LEA-128 shows similar performance to [5]. The reason for the performance difference is that there is a part that calculates a cache table.

The reason for the performance difference compared to the separation version is that the online version combines the generation process of precomputation and the encryption process in order to reduce additional function calls.

The optimized LEA CTR mode implementations (denoted as $\left(c\right)$ in the figure) clearly outperform the works from [3,4,5]. It shows around 4.8% performance improvement in case of LEA-128/128 compared with the work from [5]. In case of LEA-128/192, and LEA-128/256, our implementations provide around 6.3% and 6.3% improved performance compared to [3]. Our LEA implementations provide the fastest performance on 8-bit AVR platform compared with the previous results.

6.2. HIGHT-CTR on 8-Bit AVR Microcontrollers

The HIGHT is a 64-bit block cipher and until now there has only been one previous study for optimization on the AVR platform. Thus, we compare our implementation to the previous work [4], and the results are represented in Figure 13. Like performance analysis of LEA implementation described in the previous subsection, there are three HIGHT implementation versions such as the separation version, online version, and optimized CTR implementation, which are denoted as $(c,s)$, $(c,o)$, and $\left(c\right)$, respectively, in Figure 13.

The separation version (denoted as $c,s$) has about 9.9% lower performance than [4]. However, the online version (denoted as $c,o$) provides a slightly better performance. The reason for this result is that the separation version performs encryption after calculating a precomputation table in independent functions. On the other hand, the online version keeps executing an encryption process, while generating the precomputation table. By using this, additional function calls overhead for generating a precomputation table can be reduced. Given these points, the online version has better performance compared with the separation version.

Finally, an optimized CTR mode of operation version (denoted as c) gets 3.8% better performance than [4]. This is because some of the calculation intervals are skipped through the use of precomputed values, and this is the fastest timing compared with the previous best results on the same platform.

6.3. CTR_DRBG on 8-Bit AVR Microcontrollers

The proposed CTR_DRBG was implemented in Atmel Studio 7, as the same implementation environment as Section 6.1. In addition, the code was complied in an -O2 option. We implemented CTR_DRBG using the optimization method proposed in Section 4 and Section 5. Therefore, we measured the ratio of performance improvement by comparing our proposed implementation of CTR_DRBG (using optimized LEA-CTR, and optimized HIGHT-CTR) and CTR_DRBG with LEA [3,5], and HIGHT [4]. Since until now there have been no implementations of CTR_DRBG, we implement the naive version ourselves. As the underlying block cipher, we utilize the previous works of LEA implementation from [3,5], and of HIGHT from [4].

Table 7. Performance improvement of proposed Derivation function and Update function compared the naive implementation version on 8-bit AVR MCUs [3,4,5]. The result is based on the number of extracted random numbers, where B, $D.Fnc$, $U.Fnc$, and $E.Fnc$ represent byte, Derivation Function, Update Function, and Extract Function, respectively.

Block Cipher		LEA-128/128	LEA-128/192	LEA-128/256	HIGHT-64/128
$D.Fnc$		10.1%	13.4%	14.1%	5.6%
$U.Fnc$		51.1%	69.4%	72.4%	40.6%
32B	$E.Fnc$	13.6%	22.0%	23.5%	1.4%
64B	$E.Fnc$	16.7%	25.1%	26.5%	1.9%
128B	$E.Fnc$	20.2%	28.7%	29.9%	2.4%
256B	$E.Fnc$	23.4%	31.9%	32.8%	3.0%
512B	$E.Fnc$	25.8%	34.3%	35.0%	3.3%
1024B	$E.Fnc$	27.3%	35.8%	36.4%	3.5%

shows the ratio of performance improvement to Derivation Function and Update Function, and shows the ratio of performance improvement in Extract Function depending on the length of the extracted random number. When measuring the ratio of performance improvement, an Input Data of Derivation Function was fixed at 64 bytes (which is reasonable because, on AVR platforms, the noise data are typically collected from hardware noise sources, which contain larger entropy than software noise sources). The encryption process as much as Len_seed is omitted in the Derivation Function proposed in Section 5. The block ciphers except HIGHT-64/128 show a performance improvement of more than 10% in Derivation Function as the Block size is 128-bit.

The actual computation of the method, proposed in Section 5, in the Update Function is only the XOR operation for the length of the seed. Since, in the Update Function as much encryption process as Len_seed has been omitted, the ratio of performance improvement is much larger than that of Derivation Function. We measure performance according to the length of the extracted random number in the Extract Function. In addition, we implemented the Extract Function using methods proposed in Section 4 and Section 5. In other words, our implementation generates a look-up table when the Counter equals V+1, and uses a look-up table when the Counter more than V+2. Therefore, it can be seen that the longer the length of the extracted random number, the greater the ratio of the performance improvement of the Extract Function for each algorithm.

Figure 14 shows the ratio of performance improvement for CTR_DRBG with the target block ciphers according to the length of the extracted random number. The ratio of performance improvement is measured by comparing the previous best results shown in [3,4,5].

Table 8. The best performance improvement ratio (%) of CTR_DRBG using our LEA and HIGHT implementation compared to CTR_DRBG using previous LEA and HIGHT implementation [3,4,5]. The result is based on the number of extracted random numbers, Byte represents the number of bytes with best performance of CTR_DRBG.

Block Cipher		LEA-128/128	LEA-128/192	LEA-128/256	HIGHT-64/128
Byte		1024	1024	1024	32
CTR_DRBG		26.7%	36.2%	37.2%	8.7%

shows the ratio of performance improvement, which shows the best performance among the ratios in Figure 14.

The optimized implementations of CTR_DRBG used LEA-128/128, LEA-128/192, and LEA-128/256 increase the ratio of performance improvement as the length of the extracted random number increases. In Table 7, the ratio of performance improvement to Extract Function for LEA-128/128, LEA-128/192, and LEA-128/256 increases by a greater width than HIGHT-64/128 as the length of the extracted random number increases. Therefore, the ratio of performance improvement to Extract Function for LEA-128/128, LEA-128/192, and LEA-128/256 affects the performance improvement ratio of CTR_DRBG over the ratio of performance improvement for Derivation Function and Update Function. HIGHT-64/128 has a difference of approximately 2.1% in the ratio of performance improvement between 32 bytes and 1024 bytes extracted random number, and the overall ratio of performance improvement of CTR_DRBG does not increase. In other words, in the case which uses HIGHT-64/128, the ratio of performance improvement for Extract Function has less effect on the ratio of performance improvement in CTR_DRBG than the ratio of performance improvement for Derivation Function and Update Function.

The ratio of performance improvement of CTR_DRBG using HIGHT-64/128 drops as the length of the extracted random number increases. Table 7 shows that the performance increase in the Extract Function of HIGHT-64/128 results in a performance improvement of less than 3% as the length of the extracted random number increases. According to our observation, in the ratio of performance improvement to the extracted 32 byte random numbers and 1024 byte random numbers from the Extract Function, if the difference between the ratio of performance improvement when extracting random numbers is less than 8.3%, the ratio of performance improvement in CTR_DRBG does not increase depending on the length of the extracted random number. The longer the extracted random number is, the more encryption process is added. The longer the extracted random number, the more encryption process is added. Therefore, if the ratio of performance improvement of the Extract Function is significantly less than the ratio of performance improvement for Derivation Function and Update Function, the ratio of performance improvement for CTR_DRBG is lower. Our work of optimized CTR_DRBG in this paper shows up to 37.2% performance improvement when using proposed LEA implementation, and up to 8.7% performance improvement when using proposed HIGHT-64/128 implementation.

7. Conclusions

In this paper, we have presented optimized implementations of ARX-based Korean block ciphers (LEA and HIGHT) with CTR mode of operation, and CTR_DRBG using them on low-end 8-bit AVR microcontrollers. With respect to CTR mode optimization, the proposed implementation method for generating look-up tables has the advantage of reducing additional function calls compared to the existing naive methods. By using this technique, our proposed table generation method reduced the cost of building precomputation table by around 6.7% and 9.1% in the case of LEA and HIGHT, respectively. In addition, using the generated look-up table in a fixed key scenario, our CTR implementations based on LEA and HIGHT provide 6.3% and 3.8% improvements compared with the previous best results, respectively. Our CTR implementations are the fastest compared to existing LEA and HIGHT implementations. Regarding CTR_DRBG optimization, we proposed to precompute several parts of CTR_DRBG, which results in performance improvement. The proposed method is the first CTR_DRBG optimization technique, and can be applied regardless of any cipher used for CTR_DRBG. By using this, our CTR_DRBG’s implementations using LEA and HIGHT on 8-bit AVR MCUs provide 37.2% and 8.7% of performance improvement compared with the previous naive implementation. We believe that our work can be widely used for building various types of secure IoT services. Furthermore, the optimization techniques from this work can be applied to the other platforms without difficulties.