Compiled Constructions towards Post-Quantum Group Key Exchange: A Design from Kyber
Abstract
:1. Introduction
2. Preliminaries
2.1. Abdalla et al.’s Compiler
- Each user owns a pair consisting of a public key and a secret key , and all needed public keys may be distributed to all protocol participants during the initialization phase.
- Each pair of users , , shares a high entropy symmetric key, or the complete set of participants shares one common secret (different instances of a user may hold different long-term secrets).
- Each pair of users , , shares a low entropy password. In this case, we assume a publicly available dictionary from which passwords are chosen uniformly at random.
- A non-interactive non-malleable commitment scheme that is perfectly binding and achieves non-malleability for multiple commitments.
- A collision-resistant pseudorandom function family with to be indexed by a set of polynomial size, and two publicly known values and such that no ppt adversary can find two different indices such that , .
- A hash function selected from a family of universal hash functions that maps the concatenation of bitstrings from and the set of participants onto , where n is the number of participants in and .
2.2. Security in a Post-Quantum Setting
- Collision-freeness. In [12], it is proven that the best quantum algorithm for finding a collision for a random function (i.e., a pair of distinct such that ) is . (Notation “wipes out” logarithmic factors in , namely, ). The analogous classical bound is While being suboptimal in number of queries, this algorithm is the most efficient in terms of time complexity with small quantum memory. Thus, in the sequel, we may assume that (even for a quantum adversary) finding a collision pair for a quantum-accessible random oracle can only be done with negligible probability (this is used in Section 4.3.1).
- Pseudorandomness. Following again Hövelmanns et al. [9], we use the argument of Zhandry (see [13]) stating that no quantum algorithm, making at most q quantum queries to a quantum random oracle implementing a random function , can distinguish between and a random polynomial of degree defined over the field As a result, if the input to a quantum random oracle contains enough entropy, then the probability of distinguishing its output from a value chosen uniformly at random is negligible. In other words, when the input is unknown and chosen uniformly at random, the fact that the random oracle can be queried in superposition is of no help in distinguishing the oracle’s output from a randomly chosen element. This is used in the quantum random oracle proof from Section 4.3.
3. Post-Quantum Primitives: and Commitment Scheme
3.1. Kyber’s IND-CPA PKE
| Algorithm 1:Kyber.CPA.KeyGen() |
| 1
2 3 4 5 return |
| Algorithm 2:Kyber.CPA.Enc() |
| 1 2 3 4 5 6 return |
| Algorithm 3:Kyber.CPA.Dec() |
| 1 2 3 return |
3.2. The Transformation: From PKE to AKE
- The attacker knows either the long-term secret key or the secret state information (but not both) of both parties involved in the test session, as long as it did not modify the message received by the test session.
- If the attacker modified the message received by the test session, as long as it obtained neither the long-term secret key of the test session’s peer nor the test session’s state.
3.3. The Commitment Scheme
| Algorithm 4:() |
| 1 2 3 k := H(m) 4 return |
| Algorithm 5:() |
 |
4. Our Post-Quantum Group Key Exchange
4.1. Security Model
4.1.1. Protocol Instances
- indicates whether this instance is or has been used for a protocol run. The flag can only be set through a protocol message received by the instance due to a call to the - or to the -oracle (see below).
- keeps the state information needed during the protocol execution as well as the long term keys needed for authentication.
- shows if the execution has terminated.
- denotes a public session identifier that can serve as identifier for the session key Note that, even though we do not construct session identifiers as session transcripts, the adversary is allowed to learn all session identifiers.
- stores the set of identities of those users that aims at establishing a key with—including himself.
- indicates if the protocol instance was successful, i. e., the user accepted the session key.
- stores the session key once it is accepted by Before acceptance, it stores a distinguished null value.
4.1.2. Communication Network
4.1.3. Adversarial Capabilities
- This sends message M to the instance and returns the reply generated by this instance. If queries this oracle with an unused instance and a set of identities of principals, the -flag is set, initialized with , and the initial protocol message of is returned.
- This executes a complete protocol run among the specified unused instances of the respective users. The adversary obtains a transcript of all messages sent over the network. A query to the Executeoracle is supposed to reflect a passive eavesdropping.
- This yields the value stored in .
- Let b be a bit chosen uniformly at random. Provided that the session key is defined (i. e., and ) and instance is fresh (see the definition of freshness below), can execute this oracle query at any time when being activated. Then, the session key is returned if and a uniformly chosen random session key is returned if . In this model, an arbitrary number of Testqueries is allowed for the adversary , but, once the oracle has returned a value for an instance , it will return the same value for all instances partnered with (see the definition of partnering below).
- This returns all long-term secrets of user —in our case, the private keys used for authentication in .
4.1.4. Correctness, Integrity and Secrecy
- For some , a query was executed before a query of the form has taken place, for some message (or set of identities) M and some .
- The adversary earlier queried with and being partnered.
4.2. Our Construction
- We simplify the session key and session identifier computation using two hash functions to extract them from the shared master key K. Indeed, as the we use as building block is proven secure in the (quantum) random oracle model, it no longer makes sense to use the (somewhat complicated) key extraction procedure defined in [8] to dodge idealized hash functions. Thus, we forgo Tools 1 and 2 mentioned in Section 2.1 and use two hash functions and instead. Thus, at the final Computation phase, each user will set the session key as and the corresponding session identifier as , where K is the master key shared by everyone involved in the execution.
- Further, we make an additional requirement on the compiled , needed for the security proof. Indeed, as pointed out by Nam in [18], an extra condition on the two party protocol used as a base must be imposed in Theorem 1 of [8]. Indeed, the underlying should fulfill integrity in order to thwart a simple replay attack (in the proof of Theorem 1 of [8], it is actually assumed that integrity is fulfilled—see the argument related to Game 1). We thus slightly tune up the two-party to make sure integrity is achieved.
4.3. Security Arguments and Proofs
- (i)
- (ii)
- The encryption scheme yields a non-interactive commitment scheme that is both non-malleable for multiple commitments and perfectly binding. This comes straightforward as a result of this scheme being IND-CCA (see Section 3.3 and [15]).
4.3.1. A Variant of Attaining Integrity
4.3.2. Security of Our Proposed Group Protocol
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Non-Perfect Correctness of Kyber.CPA′
- Choose uniformly-random
- return
Appendix B. Transformation from IND-CPA PKE to Secure 2AKE
Appendix C. Transformation from IND-CPA PKE to IND-CCA KEM
References
- Fujioka, A.; Takashima, K.; Yoneyama, K. One-Round Authenticated Group Key Exchange from Isogenies. ProvSec. Lect. Notes Comput. Sci. 2019, 11821, 330–338. [Google Scholar]
- Apon, D.; Dachman-Soled, D.; Gong, H.; Katz, J. Constant-Round Group Key Exchange from the Ring-LWE Assumption. PQCrypto. Lect. Notes Comput. Sci. 2019, 11505, 189–205. [Google Scholar]
- Katz, J.; Yung, M. Scalable Protocols for Authenticated Group Key Exchange. In Advances in Cryptology— CRYPTO 2003, 23rd Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2003, Proceedings; Boneh, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2729, pp. 110–125. [Google Scholar] [CrossRef] [Green Version]
- Choi, R.; Hong, D.; Kim, K. Constant-round Dynamic Group Key Exchange from RLWE Assumption. IACR Cryptol. ePrint Arch. 2020, 2020, 35. [Google Scholar]
- Persichetti, E.; Steinwandt, R.; Corona, A.S. From Key Encapsulation to Authenticated Group Key Establishment—A Compiler for Post-Quantum Primitives †. Entropy 2019, 21, 1183. [Google Scholar] [CrossRef] [Green Version]
- González Vasco, M.; Pérez del Pozo, A.; Steinwandt, R. Group Key Establishment in a Quantum-Future Scenario. Informatica 2020, 1–18. [Google Scholar] [CrossRef]
- Bos, J.W.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehlé, D. CRYSTALS—Kyber: A CCA-Secure Module-Lattice-Based KEM. In Proceedings of the 2018 IEEE European Symposium on Security and Privacy (EuroS&P), London, UK, 24–26 April 2018; pp. 353–367. [Google Scholar]
- Abdalla, M.; Bohli, J.; Vasco, M.I.G.; Steinwandt, R. (Password) Authenticated Key Establishment: From 2-Party to Group. TCC. Lect. Notes Comput. Sci. 2007, 4392, 499–514. [Google Scholar]
- Hövelmanns, K.; Kiltz, E.; Schäge, S.; Unruh, D. Generic Authenticated Key Exchange in the Quantum Random Oracle Model. In Public-Key Cryptography—PKC 2020; Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 389–422. [Google Scholar]
- Cramer, R.; Shoup, V. Design and Analysis of Practical Public-Key Encryption Schemes Secure against Adaptive Chosen Ciphertext Attack. SIAM J. Comput. 2003, 33, 167–226. [Google Scholar] [CrossRef]
- David Jao, E.A. Supersingular Lsogeny Key Encapsulation. Submission to NIST Post-Quantum Project. 2017. Available online: https://sike.org/#nist-submission (accessed on 16 October 2020).
- Chailloux, A.; Naya-Plasencia, M.; Schrottenloher, A. An Efficient Quantum Collision Search Algorithm and Implications on Symmetric Cryptography. In Advances in Cryptology—ASIACRYPT 2017—23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Takagi, T., Peyrin, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10625, pp. 211–240. [Google Scholar] [CrossRef]
- Zhandry, M. Secure Identity-Based Encryption in the Quantum Random Oracle Model. In Advances in Cryptology—CRYPTO 2012—32nd Annual Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2012; Safavi-Naini, R., Canetti, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7417, pp. 758–775. [Google Scholar] [CrossRef] [Green Version]
- Boneh, D.; Dagdelen, Ö.; Fischlin, M.; Lehmann, A.; Schaffner, C.; Zhandry, M. Random Oracles in a Quantum World. In Advances in Cryptology—ASIACRYPT 2011—17th International Conference on the Theory and Application of Cryptology and Information Security, Seoul, Korea, 4–8 December 2011; Lee, D.H., Wang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 7073, pp. 41–69. [Google Scholar] [CrossRef] [Green Version]
- Hövelmanns, K.; Kiltz, E.; Schäge, S.; Unruh, D. Generic Authenticated Key Exchange in the Quantum Random Oracle Model. IACR Cryptol. ePrint Arch. 2018, 2018, 928. [Google Scholar]
- Bellare, M.; Pointcheval, D.; Rogaway, P. Authenticated Key Exchange Secure against Dictionary Attacks. In Advances in Cryptology—EUROCRYPT 2000, International Conference on the Theory and Application of Cryptographic Techniques, Bruges, Belgium, 14–18 May 2000; Preneel, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1807, pp. 139–155. [Google Scholar] [CrossRef] [Green Version]
- Bohli, J.; Vasco, M.I.G.; Steinwandt, R. Secure group key establishment revisited. Int. J. Inf. Sec. 2007, 6, 243–254. [Google Scholar] [CrossRef]
- Nam, J.; Paik, J.; Won, D. A security weakness in Abdalla et al.’s generic construction of a group key exchange protocol. Inf. Sci. 2011, 181, 234–238. [Google Scholar] [CrossRef]
- Hofheinz, D.; Hövelmanns, K.; Kiltz, E. A Modular Analysis of the Fujisaki-Okamoto Transformation. TCC (1). Lect. Notes Comput. Sci. 2017, 10677, 341–371. [Google Scholar]



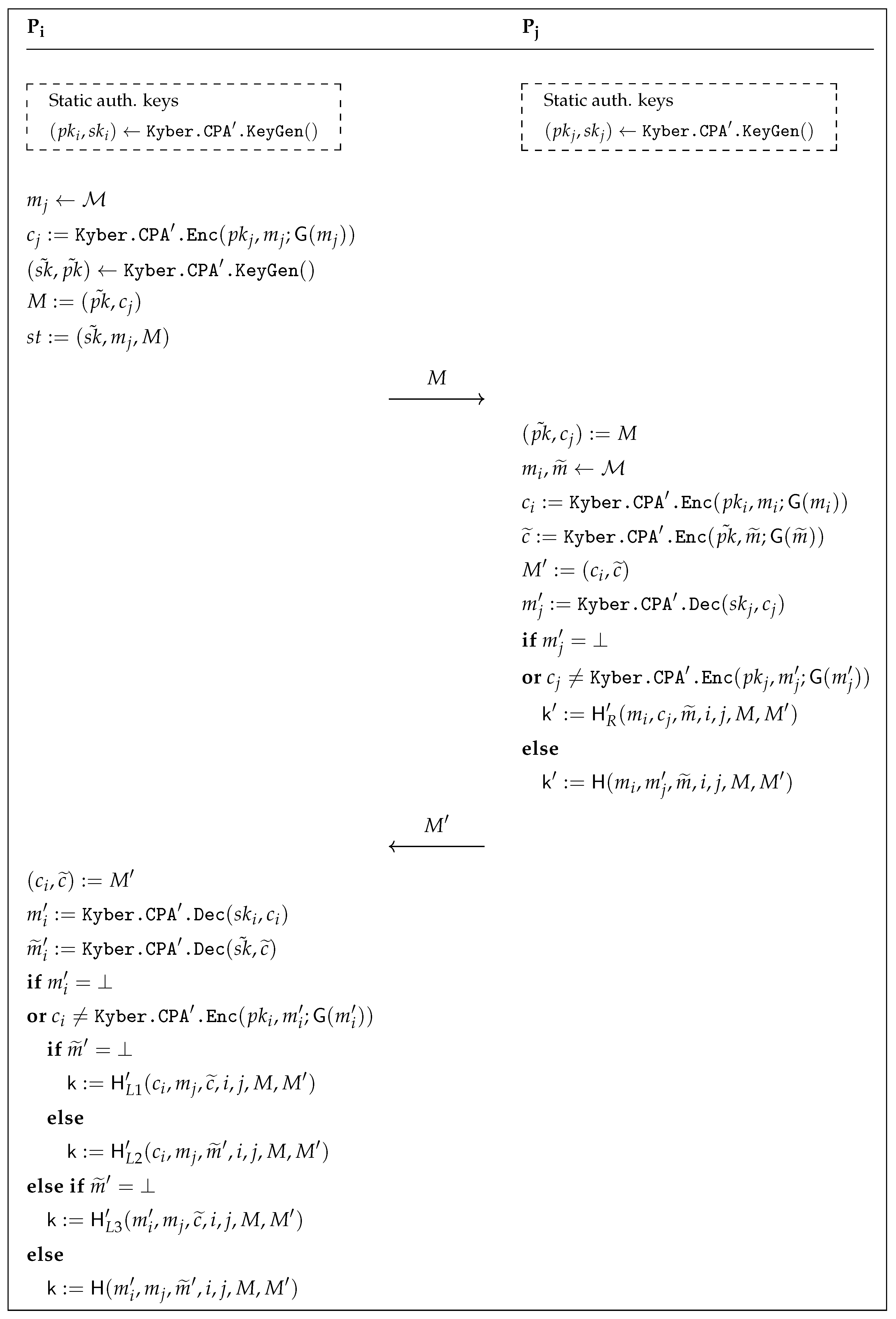

| Protocol | # Rounds | Avoids PQ-Sign. | # Broadcast Messages | # PtP Messages |
|---|---|---|---|---|
| n-UM [1] | 1 | Yes | n | 0 |
| BC n-DH [1] | 1 | Yes | n | 0 |
| Apon et al. [2] | 3 | Yes (but is unauth.) | 0 | |
| STAG [4] | 3 | No | 0 | |
| Pers. et al. [5] | 3 | No | n | |
| Gonz. et al. [6] | 2 | Yes | n | |
| This work | 4 | Yes |
| Protocol | Assumption Type | Model | FutQ/PostQ | Authent. |
|---|---|---|---|---|
| n-UM [1] | Isogeny | QROM | PostQ | Yes |
| BC n-DH [1] | Isogeny | ROM | PostQ | Yes |
| Apon et al. [2] | Lattice | ROM | PostQ | No |
| STAG [4] | Lattice | ROM | PostQ | Yes |
| Pers. et al. [5] | Compiler | No RO added | PostQ | Yes |
| Gonz. et al. [6] | Compiler | No RO added | FutQ | Yes |
| This work | Lattice | QROM | PostQ | Yes |
| Notation | Representation |
|---|---|
| Bold lower-case | Vectors with coefficients in R or . All vector will be column vectors by default. |
| Regular font letter | Elements in R or . |
| Bold upper-case | Matrices. |
| If S is a set, s is chosen uniformly at random from S. If S is a distribution, s is chosen according to such distribution S. | |
| where Sam is an eXtendable Output Function (XOF) | Value y that is distributed according to distribution S (or uniformly over a set S). This is a deterministic procedure. |
| , | is generated from a distribution where each of its coefficients are generated from . A k-dimensional vector of polynomials can be generated according to the distribution . |
| is the rounding function i.e., where and is the floor function. | |
| For an even (respectively, odd) integer , is the unique element in the range (respectively, ) such that . |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escribano Pablos, J.I.; González Vasco, M.I.; Marriaga, M.E.; Pérez del Pozo, Á.L. Compiled Constructions towards Post-Quantum Group Key Exchange: A Design from Kyber. Mathematics 2020, 8, 1853. https://doi.org/10.3390/math8101853
Escribano Pablos JI, González Vasco MI, Marriaga ME, Pérez del Pozo ÁL. Compiled Constructions towards Post-Quantum Group Key Exchange: A Design from Kyber. Mathematics. 2020; 8(10):1853. https://doi.org/10.3390/math8101853
Chicago/Turabian StyleEscribano Pablos, José Ignacio, María Isabel González Vasco, Misael Enrique Marriaga, and Ángel Luis Pérez del Pozo. 2020. "Compiled Constructions towards Post-Quantum Group Key Exchange: A Design from Kyber" Mathematics 8, no. 10: 1853. https://doi.org/10.3390/math8101853
APA StyleEscribano Pablos, J. I., González Vasco, M. I., Marriaga, M. E., & Pérez del Pozo, Á. L. (2020). Compiled Constructions towards Post-Quantum Group Key Exchange: A Design from Kyber. Mathematics, 8(10), 1853. https://doi.org/10.3390/math8101853






