Analysis of the Upper Limitation of the Most Convenient Cadence Range in Cycling Using an Equivalent Moment Based Cost Function

Abstract

The article presents the study of the pedalling rates obtained by minimizing a cost function based on a kinetic approach and which can be estimated with more easily achievable experimental data as input than other cost functions. Simulations based on data available in the literature were used to compare the cadences obtained by minimizing well-known joint moment-based cost functions and the proposed cost function. The influence of the power output and of the body mass index on the pedalling rates that minimize the cost function was investigated. Experimental tests performed by four competitive cyclists in the field were used as comparison for the results based on simulations. From simulations emerged that results obtained with the cost function proposed in this work were similar to those based on the absolute average joint moments. We found that the upper limit of the more convenient pedalling rate range decreases linearly with the body mass index, while it increases non-linearly with power output. Furthermore, a polynomial regression of the correlation of the pedalling rate obtained through the method and body mass index and power was found. Experimental results confirmed that the proposed model, finding an approximation of the minimum of muscular effort (not including negative muscular work), is able to estimate the upper limit of an optimal range of cadence. All tested cyclists freely choose to pedal at a cadence under this limit.

1. Introduction

The identification and the analysis of correlations between human movement performance and motion parameters is of a considerable importance for both scientists and athletes and is the issue of a huge number of biomechanical studies [1,2,3].

In cycling, pedalling rate significantly affects rider energy expenditure and consequently the overall performance. The metabolic energy cost (oxygen consumption), the muscular efforts, the leg joints torques, the negative muscle work, at a given power output, are all influenced by the pedalling cadence, typically with different optimal ranges. Several studies in the literature searched for an optimum criterion and most of them are based on the minimization of a specific cost function. The use of a cost function [1,4,5] allows to quantify the movement cost by a single value obtained by substituting the values of several variables in a mathematical expression. Most common cost functions used in the biomechanics of cycling are based on the energy consumption [6,7,8,9], the muscle electrical activity (with electromyography, EMG) [10], the leg joint moments (which bear some relation to the muscular effort) [11,12,13], the negative muscle work [14], neuromuscular fatigue-related quantities [15] and the rating of perceived exertion (RPE) during cycling [16,17]. Seabury [6] and Marsh [7] founded that the oxygen consumption for power outputs less than 200 W is minimized for cadences between 40 and 65 rpm; for power outputs of about 300 W the optimal range for oxygen consumption is between 70 and 80 rpm [15,18]. Furthermore, gross muscular efficiency (the oxygen consumption divided by the power output) for low/moderate effort intensities decreases with increasing pedalling rates [19], while during high intensity cycling it remains almost constant with increasing pedalling rates. In [20] Neptune et al. founded, for most of the tested subjects, a minimum in the summed iEMG across all muscles at the cadence of 90 rpm. A further analysis [15], based on simulations, showed that at 90 rpm occurred the minimum of all nine neuromuscular quantities applied to the sum across muscles of individual activations (average, integrated and peak activation, average and peak force, average and peak stress, average and peak endurance). Redfield and Hull [11] and Marsh et al. [13] examined in detail the relation between cadence and leg joint moments at constant power. A cost function based on the average of the absolute leg joint moments during a pedalling cycle was proposed and validated by experimental data. The optimum resulting from these studies corresponds to cadences in the neighbourhood of 90-100 rpm increasing with the power output. From the study of Neptune in [14] emerged that at pedalling cadences higher than 90 rpm the negative muscle work increases, with the consequent decreasing of muscular efficiency. In [17], Jameson obtained that cadence does not affect significantly central sensations and a minimum in the muscle pain ratings at about 70 rpm.

Therefore, optimal cadence actually depends on which criterion is considered. Furthermore, each cyclist freely chooses a cadence depending on a series of peculiar physiological and environmental factors that makes the problem even more complex [21]. As a consequence, it is not possible to determine an exact optimal rate of pedalling, whereas it can be defined a range of compromise between energy cost and muscular work optimum, within which each rider self-regulates his cadence [22]. A confirmation of this is the well-known experimental evidence that pedalling rates freely chosen by cyclists (85-100 rpm) are higher than metabolically optimum cadences (50–70 rpm), while the cadences that minimize the joint moments can be even higher (90–110 rpm) [23]. In other words, the optimal cadence for a cyclist can be identified in a compromise between a minimum peripheral muscular force and a minimum metabolic cost.

In this work, it is analysed an alternative easy to evaluate cost function, based on an approximate maximum peak of muscular power exerted during a cycle, that can be converted in an equivalent global moment generated by the leg joints. To this aim, a kinetic method is used: the inverse dynamics problem is solved by an energetic formulation in order to find an approximate trend of the power law generated by the muscles. The advantage of the energetic approach, with respect to a Newton–Euler formulation, is due to the limited set of experimental data required, namely the power law applied to the crank during a cycle. In [24], Neptune and Van den Bogert demonstrated that kinetic methods underestimate the mechanical energy expenditure of muscles, with errors of 24% in a simulation and of the 5% in a second simulation, due to the inability of such methods to account for co-contraction of antagonistic muscles during movement. In [14] a quantification of the amount of negative muscular crank torque at different pedalling rate is investigated. From the study, performed at a power output of 260 W, it emerged that no negative muscle work was present at 60 rpm, a negligible amount at 75 and 90 rpm and substantial negative muscular crank torque was generated at 105 and 120 rpm. On the basis of these findings, it could be supposed that a kinetic approach at low pedalling rates can substantially allow to obtain muscular effort values close to the real ones, whereas at high pedalling frequencies it could underestimate the effective efforts. Therefore, it can provide optimal cadence values higher than those that minimize muscle effort, providing an upper limitation for the most convenient cadence range.

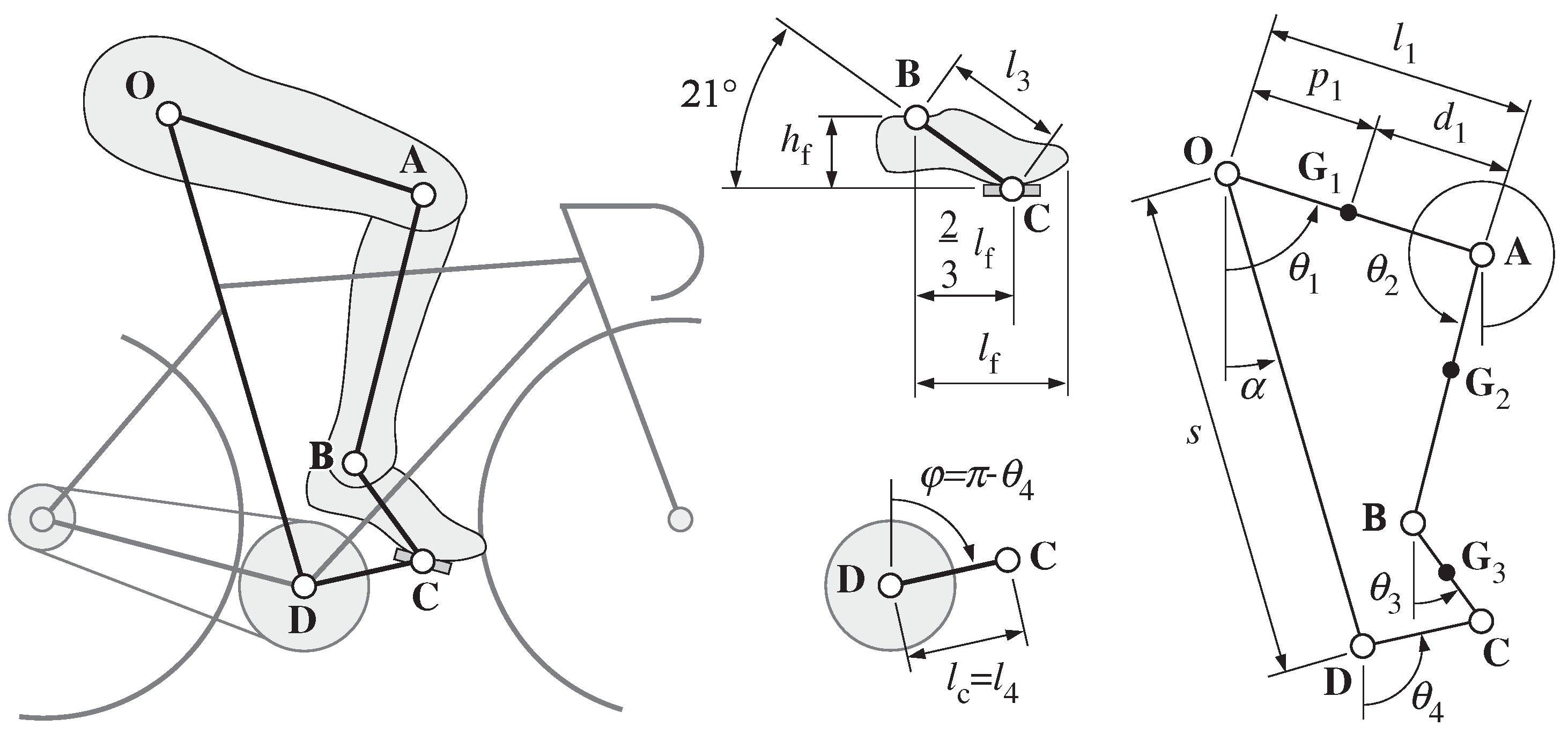
Biomechanical analysis of cycling movements can be carried out with two approaches: a standard inverse dynamics approach with simplified planar skeletal models [11,25] or musculoskeletal modelling combined with optimal control analysis by means of multibody biomechanical analysis software (OpenSim, Anybody, SIMM etc…) [15,26,27,28]. In the comparison, the first is characterized by a greater simplicity, a smaller number of parameters and input data to be identified, but a more limited number of quantities that can be calculated and a greater approximation. The second is a powerful method to study multi-joints movements with respect to individual muscle mechanics and energetics, providing considerable information on system individual muscle kinetics and kinematics, but the number of parameters that have to be identified and the complexity are significantly higher. With the aim of studying a methodology that allows to identify the limits of the most convenient pedalling cadences with a method that is simple to implement, we have chosen to follow the first approach.

Two formulations of the dynamic problem (the first based on Newton–Euler equations, the second on the power flow balance) are implemented in order to define two different cost functions: the first, called Moment based Cost Function (MCF), is the one inherited from [11,13]; the second, proposed by the authors, is the Equivalent Moment based Cost Function (EMCF). A series of simulations on six hypothetical athletes confirm that the model based on EMCF gives similar results with the MCF method, which is considered to be a term of comparison well established in literature and supported by experimental evidence. Data from simulations are also used for a polynomial regression that allows to obtain an easy approximated formula. Then, a series of tests have been performed in the field, collecting data that confirms the validity of the proposed model. The novel EMCF cost function is able to identify the upper limit of the range of more convenient cadences (henceforth $C_{lim}$), similarly to other established methods based on the average of the absolute leg joint moments, but with the advantage of a simpler formulation and an easier calculation method. A comparison is made between the values of the cost function (MCF) obtained with the kinetic method and those of the EMCF cost function to verify the validity of the proposed approach. Subsequently an analysis of the dependence between $C_{lim}$ and power and body mass index is carried out, identifying an approximate polynomial form relationship of this dependence. Finally, experimental tests are conducted to compare the $C_{lim}$ obtained with the EMCF cost function and the cadences chosen by competitive cyclists for different power levels.

Focusing on the general approach and methodology, this paper offers an example on how mathematical models and numerical methods can be exploited to perform a model-based study of a biomechanical problem. Thus, the paper is in line with the aim of this Special Issue (Mathematical Modeling in Biomechanics and Mechanobiology), where similar papers can be found [29]. The article is structured as follows. Section 2 is devoted to Methods and Materials, with a detailed description of the planar model used to formulate the kinematics and the dynamics of the pedalling, the equations of kinematics for position, velocity and acceleration, the equations of dynamics, the formulation of the cost functions MCF and EMCF and the experimental tests. Results, discussion and conclusions are provided in Section 3, Section 4 and Section 5, respectively.

2. Methods and Materials

2.1. Kinematic Model

By means of a biomechanical multibody model, quantities not directly measurable, like joint moments, can be estimated indirectly. In particular, the solution of the inverse dynamics problem, once the motion is assigned to the model and external forces are known, allows to determine the joint moments and the internal forces laws [26,30]. A detailed description of the planar model used to formulate the kinematics and dynamics of the pedalling is given in Section 2.1, where also the equations of kinematics for position, velocity and acceleration are given. Then, the equations of dynamics are derived in Section 2.2 and then exploited to formulate the cost functions MCF and EMCF. Finally, methods used for tests are described in Section 2.3.

Inspired to [11,31], the bicycle–leg system has been modelled as a planar five bar linkage characterized on the basis of anthropometric scale factors [32,33]. Figure 1 shows the skeletal model adopted and gives the basic nomenclature used to describe the kinematics of the system. The vector $\mathbf{\theta }={\left[{\theta }_1{\theta }_2{\theta }_3{\theta }_4\right]}^T$ contains the absolute orientation from the vertical axis of the four moving segments of the system, assuming as positive an anticlockwise rotation. The subscripts i (i = 1:4) refers in the order to: thigh, shank, foot and crank. The length of the ith link is indicated by $l_i$. Lengths $p_i$ and $d_i$ indicate the proximal and distal position of the center of mass ${\mathbf{G}}_i$ with respect to the extremities of the ith body segment, so that $p_i+d_i=l_i$. The length $l_3$ has been determined, as shown in Figure 1, assuming that the pedal spindle is fixed at two thirds of the total length of the foot; as a result, the segment $\left(\mathbf{C}-\mathbf{B}\right)$ forms with the pedal a constant angle equal to ${21}^{\circ }$. The seat tube angle is set to an average value between road and triathlon, i.e., $\alpha ={75}^{\circ }$. Based on the $109\%$ saddle height method [34,35], the $\mathbf{OD}$ constant distance s is determined by the following formula:

$$s=1.09h_{ins}-l_c=1.09\left(0.48h\right)-l_c$$

(1)

where $h_{ins}$ is the inseam height, estimated as the 48% of the total height h; $l_c$ represents the length of the pedal crank ($l_c=l_4$ in the scheme of Figure 1) and it is fixed to a typical value for road bicycles ($l_c=170\mathrm{mm}$).

To solve the position problem, a closed loop can be defined along the path $\mathbf{O}-\mathbf{A}-\mathbf{B}-\mathbf{C}-\mathbf{D}-\mathbf{O}$, resulting in the following system of equations:

$$\left\{\begin{array}{c}{\displaystyle \sum _{i=1}^3}{l}_{i}sin{\theta }_i-l_{4}sin{\theta }_4-ssin\alpha =0\hfill \\ {\displaystyle \sum _{i=1}^3}{l}_{i}cos{\theta }_i-l_{4}cos{\theta }_4-scos\alpha =0\hfill \end{array}\right.$$

(2)

All length variables in Equation (2) are known, as the angle $\alpha$. As shown in Figure 1, the crank angle $\phi$ increases clockwise from the top dead center (TDC). Thus, ${\theta }_4$ is related to $\phi$ by the relation:

$${\theta }_4\left(\phi \right)=\pi -\phi$$

(3)

The foot angle ${\theta }_3$ must be related to the crank angle, with a relation ${\theta }_3={\theta }_3\left(\phi \right)$. To this aim, experimental data extracted from [31] have been used. A good fitting of such data, shown in Figure 2a, was found using a law of the form:

$${\theta }_3\left(\phi \right)={\gamma }_a+{\gamma }_{b}sin\left(\phi -{\gamma }_c\right)$$

(4)

After an optimization procedure (fminsearch function in MATLAB, based on a derivative-free optimization method), ${\gamma }_a=26.{25}^{\circ }$, ${\gamma }_b=27.{55}^{\circ }$ and ${\gamma }_c=26.{56}^{\circ }$ resulted the best fit values for constants in Equation (4). A similar trend for the foot angle vs. the crank angle was also found in [36], validating the adopted fitting law.

Once the relations ${\theta }_3\left(\phi \right)$ and ${\theta }_4\left(\phi \right)$ are defined, the two remaining unknowns of the problem, i.e., ${\theta }_1$ and ${\theta }_2$, can be found as functions of $\phi$ solving the system (2) in combination with Equations (3) and (4).

A linear form for the velocity problem can be found by derivation of the position equations:

$${\mathbf{J}}_1{\left[\begin{array}{cc}{\dot{\theta }}_1& {\dot{\theta }}_2\end{array}\right]}^T+{\mathbf{J}}_2{\left[\begin{array}{cc}{\dot{\theta }}_3& {\dot{\theta }}_4\end{array}\right]}^T=\mathbf{0}$$

(5)

$${\left[\begin{array}{cc}{\dot{\theta }}_1& {\dot{\theta }}_2\end{array}\right]}^T=-{\mathbf{J}}_1^{-1}{\mathbf{J}}_2{\left[\begin{array}{cc}{\dot{\theta }}_3& {\dot{\theta }}_4\end{array}\right]}^T$$

(6)

Jacobian matrices in the previous equations are defined as:

$${\mathbf{J}}_1=\left[\begin{array}{cc}{l}_{1}sin{\theta }_1& l_{2}sin{\theta }_2\\ l_{1}cos{\theta }_1& l_{2}cos{\theta }_1\end{array}\right]{\mathbf{J}}_2=\left[\begin{array}{cc}{l}_{3}sin{\theta }_3& -l_{4}sin{\theta }_4\\ l_{3}cos{\theta }_3& -l_{4}cos{\theta }_4\end{array}\right]$$

(7)

A further derivation of Equation (6) brings to the expression of the accelerations:

$$\begin{array}{c}\hfill {\left[\begin{array}{cc}{\ddot{\theta }}_1& {\ddot{\theta }}_2\end{array}\right]}^T=-{\mathbf{J}}_1^{-1}\left({\mathbf{J}}_2{\left[\begin{array}{cc}{\ddot{\theta }}_3& {\ddot{\theta }}_4\end{array}\right]}^T\right.+\left.{\mathbf{J}}_3{\left[\begin{array}{cccc}{\dot{\theta }}_1^2& {\dot{\theta }}_2^2& {\dot{\theta }}_3^2& {\dot{\theta }}_4^2\end{array}\right]}^T\right)\end{array}$$

(8)

where the Jacobian related to the centrifugal terms is defined as:

$${\mathbf{J}}_3=\left[\begin{array}{cccc}{l}_{1}cos{\theta }_1& l_{2}cos{\theta }_2& l_{3}cos{\theta }_3& -l_{4}cos{\theta }_4\\ -l_{1}sin{\theta }_1& -l_{2}sin{\theta }_2& -l_{3}sin{\theta }_3& l_{4}sin{\theta }_4\end{array}\right]$$

(9)

2.2. Dynamic Model

For the dynamic modelling of the system, two different formulations have been considered. Basically, the first follows the Newton–Euler method, whereas the second is based on energy and power flow principles. The first formulation allows to calculate the Moment-Based Cost Function (MCF) already presented in [11,13], while the second formulation is used to determine an Equivalent Moment-Based Cost Function (EMCF), defined by the authors in the present work.

2.2.1. Moment-Based Cost Function (MCF)

External forces applied to the system are required for the Newton–Euler method, in particular the force applied to the foot by the pedal. Experimental data, given as average trend between different subjects and conditions, are available from [36]. Effective and radial components of the force ($F_e$ and $F_r$, respectively) are given versus the crank angle, as shown in Figure 2b,c. Data refers to a pedalling cadence of ${\dot{\phi }}^{*}=90\mathrm{rpm}$ and an average net power, hereafter called resistant power, of ${\overline{P}}_r^{*}=385\mathrm{W}$. Once the cadence $\dot{\phi }$ and the power ${\overline{P}}_r$ of a different pedalling regimen are defined, the forces must be scaled by the ratio $\tau$ as follows:

$$F=\tau F^{*}\tau ={\displaystyle \frac{{\dot{\phi }}^{*}}{{\overline{P}}_r^{*}}}{\displaystyle \frac{{\overline{P}}_r}{\dot{\phi }}}$$

(10)

where $F^{*}$ indicates the experimental force data given in [36], that refers to ${\dot{\phi }}^{*}$ and ${\overline{P}}_r^{*}$.

The above mentioned scaling procedure represents a source of error since the shape of force curves will remain the same even at different cadences and power outputs; this is in contrast, for example, with the study presented in [37], where a certain variability is shown. Nevertheless, a simple scaling method is justified once an optimization problem based on pedalling cadence and power output must be formulated, and the choice of an average trend, as obtained in [36], is reasonable. Furthermore, if the error in the scaling of the force curves could be appreciable, it results much less significant if the global torque at the crank is scaled ( Figure 3a). In this case, the contribution of the two legs, acting with a shift of a half cycle, gives a curve shape that is fully similar to a sinusoidal function whose average value must be equal to the average power ${\overline{P}}_r$; thus the only variability is about the amplitude, with the further limitation that the curve must be always positive. Definitely, it is reasonable to expect that a proportional scaling of $P_r$ starting from the experimental data set $P_r^{*}$ will result on a faithful trend even at conditions different from experiments.

Besides the scaling procedure, a fitting of experimental force curves has been adopted in order to obtain smooth curves. To this aim, a three terms Fourier series has shown a good capability to fit the data; thus, the effective component (and analogously the radial component) of the pedal force can be approximated by:

$$F_e=F_0+\sum _{i=1}^3{F}_{i}sin(\phi +{\beta }_i)$$

(11)

Coefficients $F_i,i=0,1,\cdots ,3$ and ${\beta }_i,i=1,\cdots ,3$ can be found by a minimization procedure where the cost function is defined as the deviation between fitted and experimental data. The result of such operation is shown in Figure 2b,c, where the fitted and experimental curves of $F_e$ and $F_r$ are compared; the corresponding best fit parameters are collected in

Table 1. Best fit coefficients for Equation (11).

${\mathit{F}}_{\mathit{e}}$
$F_0\left[\mathrm{N}\right]$	$F_1\left[\mathrm{N}\right]$	${\beta }_1{[}^{\circ }]$	$F_2\left[\mathrm{N}\right]$	${\beta }_2{[}^{\circ }]$	$F_3\left[\mathrm{N}\right]$	${\beta }_3{[}^{\circ }]$
121.89	189.03	107.11	33.10	1.42	−41.41	184.50
${\mathit{F}}_{\mathit{r}}$
$F_0\left[\mathrm{N}\right]$	$F_1\left[\mathrm{N}\right]$	${\beta }_1{[}^{\circ }]$	$F_2\left[\mathrm{N}\right]$	${\beta }_2{[}^{\circ }]$	$F_3\left[\mathrm{N}\right]$	${\beta }_3{[}^{\circ }]$
49.49	155.02	−116.72	−21.02	−73.62	−0.78	−26.09

.

The scheme of Figure 4 shows the free body diagram of the leg used to formulate the dynamic model by means of the Newton–Euler method. The horizontal and vertical components of the pedal force, $F_h$ and $F_v$ respectively, are calculated starting from the fitting law (11) of $F_e$ and $F_r$, as expressed by the first two equations of the system (12):

$$\left\{\begin{array}{c}{F}_h=F_{r}sin\phi +F_{e}cos\phi \hfill \\ F_v=F_{r}cos\phi -F_{e}sin\phi \hfill \\ \\ H_B=m_3{a}_{G_{3}x}+F_h\hfill \\ V_B=m_3\left(g+a_{G_{3}y}\right)+F_v\hfill \\ H_A=m_2{a}_{G_{2}x}+H_B\hfill \\ V_A=m_2\left(g+a_{G_{2}y}\right)+V_B\hfill \\ \\ M_a=-I_{G_3}{\ddot{\theta }}_3-\left(F_{v}sin{\theta }_3+F_{h}cos{\theta }_3\right)l_3-m_3\left(gsin{\theta }_3-a_{G_{3}x}cos{\theta }_3-a_{G_{3}y}sin{\theta }_3\right)p_3\hfill \\ M_k=M_a+I_{G_2}{\ddot{\theta }}_2+\left(V_{B}sin{\theta }_2+H_{B}cos{\theta }_2\right)l_2+m_2\left(gsin{\theta }_2-a_{G_{2}x}cos{\theta }_2-a_{G_{2}y}sin{\theta }_2\right)p_2\hfill \\ M_h=-M_k-I_{G_1}{\ddot{\theta }}_1-\left(V_{A}sin{\theta }_1+H_{A}cos{\theta }_1\right)l_1-m_1\left(gsin{\theta }_1-a_{G_{1}x}cos{\theta }_1-a_{G_{1}y}sin{\theta }_1\right)p_1\hfill \end{array}\right.$$

(12)

The following four equations relate to the internal forces at the ankle and knee joints, while the last three equations are the expressions of $M_a$, $M_k$, and $M_h$, namely the joint moments at the ankle, the knee and the hip.

Deriving from [13], the MCF cost function, based on the average absolute lower extremity joint moments, can now be defined as:

$$MCF={\displaystyle \frac{1}{2\pi }}\underset{0}{\overset{2\pi }{\int }}\left({\displaystyle \frac{|M_a|+|M_k|+|M_h|}{3}}\right)\mathrm{d}\phi$$

(13)

2.2.2. Equivalent Moment-Based Cost Function (EMCF)

A power balance formulation has been exploited to obtain an approximate trend of the overall muscular power law, resulting from the sum of the resistant power at the crank and the derivative of the mechanical energy of the system. The approximation in this estimation is due to the impossibility of the method to take into account the action of the antagonist muscles [24].

Starting from data relative to the effective force given in [36] and assuming a perfect symmetry between the left and the right leg during the pedalling, the power applied to the central axis of the crankset can be determined as:

$$P_r=\left[F_e\left(\phi \right)+F_e\left(\phi +\pi \right)\right]l_c\dot{\phi }$$

(14)

The plot of the previous expression is shown by the solid line in Figure 3a. The dashed line refers to the fitting of such curve, that is possible by means of the following simplified expression:

$$P_r={\overline{P}}_r\left[1-kcos\left(2\phi +\beta \right)\right]$$

(15)

with $k=0.89$ and $\beta =6.{18}^{\circ }$. Thus, the resistant power is easily scalable, keeping constant the factors k and $\beta$, whereas the average resistant power ${\overline{P}}_r$ must be set to the desired value.

During the pedalling a certain amount of mechanical energy, defined as the sum of the potential V and kinetic T energy, is stored or released by the leg. Even if the mechanical energy of the system is periodically constant (at a constant pedalling cadence), the oscillation of such energy inside the revolute affects the shape of the instantaneous power curve that must be exerted by the muscles. The power balance law, in fact, can be expressed as:

$$P_m=P_r+{\displaystyle \frac{\mathrm{d}T}{\mathrm{d}t}}+{\displaystyle \frac{\mathrm{d}V}{\mathrm{d}t}}$$

(16)

where $P_m$ is the approximated power generated by the muscular apparatus, $P_r$ is the power delivered to the crankset, T and V are the kinetic and potential energy of the leg respectively. While $P_r$ in the previous equation is provided by Equation (15), the potential and kinetic energy of the system must be determined by the expressions:

$$T=\sum _{i=1}^4\left[{\displaystyle \frac{1}{2}}{m}_i\left({\dot{x}}_{G_i}^2+{\dot{y}}_{G_i}^2\right)+{\displaystyle \frac{1}{2}}{I}_{G_i}{\dot{\theta }}_i^2\right]V=\sum _{i=1}^4{m}_{i}g{y}_{G_i}$$

(17)

Coordinates $\left(x_{G_i},y_{G_i}\right)$ and their derivatives express the position and the velocity of the center of mass of the ith segment with respect to the conventional axes system (x sagittal, y vertical); they can be determined as a function of $\phi$ and $\dot{\phi }$ using the Equations (2) and (6) of the kinematic model.

Expressions (17) refers to a single leg, thus the global energy of the system can be obtained considering both legs, with an angular shift of $\pi$ between left and right. Furthermore, the mechanical energy stored in the pedals and in the crank is neglected, being their mass much lower than the leg mass. Moreover, the crank kinetic energy is constant since the angular velocity $\dot{\phi }$ is considered constant; also its gravitational potential energy is constant, since the height of the center of mass (corresponding to the spindle of the crank) is fixed. Thus, when Equation (16) is expanded, the derivative of the kinetic and potential energy of the crank is null.

As an example, Figure 3b shows the approximated muscular power curve ($P_m$, solid line) obtained by Equation (16) and the contribution of each single term (dashed lines) for a cyclist with $70\mathrm{kg}$ mass and $1.75\mathrm{m}$ height exerting an average power of $385\mathrm{W}$ at a cadence of $90\mathrm{rpm}$.

Exploiting the formulation described in this section, a novel cost function can be introduced as an equivalent global moment defined as:

$$EMCF={\displaystyle \frac{max\left(P_m\right)}{\dot{\phi }}}$$

(18)

where the angular velocity $\dot{\phi }$ of the crank is supposed constant and expressed in rad/s. The equivalent moment, that is the ratio $P_m/\dot{\phi }$, represents an approximate global estimate of the muscular effort. Thus, the minimum of the function EMCF represents an upper limit for the range of cadences that is most convenient from an energetic point of view ($C_{lim}$).

The similarity between MCF and EMCF results evident, since the first one is correlated to the average absolute value of the joint torques, which is conceptually near to the definition of the equivalent moment given in this section. The same kinematic experimental data, i.e., the angle of the pedal vs. crank rotation, are necessary in both cases to define the cost functions; nevertheless, dynamic data required to define MCF include force components at pedals, that are complex measurements, whereas the definition of EMCF requires only the estimation of the resistant power $P_r$, that is equivalent to measure the torque applied to the crank. In this sense, once the similarity of the two functions is assessed, an advantage can be found in the EMCF.

2.3. Experimental Method

Four competitive cyclists have been tested in the field (mass $66.3\pm 7.8\mathrm{kg}$, height $174.3\pm 6.8\mathrm{cm}$, age $27.5\pm 2.4\mathrm{years}$).

Table 2. Anthropometric data of tested competitive cyclists.

Cyclist	Age	m [kg]	h [m]	BMI $[\mathbf{kg}/{\mathbf{m}}^2]$	$\mathit{I}=\mathit{m}\mathit{h}$ [kg m]
CS	25	55	1.65	20.2	90.8
GM	26	67	1.77	21.4	118.6
FF	29	72	1.74	23.8	125.3
FC	30	71	1.81	21.7	128.5

collects anthropometric data of each subject. Informed consent was obtained before the experiment. All the subjects rode their own racing bicycle along an uphill road with an average gradient of $5\%$. Five different levels of power normalized with respect to the mass of the cyclist have been tested, ranging from 1.63 W/kg to 5.44 W/kg. It was asked to each subject to perform five trials of 2’ at increasing levels of constant power, with rest intervals of 2’ between each exercise. In all cases the cadence was free. Data were collected from commercial cycling computers and power meter installed on the bicycles; average cadence and power during each trial were then calculated. To verify that fatigue did not influence the tests, two of the subjects repeated the trials with a random sequence of power, showing results comparable with the increasing sequence.

3. Results

In this section it is firstly given the comparison between MCF and EMCF when they are involved in the minimization problem; the comparison is done at increasing average power outputs, corresponding to increasing values of upper limit cadences. Figure 5 shows the comparison between MCF and EMCF, plotted versus the pedalling cadence. Both cost functions have been normalized by their minimum value, so that $C_{lim}$ occurs when the CF is equal to 1. Plots, based on simulations, refers to a cyclist with $m=70\mathrm{kg}$ and $h=1.75\mathrm{m}$ exerting a power output from 100 W to 400 W. Values of $C_{lim}$ are comparable in all cases, with greater values at increasing powers, as evidenced by experiments in literature [23]. Therefore, it can be said that the minimization of the equivalent moment gives similar results with respect to the minimization of the approximated average muscular stress.

The study can be extended to different body characteristics: once the mass and the height are given, all the geometric and inertial properties of the kinematic and dynamic models can be obtained by means of a scaling procedure based on anthropocentric average factors [32,33]. As explained in Section 2.2.2, also the power $P_r$ applied to the crankset can be scaled on the basis of the imposed average power output. Thus, the upper limit of most convenient cadence rate has been investigated for a series of cases, ranging the mass from 50 to $100\mathrm{kg}$, the body mass index (BMI) from 19 to $25\mathrm{kg}/{\mathrm{m}}^2$ and the power output from 100 to $400\mathrm{W}$. Results are plotted in Figure 6. Solid black lines are iso-height curves, while markers refer to six different professional riders considered for simulations; the three white markers, in particular refer to sprinters (sp), whereas black markers correspond to climbers (cl). It results clear from plots, as confirmed by the facts, that climbers have higher optimal cadences than sprinters. Furthermore, for all cyclists $C_{lim}$ increases for increasing powers. Anthropometric data of the six the simulated cyclists are collected in

Table 3. Anthropometric data of six professional cyclists considered for simulations (sp: sprinter, cl: climber).

Cyclist		m [kg]	h [m]	BMI $[\mathbf{kg}/{\mathbf{m}}^2]$	$\mathit{I}=\mathit{m}\mathit{h}$ [kg m]
A	sp	85	1.86	24.6	158.1
B	sp	82	1.88	23.2	154.2
C	cl	67	1.86	19.4	124.6
D	sp	70	1.75	22.9	122.5
E	cl	64	1.82	19.3	116.5
F	cl	56	1.67	20.1	93.5

, whereas $C_{lim}$ obtained with each one of the cost functions are reported in

Table 4. Upper limit cadences ($C_{lim}$ [rpm]) obtained with EMCF and MCF at different power outputs for the group of six cyclists considered for simulations.

Power	A			B			C
$\left[\mathrm{W}\right]$	EMCF	MCF	$\Delta \%$	EMCF	MCF	$\Delta \%$	EMCF	MCF	$\Delta \%$
100	66	59	11	66	60	9	71	68	4
200	83	85	2	84	86	2	90	95	5
300	95	101	6	96	102	6	103	109	6
400	105	110	5	106	111	5	113	119	5
Power	D			E			F
$\left[\mathrm{W}\right]$	EMCF	MCF	$\Delta \%$	EMCF	MCF	$\Delta \%$	EMCF	MCF	$\Delta \%$
100	71	68	4	73	70	4	78	77	1
200	90	95	5	92	97	5	98	102	4
300	103	108	5	105	110	5	112	117	4
400	113	119	5	116	122	5	124	129	4

. Results are comparable in all cases; the average error between the two methods is $5\%$, exceeding this value in few cases related to low power outputs (100 W).

Riders in s Table 3 and Table 4 are listed with a descending order of the index I, defined as $I=mh$, that it was found to correspond to an ascending ordering of $C_{lim}$ values. The correlation between $C_{lim}$ (hereafter always determined minimizing the EMCF) and the anthopometric index I becomes even more evident in Figure 7a: data obtained varying the index I while keeping fixed a specified power P substantially align on a straight line. Therefore, we can expect that a polynomial regression of $C_{lim}=C_{lim}\left(I,P\right)$ is possible. A satisfying approximation has been found using a polynomial form of the 1st order with respect to I and of the 2nd order with respect to P:

$$C_{lim}=a+bI+cP+dIP+e{P}^2$$

(19)

Values of coefficients $a,b,c,d,e$ that give the best fit (least-square fitting) are collected in

Table 5. Best fit coefficients for Equation (19).

$\mathit{I}=\mathit{m}\mathit{h}{\mathit{C}}_{\mathit{lim}}=\mathit{a}+\mathit{b}\mathit{I}+\mathit{c}\mathit{P}+\mathit{d}\mathit{IP}+\mathit{e}{\mathit{P}}^2$
$a\left[\mathrm{rpm}\right]$	$b\left[\mathrm{rpm}{\left(\mathrm{kg}\mathrm{m}\right)}^{-1}\right]$	$c\left[\mathrm{rpm}{\mathrm{W}}^{-1}\right]$	$d\left[\mathrm{rpm}{\left(\mathrm{kg}\mathrm{m}\mathrm{W}\right)}^{-1}\right]$	$e\left[\mathrm{rpm}{\mathrm{W}}^{-2}\right]$
$64.97$	$-1.26\times {10}^{-1}$	$2.81\times {10}^{-1}$	$-3.01\times {10}^{-4}$	$-2.04\times {10}^{-4}$

, while a further graphical representation of Equation (19) is given in Figure 7b: the diagram provides the optimal cadence versus the power output P for a discrete series of indexes I. This result is of a certain interest since it becomes immediate for a cyclist to obtain an approximate estimate of the upper limit of the most convenient range of cadence in terms of muscular effort at a given power output.

As discussed in Section 2.3, a series of tests have been performed on four competitive cyclist ( Table 2). Experimental data are collected in Figure 8a. All subjects confirm the tendency of an increase in cadence due to an increase in power. A global view of the data is given in Figure 8b, where trends and variation’s ranges of experimental data are shown; the average of the experimental data trend goes approximately from 70 rpm at 100 W to 90 rpm at 450 W, with a decreasing dispersion moving toward high power outputs. On the same figure it is plotted the range of cadence estimated by the EMCF minimization method applied to the tested subjects; values are higher than experimental data for all power outputs. Furthermore, experimental data obtained by [6] are reported; such data represent cadences that minimize the oxygen uptake, i.e., the energy expenditure, calculated as the average of the three subjects tested by Seabury.

4. Discussion

The cost function proposed in this work resulted to be similar to those based on the absolute average joint moments, as presented in [11]. In the same work it is shown how the joint moments can be divided into two parts, the first one called quasistatic moment, that produces positive work in order to counteract the resistant forces, the second one called kinematic moment, that is due to inertial terms and generates a null work in a cycle. The quasistatic moment decreases at high cadences, while the kinematic moment does the opposite. As a result, being the total moment the sum of the two components, an optimum can be found in the minimization of the MCF cost function.

The EMCF cost function is based on the peak of an equivalent moment obtained from the muscular power curve; such peak increases at high cadences due to a larger influence of the kinematic moments related to the inertial terms, whereas the peak increases at low cadences due to larger quasistatic moment components, in agreement to the analysis of Redfield and Hull [11].

The approach followed in [13] is similar: it is experimentally evaluated the absolute average joint moment (comparable to the MCF) during a cycle; different groups of participants pedalling at increasing imposed frequencies and powers are analysed. Basically, it emerges that the minimum of the average moment occurs at cadences that are comparable to those obtained with the minimization of EMCF. Furthermore, the values of the optimal cadences increase with the power, as evidenced in the present study. The same paper shows how the pedalling rate freely chosen by the participants is in general similar but different from the cost function minimum. Moreover, cadences preferred by participants are nearly constant varying the power, exhibiting also a significantly large variance. This aspect confirm the considerations made by [21,22], i.e., that the preferred cadence is determined by a very complex combination of factors. Among them, however, the minimization of the muscular effort can be considered one of the most influencing. This minimization, by approximating the muscular effort through a kinematic approach, can can be used to estimate the upper limit of the optimal range of cadence for a cyclist, whereas the lower limit can be found considering the minimization of the energy consumption.

With the increase of the pedalling frequency the negative muscular work increases [14]. On the other hand as the output power increases the most convenient cadence increases; consequently, considering the combined effect of these two behaviours, it is expected that the difference between the value of $C_{lim}$ and the cadence chosen by cyclists increases with power.

Experimental data obtained in this work, notwithstanding a certain dispersion and variability, give evidence to previous considerations. The analysis of data shows that the dispersion is mainly attributable to subjects FF and FC. A reason can be found in a change of gear ratio between low and high power exercises, resulting in a discontinuity that gives an “S” shape to the plot. Subjects CS and GM do not show such trend: in these cases data fit with high accuracy with a linear law. Aggregate data are well represented by the linear fit of Figure 8b; as supposed, cadences adopted by cyclists are placed in the central area, between cadences that minimize the muscular effort (EMCF minimization) and cadences that minimize the energy expenditure (data from Seabury [6]).

5. Conclusions

Far from the claim of finding the cadence corresponding to the one freely chosen by a cyclist, the ambition of the present study was definitely to create a model that can be easily identified and verified in laboratory and that can offer practical indications also in field activities. Through the model it is possible to obtain an upper limitation of the range of cadences which are most convenient from the point of view of muscular effort. The optimum pedalling rate for a cyclist in a certain condition can be influenced by other factors (e.g., the metabolic cost or the maximum speed), the muscular work criterion returns a useful indication that the rider can consider at any rate to monitor his exercise.

The advantages of the approach proposed in this work is due to a simple mathematical formulation that requires few experimental data as input. The validity of the method is proved referring to data and methods available from other studies. A series of experimental tests confirmed that the EMCF method can be used to identify the upper limit of the optimal cadence range, whereas the lower limit can be obtained by other methods based on the minimization of the energy consumption.

In order to give more strength to the evidences outlined in this study future works will concern the project of a dedicated test bench that will be used to give a deeper experimental validation of the EMCF by means of a wide campaign of tests, varying both the characteristics of the participants and the setup or the type of bicycle. Furthermore, on the basis of a validation procedure based on a significant number of experimental measurements, it could be possible to think of introducing a correction term within the proposed model, in order to obtain in a simple way an estimate of the optimal cadence from the point of view of muscular effort.