Expanded Fréchet Model: Mathematical Properties, Copula, Different Estimation Methods, Applications and Validation Testing
Abstract
1. Introduction
2. Copula
2.1. Via FGM Copula
2.2. Via Modified FGM Copula
- Type-I
- Type-II
- Type-III
- Type-IV
2.3. Via Clayton Copula
2.4. Via Renyi’s Entropy
3. Mathematical Properties
3.1. Useful Representations
3.2. Moments and Incomplete Moments
3.3. Moment Generating Function (MGF)
3.4. Residual Life and Reversed Residual Life Functions
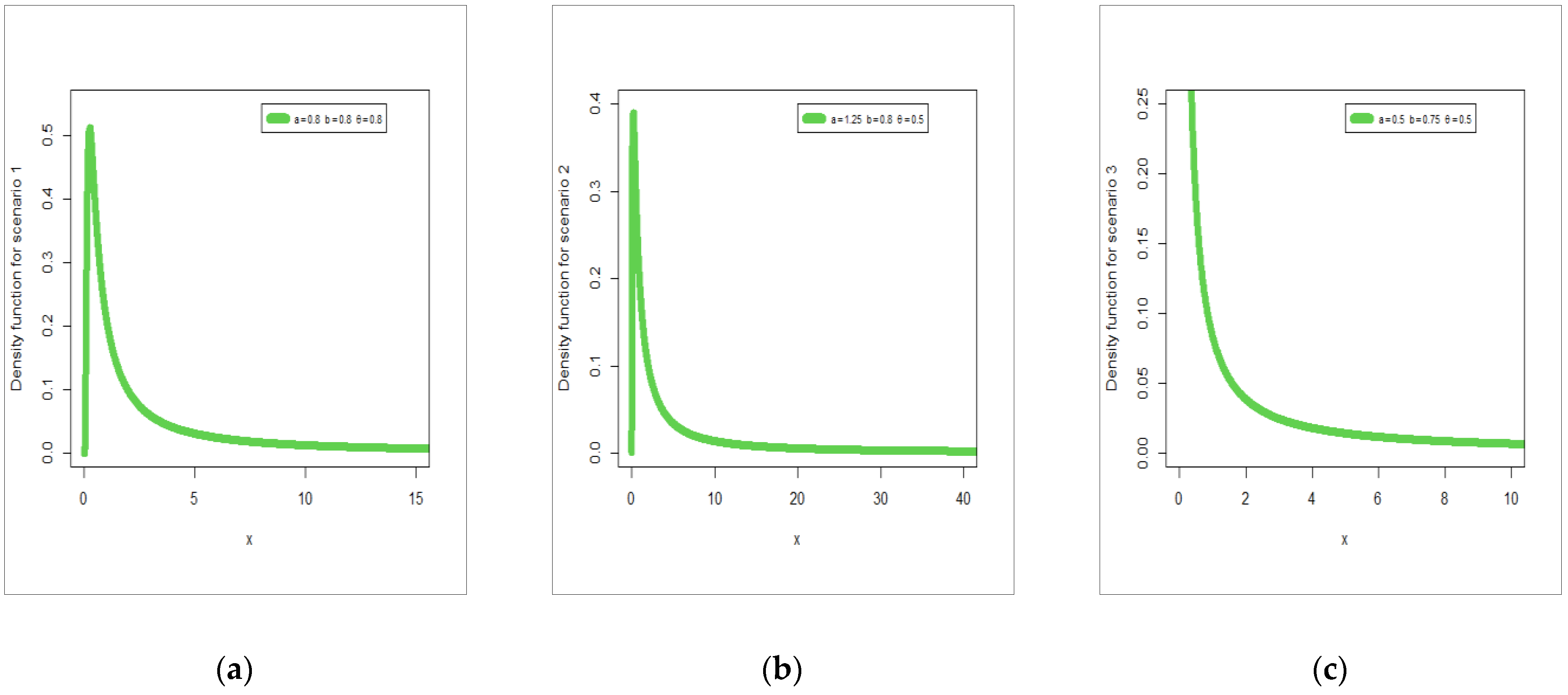
3.5. Numerical Calculations and Relevant Analysis
4. Classical Estimation under Uncensored Scheme
4.1. The MLE Method
4.2. The CVME Method
4.3. OLS Method
4.4. WLSE Method
4.5. The ADE Method
4.6. The Method
4.7. The Method
5. Simulation Studies for Comparing Estimation Methods under Uncensored Scheme
- Bias
- Root mean-standard error
- The mean of the absolute difference between the theoretical and the estimates ; and
- The maximum absolute difference between the true parameters and estimates .
- The BIAS (BIAS(a), BIAS(b) and BIAS(θ)) tends to when n increases and tends to which means that all estimators are non-biased.
- The RMSE (RMSE(a), RMSE (b) and RMSE (θ)) tends to when n increases, and tends to , which means incidence of consistency property.
- For “a = b = θ = 0.8” (see Table 3), the MLE has the lowest RMSE as illustrated below:
- RMSE (a)= (0.100754, 0.06959, 0.039482, and 0.03039).
- RMSE (b)= (0.117999, 0.082085, 0.046039, and 0.03483).
- RMSE (θ)= (0.09090, 0.060655, 0.03379, and 0.02604).
- For “a = 1.25, b = 0.8 and θ = 0.5” (Table 4), the MLE has the lowest RMSE as illustrated below:
- RMSE(a)= (0.158557, 0.108888, 0.060440, and 0.045951).
- RMSE(b)= (0.118178, 0.084967, 0.044982, and 0.035669).
- RMSE(θ)= (0.060194, 0.041468, 0.022886, and 0.017223).
- For “a = 0.5, b = 0.75 and θ = 1.5” (Table 5), the MLE has the lowest RMSE as illustrated below:
- RMSE(a)= (0.062856, 0.04356, 0.043363, and 0.019156).
- RMSE(b)= (0.11083, 0.074849, 0.058097, and 0.033038).
- RMSE(θ)= (0.146539, 0.102224, 0.001031, and 0.044046).
6. Modeling Uncensored Real Data for Comparing the Competitive Models
6.1. Stress Data
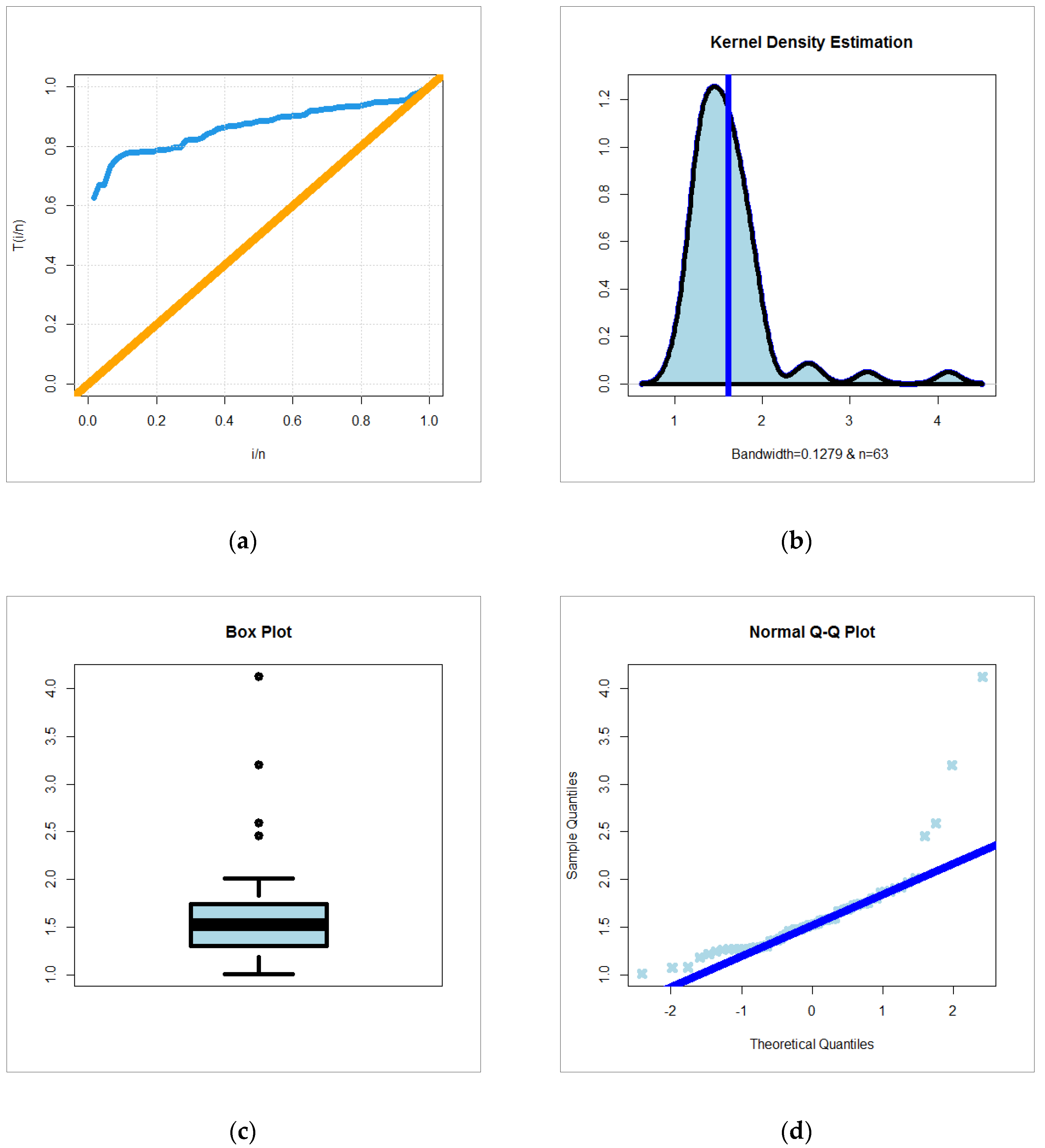
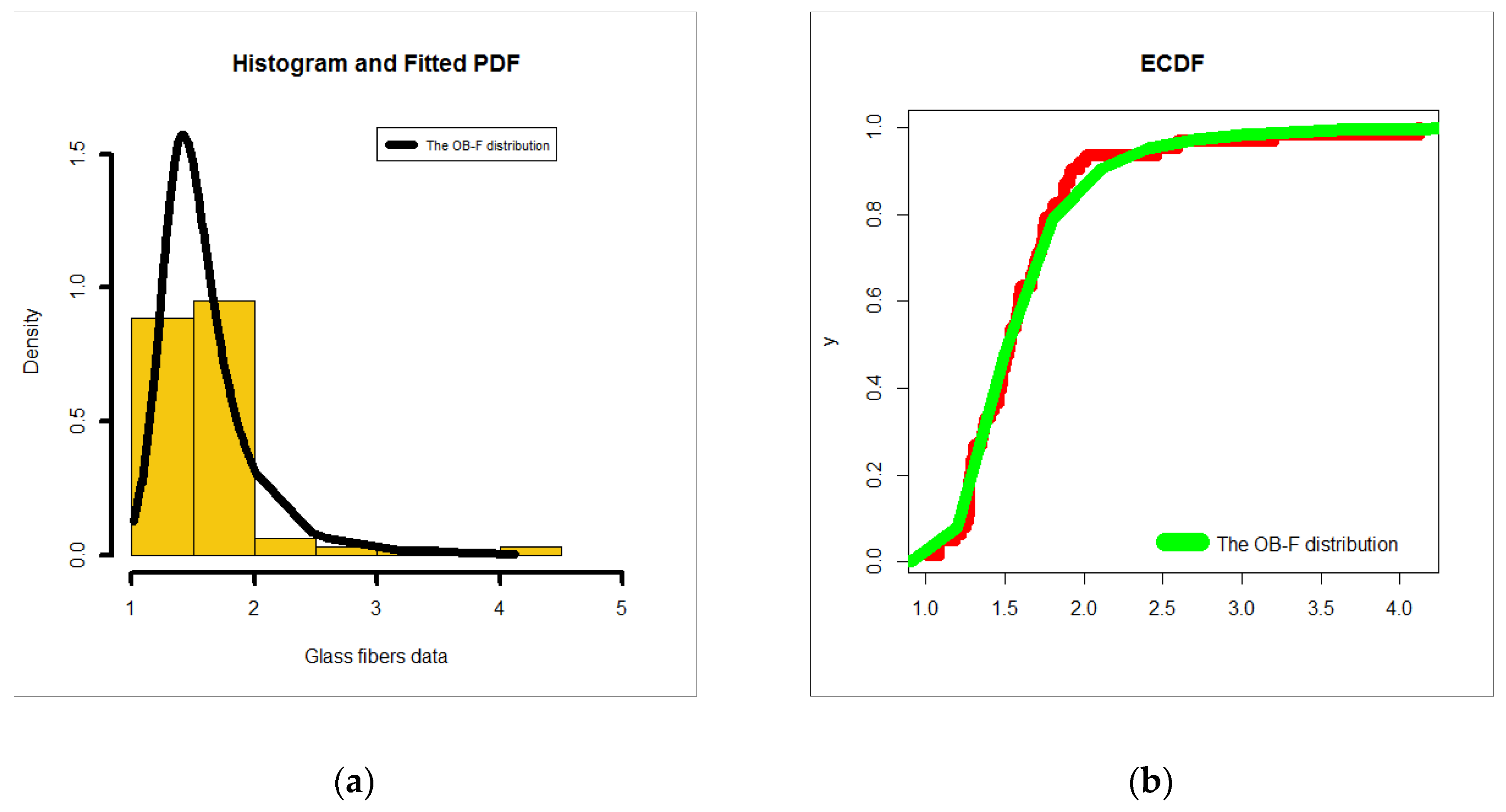
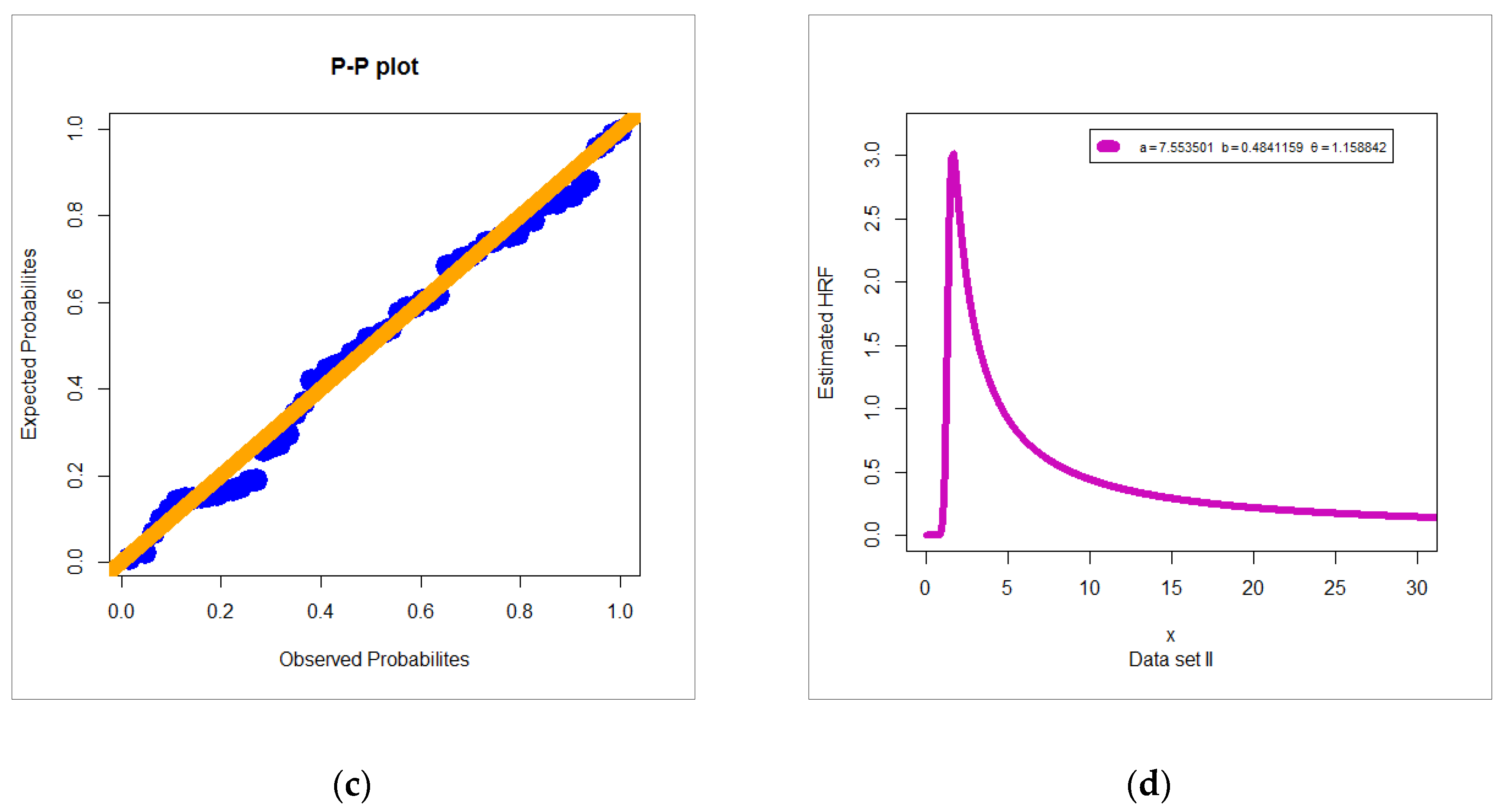
6.2. Glass Fibers Data
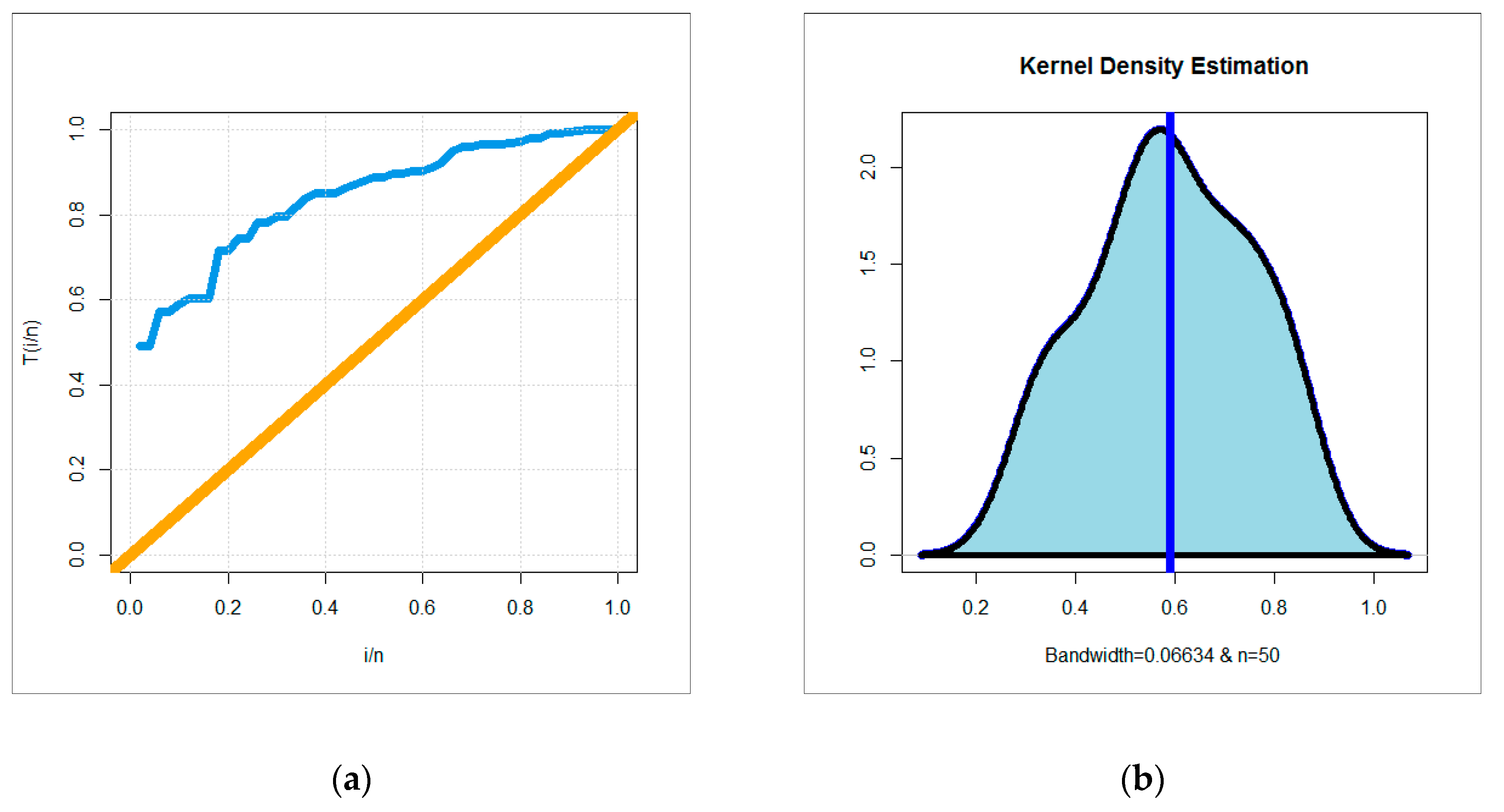
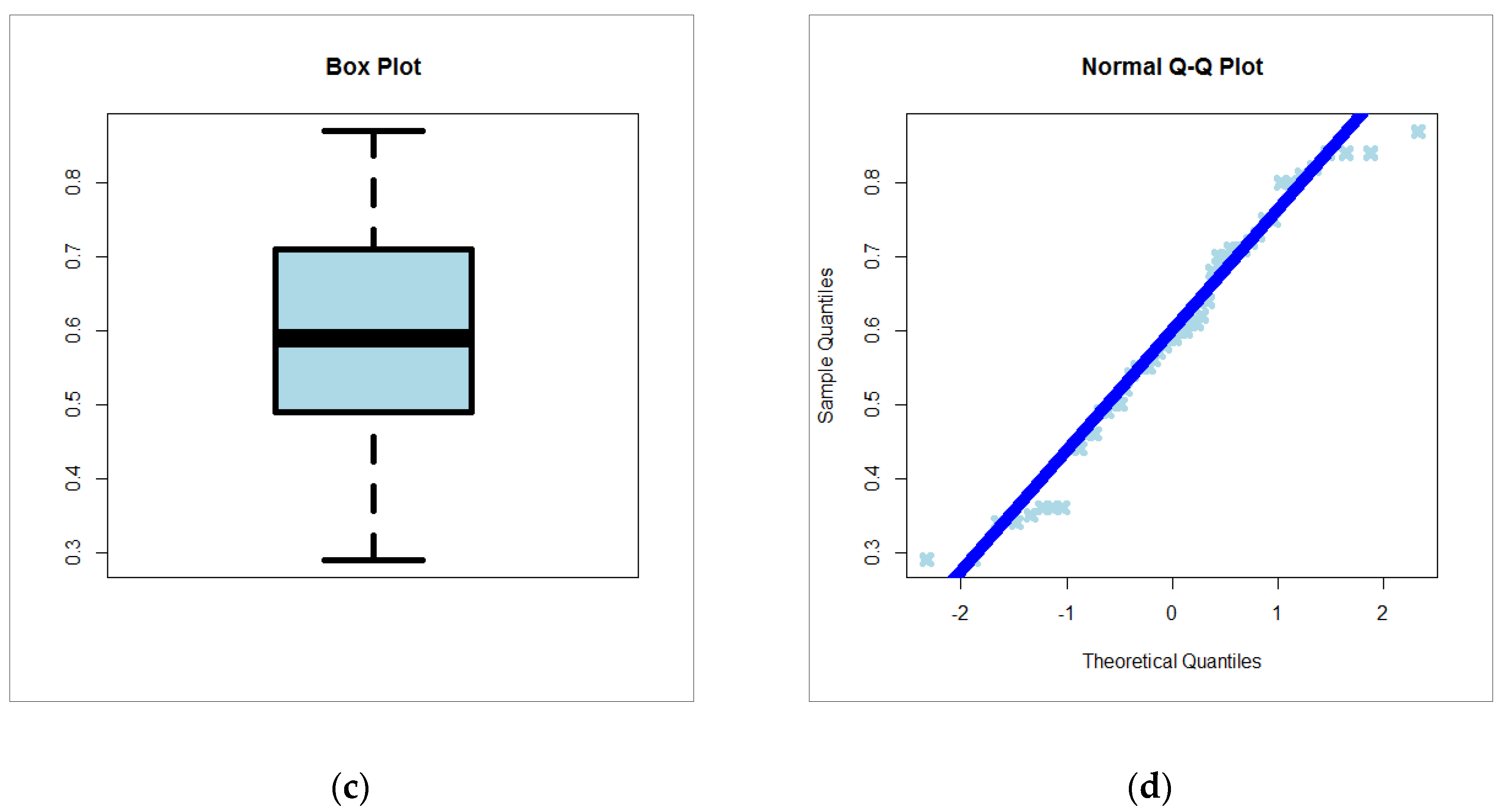
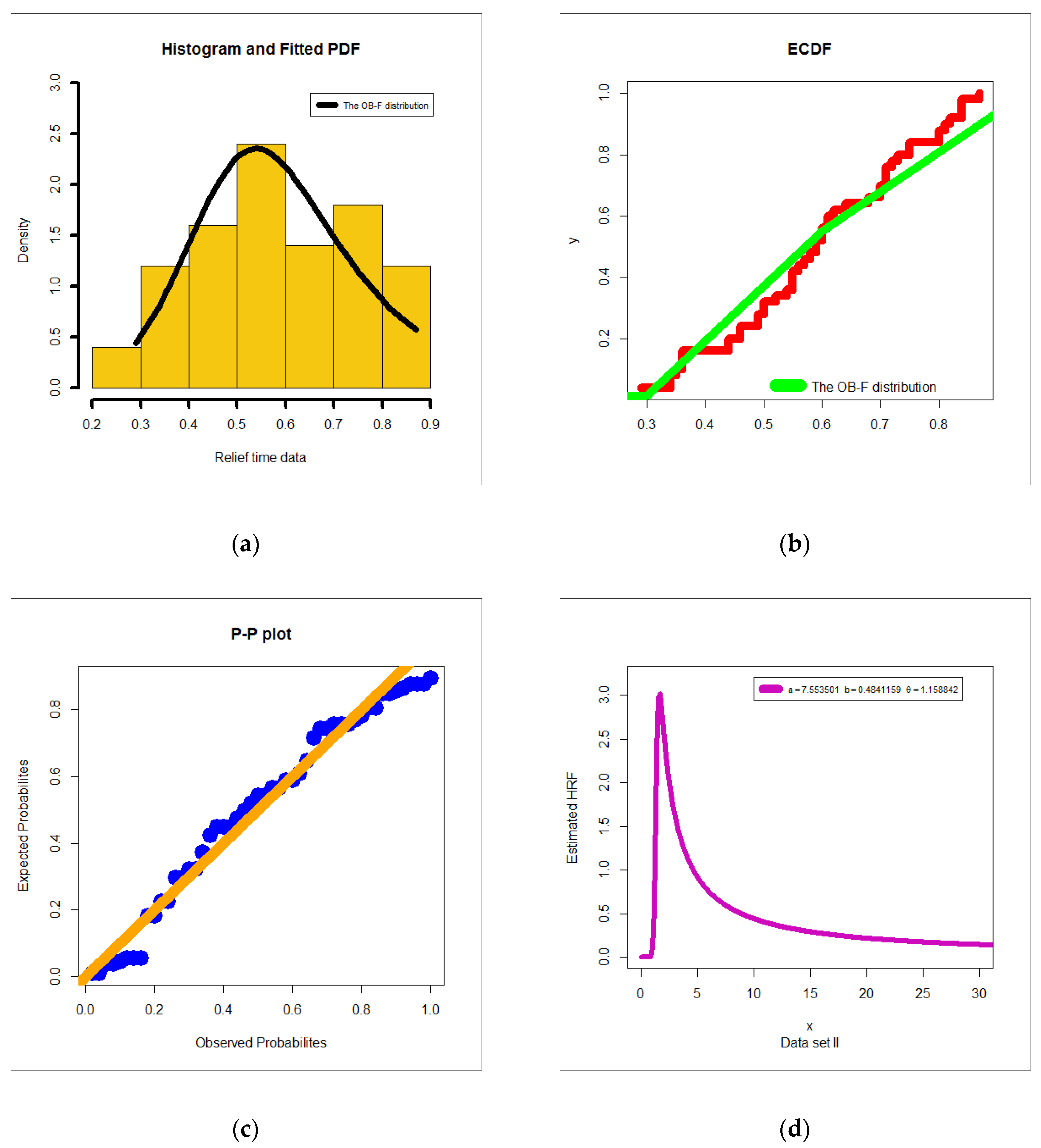
6.3. Relief Time Data
7. Validation under Censored Scheme
7.1. Maximum Likelihood Estimation for Censored Data
7.2. Test Statistic for Right Censored Data
7.3. Criteria Test for OB-F
7.4. Simulations
7.5. Test Statistic
8. Application to Leukemia Free-Survival Times
9. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fréchet, M. Sur la loi de probabilité de lécart maximum. Ann. Soc. Pol. Math 1927, 6, 93–116. [Google Scholar]
- Von Mises, R. La distribution de la plus grande de nvaleurs. Rev. Math. Union Interbalcanique 1936, 1, 141–160. [Google Scholar]
- Von Mises, R. Selected papers of Richard von Mises. Am. Math. Soc. 1964, 1. [Google Scholar]
- Kotz, S.; Johnson, N.L. Breakthroughs in Statistics: Foundations and Basic Theory; Springer: Berlin, Germany, 1992; Volume 1. [Google Scholar]
- Nadarajah, S.; Kotz, S. The exponentiated Fréchet distribution. Interstat Electron. J. 2003, 14, 1–7. [Google Scholar]
- Eliwa, M.S.; El-Morshedy, M.; Afify, A.Z. The odd Chen generator of distributions: Properties and estimation methods with applications in medicine and engineering. J. Natl. Sci. Found. Sri Lanka 2020, 48, 113–130. [Google Scholar] [CrossRef]
- Yousof, H.M.; Jahanshahi, S.M.A.; Sharma, V.K. The Burr X Fréchet Model for Extreme Values: Mathematical Properties, Classical Inference and Bayesian Analysis. Pak. J. Stat. Oper. Res. 2019, 15, 797. [Google Scholar] [CrossRef]
- Eliwa, M.S.; El-Morshedy, M.; Sajid, A. Exponentiated odd Chen-G family of distributions: Statistical properties, Bayesian and non-Bayesian estimation with applications. J. Appl. Stat. 2020, 1–27. [Google Scholar] [CrossRef]
- Krishna, E.; Jose, K.K.; Alice, T.; Risti, M.M. The Marshall-Olkin Fréchet distribution. Commun. Stat. Theory Methods 2013, 42, 4091–4107. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.S. The odd flexible Weibull-H family of distributions: Properties and estimation with applications to complete and upper record data. Filomat 2019, 33, 2635–2652. [Google Scholar] [CrossRef]
- Al-Babtain, A.A.; Elbatal, I.; Yousof, H.M. A new three parameter Fréchet model with mathematical properties and applications. J. Taibah Univ. Sci. 2020, 14, 265–278. [Google Scholar] [CrossRef]
- Al-babtain, A.A.; Elbatal, I.; Yousof, H.M. A New Flexible Three-Parameter Model: Properties, Clayton Copula, and Modeling Real Data. Symmetry 2020, 12, 440. [Google Scholar] [CrossRef]
- Yousof, H.M.; Altun, E.; Hamedani, G.G. A new extension of Frechet distribution with regression models, residual analysis and characterizations. J. Data Sci. 2018, 16, 743–770. [Google Scholar]
- Elsayed, H.A.H.; Yousof, H.M. The generalized odd generalized exponential Fréchet model: Univariate, bivariate and multivariate extensions with properties and applications to the univariate version. Pak. J. Stat. Oper. Res. 2020, 16, 529–544. [Google Scholar] [CrossRef]
- Korkmaz, M.C.; Yousof, H.M.; Ali, M.M. Some theoretical and computational aspects of the odd Lindley Fréchet distribution. İstatistikçiler Dergisi: İstatistik ve Aktüerya 2017, 10, 129–140. [Google Scholar]
- Yousof, H.M.; Butt, N.S.; Alotaibi, R.M.; Rezk, H.; Alomani, G.A.; Ibrahim, M. A new compound Fréchet distribution for modeling breaking stress and strengths data. Pak. J. Stat. Oper. Res. 2019, 1017–1035. [Google Scholar] [CrossRef]
- Alizadeh, M.; Cordeiro, G.M.; Nascimento, A.D.; Lima, M.D.C.S.; Ortega, E.M. Odd-Burr generalized family of distributions with some applications. J. Stat. Comput. Simul. 2017, 87, 367–389. [Google Scholar] [CrossRef]
- Gleaton, J.U.; Lynch, J.D. Properties of generalized loglogistic families of lifetime distributions. J. Probab. Stat. Sci. 2006, 4, 51–64. [Google Scholar]
- Gupta, R.C.; Gupta, R.D. Proportional reversed hazard rate model and its applications. J. Stat. Plan. Inference 2007, 137, 3525–3536. [Google Scholar] [CrossRef]
- Farlie, D.J.G. The performance of some correlation coefficients for a general bivariate distribution. Biometrika 1960, 47, 307–323. [Google Scholar] [CrossRef]
- Gumbel, E.J. Bivariate logistic distributions. J. Am. Stat. Assoc. 1961, 56, 335–349. [Google Scholar] [CrossRef]
- Gumbel, E.J. Bivariate exponential distributions. J. Am. Stat. Assoc. 1960, 55, 698–707. [Google Scholar] [CrossRef]
- Morgenstern, D. Einfache beispiele zweidimensionaler verteilungen. Mitteilingsblatt Mathematische Statistik 1956, 8, 234–235. [Google Scholar]
- Rodriguez-Lallena, J.A.; Ubeda-Flores, M. A new class of bivariate copulas. Stat. Probab. Lett. 2004, 66, 315–325. [Google Scholar] [CrossRef]
- Pougaza, D.B.; Djafari, M.A. Maximum entropies copulas. In Proceedings of the 30th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Chamonix, France, 4–9 July 2010. [Google Scholar]
- Mead, M.E.; Abd-Eltawab, A.R. A note on Kumaraswamy Fréchet distribution. Australia 2014, 8, 294–300. [Google Scholar]
- Mahmoud, M.R.; Mandouh, R.M. On the transmuted Fréchet distribution. J. Appl. Sci. Res. 2013, 9, 5553–5561. [Google Scholar]
- Karamikabir, H.; Afshari, M.; Yousof, H.M.; Alizadeh, M.; Hamedani, G.G. The Weibull Topp-Leone Generated Family of Distributions: Statistical Properties and Applications. J. Iran. Stat. Soc. 2020, 19, 121–161. [Google Scholar] [CrossRef]
- Barreto-Souza, W.M.; Cordeiro, G.M.; Simas, A.B. Some results for beta Fréchet distribution. Commun. Stat. Theory Methods 2011, 40, 798–811. [Google Scholar] [CrossRef]
- Shahbaz, M.Q.; Shahbaz, S.; Butt, N.S. The Kumaraswamy-Inverse Weibull Distribution. Pak. J. Stat. Oper. Res. 2012, 8, 479–489. [Google Scholar] [CrossRef]
- Nichols, M.D.; Padgett, W.J. A Bootstrap control chart for Weibull percentiles. Qual. Reliab. Eng. Int. 2006, 22, 141–151. [Google Scholar] [CrossRef]
- Yousof, H.M.; Rasekhi, M.; Altun, E.; Alizadeh, M. The extended odd Frechet family of distributions: Properties, applications and regression modeling. Int. J. Appl. Math. Stat. 2018, 30, 1–30. [Google Scholar]
- Chakraborty, S.; Handique, L.; Altun, E.; Yousof, H.M. A New Statistical Model for Extreme Values: Properties and Applications. Int. J. Open Probl. Compt. Math 2019, 12, 67–84. [Google Scholar]
- Haq, M.A.; Yousof, H.M.; Hashmi, S. A New Five-Parameter Fréchet Model for Extreme Values. Pak. J. Stat. Oper. Res. 2017, 617–632. [Google Scholar] [CrossRef]
- Yousof, H.M.; Afify, A.Z.; Abd El Hadi, N.E.; Hamedani, G.G.; Butt, N.S. On six-parameter Fréchet distribution: Properties and applications. Pak. J. Stat. Oper. Res. 2016, 12, 281–299. [Google Scholar] [CrossRef]
- Aarset, M.V. How to identify a bathtub hazard rate. IEEE Trans. Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]
- Smith, R.L.; Naylor, J.C. A comparison of maximum likelihood and bayesian estimators for the three-parameter Weibull distribution. Appl. Stat. 1987, 36, 358–369. [Google Scholar] [CrossRef]
- Wingo, D.R. Maximum likelihood methods for fitting the Burr type XII distribution to life test data. Biom. J. 1983, 25, 77–84. [Google Scholar] [CrossRef]
- Bagdonavičius, V.; Nikulin, M. Chi-squared goodness-of-fit test for right censored data. Int. J. Appl. Math. Stat. 2011, 24, 30–50. [Google Scholar]
- Goual, H.; Yousof, H.M. Validation of Burr XII inverse Rayleigh model via a modified chi-squared goodness-of-fit test. J. Appl. Stat. 2020, 47, 393–423. [Google Scholar] [CrossRef]
- Goual, H.; Yousof, H.M.; Ali, M.M. Lomax inverse Weibull model: Properties, applications, and a modified Chi-squared goodness-of-fit test for validation. J. Nonlinear Sci. Appl. 2020, 13, 330–353. [Google Scholar] [CrossRef]
- Goual, H.; Yousof, H.M.; Ali, M.M. Validation of the odd Lindley exponentiated exponential by a modified goodness of fit test with applications to censored and complete data. Pak. J. Stat. Oper. Res. 2019, 15, 745–771. [Google Scholar] [CrossRef]
- Mansour, M.M.; Ibrahim, M.; Aidi, K.; Shafique Butt, N.; Ali, M.M.; Yousof, H.M.; Hamed, M.S. A New Log-Logistic Lifetime Model with Mathematical Properties, Copula, Modified Goodness-of-Fit test for Validation and Real Data Modeling. Mathematics 2020, 8, 1508. [Google Scholar] [CrossRef]
- Mansour, M.; Korkmaz, M.C.; Ali, M.M.; Yousof, H.M.; Ansari, S.I.; Ibrahim, M. A Generalization of the exponentiated Weibull Model with Properties, Copula and Application. Eurasian Bull. Math. 2020, 3, 84–102. [Google Scholar]
- Mansour, M.; Rasekhi, M.; Ibrahim, M.; Aidi, K.; Yousof, H.M.; Elrazik, E.A. A New Parametric Life Distribution with Modified Bagdonavičius-Nikulin Goodness-of-Fit Test for Censored Validation, Properties, Applications, and Different Estimation Methods. Entropy 2020, 22, 592. [Google Scholar] [CrossRef]
- Ravi, V.; Gilbert, P.D. BB: An R package for solving a large system of nonlinear equations and for optimizing a high-dimensional nonlinear objective function. J. Stat. Softw. 2009, 32, 1–26. [Google Scholar]
- Ibrahim, M.; Yadav, A.S.; Yousof, H.M.; Goual, H.; Hamedani, G.G. A new extension of Lindley distribution: Modified validation test, characterizations and different methods of estimation. Commun. Stat. Appl. Methods 2019, 26, 473–495. [Google Scholar] [CrossRef]
- Yadav, A.S.; Goual, H.; Alotaibi, R.M.; Ali, M.M.; Yousof, H.M. Validation of the Topp-Leone-Lomax model via a modified Nikulin-Rao-Robson goodness-of-fit test with different methods of estimation. Symmetry 2020, 12, 57. [Google Scholar] [CrossRef]
- Abouelmagd, T.H.M.; Hamed, M.S.; Handique, L.; Goual, H.; Ali, M.M.; Yousof, H.M.; Korkma, M.C. A new class of distributions based on the zero truncated Poisson distribution with properties and applications. J. Nonlinear Sci. Appl. 2019, 12, 152–164. [Google Scholar] [CrossRef]
- Abouelmagd, T.H.M.; Hamed, M.S.; Hamedani, G.G.; Ali, M.M.; Goual, H.; Korkmaz, M.C.; Yousof, H.M. The zero truncated Poisson Burr X family of distributions with properties, characterizations, applications, and validation test. J. Nonlinear Sci. Appl. 2019, 12, 314–336. [Google Scholar] [CrossRef]


| E(Z) | Var(Z) | Skew(Z) | Kur(Z) | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 0.25 | 24575.64 | 10930984115 | 5.873463 | 40.9488 | 24575.64 | 11534945965 |
| 5 | 336.9234 | 86392744 | 61.89353 | 4675.322 | 336.9234 | 86506262 | ||
| 10 | 11.25069 | 60850.12 | 1681.481 | 4309801 | 11.25069 | 60976.70 | ||
| 50 | 1.9 | 2.1 | 1.92903 | 2.09453 | ||||
| 2 | 0.05 | 1.25 | 25403.99 | 11209836646 | 5.78075 | 39.75302 | 25403.99 | 11855199133 |
| 0.15 | 3374.045 | 1286326804.0 | 17.1300 | 345.0779 | 3374.045 | 1297710986 | ||
| 0.25 | 296.3798 | 80743061 | 64.40085 | 5042.712 | 296.3798 | 80830902 | ||
| 0.35 | 39.3637 | 4372214.0 | 253.2212 | 82348.29 | 39.3637 | 4373764 | ||
| 5 | 0.5 | 0.01 | 5266.967 | 2675972773 | 12.82974 | 186.0085 | 5266.967 | 2703713717 |
| 0.25 | 336.9234 | 86392744.0 | 61.89353 | 4675.322 | 336.9234 | 86506262 | ||
| 0.35 | 37.53839 | 4461785 | 249.7617 | 80324.18 | 37.53839 | 4463194 | ||
| 0.45 | 9.305143 | 230220.7 | 970.2972 | 1318254 | 9.305143 | 230307.3 | ||
| 0.5 | 6.235529 | 52934.94 | 1859.104 | 5140488 | 6.235529 | 52973.83 | ||
| 0.55 | 4.731619 | 12405.41 | 3448.200 | 19161060 | 4.731619 | 12427.8 | ||
| 0.5 | 0.5 | 0.5 | 23851.02 | 10675812761 | 5.960493 | 42.09073 | 23851.02 | 11244684106 |
| 1 | 1 | 1 | 13.2383 | 999816.3000 | 500.0971 | 333428.8 | 13.2383 | 999991.6000 |
| 0.15 | 0.15 | 1 | 14391.58 | 6992893577 | 7.685724 | 68.12830 | 14391.6 | 7200011193 |
| 0.25 | 0.05 | 0.25 | 2073.379 | 1038694167 | 20.62117 | 479.5531 | 2073.379 | 1042993067 |
| 0.01 | 0.01 | 0.01 | 0.7453203 | 371968.3000 | 1092.416 | 1342959 | 0.745320 | 371968.9000 |
| E(Z) | Var(Y) | Skew(Z) | Kur(Z) | |||
|---|---|---|---|---|---|---|
| 4.001 | 1.22533 | 0.270577 | 5.60111 | 54524.95 | 1.225334 | 1.772017 |
| 4.010 | 1.22459 | 0.268511 | 5.56508 | 5436.60 | 1.224588 | 1.768125 |
| 4.100 | 1.21739 | 0.249111 | 5.23632 | 529.592 | 1.217387 | 1.731142 |
| 4.250 | 1.20633 | 0.221216 | 4.79036 | 204.831 | 1.206332 | 1.676453 |
| 4.500 | 1.19015 | 0.184256 | 4.23884 | 98.8015 | 1.190151 | 1.600716 |
| 5 | 1.16423 | 0.133761 | 3.53507 | 48.0915 | 1.16423 | 1.489192 |
| 7 | 1.10577 | 0.053272 | 2.42510 | 17.5340 | 1.105767 | 1.275993 |
| 10 | 1.06863 | 0.022262 | 1.91034 | 10.9786 | 1.068629 | 1.164230 |
| 12 | 1.05555 | 0.014609 | 1.74981 | 9.46172 | 3.368633 | 1.128787 |
| 15 | 1.04317 | 0.008858 | 1.60525 | 8.28249 | 1.213482 | 3.957999 |
| 20 | 1.03145 | 0.0047328 | 1.47388 | 7.33349 | 4.382908 | 1.429566 |
| 25 | 1.02473 | 0.0029403 | 1.40049 | 6.85240 | 1.4841 | 4.840664 |
| 30 | 1.02037 | 0.0020027 | 1.35357 | 6.56231 | 4.824307 | 1.573536 |
| 35 | 1.01732 | 0.0014515 | 1.32097 | 6.36853 | 1.524658 | 4.972951 |
| 45 | 1.01333 | 0.0008625 | 1.27863 | 6.12607 | 1.438461 | 4.691805 |
| 55 | 1.010827 | 0.000571 | 1.252304 | 5.98124 | 1.290118 | 4.207958 |
| 65 | 1.009118 | 0.000406 | 1.234393 | 5.88325 | 1.118823 | 3.649247 |
| 75 | 1.007874 | 0.000303 | 1.221374 | 5.81438 | 9.473066 | 3.089815 |
| 85 | 1.006929 | 0.0002349 | 1.211503 | 5.76240 | 7.878245 | 2.569635 |
| 95 | 1.006187 | 0.0001874 | 1.203757 | 5.72214 | 6.461233 | 2.10745 |
| 100 | 1.00587 | 0.000169 | 1.20048 | 5.70518 | 1.842394 | 6.009306 |
| 102 | 1.00576 | 0.0001623 | 1.19926 | 5.69890 | 1.76644 | 5.761569 |
| n | BIAS(a) | BIAS(b) | BIAS(θ) | RMSE(a) | RMSE(b) | RMSE(θ) | |||
|---|---|---|---|---|---|---|---|---|---|
| MLE | 50 | 0.00807 | 0.00975 | 0.011514 | 0.100754 | 0.117999 | 0.09090 | 0.005825 | 0.01072 |
| CVM | −0.01243 | 0.00856 | −0.00391 | 0.12232 | 0.13539 | 0.13791 | 0.00262 | 0.0053 | |
| OLS | −0.02486 | −0.01852 | −0.02408 | 0.12368 | 0.13114 | 0.13735 | 0.01337 | 0.02473 | |
| WLS | 0.06774 | −0.02485 | 0.06358 | 0.14211 | 0.11892 | 0.12843 | 0.02101 | 0.03235 | |
| ADE | −0.02272 | 0.00426 | −0.02246 | 0.10632 | 0.12608 | 0.10436 | 0.00827 | 0.0147 | |
| RT | −0.00077 | 0.0006 | 0.00077 | 0.14007 | 0.12008 | 0.14141 | 0.00023 | 0.00177 | |
| LT | −0.01324 | 0.01587 | −0.02012 | 0.12197 | 0.15242 | 0.10291 | 0.00505 | 0.01126 | |
| MLE | 100 | 0.00839 | 0.007981 | 0.008815 | 0.06959 | 0.08209 | 0.06066 | 0.00492 | 0.00914 |
| CVM | −0.0012 | 0.0059 | 0.00315 | 0.0854 | 0.09367 | 0.09853 | 0.00213 | 0.00339 | |
| OLS | −0.00761 | −0.00762 | −0.00717 | 0.08559 | 0.09196 | 0.0978 | 0.00445 | 0.00827 | |
| WLS | 0.05163 | −0.00878 | 0.04946 | 0.09626 | 0.08525 | 0.08648 | 0.01766 | 0.02943 | |
| ADE | −0.00517 | 0.0056 | −0.0059 | 0.07434 | 0.08772 | 0.07298 | 0.00168 | 0.00446 | |
| RT | 0.00405 | 0.00318 | 0.00468 | 0.09677 | 0.08363 | 0.09794 | 0.00232 | 0.00547 | |
| LT | −0.00214 | 0.00773 | −0.00676 | 0.08418 | 0.1034 | 0.06898 | 0.0016 | 0.00434 | |
| MLE | 300 | 0.001745 | 0.002581 | 0.00208 | 0.039482 | 0.046039 | 0.03379 | 0.00130 | 0.00240 |
| CVM | 0.00091 | 0.00315 | 0.00242 | 0.04947 | 0.05326 | 0.05582 | 0.0014 | 0.00251 | |
| OLS | −0.00261 | −0.00131 | −0.00204 | 0.04906 | 0.05374 | 0.0552 | 0.00114 | 0.00211 | |
| WLS | 0.02453 | −0.00271 | 0.02406 | 0.05089 | 0.0477 | 0.04483 | 0.00886 | 0.01500 | |
| ADE | −0.00258 | −0.00145 | −0.00351 | 0.04331 | 0.04882 | 0.04256 | 0.00147 | 0.00362 | |
| RT | 0.00115 | 0.00159 | 0.0016 | 0.05452 | 0.04804 | 0.05515 | 0.00087 | 0.00261 | |
| LT | −0.00112 | 0.00422 | −0.00228 | 0.05039 | 0.0603 | 0.0396 | 0.00101 | 0.00251 | |
| MLE | 500 | 0.000087 | 0.00033 | 0.002176 | 0.03039 | 0.03483 | 0.02604 | 0.00088 | 0.00157 |
| CVM | −0.00162 | −0.00112 | −0.00159 | 0.03845 | 0.03965 | 0.04254 | 0.00084 | 0.00156 | |
| OLS | −0.00191 | −0.0033 | −0.00261 | 0.03842 | 0.03999 | 0.04284 | 0.00162 | 0.00297 | |
| WLS | 0.01934 | −0.00232 | 0.01896 | 0.03948 | 0.03627 | 0.03472 | 0.00699 | 0.01178 | |
| ADE | −0.00153 | 0.00096 | −0.00156 | 0.03339 | 0.0379 | 0.03251 | 0.00049 | 0.00176 | |
| RT | −0.00003 | −0.00068 | −0.00017 | 0.04258 | 0.03645 | 0.04276 | 0.00023 | 0.00134 | |
| LT | 0.00097 | −0.00057 | −0.00055 | 0.03775 | 0.0438 | 0.03037 | 0.00018 | 0.0012 |
| n | BIAS(a) | BIAS(b) | BIAS(θ) | RMSE(a) | RMSE(b) | RMSE(θ) | |||
|---|---|---|---|---|---|---|---|---|---|
| MLE | 50 | 0.023764 | 0.015476 | 0.009473 | 0.158557 | 0.118178 | 0.060194 | 0.009302 | 0.017345 |
| CVM | 0.00057 | 0.01991 | 0.01226 | 0.19723 | 0.14069 | 0.09586 | 0.00954 | 0.01659 | |
| OLS | −0.02333 | −0.01548 | −0.00822 | 0.19277 | 0.13196 | 0.0894 | 0.00906 | 0.01685 | |
| WLS | 0.11877 | −0.02027 | 0.03617 | 0.22408 | 0.12112 | 0.07859 | 0.02202 | 0.03713 | |
| ADE | −0.02229 | 0.00738 | −0.00574 | 0.1661 | 0.1261 | 0.06905 | 0.00366 | 0.00672 | |
| RT | 0.01091 | 0.00561 | 0.00498 | 0.21508 | 0.11939 | 0.08265 | 0.00416 | 0.00863 | |
| LT | −0.00621 | 0.0156 | −0.01253 | 0.19069 | 0.15363 | 0.06628 | 0.00311 | 0.0072 | |
| MLE | 100 | 0.012492 | 0.007061 | 0.004961 | 0.108888 | 0.084967 | 0.041468 | 0.004651 | 0.008701 |
| CVM | 0.00045 | 0.00364 | 0.00351 | 0.13773 | 0.09388 | 0.06539 | 0.00221 | 0.00394 | |
| OLS | −0.01263 | −0.0079 | −0.00407 | 0.13407 | 0.09501 | 0.06444 | 0.00462 | 0.00863 | |
| WLS | 0.07746 | −0.01107 | 0.02659 | 0.14821 | 0.0864 | 0.05507 | 0.01589 | 0.02729 | |
| ADE | −0.01174 | 0.00377 | −0.00259 | 0.11517 | 0.09125 | 0.05095 | 0.00181 | 0.0037 | |
| RT | 0.0064 | 0.00315 | 0.00289 | 0.15524 | 0.08717 | 0.06034 | 0.0024 | 0.00523 | |
| LT | −0.00251 | 0.00733 | −0.00609 | 0.13087 | 0.10775 | 0.04765 | 0.00145 | 0.00367 | |
| MLE | 300 | 0.00250 | 0.004189 | 0.001343 | 0.060440 | 0.044982 | 0.022886 | 0.001799 | 0.003203 |
| CVM | −0.00046 | 0.0032 | 0.00139 | 0.04903 | 0.05418 | 0.05534 | 0.00113 | 0.00179 | |
| OLS | −0.00374 | −0.00047 | −0.00042 | 0.07542 | 0.05235 | 0.0353 | 0.00066 | 0.00124 | |
| WLS | 0.03905 | −0.00102 | 0.01497 | 0.08009 | 0.04668 | 0.02983 | 0.00937 | 0.01681 | |
| ADE | −0.00413 | 0.00350 | −0.00031 | 0.06396 | 0.04941 | 0.02798 | 0.00086 | 0.00206 | |
| RT | 0.00414 | 0.00281 | 0.00191 | 0.08320 | 0.04685 | 0.03209 | 0.00175 | 0.00386 | |
| LT | −0.0028 | 0.00251 | −0.00294 | 0.07627 | 0.0586 | 0.02573 | 0.00095 | 0.00214 | |
| MLE | 500 | 0.000621 | −0.000011 | 0.000328 | 0.045951 | 0.035669 | 0.017223 | 0.00018 | 0.00033 |
| CVM | −0.00061 | −0.00061 | −0.00055 | 0.03839 | 0.04001 | 0.04284 | 0.00035 | 0.00065 | |
| OLS | −0.00415 | −0.00237 | −0.00151 | 0.05778 | 0.05778 | 0.02771 | 0.00151 | 0.00284 | |
| WLS | 0.02756 | −0.00279 | 0.01058 | 0.05966 | 0.03746 | 0.02229 | 0.0063 | 0.01105 | |
| ADE | −0.00405 | −0.00012 | −0.00127 | 0.04947 | 0.03904 | 0.02188 | 0.00093 | 0.00225 | |
| RT | −0.0011 | −0.00045 | −0.00028 | 0.0653 | 0.03703 | 0.02523 | 0.00031 | 0.00118 | |
| LT | −0.00237 | 0.00264 | −0.00148 | 0.05933 | 0.04566 | 0.02094 | 0.00054 | 0.00172 |
| n | BIAS(a) | BIAS(b) | BIAS(θ) | RMSE(a) | RMSE(b) | RMSE(θ) | |||
|---|---|---|---|---|---|---|---|---|---|
| MLE | 50 | 0.004824 | 0.008576 | 0.017762 | 0.062856 | 0.11083 | 0.146539 | 0.005268 | 0.009642 |
| CVM | −0.00328 | 0.00745 | −0.00994 | 0.08249 | 0.13242 | 0.24642 | 0.00185 | 0.00391 | |
| OLS | −0.01345 | −0.01617 | −0.03945 | 0.0814 | 0.12269 | 0.24364 | 0.01201 | 0.02205 | |
| WLS | 0.03881 | −0.02391 | 0.11541 | 0.09030 | 0.11182 | 0.22718 | 0.01998 | 0.03209 | |
| ADE | −0.01273 | 0.0046 | −0.04379 | 0.06803 | 0.11777 | 0.17922 | 0.00808 | 0.01505 | |
| RT | 0.00023 | 0.00116 | 0.00112 | 0.08905 | 0.11295 | 0.26643 | 0.00049 | 0.00385 | |
| LT | −0.00843 | 0.01549 | −0.02432 | 0.07607 | 0.14224 | 0.17088 | 0.00431 | 0.01136 | |
| MLE | 100 | 0.00216 | 0.006975 | 0.010667 | 0.04356 | 0.074849 | 0.102224 | 0.003484 | 0.00628 |
| CVM | 0.00175 | 0.01084 | 0.00553 | 0.05642 | 0.08787 | 0.16508 | 0.00411 | 0.00699 | |
| OLS | −0.00700 | −0.00502 | −0.02016 | 0.05542 | 0.08567 | 0.16202 | 0.00539 | 0.00975 | |
| WLS | 0.02786 | −0.01039 | 0.07939 | 0.05873 | 0.07681 | 0.14387 | 0.01518 | 0.02409 | |
| ADE | −0.0048 | 0.00555 | −0.01785 | 0.0465 | 0.0809 | 0.11966 | 0.00278 | 0.00707 | |
| RT | 0.00164 | 0.00337 | 0.00474 | 0.05934 | 0.07746 | 0.17643 | 0.00179 | 0.00534 | |
| LT | −0.00574 | 0.01244 | −0.01276 | 0.05401 | 0.1003 | 0.12148 | 0.00305 | 0.00815 | |
| MLE | 300 | −0.000001 | 0.002677 | 0.002529 | 0.02484 | 0.043363 | 0.058097 | 0.001031 | 0.001723 |
| CVM | −0.00042 | 0.0017 | −0.00124 | 0.03171 | 0.05039 | 0.09336 | 0.00046 | 0.00069 | |
| OLS | −0.00309 | −0.00188 | −0.00834 | 0.0316 | 0.05064 | 0.09313 | 0.00223 | 0.00403 | |
| WLS | 0.01449 | −0.00199 | 0.04067 | 0.03221 | 0.04515 | 0.07681 | 0.00845 | 0.01409 | |
| ADE | −0.00302 | 0.00031 | −0.00981 | 0.02675 | 0.04743 | 0.06873 | 0.00195 | 0.00501 | |
| RT | −0.00051 | 0.00077 | −0.00105 | 0.03376 | 0.04436 | 0.10063 | 0.00022 | 0.00235 | |
| LT | −0.00309 | 0.00518 | −0.00618 | 0.03032 | 0.05385 | 0.06829 | 0.00138 | 0.0047 | |
| MLE | 500 | 0.00018 | 0.000744 | 0.00097 | 0.019156 | 0.033038 | 0.044046 | 0.000348 | 0.000621 |
| CVM | −0.00061 | 0.00048 | −0.00183 | 0.02386 | 0.03801 | 0.0702 | 0.00032 | 0.00056 | |
| OLS | −0.00150 | −0.00102 | −0.00410 | 0.02475 | 0.0377 | 0.07232 | 0.00111 | 0.00201 | |
| WLS | 0.01072 | −0.00200 | 0.02987 | 0.02404 | 0.03453 | 0.0568 | 0.00616 | 0.01019 | |
| ADE | −0.00205 | 0.00152 | −0.00621 | 0.02039 | 0.03665 | 0.05255 | 0.00111 | 0.00351 | |
| RT | −0.00042 | −0.00025 | −0.00121 | 0.02642 | 0.03386 | 0.07828 | 0.00031 | 0.00243 | |
| LT | −0.00071 | 0.00149 | −0.00204 | 0.02330 | 0.04110 | 0.05204 | 0.00038 | 0.00245 |
| Competitive Models (Abbreviation) | Author(s) |
|---|---|
| Kumaraswamy Fréchet (Kum-F) | [26] |
| Transmuted Fréchet (T-F) | [27,28] |
| Exponentiated Fréchet (EF) | [5,28] |
| Beta Fréchet (B-F) | [29] |
| Marshal–Olkin-Fréchet (MO-F) | [9] |
| McDonald Fréchet (Mc-F) | [30] |
| odd log-logistic inverse Rayleigh (OLL-IR) | [13] |
| Fréchet (F) | [1] |
| odd log-logistic exponentiated Fréchet (OLL-EF) | New |
| odd log-logistic exponentiated inverse Rayleigh (OLL-EIR) | New |
| Generalized odd log-logistic inverse Rayleigh (GOLL-IR) | New |
| Model | Goodness of Fit Criteria | |||
|---|---|---|---|---|
| K-S | P-V | |||
| OB-F | 0.0669 | 0.473 | 0.06317 | 0.8198 |
| OLL-EF | 0.1203 | 0.9639 | 0.5561 | 2.2 × 10⁻¹⁶ |
| OLL-EIR | 0.1553 | 1.21197 | 0.65497 | 2.2 × 10⁻¹⁶ |
| OLL-IR | 0.15532 | 1.21201 | 0.6550 | 2.2 × 10⁻¹⁶ |
| F | 0.1090 | 0.7657 | 0.0874 | 0.4282 |
| Kum-F | 0.0812 | 0.6217 | 0.0759 | 0.6118 |
| EF | 0.1091 | 0.7658 | 0.0874 | 0.4287 |
| Beta-F | 0.0809 | 0.6207 | 0.0757 | 0.6147 |
| T-F | 0.0871 | 0.6209 | 0.0782 | 0.5734 |
| MO-F | 0.0886 | 0.6142 | 0.0763 | 0.5168 |
| Mc-F | 0.1333 | 1.0608 | 0.0807 | 0.5332 |
| Model | Estimates | ||||
|---|---|---|---|---|---|
| a | b | c | β | θ | |
| OB-F | 5.8786 | 0.5825 | 1.1017 | ||
| (0.6645) | (0.1711) | (0.1801) | |||
| OLL-EF | 0.1351 | 3.7216 | 0.9296 | 21.319 | |
| (0.011) | (0.0034) | (0.0033) | (0.0034) | ||
| OLL-EIR | 0.4946 | 0.067 | 1.74262 | ||
| (0.04135) | (0.7195) | (9.3007) | |||
| OLL-IR | 0.49459 | 0.45242 | |||
| 0.04135 | 0.03869 | ||||
| F | 1.3968 | 4.3724 | |||
| (0.0336) | (0.3278) | ||||
| Kum-F | 0.8489 | 1.6239 | 1.6341 | 3.4208 | |
| (16.083) | (0.6979) | (9.049) | (0.7635) | ||
| EF | 0.9395 | 1.4169 | 0.9395 | ||
| (3.543) | (2.568) | (0.3278) | |||
| Beta-F | 0.7346 | 1.5830 | 1.6684 | 3.5112 | |
| (1.5290) | (0.7132) | (0.7662) | (0.9683) | ||
| T-F | −0.7166 | 1.2656 | 4.7121 | ||
| (0.2616) | (0.0579) | (0.3657) | |||
| MO-F | 0.0033 | 6.2296 | 1.2419 | ||
| (0.0009) | (1.0134) | (0.1181) | |||
| Mc-F | 0.8503 | 44.423 | 19.859 | 0.0203 | 46.974 |
| (0.1353) | (25.100) | (6.706) | (0.0060) | (21.871) | |
| Model | Goodness of Fit Criteria | |||
|---|---|---|---|---|
| K-S | P-V | |||
| OB-F | 0.0548 | 0.38734 | 0.0705 | 0.8914 |
| OLL-EF | 0.10487 | 0.8325 | 0.55196 | 6.7 × 10⁻¹⁶ |
| OLL-EIR | 0.1502 | 1.14697 | 0.67949 | 6.7 × 10⁻¹⁶ |
| OLL-IR | 0.15021 | 1.14697 | 0.67951 | 6.7 × 10⁻¹⁶ |
| F | 0.0707 | 0.5332 | 0.0772 | 0.8185 |
| Kum-F | 0.0634 | 0.4981 | 0.0715 | 0.8810 |
| EF | 0.0707 | 0.5332 | 0.0772 | 0.8187 |
| Beta-F | 0.0640 | 0.5008 | 0.0716 | 0.8804 |
| T-F | 0.0655 | 0.4939 | 0.0735 | 0.8470 |
| MO-F | 0.0629 | 0.4902 | 0.0813 | 0.7685 |
| Mc-F | 0.1161 | 0.9193 | 0.0831 | 0.7455 |
| Model | Estimates | ||||
|---|---|---|---|---|---|
| a | b | c | β | θ | |
| OB-F | 7.5535 | 0.4841 | 1.1588 | ||
| (1.13) | (0.184) | (0.192) | |||
| OLL-EF | 0.1449 | 0.0088 | 1.2997 | 24.878 | |
| (0.013) | (0.000) | (0.000) | (0.000) | ||
| OLL-EIR | 0.5025 | 0.0716 | 1.7048 | ||
| (0.053) | (1.1306) | (13.47) | |||
| OLL-IR | 0.50251 | 0.45599 | |||
| 0.05295 | 0.04865 | ||||
| F | 1.4108 | 5.4377 | |||
| (0.0344) | (0.5192) | ||||
| Kum-F | 0.2855 | 1.2824 | 1.9142 | 4.7731 | |
| (9.1338) | (0.6388) | (12.836) | (1.3134) | ||
| EF | 0.9059 | 1.4367 | 5.4379 | ||
| (2.764) | (4.324) | (0.5193) | |||
| B-F | 1.2996 | 1.2649 | 1.3945 | 4.7927 | |
| (4.4378) | (0.6640) | (0.9304) | (1.4641) | ||
| T-F | 0.7778 | 1.5491 | 4.3139 | ||
| (0.2477) | (0.0655) | (0.5849) | |||
| MO-F | 0.0023 | 5.2383 | 1.4537 | ||
| (0.0004) | (0.8209) | (0.1650) | |||
| Mc-F | 56.227 | 14.953 | 0.0073 | 29.104 | |
| (30.539) | (4.733) | (0.0013) | (11.304) | ||
| Model | Goodness of Fit Criteria | |||
|---|---|---|---|---|
| K-S | P-V | |||
| OB-F | 0.1038 | 0.8163 | 0.1043 | 0.6482 |
| GOLL-IR | 0.1955 | 1.3498 | 0.11008 | 0.5797 |
| OLL-EF | 0.1577 | 1.09876 | 0.53498 | 7.4 × 10⁻¹³ |
| F | 0.3233 | 2.0301 | 0.1506 | 0.2066 |
| EF | 0.3233 | 2.0301 | 0.1506 | 0.2064 |
| Beta-F | 0.3611 | 2.5131 | 0.1433 | 0.3601 |
| T-F | 0.2823 | 1.8152 | 0.1370 | 0.3045 |
| Model | Estimates | ||||
|---|---|---|---|---|---|
| a | b | c | β | θ | |
| OB-F | 29.50356 | 0.64127 | 0.14316 | ||
| (49.14) | (0.083) | (0.238) | |||
| GOLL-IR | 1.961 | 0.111 | 1.4123 | ||
| (0.234) | (0.000) | (0.000) | |||
| OLL-EF | 0.0669 | 0.0046 | 0.3558 | 32.561 | |
| (0.0076) | (0.003) | (0.0047) | (0.006) | ||
| F | 0.4859 | 3.2078 | |||
| (0.023) | (0.326) | ||||
| EF | 0.9047 | 0.5013 | 3.2077 | ||
| (18.784) | (3.244) | (0.326) | |||
| Beta-F | 4.015 | 1.3349 | 2.0022 | 0.87017 | |
| (0.111) | (0.147) | (0.321) | (0.0033) | ||
| T-F | −0.5816 | 0.4400 | 3.4974 | ||
| (0.2787) | (0.0290) | (0.3527) | |||
| N = 10,000 | h₁ = 15 | h₂ = 25 | h₃ = 50 | h₄ = 130 | h₅ = 350 | h₆ = 500 |
|---|---|---|---|---|---|---|
| a | 1.9568 | 1.9612 | 1.9734 | 1.9786 | 1.9856 | 1.9923 |
| MSE | 0.0137 | 0.0109 | 0.0090 | 0.0073 | 0.0048 | 0.00029 |
| b | 0.5436 | 0.5326 | 0.5289 | 0.5203 | 0.5176 | 0.5066 |
| MSE | 0.0186 | 0.0152 | 0.0123 | 0.0095 | 0.0078 | 0.0059 |
| θ | 1.5286 | 1.5243 | 1.5182 | 1.5126 | 1.5064 | 1.5022 |
| MSE | 0.0158 | 0.0128 | 0.0092 | 0.0079 | 0.0062 | 0.0046 |
| N = 10,000 | h = 50 | h = 130 | h = 350 | h = 500 |
|---|---|---|---|---|
| ε = 1% | 0.0079 | 0.0092 | 0.0098 | 0.0107 |
| ε = 5% | 0.0461 | 0.0478 | 0.0492 | 0.0503 |
| ε = 10% | 0.0971 | 0.0985 | 0.0990 | 0.1002 |
| 4.425 | 8.702 | 14.253 | 22.968 | 56.086 | |
| 6 | 11 | 9 | 14 | 11 | |
| −1.635 | −1.236 | −0.986 | −2.635 | −7.956 | |
| 2.272 | 3.030 | 1.894 | 2.272 | 0.757 | |
| −0.723 | 1.136 | −0.986 | 0.9763 | −2.953 | |
| 5.5246 | 5.5246 | 5.5246 | 5.5246 | 5.5246 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
M. Salah, M.; El-Morshedy, M.; Eliwa, M.S.; Yousof, H.M. Expanded Fréchet Model: Mathematical Properties, Copula, Different Estimation Methods, Applications and Validation Testing. Mathematics 2020, 8, 1949. https://doi.org/10.3390/math8111949
M. Salah M, El-Morshedy M, Eliwa MS, Yousof HM. Expanded Fréchet Model: Mathematical Properties, Copula, Different Estimation Methods, Applications and Validation Testing. Mathematics. 2020; 8(11):1949. https://doi.org/10.3390/math8111949
Chicago/Turabian StyleM. Salah, Mukhtar, M. El-Morshedy, M. S. Eliwa, and Haitham M. Yousof. 2020. "Expanded Fréchet Model: Mathematical Properties, Copula, Different Estimation Methods, Applications and Validation Testing" Mathematics 8, no. 11: 1949. https://doi.org/10.3390/math8111949
APA StyleM. Salah, M., El-Morshedy, M., Eliwa, M. S., & Yousof, H. M. (2020). Expanded Fréchet Model: Mathematical Properties, Copula, Different Estimation Methods, Applications and Validation Testing. Mathematics, 8(11), 1949. https://doi.org/10.3390/math8111949








